Drying-induced hydrophobic polymer collapse

Abstract

We have used computer simulation to study the collapse of a hydrophobic chain in water. We find that the mechanism of collapse is much like that of a first-order phase transition. The evaporation of water in the vicinity of the polymer provides the driving force for collapse, and the rate limiting step is the nucleation of a sufficiently large vapor bubble. The study is made possible through the application of transition path sampling and a coarse-grained treatment of liquid water. Relevance of our findings to understanding the folding and assembly of proteins is discussed.

For nearly a half-century, hydrophobic interactions have been considered the primary cause for self assembly in soft matter, and a major source of stability in biophysical assembly (1, 2). Studying these interactions in perhaps their most basic form, we use computer simulations to demonstrate the mechanism for the collapse of a hydrophobic polymer in water. We show that solvent fluctuations induce the transition from the extended coil to the collapsed globule state, where a vapor bubble of sufficient size is formed to envelop and thereby stabilize a critical nucleus of hydrophobic units. This mechanism is different from that usually considered, where coil to globule transitions are attributed to effective interactions between pairs of chain segments and a change in sign of second virial coefficient (3). Rather, the mechanism we find is evocative of the n-cluster model, where hydrophobic collapse is produced by solvent-induced interactions between a relatively large cluster of segments (4).

As expected from earlier work on the equilibrium theory of hydrophobicity (5), we find that the solvent length scales pertinent to hydrophobic collapse extend over nanometers. We also find that pertinent time scales extend beyond nanoseconds. Given these molecularly large lengths and times, it is understandable that no work before this has provided statistically meaningful computer simulations of the process. Our use of a statistical field model of water allows us to simulate solvent dynamics over large length and time scales that would be impractical to study with purely atomistic simulation. Spatially complex small length-scale fluctuations are analytically integrated out, thus removing the most computationally costly features from our simulation. Their integration can be performed at the outset because their relaxation is relatively fast (6) and their statistics is essentially Gaussian (7). Only the polymer degrees of freedom and a coarse-grained density field remain. The equilibrium theory for this approach has been detailed in an earlier paper (8). Here, we use a version of the model that is suitably generalized for dynamical applications.

By “small length” we refer to distances smaller than l ≈ 0.3 nm. In the absence of any strong perturbation, such as those that can occur close to a solute, these small length-scale fluctuations are the only fluctuations of significance. Larger length-scale fluctuations are generally insignificant in water at ambient conditions. The liquid is relatively cold and incompressible, and spatial correlations extend over only one or two water molecules. But the presence of a hydrophobic polymer can change this situation, making large length-scale fluctuations important. The liquid lies close to macroscopic vapor–liquid equilibrium, and vapor-like behavior is stabilized in the vicinity of a sufficiently extended hydrophobic surface (9)—a surface formed, for example, by the clustering of hydrophobic groups in a polymer chain. This effect can be captured by the behavior of a coarse-grained density field (5, 10), and such a field is conveniently simulated with a field of binary numbers (8), as we discuss now.

Equilibrium of the Solvent Model

Dividing space into a cubic grid of cells, each with side length l, this binary field is a dynamical variable given by ρ_ln_i, where ρ_l is a constant given by the bulk liquid density, and n_i is dynamical given by n_i = 1 if cell i contains “liquid,” and n_i = 0 if it contains “vapor.” This coarse-grained density is thus the “Ising” field that describes phase coexistence and gas–liquid interfaces (11). The remaining small length-scale field, δρ(r), is the difference between ρ_ln_i and the actual density at a point r in cell i. It takes on a continuum of values, obeys Gaussian statistics, and captures the granularity of the solvent (12).

Confining our attention to an ideal hydrophobic solute, namely a polymer consisting of hard spheres, the integration over δρ(r) yields the following Hamiltonian for the coarse-grained field in the grand-canonical ensemble (8):

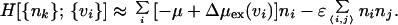1

The quantity μ is the solvent chemical potential, ɛ is the nearest-neighbor coupling energy parameter of the solvent, the sum over 〈i,j〉 includes all nearest neighbor cells, v_i denotes the volume excluded by the solute in cell i, and

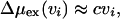2

with c = 2.67 × 10⁸ J/m³ (about 60 k_BT/nm³ at room temperature), is the reversible work to accommodate that excluded volume in the liquid. Eqs. 1 and 2 are approximations to the full results derived in ref. 8. Specifically, in comparison with Equations 19 or 23 of ref. 8, we see that Eq. 1 neglects relatively small intercell interactions. Further, Eq. 2 is a reasonable numerical approximation to the general result for Δμ_ex(v_i) that follows from Gaussian statistics for δρ(r) (7). The specific value of c is chosen so that Δμ_ex(4πR³/3) yields the excess chemical potential for a hard sphere or bubble that excludes solvent from a spherical volume of radius R = 0.5 nm (13).

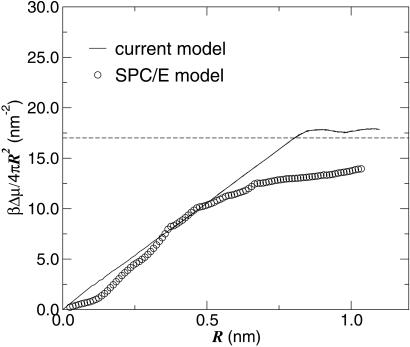
The predictions of the model for excess chemical potential or solvation free energy of a hard sphere over the range of all possible radii is shown in Fig. 1. It is seen that the agreement between the results of the model and those of an atomistic simulation is reasonable, because the model captures the appropriate free-energy scaling at small and large lengths and gives a reasonable prediction of the crossover length between the two regimes. For closer agreement between the statistical field model and the atomistic model in the crossover regime, terms neglected in Eq. 1 should be included, as demonstrated in ref. 8.

Figure 1.

The solvation energy per unit surface area for a hard sphere or bubble as a function of R, where R is the radius of the spherical volume from which the solvent, water, is excluded. The circles are the results of computer simulation for the SPC/E atomistic model of water (13). The line is the prediction of our model computed by Monte Carlo umbrella sampling (14), using the weight functional exp {−βH[{n_k}, {v_i}] }, where β⁻¹ = k_BT, and with Σ_iv_i = 4πR³/3. The parameters of the model have been chosen so as to match the isothermal compressibility, the chemical potential, and the surface tension of water at room temperature and 1 atm pressure (1 atm = 101.3 kPa). This yields l = 0.21 nm, ɛ = 3.74kJ/mol (= 1.51 k_BT at room temperature), and μ − μ_coex = 0.557 J/mol (= 2.25 × 10⁻⁴ k_BT at room temperature), where μ_coex is the chemical potential of the solvent when it is in coexistence with the vapor at room temperature. The comparison of μ − μ_coex with ɛ shows that the bulk liquid is extremely close to phase coexistence. The horizontal dashed line is placed at the value of the liquid–vapor surface tension and coincides with the large R asymptotic value of Δμ_ex/4πR² for both the model and the atomistic simulation (the surface tension of SPC/E water model is very close to that of real water; ref. 27).

The crossover occurring around R ∼ 1 nm is a collective effect. It is induced by the entropic cost of constraining small length-scale fluctuations near a hydrophobic solute. For a given cell i, the cost is Δμ_ex(v_i). When the v_i's form a connected volume of large enough extent, the net entropic cost is larger than the energetic cost for forming an interface that surrounds the volume. At this point, and for larger volumes, it becomes energetically preferable for n_i = 0 for all cells i occupied by or adjacent to the large solute, and free energetics is then dominated by the energy of the interface thus formed. Such interfaces are stable only in the neighborhood of vapor–liquid phase equilibrium. Therefore, crossover behavior can occur only when μ − μ_coex≪ k_BT, where k_BT is Boltzmann's constant times temperature (the thermal energy) and μ_coex is the chemical potential at phase coexistence between liquid and vapor. Further, because a pressure–volume term generally contributes to the free energy of a large void, crossover behavior occurs only when pressure is low enough to make this term similarly small. We will see below that the crossover in the scaling behavior of the free energy is closely related to the nucleation of oil–water demixing and the mechanism for the collapse of a hydrophobic chain.

Dynamics of the Solvent and Chain

The excluded volumes v_i are dynamical, changing as the chain configuration changes with time. The chain need not move slowly on the time scale for which disturbances in the solvent may relax. As such, reversible work surfaces, like the solvation free energy graphed in Fig. 1, are not entirely pertinent, and the dynamics of the liquid and chain should be studied together. For this purpose, we have constructed a stochastic dynamics that satisfies the basic requirements of time reversibility and the preservation of an equilibrium distribution. With this dynamics, solute particles move through space with continuous variation of coordinates while the coarse grained density evolves simultaneously through its discrete configurations. Because δρ(r) has been integrated out (its effects appear only implicitly), the trajectories can be true to nature only for times greater than those required to relax δρ(r). This time is on the order of 1 ps (6). On this time scale, the appropriate stochastic dynamics is non-inertial.

Trajectories of our model are advanced as follows: The polymer, composed of N_s = 12 spheres is moved for M_s time steps from a configuration {r_α} to a new configuration {r} according to propagation rules of Langevin dynamics, in the field of constant coarse grained density variables, {n_i}. At the end of those steps, the polymer is held fixed and the coarse grained density is moved to a new configuration {n} by carrying out a full sweep through all cells, applying Glauber Monte Carlo dynamics (17) to each cell with the Hamiltonian H[{n_i},{v_i}]. The net procedure taking the system from {r_α, n_i} to {r, n} is then repeated over and over again. The trajectories thus formed are reversible, preserve the norm of the configurational distribution function, and obey detailed balance.

For one of the M_s time steps between solvent sweeps, carrying the monomers from their configuration at time t to that at time t + δt_s, the Langevin propagation corresponds to

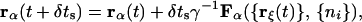3

where F_α({r_ξ(t)}, {n_i}) is the force acting on monomer α, and γ is the friction constant. The force contains a random part, δF, that is independent of configurational variables. It is the dynamical remnant of the small length-scale field, δρ(r). We take it to be isotropic, to have a correlation time of zero, and to obey Gaussian statistics with zero mean and variance 〈|δF|²〉 = 3k_BTγ. We estimate the value of γ by associating the diffusion constant of a single bead moving in water, D_s = k_BT/γ, to its Stokes estimate which gives γ = 8.39 × 10⁻¹² kg/s. The remaining contribution to the force is not random, and is given by −∇_α[V({r_ξ}) + c∑_iv_i]. The time step is δt_s = 1.4 × 10⁻¹⁴ s, which is small enough that Eq. 3 preserves the canonical distribution.

A physically meaningful value of M_s coincides with M_s ≈ δt_l/δt_s, where δt_l is the physical time associated with a sweep through the coarse-grained density of the solvent. This solvent time should coincide with the correlation time for a density fluctuation of length-scale l—i.e., δt_l = 1/[D(2π/l)²)], where D is the self-diffusion constant of liquid water. This relationship gives δt_l = 5.0 × 10⁻¹³ s, and thus M_s = 36.

With these dynamical rules, we show below that the half-life of the extended chain we consider is approximately 10⁻⁵ s at room temperature, whereas the transient time to move off a threshold between extended coil and compact globule states is of the order of 10⁻¹⁰ s. Thus, collapse transitions in this system are rare events (16). Harvesting a representative ensemble of these events without prior knowledge of transition states or mechanism is accomplished with transition path sampling (17). To apply this technique, we use the number of vapor cells, Σ_i(1 − n_i), as the order parameter to distinguish the solvated coil and globule states.

Results

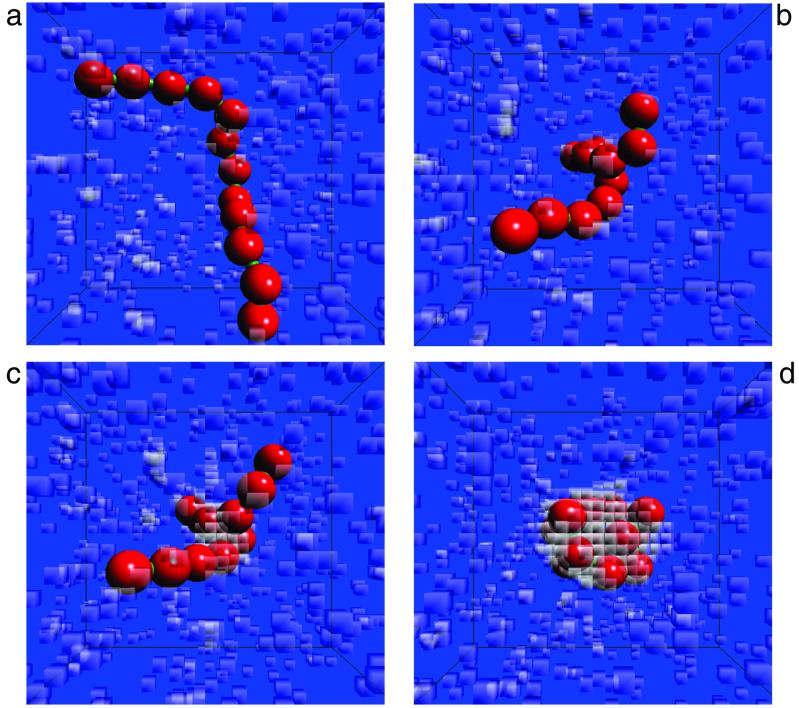
Fig. 2 illustrates a 1.5-ns trajectory in which a chain of 12 hydrophobic units collapses from an extended coil to a compact globule. The volume occupied by each separate unit is typical of that for amino acids in solution. In vacuum, this particular chain will always remain in a coil state because the global minimum in its intrachain potential energy function corresponds to the fully extended conformation. Nevertheless, the collapsed chain is very much the stable state of the solvated chain, as is evident from the free-energy surface shown in Fig. 3. Although rare, the trajectory illustrated in Fig. 2 is a representative example of the subensemble of all 1.5-ns trajectories that do exhibit the collapse transition at temperature T ≈ 300 K. The polymer is initially in the extended coil state, after which a spontaneous fluctuation in chain conformation collapses a section of the polymer. The collapsed section forms a sufficiently large hydrophobic cluster that the formation of a vapor bubble is induced. Eventually, this vapor bubble grows and drives all of the units of the polymer together.

Figure 2.

Four configurations from a trajectory where a 12-unit hydrophobic chain in water goes from the coil to the globule state. (a) A configuration from the equilibrated coil. The chain remained in configurations like that throughout a 10-ns run at room temperature (T = 0.663ɛ). On a much longer time scale, about 10⁻⁵ s, the chain typically does exhibit a transition from the coil to globule. Such events are found with transition path sampling, equilibrating from an initial high-temperature (T = 0.74ɛ), 10-ns trajectory that exhibited the transition spontaneously. Three configurations exhibiting that transition, covering a stretch of 1.5 ns, are shown in b, c, and d, with that in c being a configuration from the transition state surface. The transparent cubes denote the vapor cells. Those seen far from the chain are typical spontaneous density fluctuations in bulk liquid water. The size of the simulation box is 397 nm³, corresponding to 42,875 cells. The parameters characterizing the energy of the solvent are given in the caption to Fig. 1. The intrachain potential, V(r₁, r₂, . . . , r₁₂), is a function of the positions of the centers of each of the 12 hydrophobic spheres (the red particles in the figure). It contains three parts: (i) steep (essentially hard sphere) repulsions between solute particles such that their interparticle separations are larger than σ = 0.72 nm; (ii) stiff harmonic potentials bonding adjacent particles in the hydrophobic chain, ½k_s(σ − |r_α+1 − r_α|)², with k_s = 14.1 J/m²; (iii) a bending potential favoring an extended chain, ½k_θθ_α², where θ_α is the angle between (r_α+2 − r_α+1) and (r_α+1 − r_α), and k_θ = 1.85 × 10⁻²⁰ J/rad². The volumes v_i excluded from water by the chain are dynamic because they change with changing chain configuration—i.e., v_i = v_i({r_α}). Specifically, these volumes are computed by assuming water molecules have van der Waals radii equal to 0.14 nm, and that the diameter of each hydrophobic unit is σ = 0.72 nm. That is, points in the excluded volume, r, are those in the union of all volumes inscribed by |r − r_α| < 0.5 nm, α = 1, 2, . . . , N_s.

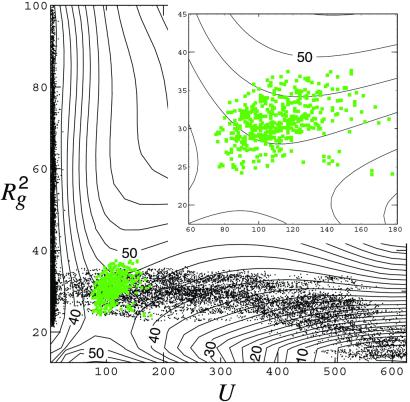
Figure 3.

Contour plot of the free-energy landscape for the collapse of our hydrophobic polymer, computed by Monte Carlo umbrella sampling (14), using the weight functional exp{−βH[{n_k}, {v_i}] − βV[{r_α}] }, where the intrachain potential, V[{r_α}], and the excluded volumes, v_i[{r_α}], are determined as described in the caption to Fig. 2. The curves of constant free energy are drawn as a function of the squared radius of gyration and the size of the largest bubble in the system (see text). Neighboring lines are separated by 2.5 k_BT. Superimposed is a scatter plot (in black) of the harvested 150-ps trajectories going from the coil to the globule state. The transition states are indicated in green. The harvesting was performed with transition path sampling, making 8,400 moves in trajectory space, of which 75% were shooting and 25% were shifting (17). We find that the plateau regime of the flux correlation function is reached after 50–70 ps (16, 17), implying that the typical commitment time for trajectories to pass over the barrier is on the order of 0.1 ns. Given this time and the fact that the figure shows the free-energy barrier separating the extended coil and compact globule states to be about 9 k_BT, the half-life of the extended chain is about 0.1 ns × exp(9) ≈ 10⁻⁵ s.

Visual inspections of this and similar dynamical trajectories suggest that the mechanism of the collapse transition arises from an interplay between the size of the polymer and the formation of a vapor bubble. For this reason, we have mapped out the free-energy landscape in terms of variables manifesting the polymer size and the bubble size. The first of these variables, R, is the squared radius of gyration of the polymer. The other, U, is the volume of the largest vapor bubble, in units of l³. To identify the bubbles in the system, we use the criterion that any two vapor cells (i.e., cells for which n_i = 0) belong to the same bubble whenever they are nearest neighbor cells.

The contour plot for the room temperature free-energy landscape (Fig. 3) shows that the path of lowest free energy from the coil to the collapsed globule is one where, initially, the radius of gyration decreases, while the size of the largest bubble is still essentially zero. In this regime, the solvent still wets the polymer (i.e., n_i is mostly 1 for cells occupied by the solute), and the free energy hardly changes. When the radius of gyration becomes small enough, however, a bubble starts to grow. Here, the free energy increases sharply by about 9 k_BT where it reaches a saddle point at (U, R) = (98, 23.5 l²). Beyond that saddle point, the bubble grows spontaneously to a size that eventually envelopes the fully collapsed globule. The height of the barrier only weakly depends on chain stiffness because it is due primarily to solvent reorganization.

A close examination of the free-energy landscape reveals a small barrier of height 2 k_BT at (U, R) = (6.5, 70 l²). This feature, not visible on the scale of the graph plotted in Fig. 3, separates the coil from a more compact metastable intermediate. The presence of these two states arises from a competition between the entropy of the chain, which favors the coil state, and weak depletion forces, which favor a more compact state. Weak depletion forces are caused by the reduction in the volume from which the solutes exclude the solvent, when solutes come together while still wet. The attraction between two small hydrophobic objects predominantly arises from this effect (7, 18, 19), although its full description (with the characteristic oscillations in potentials of mean force) requires a more accurate evaluation of Δμ_ex (v_i) than Eq. 2. Whether evaluated to high accuracy or approximately, this driving force is relatively small, and it is not responsible for spontaneous assembly of hydrophobic units (20). The free-energy difference is 30 k_BT between the coil and the fully collapsed globule, whereas it is only a few k_BT between the coil and the intermediate state. The strong driving force for the collapse of the polymer comes from the emptying of cells (i.e., solvent cavitation or drying) and thus the demixing of the hydrophobic units and water. The resulting stabilization follows from the fact that the solvent is close to liquid–vapor equilibrium so that the large length-scale interfacial free energy of the cavity is far lower than the small length-scale entropic cost of maintaining a wet state, Σ_i Δμ_ex (v_i). Thus, nucleating the collapsed hydrophobic chain involves the same physical effect that is responsible for the crossover phenomenon discussed above in reference to Fig. 1.

To judge the extent to which R and U describe the pertinent dynamics of the collapse, and are thus good reaction coordinates, we have performed extensive transition path sampling of an ensemble of trajectories, each of length 150 ps. Points taken from these transition trajectories are shown in juxtaposition with the free-energy surface in Fig. 3. Although ten times shorter than the one illustrated in Fig. 2, the 150-ps trajectories are sufficiently long to capture the mechanism of the collapse because 150 ps is significantly longer than the time for a trajectory starting at the dynamical bottleneck to commit to a basin of attraction. Fig. 3 shows that the flow through the bottleneck in this system is primarily due to the solvent, and the solvent in this transition state regime moves on the time scale of picoseconds. To identify the bottleneck (i.e., transition-state surface), we have located the configurations on each trajectory from which newly initiated trajectories have equal probability of ending in the coil or globule states. These points in configuration space are members of the transition state ensemble (17, 21, 22). We project them onto Fig. 3, where it is seen that points in the transition state ensemble are indeed close to the saddle point in the free-energy surface. Thus, U and R are the predominant reaction coordinates for this system. The transition-state ensemble is slightly tilted in the (U, R)-plane, showing that the larger the polymer, as measured by its radius of gyration, the larger the size of the critical vapor bubble. However, the scatter of the transition-state ensemble from a line in that plane is notable, indicating that at least one other variable in addition to U and R plays a quantitative role in the reaction coordinate.

The transition paths shown in Fig. 3 differ from the lowest free-energy path, and the differences are generally larger than k_BT. This behavior shows that the polymer and the solvent move on significantly different time scales when passing through and moving beyond the dynamical bottleneck. After a vapor bubble is nucleated, the polymer does not respond on the time scale at which the bubble grows. In fact, by taking an artificially large value for M_s (3,600) to accelerate the dynamics of the chain relative to that of the solvent by a factor of 100, the projected dynamical paths closely follow the lowest free-energy path.

Discussion

Trajectories of the hydrophobic collapse are generally parallel to U as they pass over the transition state. This finding demonstrates unambiguously that the dynamics of collapse of a hydrophobic polymer in water is dominated by the dynamics of water, specifically the collective emptying of regions of space near a nucleating cluster of hydrophobic species. Further, both the solvent and chain remain out of equilibrium throughout the collapse transition. Real hydrophobic molecules have some affinity to water, and vice versa, because of ubiquitous van der Waals interactions. The ideal hydrophobic chain considered here, however, has no such property because it is composed simply of hard spheres. Nevertheless, we expect our conclusions to remain valid for more realistic models of hydrophobic species because the underlying mechanism of nucleation is largely unaffected by van der Waals interactions (23). Our findings would seem also pertinent to the mechanism of biological assembly, such as protein folding, but to demonstrate so with simulation will require an analogous simulation study of a protein-like chain. In the past, a statistically meaningful study of such folding with explicit account of solvent dynamics seemed impractical. The current analysis, however, suggests that such studies will become feasible by using a statistical field model like that used herein.

Appropriate models for hydrophobic collapse must account for both the physics of small length-scale fluctuations and the physics of phase equilibria and interfaces. This accounting is difficult to accomplish without an explicit treatment of the solvent, as we do here. Often, solvation is treated with implicit solvent models in which all solvent degrees of freedom are averaged out in some approximate fashion, assuming that all of these degrees of freedom relax quickly. Some of these models mimic the effects of the solvent through estimates of the pair potential of mean force between solute units. This approach can be correct for describing small length-scale effects, and therefore can be correct in situations where the solute remains wet. But for collections of hydrophobic solutes large enough to induce drying or cavitation, an implicit model would need to describe correlations of essentially all orders, and not simply pair correlations. For this reason, a recent study of hydrophobic effects in protein folding requires further analysis (24). Other implicit solvent models are based on estimates of exposed surface area (25, 26). This approach can be valid for large enough solutes, provided the time scales of interest are longer than nucleation times (10⁻⁵ s in the system studied here). But applying it to small unassembled solutes is incorrect because the free energy in this regime scales with excluded volume and not surface area.

The connection we stress between hydrophobic collapse and phase equilibria provides a simple explanation for both cold denaturation and pressure denaturation of proteins. Namely, the tendency for drying and its concomitant stabilization of hydrophobic clustering decreases with decreasing proximity of liquid–vapor equilibrium. Thus, the lowering temperature and the increasing of pressure destabilize hydrophobic collapse because both these actions move ambient water away from its phase equilibrium with vapor. The proximity of phase equilibria is also of relevance to free-energy barriers for hydrophobic collapse, like that illustrated in Fig. 3. These barriers will increase, for example, with increasing external pressure. Thus, the most direct measure of the importance of hydrophobic collapse in protein folding may therefore come from studying the kinetic effects of changing pressure.