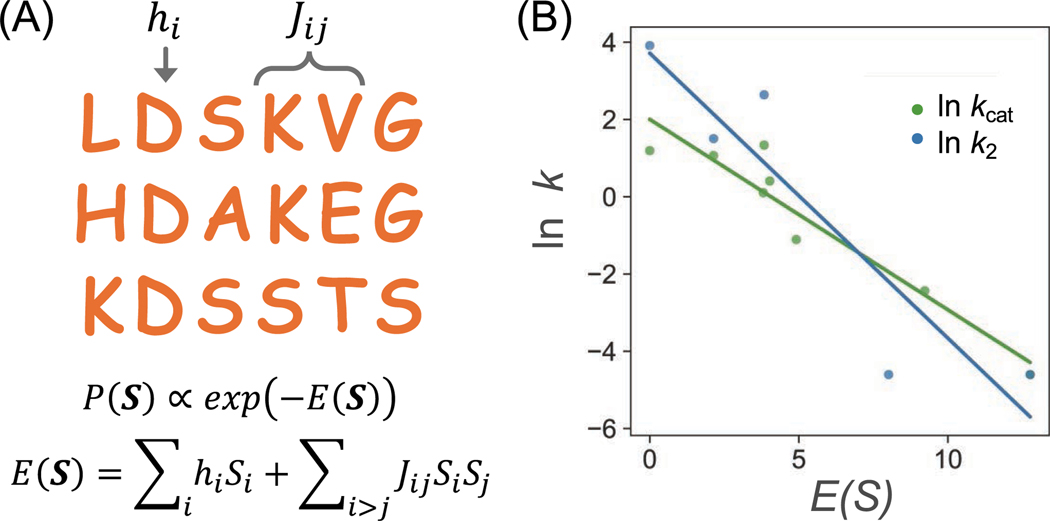Biochemical and Computational Characterization of Haloalkane Dehalogenase Variants Designed by Generative AI: Accelerating the S_N2 Step

Abstract

Generative artificial intelligence (AI) models trained on natural protein sequences have been used to design functional enzymes. However, their ability to predict individual reaction steps in enzyme catalysis remains unclear, limiting the potential use of sequence information for enzyme engineering. In this study, we demonstrated that sequence information can predict the rate of the S_N2 step of a haloalkane dehalogenase using a generative maximum-entropy (MaxEnt) model. We then designed lower-order protein variants of haloalkane dehalogenase using the model. Kinetic measurements confirmed the successful design of protein variants that enhance catalytic activity, above that of the wild type, in the overall reaction and in particular in the S_N2 step. On the simulation side, we provided molecular insights into these designs for the S_N2 step using the empirical valence bond (EVB) and metadynamics simulations. The EVB calculations showed activation barriers consistent with experimental reaction rates, while examining the effect of amino acid replacements on the electrostatic effect on the activation barrier and the consequence of water penetration, as well as the extent of ground state destabilization/stabilization. Metadynamics simulations emphasize the importance of the substrate positioning in enzyme catalysis. Overall, our AI-guided approach successfully enabled the design of a variant with a faster rate for the S_N2 step than the wild-type enzyme, despite haloalkane dehalogenase being extensively optimized through natural evolution.

Graphical Abstract

INTRODUCTION

Artificial intelligence (AI) has become a promising tool in enzyme engineering, complementing approaches like directed evolution and physics-based simulations.¹ AI models rely on data for training, and with billions of available protein sequences−there exists a vast pool of homologous enzyme sequences. These homologues are not randomly generated; their sequence patterns likely reflect principles that have ensured their survival over billions of years of evolution.^2,3 Generative AI analysis of natural sequences can quantify sequence patterns and estimate the probability of specific sequences or amino acid replacements occurring within natural protein sequences.⁴ Remarkably, sequence probability derived from generative AI has been linked to protein fitness, as measured in phenotype-based deep mutational scanning experiments.³ Furthermore, sequence probability correlates with enzyme activity measured in biochemical assays.⁵ Additionally, generative AI-based sequence analysis has successfully generated functional enzyme variants, showcasing the potential of AI in enzyme engineering.^6–9 For example, Russ et al. applied a maximum-entropy (MaxEnt) model to design chorismate mutase homologues, achieving a success rate of approximately 30% in generating functional sequences.⁹ However, AI-designed sequences often do not exceed the performance of wild-type enzymes. Besides, previous efforts have focused on higher-order protein variants, which are challenging to interpret in terms of their molecular differences from wild-type enzymes. It remains uncertain whether all mutated residues contribute to the observed changes or if many are neutral. Analyzing AI-designed lower-order protein variants could provide key insights into how individual residues impact catalytic performance.¹⁰

The complexity of enzyme catalysis also complicates the understanding of how generative AI operates in enzyme engineering. Enzyme catalysis typically involves multiple reaction steps. For example, haloalkane dehalogenase from Xanthobacter autotrophicus GJ10 (DhlA) catalyzes an S_N2 reaction, in which a halogen atom is removed from the substrate, followed by a hydrolysis step that introduces a hydroxyl group. Haloalkane dehalogenase from different species exhibits varying rate-limiting steps in the reaction, with halide ion release being rate-limiting in wild-type DhlA.¹¹ During enzyme evolution, multiple steps may be optimized simultaneously, making it difficult to discern how sequence information correlates with the catalytic properties of individual steps or the overall reaction. We previously demonstrated that the generative MaxEnt model can predict the effects of amino acid substitutions on DhlA’s overall catalytic activity.⁵ However, it remains unclear how the model performs in predicting the impact of amino acid replacements on specific reaction steps.

In this study, we employed generative AI, along with biochemistry and computation, to explore how sequence information can predict the individual reaction steps of DhlA. We first observed that generative AI-based analysis of DhlA homologues could predict not only the overall catalytic activity of protein variants, as previously shown, but also the catalytic activity of the S_N2 step. To validate these predictions, we characterized the top-predicted DhlA variants, including two single and three double variants. Notably, we found that the L262V variant doubled the catalytic activity of the S_N2 step, while the F128L/L262I variant improved overall catalytic activity, demonstrating the effectiveness of generative AI in enhancing enzyme performance through evolutionary sequence information. To gain deeper molecular insights into the S_N2 step, we calculated the activation barriers of these protein variants using the empirical valence bond (EVB) simulations, which were consistent with the kinetic data. EVB simulations explored various factors that could contribute to the observed effects, including electrostatic interactions and water penetration effects. Additionally, metadynamics simulations were employed to examine the substrate’s positioning in the near-transition state. We highlighted the role of maintaining collinearity between the attacking nucleophile and the cleaved bond in the S_N2 step. Overall, this study provides a comprehensive evaluation of generative AI-generated protein variants and offers valuable insights into how sequence information can be leveraged to navigate the complexities of enzyme catalysis and design.

RESULTS AND DISCUSSION

Generative MaxEnt Model Predicts Catalytic Activity and Designs DhlA Protein Variants.

Nature has evolved preorganized active sites in DhlA to efficiently catalyzes the dehalogenation of short-chain haloalkanes, such as 1,2-dichloroethane (DCE), to yield alcohols.^12,13 In the S_N2 step, the C−Cl bond is broken through a nucleophilic attack by D124, forming a covalent intermediate; the hydrolysis is facilitated by the general base H289 (Figure 1A).¹³ Beyond the catalytic residues, other surrounding residues also play a crucial role in modulating enzyme activity (Figure 1B).^14–16 For example, W125 and W175 stabilize the chloride ion during the S_N2 reaction.¹⁷ Interestingly, previous studies have shown that changing amino acid in active site residues can shift the rate-limiting step between the S_N2 reaction and hydrolysis. In wild-type DhlA, halide ion release is believed to be the rate-limiting step for DCE; however, either the S_N2 reaction or hydrolysis can become rate-limiting depending on specific amino acid substitutions.^14–16

Figure 1.

DhlA-catalyzed reaction and the structure of DhlA. (A) Reaction Scheme. S_N2 displacement of the chlorine atom from DCE, involving covalent bonding of DCE to the carboxylate group of D124, followed by hydrolysis, producing 2-chloroethanol. (B) Crystal structure of DhlA bound to DCE (PDB ID: 2DHC). (C) Close-up of the substrate (carbon atoms are in blue, chlorine atoms are in green) and selected active site residues, with F128 and L262 (underlined) highlighted as the mutated positions in the designs.

Despite the complexity of enzymatic reactions, we have demonstrated that generative MaxEnt models could uncover the sequence-activity relationship for DhlA within its active sites.⁵ The MaxEnt model is parametrized using DhlA homologues. We first constructed the multiple sequence alignment (MSA). The MSA statistics, including single-point conservation and pairwise co-occurrence at two sites, were used as constraints while maximizing sequence information entropy. This process yielded a sequence probability for any amino acid replacement or new sequence within the protein family. The sequence probability $P(S)$ of a sequence $S$ writes $P(S)\propto \exp (-E(S))$, where $E\left(S\right)={\Sigma }_i{h}_i{S}_i+{\Sigma }_{i>j}{J}_{ij}{S}_i{S}_j$ represents the statistical energy of the sequence (Figure 2A). The model parameters h_i and $J_{ij}$ can be effectively trained using gradient-based optimization techniques.⁵ Interestingly, the sequence probability P(S) or its corresponding energy E(S) correlates with $k_{\text{cat}}$ (the overall catalytic activity) with a Spearman’s correlation value of −0.95 and a p-value <0.001 as shown in ref 5 and Figure 2B. However, whether sequence information can predict individual reaction steps remains unclear. This is particularly important because enzymatic reactions typically involve multiple steps, and without such information, it is not possible to rationally improve a specific step using sequence data. To address this, we collected kinetic data for mutants characterized under the same experimental conditions (Table S1 of the SI). Remarkably, $k_2$ (the catalytic activity for the S_N2 step) can also be predicted from sequence information (Figure 2B). The Spearman’s correlation value between $E(S)$ and $k_2$ is −0.87 and a p-value is 0.023.

Figure 2.

Predicting the catalytic activity of DhlA using the generative MaxEnt model. (A) Schematic representation of the MaxEnt model. The model captures both site conservation and pairwise site couplings in the MSA constructed with DhlA homologues. (B) The MaxEnt model predicts both the overall catalytic activity (k_cat) and the S_N2 step (k₂). Lower $E(S)$ (or higher $P(S)$) indicates higher activity. The k_cat, k₂ and statistical energies $E(S)$ are presented in Table S1.

We then redesigned the active sites of DhlA using generative AI, focusing on residues within 8.5 Å of the substrate DCE in the crystal structure (PDB ID: 2DHC). Thirteen key residues were initially identified: E56, D124, W125, F128, F164, F172, W175, F222, P223, V226, L262, L263, and H289. However, F164 was excluded during the postprocessing of the MSA due to a gap ratio exceeding the threshold, leaving 12 active sites residues. Using the MaxEnt model, we sampled the energy landscape $E(S)$ using Monte Carlo simulation and obtained many protein variants with lower $E(S)$ (or higher $P(S)$) than the wild-type DhlA, indicating their potential for improved catalytic activity. Further details on the model and sampling can be found in ref 5.

We selected five protein variants for further biochemical and computational analysis, including the top single variants, F128L and L262V, as well as the top double variants: F128L/L262V, F128P/L262V, and F128L/L262I. Interestingly, all double protein variants involved the same two sites as the single protein variants. Our focus on lower-order protein variant is based on several key considerations. While generative AI has successfully designed functional higher-order protein variants, producing sequences that outperform the wild-type enzyme remains a significant challenge. Additionally, it is difficult to pinpoint the specific contributions of individual amino acid substitutions to the overall change in higher-order protein variants. This creates a gap between generative AI-based engineering and the mechanistic understanding of the design. In contrast, lower-order protein variants have a higher success rate in improving enzyme activity¹⁸ and are easier to rationalize.

AI-Generated Lower-Order Protein Variants Are Generally Well-Folded and Exhibit Varied Stability.

Starting with the wild-type enzyme, we performed site-directed mutagenesis and protein production for the designed protein variants (Sections S2.1 and S2.2 of the SI). We assessed the protein secondary structure and folding using circular dichroism (CD) spectroscopy (Figure S3 in Section S2.3 of the SI). Far-UV CD spectra at 15 °C confirm that all protein variants, except F128P/L262V, retained proper folding and secondary structure similar to the wild type. The spectra for most protein variants display a positive peak at approximately 195 nm and two negative peaks at around 208 and 220 nm, characteristic of α-helical content. While some minor deviations from the wild-type spectra were observed, these likely reflect subtle conformational changes. However, the F128P/L262V variant exhibited significantly altered spectra, indicating a disrupted structure. Consequently, F128P/L262V was excluded from further experiments due to its compromised structural integrity.

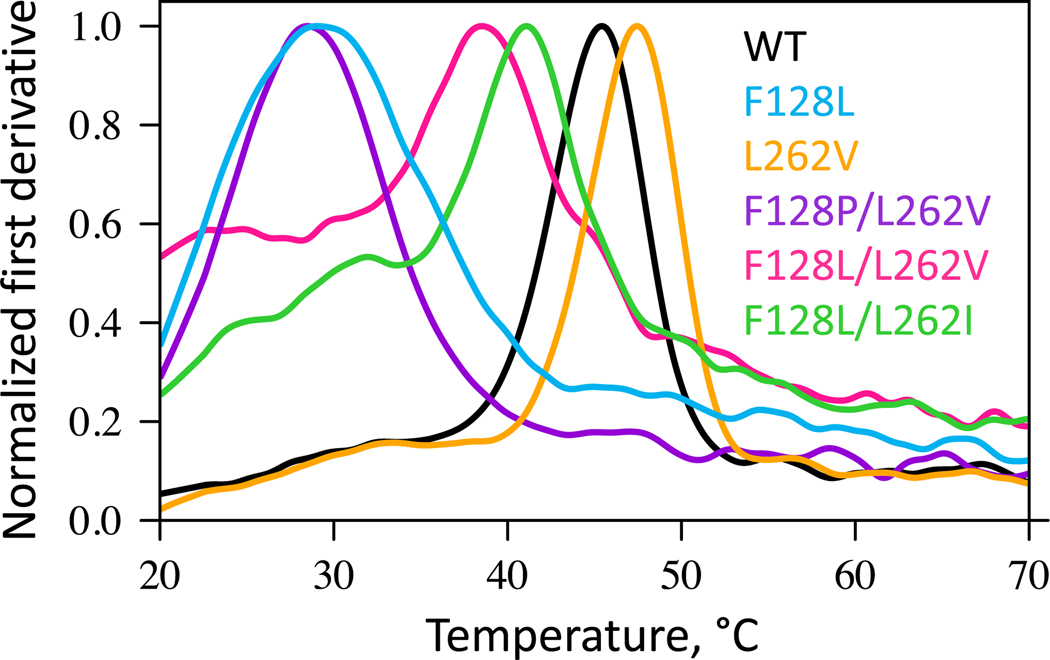
We then characterized the thermostability of these protein variants using differential scanning fluorimetry (Section S2.4 of the SI). The melting temperatures (T_m) were extracted from the first derivative of the thermal unfolding data (Figure 3 and Table 1). T_onset was defined as a temperature with a 20% increase of the signal from the baseline, and its order is consistent with the T_m values. Notably, the L262V variant increases the T_m from 45.2 °C in the wild type to 47.3 °C, indicating enhanced thermostability. In contrast, the F128L variant significantly decreases the T_m to 29.2 °C. The double variant L262V/F128L exhibits a T_m of 38.6 °C, which is approximately the average of the T_m values of the two single protein variants. This suggests that L262V may partially offset the destabilizing effect of the F128L variant. The other two double protein variants, F128P/L262V and F128L/L262I, have T_m values of 28.6 and 40.7 °C, respectively. The observed trends in thermostability for these DhlA protein variants differ markedly from previous studies on Renilla luciferase, where top active site variants designed by the same strategy have minimal impact on thermostability.¹⁸ The low T_m of F128P/L262V, consistent with its disrupted structure, led to the exclusion of this variant from further experiments due to its compromised structural integrity.

Figure 3.

Normalized first derivative curves from differential scanning fluorimetry for DhlA protein variants. The peak maxima correspond to the melting temperatures (T_m), measured in 100 mM glycine buffer at pH 8.6.

Table 1.

Melting Temperature of DhlA Protein Variants

variant	Tonset (°C)	Tm (°C)
wild type	40.4	45.2
F128L	20.0	29.2
L262V	43.3	47.3
F128P/L262V	20.0	28.6
F128L/L262V	36.5	38.6
F128L/L262I	35.1	40.7

Steady-State Kinetic Analysis Provided Initial Comparison of Catalytic Performance.

We measured the steady-state kinetics of the selected enzyme variants using isothermal titration calorimetry (ITC). We first determined the dependence of the initial reaction rate on substrate concentration, using DCE as the substrate. We conducted all kinetic analysis at 15 °C due to the low T_onset of the engineered protein variants. The ITC data were fitted to steady-state kinetic models (eqs 1A and 1B) to derive respective kinetic parameters (Table 2), including the turnover number k_cat, the Michaelis−Menten constant (K_M), and the substrate inhibition equilibrium coefficient (K_SI). The steady-state kinetic data, along with results from conventional nonlinear regression analysis, are presented in Figure S5 of the SI.

Table 2.

Steady-State Kinetic Constants of DhlA Protein Variants with DCE^a

variant	kcat (s−1)	KM (mM)	KSI (mM)
wild type	0.27 ± 0.01 (0.05)	0.06 ± 0.01 (0.05)	3.21 ± 0.22 (1.16)
F128L	0.05 ± 0.01 (0.05)	0.70 ± 0.03 (0.16)	4.58 ± 0.54 (2.86)
L262V	0.25 ± 0.01 (0.05)	0.25 ± 0.03 (0.16)	6.91 ± 1.64 (8.68)
F128L/L262V	0.18 ± 0.01 (0.05)	1.04 ± 0.06 (0.32)	n.d.
F128L/L262I	0.36 ± 0.02 (0.11)	1.08 ± 0.10 (0.53)	3.83 ± 0.96 (5.08)

^aParameters were determined in 100 mM glycine buffer, pH = 8.6 at temperature 15 °C, n.d. = not determined. Data reported as a best fit value ± standard error (standard deviation). Standard deviations indicate reduced accuracy of certain steady-state kinetic parameter estimates (e.g., for F128L/L262I) due to the limited substrate concentration range.

Compared to the wild type, k_cat is preserved in the L262V variant and slightly increases in the F128L/L262I variant, indicating that the AI predictions can identify protein variants with enhanced catalytic activity. However, for the other protein variants, the k_cat value decreases, highlighting the necessity for further refinement of the generative models. The Michaelis constant (K_M) was increased in all the protein variants, suggesting a lower affinity for the substrate in comparison to the wild-type enzyme. Additionally, the steady-state kinetic analysis revealed the presence of substrate inhibition (K_SI), a phenomenon commonly observed in haloalkane dehalogenases. In the reaction of DhlA with DCE, substrate inhibition was relatively mild and only slightly impacted the catalytic efficiency of the enzyme at high substrate concentrations (Figure S5 of the SI).

Fitting of steady-state kinetic data. (A) Michaelis−Menten equation.

$$\frac{v_0}{\left[E_0\right]}=\frac{k_{\text{cat}}[\text{S}]}{K_{\text{M}}+[\text{S}]}$$ (1A)

(B) Michaelis−Menten equation modified to account for substrate inhibition.

$$\frac{v_0}{\left[E_0\right]}=\frac{k_{\text{cat}}[\text{S}]}{K_{\text{M}}+[\text{S}]+\frac{{[\text{S}]}^2}{K_{\text{SI}}}}$$ (1B)

Transient Kinetic Analysis Reveals a Variant with Improved S_N2 Catalytic Activity.

To determine the rate constants for individual steps, including the S_N2 step (k₂), we employed transient kinetics with the stopped-flow method. This was combined with global numerical analysis of the kinetic data. When DhlA variants were rapidly mixed with DCE, we observed quenching of intrinsic tryptophan fluorescence (left panels in Figure S6 of the SI). Global fitting was performed using KinTek Explorer (KinTek corporation), allowing simultaneous fitting of both transient fluorescence data and steady-state data obtained by ITC (Figure S6 of the SI). The data fitting used numerical integration of rate equations from the minimal kinetic model (Figure 4) for the haloalkane dehalogenase reaction,¹⁹ including the substrate inhibition pattern in the case of the wild type and L262V. For the F128L/L262V and F128L/L262I protein variants, we were unable to distinguish between the final two steps, namely the formation and dissociation of the enzyme−product (EP) complex. As a result, it was not possible to determine k₃ and k₄ as separate individual steps. The kinetic mechanism was simplified to three steps, where the formation of an alkyl-enzyme intermediate (S_N2, k₂) is followed by a single third step that yields the free enzyme and the reaction products.

Figure 4.

Model used for fitting transient kinetic data of DhlA protein variants.

The resulting kinetic constants are summarized in Table 3. Interestingly, L262V leads to an increase in the rate of nucleophilic substitution. On the other hand, the nucleophilic attack is repressed in F128L/L262V making it the rate-limiting step. F128L/L262I retains a similar value as the wild type. F128L does not show any substrate saturation and only the k₂/K_S ratio could be derived from the kinetic data. A detailed description of the global kinetic analysis and the parameters, including scaling factors, is provided in Figure S6 and Table S9 of the SI. In addition to the standard error values presented in Table 3, a more rigorous analysis of the variation of the kinetic parameters was accomplished by confidence contour analysis (Figure S7 of the SI); the lower and upper confidence limits for each parameter were derived for χ² threshold at 0.98.

Table 3.

Transient-State Kinetic Constants of DhlA Protein Variants with DCE^a

variant	$K_{\text{S}}$ (μM)	$k_2\left({\text{s}}^{-1}\right)$	$\begin{array}{c}{k}_2/K_{\text{S}}\\ \left(\mu {\text{M}}^{-1}{\text{s}}^{-1}\right)\end{array}$	$k_3\left(s^{-1}\right)$	$k_4\left({\text{s}}^{-1}\right)$
wild type	291 ± 58 (247; 320)	7.6 ± 0.8 (6.6; 8.8)	0.026	0.19 ± 0.02 (0.18; 0.20)	3.6 ± 0.3 (2.3; 5.5)
F128L	n.d.	n.d.	0.004	0.0033 ± 0.0001 (0.0032; 0.0034)	6.5 ± 0.4 (3.8; 10.9)
L262V	1520 ± 30 (1100; 1560)	14.1 ± 0.2 (10.3; 14.5)	0.009	0.24 ± 0.01 (0.23; 0.24)	5.9 ± 0.1 (5.88; 8.29)
F128L/L262V	1221 ± 90 (1110; 1270)	0.134 ± 0.001 (0.125; 0.140)	0.0001	10.6 ± 0.4 (7.8; 15.2)	n.d.
F128L/L262I	2420 ± 70 (1980; 2960)	7.4 ± 0.2 (6.3; 8.7)	0.003	0.16 ± 0.01 (0.15; 0.17)	n.d.

^aDetermined in 100 mM glycine buffer, pH = 8.6, temperature 15 °C, n.d. − not determined. Values reported as best fit values ± standard error (lower; upper confidence limits). The standard error was calculated from the covariance matrix during nonlinear regression. Confidence intervals of the parameters were obtained by confidence contour analysis for χ² threshold of 0.98 (Supporting Figure S7).

EVB Simulation Confirms the Experimentally Observed S_N2 Catalytic Activity.

The rate constant for the S_N2 reaction shows a clear difference between the wild type and both the L262V and F128L/L262V protein variants. To gain a detailed understanding of the electrostatic interactions and structural changes in the active site resulting from sequence variation, molecular dynamics (MD) simulations were conducted using the empirical valence bond (EVB) method.^19,20 EVB is a semiempirical QM/MM approach based on a calibration of the free energy profile of the reference reaction in water. The calibrated parameters of the diabatic potentials of the reactant state and product state are then applied to model the same reaction within the more complex protein environment.^20,21 The method has proven its applicability in numerous biochemical studies^22–25 and has demonstrated its strength and reliability by accurately reproducing key structural and energetic changes in proteins due to sequence variation.^26–29

We computed the activation free energies (ΔG^‡) for the S_N2 reaction in both aqueous and protein environments for the wild-type, L262V, F128L/L262V, and F128L/L262I protein variants. The results are shown in Figure 5A, alongside experimental estimates. EVB successfully captures the differences between the aqueous and protein environments. The results for the wild-type and L262V protein variants are in excellent agreement with the experiment, while the ΔG^‡ values for the F128L/L262V and F128L/L262I variants are slightly underestimated. This promising outcome, indicating the overall catalytic effect, is the primary focus of our EVB studies. However, it remains important to identify the factors responsible for the changes in the ΔG^‡.

Figure 5.

EVB simulations of DhlA protein variants. (A) Comparison of computed (pink) and experimental (blue) activation energies (ΔG^‡) for the S_N2 reaction. Experimental ΔG^‡ values are derived from the Eyring equation based on k₂. (B−E) Representative molecular structures of native DhlA in its reactant state (B) and transition state (C), and of the L262V variant in its reactant state (D) and transition state (E). Only DCE and the side chains of key amino acids (D124, W125, F128, W175, V262) are shown. Atom color code: H in gray, C in slate blue, N in deep blue, O in red, Cl in green.

We examined the electrostatic contributions to the free energy of the S_N2 reaction, ΔG, and the structural features of mutated and neighboring residues. The data on group, electrostatic, and van der Waals contributions of key active site residues are presented in Tables S11–S13 of the SI. The effect of sequence variation, however, is not pronounced. For example, the energy of W175, a key residue stabilizing the chloride anion, increases in F128L/L262V and decreases in F128L/L262I (Table S11 of the SI). Notably, replacing phenylalanine with leucine at position 128 increases the contributing energy of this residue, which is observed in both F128L/L262V and F128L/L262I (Table S12 of the SI). The electrostatic contribution to the reorganization energy is higher in all protein variants compared to the wild type (Table S13 of the SI).

Since the above considerations did not lead to unique conclusions regarding the origin of the differences in activation free energies, we decided to explore the overall effect of ground-state stabilization/destabilization and transition-state stabilization. The corresponding study was done by evaluating the electrostatic and nonelectrostatic contributions to the ground-state and transition-state of the wild-type and L162V variants. The calculations were done by the PDLD/S-LRA-β.²³ The results of the calculations are given in Table S14, where we can see that the ground state of the variant is destabilized relative to the wild type and that this result is due to electrostatic effects. Thus, the most likely reason for the small reduction in the S_N2 barrier is a ground-state destabilization. This is usually not the way that enzymes reduce a rate-determining S_N2 step, where the major changes are always done by electrostatic transition-state stabilization.^30,31 However, here we have a relatively small change, which is associated with a reduction in binding (increase K_M). Such a change is not favored by evolution and is not expected to occur in native enzymes. At any rate, using computers to find this way of improving k₂ is not trivial and is a significant accomplishment of the maximum entropy approach.

Next, we focused on the structural changes in the active site due to amino acid replacements, emphasizing five key residues: the nucleophile D124, the mutated residues L262 and F128, along with W125 and W175 which stabilize the leaving chloride anion. Figure 5B–E display the structural changes for the native enzyme and the L262V variant in both the reactant and transition states, while other protein variants are shown in Figure S9 of the SI. The most noticeable structural difference is the distance between the nonreactive chlorine atom and the residues at positions 128 and 262. Specifically, the replacement of the aromatic side chain with an alkyl group in the F128L/L262V and F128L/L262I protein variants leads to the elongation of the intermolecular Cl−H contacts. The elimination of the phenyl ring also results in the loss of T-shaped π−π stacking interactions between F128 and W125, as well as the emergence of possible clashes with neighboring aliphatic residues such as M152. The size effect of F128 in DhlA was previously highlighted through comparison of multiple aligned sequences in ref 32: the bulk of this residue may hinder efficient catalytic activity with larger substrates. Thus, shortening the length of the residues at positions 128 and 262 leads to an enlargement of the active site cavity, which could be beneficial for accommodating larger ligands such as 1,2-dibromoethane or even 1-chlorohexane.

According to the experimental structural data, the active site of DhlA is primarily hydrophobic, with one water molecule present. This molecule is located near the H289 and D124 residues and plays a key role in the final chemical step−hydrolysis. As the cavities in the catalytic center are increased due to the amino acid replacements, we also examined the effect of inserting an additional water molecule near the reactive center. The introduction of a second water molecule increases the activation barrier in all protein variants and aligns well with the experimental estimate for the double-point variant F128L/L262V (Figure S11 and Table S15 of the SI). Detailed data on the electrostatic interactions and structural changes in the active site are provided in Section S3.4 of the SI. Adding more water molecules can influence the energetics of the S_N2 reaction and raise the activation barrier by stabilizing the nucleophile in its ground state. This correlates with the experimentally estimated rate constant k₂ for F128L/L262V, which shows a slowdown in chlorine displacement but an acceleration in the hydrolysis step.

Metadynamics Simulation Reveals Molecular Features Correlated with S_N2 Catalytic Activity.

In addition to EVB simulations, we conducted metadynamics simulations to explore molecular features that may correlate with the enzyme activity of the S_N2 step. While classical MD simulations cannot directly capture the enzymatic reaction, these features can be leveraged for enzyme engineering in the future. Here we applied well-tempered metadynamics³³ to examine the process of moving from reactant to a configuration closer to the transition state in DhlA. Metadynamics uses a history-dependent potential to accelerate the sampling of the collective variables (CVs). During the simulation, a Gaussian-shaped potential is periodically added to bias the system at the current CVs’ position, with the height of the Gaussian decreasing in well-tempered metadynamics as bias accumulates. Technical details of these calculations can be found in Section S4 of the SI.

In the S_N2 reaction, characterized by a backside attack, the carboxylic acid group of D124 acts as the nucleophile, attacking the carbon atom in the DCE substrate opposite the leaving chlorine atom. In our metadynamics simulations, we employed two CVs: the distance between the oxygen of D124 and the carbon of DCE (denoted as d(O−C)), and the angle formed by D124-O, DCE-C, and DCE-Cl (denoted as θ(O− C−Cl)). After 100 ns simulation and reweighting, we obtained the distribution of θ(O−C−Cl) as a function of the d(O−C).

The θ(O−C−Cl) angle is expected to be nearly collinear, close to 180°, in the transition state of the S_N2 reaction. Any deviations from this ideal angle could suggest a less optimal alignment, potentially resulting in a slower reaction rate. As shown in Figure 6, the θ(O−C−Cl) angle increases as the d(O−C) distance decreases across all systems, consistent with substrate positioning within the enzyme pocket. The smallest d(O−C) distance in our simulation is around 2.5 Å, which provides insight into the near-transition state region. In this region, the angle is around 135° in the wild type (Figure 6A). Interestingly, the L262V variant exhibits an average θ(O−C−Cl) greater than 140° (Figure 6B). This angle increase aligns with the S_N2 reaction mechanism and correlates with the observed increase in the catalytic rate for L262V in the experiment. For the F128L/L262V variant, the angle is less than 120° (Figure 6C), indicating reduced enzyme activity, which also matches the experimental data. The F128L/L262I variant shows an angle of approximately 130° (Figure 6D), similar to the wild type. These findings align with our earlier study on the near-attack conformation (NAC) proposal, where a similar correlation was observed.³⁴ The NAC angle can be an important factor in assessing the catalytic effect of the different variant, which has also been pointed out by Janssen and coworkers.³⁵ Overall, these angle variations align with the experimental enzyme kinetics, offering molecular insights that correlate with the observed differences in enzyme activity in the engineered protein variants.

Figure 6.

Metadynamics simulations of DhlA protein variants. Angle θ(O−C−Cl) as a function of distance d(O−C) in (A) wild type, (B) L262V, (C) F128L/L262V, and (D) F128L/L262I.

It remains unclear whether the correlation between θ(O−C−Cl) angle and k₂ itself reflects transition state stabilization or ground state destabilization, such as the NAC effect. However, the improvement of the S_N2 rate in L262V is likely to reflect ground-state destabilization as demonstrated in the energetics calculation. Nevertheless, it is important to reemphasize that in enzymes refined by evolution, the barriers for the S_N2 step are significantly lowered (relative to water) through substantial electrostatic stabilization of the transition state.³⁰

CONCLUSIONS

This study provides a comprehensive biochemical and computational analysis of DhlA protein variants designed using the MaxEnt model. Unlike other studies that focus on higher-order protein variants to highlight the generative capacity of AI models, we focused on single and double protein variants, where it is easier to analyze their differences from those of the wild type. We successfully identified protein variants that enhanced the catalytic activity of either a single reaction step, such as the S_N2 step, or the overall catalytic activity, using a minimal number of designs. In addition to experimental validation, our computational methods provided further insights. EVB simulations produced activation energy profiles that closely matched the experimentally measured S_N2 reaction rates. The simulations also help in determining the effects of sequence change on the electrostatic transition-state stabilization and on water penetration. Metadynamics simulations also revealed the importance of maintaining collinearity between the attacking nucleophile and the bond, which were consistent with the observed changes in enzyme activity.

In considering refinements of naturally evolved enzymes we note that improving the overall performance of an enzyme above that of the wild type is close to impossible. This is true for dehalogenase where the evolutionary pressure on this enzyme is high as the bacterium needs a huge amount of the enzyme to sustain its metabolism. At the same time, the enzyme is extremely conserved, which suggests the gene is very hard to improve further.³⁶ However, the improvement of the S_N2 step is not necessarily a factor that makes the enzyme work better. In fact, the increase in the corresponding rate constant may involve a decrease in k_cat/K_M, which leads to a decrease in the enzyme efficiency. Thus, it is possible to reduce a chemical barrier without competing with evolution.

Finally, it is worth emphasizing that achieving an enzyme with a rate constant faster than the corresponding rate in the wild-type protein variant is a significant accomplishment of an AI-driven approach. It is true that the effectiveness of the wild-type enzyme was not enhanced above the overall activity archived by evolution and that the increase in rate was accomplished by a way that is not used by evolution (namely, ground-state destabilization). However, predicting which mutation will lead to rate enhancement is far from trivial. We also like to clarify that improving a rate constant in a naturally evolved enzyme is by far harder than doing so in an artificial enzyme that was designed for a new substrate with a very low initial activity, where many changes can lead to improvement (see the case of Kemp eliminase e.g., ref 27). Overall, this study lays the foundation for a more refined and effective strategy in enzyme engineering, especially for complex, multistep catalytic processes.

Supplementary Material

ASSOCIATED CONTENT

Supporting Information

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.4c15551.

Detailed description of the experimental and computational methods, as well as additional supporting results; the experimental k_cat and k₂ of previously examined haloalkane dehalogenase’s protein variants along with computed statistical energies E(S) (page S1, and Table S1); the production, purification, and biochemical characterization of the proteins (pages S3–S14, Tables S2–S9, Figures S1–S7); details of the quantum chemical and EVB calculations, along with additional EVB results (pages S15–S22, Tables S10–S17 and Figures S8–S12); information on the metadynamics simulations (pages S23–S24) (PDF)