Mailborne transmission of anthrax: Modeling and implications

Abstract

A mathematical model is developed to analyze the transmission of inhalational anthrax through the postal system by cross-contamination of mail. The model consists of state vectors describing the numbers of cross-contaminated letters generated, the numbers of anthrax spores on these letters, the numbers of resulting infections in recipients, and matrices of transition probabilities acting on these vectors. The model simulates the recent outbreak in the United States, and provides a general framework to investigate the potential impact of possible future outbreaks.

Anthrax has been a scourge of humans and domesticated animals since ancient times, and its causative agent, Bacillus anthracis, has long been considered a weapon of biological warfare or terrorism (1, 2). Spores of B. anthracis can survive indefinitely in a wide range of environments (3), and a relatively modest dose delivered to mammalian skin or lungs can result in cutaneous or inhalational anthrax, respectively (4–7). Gastrointestinal anthrax also occurs in certain regions of the world (8), although inhalational anthrax is the most lethal form (9).

Since October 2001, both inhalational and cutaneous cases of anthrax have been recognized in the United States (10, 11), after a hiatus of more than 20 years (12). Of the 22 cases reported to date (December 15, 2001), 11 have been cutaneous and 11 have been inhalational; 5 persons with inhalational anthrax have died, with a case fatality rate of 45%. All cases of inhalational anthrax have occurred in persons above 43 years of age (median 56 years, range 43 to 94; refs. 11 and 13). After a 1979 accident at a Soviet factory producing anthrax spores in Sverdlovsk, a city of 1.2 million people, 79 persons were reported to have developed inhalational anthrax, and 68 of these died (1). All of the cases were clustered in a single quadrant of the city and its outskirts, corresponding to the area downwind of the plume released from the factory. Despite the large number of persons of all ages potentially exposed to this plume, no cases were reported in persons <24 years old (1). Both the Russian accident (1) and the current U.S. cases (11, 13) suggest that older persons have increased risk for contracting inhalational anthrax after environmental exposure.

Most of the current U.S. cases have been traced to letters heavily contaminated with anthrax spores that were sent through the U.S. mail (14). All strains recovered from mail and from clinical specimens reportedly have the same molecular fingerprint (14), indicating their dissemination from a single source. These mail-related cases have occurred among the intended recipients of the letters or others in their work environment (n = 7), or among postal workers (n = 11). In addition, there have been four other cases, two cutaneous, and two inhalational (both fatal) in elderly women, in which the victims appear unrelated to either the intended recipients or the postal milieu (11).

We propose that these “unrelated” cases occurred as a result of their receiving mail that had been cross-contaminated as a consequence of heavily contaminated letters traversing the postal system, as has been considered by the investigating authorities (11). To explain these cases, we have developed a mathematical model that is based on probabilistic assumptions concerning the proliferation of contaminated letters through the postal system, and the infection of recipients of these letters. Our model allows analysis of risk at sequential steps in the pathways of the mail, and of vulnerabilities of our postal system that require immediate attention. Analysis of the results generated by this model suggests practical steps for improving safety.

Methods

Mathematical Model.

The mathematical model consists of vectors describing the number of contaminated letters at a series of postal nodes, one vector describing the number of inhalational anthrax cases generated in recipients of these letters at the last node, and matrices that transition these vectors (15–17). As the contaminated letters travel through the nodes, there is a probability that they transfer spores to other letters, and thus proliferate the number of contaminated letters in successive generations. At each node, the letters are classified according to spore count and according to the generation level of cross-contamination. The recipients of letters at the last node are classified by their age, which determines the probability of becoming infected as a function of the spore count of the letter received. The model thus allows computation of the number of infections, distinguished by the spore count of letters received, their cross-contamination generation level, and by the age of letter recipients. The parameters chosen for the model should be viewed as preliminary estimates based on intuition and the limited information available. The main purpose of the model is to provide a general framework to apply to other situations that may arise.

Assumptions on the Number of Letters.

A.1.

Letters travel sequentially through nodes, which are designated as follows: node 1 (mailboxes or other points of entry into the postal system of the original contaminated letters), node 2 (local postal destinations), node 3 (regional or central postal destinations), node 4 (local postal destinations), and node 5 (final destinations, such as households, businesses, or offices). The assumption of five nodes of the character described above is made for simplicity, and is viewed as the routing of a typical piece of mail. The model is easily adapted to more complex routing (for example, additional nodes or recipients at multiple nodes). The original contaminated letters are capable of producing cross-contaminated letters by contact at each node, and cross-contaminated letters can produce further cross-contaminated letters (Fig. 1). The number of contaminated letters that routes through each node m = 1, 2, 3, 4, 5 is represented by a vector L̃[m] = [L[m]₁,L[m]₂,L[m]₃,L[m]₄]^t with four components (t denotes vector transpose). At each node m = 1, 2, 3, 4, 5, the first component L[m]₁ corresponds to the number of original contaminated letters, each of which is assumed to have >10¹⁰ spores; the second component L[m]₂ corresponds to the number of cross-contaminated letters, each having 10³ to 10⁴ spores; the third component L[m]₃ corresponds to the number of cross-contaminated letters, each having 10² to 10³ spores; and the fourth component L[m]₄ corresponds to the number of cross-contaminated letters, each having 10¹ to 10² spores. It is assumed that there are N originally contaminated letters at node 1 locations, and because only original contaminated letters arrive at node 1, L̃[1] = [N, 0, 0, 0]^t.

Figure 1.

Schematic of the matrix model of mailborne transmission of anthrax spores, based on cross-contamination. N letters entering node 1 (e.g., mailboxes), each with >10¹⁰ spores, cross-contaminate letters at nodes 2, 3, … , which in turn cross-contaminate additional letters in successive generations. The coefficients c[m]_jk of the contamination matrices indicate cross-contamination from node m and spore class k to node m+1 and spore class j. The model can be extended to additional nodes and additional classes of spore counts.

A.2.

At each node m = 1, 2, 3, 4, a contaminated letter in class L[m]_k (k = 1, 2, 3) produces an average c[m]_jk cross-contaminated letters arriving at node m + 1 in class L[m + 1]_j (j = k + 1, … ,4). The value of c[m]_jk accounts for all cross-contamination events at a node m location or in route between a node m location and a node m + 1 location. For example, an original contaminated letter may cross-contaminate letters in a node 1 mailbox and then arrive at node 2 locations, which are accounted for in the values of c[1]_j1, j = 2, 3, 4. At the node 2 locations or in route to node 3 locations, these cross-contaminated letters may cross-contaminate other letters, which are accounted for in the values of c[2]_j2, j = 3, 4. The original contaminated letters also arrive at node 2 locations, and there or in route to node 3 locations may cross-contaminate other letters, which are accounted for in the values of c[2]_j1, j = 2, 3, 4. For each m = 1, 2, 3, 4, define the 4 × 4 matrix C[m] (the cross-contamination matrix at node m) as follows:

For simplicity, conservation of spores is not considered specifically, and it is assumed that no letters are lost in routing and all remain in the same spore class as they move from node to node. Under the assumptions A.1 and A.2, the number of originally contaminated and cross-contaminated letters at nodes m = 1, 2, 3, 4 is given by L̃[m + 1] = C[m] L̃[m].

The number of cross-contaminated letters of each generation can be determined at each node from the cross-contamination matrices. A first generation cross-contaminated letter at nodes m = 2, 3, 4, 5 is a letter cross-contaminated by an original contaminated letter. A second generation cross-contaminated letter at nodes m = 3, 4, 5 is a letter cross-contaminated by a first generation cross-contaminated letter. A third generation cross-contaminated letter at nodes m = 4, 5 is a letter cross-contaminated by a second generation cross-contaminated letter. An example of a second generation cross-contaminated letter is one that is received by a node 5 recipient that was never at the same node as an original contaminated letter, but was cross-contaminated by a first generation letter that was. Let G[m]_kh be the number of cross-contaminated letters at nodes m = 2, 3, 4, 5, in spore classes k = 2, 3, 4, and in generations h = 1, 2, 3. The formulas for G[m]_kh are G[m]_kh = 0 if k ≤ h, and

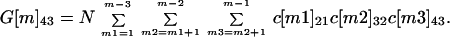Assumptions on the Number of Inhalational Anthrax Cases Produced at Each Node from Cross-Contaminated Letters.

A.3.

The probability that an individual becomes infected depends on the number of spores inhaled and the age of the individual. Individuals are divided into four age brackets as follows: <25 years (age bracket 1), 25–44 years (age bracket 2), 45–65 years (age bracket 3), and >65 years (age bracket 4). It is assumed that a fraction f[n] of the recipients are in age bracket n = 1, 2, 3, 4. For example, f[1] = 0.05,f[2] = 0.35,f[3] = 0.35, and f[4] = 0.25. For age bracket n = 1, 2, 3, 4, the probability of infection when S spores are inhaled is given by Pr[n](S) = b[n] (exp(S/a[n]) − 1)/(1 + b[n] (exp(S/a[n]) − 1)), where a[n] and b[n] are specified constants. The functions Pr[n] are sigmoidal and satisfy Pr[n](ID[n]₅₀) = 0.5 and Pr[n](ID[n]₁₀) = 0.1, where ID[n]₅₀ and ID[n]₁₀ are the number of inhaled spores that produce inhalational anthrax infection in 50% and 10%, respectively, of individuals in age bracket n. The two values ID[n]₅₀ and ID[n]₁₀ completely determine the curve Pr[n](S) when the constants a[n] and b[n] are chosen so that exp(ID[n]₅₀/a[n]) − 1.0 = 9.0 (exp(ID[n]₁₀/a[n]) − 1.0) and b[n] = 1.0/(exp(ID[n]₅₀/a[n]) − 1.0).

A.4.

The average number of individuals exposed to cross-contaminated letters at node m is E[m], m = 2, 3, 4, 5. For example, if an average of 1.5 recipients handle the arriving cross-contaminated letter at node 5, then E[5] = 1.5.

A.5.

The average number of spores inhaled at nodes 2, 3, 4, and 5 by individuals exposed to cross-contaminated letters is a fraction I[m] of the spore count of the letter. For example, if a recipient inhales on average 3% of the spores carried by a cross-contaminated letter at node 5, then I[5] = 0.03.

Calculation of the Number of Cases at Node 5 Produced by Cross-Contaminated Letters.

Let A[5]_2n, A[5]_3n, A[5]_4n be the average number of inhalational anthrax cases produced at node 5 by cross-contaminated letters having 10³ to 10⁴,10² to 10³,10¹ to 10² spores, respectively, in individuals in age bracket n (n = 1, 2, 3, 4). Under the assumptions A.1–A.5,

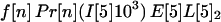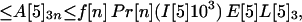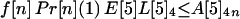If the average values for the inequalities are assumed, then the average number of inhalational anthrax cases A[5]_2n, A[5]_3n, A[5]_4n produced at node 5 by cross-contaminated letters having 10³ to 10⁴, 10² to 10³, 10¹ to 10² spores, respectively, in individuals in age bracket n (n = 1, 2, 3, 4), are

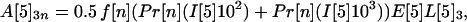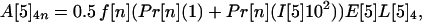and the total number of cases is ∑ ∑ A[5]_kn.

Results

An Example Corresponding to the Outbreak in the U.S. in 2001.

The model can be used to simulate the events in the U.S. in October, 2001, in which it is hypothesized that six original contaminated letters (14) led to two cases of inhalational anthrax as a result of cross-contaminated mail, one in the Bronx, NY and one in Oxford, CT (11). The parameters in the model are designed to yield this outcome. Take N = 6, E[5] = 1.5, I[5] = .03, and define the contamination matrices as

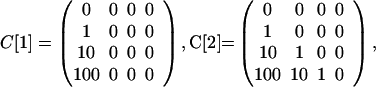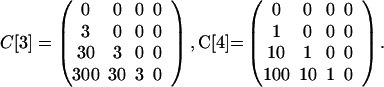Because precise values are not available, the entries in these matrices are estimates; however, the facts available provide information to help in their estimation. On October 9, 2001, two anthrax-laden letters addressed to two U.S. Senators were processed through the Hamilton Township sorting center near Trenton, New Jersey (11). In a <1-min period, 300 letters passed through the same sorting machines as each of these two original contaminated letters (11). These 600 letters (and more) were most likely first generation cross-contaminated letters. All were identifiable by postal bar code data and traceable to their destinations. One was found to have gone to a recipient in Seymour, CT, who lived about a mile from a 94-year-old woman in Oxford, CT, who died of inhalational anthrax on November 21. The Seymour letter was found to contain small numbers of spores, and almost certainly was a first generation cross-contaminated letter. No letter with spores was found in the home of the 94-year-old woman, but the fact that she received no mail that passed through the New Jersey station within the <1-min period is consistent with the hypothesis that she was infected by a second generation cross-contaminated letter. The entries of the cross-contamination matrices reflect this information, with C[3] corresponding to more vigorous processing at regional postal centers, and C[1], C[2], and C[4] corresponding to less handling in local centers.

The number of cross-contaminated letters resulting from these parameter values for the model are shown, according to spore count and node (Table 1), and according to spore count and generation level at node 5 (Table 2). The parameters for the infection of letter recipients at node 5 are shown in Table 3, and the infectious dose curves Pr[n](S), n = 1, 2, 3, 4 are shown in Fig. 2. The infection dose parameterization is suggested by expert-elicited information that is currently available (18). The number of cross-contamination inhalational anthrax cases produced at node 5 according to spore count of the letter received, age of the recipient, and the proportion in each generation level, is shown in Table 4. The model predicts, with probability of approximately 0.5, that each spore count class of cross-contaminated letters will produce one case, all in recipients >65 years. The generation level of the letters producing these three cases is inferred from the proportions of the first, second, and third generation cross-contaminated letters in each spore count class (G[5]_kh/L[5]_k, k = 2, 3, 4, h = 1, 2, 3). Thus, the case resulting from a letter with spore count 10³ to 10⁴ can be considered a first generation cross-contamination case. The case resulting from a letter with 10² to 10³ spores occurred with probability 0.83 from a first cross-contaminated letter and probability 0.17 from a second generation cross-contaminated letter. The case resulting from a letter with 10¹ to 10² spores occurred with probabilities 0.71, 0.28, and 0.01 from first, second, and third generation cross-contaminated letters, respectively.

Table 1.

Number of contaminated letters at nodes 1, 2, 3, 4, 5 by spore count

Spore Count	Node
	1	2	3	4	5
1010	6	6	6	6	6
103 to 104	0	6	12	30	36
102 to 103	0	60	126	342	432
101 to 102	0	600	1,320	3,858	5,100

Table 2.

Number of cross-contaminated letters at node 5 by generation level

Spore count	Generation level
	Original	First	Second	Third
1010	6	0	0	0
103 to 104	0	36	0	0
102 to 103	0	360	72	0
101 to 102	0	3,600	1,440	60

Table 3.

Parameters for the infection of recipients

Age bracket, years	Fraction of recipients (f[n])*	Infectious dose
		ID50	ID10
<25	0.05	15,000	4,500
25–44	0.35	10,000	3,000
45–65	0.35	6,000	1,800
>65	0.25	1,500	450

^*Estimate of the proportions of all likely mail recipients. 

Figure 2.

Relationship of number of spores S to which a recipient is exposed and the probability of developing inhalational anthrax, according to age of the recipient. The probabilities are given by the formulas Pr[n](S) = b[n] (exp(S/a[n]) − 1) / (1 + b[n] (exp(S/a[n]) − 1)), n = 1, 2, 3, 4, where the two parameters a[n] and b[n] are determined by the infectious doses that produce infections in 50% (ID₅₀) and 10% (ID₁₀) of exposed persons. The values ID₅₀ and ID₁₀ for the four age brackets are given in Table 3. (A) <25 years. (B) 25–44 years. (C) 45–65 years. (D) >65 years.

Table 4.

Number of cross-contamination cases at node 5 by letter spore count, and the age of recipient and the proportion in each generation level

Spore count	Number of cases by age of recipient, years				Proportion of cases by generation level of letter received
	<25	25–44	45–65	>65	First	Second	Third
103 to 104	0.007	0.08	0.14	0.45	1.0	0.0	0.0
102 to 103	0.009	0.10	0.16	0.47	0.83	0.17	0.0
101 to 102	0.011	0.11	0.19	0.54	0.71	0.28	0.01

An Example Corresponding to a Larger-Scale Attack.

The previous example can be modified to show the effects of a larger-scale attack. One amplification is to increase the number N of originally contaminated letters. Another amplification is to increase the entries in the cross-contamination matrices. Let p be a parameter ≥1 that corresponds to this amplification, as in the following definitions:

Higher values of p could correspond to the original contaminated letters being left unsealed or deliberately designed to leak spores. Let N = 100, let C be as above, and assume all of the other parameter values are the same as in the previous example. The model predicts that a larger number of originally contaminated letters (N = 100) and their greater capacity for cross-contamination (p as high as 250) would result in millions of cross-contaminated letters and thousands of infections (Fig. 3).

Figure 3.

Effects of a larger-scale attack. The number of originally contaminated letters is N = 100 (instead of N = 6). The entries in the first columns of the contamination matrices C increase as p increases from 1 to 250, corresponding to an increased capacity to cross-contaminate. The number of contaminated letters (A) and the number of infections (B) increase linearly with p rather than as a higher power of p, because the mechanisms of cross-contamination are only affected by an increased capacity of the original letters to cross-contaminate, and not the subsequent generations.

Discussion

The U.S. postal system is relatively open and designed to optimize the efficient and timely movement of ≈4 billion pieces of mail per week. The mail has previously been used for terrorist purposes, involving shipments of both explosives and toxic substances intended for their recipients. In the current bioterrorist attack in the U.S., the letterborne transmission of spores of B. anthracis also has had the consequence of infecting intermediaries in the postal delivery network (14), and we strongly suspect, individuals who have no other relationship to the intended recipient than their receipt of mail. Because evidence suggests that they acquired anthrax through handling or receipt of mail that had become cross-contaminated during processing of the original letter or one that had itself become contaminated, we develop a mathematical model to examine this phenomenon.

The model does not prove the hypothesis that the two “unrelated” cases were due to mailborne transmission. Another hypothesis to explain the unrelated cases is that they were airborne. It is known that the wind was blowing 47°NE from the postal facility in Trenton, NJ on October 9, directly toward the locations of these two cases, Bronx, NY, and Oxford, CT (19). This information supports the hypothesis that the two cases involved airborne transmission. The explanation of these cases remains unresolved, but our model provides a framework to analyze the critical elements in the hypothesized mailborne transmission process, and their extrapolation to other contexts. These elements are the numbers of letters involved through successive transfers of contamination, the magnitude of contamination (number of spores carried) of the letters, the magnitude of the risk to recipients of these letters in terms of the numbers of spores to which they are exposed, and the probabilistic computation of the infections that ensue. It is unavoidable that the model parameterization relies on uncertain information concerning the mechanics of spore transfer and the data on human infection doses. Calibration of parameters based on experimental data are feasible, but beyond the scope of this study.

One key assumption in this model, applied to the recent outbreak, is that there was a leakage of spores from the original letters, at least six of which were sent. Considering the extremely large number of spores contained in the original letters, and typical amounts of jostling during processing, contamination to adjacent environments was likely, which was confirmed by the examination of involved postal facilities, mailrooms, and mailbags (11, 14). A plausible mechanism for release of spores from the interior of an envelope is the bellows action of the processing machines, which may draw spores on or into following envelopes. The model demonstrates that the observed number of cases in mail recipients is consistent with the cross-contamination of thousands of pieces of mail, most with very low numbers of spores, probably <10³ per letter.

Another key assumption in the model was that the delivered dose of spores that produce illness was <10⁴. Under this assumption, the model simulations provide substantial agreement with the known number of cases in this outbreak. The model assumes that the highest level of cross-contamination is 10⁴ spores, because an order of magnitude greater produces an order of magnitude greater number of cases than was observed. Similarly, the model assumes that the lowest level of cross-contamination is 10¹ spores, because letters with less have negligible contribution to the yield of cases.

For many infectious diseases, the dose to which susceptible individuals are exposed is an important determinant of the attack rate. Thus, for Salmonella species, while the ID₅₀ (dose that will result in infection of 50% of exposed persons) may be approximately 10⁴ bacterial cells, the ID₁₀ may be only 10¹ to 10² cells (20). Similarly, in cynomolgus monkeys exposed to aerosols of virulent B. anthracis spores, the LD₄₄ (dose causing lethality in 44% of animals) was approximately 5,000 spores, whereas the LD₇ was about 300 spores (4). For cutaneous anthrax, the ID₇ in humans is believed to be substantially lower (5), explaining why most naturally occurring cases are cutaneous. Although much of the prior data concerning susceptibility to inhalational anthrax considered lethal doses (e.g., LD₅₀), we chose to study infectious doses (e.g., ID₁₀). Although high (45%), the case-fatality rate in this outbreak was lower than was previously assumed (1–9), and with improved early recognition and treatment, rates may further fall, but to an unknown extent. It is probable that advanced age has even greater effects on lethal doses than on infectious doses. Variation in virulence among B. anthracis strains is another source of uncertainty in this model.

The rapid and widespread usage of antibiotics among postal workers and persons in the immediate environment of the received original letters (21) probably averted a substantial number of cases. Specific practices that lead to the aerosolization of letterborne infectious particles in postal facilities need to be identified and their use curtailed. The capacity of contaminated letters to cross-contaminate both the environment and other letters must be interdicted by procedures that lessen both phenomena. Ongoing surveillance of mail-related illnesses and rapid tracking of the chain of contamination is necessary. Vaccination of all postal workers and other professional mail-handlers with the present or an improved anthrax vaccine may be desirable, as reflected by the scale of the potential problem shown in Fig. 3. In the interim, periodic serologic screening of postal workers for responses to B. anthracis antigens (22, 23) may be useful to both calibrate the extent and locale of contamination, as well as to provide baseline samples in case of wider contamination events. The model predicts that a larger scale attack could result in millions of contaminated letters and thousands of infections (Fig. 3), which could necessitate the complete suspension of the U.S. postal system. The model provides a means to quickly assess critical steps and magnitude of risks if such an attack occurs. As the epidemic unfolds, the parameters could be estimated with increased confidence as new data become available.

Our model recognizes and addresses the age-skew present in this and the Sverdlovsk outbreaks, which suggest an enhanced susceptibility to inhalational anthrax associated with aging. Such a phenomenon would not be highly unusual for an infectious disease, and its confirmation would better inform public health decisions. Advanced age also may be a proxy for less common forms of host compromise, including immunosuppression, immunodeficiency, and chronic illness. Although the two fatalities resulting from apparent cross-contamination in the present outbreak were elderly, it is misleading to assume that in a wider attack nearly all cases would be so. If the assumptions of the model are correct, approximately one-third of the cases would be in the middle age range in a larger scale attack.

The dangers inherent in the current U.S. postal system exposed by this model are not easily allayed, and risk reduction will both reduce efficiency and inherent user freedoms, as well as increase economic costs. Although individuals may opt for safer (cyberspace) forms of communication, the openness of the Internet also poses infectious threats of a different nature (24). Thus, in a hostile world, there exists a continuum of risk implicit in our systems of communication. In the event of further bioterrorist attack by mailborne anthrax, early cases can be recognized by prepared governmental and medical sectors, and an informed society can understand, confront, and counter the consequent risks.