Implant density reduction to avoid proximal junctional failure in adult spine surgery: Computer models and simulations

Abstract

Background

Proximal Junctional Failure (PJF) is a common complication in Adult Spine Deformity (ASD) surgeries, often leading to reoperations. While revision surgeries with osteotomies carry high complication rate of 34.8%, alternatives such as hardware proximal extension may increase PJF risk in patients with severe Global Alignment and Proportion (GAP) scores. Implant Density Reduction (IDR) has emerged to mitigate PJF risk. This study assessed the impact of IDR on PJF risk and explored sub-optimal strategies.

Methods

Two patient-personalized Finite Element (FE) models were used and expanded into a virtual cohort. Implant Density (ID), rod material, bone quality, and GAP were systematically varied. Thoracolumbar FE models were developed using structured Statistical Shape Modeling (SSM). Biomechanical metrics of Intervertebral Disk (IVD) fiber strain, Screw Pull-out Force (SPF), and rod stress, were evaluated. Trade-off analyses could determine sub-optimal configurations avoiding PJF.

Results

IDR significantly decreased IVD strain (up to −70%) and improved screw stability (up to +142%), for patients with titanium (Ti) rods and normal bone. However, IDR effectiveness was limited for cases with GAP ≥12, osteoporotic bone, and Cobalt-Chromium (Cr-Co) rods. No IDR strategy could prevent PJF for cases with GAP 12 or 13, regardless of rod type. For cases with GAP 11 and Upper Instrumented Vertebra (UIV) at T10, IDR was effective with only Ti rods. For cases with GAP 13 and UIV at T3, none of IDRs, independent of rod material, offered benefit. Notably, Ti rods may support IDR-based risk reduction in borderline cases, such as GAP 12, UIV at T3.

Conclusions

IDR is a promising strategy to lower PJF risk in high-risk spine revision cases, though its effectiveness depends on surgical and anatomical factors. This study provides an in-silico tool to support personalized surgical planning and guide future clinical trials aimed at reducing reoperations and healthcare costs.

Introduction

Adult Spine Deformity (ASD) is a complex condition marked by abnormal spinal alignment. Surgical treatment focuses on restoring sagittal balance and improving Health-Related Quality of Life (HRQOL) outcomes [1]. However, post-operative (post-op) mechanical complications, such as Proximal Junctional Failure (PJF), occur in 8.7% to 36% of ASD surgeries [2], typically within 3–6 months after surgery [3]. It includes Intervertebral Disc (IVD) degeneration, ligament damage, hardware loosening, and fractures at Upper Instrumented Vertebra (UIV) [4].

Patients with PJF often need revision surgery due to increased pain and progression of Proximal Junction Angle (PJA) [5]. These revisions aim to realign the spine by removing prior implants, perform lumbar osteotomies, and extend hardware proximally, especially in cases where the original construct ended in a biomechanically vulnerable region [6,7]. Although lumbar osteotomies are effective for sagittal realignment, they carry a high complication rate of 34.8% [8], which may discourage their use in revision settings for PJF patients. Consequently, surgeons may opt to extend instrumentation proximally without fully correcting spinal alignment, a strategy that can elevate the Global Alignment and Proportion (GAP) score [9] and potentially increase PJF risk. GAP above 7 predict high PJF risks [10], making early prevention techniques essential to reduce successive PJFs and, hence, avoid revision surgeries.

Prevention techniques aimed to reduce proximal stress concentrations. These techniques were classified as: Implant Density Reduction (IDR), sublaminar tethers, sublaminar tape, pretensioned suture loops, transverse or laminar hooks, and etc. [11]. A few studies focused on IDR effects. Durand et al. found that Screw per Level (SpL) or Implant Density (ID) fewer than 1.8 was associated with low PJF risks [12]. However, it was still unclear whether sub-optimal screw density patterns could avoid PJF risks in both first and successive revision surgeries. Moreover, because ID and SpL were global metrics that did not capture the distribution of screws near the junctional region, the authors in [12] highlighted the need for localized biomechanical analyses to assess PJF risk more precisely.

Recently, Finite Element (FE) modeling has become an effective tool to explore spinal biomechanics and simulate surgical strategies. Biomechanical effects of semi-rigid junctional fixation (transverse process hooks, clamped, and knotted tapes) were studied in [13]. In another study, Zhao et al. found that the ligament strengthening configuration of 3-level posterior tethers might decrease Proximal Junctional Kyphosis (PJK) risks [14]. Moreover, posterior tethers biomechanical effects were studied in [15,16], highlighting low PJK risks by creating gradual transition in adjacent-segment stress. Zhu et al. also found that localizing UIV at either proximal or distal thoracic vertebrae could increase PJF risks [17]. Polycarbonate-urethane rod could also decrease screw pull-out risk [18]. Fradet et al. found that the buckling effect of post-op functional loads on the proximal junctional segments, was a potential risk for PJF [19]. Metzger el al. also showed that laminar hooks could reduce stress concentrations at proximal segments, avoiding PJK [20]. Park et al. found that distal fusion levels led to increase in PJK/PJF risks [21]. However, there were lacks of computational studies exploring the biomechanical effects of IDR, sub-optimal ID patterns, and the influence of GAP, rod, and bone properties on safe ID surgery planning.

Therefore, this study aims to evaluate how ID patterns influence the risk of PJF through FE simulations. The analysis focuses on understanding the biomechanical impact of IDR strategies in patients with severe GAP scores, with the goal of preventing both primary and revision-stage PJF. In addition, the study further investigates how sub-optimal ID patterns can still achieve biomechanical safety by performing trade-off analyses. These analyses help identify screw configurations that minimize PJF risk while accounting for key clinical factors such as alignment severity (GAP score), rod stiffness, and bone quality.

Methodology

Clinical cases were selected, and corresponding patient-personalized FE models were employed. Case-derived implants were inserted to replicate surgical procedures, while virtual implants were also used to model variations in ID configurations for the clinical cases. Here, the goal was to simulate biomechanical conditions associate with PJF, and to identify implant strategies, especially involving ID reduction, that may reduce PJF risk in the selected clinical cases. These cases served as reference points for broader analysis of a virtual cohort. This virtual cohort allowed to systematically vary surgical (e.g., ID, UIV, and rod material), and anatomical (e.g., sagittal alignment via GAP scores, and bone quality) parameters. The subsequent FE simulations enabled a comprehensive evaluation of how these variations influence key biomechanical risk indicators associated with PJF (see section 2.4). A total of 104 FE simulations were conducted, including 2 real-world clinical cases, 11 case-derived ID variations (5 for the first case and 6 for the second), and virtual cohort of 91 diverse models. The summarized workflow followed 4 main steps: Clinical model generation: Two patient-personalized thoracolumbar FE models were created to represent distinct clinical scenarios (see sections 2.1 and 2.2).

• 1.Surgical replication: Two patient-personalized models were instrumented to match their respective clinical imaging data (see sections 2.3.1 and 2.3.2).
• 2.ID variation modeling and simulation: 11 additional FE models were generated by varying ID configurations within the 2 clinical cases to evaluate biomechanical effects of ID strategies aimed at mitigate PJF risks (see section 2.3.3).
• 3.Virtual cohort analysis: A virtual population of 91 FE models was evaluated by systematically varying key surgical and anatomical parameters to explore a wider range of biomechanical outcomes to mitigate PJF risks (see section 2.4).

Clinical cases

Two clinical cases were selected, each reflecting a distinct surgical context:

• •Case 1 (Primary Surgery, T10-int case (i.e., initial (int) UIV at T10, and PJF at T10 level)): This case represents a patient who developed early-onset PJF following a primary spinal fusion terminating at the thoracolumbar junction (T10). This transitional region is biomechanically vulnerable due to abrupt curvature and stiffness transitions, making it a common site for junctional complications.
• •Case 2 (Revision Surgery, T11-T3 case [i.e., initial UIV at T11, PJF at T11, and UIV extension to T3 level]): This case reflects a revision surgery scenario, where the patient initially underwent instrumentation at T11 and later required proximal extension to T3 due to failure. This case illustrates a progressive failure cascade and highlights the challenges of mitigating junctional risk in a revision context. Inclusion criteria for the selection of 2 initial cases were as follows:
• •PJF at 1st operation (1st case)
• •At least 2 successive PJF (2nd case)
• •Lower thoracic hardware extension (1st case)
• •Extension of hardware, from prior instrumentation at 1st PJF in lower thoracic to upper thoracic levels before 2nd PJF (2nd case)
• •No spine curve correction between 1st and 2nd PJF (2nd case)
• •No PJF prevention techniques at UIV/UIV+1,2 (both cases)
• •Minimum GAP 9 at immediate post-op (both cases)
• •Age 50 to 75 yrs (both cases)
• •PJF criteria: Hart et al. [4] (both cases)

Case 1 (T10-int)

Case 1 was a 55-year-old anonymized female, selected from a retrospective cohort of 57 PJF cases [10] (IRCCS, Galeazzi-Sant'Ambrogio Hospital, Milan). This case had PJF at T10 after 8 months (Fig. 1). Sagittal geometrical parameters were measured using sterEOS software (EOS Imaging, Paris, France) [10] and verified by a spine orthopedic surgeon. Thoracic Kyphosis (TK) at immediate post-op was high, 60° (normal TK 35° to 50° [22]), then post-op increase in Lumbar Lordosis (LL) worsen TK (in accordance with [23]), resulting in PJK, then PJF.

Fig. 1.

Pre-op, first-op and 8 months follow-up for the first case (T10-in): female, 55 y.o., PJF at T10 (PJA, proximal junction angle; PJF, proximal junctional failure; UIV, upper instrumented vertebra; GAP, Global Alignment and Proportion).

Case 2 (T11-T3)

Case 2 was a 76-year-old anonymized female, selected from IMIM (Hospital del Mar, Barcelona) database. Selection process was in accordance with the ethical guidelines set by Ethics Committee of Hospital del Mar. This case had 1st PJF at T11, need to extend implants from T11 to T3 while retaining the prior hardware. 2nd PJF occurred at T3 after 8 months post-operatively (Fig. 2). Spine sagittal parameters were measured using Surgimap® (Massachusetts, USA), and confirmed by an orthopedic surgeon.

Fig. 2.

First-op, second-op (GAP 11) and 3 months follow-up for case T11-T3: female, 76 y.o., 1st PJF at T11 and 2nd PJF at T3 (PJF, proximal junctional failure; UIV, upper instrumented vertebra; GAP, global alignment and proportion).

Spine geometrical annotations derived from clinical imaging data were later used to generate detailed FE models for both clinical cases by matching them to a database of pre-generated models.

Patient-personalized modeling

Two patient-personalized thoracolumbar spine FE models were developed to represent the T10-int (pre-operative) and T11-T3 (2nd surgery) clinical cases using corresponding geometrical annotations. These geometrical parameters were searched among the geometrical descriptors of 16,807 structured patient-personalized models (https://thc.spineview.upf.edu/) [24]. Two corresponding FE meshes were selected based on their highest similarity to the annotations (Fig. 3A for T10-int and Fig. 3B for T11-T3). Clinical spinopelvic parameters were compared with the retrieved models (Table 1), showing acceptable differences of approximately 5% compared to clinical measurements, consistent with the ASME V&V 40 standard for computational models, detailed in [25]. These results indicate a high degree of anatomical fidelity in the geometric reconstruction of the models. In addition to anatomical verification, biomechanical validations were also carried out via Range of Motion (RoM), and FE computational validations (previously published in [24]). In RoM validation, mono-segmental and multi-segmental ROM of lumbar, thoracic, and thoracolumbar aligned spines (GAP 1) were validated against previous in-vitro or in-vivo experiments [24], showing deviations within ±15% (in average) of reported values. In FE computational validation, aligned spine biomechanical behaviors were validated against previous in-vitro results [24], with discrepancies within 10% (in average) of experimental ranges. All these validation metrics confirm that the models offer a robust and physiologically relevant representation of real-world thoracolumbar spines, satisfying the verification and validation criteria outlined in the ASME V&V 40 framework.

Fig. 3.

(A) Triangulated mesh and osteo-ligamentous spine hexahedral FE mesh for case 1 (T10-int, pre-op); (B) Triangulated mesh and osteo-ligamentous spine hexahedral FE mesh for case 2 (T11-T3) (SS, sacral slope; LL, lumbar lordosis; TK, thoracic kyphosis; GT, global tilt).

Table 1.

Clinical and model spinopelvic parameters for T10-in and T11-T3 cases

Cases	Measurements	PI	SS	LL	TK	GT	GAP	Max Difference %
pre-op T10-int	Model	69°	32°	-41°	61°	47°	10	2.85%
	Clinical	71°	33°	-41°	60°	46°	10
2nd-op T11-T3	Model	38°	24°	-32°	46°	23°	11	5.43%
	Clinical	38°	23°	-31°	47°	24°	11

PI, pelvic incidence; SS, sacral slope; LL, lumbar lordosis; TK, thoracic kyphosis; GT, global tilt; GAP, global alignment and proportion.

Overall, Rasouligandomani et al. sampled 16,807 patient-personalised models using Eq. 1, which incorporated the first 5 shape modes of a structured Statistical Shape Model (SSM), with each mode discretized into 7 Standard Deviations (SD) [24].

$$\text{Sample}\text{Shape}=\text{Mean}+Pb$$ (1)

where Mean represents average shape, P is matrix of eigenvectors (shape modes), and b is SD. The structured SSM was developed by integrating unstructured SSM data with mesh morphing techniques [24]. Unstructured SSM was created using 42 pre-op EOS images (IRCCS database), converted into 3D surface models with sterEOS software. Principal Component Analysis (PCA) was applied to analyse shape variations, identify principal modes of variation, and compute the eigenvectors of the covariance matrix [26]. The unstructured mean model, later, was transformed into a structured hexahedral FE model by morphing a pre-existing 3D FE spine template [27] to match the mean shape geometry. Soft tissue and vertebral meshes were adapted using the Bayesian Coherent Point Drift (BCPD++) algorithm [28]. The final models incorporated 17 IVD meshes and 6 ligament groups [24]. Finally, by transferring the eigenvectors of the unstructured SSM to the structured FE mean mesh, a structured SSM was created, enabling the sampling of osteo-ligamentous spine hexahedral FE meshes (See more details in [24]).

Surgical instrumentations and ID variation modeling

Screws were designed using a Computer-Aided Design (CAD) software based on a commercial poly-axial pedicle screw (STL Poly-axial Pedicle Screw Fixation System, 2B1 S.r.L, Italy; Fig. 4A). A simplified model was created (Fig. 4B), involving 2 main parts: the head and the shaft. Screw dimensions were tailored to spinal regions per manufacturer standards (Table 2). Rods were modeled as beam elements aligned with smoothed screw head trajectories, radially expanded to a 5.5 mm diameter. To position the screws, Boolean/cut operations in Abaqus v2019 software (SIMULIA, Dassault Industries) created preparation holes in pedicles and vertebral bodies. Screw shafts were placed into these holes using kinematic constraints. Xu et al. showed that contact between screw and bone must be modeled as a relative frictional movement [29], therefore, here screw-bone interface was defined as a tight surface-to-surface contact with friction coefficient of 0.61, experimentally quantified in [30], to reflect realistic bone conditions and calculate the contact forces. Screw Pull-out Forces (SPF), as shown by Varghese et al., were calculated as sum of average axial and perpendicular contact forces (normal + shear) [31]. SPF refers to the maximum force required to extract a screw from the bone and it quantifies the resistance of the bone–screw interface to failure. Moreover, regarding ASTM F543 standards, the pedicle screws were modelled with 30° half-thread angle, 1.25 mm pitch distance, 4 mm bolt major diameter, and 3.5 mm mean thread diameter [32]. Tie constraints ensured a fixed connection between the screw head and shaft, while additional tie contacts seamlessly coupled the tetrahedral mesh of the pedicles with the hexahedral mesh of the vertebral bodies.

Fig. 4.

(A) Poly-axial real screw (2B1 S.r.L, Italy); and (B) simplified screw created by a CAD software.

Table 2.

Screw dimensions

Zone	Sacrum	Lumbar	T12 to T8	T7 to T1
Dimensions (Length$\times$Diameter) in mm	35$\times$7	45$\times$6	40$\times 5$	35$\times$4.5

Surgical instrumentation: T10-int case

T10-int implants were modeled based on immediate post-op geometry. A pre-op spine model was previously selected (Fig. 3A, pre-op in Fig. 1). Both pre-op model and implants were simultaneously imported into Abaqus v2019 software (SIMULIA, Dassault Industries). Kinematic constraints were later applied to the pre-op model to simulate surgical correction process. These constraints were applied as velocity fields during FE simulation in step 2 of 1st case, and defined as 3 rotational degrees of freedom (R_x, R_y, R_z) in the vertebral local coordinates, measured from landmark’s rotations between pre-op and immediate post-op vertebrae. A "dummy model" representing the immediate post-op geometry was retrieved from a shared database [24] (Fig. 5a) just to isolate and transfer instrumentation geometry. This dummy model was then instrumented with pedicle screws and rods, matching with clinical data shown in Fig. 1.

Fig. 5.

(A) First-op dummy model for the 1st case and dummy instrumented model in a CAD software; (B) Second-op instrumented model for the 2nd case in a CAD software.

Surgical instrumentation: T11-T3 case

T11-T3 second-op model was instrumented from T11 to T3 without correcting spine's curvature, maintaining GAP 11. The second-op model (Fig. 3B) was instrumented with pedicle screws and rods (Fig. 5B), aligned with clinical data in Fig. 2.

ID variation modeling

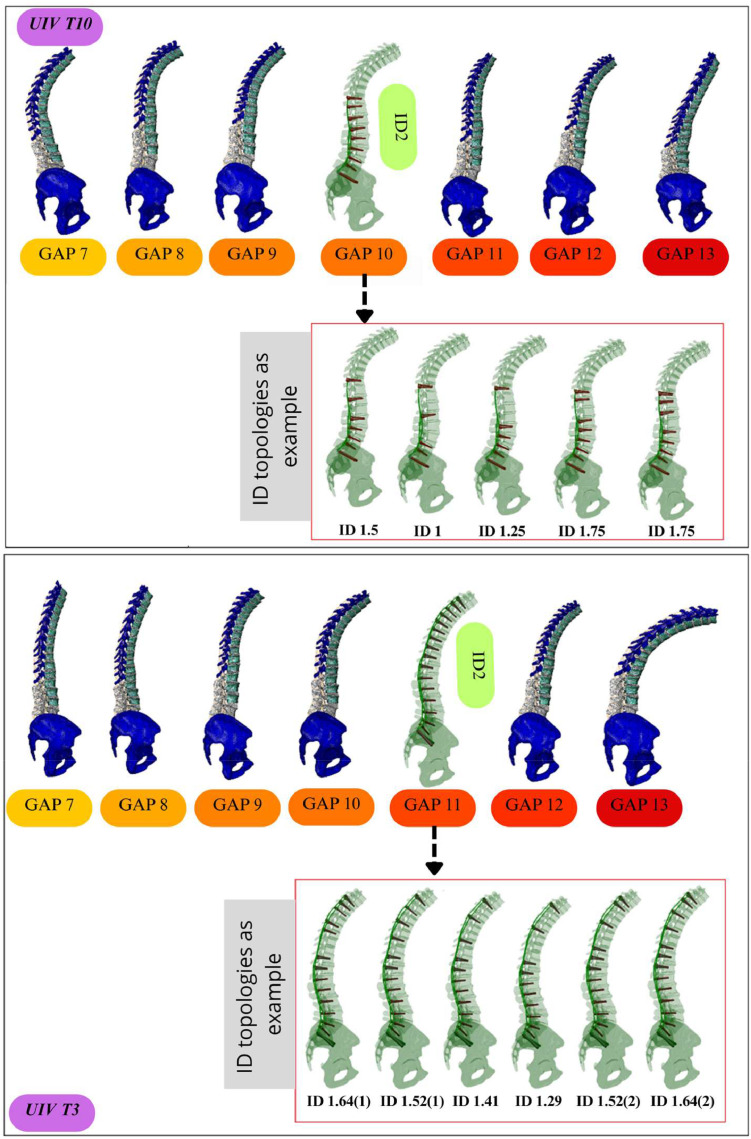
For the 2 clinical cases, ID variations were defined based on retrospective clinical data, indicating that ID or SpL, calculated as total number of screws divided by number of instrumented levels, of less than 1.8 is associated with the reduced PJF risk [12]. Among 57 control cases (no complications) collected from IRCCS [10], 23 cases (40%) had at least 1 level with missing screws (yellow cells in Fig. 6), all of which had ID of less than 1.8 (Fig. 6). For T10-int case, 6 control cases with UIV T10 (Fig. 6) were identified as different screw-missing scenarios from UIV-1 to UIV-4, therefore, 5 virtual ID scenarios, along with the real clinical case, were selected (Fig. 7a). For T11-T3 case, 5 control cases with UIV T3 (Fig. 6) were identified, therefore, 6 virtual ID scenarios along with the real clinical case, were selected (Fig. 7B).

Fig. 6.

23 control cases from IRCCS, Galeazzi-Sant'Ambrogio Hospital, Milan, each employing different ID strategies (green cell means fused level, yellow cell means non-instrumented level) (ID, implant density; UIV, upper instrumented vertebra; GAP, global alignment and proportion).

Fig. 7.

Different instrumentation scenarios for 1st (A), and 2nd (B) cases (ID, implant density; IDR, implant density reduction).

Virtual FE models and systematic variation of surgical and anatomical parameters

A virtual cohort of 91 FE spine models was expanded by systematically varying both surgical and anatomical parameters. This approach was used to (1) assess the biomechanical effects of IDR across a range of alignment severities, (2) identify safe screw configurations, and (3) evaluate interactions between alignment, rod stiffness, and bone quality in terms of soft tissues biomechanical responses. The systematic variations involved:

• •GAP score variation: a wide range of sagittal alignment conditions were considered, by generating models with GAP scores ranging from 7 to 13, spanning from borderline to severe malalignment. These values are clinically relevant, as GAP ≥7 is associated with a high risk of PJF [10].
• •ID: For each GAP level, different screw configurations were tested, with ID ranging from 1.0 to 2.0 SpL, based on retrospective control cases (see Fig. 6). Scenarios included full instrumentation as well as screw-missing patterns at various levels near the UIV (see Fig. 8).
• •UIV: Two UIV were investigated, T10 and T3, to evaluate the effect of construct termination location on biomechanical outcomes.
• •Rod material properties: sensitivity analyses were used with both titanium alloy (Ti6Al4V, Ti) and Cobalt-Chromium (Cr-Co) rods to account for different construct stiffnesses (see section 2.5).
• •Bone quality variation: 3 bone conditions (normal, osteopenia, and osteoporosis) were simulated by adjusting the material properties to generic bone stiffness values associated with each group of bone quality, for all the vertebrae of the models (see section 2.5).

Fig. 8.

Virtual FE models incorporating different ID strategies and GAP scores from 7 to 13 (ID, implant density; FE, finite element; GAP, global alignment and proportion; UIV, upper instrumented vertebra).

These models were selected from a previously validated database of personalised FE meshes in [24] (https://thc.spineview.upf.edu/), thanks to the SSM and mesh morphing techniques. The spine geometries were selected to match the desired spinopelvic parameters and GAP scores, and were modeled without curvature correction or kinematic constraints to represent sub-optimal revision scenarios. For each combination of GAP, ID, and UIV, the corresponding FE model was instrumented with pedicle screws and rods. Among 91 FE models, 42 represented UIV T10 and 49 represented UIV T3. Seven models for both UIV T10 and T3 (GAP 7 to 13) with ID 2 were presented (Fig. 8), along with 2 ID strategy examples for each subset. For UIV T10 with GAP 10, 5 scenarios were tested with varying ID (1.5, 1, 1.25, and 1.75), and for UIV T3 with GAP 11, 6 scenarios were explored. The rest of FE models followed similar ID configurations with variations in GAP. This virtual cohort enabled the trade-off analyses (see section 2.7) that informed surgical recommendations for different patient profiles (as reported in Results, see section 3.4).

Material properties

Implants: The screws and rods were modeled using titanium (Ti) with elastic-plastic material properties defined as: Young’s modulus (E) = 115 GPa, Poisson’s ratio (ν) = 0.3, and yield stress (σ_y ) = 880 MPa [33]. For sensitivity analysis, Cr-Co was also considered for the rods, with following properties: E = 210 GPa, ν = 0.29, and σ_y ​ = 1585 MPa [33].

Bones: Three material properties (normal, osteopenia, and osteoporotic) were used for vertebras (Table 3). These properties were derived from state-of-the-art literatures [[34], [35], [36], [37], [38], [39]]. For osteoporotic pedicle elements, Young’s modulus was assumed to be reduced by 80% compared to normal posterior elements [39]. Osteopenia bone properties were also estimated as mean of normal and osteoporotic values (Table 3). It was also assumed that 14 screw threads (14T) were fully engaged in the bone. Jendoubi et al. [40] reported ultimate SPF (14T) of 2300 N for normal and 900 N for osteoporotic bones. Ultimate SPF for osteopenia was also calculated as the average of SPF for normal and osteoporotic.

Table 3.

Vertebra material properties

Vertebra Sections	E (MPa)	υ	References
Normal bone density
Cortical	12000	0.3	[34]
Trabecular	200	0.315	[35]
Pedicle	3500	0.25	Calculated by [36]
Osteopenia bone density
Cortical	8350	0.3	Assumed as mean properties between normal and osteoporotic bone
Trabecular	173	0.315	Assumed as mean properties between normal and osteoporotic bone
Pedicle	3150	0.25	Assumed as mean properties between normal and osteoporotic bone
Osteoporotic bone density
Cortical	4700	0.3	[37]
Trabecular	146	0.315	[38]
Pedicle	2800	0.25	Assumed by [39]

Soft Tissues: Ligament material properties were modeled as hypo-elastic [41]. IVDs were assumed to be pre-swelled before surgery, with swelling driven by osmotic pressure. The Nucleus Pulposus (NP) contains proteoglycans and water, creating an osmotic gradient that attracts ions and water. Therefore, IVDs were modeled as poroelastic materials, consisting of a solid phase (collagen, elastin, proteoglycans) and a fluid phase (water and solutes) [27]. The Annulus Fibrosus (AF) was modeled using an anisotropic hyperelastic formulation, applying the Holzapfel-Gasser-Ogden strain energy potential (Eq. 2, [42]) to account for the AF’s fiber reinforcement along preferential directions.

$$\begin{array}{c}U=C_{10}\left({\overline{I}}_1-3\right)+\frac{1}{D}\left(\frac{J_{el}^2-1}{2}-\ln J_{el}\right)+\frac{K_1}{2K_2}\sum _{\alpha =1}^N\left(\exp \left[K_2{{\overline{E}}_{\alpha }}^2\right]-1\right)\\ {\overline{E}}_{\alpha }\stackrel{\text{def}}{=}k\left({\overline{I}}_1-3\right)+(1-3k)\left({\overline{I}}_{4\left(\alpha \alpha \right)}-1\right)\end{array}$$ (2)

where K₁ is fiber stiffness, K₂ is fiber nonlinearity, k is fiber dispersion, C₁₀ is constant related to the stiffness of the matrix, N is number of families of fibers and D is incompressibility modulus. For AF, 2 families of fibers were oriented with angle of $\pm 30$° with respect to the local horizontal plane. The values in Eq. 2, were found in the literature as: K₁ = 2.02 MPa, K₂ = 86.53, k = 0.113, C₁₀ = 0.0154 MPa and D = 0.306 1/MPa [27].

Loading conditions

Body mass (BM) distributions were translated into punctual static loads, as detailed in [43]. Briefly, these loads were applied along an eccentric path passing through the center of mass at each vertebral level, positioned at an effective distance (d_eff) from the Vertebral Center (VC) [10,43]. The total force (F) at each vertebral level was calculated as the sum of upper body loads, and d_eff was determined using the Huygens-Steiner theorem ([10,43], Eq. 3). To calculate upper body load at UIV+1, a Segmental Body Mass (SBM_i) was introduced based on fixed percentages of total BM assigned to each vertebral level [44,45].

$$d_{eff}={\left(\frac{I{z}_{eff}}{{\sum }_{i=1}^{Upper}SB{M}_i}\right)}^{-\frac{1}{2}}$$ (3)

where I_zeff was effective moment of inertia at each vertebra level [10,43]. BM loads were incorporated into the FE simulation steps for both T10-int and T11-T3 cases (Table 4). For both the clinical case ID variations (see section 2.3.3) and virtual FE models (see section 2.4), a consistent BM of 70.8 kg [43] was applied as eccentric load to ensure uniform loading conditions and enable meaningful comparative analysis across all models.

Table 4.

BM loads applied along the eccentric path for the 1st and 2nd cases

Vertebrae Level	BM loads (N)
	T10-in	T11-T3
T1	14.05	17.10
T2	15.75	18.20
T3	16.81	19.58
T4	17.80	20.88
T5	18.83	22.22
T6	19.86	23.57
T7	20.95	24.99
T8	22.11	26.51
T9	23.33	28.10
T10	24.87	30.12
T11	26.48	32.21
T12	28.41	34.73
L1	30.24	37.12
L2	32.07	39.52
L3	33.90	41.91
L4	35.89	44.51
L5	37.92	47.15

BM, body mass.

Surgery-adapted FE simulation workflow

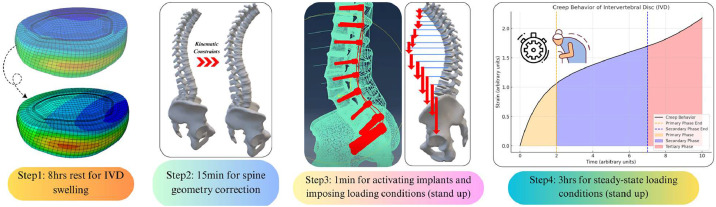
FE simulation workflow was adapted in the following steps to mimic conditions observed in the spine surgery (Fig. 9).

• 1-Step 1: Pre-swelling of IVDs: For T10-int (see sections 2.2 and 2.3.1), T11-T3 (see sections 2.2 and 2.3.2), clinical case ID variations (see section 2.3.3), and virtual FE models (see sections 2.4), IVDs were pre-swelled over 8 hours without external loads applied. This step pressurized the water content in NP and pretensioned AF fibers, as governed by osmo-poroelastic constitutive model [46].
• 2-Step 2: Spine Curvature Correction: For T10-int surgery, Capsular Ligaments (CLs) were de-activated using "Model Change" in Abaqus (SIMULIA, Dassault Industries), and kinematic constraints (see section 2.3.1) were applied to mimic the curvature correction, achieving 1st-op geometrical parameters (Fig. 1). Spine curvature was corrected over 15 minutes, aligning with clinical process at Hospital del Mar, Barcelona. No curvature correction was applied to T11-T3 (see section 2.3.2), clinical case ID variations (see section 2.3.3), and virtual FE models (see sections 2.4).
• 3-Step 3: Instrumentations and Loading Conditions: Screws and rods were activated using the "Model Change" for T10-int (see section 2.3.1), T11-T3 (see section 2.3.2), clinical case ID variations (see section 2.3.3), and virtual FE models (see section 2.4). Contact models between screws and vertebras were also activated immediately after implant placement. BM loads were applied (see section 2.6) over 1 minute to ensure numerical stability and proper convergence of poromechanical solver in IVDs.
• 4-Step 4: Steady-State Analysis: Further 3 hours simulations allowed IVD internal loads to reach a steady-state. This step, representing the secondary creep behavior of IVD, was characterized by a stabilized deformation rate where a balance was achieved between the applied load and the viscoelastic resistance of IVD.

Fig. 9.

Surgery-adapted FE simulation workflow (FE, finite element).

A total of 104 (2 clinical cases + 5 case-derived ID variations for T10-int + 6 case-derived ID variations for T11-T3 + 91 virtual) FE simulations were performed (Figures 7A, B, and 8). Following biomechanical parameters were assessed:

• •IVD fibers Maximum Principal Strain (MPSN)
• •SPF
• •Maximum Principal Stress (MPSS) in rods

Maximum Principal Strain or MPSN and Maximum Principal Stress or MPSS represent the largest normal strain and stress, respectively, experienced by a material at a given point, each acting along a direction where the corresponding shear component, strain or stress, is zero. To reduce discontinuity between IVDs and vertebras, the average MPSN was calculated in AF elements, excluding those shared with vertebral elements at top and bottom. For surgery planning, rod property was selected initially for a given ID scenario. Trade-off analyses between key biomechanical parameters were then conducted across different bone qualities. If all values were below the control cut-offs for a specific scenario and bone quality, the corresponding ID was recommended for the surgery. Additional analyses were conducted to systematically assess variations in surgical and anatomical parameters (see section 2.4).Results

Biomechanical descriptors for T10-int case

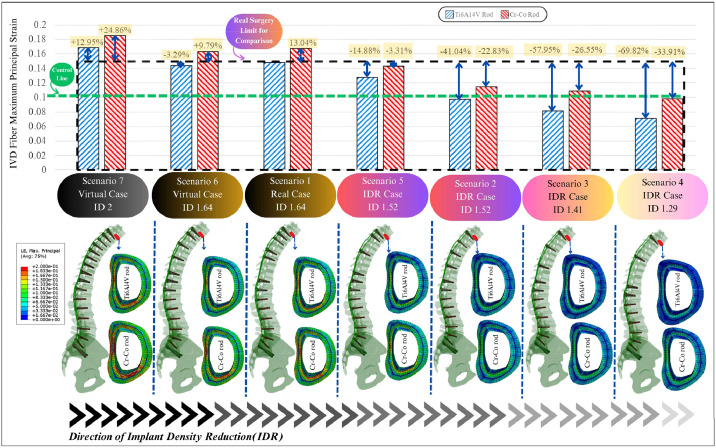
The average MPSN in the AF fibers at the T10/T9 IVD was compared against the established control cut-off of 0.1056 [42] (Fig. 10). Across different IDR scenarios using Ti rods, strain reductions ranged from 5.5% to 61.5% relative to the real surgical case (scenario 1). Scenarios 3 and 4 achieved the greatest reductions and were the only ones to bring fiber strain below the control threshold. Scenarios 1, 2, 5, and 6 still exceeded the threshold, indicating continued risk. Replacing Ti rods with stiffer Cr-Co rods led to an average 20.3% increase in fiber strain across all configurations. Notably, scenario 4 remained below the cut-off even with Cr-Co rods, although this material change pushed scenario 3 above the threshold, highlighting the sensitivity of outcomes to rod stiffness.

Fig. 10.

IVD fiber maximum principal strain at T10/T9 for 6 scenarios (T10-int case) (IVD, intervertebral disc; ID, implant density).

SPFs at the UIV T10 were also analyzed under different conditions (Fig. 11). Compared to the baseline case (scenario 1, Ti rod), IDR scenarios increased SPF by up to 101% in normal bone. For osteopenia and osteoporotic bone models, SPFs rose by approximately 30% and 55%, respectively. Safe SPFs were defined as values below the cut-offs for each bone quality, as detailed in [40]. Only scenarios 3 and 4 (Ti rods) remained below the failure cut-offs for osteopenia; for osteoporosis, they exceeded safe thresholds. In scenario 2, while SPF for osteoporotic bone with Ti rods remained below the cut-off, this scenario had high risk of overstretching IVD fibers (Fig. 10). Switching to Cr-Co rods further elevated SPFs by an additional 20% to 30%, depending on bone quality. The most notable increase occurred in scenario 4, with SPF rising by up to 46% in osteoporotic bone. Although fiber strains were retained below the cut-offs with Cr-Co rods in scenario 4, calculated SPF exceeded the cut-offs for osteopenia and osteoporotic bones. Scenario 1 exhibited the lowest increase rates (+11%, +15%, and +20% for normal, osteopenia, and osteoporotic bones, respectively).

Fig. 11.

Screw pull-out force (N) at T10 for 6 scenarios (T10-int case) (Ti, Ti6Al4V; ID, implant density; CF, contact force).

None of the calculated rod MPSS exceeded the yield stress of either Ti or Cr-Co materials.

Biomechanical descriptors for T11-T3 case

The average and continuous AF fiber strain (MPSN) at the T3/T2 IVD was compared to the same control cut-off (0.1056 [42]) (Fig. 12). Among the IDR scenarios using Ti rods, fiber strain was reduced by 41% in scenario 2, 58% in scenario 3, and 70% in scenario 4. These scenarios successfully lowered fiber strain below the cut-off, indicating reduced PJF risk. In contrast, the original surgical scenario (scenario 1) and scenarios 6 and 7 still exceeded the cut-off, reflecting higher risk. When switching to Cr-Co rods, fiber strain increased by an average of 19.3% across all scenarios. Scenario 4 again showed the highest increase (+36%), though it still remained under the threshold. Scenario 7 had the smallest increase (+9%) but remained above the cut-off. Only scenario 4 with Cr-Co rods could keep the fiber strain below the critical limit.

Fig. 12.

IVD fiber maximum principal fiber strain at T3/T2 for 7 scenarios (T11-T3 case) (IVD, intervertebral disc; ID, implant density).

SPF at UIV T3 was also evaluated under varying conditions (Fig. 13). Compared to the original surgery (scenario 1, Ti rod), from scenarios 2 to 6, SPF was increased ranging from 4% to 142% in normal bone. For osteopenia and osteoporotic bone, SPF increased by 27% and 56%, respectively, over normal bone levels. Although scenarios 3 and 4 (Ti rods) showed favorable strain reductions, they exceeded SPF cut-offs in osteoporotic bone. In contrast, scenario 2 (Ti rod) maintained SPF within safe limits across all bone types, but failed to control fiber strain adequately. Switching from Ti to Cr-Co rods increased SPF by averages of 18.7%, 28%, and 23% for normal, osteopenia, and osteoporotic bones, respectively. Scenario 4 showed the highest SPF rise (+46%) with Cr-Co in osteoporotic bone. While scenario 4 with Cr-Co rods kept fiber strain below threshold, it only provided safe SPF values in normal bone, not in weaker bone conditions.

Fig. 13.

Screw pull-out force (N) at T3 for 7 scenarios (T11-T3 case) (Ti, Ti6Al4V; ID, implant density; CF, contact force).

None of the calculated rod MPSS exceeded the yield stress of either Ti or Cr-Co materials.

Biomechanical trade-off analyses and surgery planning for T10-in & T11-T3 cases

Regarding the results in sections 3.1 and 3.2, a color-coded map (red: failure or high-risk; green: safe or low-risk) of PJF risk associated with fiber MPSN at UIV/UIV+1 and SPF at UIV, was shown in Fig. 14 for various bone and rod properties. Results showed that SPFs did not pose a risk for T10-int or T11-T3 cases when the bone was non-osteoporotic, and the rod was Ti. In contrast, Cr-Co rods might represent PJF risk in scenarios 4, when the bone was either osteoporotic or osteopenia. Moreover, for fiber strains at T10-in case, Ti rods would allow scenarios 3 and 4 to be safe in a non-osteoporotic patient. However, no safe scenario could be found is T10-in case with osteoporosis. When rod was Cr-Co, only scenario 4 would be safe if T10-int case had normal bone. Furthermore, for fiber strains in T11-T3 case with Ti rods, IDR scenario 1 would be fully safe, while the safety of scenarios 3 and 4 would be limited for non-osteoporotic bones. Moreover, when rod was Cr-Co, only IDR scenario 4 would be safe, only if T11-T3 case had normal bone. These results highlight the need to tailor IDR strategies based on patient-specific and surgery planning factors, especially bone quality and rod stiffness. While Ti rods generally offered safer configurations, Cr-Co rods may only be appropriate in limited, well-defined scenarios.

Fig. 14.

Trade-off analyses between IVD fiber strain, and screw pull-out force (green means allowed (safe, low-risk), red means rejected (failure, high risk)) (IVD, intervertebral disc; ID, implant density).

Systematic assessment of surgical and anatomical parameter variations

The analysis revealed that patients with GAP scores ≤9 and normal or osteopenia bone could accommodate a wider range of implant configurations with acceptable biomechanical risk. In contrast, GAP scores ≥10, particularly in combination with osteoporotic bone, significantly limited safe surgical options due to reduced construct stability. Moreover, material choice had a notable impact:

• •Ti rods demonstrated better biomechanical adaptability in high GAP (≥10), helping to reduce stress on both instrumentation and surrounding bone structures.
• •Cr-Co rods, due to their higher stiffness, tended to concentrate stress, resulting in increased SPF and excessive annulus fiber MPSN risks.

At the most severe alignment conditions, GAP ≥12 presented the greatest challenge:

• •For UIV at T10, no IDR configuration was deemed safe at GAP 12 or 13, and Cr-Co rods failed to mitigate PJF risk for GAP 11.
• •For UIV at T3, GAP 13 also lacked safe options, however, GAP 12 could be managed safely with Ti rods, under careful planning.

These findings emphasize the importance of individualizing surgical planning based on the interplay between alignment severity, bone quality, and implant stiffness.

Discussion

Spine surgery IDR strategies aim to balance mechanical stability while reducing rigidity to minimize local stress concentrations [47]. Although IDR is well explored in scoliosis surgeries [[48], [49], [50], [51], [52], [53], [54], [55], [56], [57], [58]], its role in sagittal alignment correction remains unclear. Behrbalk et al. [59] linked lower screw density to fewer complications in Scheuermann Kyphosis surgeries, while McClendon et al. [60] observed that higher implant density was associated with an increased risk of PJK. Charles et al. also found that high screw density (ID 1.5–2) reduced screw loosening risk but increased the odds of pseudarthrosis by 4.3 times [61]. Successful spinal fusion might require balanced mechanical stability and micromotions to promote endochondral ossification, in the regions to be fused [62]. As such, overly rigid constructs might not be optimal. In contrast, surgeries employing lower screw densities were needed to obtain an optimal correction and avoid pseudarthrosis [48,[63], [64], [65]]. In turn, Chanbour et al. [66], and Barton et al. [67] found no significant link between screw density and pseudarthrosis, though, most of the patients suffering from pseudarthrosis had missing screws at or within 2 levels [66]. Chanbour et al. also showed there was no association between screw density and PJK [66]. However, Durand et al. [12] observed that patients with SpL ≤1.8 had low PJF risks. This apparent lack of consensus about the relationship between SpL and risk of pseudarthrosis might be explained by the fact that PJF is a local event at the proximal end of the instrumentation, whereas SpL is a global metric over the entire spine. Hence, a specific SpL values can involve different screw distributions, leading to different potential risks of pseudarthrosis. This study bridged the gaps between global metrics and local events, using FE simulations to assess sub-optimal screw patterns, emphasizing the importance of localized metrics over global averages for personalised surgical planning to limit PJF risks.

Park et al. revealed stress increases in IVDs and adjacent vertebras [21]. Jang et al. also found that pre-operative unhealthy discs were more likely to collapse early due to their reduced capacity to absorb axial loads [68]. AF anisotropic fiber reinforcement enabled it to resist complex loading patterns and prevent excessive motion [69,70]. In this study, fiber strain was identified as 1 of the key biomechanical parameters for assessing PJF risk, in accordance with findings by Hashimoto et al., who linked excessive strain in adjacent spinal segments to IVD degeneration and PJF [71]. Later, fiber strain at UIV/UIV+1 was compared with a control strain of 0.1056, cut-off for AF lamellar damage [42].

The effects of IDR on fiber strain and SPF were evaluated in T10-int and T11-T3 clinical cases, in which in silico models were included, validated in [24], and their credibility was assessed using ASME V&V40 standard [25]. Reducing SpL/ID from 1.66 to 1 in the T10-int case lowered fiber strain by 47.76%, aligning with findings at [47] which IDR reduced construct rigidity and stress at fused-mobile segment interfaces. Across scenarios, fiber strain reductions ranged from 5.52% to 61.47%. However, SPF increased by 7% to 101% for normal bones, consistent with Doodkorte et al. [11], who reported increased SPF with IDR. Ti rods raised SPF by 30%–55% in osteopenia and osteoporotic bones compared to normal bone (in accordance with Jendoubi et al. [40]), while Cr-Co rods further increased SPF by 20%–30% across bone conditions, corroborating Han et al.’s [72] findings on Cr-Co rods. Rod failure risks were assessed, showing no immediate risk of breakage; however, further fatigue analyses are required to determine rod fracture cycles.

For the T11-T3 case, IDR reduced fiber strain by 41%–70% (Ti rod) but increased SPF (Ti rod) by 41%–142% for normal bone, with greater increases for osteopenia (27%) and osteoporotic bones (56%). Cr-Co rods raised SPF by 18.7%–28% across bone conditions. While IDR enhances flexibility and reduces strain, it elevates SPF, especially with Cr-Co rods and in weaker bones, highlighting trade-offs in biomechanical outcomes.

FE simulations suggested that for patients with severe GAP 10 and UIV at T10, IDR scenarios involving 2- or 3-level screw reductions (scenarios 3 and 4, T10-int case) with Ti rods might prevent PJF in normal or osteopenia bone. For osteoporotic bone, no IDR scenario was safe, hence, cement-augmented screws are recommended. In the current model, the bone-screw interface was idealized using the tight surface-to-surface contact to represent full contact without micro-motion. While this approach allows isolation of the effects of implant configuration, it does not account for interface variations such as screw loosening or cement augmentation. Future studies should incorporate more detailed bone-screw interface models, such as contact-based or cohesive zone methods, to more accurately simulate augmented fixation strategies and evaluate the biomechanical benefits of cementation, particularly in osteoporotic bone. Cr-Co rods might only be suitable for scenario 4 (T10-int case) in normal bone due to the increased pull-out risk in weaker bones, aligning with Han et al. [72]. For patient with severe GAP 11 and PJF at T11, extending fixation to T3 with 1-level IDR (scenario 2, T11-T3 case) and Ti rods might avoid further PJF. For revision surgeries, IDR scenarios involving 2- or 3-level reductions (scenarios 3 and 4, T11-T3 case) with Ti rods might avoid 2nd PJF for normal or osteopenia bone but not for osteoporotic cases. Cr-Co rods might only be used in scenario 4 (T11-T3 case) for patients with normal bone.

FE virtual case studies revealed that the effectiveness of IDR strategies was highly dependent on GAP scores. Higher GAP reduced IDR effectiveness, with failure to prevent PJF observed at GAP 13 for both UIV T3 and T10, regardless of rod type. At GAP 12 with UIV T3, Ti rods were effective, while Cr-Co rods were not. In contrast, GAP 7 allowed for broader safe IDR scenarios. In patients with high GAP scores (≥7) and compromised bone quality (osteopenia or osteoporosis), safe surgical plans were still achievable using IDR scenarios of 1.5 or 1.75, particularly with Ti rods and removal of the T12 or L1 screw. This approach reduced predicted mechanical failure risk by 15–22% compared to non-optimized configurations. For patients with lower GAP scores (≤10) and normal or osteopenia bone, IDR values as low as 1.25, especially with Cr-Co rods, were safe and associated with a 10–15% reduction in expected revision rates. In elderly patients or those with severe osteoporosis, configurations beyond GAP 11 should be avoided, as no safe ID combinations were identified. These findings highlight the need to stratify surgical plans by alignment score, bone quality, and instrumentation strategy to enable personalised and biomechanically informed care. These findings (Table 5) were also aligned with a retrospective cohort (Fig. 6), including a case with UIV T10, GAP 8, and ID 1.5 that remained stable for 22 months, confirming PJF prevention regardless of bone or rod properties. A larger clinical cohort is needed for broader validation and to establish statistical correlations in future works.

Table 5.

Allowed (safe, low-risk) surgery plans in different GAP scores

This study was built upon and extended previous studies addressing PJF and IDR by offering a comprehensive computational biomechanical framework that incorporated worse-case loading conditions, as well as detailed patient-personalised modeling. Earlier investigations by Lopez Poncelas et al. emphasized the role of lordosis correction location [73] and proximal implant configurations [74] in modulating PJF risks. While these studies provided key clinical insights, they relied primarily on clinical correlations and limited biomechanical validation. Further biomechanical strategies, such as the use of polyethylene tethers [75] and tethered pedicle screw constructs [76], have shown promise in mitigating PJK, a precursor to PJF. Within this context, IDR emerged as a distinct biomechanical strategy compared to other interventions like sublaminar tethers. IDR involved selectively reducing the number of fixation points, such as pedicle screws, at specific spinal levels to create a smoother transition in stiffness between instrumented and adjacent non-instrumented segments. In contrast, sublaminar tethers reduced PJF risk by applying dynamic posterior tension at the proximal junction, thereby controlling kyphosis progression while maintaining segmental mobility. Other complementary approaches had also gained traction, including biologic augmentation (e.g., transpedicular rhBMP-2 with β-tricalcium phosphate [77]), optimized fixation techniques [78], and pharmacologic treatments such as teriparatide for osteoporosis [79]. Moreover, preoperative assessments of frailty and sarcopenia [80] were increasingly recognized as critical elements of surgical planning. Despite these advances, key biomechanical aspects remain underexplored in computational models, such as rib cage contributions, dynamic loading conditions, and the behavior of cement-augmented screws [43,81]. The current study utilized a unique computational framework to address these gaps by integrating pathology-specific biomechanical insights into a high-fidelity simulation environment, enabling a more realistic evaluation of construct behavior under PJF conditions. Moreover, with regards to cement-augmented screws, IDR strategies were different in both purpose and mechanism. Cement-augmented screws were primarily used to enhance fixation strength, particularly in osteoporotic bone, to reduce the risk of screw pull-out and vertebral fractures. In contrast, IDR aimed to decrease construct stiffness, promoting smoother stress transitions across spinal segments. As such, IDR represented a distinct approach within the broader set of techniques for preventing PJF, with its use tailored to patient-specific factors such as bone quality, sagittal alignment, and overall construct design.

One of the limitations in this study was focusing solely on anterior body weight distribution, representing a worst-case scenario in a PJF case-control study [10]. Another limitation was absence of basic data like weight or BMI, leading to use of correlation models (O'Neill [82] and Bozeman [83]) for BMI estimation (detailed in [10]). Limited computational resources restricted the number of FE simulations. Patient-specific bone properties were unavailable in EOS images, so sensitivity analyses were used for SPF assessment across 3 bone properties. As another limitation, this study relied on static FE simulations, which do not capture time-dependent biomechanical phenomena, such as viscoelastic creep, muscle activation, neuromuscular feedback, or dynamic activities like walking or transitioning postures. Additionally, the biomechanical risk indicators used, such as annulus fiber strain and screw pull-out force, were derived from validated in-vitro and computational studies. Whereas these thresholds provide valuable insights into the mechanical conditions that may predispose to PJF, they do not account for patient-specific biological or behavioral factors. Possible screw misalignments were not considered, either. Therefore, even though reductions in these parameters suggest a lower mechanical risk in terms of clinical PJF, proper contextualization and contrasting of our results remain necessary through further supporting clinical data and outcome. Importantly, the mechanical outcomes hereby targeted shall be considered as short-term outcomes, as the models and simulations do not capture tissue growth and remodeling and cannot, therefore predict complications such as pseudarthrosis. To strengthen the clinical relevance of the current findings, future studies should include retrospective or prospective patient cohorts, to correlate robustly virtual risk predictions with real-world postoperative outcomes. Specifically, follow-up studies combined with the present modeling and simulation approach, should confirm whether elevated annulus fiber strain, increased screw pull-out forces, or specific implant configurations represented by the models, correlate with actual incidences of PJF. Establishing such correlations would be a critical step towards patient-specific surgical planning. Additional research should also explore the impact of obesity, weight loss, and UIV selection on ID and alignment. Methodologically, future work would benefit from incorporating uncertainty quantification, dynamic simulations, musculoskeletal-FE coupling, feedback control mechanisms, and patient-specific modeling using larger and multicenter datasets. Furthermore, integrating assessments of frailty, sarcopenia, and complications such as pseudarthrosis, along with leveraging machine learning or multi-physics approaches, will further refine and validate the proposed IDR strategies.

Conclusion

This research highlights the clinical significance of personalised FE simulations and virtual surgery planning in addressing challenges related to sub-optimal spine sagittal correction. The findings demonstrate that IDR can effectively reduce the risk of PJF in severe GAP by considering factors such as bone properties, rod materials, and screw distribution. By alleviating the load on adjacent IVDs, IDR lowers PJF risk, and trade-off analyses help identify optimal screw density configurations. Clinically, IDR can minimize the need for revision surgeries, reduce hospital stays, blood loss, mortality, and lower overall surgery costs. Additionally, post-operative GAP estimation can guide safe configuration choices, improving patient outcomes.

Funding disclosures

This study was supported by DTIC-UPF, Hospital del Mar - IMIM, and IRCCS Galeazzi-Sant'Ambrogio Hospital, as well as by the Spanish Government (CEX2021-001195-M) and a mobility grant from European Society of Biomechanics (ESB). This work also received funds from the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. This work was supported by the European Research Council (ERC) (grant agreement: ERC-2021-CoG-O-Health-101044828).

Declaration of competing interest

One or more of the authors declare financial or professional relationships on ICMJE-NASSJ disclosure forms.