Reproductive skew in the polygynandrous acorn woodpecker

Abstract

Reproductive skew models, which focus on the degree to which reproduction is shared equally (low skew) or monopolized by a single individual (high skew) within groups, have been heralded as providing a general unifying framework for understanding the factors determining social evolution. Here, we test the ability of optimal skew, or “transactional,” models, which predict the level of skew necessary to promote stable associations of dominants and subordinates, rather than independent breeding, to predict reproductive partitioning in the acorn woodpecker (Melanerpes formicivorus). This species provides a key test case because only a few vertebrates exhibit polygynandry (multiple breeders of both sexes within a group). Contrary to the predictions of the models, joint-nesting females share reproduction more equitably than expected, apparently because egg destruction and the inability of females to defend their eggs from cobreeders eliminate any possibility for one female to control reproduction. For males, however, reproductive skew is high, with the most successful male siring over three times as many young as the next most successful male. Although this result is consistent with optimal skew models, other aspects of male behavior are not; in particular, the reproductively most successful male frequently switches between nests produced by the same set of cobreeders, and we were unable to detect any phenotypic correlate of success. These results are consistent with an alternative null model in which cobreeder males have equal chance of paternity, but paternity of offspring within broods is nonindependent as a consequence of female, rather than male, control.

Optimal skew models focusing on the degree to which individuals monopolize reproduction within social groups are appealing to behavioral ecologists because they tie together individual and ecological factors into a unifying framework for predicting group stability and the extent of reproductive sharing between dominants and subordinates. Such models optimize fitness payoffs to group members in relation to the productivity advantages of association, the prospects of independent breeding by subordinates, and the relatedness of dominants to subordinates. Early transactional or “concessions” models (1) assumed that dominants have complete control over subordinates and concede only the amount of reproduction necessary to induce subordinates to remain in the group (2–6). More recent “restraint” models relax the assumption of complete control and only assume that dominants are capable of evicting subordinates or preventing them from joining their group (7). According to this latter type of transactional model, subordinate reproduction is restrained only by the threat of eviction by the dominant. An alternative to transactional models are “compromise” models in which reproductive skew is determined by intrasexual contests among group members rather than factors affecting group stability (8).

Proponents of transactional models based on concessions have found support (9, 10) and generated a flurry of theoretical interest (7, 8, 11–14). However, considerable controversy remains as to whether the assumptions of these models are adequately met (1, 7, 15, 16). Furthermore, no empirical study thus far has taken into account the possibility that observed values of skew might be explained by null models assuming random mating patterns (17, 18). Such models are especially important in vertebrate societies where average reproductive output is low and parentage of individual offspring within broods or clutches may not be independent of each other.

Acorn woodpeckers (Melanerpes formicivorus) are one of the few vertebrate societies that contain multiple cobreeder males and females (polygynandry), making them a model case for examining alternative models of reproductive skew (9, 18). Social groups can contain coalitions of up to seven cobreeder males vying for mating with up to three joint-nesting females, but groups with more than three males or two females are uncommon. Joint-nesting females lay their eggs communally in the same nest, and all group members participate in caring for young and territorial defense. Both cobreeder males and joint-nesting females are usually close relatives, but breeders of the opposite sex are unrelated and incest is rare (19, 20). Groups can also contain up to 10 nonreproductive adult helpers from previous nesting attempts. Helpers attain breeding status either by dispersing to a new territory or by inheriting their natal territory after the death and replacement (by unrelated immigrants) of all breeders of the opposite sex.

A quantitative test of transactional models depends on estimates of the relatedness between dominants and subordinates, the fitness advantages of association, and the degree to which ecological constraints constrain dispersal and independent reproduction. Because few of these values are generally known, prior tests have focused either on qualitative examination of assumptions (15) or on equally qualitative comparisons between the sexes or between populations that are known to have different values for one or more of these parameters (10). In particular, concessions theory predicts that with increasing levels of ecological constraints (or other relative benefits of group living caused by higher relatedness of group members or greater fitness advantages of groups), subordinates will require less incentive to remain in the group and will thus obtain a smaller share of reproduction. Transactional theories based on restraints predict the opposite, because as independent reproduction becomes harder, the subordinate will be able to garner a larger proportion of the group's reproduction before it will pay the dominant to force eviction.

In acorn woodpeckers, ecological constraints on independent dispersal and breeding are considerable for both sexes, as indicated by a high proportion (33.6% of females, 40.0% of males; ref. 21) that delay dispersal and remain on their natal territory as helpers for at least 1 year. However, both relatedness among cobreeders and the fitness advantages of group living are greater for males compared with females (Table 1). Ecological constraints are also greater for males compared with females as indicated by the higher fraction that remain as helpers (21) and a lower probability that an adult nonbreeder male will obtain breeding status by dispersing compared with a female (22). Consequently, concessions theory predicts that reproductive skew should be greater among cobreeder males than joint-nesting females, but that it should be considerable for both. Furthermore, because concessions models are predicated on one dominant individual being in control of reproduction, the bird gaining the most parentage should generally be the largest or oldest individual, and is generally expected to be the same individual in successive nests. In acorn woodpeckers, both age and size appear to influence dominance relationships. For example, larger juveniles are dominant over smaller juveniles in aggressive interactions (23) and older helpers are dominant over younger helpers in competition for access to stored acorns when the acorn crop is poor (24).

Table 1.

Variables used in calculating expected values of reproductive skew

Variable	Definition	Values
		Males	Females
n	Life span (years)	15	15
d	Probability of successful dispersal	0–1	0–1
r	Coefficient of relatedness between breeders	0.46	0.41
lc	Annual survivorship of a cobreeder	0.73	0.69
ls	Annual survivorship of a breeder nesting singly	0.72	0.72
lh	Annual survivorship of a potential breeder that forgoes breeding and acts as a helper	0.75	0.75
mc	Annual fecundity of a group with cobreeders	2.79	3.04
ms	Annual fecundity of a group with a single breeder	2.41	2.50

Study Site and Methods

Demography of Males and Females.

To calculate patterns of reproductive partitioning predicted by optimal skew theory, demographic data are needed on mean relatedness of cobreeders, the relative fecundity and survivorship of birds breeding by themselves and in coalitions, and the ecological constraints to independent reproduction (8). We estimated these parameters from 28 years of continuous study (1972 to 1999) on a marked population at Hastings Reservation in Monterey County, CA (19–27), during which time we followed the life-histories of over 3,000 color-banded individuals (Table 1).

Mean relatedness based on pedigrees was slightly, but not significantly, higher among pairs of cobreeder males than pairs of joint-nesting females (mean r = 0.46 ± 0. 01 versus 0.41 ± 0.03, Wilcoxon two-sample test, n = 40, 22, z = 1.74, P = 0.08). Reproductive gains caused by the presence of a second breeder were significant but modest for both sexes. Males experienced a 15.8% increase in young fledged per group-year from 2.41 young as a singleton to 2.79 in a cobreeding duo (ANOVA, F _1,622 = 4.4, P < 0.05). Females experienced a 21.6% increase in young fledged per group-year from 2.50 as a singleton to 3.04 in a joint-nesting duo (F _1,740 = 7.6, P < 0.01). Neither of these values are compromised by extra-group parentage, which is rare or nonexistent in this population (20, 28). Despite this slight advantage for females, the benefits of cobreeding are higher for males than for females (see calculation of k below) because joint nesting entails a small but significant 3.7% decrease in annual survival probability for females from 72.1% to 69.4% (logistic regression, χ² = 7.6, n = 785 breeder years, P < 0.001), whereas cobreeding nonsignificantly increases survival by 1.1% for males from 72.2% to 73.0% (logistic regression; males: χ² = 3.1, n = 1171 breeder years, P = 0.08).

In contrast to fecundity and survivorship, ecological constraints on dispersal (d) proved difficult to quantify. The annual probability that an adult nonbreeder will obtain breeding status by dispersing is 27% for males and 50% for females, based on life-time values (22) divided by the mean number of years spent as a helper. For birds with breeding status, d is likely to be related to, but lower than, estimates for nonbreeders, assuming that age confers some advantage in competitive contests for breeding positions. However, because we cannot assume that all breeders are attempting to disperse (they only do so occasionally), it is difficult to quantify how difficult it would be for them to do so. Therefore, we allowed d to vary and determined the range of values that predict group stability for transactional models based on concessions and restraints.

Estimation of Skew Predicted by Transactional Models.

We limited our analyses to associations of two individuals to keep the calculations and predictions tractable (30, 31) and because groups with either cobreeding males or joint-nesting females most commonly involve only two cobreeders (62% and 88% of male and female groups, respectively). Calculations were made using the basic concessions and restraint models summarized by Johnstone (8). Because acorn woodpeckers may live several years, we considered the potential lifetime fitness consequences of different strategies rather than restricting estimates to single year effects. For concessions, the expected minimum share of reproduction that the subordinate will demand to remain the group (the evolutionarily stable level of skew) is given by

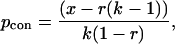1

where x is the expected lifetime reproductive success of a subordinate that attempts to breed independently relative to an established lone breeder, r is the relatedness coefficient, and k is the lifetime productivity advantage of a cobreeding association relative to that of an established lone breeder. For restraints,

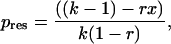2

where p_res is the maximum share of reproduction obtained by the subordinate. To estimate x and k we used the equations of Mumme et al. (28), where the expected lifetime reproductive success of an established lone breeder is

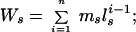3

the expected reproductive success of a subordinate that attempts to breed independently is

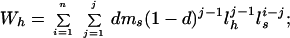4

and the expected lifetime reproductive success for two cobreeders (as indicated by the subscript c2) is

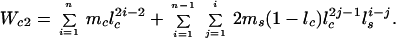5

Eq. 4 considers that the subordinate has a probability of 1 − d of initially being unable to secure his or her own territory, and thus will have to spend a variable number of years (j − 1) as a nonbreeding helper with annual survivorship of l_h. In Eq. 5, the first term is the lifetime reproductive success of the two cobreeders while both are still living and breeding together, whereas the second term considers the reproductive success of the surviving breeder nesting singly after one or the other of the birds dies after j years of cobreeding. Finally, we estimated the productivity of cobreeding relative to a single individual that has secured a breeding position as

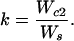Thus, by using the demographic values summarized in Table 1, k = 1.529 for males (that is, a cobreeder male produces an estimated 52.9% more offspring than a male breeding singly), whereas k = 1.472 for females.

Similarly, the lifetime reproductive success of a subordinate that attempts to disperse to breed independently relative to a single individual that has secured a breeding position is

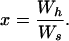7

The value of W_s and hence x is a function of d (the probability of successful dispersal by a cobreeder) which, as discussed above, we allowed to vary between 0 and 1.

Simulations of Expected Skew.

The standard null model involved trials in which we assumed that parentage of each nestling was independent of all other nestlings within broods. We then randomly assigned paternity/maternity to each offspring produced by a cobreeder/joint-nesting duo (combining all nests produced by the same set of cobreeders) and calculated the resulting average proportion of young parented by the individual receiving the smaller proportion of offspring (the presumed subordinate). Values were based on 5,000 trials. This method amounts to flipping a coin to determine parentage for each nestling and yields the expected proportion of offspring parented by the presumed subordinate (p_s) given equal, random probability of parentage by cobreeders. Simulated values were tested against the observed values by determining the proportion of trials yielding p_s values more or less extreme than those observed.

For the alternative null models assuming nonindependence of paternity within clutches, paternity of some or all entire broods was assigned randomly. In contrast to the first model, this method amounts to flipping a coin only once to determine paternity of entire broods. Two versions of this model were considered. In the first, all broods were assigned to one or the other cobreeder at random. In the second version, the probability that an entire clutch was assigned to a single male versus determined independently was set equal to the observed frequency of nests whose offspring were parented by only one of two cobreeders. In the remaining broods, paternity of each offspring was determined independently. As with the standard null model, multiple nests produced by the same set of cobreeders were combined and the overall proportion of offspring parented by the presumed subordinate (again based on the individual receiving the smaller proportion of offspring) was calculated.

Results

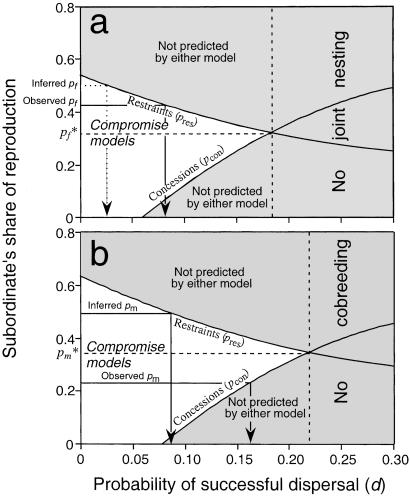
Reproductive skew predicted by both concessions and restraints models for male and female acorn woodpeckers are summarized in Fig. 1. The x coordinates of the intersections of the lines generated by the two models indicate the maximum annual probability of successful dispersal that results in a stable association of two breeders (22% for males and 18% for females). Annual probabilities of successful dispersal above these values produce a population that consists only of independently breeding individuals because the maximum amount of reproduction that a dominant will tolerate is greater than the minimum amount a subordinate requires to remain in the group. The y coordinates (p_f and p_f) of the intersections of the lines determines the maximum level of subordinate reproduction expected based on concessions (0.35 for males and 0.32 for females) or, conversely, the minimum amount of subordinate reproduction predicted based on restraints. Values between the lines and demarcated by the white triangular area of the graphs represent values consistent with mixed or compromise models (8).

Figure 1.

The expected subordinate's share of reproduction in relation to ecological constraints (measured as the probability of successful dispersal by a cobreeder) for females (a) and males (b). The two curved lines in each panel represent the expected subordinate's share of reproduction according to transactional models based on concessions (2–4, 8) (p_con) and restraints (7, 8, 14) (p_res). p_con assumes dominants are in complete control and offer the minimal necessary incentive needed to induce subordinate to remain in the group, whereas p_res assumes that subordinates obtain the maximum amount of reproduction they can without being evicted by the dominant. Thus, the white triangular areas bounded by these lines represent the potential range of values for p_sub, the subordinate's share of reproduction, consistent with transactional models. Values for p_sub within this area (but not on the lines themselves) are those predicted by mixed or “compromise” skew models (8). Values above and below this area are not predicted by either concessions or restraints models. Cobreeding/joint nesting is not predicted to occur at all in the area to the right of the dotted vertical line, defined by the probability of successful dispersal where p_con and p_sub cross. In this area, where cobreeding is predicted to be unstable, constraints are so low (i.e., the probability of successful dispersal is high) that subordinates will always do better by dispersing and breeding on their own. The horizontal broken lines determine p*_f and p*_m, the maximum level of subordinate reproduction possible for females and males, respectively, based on concessions models and, alternatively, the minimum level of subordinate reproduction possible based on restraints models. The observed level of subordinate reproduction (where subordinates are defined as the individual achieving the lower proportion of parentage) are indicated the “observed p_f ” and “observed p_m ” lines. Lines dropping vertically to the x axis (marked by the arrows) from where these values meet the p_res (females) or p_con (males) curves indicate the maximum probability of successful dispersal (d) consistent with cobreeding given our demographic and parentage estimates. Finally, the dotted lines indicate the level of subordinate reproduction implied by the basic (for females) and alternative (for males) simulation models (“inferred p_f ” and “inferred p_m ” = 0.5). These lines are also accompanied by a vertical dotted line dropping to the x axis indicating the maximum probability of successful dispersal consistent with this level of subordinate reproduction.

How do the predictions of these models compare with the observed values for subordinate reproduction? To control for bias in skew caused by low reproductive output (17), we compared observed values of the subordinate's share of reproduction (p_s) to those obtained from a computer simulation that randomly assigned parentage to the presumed dominant and subordinate with equal probability. As described above, we presumed that dominants were the individuals obtaining the larger share of reproduction in a cobreeder or joint-nesting coalition.

Among broods of joint-nesting females, only 20% of nests (n = 38) produced offspring mothered by a single female, and thus mixed maternity was the rule. On average, subordinate joint-nesting females obtained maternity of 42% of offspring within a nest (observed p_f), which is a higher proportion of reproduction than expected from the simulation in which maternity was assigned independently to each nestling (Table 2). That is, females are egalitarian and share parentage more equally than expected by chance. This observation implies that the expected subordinate's share of reproduction (inferred p_f) is 0.5. Both the observed and the inferred values are greater than p*_f (Fig. 1) and thus greater than any value consistent with the concessions model. It is potentially consistent with the restraints model (or compromise models based primarily on restraints), but only if there is an improbably low (≤0.026 for the inferred d_f) annual probability of successful dispersal (where the dotted line meets the x axis in Fig. 1a).

Table 2.

Observed and expected values for the p_s, the presumed subordinate's (less successful bird's) share of reproduction in groups with two breeders

	Groups	Nests	Mean N offspring ± SE	Observed ps	Expected ps
					By nestling	By clutch	By observed proportion
Females
All data	19	40	8.9  ± 1.2	0.42	0.35**	–	–
Males
All data	25	71	8.2  ± 1.0	0.23	0.34**	0.19	0.24
Cobreeders with at least 3 nests	14	56	11.5  ± 0.9	0.29	0.38**	0.28	0.31

Nests produced by the same set of birds are combined. Parentage assignment was based on multilocus DNA fingerprinting combined with observational data of egg-laying by joint-nestling females (20). Lower values indicate higher skew (greater monopolization of reproduction by the presumed dominant). Expected values were generated by simulations in which cobreeders had an equal probability of parenting either an offspring or entire clutches. “By nestling” assumes independence of parentage of each nestling; “by clutch” (males only) assigns paternity of clutches on a winner-take-all basis; “by observed proportion” (males only) divides nests into two groups based on the observed frequency of single-sired nests (72%) and assigns paternity of clutches on a winner-take-all basis for this proportion and on a nestling-by-nestling basis for the remaining nests. 

^**, P < 0.01; 

^**, P < 0.001; other, P > 0.05. 

For broods produced by cobreeder males, mixed paternity was unusual, with 72% of such nests (n = 65) yielding young sired by only one of the two males. The subordinate's share of reproduction using all nests (observed p_m) was 23%, significantly less than expected by chance under the null model assigning paternity of each nestling with equal probability to either breeders (Table 2). This finding suggests high reproductive skew between cobreeder males. In contrast to the situation for females, the probability of parenting offspring by the subordinate is below the minimum level consistent with restraint models (p*_m = 0.35) and within the range predicted by concessions models (Fig. 1b). Skew among cobreeder males is also greater than that among joint-nesting females (P < 0.001), as predicted by concessions theory.

The high skew among cobreeder males is consistent with optimal skew models. However, other expectations of these models were not met. First, concessions theory demands that there be a clear dominant in control of reproductive partitioning within groups. As defined here, this would mean that the high observed skew should be achieved by the same male (the presumed dominant) generally gaining the greater share of paternity within successive clutches. In contrast, the identity of the more successful male often differed between successive breeding attempts between years, and often between nests within the same year. Among cobreeder males that produced at least two nests together (whether in the same or different years), the same male consistently obtained the dominant share of reproduction in only 8 of 25 cases (32%). Even restricting analysis to only those groups in which the breeder males fledged from different nests and thus were known to differ in age, the older male achieved the dominant share of reproduction in only 5 of 17 cases (29%). Such switching of reproductive domination results in decreasing skew (increased p_s) as cobreeders produce more nests (Table 2, row labeled “cobreeders with at least 3 nests”) and is directly contrary to a key assumption of concessions theory.

A second expectation of optimal skew theory is that the dominant individual in charge of reproductive partitioning is likely to be the older, larger, or otherwise stronger individual. In contrast, age, weight, and condition all failed to correlate with reproductive success (Table 3). This observation was even true when restricting analyses to groups where cobreeders were either a father and son or an uncle and nephew, and thus where the age difference was unambiguous. There are at least two plausible explanations for these results. First, it is possible that reproductive sharing between cobreeder males matches skew theory for individual nests, but dominance switches for unknown reasons between nesting attempt. Alternatively, there may be no consistent pattern of reproductive dominance between males, and the pattern of skew observed in our data may instead result from nonindependence of paternity within broods. Predictions of this latter possibility were compared with our results by using the alternative null models described above in which paternity of some (Table 3, column labeled “by observed proportion”) or all (Table 3, column labeled “by clutch”) broods was assigned in an “all or none” fashion to one of the two cobreeders.

Table 3.

The relationship between reproductive success and variables likely to correlate with behavioral dominance

	Hierarchy determination
	Age	Weight	Condition
Joint-nesting females
Proportion of offspring produced by alpha (N)	0.50 (175)	0.52 (103)	0.50 (103)
Proportion of groups in which alpha was the most successful (N)	0.32 (19)	0.54 (13)	0.46 (13)
Cobreeding males (all data)
Proportion of offspring produced by alpha (N)	0.51 (204)	0.41 (182)	0.38 (182)
Proportion of groups in which alpha was the most successful (N)	0.48 (25)	0.35 (20)	0.30 (20)
Cobreeding males (siblings)
Proportion of offspring produced by alpha (N)	0.56 (147)	0.38 (110)	0.38 (110)
Proportion of groups in which alpha was the most successful (N)	0.56 (18)	0.29 (14)	0.29 (14)
Cobreeding males (father/son or uncle/nephew)
Proportion of offspring produced by alpha (N)	0.39 (57)	0.52 (54)	0.41 (54)
Proportion of groups in which alpha was the most successful (N)	0.29 (7)	0.50 (6)	0.33 (6)

In all cases, two cobreeders were compared, and “alpha” refers to the bird that was older, larger, or in better condition. Age differences ranged from several hours (for nestmates hatching asynchronously) to 3 years. Weight hierarchy was determined from measurements taken at the same time when possible, but otherwise by comparing residuals after controlling for year and season in which the measurements were taken. Condition was estimated by regressing wing chord on weight and comparing residuals after controlling for year and season. 

Observed levels of skew in simulations for both our complete data set and considering only sets of male cobreeders that produced at least three nests together are almost identical to and not significantly different from simulated values by using either version of the alternative null model (Table 2). That is, observed reproductive partitioning among cobreeder males is consistent with what is predicted if paternity of either all broods, or of the same proportion of broods as observed, is determined by a single flip of a coin.

Thus, if we assume nonindependence of paternity, high skew among cobreeder males is consistent with equal probability of paternity. As with joint-nesting females, this finding suggests the possibility that the expected subordinate's share of reproduction (inferred p_m) is equal to 0.5, a value that is greater than p*_m (Fig. 1b) and any value consistent with the concessions model regardless of the degree of ecological constraints. As in the case for joint-nesting females, it is consistent with restraints models, but only if the probability of successful dispersal is low (d_m ≤ 0.08).

Discussion

Assuming the standard assumption that paternity of offspring is determined independently, our results indicate an absence of skew among joint-nesting females and a relatively high skew between cobreeder males. This result is consistent with the predictions of concessions models, both qualitatively in that male skew is greater than female skew, and quantitatively in that male skew falls within the range predicted by concessions models (Fig. 1b).

However, other key findings are not consistent with optimal skew theory. First consider females. Concessions theory predicts a moderate degree of skew, with a proportion of young sired by the subordinate (p_s) no higher than 0.32 (Fig. 1a, p^*_f). This value is considerably lower than the observed p_f of 0.42; in fact, observed skew is significantly lower than expected by chance (Table 2).

A key assumption of skew theory is that dominants have complete control of reproduction by subordinates. Behavioral data fails to support this assumption for joint-nesting females. Regardless of age, all females with breeding status have equal access to nest cavities and equal ability to remove and destroy their cobreeders' eggs before laying their own eggs (26, 32). Because females do not discriminate their own eggs, such egg destruction synchronizes egg-laying and effectively assures that joint-nesting females lay similar numbers of eggs in the communal nest. Thus, as in meerkats (15), dominant females are neither able to control reproduction nor in a position to grant reproductive concessions to subordinates.

The situation is more complicated for cobreeder males. Although skew is high and within the range predicted by the concessions model (using the standard assumption that paternity is independently determined for each offspring), other results again counter the expectations of concessions theory. Assuming that there is a clearly dominant male, he should father the majority of offspring in most or all nests. Furthermore, dominance itself should correlate with some phenotype attribute such as age, size, or condition. Neither of these predictions was met. First, the male siring the majority of young switched between nests in the majority of cases where we were able to determine paternity of more than one brood produced by the same set of cobreeders, thus leading to decreasing skew as more nests were included (Table 2). Second, we found no relationship between the male siring the majority of young (the presumed dominant) and either age, body mass, or condition (Table 3).

This apparent lack of a clear dominant and switching of paternity between nests is consistent with the observed pattern of reproductive partitioning between cobreeder males if we revise the standard assumption of how parentage is determined and consider the possibility that paternity may be largely an all-or-none affair within broods. This possibility would effectively decrease the sample sizes for cobreeder males by nearly two-thirds, from 205 nestlings to 71 nests, with a corresponding increase in the degree of reproductive skew expected by chance alone. Measured by the subordinate's share of reproduction (p_s), the expected value considering all data drops from 0.34 (significantly greater than the observed value of 0.23) when paternity is determined independent for each nestling to 0.19 (less than the observed value, but not significantly so; Table 2) when it is not and paternity is instead determined randomly on a clutch-by-clutch basis.

We currently can only speculate concerning the mechanisms leading to this situation. In contrast to females, males have no readily apparent way to subvert potential dominance, and the precise mechanisms by which paternity is determined remain unknown. Possibly females choose which males to mate with, and do so on some basis other than dominance. Copulations are almost never observed in acorn woodpeckers (25) and are presumably under the control of females. It may be to a females' advantage to obfuscate paternity if this reduces the chances of a male either withholding parental care or destroying a nest in which he has little or no confidence of parentage (27, 33). Thus, the pattern of skew among cobreeder males is possibly a consequence of female control rather than exclusively because of male–male interactions. Such as situation would be comparable to that of dunnocks Prunella modularis, in which sexual conflict with females, rather than male–male competition alone, determines patterns of parentage within nests produced by (in this case unrelated) cobreeding males (33, 34).

In summary, the observed pattern of skew between joint-nesting females is not consistent with concessions theory, primarily because the key assumption that one individual is in control of reproductive partitioning is not met. For cobreeder males, skew is high and consistent with the optimal skew. However, other predictions of skew theory do not appear to be met, and our data are also consistent with an alternative hypothesis that the probability of paternity is equal between cobreeders but that female control renders paternity mostly an all-or-none affair within broods. This alternative hypothesis is consistent with lack of control; that is, with there being no dominant male that is able to determine paternity.

Reproductive skew theory attempts to unify social and ecological factors into a single framework, providing promise of a coherent explanation for variation in reproductive partitioning. Our results indicate that, in acorn woodpeckers, the assumptions of skew theory may not be met by either sex, and are definitely not met by one of them (females). Combined with results suggesting that skew theory cannot explain reproductive partitioning in meerkats Suricata suricatta, a highly social mammal (15), this finding indicates that increased attention to alternative models of reproductive partitioning in vertebrate societies is needed.