Sustainable Dyeing Process Modeling for Recycled PET/PCT Microfibers via Gaussian Process Regression

Abstract

As the textile industry moves toward more sustainable and resource-efficient manufacturing, minimizing the experimental burden in dyeing processes has become increasingly critical. This study presents a Gaussian process regression (GPR)-based framework for predicting the colorimetric outcomes of dyeing processes involving ecofriendly fiber blends composed of recycled polyethylene terephthalate and polycyclohexylene dimethylene terephthalate. Using only 52 experimental data points, the model was trained to predict CIELAB color coordinates (L*, a*, b*) as well as the K/S value based on dyeing variables such as temperature, time, and dye concentration. The GPR model achieved high prediction accuracy with coefficients of determination (R ²) of 0.96, 0.96, 0.73, and 0.95 for L*, a*, b*, and K/S, respectively. Moreover, the probabilistic nature of GPR enables uncertainty quantification through posterior predictive distributions, offering both mean estimates and 95% confidence intervals. This capability supports robust decision-making in dyeing process design and quality control, especially in low-data regimes. The proposed approach demonstrates significant potential for reducing resource consumption and experimental iterations in fiber coloration, contributing to the development of data-efficient and environmentally sustainable dyeing systems.

1. Introduction

In the textile industry, there is a growing need for precise and efficient dyeing technologies that can simultaneously achieve quality control, process optimization, and reduction of environmental impact. − In particular, dyeing is the most resource-intensive stage in textile processing, consuming large amounts of water, energy, and chemicals. As a result, there is growing interest in sustainable production methods that aim to reduce water usage, improve energy efficiency, and minimize chemical pollution and waste. − In conventional dyeing processes, achieving consistent color reproduction requires repeated experiments and manual adjustment of process conditions, which significantly increases the required time as well as costs and waste generation. Consequently, machine-learning prediction models have been explored as a way to reduce the number of repeated experiments and improve dyeing efficiency. −

Machine learning-based prediction models offer the advantage of identifying dyeing conditions that yield colors close to the desired target without repeated experiments by learning from existing experimental data and predicting outcomes under new conditions. , The L*, a*, and b* in the widely used CIELAB color space are closely related to visual color perception. In addition, the K/S value, which represents the ratio of absorption to scattering, is another important indicator of color yield in dyed fabrics. By incorporating this color strength metric into the prediction model, it is possible to more comprehensively evaluate dye uptake and color intensity, which are closely associated with fastness, a major indicator of fiber performance in textile applications. A model that accurately predicts these values can be highly useful for evaluating dyeing quality and designing dyeing processes. − However, developing such a model requires sufficient amount of training data, which is often difficult to obtain due to the physical and economic limitations of actual textile dyeing experiments. During the early stages of research on a single color or a specific material, only a small sample size is typically available. In such small-sample settings, commonly used machine learning techniques such as support vector machine (SVM) and artificial neural network (ANN) tend to overfit, resulting in poor generalization performance, making it difficult to achieve accurate predictions. −

In this study, a Gaussian process regression (GPR) model was introduced to address the challenge of a small sample size, aiming to achieve high predictive performance even with limited data. − GPR is a probabilistic, Bayesian regression method that provides not only a single predicted value but also a confidence interval associated with the prediction. − This characteristic provides a practical advantage over conventional linear regression models because it enables a quantitative assessment of prediction certainty. Such capability is particularly valuable for experimental design and dyeing process control. GPR is especially effective in environments with limited training data, as it helps prevent overfitting while maintaining strong generalization performance. ,

In this study, a GPR-based prediction model was developed using 52 experimental samples. The dyeing temperature, time, and dye concentration served as input variables, and the corresponding L*, a*, b*, and K/S values of the dyed PCT fabric were the output variables to be predicted. To identify the optimal kernel function, cross-validation was performed on several possible kernels, and the model performance was evaluated using quantitative metrics such as mean squared error (MSE), mean absolute error (MAE), and R². Furthermore, the posterior predictive distribution was analyzed to visualize predictive uncertainty, which is one of the core strengths of GPR. The agreement between predicted and actual values was also examined using several validation methods.

The approach proposed in this study serves as a foundation for future smart dyeing processes that enable color control without repeated experiments. By leveraging GPR’s probabilistic predictions, the model can increase confidence in process design decisions and support decision-making while minimizing resource waste. − It can also be applied to quality control and experimental design optimization, either as an alternative to conventional empirical approaches or as a complementary method. − This study demonstrates that the GPR model can achieve high-confidence predictions even with a small sample size, highlighting its potential to contribute to the development of eco-friendly, sustainable dyeing processes.

2. Experimental Section

2.1. Materials

The fabric samples used in this study were sea–island type microfiber suede fabrics provided by Huvis Co., Ltd., South Korea and the characteristics of the dyed fabrics are shown in Table .

1. Specifications of Suede Fabric.

parameter	value
Yarn spec.	Recycled PET 50%: PCT 50%
Suede spec.	Yarn 70%: PU 30%
Type	Nonwoven fabric
Size (mm)	130
Thickness (mm)	1.18
Weight (g/m2)	13.5

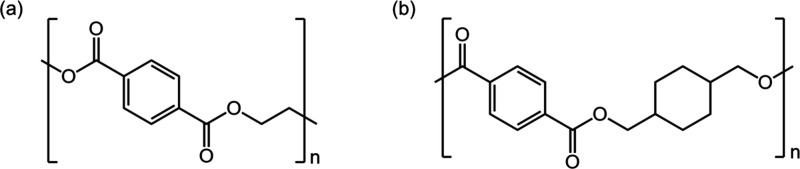
The suede was produced by blending recycled polyethylene terephthalate (PET) and polycyclohexylene dimethylene terephthalate (PCT) microfiber in a 50:50 ratio, followed by 30% impregnation with polyurethane (PU) resin. Figure shows the chemical structures of the recycled PET and PCT polymers used.

1.

Chemical structure of fabric (a) recycled PET, and (b) PCT.

Figure (a) shows the chemical structure of recycled PET, which was obtained by mechanically and chemically recycling waste PET bottles. Figure (b) presents the chemical structure of PCT, a copolyester fiber material synthesized through an ester polycondensation reaction of terephthalic acid (TPA) or dimethyl terephthalate (DMT) with the precursor 1,4-cyclohexane dimethanol (CHDM). The disperse dye used for dyeing was Dorospers Dark Gray KKL, an anthraquinone-based dye (Archroma Co., Ltd., Switzerland). The dispersing agent used in the dye bath was Sunsolt RM-340S (NICCA KOREA Co., Ltd., Japan), and the pH of the dye bath was adjusted using acetic acid (CH₃COOH) (SAMIL Co., Ltd., South Korea). For the reduction cleaning process, the reducing agent Sera Con M-FAS (Dystar, Singapore) and NaOH (SAMIL Co., Ltd., Korea) were used.

2.2. Dyeing

Figure illustrates the dyeing and reduction cleaning process of suede fabric.

2.

Schematic diagram of the dyeing and reduction cleaning process of the suede fabric.

A dye bath was prepared using a liquor ratio of 1:20 for 13.5 g of suede fabric. Disperse dye was added at concentrations of 5% and 10% owf (on weight of fabric). Additionally, 1.89 mL of a 2 wt % dispersing agent and 5 wt % acetic acid were added to adjust the pH of the dye bath to 5. Dyeing was performed in an infrared dyeing machine (DL-6000, Daelim Starlet Co., South Korea) at 100–135 °C for 10–60 min. After dyeing, a reduction cleaning step was conducted to remove any unfixed dye from the fabric surface. A cleaning solution with a 1:20 liquor ratio, containing 6 g/L of the reducing agent (Sera Con M-FAS) and 6 mL/L of NaOH, was applied at 85 °C for 30 min to carry out the reduction cleaning process. The cleaned fabrics were rinsed with lukewarm water and dried, resulting in a total of 52 dyed samples under various process conditions.

2.3. Color Measurement

To evaluate the dye uptake of the dyed fabrics, a spectrophotometer (SCINCO Co., Ltd., South Korea) was used to measure surface reflectance at 20 nm intervals within the visible wavelength range of 360–740 nm under a 10° standard observer and D65 illumination conditions. From these measurements, the L*, a*, and b* values were obtained. To minimize measurement error, each fabric sample was measured four times, and the average value was used as the final data.

2.4. Dye Uptake Characteristics

The adsorption and diffusion behavior of disperse dyes depends on the microstructure and chemical affinity of the fiber substrate. Polyester fibers such as rPET and PCT lack charged groups, so ionic bonding with dyes is negligible. Heating the fabric above its glass transition temperature expands the amorphous regions and allows anthraquinone dyes to diffuse into the polymer’s free volume. The absorbed dye remains in the fiber chiefly through hydrophobic and π–π interactions between its aromatic rings and the polymer chains, assisted by weaker dipole and hydrogen-bond forces. In this study, the interaction strength between dye and fiber in rPET/PCT microfibers was quantified using the Kubelka–Munk K/S value. The Kubelka–Munk equation is presented in Eq. .

$$K/S=\frac{{(1-R)}^2}{2R}$$ 1

where K is the absorption coefficient, S is the scattering coefficient, and R is the reflectance of the sample. Surface reflectance spectra were measured with a spectrophotometer, and the highest K/S value among all measured wavelengths was taken as the final result.

2.5. Model Selection

In this study, dyeing time (min), temperature (°C), and dye concentration (% owf) were used as input variables, and the output variables were the L*, a*, b*, and K/S values of the dyed fabric. The machine learning model used was GPR, a Bayesian regression method that estimates the distribution of functions based on given inputs. Given the limited data set (52 samples), GPR was selected for its ability to provide reliable predictions and strong generalization performance with small data. All modeling was implemented in Python 3.10.0 using scikit-learn 1.6.1.

2.6. Model Evaluation Criteria

To quantitatively evaluate the performance of the GPR model in predicting color data based on dyeing process variables, three representative regression metrics were used: MAE, MSE, and R ². MAE represents the mean absolute difference between predicted and actual values and provides an intuitive measure of prediction error. The MAE was calculated by eq .

$$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{n}\sum _{i=1}^n|y_i-{ŷ}_i|$$ 2

where y _i is the actual measured value from the experiment, and ŷ _i is the predicted value from the model. MSE is more sensitive to large errors and is useful for evaluating the robustness of the model. The MSE formula is presented as eq .

$$\mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{n}\sum _{i=1}^n{(y_i-{ŷ}_i)}^2$$ 3

The R ² value indicates how well the model explains the actual data. A value closer to 1 suggests that the model has higher explanatory power. The formula for calculating R ² is presented as eq .

$$R^2=1-\frac{\sum _{i=1}^n{(y_i-\mathrm{y̅})}^2}{\sum _{i=1}^n{(y_i-{ŷ}_i)}^2}$$ 4

where y̅ denotes the mean of the actual experimental values. In addition, considering the small training data set in this study, a 5-fold cross-validation (CV) was performed to control overfitting and evaluate the model’s generalization performance. The entire data set was randomly divided into five subsets, with one subset used for validation and the remaining subsets used for training. This process was repeated five times, and the average values of the evaluation metrics were used as the final performance results.

3. Results and Discussion

3.1. Data Analysis

To quantitatively examine the degree of interaction among variables and to assess how each input variable contributes to predicting the output, the correlations were analyzed among the dyeing process parameters (dyeing temperature, time, and dye concentration) as well as between the input variables and the output color coordinates (L*, a*, and b*) and color strength (K/S value). The analysis was conducted by calculating the Pearson correlation coefficient (PCC) based on the Pearson correlation formula, which is presented in eq .

$$r_{xy}=\frac{\sum _{i=1}^n(x_i-\mathrm{x̅})(y_i-\mathrm{y̅})}{\sqrt{\sum _{i=1}^n{(x_i-\mathrm{x̅})}^2\sum _{i=1}^n{(y_i-\mathrm{y̅})}^2}}$$ 5

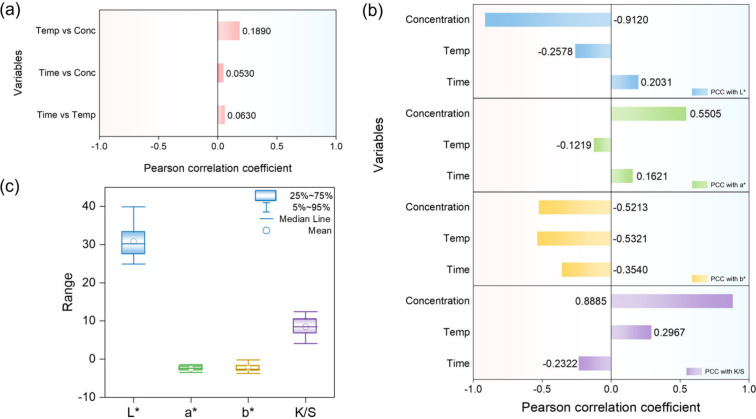
The PCC ranges from −1 to 1, where a value of 1 indicates a perfect positive correlation, −1 indicates a perfect negative correlation, and 0 indicates no correlation. , A higher absolute PCC value indicates a stronger relationship between two variables, meaning that changes in one variable are closely associated with changes in the other. On the other hand, a lower absolute value indicates that the relationship is weak and difficult to interpret. The analysis revealed that the relationships among the input variables were generally weak. In contrast, certain input variables showed relatively strong relationships with specific output variables, suggesting that some dyeing conditions significantly affect particular color coordinates. The PCC results for both input–input and input–output variable pairs, along with the box plots illustrating the distribution of the output variables, are presented in Figure .

3.

(a) Pearson correlation coefficient between input variables, (b) Pearson correlation coefficient between input and output variables, and (c) Box plots of the output variables.

Figure (a) shows the correlations among the three input variables, which are dyeing temperature, time, and dye concentration. All correlation coefficients are below 0.2, indicating very weak relationships and suggesting minimal influence among the input variables. Figure (b) presents the correlations between each input variable and the output variables, specifically the L*, a*, b*, and K/S values that represent the fabric’s color characteristics. The strongest correlation is observed between dye concentration and the L* value, which represents the lightness of the fabric. The correlation coefficient is approximately −0.91, indicating that the lightness significantly decreases as the dye concentration increases. Dye concentration is also strongly and positively correlated with the K/S value, reflecting the intuitive increase in overall color strength as the amount of dye increases. Similarly, the a* value, which represents the red-green axis of the color space, tends to increase with higher dye concentrations, shifting the fabric color toward red. Conversely, the b* value, reflecting the yellow-blue axis, tends to decrease, shifting the color toward blue. Temperature shows a moderate positive correlation with the K/S value, while dyeing time exhibits a weak negative correlation, suggesting that prolonged time alone does not necessarily enhance color yield under the studied conditions. As shown in Figure (c), the L* value exhibited a low correlation with dyeing temperature and time. Similarly, the a* and b* values showed weaker correlations with temperature and time than with dye concentration, partly due to their relatively narrow data distributions, which made such relationships more difficult to identify. The K/S value follows the same trend, where dye concentration is the dominant factor, while temperature and dyeing time have only a minor impact. These results suggest that the input variables can be considered largely independent, with dye concentration being a more critical factor for color change compared to temperature and time. The strong correlations between dye concentration and the L*, a*, b*, and K/S values confirm that the fabrics in the data set were properly dyed under the given experimental conditions, accurately representing both color depth and chromatic characteristics.

3.2. Model Configuration

The data set consisted of 52 experimental samples, of which 80% were randomly selected as training data and the remaining 20% were used as test data. Since the input variables had different units, standardization was performed by adjusting the mean to 0 and the standard deviation to 1 to ensure that all variables contributed equally to model training. The same standardization was applied to the test set. The kernel function is a core component of the GPR model, enabling it to learn nonlinear relationships between input variables and directly influencing its predictive accuracy and generalization performance. Therefore, the choice of kernel is critically important. − In this study, various kernel function combinations were constructed by incorporating the White kernel into existing kernels to model measurement noise and observation errors more accurately and to better reflect the uncertainty present in actual data. , Among these combinations, the kernel function combination with the lowest MSE value from the CV was selected for the final model. The CV MSE results for each kernel function combination are presented in Table .

2. CV MSE Results for Different Kernel Combinations.

kernel function	CV MSE
Matern + White	0.926
Rational quadratic + White	0.949
RBF + Matern + White	0.971
RBF + White	1.043

Among all the combinations tested, the combination of the Matern kernel and White kernel showed the lowest MSE and was selected as the final model. The length-scale parameter ( $\mathcal{l}$ ), which controls the range of influence over input correlations in the kernel function, was set to 1. The smoothness parameter (ν) of the Matern kernel, which determines the complexity and variability of the function to be learned, was set to 1.5. This kernel combination achieved the lowest MSE and effectively captured underlying data patterns even with the small sample size, which justifies its selection as the final model. The final model was trained using the entire data set with standardized input values. Hyperparameters such as the length scale and noise level were optimized by repeating the training process up to 10 times. This multi-iteration optimization helped the model approach a global optimum and improved its generalization performance. Since the GPR model predicts four outputs, the model was designed to predict them in parallel while sharing the same kernel across all outputs.

3.3. Model Performance Evaluation

The predictive performance of the GPR model was evaluated using 5-fold CV on the data set of 52 dyeing experiments. The MAE, MSE, and R ² values for each output variable of the GPR model are presented in Table .

3. Predictive Performance Metrics of the GPR Model Based on 5-fold CV.

metrics	L*	a*	b*	K/S
MAE	0.4950	0.1129	0.2441	0.3608
MSE	0.3444	0.0183	0.0993	0.1857
R 2	0.9566	0.9573	0.7295	0.9451

The prediction results for each output variable demonstrated consistently high accuracy. As shown in Table , the predicted MAE and MSE for the L* were 0.4950 and 0.3444, respectively, which are very low given that the lightness scale ranges from 0 to 100. Similarly, the MAE values for a* and b* were 0.1129 and 0.2441, and the MSE values were 0.0183 and 0.0993, indicating minimal differences between the predicted and actual values. For the K/S output, the MAE and MSE were 0.3608 and 0.1857, respectively, showing that the predicted color strength values closely matched the experimental measurements as well. The R ² values confirm the model’s strong predictive capability: 0.9566 for L* and 0.9573 for a* (indicating that about 95% of the variance is explained in each case), 0.7295 for b*, and 0.9451 for K/S. The somewhat lower R ² for b* suggests that b* is harder to predict, possibly due to its narrower range or higher noise, but it still indicates a reasonable fit. These results suggest that, despite the small sample size, the GPR model successfully captured the complex nonlinear relationships in the dyeing process, resulting in reliable predictions for all color components and the K/S value confirming the model’s suitability for this application.

3.4. Model Validation

To validate the trained GPR model, the relationship between the predicted and actual values was examined using linear regression analysis. The results of the regression analysis, including the regression lines representing the relationship between the predicted and actual values, are presented in Figure .

4.

Result of linear regression analysis with (a) L* values, (b) a* values, (c) b* values, and (d) K/S values.

Figure presents a linear regression analysis with the actual values on the x-axis and the predicted values on y-axis, illustrating the relationship between the known measurements and the predictions generated by the model. A high prediction accuracy is indicated when the data points lie close to the regression line. The results show that all output variables exhibit a strong linear relationship between actual and predicted values, with most points distributed near the ideal y = x line. The predicted L* values are tightly clustered along the line, demonstrating a high degree of agreement with the actual values. The a* and b* values also show strong correlations, despite some minor deviations. Likewise, the K/S predictions align closely with the ideal y = x line, indicating accurate modeling of color strength. The equations of the regression lines indicate that the slopes are close to 1 and the intercepts are near 0 for all output variables, suggesting that the predictions are unbiased and consistent with the actual values. In addition to the regression analysis, this study also examined the quantification of predictive uncertainty, one of the main advantages of the GPR model. Rather than producing a single point estimate, GPR provides a distribution of possible outcomes for each input within a Bayesian regression framework. This allows the model to quantify the confidence of each prediction. Figure visualizes the posterior predictive distribution for each output variable, including the predicted mean and the 95% confidence intervals (±1.96σ).

5.

GPR-based posterior predictions of each output variable (a) L* values, (b) a* values, (c) b* values, and (d) K/S values.

The analysis showed that the confidence intervals were narrow for most data points, indicating that the model generated predictions with a high level of certainty. The centers of the predictive distributions were also closely aligned with the actual measured values, visually confirming that the predictions were generally unbiased and reasonably accurate. To further evaluate the reliability of the predictive distributions, the absolute errors between the actual and predicted values were compared against the 95% confidence intervals for each output variable. The results of this comparison are presented in Figure .

6.

Comparison between prediction errors and 95% confidence intervals for (a) L* values, (b) a* values, (c) b* values, and (d) K/S values.

For all samples of each output variable, the absolute errors were smaller than the corresponding confidence intervals, indicating that the actual values were well contained within the confidence bounds provided by the GPR model. These results confirm that the GPR model demonstrated consistent performance in both prediction accuracy and uncertainty estimation, suggesting its potential as a reliable predictive tool in dyeing processes where repeated experiments are challenging.

3.5. Posterior Prediction Surface Analysis

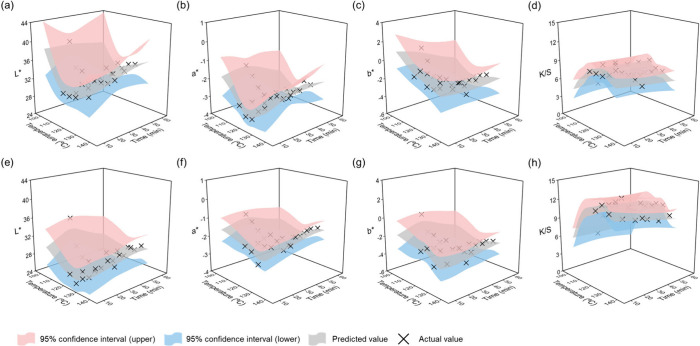
One of the main advantages of the GPR model is its ability to generate and analyze posterior predictive distributions for new inputs. Based on this property, prediction surfaces were constructed for each output variable by setting dyeing time and temperature as independent variables, while fixing dye concentration at 5% and 10%. The actual measured values corresponding to each condition were also visualized alongside the predictions. The posterior prediction results are presented in Figure .

7.

Posterior predictive surfaces of (a) L* value, (b) a* value, (c) b* value, (d) K/S value at 5% dye concentration, and (e) L* value, (f) a* value, (g) b* value, (h) K/S value at 10% dye concentration, plotted against dyeing temperature and time with 95% confidence intervals and actual values.

For a dye concentration of 5%, Figure (a–d) presents the predicted mean surfaces for L*, a*, b*, and K/S, respectively. Similarly, Figure (e–h) shows the corresponding surfaces for L*, a*, b*, and K/S at a dye concentration of 10%. Within the temperature and time ranges where training data were concentrated, the predicted surfaces closely matched the actual measured values, and most data points fell within the 95% confidence intervals provided by the GPR model. This indicates that the model maintained high predictive accuracy in these regions and provided reliable estimates of output variability. In areas where the confidence intervals appeared relatively narrow, the model demonstrated high certainty in its predictions under those specific conditions. In contrast, regions with limited or no training data showed more abrupt changes in the surface slope and broader confidence intervals, reflecting increased uncertainty in those extrapolated areas. Predictions that extrapolate beyond the original data range carry increased risk and require cautious interpretation, underscoring an inherent limitation in the model’s ability to generalize. These results highlight the relationship between data density in the input space and predictive uncertainty, offering a practical means of identifying less stable prediction zones. Such visual analysis based on posterior distributions underscores the value of GPR not only in generating point predictions but also in quantifying the level of certainty associated with each prediction. This capability is particularly useful for designing dyeing process conditions with greater confidence and identifying potential risks in experimental settings where repeated trials are limited. The current data set comprises dye concentrations of 5% and 10% owf, which are sufficient for the present analysis. Incorporating intermediate concentrations and additional types of disperse dyes in future work would enable the model to encompass a broader concentration range and enhance its generalizability.

3.6. Comparative Analysis

3.6.1. Comparison with Actual Data

To visually compare the performance of the GPR model, the predicted color values were plotted alongside the actual experimental values in a three-dimensional space. The comparison results are presented in Figure .

8.

Comparison of color values in 3D space (a) predicted values by GPR model, (b) actual values by experiment, (c) combined scatter plot of predicted and actual values, (d) absolute error between predicted and actual values.

Figure (a) shows the GPR model’s predicted color coordinates for the test samples in a 3D Lab space, while Figure (b) plots the actual experimental color values for those samples. The points in (a) and (b) are clustered in similar regions, indicating that the GPR model effectively captures the real color distribution. In Figure (c), the predicted and actual points are superimposed, and their close proximity suggests that the differences are minimal. Figure (d) visualizes the absolute errors of each test sample, showing that most points are concentrated near the origin. This result confirms that the differences between predicted and actual values are small, demonstrating the model’s overall high accuracy. Table summarizes the experimental values, predicted values, and corresponding absolute errors for each test sample.

4. Comparison of Actual and Predicted Values with Absolute Errors for Each Test Sample.

	actual values				predicted values				absolute error
sample	L*	a*	b*	K/S	L*	a*	b*	K/S	L*	a*	b*	K/S
1	24.76	–1.78	–2.17	12.48	25.72	–1.97	–2.90	11.68	0.96	0.19	0.73	0.80
2	27.53	–1.89	–3.21	10.37	28.00	–1.99	–3.20	9.78	0.47	0.10	0.01	0.59
3	28.64	–1.85	–3.37	9.29	28.28	–1.97	–3.19	9.80	0.36	0.12	0.18	0.51
4	31.69	–3.02	–3.00	7.76	32.59	–3.04	–2.91	7.27	0.90	0.02	0.09	0.49
5	26.33	–2.66	–3.55	11.57	26.22	–2.45	–3.18	11.52	0.11	0.21	0.37	0.05
6	26.63	–1.81	–2.12	10.81	27.12	–1.78	–2.26	10.27	0.49	0.03	0.14	0.54
7	25.56	–2.05	–2.63	11.91	25.23	–1.97	–2.54	12.04	0.33	0.08	0.09	0.13
8	33.73	–2.34	–2.60	6.38	33.52	–2.40	–2.34	6.33	0.21	0.06	0.26	0.05
9	28.76	–1.42	–1.99	8.79	29.79	–1.47	–1.53	8.42	1.03	0.05	0.46	0.37
10	30.74	–3.47	–1.53	8.32	30.63	–3.37	–1.30	8.48	0.11	0.10	0.23	0.16
11	32.19	–3.28	–2.89	7.58	32.67	–3.02	–2.77	7.30	0.48	0.26	0.12	0.28

For the L*, the mean absolute error was approximately 0.50. The a*, b*, and K/S also showed low average errors of around 0.11, 0.24, and 0.36, respectively. These values indicate color differences that are difficult to distinguish visually, confirming the high predictive performance of the model.

3.6.2. Comparison with the ANN Model

To compare the predictive performance of the GPR model with that of another model using a limited data set, an ANN model was constructed based on the same experimental data. The ANN model was trained on 80% of the data and tested on the remaining 20%. The network consisted of an input layer, two hidden layers (with 64 and 32 neurons), and an output layer with 4 neurons to predict L*, a*, b*, and K/S values simultaneously. Rectified Linear Unit (ReLU) was applied to the hidden layers, and the network was trained using the Adam optimizer. Figure summarizes the ANN’s performance.

9.

Linear regression analysis of ANN predictions with (a) L* values, (b) a* values, (c) b* values, (d) K/S values, and (e) comparison of MAE and MSE values between ANN and GPR models.

Figure (a), (b), and (d) show the linear regression analysis results for the ANN’s predictions of L*, a*, and K/S values, respectively. While the predicted values generally align with the actual values, the deviations from the regression line are larger compared to those of the GPR model, and several outliers can be observed. Figure (c) shows the ANN’s predictions for b* values, which appear less accurate than the other three outputs and exhibit the greatest dispersion among the data points. Figure (e) compares the MAE and MSE of the ANN and GPR models. The GPR model achieved lower error values on all metrics compared to the ANN. These results suggest that GPR is more robust and achieves better generalization performance than ANN for regression tasks with a small sample size. As a Bayesian regression model, GPR naturally guards against overfitting and provides an uncertainty estimate with each prediction, quantifying the confidence in the output values. This capability makes GPR a practical choice for predictive modeling on experimental data, especially in cases of limited sample sizes. Similar trends have been reported in previous studies, and the results of this study are consistent with such findings. − The ANN model underperformed compared to the GPR model in this study. This was mainly due to the limited size of the data set. However, with a larger amount of data, ANN may offer advantages in terms of scalability and training efficiency. Therefore, it is important to select an appropriate model depending on the size of the data set and the specific application context.

4. Conclusion

In this study, a GPR model was constructed using 52 experimental samples to predict the relationship between dyeing process variables (dyeing temperature, time, and concentration) and the resulting color coordinates (L*, a*, and b*) and K/S value. To improve predictive performance, multiple kernel functions were compared via cross-validation, and the best-performing kernel combination was selected. The model achieved R ² values of 0.96, 0.96, 0.73, and 0.95 for L*, a*, b*, and K/S respectively, demonstrating strong explanatory power. Furthermore, for all four outputs the MAE and MSE were both below 0.5, confirming the model’s high predictive performance on quantitative metrics.

One main advantage of GPR is its ability to generate posterior predictive distributions, which provide both point estimates and a measure of uncertainty. Using this feature, the model’s confidence was evaluated both visually (via 95% confidence intervals) and quantitatively. Most predictions closely matched the experimental data, and the narrow 95% confidence intervals indicated a high level of certainty in those predictions. Additionally, the prediction errors for all test samples were smaller than the model’s predicted standard deviations, confirming that the GPR model can reliably reproduce the experimental outcomes within its uncertainty bounds.

This study experimentally demonstrated that the GPR model can be effectively applied to predict the color coordinates of dyed fabrics based on dyeing process variables. In summary, the results of this study establish GPR as a promising approach for achieving high predictive accuracy even with very limited data. By reducing the need for iterative dyeing experiments, this approach can potentially cut down wastewater generation and the consumption of water, energy, and chemicals, contributing to more environmentally sustainable dyeing practices. It also provides a practical foundation for efficient quality control and process design, with potential applications in smart dyeing systems, real-time control in manufacturing, digital twin-based process control, and eco-friendly textile product development. Applying the GPR model directly on the factory floor can facilitate adaptive optimization, thereby enhancing sustainability and productivity in large-scale dyeing operations.

The authors declare no competing financial interest.