When can we infer mechanism from parasite aggregation? A constraint-based approach to disease ecology

Abstract

Few hosts have many parasites while many hosts have few parasites - this axiom of macroparasite aggregation is so pervasive it is considered a general law in disease ecology, with important implications for the dynamics of host-parasite systems. Because of these dynamical implications, a significant amount of work has explored both the various mechanisms leading to parasite aggregation patterns and how to infer mechanism from these patterns. However, as many disease mechanisms can produce similar aggregation patterns, it is not clear whether aggregation itself provides any additional information about mechanism. Here we apply a “constraint-based” approach developed in macroecology that allows us to explore whether parasite aggregation contains any additional information beyond what is provided by mean parasite load. We tested two constraint-based null models, both of which were constrained on the total number of parasites P and hosts H found in a sample, using data from 842 observed amphibian host-trematode parasite distributions. We found that constraint-based models captured ~85% of the observed variation in host-parasite distributions, suggesting that the constraints P and H contain much of the information about the shape of the host-parasite distribution. However, we also found that extending the constraint-based null models can identify the potential role of known aggregating mechanisms (such as host-heterogeneity) and disaggregating mechanisms (such as parasite-induced host mortality) in constraining host-parasite distributions. Thus, by providing robust null models, constraint-based approaches can help guide investigations aimed at detecting biological processes that directly affect parasite aggregation above and beyond those that indirectly affect aggregation through P and H.

Introduction

Disease ecology has traditionally emphasized mechanistic descriptions of infection patterns (Anderson and May 1978, Duerr et al. 2003, Poulin 2007). One particular pattern observed in macroparasites, such as parasitic helminths and arthropods that do not directly reproduce within their host (Anderson and May 1979), is that many hosts in a population tend to have few parasites and a few hosts tend to have many. In statistical parlance this means that parasites tend to be aggregated within their hosts. This pattern is so ubiquitous in parasites that is has been called one of the few general laws in disease ecology (Poulin 2007).

Canonical models of host-macroparasite dynamics have illustrated that a balance between parasite pathogenicity and parasite aggregation plays an important role in the ability of a parasite to regulate a host population (Anderson and May 1978, Tompkins et al. 2002). In general, the stability of a host-parasite system and the regulation of a host population by parasites requires some level of parasite aggregation and that parasite pathogenicity is not too high (Anderson and May 1978). Because of the importance of parasite aggregation, much empirical and theoretical work has sought to understand both the mechanisms that can lead to aggregation in host-macroparasite systems (Anderson and Gordon 1982, Wilson et al. 2002, Raffel et al. 2011, Gourbière et al. 2015), and how to infer the dominant mechanisms structuring a host-parasite system from observed aggregation patterns (Duerr et al. 2003, Grear and Hudson 2011, Wilber et al. 2016).

Traditionally, studies of macroparasite aggregation have relied on a process-based approach where various aggregating and disaggregating mechanisms are sequentially incorporated into unaggregated null models until observed levels of aggregation are obtained (Anderson and Gordon 1982, Isham 1995, Chan and Isham 1998, Pugliese et al. 1998, Rosà and Pugliese 2002, Rosà et al. 2003, Grear and Hudson 2011, Fowler and Hollingsworth 2016). While the process-based approach has usefully illuminated various aggregating and disaggregating mechanisms in host-parasite systems (summarized in Wilson et al. 2002), it suffers from the “many-to-one problem” inherent in much of ecology (Frank 2014): there are many process-based models that can result in similar levels of parasite aggregation making it difficult to identify the specific processes leading to aggregation from patterns alone. When lab or field experiments are not a viable option to identify mechanism in host-parasite systems, it would be useful to have some criteria to identify when observed patterns of parasite aggregation may provide some information about the mechanisms influencing a host-parasite system or when most of the information is provided in the mean parasite abundance.

Recently developed constraint-based models used in macroecology provide such a criteria. These models are different from the process-based approach in that they attempt to predict the most-likely form of a population- or community-level distribution using only a known set of statistical constraints (Harte 2011, Locey and White 2013, Newman et al. 2014, Xiao et al. 2015b). The constraint-based approach does not propose that biological mechanisms are not acting in a system; it contends that many different combinations of these mechanisms lead to similar patterns of aggregation with predictable statistical properties (Frank 2009, McGill and Nekola 2010, Frank 2014). This is important because these models can then be used as robust null models (i.e. models that do not trivially fail) to identify when a given observed distribution contains biological information beyond that given by the constraints used to predict the distribution (Locey and White 2013, Harte and Newman 2014). Similarly, null model approaches have been used in community ecology to identify when signals of an ecological process can be discerned from observed changes in a community metric (e.g. changes in β diversity) when a change in this metric can also be a concomitant result of changes in another metric (e.g. changes in α diversity; Chase and Myers 2011, Chase et al. 2011). These constraint-based and null model approaches have had much success in understanding patterns in free-living populations and communities (Leibold and Mikkelson 2002, White et al. 2012, Ulrich and Gotelli 2013, Harte et al. 2015) and we argue that they can also be useful in addressing mechanistic questions about parasite aggregation in disease ecology.

For example, any observed host-parasite distribution is constrained by the total number of parasites P and the total number of hosts H in the sample. Given this, there are only a finite number of shapes that this sampled host-parasite distribution can take (i.e. the feasible set of the host-parasite distribution, Locey and White 2013). If the shape of this observed host-parasite distribution is similar to the most likely distribution within this feasible set, then making inferences about the biological mechanisms leading to the shape of this distribution is difficult as the observed distribution is simply the most-likely distribution of all possible distributions (Haegeman and Loreau 2009). In other words, many different combinations of host and/or parasite-related processes will lead to the same host-parasite distribution, and this is the distribution that is predicted by the constraint-based model.

This has important implications for disease ecology where one often wants to understand something about the mechanisms affecting a host-parasite system from the level of aggregation observed (Anderson and Gordon 1982). Having some robust criteria for when a sampled host-parasite distribution shows “unusual” aggregation can help identify host-parasite systems where particular aggregating or disaggregating mechanisms are disproportionately constraining the distribution beyond the inherent (but biologically important) constraints imposed by P and H. We define “unusual” aggregation as a level of aggregation that is significantly different than the level of aggregation predicted by the most likely distribution in the feasible set (e.g. Locey and White 2013, Harte and Newman 2014).

The traditional null model for the distribution of parasites across hosts follows a Poisson distribution, which is typically derived from a death-immigration process (Anderson and Gordon 1982). The constraint-based approach for aggregation is asking a different question than tests of the traditional Poisson null model. Rejecting the Poisson null model indicates that this simple model is not capturing the important aggregating or disaggregating mechanisms in a host-parasite system, however failing to reject the Poisson null model is not proof that a system is following a simple death-immigration process. In contrast, the constraint-based null models make no assumptions about the particular processes leading to its predicted level of aggregation and simply predict the most likely level of aggregation for a system with P parasites and H hosts. Unlike the classic Poisson null hypothesis, failing to reject the constraint-based model tells us something important: our empirical pattern of aggregation does not contain any information about process beyond that already contained in P and H (Harte and Newman 2014). Because this approach robustly identifies “unusual” aggregation, it can help us better understand when the effects of processes, such as parasite-induced mortality or host-heterogeneity, can be reliably inferred from observed host-parasite distributions.

This study has two goals. First, we use a dataset consisting of 22 unique amphibian host-trematode parasite pairings with over 8000 amphibians sampled at 205 sites over 5 years to test whether constraint-based models used in free-living systems also provide robust null models for host-parasite distributions. Second, we explore how, upon failing to describe host-parasite distributions, these constraint-based models can be extended to account for known aggregating mechanisms (such as host-heterogeneity) and disaggregating mechanisms (such as parasite-induced host mortality) in host-parasite systems. We find that the shape of host-macroparasite distributions are generally well-predicted by the constraint-based approach. These results show that to reliably infer something about biological mechanism directly affecting patterns of parasite aggregation, one must first account for the strong constraints imposed on aggregation by P and H.

Methods

The methods section is organized as follows. The first section gives an overview of two constraint-based null models that have been recently used in the macroecological literature (Haegeman and Etienne 2010, Locey and White 2013, Xiao et al. 2015a). The second section describes how we generated predicted host-parasite distributions from these two constraint-based null models. The third section describes how we compared the constraint-based null models to data. Finally, the fourth section describes how we extended these constraint-based null models to account for known aggregating and disaggregating mechanisms in host-parasite systems. Table 1 contains a list of terms and definitions used to define the constraint-based models.

Table 1:

Definitions of terms used to describe the constraint-based null models.

Term	Definition
Labeled	Hosts or parasites are distinguishable
Unlabeled	Hosts or parasites are indistinguishable
Macrostate	Unordered vector of unlabeled parasite abundances. e.g. Given P = 3 and H = 2, the vector {3, 0} is a macrostate
Configuration	Ordered vector of unlabeled parasite abundances. e.g. Given P = 3 an H = 2, the macrostate {3, 0} has two configurations: (3, 0) and (0, 3)
Feasible set	All possible macrostates given P and H. e.g. The feasible set given P = 3 and H = 2 is {{3, 0}, {2, 1}}
Weighted feasible set	Feasible set in which macrostates have particular weights.
Partition model	Weights each macrostate in the feasible set by assuming unla-beled hosts and parasites. All macrostates have equal weights.
Composition model	Weights each macrostate in the feasible set by assuming labeled hosts and unlabeled parasites. Analogously, each macrostate can be realized by multiple configurations.

Defining the weighted feasible sets for constraint-based null models of parasite aggregation

The constraint-based null models that we consider have two constraints inherent in any sampled host-parasite distribution: the total number of parasites sampled P and the total number of hosts sampled H. Given these constraints, both models proceed by enumerating the feasible set of all possible macrostates of P parasites and H hosts (Locey and White 2013). We define a macrostate as one possible unordered host-parasite distribution resulting from distributing P parasites among H hosts (Table 1). For example, the feasible set of possible macrostates that we can observe given P = 3 parasites and H = 3 hosts is F = {{3, 0, 0}, {2, 1, 0}, {1, 1, 1}}. The macrostate {3, 0, 0} specifies that one host has three parasites and two hosts have zero parasites.

After specifying all of the possible macrostates in a feasible set constrained by P and H, each macrostate is then assigned a weight. For example, some macrostates may be combinatorially more likely to occur than others and thus will have a larger weight in the feasible set. Determining how to weight each macrostate depends on whether hosts and/or parasites are considered labeled or unlabeled (Table 1; Haegeman and Etienne 2010).

One option is to specify that both hosts and parasites are unlabeled such that all possible macrostates are equally likely to occur. This is equivalent to integer partitions used in combinatorics (Bóna 2006, Xiao et al. 2015a), so we call this model the “partition model”. The partition model is process-independent and makes no assumptions about any potential mechanisms leading to a given macrostate (Locey and White 2013). Therefore, no macrostate is more likely to occur than any other macrostate (Xiao et al. 2015a). Assuming that each macrostate is equally likely is not equivalent to assuming that any single host is equally likely to have a parasite abundance from zero to P. The probability of a single host having a parasite abundance of x = 0, …, P is p(x|P, H) = ∑_m∈F p(x|m, P, H)p(m|P, H) where m is a macrostate in the feasible set F. Using our example from above, the partition model assigns each of the three macrostates in the feasible set an equal probability of 1/3. The probability of observing a single host with x = 0, 1, 2, or 3 parasites is p(0) = 3/9, p(1) = 4/9, p(2) = 1/9, and p(3) = 1/9.

A second option for weighting macrostates is to again assume that parasites are unlabeled, but now assume that hosts are labeled. This is equivalent to integer compositions used in combinatorics (Bóna 2006, Xiao et al. 2015a), so we call this model the “composition model”. Using the composition model, particular macrostates are more likely to occur because they are associated with a larger number of possible configurations. For example, given labeled hosts and unlabeled parasites, the macrostate {3, 0, 0} could be realized from three different configurations: (3, 0, 0), (0, 3, 0), and (0, 0, 3). Enumerating all the configurations for the other macrostates in our example feasible set, we see that the macrostate {2, 1, 0} can occur six ways and {1, 1, 1} can occur one way. Therefore, the macrostate {3, 0, 0} has a weight of 3/10, {2, 1, 0} has a weight of 6/10, and {1, 1, 1} has a weight of 1/10. The probability of observing a single host with x = 0, 1, 2, or 3 parasites is P(0) = 4/10, P(1) = 3/10, P(2) = 2/10, and P(3) = 1/10.

More generally, for any macrostate m in a feasible set with P unlabeled parasites and H unlabeled hosts there are a total of $b_m=\frac{H!}{{\Pi }_{i\in A}{h}_i!}$ configurations with unlabeled parasites and labeled hosts (Brualdi 2010). A is a set containing the unique parasite abundances found in macrostate m, i is a particular member of that set, and h_i is the number of hosts in macrostate m that have a parasite abundance i. Note that ∑_i∈A h_i = H. The total number of possible configurations of all macrostates using the composition model is given by $D=\frac{(H+P-1)!}{P!(H-1)!}$ (Harte 2011). Taken together, the weight on any particular macrostate m using the composition model is $\frac{b_m}{D}$.

In summary, both the composition and partition models place our observed host-parasite distribution in the context of all possible observable host-parasite distributions. In particular, this allows us to ask an important question in parasite ecology: does a host-parasite distribution contain any information about biological mechanism beyond that already contained in P and H? Because there is no general consensus on which approach is preferable (Haegeman and Etienne 2010, Xiao et al. 2015a), we consider both the partition model and the composition model in this study. Figure 1 gives a visual comparison of these two models.

Figure 1:

A. and B. show how the predictions from the partition model and composition model were generated. Random macrostates were drawn from the weighted feasible set (light gray lines) and the predicted distribution was computed as the central tendency of these randomly drawn weighted macrostates (thick lines with dots). Each dot represents a host in the predicted distribution with a given parasite abundance and rank. Hosts with low ranks (low ln(ranks)) have a larger number of parasites than hosts with high ranks (high ln (ranks)). C. and D. compare the partition and composition models for two different values of P and H. The more familiar Poisson model is also included for reference. The partition and composition models predict more aggregated host-parasite distributions than the Poisson model and the partition approach tends to produce more aggregated distributions than the composition model. The degree that the predictions from the partition and composition models differ depends on the values of P and H.

We could have also considered two other approaches: labeled hosts and labeled parasites or unlabeled hosts and labeled parasites. We chose not to consider these approaches because assuming labeled parasites is neither consistent with the pattern that we are interested in (i.e. the host-parasite distribution) nor how host-parasite systems are sampled. Assuming labeled parasites tracks the location of each individual parasite in the host population, whereas we are interested in the population-level distribution of parasites across hosts (see Xiao et al. 2015a, for the equivalent argument in free-living individuals). Moreover, specifying labeled parasites assumes that the system could be sampled by randomly choosing a parasite and assigning it a unique label and a label corresponding to the host in which it was found (assuming labeled hosts). This process would then be repeated until some number of P parasites were sampled. The total number of hosts H would then be given by the number of unique host labels on our P sampled parasites. This is not how host-parasite systems are sampled. Instead, H hosts are randomly sampled and the P parasites within these hosts are counted. This is more consistent with unlabeled parasites.

Despite these issues, the case with labeled hosts and labeled parasites is noteworthy because it results in a Poisson distribution of parasites across hosts (see Appendix S1). However, the model resulting in the Poisson distribution has exactly the same number of assumptions as the partition and composition models, so there is no a priori reason to favor one model over the other. The only way to discriminate between the approaches is to compare them to empirical host-parasite distributions (Haegeman and Loreau 2009, Haegeman and Etienne 2010, Xiao et al. 2015a), against which the Poisson almost universally fails (Shaw and Dobson 1995, Shaw et al. 1998, Wilson et al. 2002). Appendix S6: Figure 1 illustrates the completely unsurprising result that the Poisson distribution also does not capture the level of parasite aggregation in the data we present here.

Moving from weighted feasible sets to constraint-based null model predictions

The proceeding section described how we enumerated and weighted the feasible sets for the partition and composition models. This section describes how we generate the predicted host-parasite distributions from these two models.

Given a weighted feasible set of macrostates from either the partition or composition model, the central tendency of this feasible set provides a prediction for the most likely host-parasite distribution given the constraints P and H (Locey and White 2013). We define the central tendency of a weighted feasible set as the vector of marginal medians of this feasible set (Appendix S2). For most realistic values of P and H it is computationally intractable to enumerate all possible macrostates in the feasible set to compute this central tendency. To address this problem, we used the algorithms provided by Locey and McGlinn (2013) to randomly draw macrostates from all possible macrostates in a feasible set defined by P and H. We then computed the central tendency of this sample as an estimate of the central tendency of the full feasible set (Figure 1; Locey and White 2013). To generate the predicted host-parasite distribution for the partition model, we drew 1000 random macrostates from a feasible set defined by P and H and used the central tendency of this sample as our predicted host-parasite distribution (Figure 1).

While we could have used the same approach to compute the predicted host-parasite distribution for the composition model by weighting each randomly drawn macrostate m by b_m/D, we instead used the analytical result from maximum entropy theory that the probability p(x|P, H) of a single host having x parasites under the composition model is (Haegeman and Etienne 2010)

$$p(x|P,H)=\frac{\left(\begin{array}{c}P-x+H-2\\ P-x\end{array}\right)}{\left(\begin{array}{c}P+H-1\\ P\end{array}\right)}$$ (1)

The predicted rank abundance distribution of equation 1 is equivalent the central tendency of the weighted feasible set for the composition approach (Appendix S2). Moreover, equation 1 shows us that the composition approach is equivalent to assuming that host-parasite distributions follow a finite negative binomial distribution with k = 1 (Zillio and He 2010). Note that we are not arbitrarily setting k = 1 – this is a direct result from maximizing entropy with respect to the constraints P unlabeled parasites and H labeled hosts. Moreover, the finite nature of this distribution is a direct result of the constraint P, which can lead to better descriptions of aggregation in finite populations (Zillio and He 2010). However, P is similar to the number of trials in a binomial distribution and cannot be tuned to improved the fit of the model.

In summary, we used both a sampling based approach and an analytical formula to generate predicted host-parasite distributions from the weighted feasible sets of our two constraint-based null models. In the context of more commonly used distributions in disease ecology, these two constraint-based null models have one less parameter than a negative binomial model, which is a very flexible distribution that often fits host-parasite distributions very well (Shaw et al. 1998). We stress that the goal of this study is not to ask whether these distributions do better or worse than a negative binomial in predicting a host-parasite distribution, but whether host-parasite distributions tend to contain information beyond what is given by P and H.

Comparing constraint-based models to empirical data

Description of empirical data

To test whether empirical host-parasite distributions contained information beyond that given by the constraints P and H, we used an extensive dataset of all macroparasites found in 8099 amphibian hosts across 205 ponds (sites) in the East Bay region of California (Alameda, Contra Costa and Santa Clara counties) from 2009–2014 (Johnson et al. 2013). This included ponds from publicly accessible parks, open space preserves, municipal watershed districts, and private ranches. In this field study, we sampled recently metamorphosed amphibians, as these provide a reliable and standardized indicator of infections acquired during aquatic development from the associated pond. In a given survey event, we randomly collected at least 10 of each host species as they approached metamorphosis using the methods described in Johnson et al. (2016). To measure parasite abundance, we performed a systematic examination of all major tissues and organs in the sampled hosts for parasites (Hartson et al. 2011). The sampled amphibians consisted of Pseudacris regilla (Pacific chorus frog, n = 4431), Anaxyrus boreas (Western toad, n = 1309), Lithobates catesbeianus (American bullfrog, n = 410), Taricha torosa (California newt, n = 1568), and Taricha granulosa (Rough-skinned newt, n = 381).

We focused the following analyses on the five most common macroparasites in the system in terms of both prevalence and abundance. These were the larval trematodes Ribeiroia ondatrae (RION), Echinostoma sp. (ECSP), Alaria sp. (ALAR), Cephalogonimus sp. (CEPH), and Manodistomum sp. (MANO). All of these trematodes have complex life cycles in which their first intermediate hosts are pulmonate snails, their second intermediate host can be amphibians, snails or fishes, and their definitive hosts are water-associated vertebrates (reptiles, amphibians, birds, or mammals) (Johnson and McKenzie 2008).

Comparing models to data

We determined whether the empirical distributions of parasites across hosts deviated from the predictions of our two constraint-based models for each combination of host species and parasite species at each site during each year. We included a year-by-site-by-host-by-parasite distribution only if it had at least 10 parasites and 10 hosts. Given this criterion, we were able to compare the constraint-based models to 842 host-parasite distributions. As expected, 837 of these distributions were aggregated with a ln(variance to mean ratio) greater than zero (Appendix S6: Figure 1). For each of these distributions, we extracted the total number of individuals of a given amphibian species (H) and parasites of a given trematode species (P) and calculated the corresponding rank abundance distribution (RAD) for the constraint-based models as the central tendency of the weighted feasible set (see Moving from weighted feasible sets to constraint-based null model predictions). The RAD gives the predicted parasite abundances from a given distribution for H hosts and assigns a rank of 1 to the host with highest abundance and a rank of H to the host with the lowest abundance (Harte 2011, White et al. 2012).

To determine whether an observed host-parasite distribution deviated from the central tendency of a constraint-based model, we plotted the observed RAD (obs_i) versus the predicted RAD (pred_i). We then calculated the R² value based on a fit to the 1:1 line using the equation (White et al. 2012, Xiao et al. 2015b)

$$R^2=1-\frac{{\sum }_i(\text{ln}\left({\text{obs}}_i+1\right)-\text{ln}{\left({\text{pred}}_i+1\right)}^2}{{\sum }_i{\left(\text{ln}\left({\text{obs}}_i+1\right)-\overline{\text{ln}\left({\text{obs}}_i+1\right)}\right)}^2}$$ (2)

where i is the rank (i = 1, …, H) of each observed or predicted host in a distribution. R² to the 1:1 line describes how much variance in the observed data is described by the model prediction. If the model describes a large portion of the variation in the observed data then the R² value will be larger, with unity being a perfect prediction. If the model is a poor fit, the R² value will be much less then unity and possibly negative if the 1:1 line was a worse fit than assuming that each host had a parasite abundance equal to the mean of the observed distribution (White et al. 2012). We calculated R² values for each distribution independently as well as for all distributions combined. We also explored a number of alternative measures of goodness-of-fit that gave consistent results (Appendix S3).

Extending the constraint-based null models to account for aggregating and disaggregating mechanisms

When an observed host-parasite distribution deviated from the central tendency of a constraint-based null model, this provided evidence that additional constraints/mechanisms beyond just P and H were disproportionately affecting the system (Harte and Newman 2014). We developed two ways to extend the constraint-based null models to detect whether classic aggregating and disaggregating mechanisms may be affecting host-parasite distributions beyond P and H.

Accounting for disaggregating mechanisms

Disaggregating mechanisms such as parasite-induced host mortality can play an important role in structuring empirically observed host-parasite distributions (Anderson and Gordon 1982). The parasite Ribeiroia ondatrae is known to have a strong, intensity-dependent effect on the survival of some amphibian hosts where increased parasite intensity leads to increased limbmalformations and decreased survival (Johnson 1999). This means that hosts with large parasite burdens are removed from the system, making the parasite distribution more uniform. Therefore, Ribeiroia-induced host mortality may interact with P and H to further constrain the shape of host-Ribeiroia distributions.

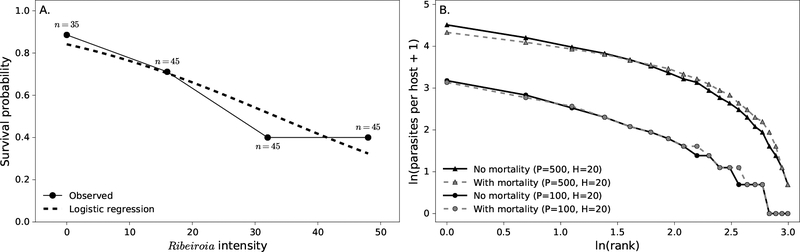
We included Ribeiroia-induced host mortality as an additional constraint on the partition and composition null models. To do this, we used laboratory-derived survival curves that describe how Ribeiroia intensity affects amphibian host survival probability (Johnson et al. 2012). We focused on the amphibian species Pseudacris regilla because Ribeiroia-induced mortality and malformations in this species have been documented in the field and in the lab (Johnson 1999, Johnson and McKenzie 2008) and there were a large number of P. regilla-Ribeiroia distributions in the dataset on which to test the extended models (n = 133). The intensity-dependent survival curve specified the probability of an amphibian host surviving from larva to recent metamorph with some observed parasite intensity. We assumed that this curve followed a logistic function and estimated the parameters of this function from independent laboratory data (Figure 2A; Appendix S4; Johnson 1999).

Figure 2:

A. The black line and dots give the parasite-induced host mortality data from Johnson (1999) where Pseudacris regilla hosts were infected with varying Ribeiroia intensities. Frogs were exposed to Ribeiroia cercariae as tadpoles and the experiment was stopped after tadpoles metamorphosed. The dashed line gives the mean predictions of the logistic regression model fit to the data. This logistic regression was then imposed as a mortality constraint on the partition model and the composition model. B. An example of the effect of including the laboratory-estimated survival curve on the predictions of partition models with P = 500 parasites and H = 20 hosts and P = 100 and H = 20. The symbols indicate a given host in a predicted distribution with a particular parasite abundance and rank. Hosts with low ranks (low ln(ranks)) have a larger number of parasites than hosts with high ranks (high ln (ranks)). Depending on the values of P and H, the mortality constraint could noticeably reduce aggregation (triangles) or have little effect on aggregation (circles).

We then used this result to further constrain the partition and composition model predictions by assigning each macrostate a likelihood using the estimated survival function (Figure 2A). For each constraint-based model, the macrostates were then weighted by this likelihood such that macrostates with small likelihoods (e.g. ones that contained hosts with high parasite loads) were less likely to be observed than macrostates with large likelihoods. Using this weighting scheme, we sampled from models that were constrained on P, H and Ribeiroia-induced host mortality using a Metropolis-Hastings algorithm (Figure 2B; see Appendix S4 for a full description of the algorithm used).

Once we obtained estimates of the mortality-constrained partition and composition models, we compared the resulting predictions to the observed P. regilla-Ribeiroia distributions using the methods described in Comparing models to data. In addition, we also calculated an approximate AICc for the constraint-based model with and without an additional mortality constraint. We compared these models using ΔAICc where we considered an absolute value of ΔAICc > 2 as evidence that one model was better than the other (Burnham and Anderson 2002). The AICc values were approximate because there was no analytically defined likelihood for the mortality-constrained models. Therefore, we approximated the likelihood by drawing a large number of samples (e.g. 500 samples) from the mortality-constrained feasible set and computing the likelihood of a single host having x parasites using the equation $p(x|P,H)={\sum }_{m\in \widehat{F}}p(x|m,P,H)p(m|P,H)$, where $\widehat{F}$ is the sampled feasible set. As we did not perform any additional model fitting to derive the mortality-constrained model, it was not statistically inevitable that the central tendencies of the mortality-constrained models would provide a better representation of the data. Therefore, an improvement in agreement between model and data, reflected in an increased R² or decreased AICc for the mortality models relative to models without mortality, is strong evidence that Ribeiroia-induced mortality is constraining the distribution beyond P and H.

Accounting for aggregating mechanisms

Host heterogeneity, whether it be in susceptibility, parasite encounter rates, behavior or other factors, is an important mechanism leading to aggregation in host-parasite systems (Cornell 2010, Raffel et al. 2011). We accounted for this aggregating mechanism by extending the constraint-based models to include empirically observed levels of host heterogeneity. In particular, we explored discrete host heterogeneity where we assumed that overaggregation relative to the predicted model was a result of mixing discrete groups of hosts (Grafen and Woolhouse 1993, Wilson et al. 2002). This approach is different than the standard practice of fitting a negative binomial distribution to overaggregated host-parasite distributions. If the goal of an analysis is to obtain the best possible fit to an observed host-parasite distribution then it is well-known that fitting a negative binomial distribution provides an excellent model of overaggregated host-parasite distributions (Shaw et al. 1998, Calabrese et al. 2011). However, if the goal of an analysis is to determine whether a host-parasite distribution contains any information beyond what is contained in P and H, fitting a negative binomial model does not provide immediate insight into what constitutes unusual aggregation or the potential host attributes leading to this overaggregation (but see Alonso and Pascual 2006, Fowler and Hollingsworth 2016, for various mechanistic interpretations of the negative binomial k parameter). Extending a constraint-based model to include discrete host-heterogeneity, as is done here, can help generate more specific hypotheses as to the relative importance of different levels of host-heterogeneity in structuring a host-parasite distribution.

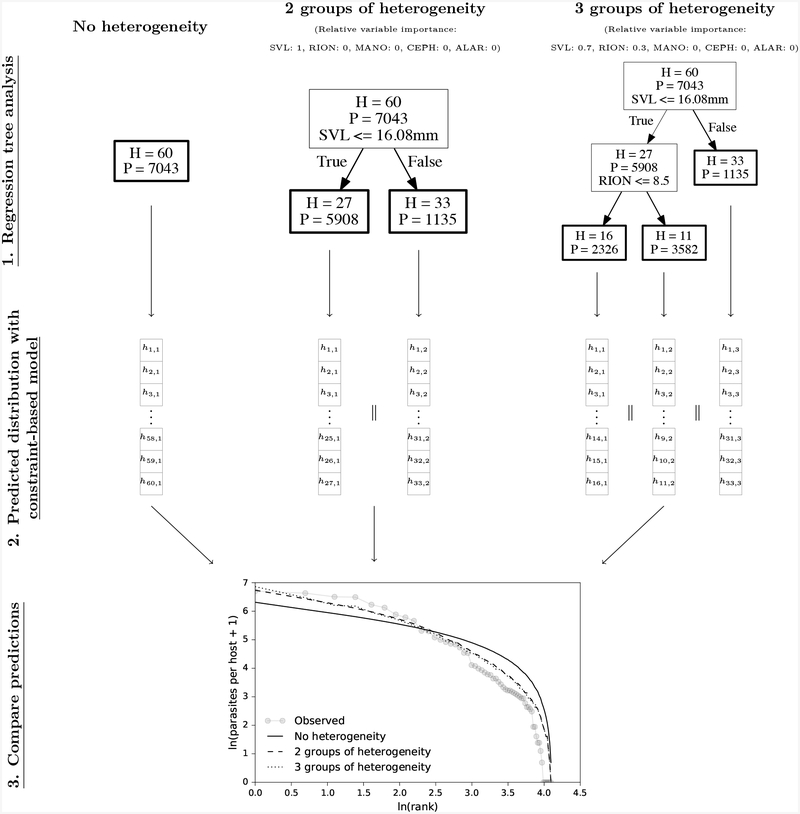
To incorporate discrete host-heterogeneity, we used 5 observed host attributes by which we could bin hosts into groups of heterogeneity. The first attribute was host body size (i.e. snout-vent length), which is a well-known attribute affecting parasite exposure and aggregation (Grutter and Poulin 1998, Poulin 2013). The other 4 host attributes were the parasite abundances of the larval trematodes, excluding the focal trematode, infecting an individual host (see Fig. 3 for an example). Coinfection can potentially increase aggregation by increasing heterogeneity in host susceptibility to the focal parasite (Cattadori et al. 2008), but can also decrease aggregation by increasing intra-host parasite negative density dependence (Pacala and Dobson 1988). Here we consider coinfection as a mechanism leading to increased aggregation.

Figure 3:

A diagram showing how host-heterogeneity can be incorporated into constraint-based models. Step 1: Consider, for example, a distribution for the parasite Echinostoma sp. in the host Pseudacris regilla with H = 60 hosts and P = 7043 parasites. When no host heterogeneity is included, the central tendency of the constraint-based model can be computed directly from H and P as described in the main text. To include groups of heterogeneity, a regression tree analysis is performed in which the response variable is Echinostoma abundance and the predictor variables are P. regilla body size (snout-vent length, SVL) and the abundance of Ribeiroia ondatrae (RION), Alaria sp. (ALAR), Cephalogonimus sp. (CEPH), and Manodistomum sp. (MANO) in a particular host. In the example above, the regression tree analysis shows that the “best” way to make two groups of heterogeneity given the predictor variables is to split the 60 P. regilla individuals into those with SVL ≤ 16.08 mm and those with SVL > 16.08 mm. To make three groups of heterogeneity, P. regilla individuals with SVL ≤ 16.08 are again split into individuals with RION abundance ≤ 8.5. For each of these regression trees, we can determine the relative importance of each variable in building the regression tree by how much they decrease the sum of squared error compared to the other predictors. Step 2: We can then compute the central tendency of the constraint-based model for each of these groups of heterogeneity (the bold boxes above) using the total number of hosts and parasites in each heterogeneity group. Each heterogeneity group has its own rank abundance distribution with h_i,j being the ith ranked host with some number of parasites in heterogeneity group j. Concatenating (‖) these rank abundance distributions together and re-ordering the resulting vector gives the predicted constraint-based model after allowing for P and H to vary with host heterogeneity. Step 3: These predicted distributions can then be compared to the observed host-parasite distribution.

Using these 5 host attributes, we used regression trees in which the response variable was the focal parasite abundance and the predictor variables were the 5 host attributes described above (Fig. 3). Separate regression trees were run for each of the 842 host-parasite distributions. For a given host-parasite distribution, we found the best regression tree with 2–5 of groups of host heterogeneity and calculated the relative importance of each predictor variable based on how much they reduced the sum of squared error compared to the other predictor variables (Fig. 3). We restricted each group to have at least 2 hosts. Within each of these j groups we determined the total number parasites P_j and the total number of hosts H_j. The regression tree approach explores how various predictor variables affect mean parasite load (James et al. 2013), which is consistent with the constraint-based assumption that much of the information about the host-parasite distribution is contained in P and H.

To generate a constraint-based model RAD from the results of the regression tree, the RADs for each group j were computed with P_j and H_j and the predicted RAD was given by the concatenation for these j vectors (Fig. 3). This predicted mixture RAD could then be analyzed using the various methods described above. We also computed approximate AICc values for each heterogeneity model that we applied to an observed distribution. As described in the previous section, we did this by drawing 500 macrostates from the heterogeneity model to generate an estimate for the probability of a single host having x parasites under either the partition or composition assumptions. Finally, we employed a randomization test to ensure that any increase in R² after including host heterogeneity was due to the host attributes considered, rather than just the act of grouping itself (described in Appendix S5).

In summary, while P and H alone may sometimes not sufficiently constrain an observed host-parasite distribution, this approach is testing whether allowing P and H to vary as a function of host heterogeneity can account for deviations from the constraint-based null models. All analyses were performed in Python (version 2.7.11) and the code to replicate the analysis can be found at https://github.com/mqwilber/feasible_parasites.

Results

Do host-parasite distributions contain information beyond that contained in P and H?

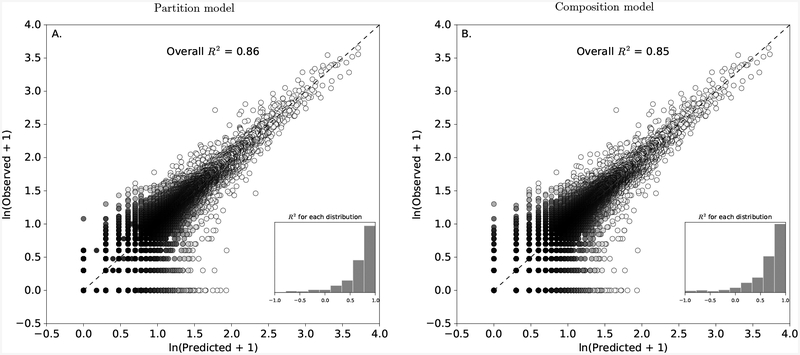
Overall, the partition model and composition model described 86% and 85% of the variation in all of the observed host-parasite distributions combined, respectively (Fig. 4A, B). For any particular host-parasite distribution, the median R² for the partition and composition models was 0.78 and 0.76, respectively (Fig. 4A, B). Examining the models with regard to host-by-parasite combinations, the median R² for the constraint-based models tended to be close to 80% for the various host-by-parasite combinations (Appendix S6: Fig. 2), with some notable exceptions for the host Lithobates catesbeianus and the parasites Alaria sp. and Cephalogonimus sp. (Appendix S6: Fig. 2–5).

Figure 4:

Plots showing the fit of the partition model A. and the composition model B. to all of the 842 observed host-parasite distributions considered in this study. The black-dashed line gives the 1:1 line and the overall R² gives the percent of variation that the constraint-based models explain in all of the observed data. Each point represents a single individual host from one of the 842 distributions with a given predicted and observed parasite abundance. Darker colors indicate a higher density of points in the region than lighter colors. The inset histogram shows the distribution of R² values calculated for each of the 842 individual host-parasite distributions.

The partition model tended to describe more variation in host-parasite distributions than the composition model (Fig. 4, Appendix S6: Fig. 6). The composition model is equivalent to a finite negative binomial model with k = 1 and many of the observed host-parasite distributions in this study had maximum-likelihood estimated k parameters $\left(\widehat{k}\right)$ less than one (Appendix S6: Fig. 6). While $\widehat{k}\ne 1$ is not necessarily incompatible with the composition model due to estimation error in the negative binomial k parameter (Lloyd-Smith 2007), the partition model did predict more aggregated distributions than the composition model (Fig. 1). This led to the partition model accounting for a larger amount of the variance in host-parasite distributions with k < 1 (Appendix S6: Fig. 6).

Accounting for disaggregating and aggregating mechanisms

Disaggregating mechanisms: Parasite-induced host mortality

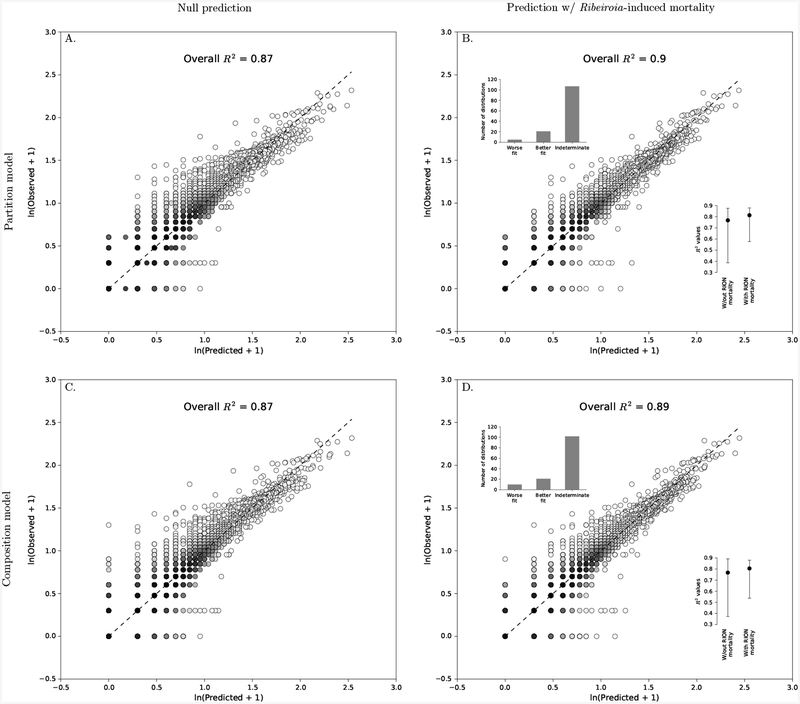
Including independently-estimated Ribeiroia-induced parasite mortality into the constraint-based models improved the overall fit of the models to Pseudacris regilla-Ribeiroia distributions. This was seen in three different metrics. First, there was a significant increase in the overall R² when the mortality constraint was included (bootstrapped 95% confidence interval for the difference in overall R² between the mortality constraint-based model and the null constraint-based model from 1000 re-samples: feasible set model, [0.019, 0.033]; maximum entropy model, [0.018, 0.035]; neither interval includes 0; Fig. 5A–D). This improvement in fit can be visualized by observing the tightening of the points to the 1:1 line when Ribeiroia-induced mortality was included in the model (Fig. 5A–D). Second, the median R² for individual Pseudacris-Ribeiroia distributions increased and the variance around the individual R² values decreased (Fig. 5B,D). Third, for individual distributions that were better fit under either the mortality or no mortality models based on the absolute value of ΔAICc > 2, a significant or marginally significant proportion were better under the mortality model (partition model: Binomial test, N = 26, better under mortality model = 21, p = 0.002; composition model: Binomial test, N = 31, better under mortality model = 21, p = 0.07; Fig. 5B,D).

Figure 5:

The effect of including empirically-estimated Ribeiroia-induced Pseudacris regilla mortality into the partition and composition models. The first column in this plot (A., C.) compares 133 observed rank abundance distributions (RAD) of Ribeiroia-P. regilla with the RADs predicted by the constraint-based models before they were constrained on parasite-induced host mortality. The second column (B., D.) compares the observed and predicted RADs after they were constrained on parasite-induced host mortality. The 1:1 line is given by the black, dashed line. Each point represents a single host with a given predicted and observed parasite abundance. Darker colors indicate a higher density of points in the region than lighter colors. The inset dot plots in B. and D. show the first through third quartiles of the R² values from each of the 133 distributions without and with Ribeiroia-induced mortality. The inset bar plots in B. and D. give the number of observed distributions that were a worse fit with the mortality constraint, a better fit with the mortality constraint, or were equally good with either (Indeterminate) based on ΔAICc.

Aggregating mechanisms: Host-heterogeneity

There were 124 unique host-parasite distributions that had R² < 0.5 and an observed variance to mean ratio greater than the variance to mean ratio of one of the constraint-based models. We considered these distributions to be overaggregated with respect to the constraint-based models. Of these 124 distributions, 48 were Echinostoma (12% of all Echinostoma distributions) 29 were Alaria (35% of all Alaria distributions), 17 were Cephalogonimus (24% of all Cephalogonimus distributions), 17 were Manodistomum (33% of all Manodistomum distributions), and 13 were Ribeiroia (5% of all Ribeiroia distributions).

Considering only these overaggregated distributions, we used the regression tree analysis described above to test whether further constraining P and H based on known host attributes improved the fit of the constraint-based models to the observed host-parasite distributions. The heterogeneity models built from the regression tree analysis improved the fit of the constraint-based models to the empirical data beyond what would be expected by the inevitable increase in fit by simply grouping hosts (overall R² greater than the 95% interval from randomly permuting hosts into groups; Fig. 6). The improvement in fit can be visualized in Figure 6 by noting how the data points compress to the 1:1 line as more groups of heterogeneity are included. Note that this increase in model fit was not achieved by minimizing or maximizing any criteria about how well the heterogeneity model fit the observed host-parasite distribution. Finally, for three or more groups of host-heterogeneity, including just host body-size heterogeneity as an additional constraint yielded better models in terms of both higher R² values and larger AICc weights than including just heterogeneity in coinfection as an additional constraint (Fig. 7A–D).

Figure 6:

The effect of discrete heterogeneity on the 124 host-parasite distributions that were overaggregated relative to at least one of the constraint-based models (all hosts and parasites shown together). The first column in this plot shows the predicted rank abundance distributions (RAD) compared to the observed RADs when no host heterogeneity was included in either of the two constraint-based models. The black, dashed line gives the 1:1 line and the overall R² describes the amount of variation the constraint-based models described in all 124 overaggregated distributions. Each point represents a single host with a given predicted and observed parasite abundance. Darker colors indicate a higher density of points in the region than lighter colors. The histogram in the lower right hand side gives the distribution of R² values for each particular host-parasite distribution. The second and third columns in this plot show the effect of adding 2 and 3 groups of host heterogeneity, respectively, on the predicted host-parasite distributions based on the results from a regression tree analysis on known host attributes in the dataset. The plots in the upper left hand corner show the mean importance of a given host attribute in structuring the regression tree for all the 124 overaggregated host-parasite distributions. The predictor variables were body-size (svl), Echinostoma sp. (ECSP), Ribeiroia (RION), Cephalogonimus (CEPH), Alaria (ALAR), and Manodistomum (MANO). The predictor importance was the same for all models within a heterogeneity group and are therefore only displayed once for each group. Finally, the 95% interval displayed in the plot gives the 95% quantiles of overall R² values based on randomly permuting parasites into the groups predicted by the regression tree analysis. If the overall R² is greater than the interval, it shows that the increase in R² from the regression tree is a result of the predictors used in the regression tree analysis, rather than just grouping itself.

Figure 7:

Plots show the effects of adding groups of heterogeneity to the constraint-based null models on two metrics: R² and AICc weights. Three heterogeneity models with different predictor variables were considered: only host body size, only coinfection with other trematodes, and both body size and coinfection with other trematodes. A. and B. show how the median R² of the 124 overaggregated distributions changes for the partition model (A.) and the composition model (B.) when heterogeneity in body size and and/or coinfection with other trematodes was considered. The points represent the median R² and the error bars give the approximate 95% confidence interval around the median. C. and D. show the median AICc weights for all 124 distributions for a given group size and heterogeneity model. For example, for the partition model every observed host-parasite distribution had 13 candidate models: the no-heterogeneity model (1 group) and three heterogeneity models times four groupings (2 groups, 3 groups, 4 groups, 5 groups). The AICc weights were calculated for these 13 models for a single distribution and then the median AICc weights for a given model was computed for all 124 overaggregated distributions. The error bars give the approximate 95% confidence intervals around these medians. These AICc weights are only comparing within a constraint-based model and are not comparing the partition model (C.) to the composition model (D.).

Discussion

The shape of a sampled host-parasite distribution is necessarily constrained by the total number of hosts H and the total number of parasites P found in that sample (Haegeman and Etienne 2010, Locey and White 2013). While there are indisputably biological mechanisms leading to the shape of this distribution (Wilson et al. 2002), inferring anything about these mechanisms may be difficult without first accounting for the constraints imposed by P and H. Here we use an extensive dataset of 22 host-parasite combinations and 842 empirical host-parasite distributions to show that aggregated host-parasite distributions tend to be consistent with the most likely distribution given P and H. This suggests that when trying to make inference about biological mechanism directly affecting patterns of parasite aggregation one must account for the mechanisms indirectly affecting aggregation through changes to P and H.

This finding has three important implications for disease ecology. First, there is a rich history in parasitology of using the shape of host-parasite distributions in combination with dynamic models and statistical techniques to infer which mechanisms may be affecting a given host-parasite system (Crofton 1971, Anderson and Gordon 1982, Grear and Hudson 2011). While these approaches are in no way inappropriate, our results show that the instances in which the shape of a host-parasite distribution contains more information beyond what is contained in P and H may be more rare than previously thought. This result is consistent with other findings showing that log mean parasite load describes up to 88% of the variation in the log variance of parasite load, leaving only 13% of the variation to be described by biological mechanisms acting on something other than the mean (Shaw and Dobson 1995, Poulin 2013). Our results take this a step further by using constraint-based models to explicitly predict the entire host-parasite distribution given P and H. We find that, similar to Poulin (2013), much of the variability in the entire host-parasite distribution (not just the variance) is well predicted by mean parasite load and how many hosts are present in the sample. As a next step, explicitly considering whether specific attributes of observed host-parasite distributions systematically deviate from constraint-based predictions, such as the number of predicted uninfected hosts, could shed additional light on when host-parasite distributions contain much information beyond P and H.

The second implication is that the success of constraint-based models in disease ecology will allow them to be adopted as robust null models against which empirical host-parasite distributions can be compared. Constraint-based models are being increasingly used as robust null models in community ecology to determine when ecological mechanism may be disproportionately affecting the shape of population- and community-level distributions (Ulrich and Gotelli 2013, Newman et al. 2014, Xiao et al. 2015b). In disease ecology, by using a constraint-based model to predict parasite aggregation given P and H, we can determine when a host-parasite system is showing unusual levels of aggregation to help direct modeling and experimental efforts. For example, future studies could explore whether factors such as the complexity of parasite life cycles (Lester and McVinish 2016), self-reinfection processes (Grear and Hudson 2011), or the composition of the host and parasite community in which a distribution is observed (Krasnov et al. 2006) lead to consistent deviations from constraint-based predictions.

Third, the general success of constraint-based models in describing host-parasite distributions has important implications for understanding the dynamics of host-macroparasite systems. Most macroparasite models explicitly model the state variables H and P (Anderson and May 1978, Dobson and Hudson 1992) and examine, in addition to other biological factors, how either fixed (Anderson and May 1978) or dynamic aggregation (Kretzschmar and Alder 1993, Rosà et al. 2003) influences host and parasite dynamics. Constraint-based models in turn predict that aggregation is largely determined by exactly these state variables. Therefore, a constraint-based approach to parasite ecology can be directly linked back to a more familiar mechanistic framework by examining the implications of constraint-based, aggregation predictions on dynamics of the total number of hosts and parasites in a system. Linking constraint-based models for describing aggregation to dynamic equations for the state variables of a system has often been alluded to in macroecology (Supp et al. 2012, White et al. 2012), but has been difficult to implement (Harte 2011). The rich empirical and theoretical understanding of biological factors affecting the total number of hosts and the total number of parasites in a system (Kretzschmar and Alder 1993, Hudson et al. 1992, Dobson and Hudson 1992) makes disease ecology an ideal field in which to make this connection.

In addition to providing robust null models and a unique opportunity to link dynamic, mechanistic models with a constraint-based approach, the constraint-based models can also be extended beyond null models to test the importance of potential aggregating and disaggregating mechanisms affecting host-parasite distributions. In this study, we extended the constraint-based models to include independently estimated relationships between parasite intensity and amphibian survival and found that accounting for the well-described negative effect of Ribeiroia on P. regilla (Johnson 1999, Johnson et al. 2012) improved the fit of the constraint-based model to empirical host-parasite distributions. While this improvement in model fit was not drastic as P and H already accounted for 87% of the variation in the distributions, it was achieved using a survival curve estimated from an independent dataset (Johnson 1999), providing strong evidence that parasite-induced mortality is influencing P. regilla-Ribeiroia distributions beyond just changes to P and H.

Moreover, we also found that extending constraint-based models to include heterogeneity in host body size and coinfection with other trematode parasites accounted for much of the overaggregation in observed distributions that were not well described by the constraint-based null models. In particular, we found evidence that host body size was generally a more important constraint on the host-parasite distribution than a host’s level of coinfection with other trematodes. This result is consistent with previous studies which have shown the importance of host age/body size heterogeneity for increasing parasite aggregation due to changes in host immunity and/or exposure to parasites with host age/body size (Pugliese et al. 1998, Poulin 2013). Moreover, while previous work has shown that coinfection can act as a type of host heterogeneity and increase parasite aggregation (Cattadori et al. 2008), this same work has also shown that host characteristics such as age/body size, sex, and breeding status can often be more important factors affecting parasite aggregation and host-parasite dynamics than coinfection. While we have considered host-heterogeneity and parasite-induced mortality separately in this study, there is no reason that the constraint-based approach cannot be extended to included multiple mechanistic constraints. However, this must be done judiciously as imposing too many constraints could lead to trivial agreements between the model and data (Haegeman and Loreau 2009).

In conclusion, constraint-based models provide a powerful framework for understanding when we can reliably infer mechanism from parasite aggregation. However, we are not advocating that the constraint-based approach should replace the process-based approach that has been so successful in disease ecology. Rather, the constraint-based approach is another tool in the disease ecologist’s belt that can highlight when observed parasite aggregation is telling us something novel about the mechanisms acting in our system and when we should acknowledge the statistical inevitability that sometimes host-parasite distributions simply look how they must look given P and H.