Evaluating the impact of trade-offs in diagnostic test accuracy, time-to-isolation, and accessibility on outbreak response for the Ebola virus: a mathematical modeling study

Abstract

Background

Ebolavirus and related filoviruses are feared pathogens due to high mortality rates, and cases are confirmed using reverse transcription-polymerase chain reaction (RT-PCR) testing. Compared to rapid diagnostic testing (RDT), RT-PCR has higher accuracy but longer turnaround time and lower testing rate. RDTs’ accuracy for Ebola does not meet the World Health Organization’s (WHO) target product profile (TPP). This TPP, however, excludes trade-offs between accuracy, time-to-isolation (the time from getting tested to getting hospitalized and isolated), and accessibility. This research aims to guide diagnostic test development and use by identifying trade-offs in accuracy, time-to-isolation, and accessibility that enable impactful outbreak response.

Methods

A mathematical compartmental model was calibrated to the 2014–2016 Sierra Leone EBOV epidemic, including test accuracy, accessibility, and time-to-isolation parameters. These parameters were varied to evaluate their impact on total epidemic size in different in isolation and in combination.

Results

Reductions in EBOV test sensitivity or specificity alone will increase the expected number of cases from 11.7 to 223%, while any decrease in time-to-isolation alone (due to a more rapid test result) or increase in testing rate alone would decrease the expected number of cases by 47.7–87.7%. When combining the three factors together, the benefits associated with an RDT would outweigh the harms, with a combined net reduction of mean cases between 71.6 and 92.3%.

Conclusions

When coupled with a more rapid turnaround time and increase in test access, the use of a lower performance test can result in significantly reduced epidemic size compared to relying on PCR alone in an EBOV outbreak in a resource-limited setting.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12879-025-11273-y.

Background

Filoviruses, including Ebolavirus and Marburgvirus, are among the most feared pathogens globally due to their high mortality rates, ranging from 30 to 90%, and the lack of specific treatments [1]. Six filovirus genera have been discovered, with six species known to be pathogenic to humans [2]. There are six species in the Ebolavirus genus, of which Zaire, Sudan, Tai Forest, and Bundibugyo are pathogenic [3]. The Marburgvirus genus includes Marburg and Ravn viruses, also pathogenic to humans. The Zaire Ebolavirus (EBOV) has historically caused the most frequent and severe outbreaks [2].

Between 1976 and 2014, 25 Ebola outbreaks were reported. Given its zoonotic transmission, future outbreaks are inevitable. The most recent Ebola outbreak occurred in 2025 in Uganda, and the latest Marburgvirus outbreak in Tanzania in 2025, highlighting ongoing risk [4–6]. The 2014–2016 West Africa Ebola virus disease (EVD) epidemic caused by EBOV was the largest filovirus outbreak to date, with 28,616 probable and confirmed EVD cases and 11,310 deaths, though the actual toll was likely higher [3].

Ebolavirus transmission occurs through mucous membranes or abraded skin. After an incubation period of 2 to 21 days (average 8–10 days), symptoms begin with non-specific febrile illness, followed by gastrointestinal symptoms, hemorrhage, and possible multi-organ failure [2, 3]. ¯Early symptoms often resemble common illnesses like malaria, complicating diagnosis, especially in under-resourced hospitals [7]. These delays, combined with limited infection control, make hospitals hotspots for transmission. Nosocomial transmission is a critical driver of outbreaks, and faster detection and isolation can reduce epidemic size [1, 7, 8].

The diagnostic gold standard for EVD is viral amplification, typically requiring high-containment or well-resourced field laboratories [9]. Reverse transcription-polymerase chain reaction (RT-PCR) is recommended for field use, but still demands molecular facilities, causing delays in diagnosis [9]. Turn-around time for a confirmed laboratory EVD case ranges from 6 h to 3 days [10]. A negative RT-PCR is only reliable if conducted 72 h post-symptom onset, testing earlier may yield false negative test results and require repeat testing. Current RT-PCR costs are too high to routinely use for every febrile illness of infectious origin, making detecting a new outbreak more challenging [7].

Target product profiles (TPPs) can help address these challenges by outlining desired diagnostic characteristics for specific diseases and use cases, including sensitivity, specificity, cost, time-to-detection, and target population [11]. TPPs can inform development of accessible, effective diagnostics to help contain future outbreaks and achieve public health goals.

In October 2014, following expert consultation, the World Health Organization (WHO) issued a TPP for rapid EBOV diagnostics, recommending clinical sensitivity and specificity of > 98% and > 99% (desired), or > 95% and > 99% (acceptable), respectively [12]. The target time-to-result was < 30 min (desired), and < 3 h (acceptable) [12]. However, the epidemiological impact of meeting these targets remains unclear.

This raises the question: What trade-offs between test accuracy, time-to-detection, and accessibility are needed for an impactful EBOV outbreak response? Using mathematical modeling, this study aimed to quantify the impact of diagnostic test properties including accuracy, time-to-detection, and accessibility, on EBOV epidemic outcomes.

Methods

Model structure

We developed a compartmental transmission model for EBOV to assess the impact of diagnostic test characteristics on epidemic size. The model reflects the 2014–2016 Sierra Leone EBOV outbreak, chosen for its scale and availability of WHO data (Figure S1). This enabled exploration of counterfactuals- how the outbreak might have changed with alternative diagnostic tools.

The model is comprised of eleven ordinary differential equations and eighteen parameters (Fig. 1; Table 1, Text S1, Table S1). Disease progression is stratified into several stages: exposed, infected, hospitalized, and dead or recovered. Susceptible (S_np and S_t⁺), exposed (E_np and E_t⁺), and infected (I_np and I_t⁺) compartments are divided between those who have tested positive (_t⁺), and those untested or testing negative (_np). Exposed individuals (E_np and E_t⁺) represent people who have been infected with the virus but are in their incubation period, in which Ebolavirus cannot be transmitted [13]. After incubation, individuals become symptomatic and infectious. Testing during incubation is assumed to have very low sensitivity (0–5%)) [14]. RT-PCR sensitivity for infectious individuals tested after 72 h of symptom onset has a high test sensitivity (95—100%) [14, 15].

Fig. 1.

Compartmental model structure. S_np: Susceptible non-positives; S_t⁺ Susceptible positives; E_np: Exposed non-positives; E_t⁺: Exposed positives; I_np: Infected non-positives; I_t⁺: Infected positives; H_i^-: Hospitalized non-infected; H_i⁺: Hospitalized infected; F: Funeral; D: Death; R: Recovered

Table 1.

Key model assumptions, including the fitted parameter ranges and distribution curves

Parameter	Description	Value ranges:			Distribution curve:	Ranges based on source:
		0-123 Days	123–190 Days	190–600 Days
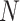
	Size of the total population in Sierra Leone (2014)	7,017,144			NA	[18]
	Transmission rate for Infected	0.12–0.30*	0.12–0.30*	0.05–0.20*	Triangular, mode: 0.24, 0.22, 0.13*	[19, 20]
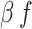
	Transmission rate for Funeral	0.16–4.74	0.16–4.74	0.16–4.74	Triangular, mode: 0.94	[16, 17, 21]
	Transmission rate for Hospitalized	0.14–1.0	0.14–1.0	0.14–1.0	Triangular, mode: 0.5	Assumption
	Testing rate for Susceptible	0.00–0.00034			Uniform	[22]
	Testing rate for Exposed	0.0–0.05			Uniform	Assumption
	Testing rate for Infected	0.5–0.9			Uniform	Assumption
	False positive rate	0.000–0.005			Beta (20/80)	[15]
	Time from symptoms to testing	3–5 days			Triangular, mode: 0.333 (3 days)	[14]
	Duration from getting tested to Hospitalized (Time-to-isolation)	1–3 days			Triangular, mode: 0.667 (1.5 days)	[10]
	Incubation period	8–10 days			Normal	[13, 23]
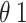
	Sensitivity for Exposed	0.00–0.05			Beta (20/80)	[14]
	Sensitivity for Infected	0.950–1.00			Beta (80/20)	[14, 15]
	Mean duration of Infected to Recovered or Funeral	8–24 days			Normal	[20]
	Mean duration of Hospitalized to Recovered or Death	4–20 days			Normal	[20]
	Mean duration of Funeral to Death	1–4 days	1–4 days	1–4 days	Triangular, mode: 0.5 (2 days)*	[16, 21]
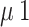
	Case fatality rate for Infected	0.25–0.60*	0.25–0.60*	0.25–0.60*	Normal	[24, 25]
	Case fatality rate for Hospitalized	0.20–0.55*	0.20–0.55*	0.20–0.55*	Normal	[24, 25]

*Parameters that were fitted; NA Not applicable

Hospitalized individuals (H_i⁻ and H_i⁺) are categorized as infected (H_i⁺) or not infected (H_i⁻). The H_i⁻ group represents false positives, who are at higher risk due to proximity to infected individuals. The H_i⁺ group includes true positives hospitalized after testing, or after exposure in hospital. Entry into H_i⁺ occurs via test-based isolation or hospital-based infection. People can also enter this compartment from being exposed or infected and tested positive (E_t⁺ and I_t⁺) at the rate of time-to-isolation. Time-to-isolation is the time it takes from getting tested to getting isolated- covering both the time-to-detection and any other delays in busy hospital settings.

Infected hospitalized individuals either recover (R) or die (D). Those dying in hospital are are assumed to have a ‘safe death’, with no further transmission at the funeral. Those dying in the community without testing are assumed to have ‘unsafe funerals’ (F), potentially infecting attendees, before transitioning to the safe death compartment (D) [16, 17]. Individuals may also recover without hospitalization or teting.

Model parameterization and calibration

The Sierra Leone epidemic was divided into three phases: early (day 0–122), middle (day 123–189), and late (day 190–578) [18]. Eighteen parameters were used, with six allowed to vary between phases- three transmission rates, two fatality rates, and the duration from funeral to death (Table 1). Allowing for these changes reflect possible shifts in resources, public awareness, and prevention behavior.

A literature review informed parameter ranges (Table 1). Distributions were selected and the model was deterministically fitted to key parameters (more on this process can be found in Table S2).

We used Monte Carlo filtering to identify baseline simulations representative of the epidemic. We ran 600,000 simulations, each with a randomly selected combination of the uncertain parameters across the identified distributions for each parameter (Table 1). These simulations were then filtered on day 179, day 480, and day 578 to cover the exponential growth phase, peak and steady state of the epidemic. Simulations that matched the WHO total case and total death data within ± 10% at each time point were considered sufficiently close to be retained in the baseline (Text S2, Tables S3, S4, Figure S2).

Scenario analysis

The calibrated model was used to evaluate scenarios varying test accuracy, accessibility, and time-to-isolation. We first varied sensitivity (85–100%), specificity (95–100%), time-to-isolation (30 min to 1.5 days), and accessibility (100-500%) individually. Second, we examined trade-offs between accuracy and accessibility, and between accuracy and time-to-isolation. Third, we assessed combined trade-offs among all three. These trade-offs evaluate whether increased testing rates and faster isolation, such as from rapid diagnostic tests, can compensate for lower test accuracy. Finally, we estimated the number of false positives in selected simulations to explore ethical implications of using lower-specificity tests.

For each scenario, we computed the mean total cases and deaths with a 95% confidence interval (CI). Since WHO declares an epidemic over after 42 days without new cases to be over when there have been no new cases for twice the maximal incubation period, i.e. 42 days. As there are no more cases or deaths after day 480 in the WHO data, day 522 was chosen as the endpoint of the epidemic, and the chosen timepoint to end the analysis. All simulations were performed using R (version 4.4.1; R Core Team, 2024) and RStudio (version 2024.04.2; Posit Software, 2024).

Ethical considerations

This project does not involve the use of human or animal subjects and did not require ethical approval.

Results

Individual scenario analysis

Decreasing test sensitivity and specificity in isolation resulted in a substantial increase in total expected cases (Fig. 2A and B, Figure S3). When sensitivity was reduced from 99 to 97.5%, total cases rose by 11.7%, from 9,150 (95% CI 8,279–9,559) to 10,218 (95% CI 9,217–11,067). At 85% sensitivity, expected cases increased by 223% to 29,556 (95% CI 22,993–41,009). Decreasing test specificity also raised case numbers, but to a lesser degree. A specificity of 99% resulted in a 14.1% increase in cases to 10,444 (95% CI 9,261–11,798), and at 95% specificity, cases increased by 35.7% to 12,412 (95% CI 9,924–17,858).

Fig. 2.

A The mean total cases on day 522 with different sensitivity values; B The mean total cases on day 522 with different specificity values; C The mean total cases on day 522 with different testing rate values; D The mean total cases on day 522 with different time-to-isolation values

In contrast, increasing the testing rate and reducing time-to-isolation led to marked case reductions. A 10% testing rate increase resulted in a 47.7% case reduction from 9,150 (95% CI 8,279–9,559) to 4,782 (95% CI 4,266–5,377). Doubling of the rate yielded a 74.2% decrease to 2,359 (95% CI 645–4,396). Further increases provided no additional benefit, with excess testing slightly increasing total cases (Fig. 2C, Figure S3). A further exploration of this relationship can be found in Text S3 and Figure S4.

Reducing time-to-isolation also reduced cases. When the time to isolation is reduced to 1 day, a 47.7% reduction in cases is expected, from 9,150 (95% CI 8,279–9,559) to 4,783 (95% CI 1,773–7,853). Although reducing the time-to-isolation consistently decreased total cases, the reduction became less pronounced each time step. When time-to-isolation was as low as 30 min, which could reasonably be expected with a rapid diagnostic test, an 87.7% reduction in cases is expected to 1,122 (95% CI 474–2,023) (Fig. 2D, Figure S3).

Trade-off scenarios

The trade-off between decreasing accuracy and decreasing time-to-isolation resulted in a substantial decrease in total expected cases in most tested scenarios compared to baseline. When decreasing the accuracy to an 85% sensitivity and a 95% specificity and decreasing time-to-isolation to 30 min, there was a 50.3% decrease in expected cases, from 9,150 (95% CI 8,279–9,559) to 4,548 (95% CI 1,276–9,296). The most considerable reduction was found with a 95% sensitivity, 99% specificity, and time-to-isolation of 30 min, with a reduction of 79.8% to total expected cases of 1,846 (95% CI 671–3,391). The smallest reduction and only scenario that did not decrease the mean total cases below reported WHO data was with an 85% sensitivity, a 95% specificity, and a time-to-isolation of 12 h; compared to baseline there was a 1.8% reduction in expected cases down to 8,986 (95% CI 2,803–18,301) (Figs. 3 and 4, left box). The mean and upper 95% CI of total deaths are shown in Figures S5 and S6 (left box).

Fig. 3.

Mean total cases at day 522, as trade-off between sensitivity & specificity, time-to-isolation, and testing rate; left box testing rate: baseline, middle box testing rate: +50%, right box testing rate: +100%

Fig. 4.

95% CI upper bound of total cases at Day 522, as trade-off between sensitivity & specificity, time-to-isolation, and testing Rate; left box testing rate: baseline, middle box testing rate: +50%, right box testing rate: +100%

The total expected cases decreased significantly more when an increased testing rate was added to the trade-off between accuracy and time-to-isolation. The most significant reduction was found with a 95% sensitivity, a 99% specificity, and a time-to-isolation of 30 min. With a testing rate of 150%, the expected cases decreased by 92.3% from 9,150 (95% CI 8,279–9,559) to 706 (95% CI 299–2,454), while a testing rate of 200% decreased the expected cases by 92.0% (expected cases 735 (95% CI 240–2,766). The smallest reduction was found with an 85% sensitivity, a 95% specificity, and a time-to-isolation of 12 h. With a testing rate of 150%, the expected cases decreased by 72.7% to 2,494 (95% CI 705–10,728), while a testing rate of 200% decreased the expected cases by 71.6% to 2,599 (95% CI 496–11,951) (Figs. 3 and 4). The mean and upper 95% CI of total deaths are shown in Figures S5 and S6.

False positives

A sub-analysis was performed to investigate the number of false positives that became infected in the hospital (Table S5). Lower specificity led to more false positives becoming infected, and higher testing rates amplified this effect. At baseline, 329 (95% CI 42–669), 4% of total cases were attributable to false positives becoming infected. In contrast, the false positives in the tested trade-off scenarios were much higher, ranging from 355 (95% CI 72–1,875) to 1,951 (95% CI 381–6,645). The percentage of mean total cases that started as false positives was also much higher, ranging from 23 to 76%.

Discussion

We found that any reductions in test sensitivity or specificity alone will increase the expected number of cases from 11.7 to 223%, while any decrease in time-to-isolation (due to a more rapid test result) or increase in testing rate would decrease the expected number of cases by 47.7–87.7%. When combining the three factors together, the benefits associated with a rapid test would outweigh the harms, as a test with lower accuracy that can decrease turnaround time and increase access would result in a net reduction of mean cases between 71.6 and 92.3%. For the 2014–2016 Sierra Leone epidemic this would have meant a reduction from 8,704 cases to as low as 670 cases.

Additionally, increasing the testing rates beyond 50% is detrimental, cautioning over-testing. However, it is important to consider the model does not allow for retesting. The trade-offs also found a higher uncertainty when increasing the testing rate instead of lowering the time-to-isolation. This means that the effect of lowering time-to-isolation is more robust than increasing accessibility when included in a trade-off with accuracy. Another important note is the high number of false positives, which raises ethical concerns about testing with a lower specificity. However, given the fact that a trade-off between accuracy, and accessibility and time-to-isolation can drastically reduce the number of people who are ultimately infected, it may become possible to properly isolate all EBOV suspects, thus reducing or even mitigating all false positive infections. Mitigating all false positive infections would lead to further 23–76% reduction in cases in our tested scenarios.

If a rapid diagnostic test meeting the WHO’s TPP criteria (sensitivity > 95%, specificity > 99%, time-to-detection < 3 h) had been used during the 2014–2016 epidemic, the model predicts a reduction in mean total cases of at least 75%, with even more significant reductions with an increased testing rate. Real-world RDTs, however, may have lower accuracy, as evidenced by a systematic review and meta-analysis that found a pooled sensitivity between 82 and 86% and a pooled specificity > 95% [26, 27]. If RDTs are assumed to have a sensitivity of 85% and a specificity of 95%, the time-to-isolation needs to be 3 h or less to achieve cases lower than the reported WHO data in the upper bound of the 95% CI. This means that current RDTs may already be able to help combat epidemics.

This is one of the first mathematical models developed to investigate the impact of diagnostic tools with different properties on the total size of an EBOV outbreak. To our knowledge, only one other model evaluated a trade-off between PCR and RDT testing in an EBOV outbreak using a modified SEIR-framework [28]. That model relied on test performance values available at the time and assessed how different testing strategies with RDT, PCR or a combination of both affected epidemic size. The authors found that using a dual testing strategy, RDT for early triage and PCR for confirmation, led to the greatest reduction in epidemic size. Interestingly, replacing PCR with RDTs alone resulted in only a 6% decrease in epidemic size during the 2014–2016 Sierra Leone epidemic. This limited impact may be partially explained by the relatively low specificity (85%) assumed in the model, leading to a higher number of false positives who were subsequently exposed and infected (Table S5).Unlike our study, this earlier model did not explore a range of hypothetical testing scenarios to systematically assess which trade-offs in sensitivity, specificity, or time-to-result might be most effective in outbreak control. Related insights can be drawn from infectious disease modelling for different pathogens. A model created for COVID-19 examined the effectiveness of repeated screening considering test sensitivities, frequency of testing, and sample-to-answer reporting time [29]. The results demonstrated that effective screening depended mostly on frequency and speed of testing results, and less on high sensitivity. Recent modelling work to support the development of new diagnostics for tuberculosis has also investigated the trade-off between accuracy and access to diagnostics, which also highlighted the trade-offs that can be made in test performance if access to testing can be improved [11]. While context and types of infections all differ across these models- as does the impact of a correct or incorrect diagnosis- the findings echo our own: that testing strategies optimized for rapid results can outperform those focused solely on test accuracy.

Our model, however, does have Limitations. We used epidemic days 179, 480, and 578 to represent the exponential growth phase, epidemic peak, and steady state. A ± 10% margin of error was used to retain a feasible number of accepted simulations while remaining closely aligned with WHO-reported total case and death counts. While fitting to the full daily case curve could offer finer resolution, we prioritized computational efficiency and interpretability over model complexity for this analysis. We do not expect that a differing approach would change our results. Second, while the deterministic nature of the model allows for a clear understanding of key parameters, it does not account for random variability that could affect early outbreak dynamics. A stochastic approach may better capture the uncertainty present in real-life epidemic scenarios, especially early in an outbreak. However, given that we were aiming to investigate the impact of diagnostics on a total epidemic size, a deterministic approach was sufficient to understand the effects. Third, the model assumes that individuals tested but not yet confirmed have the same infection rate as the infected, non-positive population. These individuals are likely to have reduced contact with others while awaiting results and, thus, a lower infection rate. This means the total reduction achieved by reducing the time-to-isolation might be overestimated. However, there was a lack of reliable data to quantify this risk. Moreover, using this infection rate implicitly includes healthcare worker infection in the model, considering they are most likely to get infected while awaiting results. Fourth, there are no reliable data on hospital length of stay for patients falsely diagnosed with Ebola. We assumed these individuals remain hospitalized for the duration of the mean incubation period before being discharged. This reflects a minimum expected stay given the need to monitor for symptoms and mitigate community risk. While this may underestimate the true duration of hospitalization in some cases, and therefore the associated infection risk, it provides a proportional mechanism for balancing discharge timing with nosocomial transmission risk. Finally, the model did not include the current ring vaccination strategy, which has been implemented in subsequent EBOV outbreaks in the Democratic Republic of Congo [30]. Integrating RDTs with the current ring vaccination strategies could provide further benefits, but unnecessary ring vaccination of false positives could also increase costs. Future research should evaluate the use of rapid diagnostic testing in conjunction with ring vaccination to understand the true cost-effectiveness and epidemic control potential of this testing strategy.

In balancing realism with parsimony, we made several simplifications based on limited available data. First individuals in the susceptible-but-test-positive (S_t⁺) compartment cannot become infected while awaiting their rest result, potentially underestimating epidemic size when time-to-isolation is long. Second, exposed individuals who test positive (E_t⁺) are assumed to enter the hospitalized infectious (H_i⁺) compartment directly, without passing through an in-hospital incubation phase. This could overestimate the proportion of infectious individuals in hospital and the resulting infection risk to false positives. However, adding a separate compartment could underestimate nosocomial infections and data to parameterize such a transition are lacking. Finally, the model does not allow for retesting of individuals who receive false-negative results, which may underestimate the full benefit of RDTs, particularly those with lower sensitivity. However, maintaining a simpler structure allowed us to more clearly explore trade-offs between test accuracy and testing rate.

Finally, the relative impact of tests with different properties evaluated here were all predicated on a comparison to the 2014–2016 EBOV outbreak. EBOV outbreaks in different settings with more rapid turnaround time/specimen transport system, or different epidemiology of disease, could result in an attenuated impact of a test that has lower performance, decreasing turnaround time, and increased access. The setting in which an EBOV outbreak occurs should be carefully evaluated to understand whether a rapid test should be deployed- and if turnaround times remain low, and access high for a higher-performance test- then this test should continue to be used.

Conclusions

The use of RDTs may reduce total epidemic size significantly compared to traditional RT-PCR testing, even with lower sensitivity and specificity. This highlights the potential of RDTs to play a vital role in epidemic control, if trade-offs between accuracy and accessibility are carefully managed. As of 2024, the WHO does not recommend the use of RDTs during an Ebola- or Marburgvirus outbreak, other than for post-mortem diagnosis [31]. However, based on our findings and prior modelling studies, we recommend that RDTs be considered for use in outbreak response, particularly in the context of established EBOV outbreaks. The study does raise ethical considerations regarding the higher number of false positives that could be infected while isolated with EBOV patients when using an RDT. With significantly lower expected cases, single-room isolation may be feasible with RDT testing, and future research should explore this. Finally, future work should explore stochastic models to better capture early outbreak variability and the role of diagnostics on not just the total size of an outbreak but also the early epidemic trajectory.

Abbreviations

EBOV

Zaire ebolavirus

EVD

Ebola viral disease

RDT

rapid diagnostic test

RT-PCR

reverse-transcriptase polymerase chain reaction

TPP

target product profile

VHF

viral hemorrhagic fever

WHO

World Health Organization

Authors’ contributions

NAB designed the model, analyzed and interpreted the modeling data, and drafted the initial manuscript. DME contributed to the initial research question and study design, validated the study results, and reviewed the manuscript. IE and EA provided additional validation of the results and reviewed the manuscript. BEN conceptualized the analysis, supported the study design and result interpretation and initial manuscript drafting, and was responsible for overall study supervision. All authors read and approved the final manuscript.

Funding

The authors received no specific funding for this work.

Data availability

The datasets analyzed during the study are available from the corresponding author upon reasonable request.

Declarations

Ethics approval and consent to participate

This project does not involve the use of human or animal data. Therefore, ethical approval was not required.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.