Abstract
Muramyl ligases are multidomain enzymes involved in intracellular steps of bacterial peptidoglycan synthesis and are considered promising targets for the development of new antibacterial agents. Among them, Mur ligase D (MurD) has been most widely used for structure-based design, but success has been limited. Here, we determine the 15N NMR spin relaxation parameters of apo and bound states of MurD in solution. We introduce a principal component analysis of the spectral densities derived from the NMR relaxation data, which provides a mechanistic insight into the dynamic events at the residue level. Compensation effects (ps-ms timescale) and conformational exchange dynamics (µs-ms timescale), the latter also measured independently, were revealed in bound and unbound MurD, which should be considered in the design of structurally novel Mur inhibitors. The mechanistic consideration used in our study can be broadly applicable to other systems for deciphering their specific dynamic mechanisms.

Subject terms: Solution-state NMR, Ligases
Mur ligase D (MurD) is a promising antibacterial target, but its dynamics remain underexplored. Here, the authors use 15N nuclear magnetic resonance to probe apo and bound states of MurD in solution, showing that dynamic events on a time scale of picoseconds to milliseconds have to be considered in the design of structurally novel Mur inhibitors.
Introduction
The Mur ligase superfamily, encompassing MurC, MurD, MurE and MurF, plays a pivotal role in intracellular peptidoglycan synthesis, thereby attracting considerable attention as potential targets for the development of novel antibacterial agents1. These ATP-dependent ligases demonstrate structural dynamics that are intrinsically linked to their capacity to bind to and catalyze the formation of considerably large peptidoglycan precursors. As the subsequent addition of amino acids to the precursors progresses from MurC to MurF, it enables the generation of increasingly larger building blocks for peptidoglycan synthesis. Consequently, the conformational dynamics among these four ligases exhibit a notable increase, reflecting their respective roles in the elongation of the peptidoglycan chain2–5.
Among the Mur ligases, MurD (UDP-N-acetylmuramoyl-l-alanyl-d-glutamate ligase) - a 47.7 kDa multidomain protein - is the most extensively studied target for inhibitor design6–20. Based on crystallographic data, it has been observed that MurD can adopt several distinct conformational states during the catalytic process, including:
An open conformation, representing the ligand-free conformation of MurD in the absence of a ligand21.
A semi-closed conformation, initially adopted upon ATP and Mg²⁺ binding to central domain (CeD, residues 94-298) at the interface with C-terminal domain (CTD, residues 299-437), which follows the binding of the substrate UDP-N-acetylmuramoyl-l-alanine (UMA) to the cleft formed between the N-terminal domain (NTD, residues 1-93) and CeD22,23.
A closed conformation, which is adopted after ATP hydrolysis, and is further characterized by d-Glu binding to CTD and the subsequent formation of the product UMAG24,25. Furthermore, the closed conformation is adopted after binding some of its most potent inhibitors, transition state analogs9–11,14,16,26, indicating that this conformation could be crucial for regulating MurD activity.
Notably, the rigid body rotation of the CTD facilitates transitions between open, semi-closed to closed conformation, as evident from crystallographic studies16,21,24,25 and shown with pseudocontact shift (PCS) NMR studies, which also reveals that this motion regulates substrate binding affinity27.
The concept of semi-closed conformation was first introduced through PCS-NMR studies27. Later, two crystal structures called intermediate-apo (PDB 5A5E) and intermediate-UMA + ADP bound (PDB 5A5F) conformation were solved23. MD simulations showed that both, together with the PCS-model, lie within the conformational ensemble of the simulated ATP-bound state, suggesting that the 5A5E and 5A5F crystal structures represent the semi-closed conformation28. The recent ATP-bound crystal structure (PDB 8VW2)22 also closely resembles these crystal structures based on RMSD comparisons (Table S1).
Recently, electron paramagnetic resonance (EPR) of frozen solutions29 and small-angle X-ray scattering (SAXS) experiments in solution30 have identified a wide range of distances between the CTD and the CeD, revealing the existence of multiple conformational states in the apo MurD. In the most populated state, this distance was consistent with the distance observed in the crystal structure of the open conformation. However, in the conformational ensemble, a state was also found in which the distance corresponds to the closed conformation. Upon inhibitor binding, the distance distribution narrowed and the conformational ensemble shifted towards the distance closely resembling those in the closed conformation observed in the crystal structures29,30. This supports the idea that conformational selection is a key mechanism in ligand binding.
While efforts to develop potent MurD inhibitors have achieved some success, the efficacy has been somewhat limited, with IC50 values reaching only into the single-digit micromolar (µM) range11,26,31. Interestingly, the campaigns to find competitive ATP inhibitors6,12,18 that could lead to multi-target inhibitors of the entire Mur ligase series yielded inhibitors that bind to UMA or d-Glu instead to the ATP binding site. Since all these efforts were based on the rigid crystallographic structures, we can speculate that the lack of knowledge about the dynamic properties of the apo and bound MurD states has hindered further development that could eventually lead to structurally novel antibacterial agents with clinical potential.
Here, by using 15N nuclear magnetic resonance (NMR) relaxation techniques in solution accompanied by a specific analysis of NMR data and supported by molecular dynamics (MD) simulations we unravel a complex dynamic behavior of three MurD states: apo MurD (MurDapo), MurD bound with stable ATP analog AMP-PCP (MurDACP), and MurD bound with the most potent sulfonamide type inhibitor (4-(6-(4-cyano-2-fluorobenzyloxy)naphtalene-2-sulfonamido)isophthalic acid, inhibitor 1) hereafter indicated as MurDinh. Reduced Spectral Density Mapping (RSDM) was employed to identify the distinct characteristics of the reduced spectral densities J(ω) along the protein backbone in the three states that depict the residues and regions with varying dynamics between the states from ps to ms time scale. By introducing Principal Component Analysis (PCA) into the spectral density data, we revealed three independent dynamic mechanisms corresponding to different intertwining of the time scales of the dynamic events that was not possible with usually applied pairwise comparison of J-terms. We have shown that an in-depth characterization of the dynamic mechanisms of apo and bound MurD forms is of paramount importance for a deeper understanding of the binding mechanism of substrates and inhibitors and consequently for the successful development of effective and more potent inhibitors.
Results
Determination of spectral densities from 15N NMR relaxation data
The TROSY-based 3D-HNCA experiments32–34 were recorded to perform the backbone 1HN and 15N chemical shift assignment of the three MurD states (Fig. 1). In the BMRB database, only the 1HN and 15N chemical shift assignment for the backbone of apo MurD was available, which was previously carried out by Saio et al.27 (BMRB entry 26641). It provided a good starting point for our assignment procedure, but could not be directly applied to MurDapo spectra due to the different buffer composition required in our studies to fulfill comparable conditions for all three MurD states. Therefore, many 15N-1HN correlation peaks in the spectra of MurDapo were shifted in different directions with respect to the published assignments, and sequential assignment using 3D HNCA experiments was crucial to obtain the resonance assignment of all three MurD states. The chemical shift assignment was obtained for 75% of the MurD non-proline residues (Table S2). Mostly, the 15N-1HN correlation signals of residues at the interface between CTD and CeD were absent in all states likely due to exchange broadening that could be attributed to the conformational exchange between open and closed MurD conformations, as previously shown by Saio et al.27.
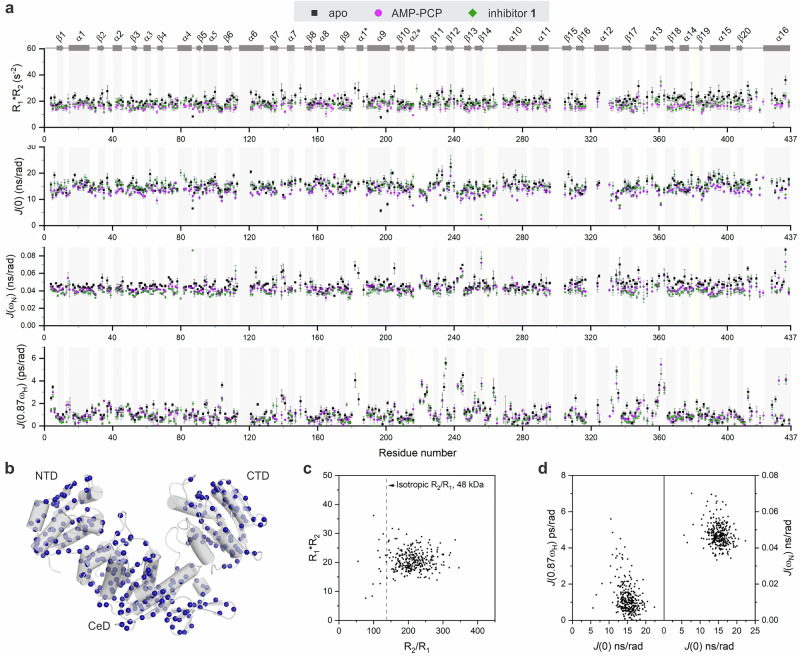
Fig. 1. Expanded regions of the NMR spectra of MurDapo (in gray), MurDACP (in magenta) and MurDinh (in green), illustrating chemical shift assignment.
a Selected 1H-13Cα slices at the 15N chemical shifts of the residues Y154-E157 from the 3D HNCA spectra, demonstrating consistent sequential assignment of the residues in all states. b Superimposed expanded regions of 2D 1H-15N TROSY spectra showing chemical shift perturbations upon ligand binding. Residue labels for which correlations are shown in the slices from 3D HNCA spectra are highlighted in bold.
The TROSY-based NMR experiments35 were conducted to measure the 15N spin-lattice relaxation rates (R1), 15N spin-spin relaxation rates (R2) and steady-state 1H-15N nuclear Overhauser enhancement (hetNOE) for MurDapo, MurDACP, and MurDinh (Fig. S1). The 15N nuclei with available relaxation data were sufficiently distributed across each MurD state (Fig. 2b) to study the dynamics of the entire protein.
Fig. 2. 15N relaxation data and reduced spectral densities.
a R1R2, J(0), J(ωN) and J(0.87ωH) for MurDapo (in black) versus MurDACP (in magenta) and MurDinh (in green). Secondary structure elements are presented and labeled as described by Bertrand et al.21. Helical turns that are observed in some X-ray structures, are marked with an asterisk. b 15N nuclei with available relaxation data (in blue spheres) for MurDapo presented on X-ray structure of open conformation (PDB 1E0D21). c Plot of R1R2 versus R2/R1 for MurDapo. d Plots of J(ωN) and J(0.87ωH) as a function of the corresponding J(0) for MurDapo. The errors in the R1R2, J(0), J(ωN) and J(0.87ωH) values were estimated through error propagation.
The distribution of 15N relaxation rates in plots of R1R2 versus R2/R1 (Fig. 2c) suggests that the three MurD states exhibit an anisotropic character36, therefore RSDM approach37 was utilized to characterize the frequency spectrum of the motions of N-H bond vectors. This approach allowed determination of reduced spectral densities at three different frequencies J(0), J(0.87ωH) and J(ωN) from relaxation rates and hetNOEs measured at a single spectrometer frequency, where J(0.87ωH) is approximated single spectral density term for linear combination of spectral densities at high frequencies (ωH, ωH ± ωN)37 (Figs. 2a, S2).
In general, increased J(0.87ωH), J(ωN) (Fig. 2a) and R1 values (Fig. S1) and lower hetNOE values (Fig. S1) were observed in the loop regions of MurD states, indicating local dynamics on the fast ps-ns (sub-nanosecond) time scale. The increased values of R1R2 and J(0) also found in α-helices and β-strands may indicate conformational exchange dynamics on the micro-to millisecond (μs-ms) timescale36,38,39. However, in order to draw conclusions about the time scale of specific dynamical events along the backbone of the three MurD states, the relationships between the three spectral densities need to be determined38.
The usual approach, applied to smaller proteins with few dynamically distinct regions38 extracts these relationships from the plots of J(ωN) and J(0.87ωH) as a function of the corresponding J(0). Moreover, for smaller proteins, it appears to be more straightforward to infer enhanced fast N-H bond motions from a high J(0.87ωH) and the presence of μs-ms exchange motions from a high J(0)40. However, for large proteins such as MurD, no specific correlation between the three densities corresponding to different dynamic properties can be recognized in these diagrams (Fig. 2d). Therefore, further details on the spectral densities, their correlations, and variations were sought for using PCA.
Mechanistic insight into dynamics of MurD states through PCA of reduced spectral densities
In our analysis, the main purpose of PCA was not dimensionality reduction, but to determine how the spectral density terms vary together and how this reflects the co-operation of dynamics on different time scales. In interpreting the PCA results, we considered J(0.87ωH) and J(ωN) to be representative of the dynamics on the fast ps-ns time scale and J(0) to be representative of the dynamics on the ns-ms time scale, where μs-ms interval refers to chemical exchange as conformational exchange41. PCA yielded a non-negligible proportion of the variance explained by each of the three PCs (Table 1), with PC1 covering more than 55% in the three MurD states. The obtained PCs describe three independent dynamic mechanisms hidden in the source spectral density data. The moderate correlations between the spectral densities in Table 1 indicate the co-operation of the dynamics over different time scales, while the correlations between the spectral densities and the PCs show the extent to which the dynamics on the time scale representative of each J-term contribute to a particular dynamic mechanism.
Table 1.
Summary of PCA

Proportion of variance explained by PCs, correlation between variables and correlation between variables and PCs for MurDapo, MurDACP and MurDinh.
The correlations between the three spectral densities in Table 1 appear to be more pronounced for MurDACP and MurDinh than for MurDapo, but nevertheless remain only moderately correlated, so that each of the three PCs is an important source of information about the dynamics. The strengths and signs of the correlation between PC1 and the original variables suggest that the PC1 axis encodes the compensation effect between the dynamics on the fast ps-ns time scale and the time scale defined by J(0). The PC2 component contains similar information about the dynamics for the MurDapo and MurDACP states, where the correlation of PC2 with J(0) predominates, while the situation is slightly different for the MurDinh state, where the correlation of PC2 with J(ωN) becomes more important. Nevertheless, it can be summarized that the PC2 axis mainly encodes the cooperation of the dynamics on the sub-nanosecond time scale, characterized by J(ωN), and on the time scale defined by J(0). The PC3 component for the MurDapo and MurDACP states shows the strengths and signs of the correlation to the original variables, indicating another compensation effect, in this case mainly between the dynamics on the sub-nanosecond time scales characterized by J(0.87ωH) and J(ωN). For the MurDinh state, this compensation effect is no longer in the foreground as it diminishes and somehow turns towards the cooperative dynamics on the sub-nanosecond time scale characterized by J(0.87ωH) (i.e., the ps regime, see 41) and the time scale defined by J(0).
Overall, comparing the proportions of variance explained by the PCs for the three states shows that the compensation effect described by PC1 gains importance, while the dynamics described by PC2 contribute less to the variability in the residue dynamics upon binding of AMP-PCP or, more markedly, upon binding of inhibitor 1. Moreover, the turnover of the percentage of variance explained by PC2 and PC3 for MurDinh suggests that the dynamic mechanisms of this state are more distinct from the other two states.
Using the PC scores for each residue, we classified the residues into five groups G1-G5 based on the dominance of one PC over the other two PCs, i.e., considering one of the dynamic mechanisms to be dominant over the other two. The classification criteria can be found in the Materials and Methods section in Table 2. The dominance of PC1 over PC2 and PC3 refers to the dominance of the compensation effect between the dynamics on the fast ps-ns time scale and the time scale defined by J(0), which can occur in one or another way and determines groups G1 and G2. The dominance of PC2 over PC1 and PC3 shows the dominance of the non-compensation effect, which is only of interest with regard to the enhancement of this effect. Group G3 was determined in this way. The dominance of PC3 over PC1 and PC2 indicates the dominance of another compensation effect, which in turn is of interest in one or the other direction of compensation and determines the groups G4 and G5. The assignment of the residues to the groups on the basis of the selected criteria is exclusive, i.e., each residue can be assigned to at most one of the groups G1-G5 or none of them. The results of this classification are shown residue by residue in Table S3 and graphically in Fig. 3. The number of residues that are classified into a particular group for each MurD state is further summarized in Table S4, based on their listing in the groups in Table S3. For example, in Table S3, MurDapo residues number 10, 56 and 89 are listed in group G5, resulting in a number of 3 in the corresponding MurDapo NTD cell of Table S4.
Table 2.
Criteria for the principal components (PC) scores determining the sets of residues of particular dynamics
| Criteria | Description and interpretation | Corresponding group of data set in Fig. 3 |
|---|---|---|
| Residues, where the decreased J(0) compensates for the increased J(0.87ωH) and J(ωN) (i.e., increased fast ps-ns dynamics) and this compensation effect prevails over the other two mechanisms (explained by PC2 and PC3) | G1, orange spheres in Fig. 3 | |
| Residues, where the increased J(0) compensates for the decreased J(0.87ωH) and J(ωN) (i.e., decreased fast ps-ns dynamics) and this compensation effect prevails over the other two mechanisms (explained by PC2 and PC3) | G2, blue spheres in Fig. 3 | |
| Residues, where J(0) (and less evidently J(ωN)) is increased without compensation on the time scale defined by J(0.87ωH) and this effect prevails over the other two mechanisms (explained by PC1 and PC3) | G3, yellow spheres in Fig. 3 | |
| Residues, where the decreased J(ωN) compensates for the increased J(0.87ωH) and this compensation effect prevails over the other two mechanisms (explained by PC1 and PC2)# | G4, pink spheres in Fig. 3 | |
| Residues, where the increased J(ωN) compensates for the decreased J(0.87ωH) and this compensation effect prevails over the other two mechanisms (explained by PC1 and PC2)# | G5, green spheres in Fig. 3 |
PC1 stands for the scores of the first principal component, PC2 for the scores of the second principal component and PC3 for the scores of the third principal component. The notation # in the table indicates a deviation from the given description for MurDinh, as explained in the text following Table 1.
Fig. 3. Categorization of residues into groups G1-G5 based on PC scores.
a Legend defining groups G1-G5, each corresponding to a distinct dynamic mechanism, captured by the first three principal components derived from spectral density data. b Chart showing changes in numbers of residues assigned to each group when comparing the apo and ligand bound states. c–e Structural mapping of classified residues onto MurD crystal structures: G1 (orange), G2 (blue), G3 (yellow), G4 (pink), and G5 (green). Left panels show PC score plots derived from the standardized data on J(0), J(ωN) and J(0.87ωH) for MurDapo. Circles denote the data points for the PC scores, with colored circles indicating residues assigned to G1-G5 based on classification criteria (Table 2), while unfilled circles indicate residues not assigned to any group. Colored cones define the classification regions in PC space which comprise the residues of a particular group. Right panels display the crystal structures of MurD in three conformational states: the open conformation of MurDapo (left, PDB 1E0D21), the semi-closed conformation with ATP (magenta) for MurDACP (middle, PDB 8VW222), and the closed conformation with inhibitor 1 (forest green) for MurDinh (right, PDB 2XPC11). Note that G4 and G5 group of residues for MurDinh contains somewhat different information than for the other two states, as indicated above. Residues shown in grey have no group assigned, while residues shown in white indicate unavailable data.
We can consider the residues in the G1 group as those whose predominant dynamic mechanism is underpinned by the increased probability of dynamics on the fast ps-ns time scale due to the decreased probability of dynamics on the time scale determined by J(0). The G1 residues are typically found in loop areas and at the termini of α-helices and β-strands, mostly at the protein’s outer surface (Fig. 3c). Such behavior of J(ω) values is typical for the sub-nanosecond flexibility of the N-H bond vector42. The G2 group, on the other hand, combines residues with the predominant mechanism of sub-nanosecond flexibility reduction due to the increased probability of dynamics on the time scale determined by J(0). The G2 residues are mainly found in secondary structural elements and at the end(s) of the loops. The total number of G1 residues remains similar for the three MurD states, while the total number of G2 residues increases upon binding of either AMP-PCP or inhibitor 1 (see Fig. 3b and c, S7, Tables S3 and S4 for details).
Group G3 represents the residues with the dominating mechanism underpinned by an increased probability of dynamics on the time scale determined by J(0) with a less intense but still present increase of probability of dynamics on the time scale determined by J(ωN), These are accompanied with the unchanged probability of dynamics on the ps time scale determined by J(0.87ωH). The total number of the residues with G3 dynamics most evidently changes upon binding of inhibitor 1 (see Fig. S7, and Table S4).
The other compensation effect within the sub-nanosecond time scale is captured by PC3 for MurDapo and MurDACP. This compensating mechanism diminishes for the MurDinh state by turning towards the mechanism of cooperative dynamics as described above. The prevalence of PC3 over the other two PCs is given in the context of groups G4 and G5, whose meaning for the MurDinh state is somewhat different from that of the other two states with regard to the mechanism described by PC3. The total number of residues classified in G4 is relatively low and spread without any particular pattern within the loops and secondary structures. The residues of group G5 turn out to be located in α-helices and β-strands as well as at the end(s) of the loops. The number of G4 residues decreases and the number of G5 residues increases upon binding of either AMP-PCP or inhibitor 1 (see Fig. S7, Tables S3 and S4 for details).
Further, we have analyzed the presence of residues of a particular group in the secondary structure elements, that we have defined as segments (such as a single α-helix, β-strand, or loop as provided in Table S3). The analysis shows that segments can contain residues from different groups. In the NTD domain for all three MurD states, about half of the segments consist of the residues belonging to only one of the five groups, together with the residues with non-significant dynamics (i.e., the residues that do not belong to any of the five groups). The other half of the segments contains the residues belonging to at least two of the five groups. In the CeD and CTD domains, there are about two-thirds of the latter and one-third of the former kind. Segments with residues belonging to different groups, i.e., the segments with PCA group variability, can be considered as with more complex dynamics, and the larger proportion of these segments supports the picture of greater complexity in the dynamics of the CeD and CTD domains.
Since the proportion of segments with greater dynamics complexity outweighs the segments with residues belonging to only one group, we assume that the segments with greater dynamics complexity bear more responsibility for the circumstances that influences the efficacy of the binding. These aspects are considered further in the following subsection together with the conformational exchange dynamics.
Common aspects of conformational exchange dynamics and PCA results for MurD states
The conformational exchange dynamics on the μs-ms time scale of the three MurD states were further investigated using TROSY-based 15N Carr–Purcell–Meiboom–Gill relaxation dispersion (CPMG-RD) NMR method43–45. The presence of conformational exchange dynamics was assessed based on the relationships between the experimental data and the data fitted with the 2-site CPMG model as derived and provided by Korzhnev et al.46. The residues with reliable evaluation of the presence of conformational exchange, as explained in the Materials and Methods section, are listed in Table S3 and with the exchange rates from the fitting in Table S5 and shown in Figs. 4 and 5.
Fig. 4. Distribution of the residues with conformational exchange and fast ps-ns dynamics.
The residues with conformational exchange dynamics on the μs-ms time scale determined at 800 MHz with CPMG-RD are labeled as backbone in yellow and the amide nitrogen as yellow spheres, while the residues with increased fast ps-ns dynamics assigned to group G1 are labeled as backbone in orange. Yellow spheres on orange backbone indicate the amide nitrogen of residues with identified conformational exchange on μs-ms time scale and increased fast ps-ns dynamics. Gray boxes indicate the percentage of residues assigned to G1 and those with an exchange contribution (kex) within each domain, as labeled. The same crystal structures11,21,22 are used to visualize these distributions for MurDapo (upper), MurDACP (middle) and MurDinh (lower), as explained in Fig. 3.
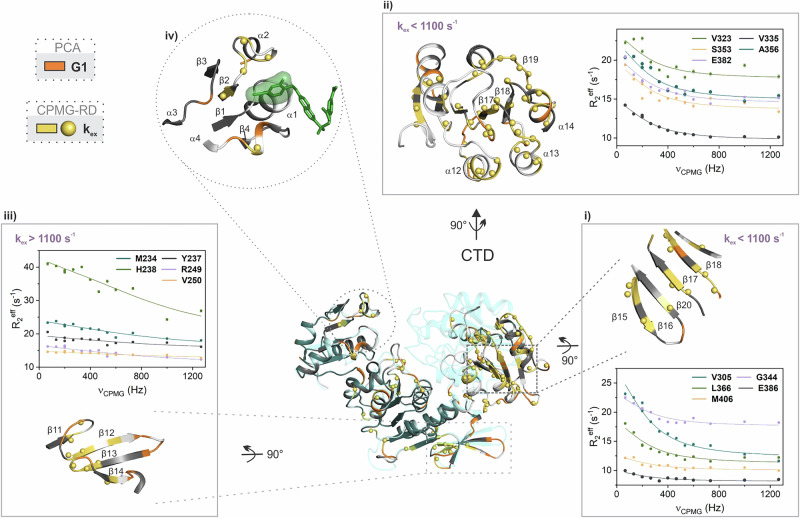
Fig. 5. Excerpts of the MurD regions with a salient pattern of conformational exchange and fast ps-ns dynamics.
The excerpted regions are shown for the MurDapo on the X-ray structure of open conformation (PDB 1E0D21) with observed conformational exchange dynamics on μs-ms time scale identified by CPMG-RD (backbone in yellow and amide nitrogen in yellow spheres) and with increased fast ps-ns dynamics assigned to G1 group (backbone in orange). Yellow spheres on orange backbone indicate the amide nitrogen of residues with identified conformational exchange on μs-ms time scale and increased fast dynamics. Residues shown in white indicate unavailable data. The closed structure (in transparent cyan, PDB 2XPC11) is overlaid over CeD. Regions shown: i) β-sheet (β15-β16-β20-β17-β18-β19) in the CTD, (ii) CTD with highlighted helices (α12, α13 and α14) and loops (α12-β17, α13-β18 and α14-β19) (iii) β−meander (β12-β13-β14) in the CeD, (iv) uracil-binding pocket (β1, β2, β1-α1, β2-α2, β3-α3 and β4-α4) with a potentially bound inhibitor shown in green. Representative CPMG-RD plots are shown, illustrating μs-ms dynamics (kex) for residues from each region. R2eff represents the effective transverse relaxation rate at each refocusing pulse train frequency (νCPMG). The errors in the R2eff values were determined based on the uncertainties of the peak intensities estimated from the background noise level of the spectra.
Screening the possible overlaps between the detected conformational exchange dynamics on the μs-ms time scale and the dynamic events recognized by PCs and the groups, we first encountered the following. We found that in MurDapo, about 60% of the segments with conformational exchange are the segments containing residues belonging to at least two different groups. This ratio increases to over 70% in the MurDACP and MurDinh states, which is due to the increase of these segments in their CeD and CTD domains. Therefore, evidence of conformational exchange for the residues in a given segment predicts with a probability of at least 60–70% the diversity of dynamics expressed by the presence of different groups in that particular segment.
On the other hand, we wanted to investigate the possibility of predicting conformational exchange dynamics on the μs-ms time scale based on information from PCA group classification. We took into account that conformational exchange should be reflected in an increased J(0) without compensation effect. PC2 appeared to be the most promising indicator with a strong positive correlation with J(0). However, it is also positively correlated with J(ωN), so that a limited predictive ability was to be expected. The segment was classified as having possible conformational exchange dynamics if it consists of at least one residue for which PC2 predominates over the other two PCs, i.e., of at least one residue belonging to G3 group. As shown in Table S6, the G3 group defined by PCA shows the best overall agreement with the observation of conformational exchange dynamics using the CPMG-RD method. Predictions using elevated values of R1R2 products are slightly less reliable, while the approximate approach to determine Rex36 is the least reliable for predicting the conformational exchange dynamics of MurD states. The best agreement between G3 and CPMG-RD per segment resolution was obtained for MurDapo, which became evidently reduced for MurDinh. This could be due to a lower number of available data for MurDinh together with a slightly changed role of PC2, where its correlation with J(ωN) starts to dominate its correlation with J(0). Nevertheless, the prediction of both the presence and absence of conformational exchange dynamics based on the G3 residues gave 65–75% agreement with the CPMG-RD results per segment resolution.
Flexibility of MurD states from the perspective of conformational exchange and fast time scale dynamics
The results of Kumar et al.47 showed how fast ps-ns motions and μs-ms conformational exchange dynamics of protein kinase p38 control its regulation and activation. Inspired by this, we similarly investigated the distribution pattern of residues with conformational exchange dynamics on the μs-ms time scale and of residues with the identified increased fast ps-ns dynamics (G1 residues). Indeed, this revealed an additional perspective on the ability (flexibility) of MurD to adapt its structure upon binding of a ligand.
The number of segments with conformational exchange is significantly lower in NTD than in the other two domains for all three states. While conformational exchange is represented to a similar extent in the CeD and CTD of MurDapo and MurDACP, it gets reduced significantly in MurDinh, especially in the CTD (Tables S3 and S4, Fig. 4). These observations suggest that the main process underlying the conformational exchange can be attributed to the movements of the CTD relative to CeD, which are not suppressed upon binding of AMP-PCP, but upon binding of inhibitor 1. The extent of the segments with G1 dynamics (Table S3, Fig. 4) is more evenly distributed across the domains for all three states. Their number overweight the number of segments with conformational exchange only in the NTD of all states and in the CTD of MurDinh.
The kex values obtained by the fit per residue for MurDapo (Table S5, Fig. 5) were considered as clues to identify subsets of structurally related residues that have a similar range of kex. For the identified subsets of residues, we performed a group fit and characterized two different global conformational exchange processes on the μs-ms time scale. One subset of residues is located in the CTD with kex values below 1100 s−1, suggesting a conformational exchange that may be related to the CTD motion. For example, these kex values are observed for contact residues within the β-sheet (β15-β16-β20-β17-β18-β19) in the outer region of CTD (Fig. 5, i), which approach the CeD in the open structure, and residues at the termini of helices α12, α13 and α14, as well as, for several residues in the α12-β17 loop, which approach the CeD in the closed structure (Fig. 5, ii). Residues with kex below 1100 s−1 from these regions were group fit resulting in a group kex of 836 s−1 and pA of 0.5. At the same time, we can observe the presence of fast ps-ns dynamics in the outer loops of CTD adjacent to the above structures with the synchronized conformational exchange, i.e., in the loops α12-β17, α13-β18 and α14-β19.
The other subset of residues is located in the CeD and exhibits various kex values above 1100 s−1. It characterizes the motion of a β-meander (β12-β13-β14) and adjacent loops β11-β12 and β13-β14 (Fig. 5, iii) positioned away from ligand binding sites, not facing the CTD. The group fit for the residues with kex above 1100 s−1 from the β-meander and adjacent loops resulted in a group kex of 2514 s−1 and pA of 0.97. Interestingly, the residues near the β-meander, specifically in the β12-β13 and β14-α10 loops, which approach the CTD in the open structure, exhibit fast dynamics on the ps-ns time scale (Fig. 5, iii).
In the MurDACP, the residues with kex values below 1100 s−1 dominate in the CTD in the above-mentioned β-sheet (Table S5, Fig. 4), and yield a group kex of 486 s−1 and pA of 0.53. In addition, the total number of segments in the CTD domain with the residues in conformational exchange does not reduce significantly. This suggests that the motion of the CTD on the μs-ms time scale is mainly preserved. We can speculate that the binding of AMP-PCP does not lock the conformation to any of those observed in the X-ray structures of MurD bound to substrates or inhibitors. This would imply that an ensemble of conformations is still available for subsequent substrate binding. The main reduction in the number of residues with conformational exchange within the β-sheet and overall in the CTD of MurDinh compared to the other two states indicates a stabilization of this domain upon binding of inhibitor 1. The fast ps-ns dynamics remains present in the loops α12-β17 and α13-β18 in both MurDACP and MurDinh.
In the β-meander (β12-β13-β14) of MurDACP and MurDinh, the number of residues with kex decreases. In the MurDACP state, the values remain mainly in the range above 1100 s−1 from the per-residue fit, while the group fit for these residues gives a group kex of 2364 s−1 and pA of 0.5. The kex values in the β-meander of MurDinh cover the ranges below and above 1100 s−1 (Table S5, Fig. 4). The fast ps-ns dynamics is preserved in the loops β12-β13 and β14-α10 upon binding of AMP-PCP and inhibitor 1.
While the conformational exchange dynamics changes significantly in the CeD and CTD of MurDinh, the fast ps-ns dynamics is preserved in the β12-β13, β13-β14 and β14-α10 loops of CeD and the α12-β17 and α13-β18 loops of CTD in all three states (Table S3, Fig. 4). These are the loops surrounding the substructures with a particular conformational exchange dynamic, as described above. Thus, it appears the loops facilitate the fast time scale flexibility of these substructures (their adaptability to the environment), which is not switched off when the ligand is bound.
In the NTD of all three states, the residues with identified conformational exchange are mainly located in the segments that form the uracil binding pocket (Fig. 4 and Fig. 5, iv), which is part of the inhibitor 1 and UMA binding sites. Their kex values extend over several scales and cannot be attributed to any overall motion of NTD. In addition, there is no particular pattern of fast ps-ns dynamics in the NTD domain. This speaks in favor of impoverished flexibility of the NTD domain in all three states.
Inhibitor 1 interacts with all three domains via 15 segments (Table S3, Fig. 6). The dynamic behavior of these segments is not uniform in any of the three states. In MurDapo, many of the segments exhibit vivid dynamics that is largely conserved in MurDACP (Table S3). Although the proportion of binding segments in conformational exchange and the variability of the PCA group are significantly reduced in MurDinh (Table S3), none of the four inhibitor 1 moieties (Fig. 6c) is exclusively surrounded by stable or flexible segments (Fig. 6a). We can still observe conformational exchange along with PCA group variability (presence of residues belonging to at least two of the PCA groups) at the inhibitor 1 binding sites of the β1-α1 and β2 segments in the NTD, β17-α13 and β20-α16 in the CTD and conformational exchange of α8 and β9-α1*-α9 in CeD (Fig. 6a, Table S3). We believe that these findings support the limited binding efficacy of inhibitor 1 and its analogs10,11,26 and call for fine-tuning of each moiety of these types of inhibitors to achieve better adaptability of these binding segments.
Fig. 6. Dynamics of the inhibitor 1 binding site.
a The inhibitor 1 binding site as determined by Simčič et al.20 highlighting residues with distinct dynamic mechanism according to PCA (G1 in orange, G2 in blue, G4 in pink, and G5 in cyan) and/or conformational exchange dynamics on μs-ms timescale as identified by CPMG-RD (yellow backbone and sphere). Residues shown in grey indicate residues with no group assigned, while residues in white indicate unavailable data. b Overlaid 1H-15N TROSY spectra of MurDapo (gray) and MurDinh (green) are shown for residues in the ligand-binding site that exhibit the strongest perturbations upon the addition of inhibitor 1 added in 4 equivalents. (c) Chemical structure of inhibitor 1 (4-(6-(4-cyano-2-fluorobenzyloxy)naphtalene-2-sulfonamido)isophthalic acid) with labeled structural moieties. LHS: Left-hand side, CU: Central unit, RHS: Right-hand side.
Common aspects of MD simulations and experimental findings for MurD states
The agreement between the results of all-atom MD simulations performed for three systems (MurDapo, MurDATP, and MurDinh), each of the simulation length 2 μs, and the experimental data per segment was sought for using the criteria in Table 3. For example, if the MD results identified at least one residue in a particular segment that met the first criterion in Table 3, and at the same time the analysis of the experimental results ranked at least one residue in group G1 for that particular segment, we considered this as a match between MD prediction and experimental results. In the same way, we looked for agreement between the MD results fulfilling the second criterion in Table 3 and the presence of G2 residue(s) in a given segment, and so on. In this regard, the prediction of the MD simulation results for the presence of the G1 group at the segment resolution was relatively high (61 – 84%), as well as for the presence of the G2 group (76 – 91%) and CPMG-RD (62 – 82%). The agreement of the simulations with the presence of the G4 and G5 groups was mostly below 50%.
Table 3.
Residue classification criteria based on the MD spectral density data
| Criteria for the classification of the residues (Res) based on the MD spectral density data | Results based on the experimental data to be compared to the MD results |
|---|---|
| G1 | |
| G2 | |
| G4 | |
| G5 | |
| CPMG-RD |
Comparison with the experimentally determined G1, G2, G4 and G5 and CPMG-RD groups. The differences d1,Res, d2,Res, d3,Res and d4,Res result from Eq. (13)
Thus, the established criteria for MD-based residue classification capture well the main dynamic mechanism described by PC1 of experimentally determined spectral densities, as the percentage of agreement with G1 and G2 is relatively high. In addition, MD successfully predicts conformational exchange per segment resolution to a similar extent. Continuing from this observation we further looked into MD simulations of the relative movements between the selected subdomains of MurD. Namely, between CTD versus NTD-CeD and between β-meander versus the rest as some specific peculiarities for these movements were identified from the experimental data as given in subsection 2.4. Figure 7 displays distributions of two-dimensional vectors representing structural arrangement during 2 μs MD simulations with a first component as the distance between the regions and a second as the relative orientation between the regions in the form of cloud patterns.
Fig. 7. Relative movements between the selected subdomains determined by the MD simulation as fluctuations in the distance between the centers of the vectors and the angle they enclose.
a Schematic representation of the selected pairs i) and ii) of subdomains with the corresponding direction vectors (n1 and n2), centers of vectors (as centers of mass, CM1 and CM2), distances between CMs (d(i) and d(ii)) and angles (ϕ(i) and ϕ(ii)) determined. b Angle distribution versus center distance and (c) centers of the data point clouds with standard deviations in the distance and angle of MurDapo(black), MurDATP(magenta), and MurDinh (green).
The distances d(i) and d(ii) between the regions (Fig. 7a, i and ii) are shown in Figure S8 as a function of simulation time, indicating more noticeable modifications in the dynamics upon binding of inhibitor 1. Further details can be seen from the data clouds in Fig. 7b. The cloud patterns capture dynamic events on a μs time scale and it is therefore to be expected that faster motions are only brought forward when slower motions decrease. Against this background, a similarly dispersed relative movement of the CTD domain relative to NTD-CeD in the MurDATP state compared to MurDapo (Fig. 7b, i) supports the essentially conserved conformational exchange dynamics observed in the experiment in the CTD domain of MurDACP. On the other hand, the dispersion cloud for the MurDinh state is shifted and reduced in size (Fig. 7b, i). This fits with the experimental findings of a significantly reduced number of residues with conformational exchange in the CTD domain and brought out increased G2 dynamics upon binding of inhibitor 1, both indicating stabilization of this domain.
Figure 7b, ii shows a reduced dispersion of the β-meander dynamics versus the rest for MurDATP and an increased dispersion of the β-meander dynamics versus the rest for MurDinh compared to MurDapo. This observation corroborates experimental data showing that the number of residues with conformational exchange in the β-meander decreases for MurDACP, with exchange rates similar to those of MurDapo (in the range above 1100 s−1) and no obvious changes in G1 and G2 dynamics. In contrast, the scattered green cloud in Fig. 7b, ii from the simulations supports the picture of the dynamics diversity of the β-meander in MurDinh. Although the conformational exchange is also reduced in the β-meander of MurDinh, the exchange rates become versatile and cover different ranges (below and above 1100 s−1). The reduction in conformational exchange brings out more evidently concentrated G1 dynamics in the vicinity of the β-meander together with basically preserved G2 dynamics compared to MurDapo.
Discussion
Typically, relationships between reduced spectral density terms are visualized as J(0) vs J(ωH) and J(ωN), where, J(0) versus J(ωH) are negatively correlated while J(0) versus J(ωN) are positively or negatively correlated in dependence of the size of the protein. However, these plots do not simultaneously account for the interdependence of all three J-terms. In our analysis using PCA, we were able to recognize the interplay between them. The main strength of the PCA performed on the spectral density data is the revelation of dynamic mechanisms underlying the protein dynamics with per residue resolution, which aids the interpretation of the interplay between protein size, dynamics, and local structural context. Each of the three PCs corresponds to a specific mechanism defined by its dependence on particular spectral density terms. The classification of residues into five groups based on PCs was crucial for analyzing the dynamics of MurD comprising 430 non-proline residues. It allowed the grouping of residues with distinct dynamics, expressed as the interplay of events on different time scales, without relying on subjective classifications or biased thresholds, on which there is often no uniform consensus in the scientific community. On this basis, we were able to investigate the mechanistic differences between distinct conformations of the MurD states. Indeed, the mechanism of increased dynamics on the fast ps-ns time scale compensated by decreased dynamics on the time scale determined by J(0) described by group G1 does not differ significantly among the three MurD states. In contrast, the opposite compensation described by G2 shows that this mechanism extends over more segments in the MurDACP and MurDinh states compared to MurDapo. The other compensation mechanism observed between the sub-nanosecond time scales and described by groups G4 and G5 is less pronounced, but still indicates an altered prevalence of these dynamics upon binding of either AMP-PCP or inhibitor 1. In addition, we observed that the total number of residues with G3 dynamics describing the non-compensation mechanism of increased dynamics on the time scale determined by J(0) obviously changes upon inhibitor 1 binding.
Investigation of the ability of the PCA results to predict conformational exchange on μs-ms time scale proved limited at residue resolution, but relatively successful at segment resolution, as the prediction of both the presence and absence of conformational exchange based on the G3 residues showed 65–75% agreement with the CPMG-RD results. This is obviously better than the prediction based on the R1R2 products, especially in predicting the absence of conformational exchange (Table S6). Thus, the PCA results provide valuable information about these important motions that are directly linked to biological function48, even for larger proteins with complex dynamic behavior on multiple time scales, such as MurD.
The independent measurements of conformational exchange dynamics with CPMG-RD indicate the existence of a conformational ensemble through slow μs-ms movements of CTD in MurDapo and MurDACP, which are only suppressed after binding of inhibitor 1. This suggests that AMP-PCP selects compatible conformations pre-existing in the apo ensemble and maintains the flexibility of the CTD to prepare the conformational ensemble favorable for substrate binding through a conformational selection process. Interestingly, 2 μs long MD simulations for MurDapo and MurDACP also show that the relative flexibility of the CTD versus the rest is not that much different for the two states, while it is significantly lower in the case of MurDinh. Nevertheless, recent crystallographic structures of apo and bound MurD showed that the closed conformation can also exist in the AMP-PNP-bound state (PDB 9DQW49) and the semi-closed conformation in the apo state (PDB 5A5E23), suggesting that occupancy of the different conformations in the ensemble may be present at a higher percentage, that is in line with our predictions from the analysis of CPMG-RD data.
The prevalence of conformational selection in the binding mechanism may be the reason for the unsuccessful design of ATP-competitive inhibitors, which was based on a specific/single crystallographic structure in the closed conformation. To effectively target the ATP-binding site, we recommend generating an ensemble of conformations that includes only those in which the site remains exposed, excluding closed conformations.
A high degree of dynamic diversity observed through group classification that inhibitor 1 cannot fully suppress could be a key factor limiting its binding efficacy. However, we should bear in mind that increasing the target flexibility in the bound state by incorporating appropriate functional groups into the ligand may have the beneficial effect of improving the lifetime of a protein-drug complex and consequently increasing the drug efficacy50. In any case, the group classification based on PCs reveals details of less and more flexible protein dynamics and can therefore serve as an advanced guide for inhibitor design.
Of note, the approach of applying PCA to the reduced spectral densities is by no means limited to the MurD system, but represents a general tool that enables a deeper insight into dynamic mechanisms specific to any other system for which spectral density data are available.
Materials and methods
Protein expression and purification
Cultures of BL21(DE3) Escherichia coli containing the pABD16 plasmid for MurD expression were cultivated on LB agar plates for 16 h at 37 °C. For preparation of U-[2H, 15N]-labeled MurD, a single colony was transferred to 20 ml of LB medium prepared with 70% 2H2O and incubated overnight at 37 °C. Cells were subsequently pelleted, resuspended, and added to U-[2H, 15N]-labeled rich OD2 medium from Silantes. For U-[2H, 13C, 15N]-labeled MurD, single colony was transferred to 20 ml of LB medium and incubated overnight at 37 °C. After pelleting, the cells were resuspended in a series of adaptation media with gradually increasing 2H2O ratios: M9 prepared in H2O, M9 with 50% 2H2O and M9 with 100% 2H2O, each at a small scale. The adaptation process started with OD600 = 0.25 and continued until reaching ~2. Finally, the cells were resuspended in large-scale M9 medium with 100% 2H2O. Each M9 minimal medium contained U-[2H, 13C]-glucose (2 g l−1) and 15NH4Cl (1 g l−1). The culture was grown at 37 °C until an OD600 of 0.7 was reached. The temperature was then decreased to 25 °C, and after a 30-min, IPTG was added to 1 mM final concentration. After 16 h of induction, cells were harvested by centrifugation and resuspended in lysis buffer (50 mM Tris-HCl, pH 8 at 4 °C, 500 mM NaCl, 5 mM MgCl2, 20 mM imidazole, protease inhibitors (Sigma Aldrich), and 2 mM TCEP). The lysate was treated with lysozyme, sonicated, and after a 15 min incubation with benzonase, clarified by centrifugation at 12,000 rpm for 30 min at 4 °C. The supernatant containing the His-tagged protein was loaded onto a His-Trap column (GE Healthcare) equilibrated with binding buffer (50 mM Tris-HCl, pH 8 at 4 °C, 500 mM NaCl, 5 mM MgCl2, 20 mM imidazole, and 2 mM TCEP). Following extensive wash with the binding buffer, the protein was eluted using elution buffer (50 mM Tris-HCl, pH 8 at 4°C, 500 mM NaCl, 5 mM MgCl2, 300 mM imidazole, and 2 mM TCEP). To exchange 2H for 1H at amide groups in regions hidden from the solvent, the protein was first unfolded by dialysis against an unfolding buffer (50 mM Tris-HCl, pH 8 at 4 °C, 6 M GuHCl, 150 mM NaCl, 5 mM MgCl2, and 3 mM DTT) and then refolded by dialysis against a refolding buffer (50 mM Tris-HCl, pH 8 at 4 °C, 150 mM NaCl, 5 mM MgCl2, and 3 mM DTT). For the second purification step involving size-exclusion chromatography, the protein was dialyzed against GF buffer (20 mM Tris-HCl, pH 7.5 at room temperature, 130 mM NaCl, 5 mM MgCl2, and 3 mM DTT) and then loaded onto a 120 mL Superdex 75 PG column (GE Healthcare) pre-equilibrated with GF buffer. The purity and molecular weight of the eluted protein were assessed using SDS-PAGE. Pure fractions were combined, concentrated, and dialyzed against NMR buffer (20 mM Tris-d6-HCl, pH 7.2 at room temperature, 100 mM NaCl, 5 mM MgCl2, 1 mM TCEP, and 0.02% NaN3). The U-[2H, 15N]-labeled MurD was flash-frozen in liquid nitrogen and stored at −80 °C.
Compound 1 was resynthesized according to the synthetic procedures described in Sosič et al.11. The 1H and 13C NMR spectra were in accordance with previously published data. Compound had > 97% purity by HPLC.
NMR spectroscopy
All experiments were recorded at 25 °C on a Bruker Avance Neo spectrometer operating at 18.8 T (800 MHz for 1H), and equipped with a 1H/13C/15N cryoprobe. Data acquisition was carried out using the pulse sequences from the Bruker’s library of pulse programs. The NMR samples were placed in 5 mm NMR Shigemi tubes and contained 0.27 mM U-[2H, 15N] or U-[2H, 13C, 15N]-labeled MurD in an NMR buffer, supplemented with 10% DMSO-d6.
Chemical shift assignment
The TROSY-based 3D-HNCA spectra were acquired with 32 scans using non-uniform sampling along the two indirect dimensions t1 and t2 containing 170 and 76 complex data points, respectively, of which only 6460-point pairs were recorded. This corresponded to an undersampling of 50%. Spectral widths 27 ppm (13C), 35 ppm (15N) and 14.2 ppm (1H), acquisition times 7 ms (13C), 30 ms (15N) and 45 ms (1H) and recycle delay of 1 s were used. The spectra were processed with Topspin 4.1.7. and analyzed with CCPNmr Assign 3.1.051. The backbone 1HN and 15N chemical shift assignments of MurDapo, MurDACP, and MurDinh are shown in the 1H-15N TROSY spectra (Figs. S3-S5).
Chemical shift perturbations (CSPs)
CSPs were tracked in 1H-15N TROSY spectra recorded with acquisition times of 45 ms (15N) and 90 ms (1H), 16 scans and a relaxation delay of 1 s. CSPs were calculated from the proton and nitrogen CSP (ΔδH and ΔδN, respectively), according to the weighted formula for the ith residue52:
| 1 |
CSP’s at binding of AMP-PCP (Fig. S6) were quantified at a protein-ligand ratio of 1:8. Subsequently, inhibitor 1 was titrated from a stock prepared in DMSO-d6. Final protein-inhibitor 1 ratio used for calculation of CSPs was 1:4 (Fig. S6). The addition of the inhibitor 1 did not exceed 2% of the NMR sample volume.
In most cases where a significant CSP was observed, the intensity of the unbound protein signal decreased with increasing ligand concentration and the new protein signal appeared with increasing intensity. The CSP could not be determined if the intensities of the new peaks were too low to obtain correlations in the HNCA spectra that would allow unambiguous assignment of the new peaks. The CSP data in the presence of AMP-PCP and inhibitor 1 indicate that MurD preferentially forms a complex with inhibitor 1 and not with both ligands. Namely, an additional set of new signals with lower intensity was observed in the ATP-binding region, also indicating the presence of a complex with both ligands. MD simulations confirmed these observations, as the complex of MurD with inhibitor 1 along the 2 μs long trajectory is far more stable and well-defined than the complex with both ligands.
15N relaxation
The 15N R1 and R2 and hetNOE measurements35 for MurDapo, MurDACP, and MurDinh were acquired with acquisition times of 45 ms (15N) and 90 ms (1H). The R1 values were determined from spectra recorded with eight relaxation delays in the following sequence: 20, 3000, 60, 2000, 160, 1280, 320, 640, and 20 ms. The recycle delay was 6 s. The R2 values were determined from spectra measured with six Carr-Purcell-Maiboom-Gill (CPMG) loop lengths in the following sequence: 10, 50, 16, 39.9, 25, 29.9 and 16 ms. The recycle delay was 1 s. 16 scans were performed for R1 and 32 scans for R2 measurements. The estimation of the experimental errors in the R1 and R2 values was determined based on the deviation between duplicated spectra. The hetNOE values were determined from two datasets, one acquired with and the other without initial proton pre-saturation. A long pre-saturation/relaxation time of 10 s was used to consider long amide 1H T1 values in perdeuterated proteins53. 16 scans were performed for MurDapo and MurDACP and 32 scans for MurDinh. The errors in the hetNOE values were determined based on the uncertainties of the peak intensities estimated from the noise level of the spectra, as described by Farrow et al.54. The R1 and R2 spectra were zero-filled to 8k in 1H dimension and processed using Topspin 4.1.7. Relaxation series were subsequently analyzed using CCPNmr Analysis 2.5.055. Relaxation rates R1 and R2 were determined using non-linear least-squares fitting, where the peak intensities were fit to the equation:
| 2 |
In this equation, both I0 and R were treated as fit parameters.
The reduced spectral densities J(0), J(0.87ωH) and J(ωN) were calculated from R1, R2, and hetNOEs using the program Relax (Version 5.0.0)56,57. The vibrationally averaged effective N-H bond length was 1.02 Å and 15N chemical shift anisotropy was −172 ppm.
The 15N CPMG-RD experiments43–45 were acquired using a constant CPMG relaxation delay (Trelax) of 30 ms. The CPMG filed strengths (νCPMG) were: 67, 133, 200 (2×), 267, 333, 400, 467, 533, 600, 733, 1000, and 1267 Hz with duplicate points included for error analysis. The spectra were measured with 24 scans and a recycle delay of 3 s. The spectra were zero-filled to 8k in 1H dimension and processed using Topspin 4.3.0 and CCPNmr Assign 3.1.051. Effective transverse relaxation rates () were calculated from the peak intensities at given CPMG frequency (Iν) relative to the intensity at νCPMG = 0 Hz (I0) using the equation:
| 3 |
were then plotted as a function of νCPMG.
The precision of the peak intensities at a given νCPMG (i.e., IνCPMG) and intensity at νCPMG = 0 Hz (i.e., I0) was determined as the mean of the background noise obtained from the random sampling for each νCPMG, i.e., ΔIνCPMG and ΔI0 (for νCPMG = 0 Hz).The error bars for the data points of in s−1 were further calculated as
| 4 |
The data points of versus νCPMG were fitted to the 2-site CPMG model presented in ref. 46. We used the nonlinear least square method implemented by the trust-region algorithm. The model is as follows:
| 5 |
where
| 6 |
The fit per residue yielded the basal transverse relaxation rate in s−1, the exchange rate constant kex in s−1 (kex = kAB + kBA), the populations pA and pB, where pB = 1- pA and pA > pB, and the 15N chemical shift Δω = ΔωN in s−1, assuming that ΔωH = 0 For the group (global) fits, the values of kex and pA were forced to be the same for the subset of residues selected from the per-residue fit based on the similar kex values within certain domain substructures. Fitting was performed using computational scripts adapted from Singh et al.58.
Evaluation of the conformational exchange
The presence of conformational exchange (CE) was assessed based on the relationships between the experimental data and the data fitted with the 2-site CPMG model46 as follows,
| 7 |
where the index i ranges from the first to the last non-zero νCPMG (excluding the repeated data point) and RMSE corresponds to the root-mean-square error of the fit.
The reliability of the conformational exchange (RE) classification was estimated based on the relation of the repeated data point, (), to the CPMG fit, , in the following way,
| 8 |
where the index i ranges from the first to the last non-zero νCPMG (excluding the repeated data point) and denotes the CPMG frequency at which the CPMG experiment was repeated.
Principal component analysis (PCA)
The spectral densities J(0), J(0.87ωH) and J(ωN) were considered for the PCA as variables with the known values for the residues of the three MurD states. Due to different scales of the original variables, standardization of the data was performed (i.e., to have a mean of zero and a standard deviation of one) to ensure that all variables contribute equally to the analysis.
By setting the specific criteria for the principal component (PC) scores, we have identified five sets of residues exhibiting exclusive dynamics (residues presented with the colored circles in Fig. 3). The criteria are presented in Table 2. For PC1 and PC3 (which indicate a compensation effect), we extracted the residues whose PC scores stand out in the positive and negative PC directions, while for PC2, which shows no compensation effect, we extracted the residues whose PC2 scores stand out from the others in the positive PC direction.
Molecular dynamics simulations
Molecular dynamics (MD) simulations of representing four MurD states (MurDapo, MurDATP, and MurDinh with and without ATP) were performed starting from the complexes presented in ref. 18 using the NAMD59 MD package and Charmm36 force field parameters60. Force field parameters for ligands were obtained by CGenFF61, while partial charges were additionally optimized by Gaussian16 (Gaussian Inc., W.C. Gaussian 16). Explicit solvent environments were generated as an aqueous solution of DMSO (molar ratio 100:3) with the addition of 0.11 M NaCl and 0.02 M MgCl2 using in-house software for random distribution of solvent molecules at a given density by considering periodic boundary conditions. For water, we used TIP3P model. All four systems were subjected to energy minimization, followed by a series of 10 ns equilibration MD simulations. Subsequently, a 2 μs production NPT simulation was performed for each system applying no position restraints. Each system consisted of ~70,000 atoms and was confined in an orthogonal 89 Å3 simulation box. The temperature was maintained at 300 K by the Nosé–Hoover thermostat and the pressure of 1 bar was kept constant by the Parrinello–Rahman barostat. Long range electrostatic interactions were calculated with the particle-mesh Ewald (PME) method. A cutoff of 1.0 nm for short-range electrostatic interactions and 1.4 nm for van der Waals interactions was used.
For the two selected pairs of MurD subdomains, we further analyzed the relative movements, namely the movement of the CTD domain versus NTD-CeD and the β-meander (β12-β13-β14) subdomain versus the rest. In this analysis, the dynamic fluctuations of selected protein subdomains were visualized by plotting 2D cloud diagrams showing the distance between the centers of masses (CM) of the selected subdomains and the relative orientation of the domains during the MD simulation. The latter was determined as the direction of the domain mass tensor axis with the lowest moment of inertia for each domain.
The motions per residue from MD simulations were analyzed via the autocorrelation function for the standard order parameter depending on the second-order Legendre polynomial of the angle between the consecutive orientations of the residue N-H backbone vector :
| 9 |
where is the second-order Legendre polynomial, and the angle brackets denote a time average over trajectory. The spectral density function describing the power of the residue motion at different frequencies ω, is the Fourier Transform of the correlation function 62:
| 10 |
The classification of the dynamics per residue was based on the relationships between the areas under the spectral density curve in the four frequency ranges. Namely,
| 11 |
where , , and We further calculated the average area under the spectral density curve in the four frequency ranges for each residue type , i.e.,
| 12 |
where is the number of the type residues, and determined the dynamical deviation of each residue of this type as the difference
| 13 |
The criteria established for these spectral density-based MD results for residue classification are shown in Table 3 along with the corresponding experimental outcomes with which they are compared. Categorization is performed for all residues in various frequency ranges while determining its dominating role based on the largest deviation from the average value for a given residue type within a given frequency range.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Description of Additional Supplementary Files
Acknowledgements
This work was supported by the Slovenian Research and Innovation Agency (Grant No. J1-4400, P1-0010, and P1-0208). We recorded NMR spectra on NMR spectrometers of the Slovenian NMR Center at the National Institute of Chemistry. We acknowledge the Ažman high-performance computing center at the National Institute of Chemistry for computational resources.
Author contributions
I.O., B.Z. and S.G.G. designed the research. I.O. performed the protein production. IS synthesized the inhibitor. I.O., B.Z., F.M. and S.G.G. acquired and analyzed the data. I.O., B.Z. and S.G.G. drafted the manuscript. All authors reviewed the manuscript.
Peer review
Peer review information
Communications Chemistry thanks the anonymous reviewers for their contribution to the peer review of this work.
Data availability
1HN, 15N chemical shifts of the MurD apo and bound states to support the NMR spectra in Fig. 1b and Fig. 6b can be found in Supplementary Data 1. Numerical data to support the graphical representation of Fig. 2, insets a, c and d, can be found in Supplementary Data 2. Numerical data to support the graphical representation of Fig. 3, insets c, d and e, can be found in Supplementary Data 3. Numerical data to support the graphical representation of Fig. 5, insets i), ii) and iii), can be found in Supplementary Data 4. The initial and final configurations of the MD trajectories of the MurDapo state can be found in Supplementary Data 5 and 6, respectively. The initial and final configurations of the MD trajectories of the MurDATP state can be found in Supplementary Data 7 and 8, respectively. The initial and final configurations of the MD trajectories of the MurDinh state can be found in Supplementary Data 9 and 10, respectively. All relevant data supporting the findings of this study are available upon request from the corresponding authors.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Barbara Zupančič, Email: barbara.zupancic@ki.si.
Simona Golič Grdadolnik, Email: simona.grdadolnik@ki.si.
Supplementary information
The online version contains supplementary material available at 10.1038/s42004-025-01675-z.
References
- 1.Theuretzbacher, U., Blasco, B., Duffey, M. & Piddock, L. J. V. Unrealized targets in the discovery of antibiotics for Gram-negative bacterial infections. Nat. Rev. Drug Discov. 22, 957–975 (2023). [DOI] [PubMed]
- 2.Shirakawa, K. T. et al. Architecture and genomic arrangement of the MurE–MurF bacterial cell wall biosynthesis complex. Proc. Natl Acad. Sci. USA120, e2219540120 (2023). [DOI] [PMC free article] [PubMed]
- 3.Miyakawa, T. et al. Structural bases for aspartate recognition and polymerization efficiency of cyanobacterial cyanophycin synthetase. Nat. Commun.13, 5097 (2022). [DOI] [PMC free article] [PubMed]
- 4.Mol, C. D. et al. Crystal structures of active fully assembled substrate- and product-bound complexes of UDP-N-acetylmuramic acid:L-alanine ligase (MurC) from Haemophilus influenzae. J. Bacteriol.185, 4152–4162 (2003). [DOI] [PMC free article] [PubMed]
- 5.Longenecker, K. L. et al. Structure of MurF from Streptococcus pneumoniae co-crystallized with a small molecule inhibitor exhibits interdomain closure. Protein Sci.14, 3039–3047 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tomašič, T. et al. 5-benzylidenethiazolidin-4-ones as multitarget inhibitors of bacterial Mur ligases. ChemMedChem5, 286–295 (2010). [DOI] [PubMed]
- 7.Zidar, N. et al. New 5-benzylidenethiazolidin-4-one inhibitors of bacterial MurD ligase: Design, synthesis, crystal structures, and biological evaluation. Eur. J. Med. Chem.46, 5512–5523 (2011). [DOI] [PubMed]
- 8.Tomašič, T. et al. Synthesis and biological evaluation of new glutamic acid-based inhibitors of MurD ligase. Bioorg Med. Chem. Lett.19, 153–157 (2009). [DOI] [PubMed]
- 9.Tomašič, T. et al. Structure-based design of a new series of D-glutamic acid based inhibitors of bacterial UDP-N-acetylmuramoyl-L-alanine: D-glutamate ligase (MurD). J. Med. Chem. 54, 4600–4610 (2011). [DOI] [PubMed]
- 10.Humljan, J. et al. Novel naphthalene-N-sulfonyl-D-glutamic acid derivatives as inhibitors of MurD, a key peptidoglycan biosynthesis enzyme. J. Med. Chem.51, 7486–7494 (2008). [DOI] [PubMed]
- 11.Sosič, I. et al. Second-generation sulfonamide inhibitors of D-glutamic acid-adding enzyme: Activity optimisation with conformationally rigid analogues of D-glutamic acid. Eur. J. Med. Chem.46, 2880–2894 (2011). [DOI] [PubMed]
- 12.Hrast, M. et al. Evaluation of the published kinase inhibitor set to identify multiple inhibitors of bacterial ATP-dependent mur ligases. J. Enzym. Inhib. Med Chem.34, 1010–1017 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hrast, M. et al. Mur ligases inhibitors with azastilbene scaffold: Expanding the structure–activity relationship. Bioorg. Med Chem. Lett.40, 127966 (2021). [DOI] [PubMed] [Google Scholar]
- 14.Zidar, N. et al. Discovery of novel 5–benzylidenerhodanine and 5-benzylidenethiazolidine-2, 4-dione inhibitors of MurD ligase. J. Med. Chem.53, 6584–6594 (2010). [DOI] [PubMed]
- 15.Perdih, A. et al. Benzene-1,3-dicarboxylic acid 2,5-dimethylpyrrole derivatives as multiple inhibitors of bacterial Mur ligases (MurC-MurF). Bioorg. Med. Chem.22, 4124–4134 (2014). [DOI] [PubMed]
- 16.Kotnik, M. et al. Structural and Functional Characterization of Enantiomeric Glutamic Acid Derivatives as Potential Transition State Analogue Inhibitors of MurD Ligase. J. Mol. Biol.370, 107–115 (2007). [DOI] [PubMed] [Google Scholar]
- 17.Rambaher, M. H., Zdovc, I., Glavač, N. K., Gobec, S. & Frlan, R. Mur ligase F as a new target for the flavonoids quercitrin, myricetin, and (–)-epicatechin. J. Comput. Aided Mol. Des.37, 721–733 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Simčič, M. et al. A novel 2-oxoindolinylidene inhibitor of bacterial MurD ligase: Enzyme kinetics, protein-inhibitor binding by NMR and a molecular dynamics study. Eur. J. Med. Chem.83, 92–101 (2014). [DOI] [PubMed] [Google Scholar]
- 19.Simčič, M. et al. NMR and molecular dynamics study of the binding mode of naphthalene-N-sulfonyl-D-glutamic acid derivatives: Novel MurD ligase inhibitors. J. Med. Chem.52, 2899–2908 (2009). [DOI] [PubMed] [Google Scholar]
- 20.Simčič, M. et al. The binding mode of second-generation sulfonamide inhibitors of MurD: Clues for rational design of potent MurD inhibitors. PLoS One7, e52817 (2012). [DOI] [PMC free article] [PubMed]
- 21.Bertrand, J. A. et al. ‘Open’ structures of MurD: Domain movements and structural similarities with folylpolyglutamate synthetase. J. Mol. Biol.301, 1257–1266 (2000). [DOI] [PubMed]
- 22.Seibold, S., Lovell, S., Liu, L. & Battaile, K. P. Crystal Structure of Apo UDP-N-acetylmuramoylalanine-D-glutamate ligase (MurD) from E. coli (ATP bound). PDB: 8VW2.
- 23.Šink, R. et al. Crystallographic Study of Peptidoglycan biosynthesis enzyme MurD: Domain movement revisited. PLoS One11, e0152075 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bertrand, J. A. et al. Crystal structure of UDP-N-acetylmuramoyl-L-alanine:D-glutamate ligase from Escherichia coli. EMBO J.16, 3416–3425 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bertrand, J. A. et al. Determination of the MurD mechanism through crystallographic analysis of enzyme complexes. J. Mol. Biol.289, 579–590 (1999). [DOI] [PubMed]
- 26.Tomašič, T. et al. Dual inhibitor of MurD and MurE ligases from escherichia coli and staphylococcus aureus. ACS Med. Chem. Lett.3, 626–630 (2012). [DOI] [PMC free article] [PubMed]
- 27.Saio, T. et al. Ligand-driven conformational changes of MurD visualized by paramagnetic NMR. Sci. Rep.5, 1–11 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nakagawa, H. et al. Conformational dynamics of a multidomain protein by neutron scattering and computational analysis. Biophys. J. 120, 3341–3354 (2021). [DOI] [PMC free article] [PubMed]
- 29.Saio, T. et al. Conformational ensemble of a multidomain protein explored by Gd3+ electron paramagnetic resonance. Biophys. J.120, 2943–2951 (2021). [DOI] [PMC free article] [PubMed]
- 30.Kawamukai, H. et al. Conformational distribution of a multidomain protein measured by single-pair small-angle X-ray Scattering. J. Phys. Chem. Lett.15, 744–750 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Azam, M. A. & Jupudi, S. MurD inhibitors as antibacterial agents: a review. Chem. Pap. 74, 1697–1708 (2020).
- 32.Favier, A. & Brutscher, B. Recovering lost magnetization: Polarization enhancement in biomolecular NMR. J. Biomol. NMR49, 9–15 (2011). [DOI] [PubMed] [Google Scholar]
- 33.Schulte-Herbrüggen, T. & Sørensen, O. W. Clean TROSY: Compensation for relaxation-induced artifacts. J. Magn. Reson.144, 123–128 (2000). [DOI] [PubMed] [Google Scholar]
- 34.Solyom, Z. et al. BEST-TROSY experiments for time-efficient sequential resonance assignment of large disordered proteins. J. Biomol. NMR55, 311–321 (2013). [DOI] [PubMed] [Google Scholar]
- 35.Zhu, G., Xia, Y., Nicholson, L. K. & Sze, K. H. Protein dynamics measurements by TROSY-based NMR experiments. J. Magn. Reson. 143, 423–426 (2000). [DOI] [PubMed]
- 36.Kneller, J. M., Lu, M. & Bracken, C. An effective method for the discrimination of motional anisotropy and chemical exchange. J. Am. Chem. Soc.124, 1852–1853 (2002). [DOI] [PubMed]
- 37.Farrow, N. A., Zhang, O., Szabo, A., Torchia, D. A. & Kay, L. E. Spectral density function mapping using 15N relaxation data exclusively. J. Biomol. NMR6, 153–162 (1995). [DOI] [PubMed]
- 38.van Ingen, H., Baltussen, M. A. H., Aelen, J. & Vuister, G. W. Role of structural and dynamical plasticity in Sin3: The Free PAH2 Domain is a Folded Module in mSin3B. J. Mol. Biol. 358, 485–497 (2006). [DOI] [PubMed]
- 39.Piai, A. et al. Structural basis of transmembrane coupling of the HIV-1 envelope glycoprotein. Nat. Commun. 11, 2317 (2020). [DOI] [PMC free article] [PubMed]
- 40.Peng, T., Zintsmaster, J. S., Namanja, A. T. & Peng, J. W. Sequence-specific dynamics modulate recognition specificity in WW domains. Nat. Struct. Mol. Biol.14, 325–331 (2007). [DOI] [PubMed] [Google Scholar]
- 41.O’Sullivan, D. B. D. et al. Dynamics of a truncated prion protein, PrP(113-231), from 15N NMR relaxation: Order parameters calculated and slow conformational fluctuations localized to a distinct region. Protein Sci.18, 410–423 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dayie, K. T., Wagner, G. & Lefèvre, J.-F. Theory and practice of nuclear spin relaxation in proteins. Annu. Rev. Phys. Chem.47, 243–282 (1996). [DOI] [PubMed] [Google Scholar]
- 43.Vallurupalli, P., Hansen, D. F., Stollar, E., Meirovitch, E. & Kay, L. E. Measurement of bond vector orientations in invisible excited states of proteins. Proc. Natl Acad. Sci. USA104, 18473–18477 (2007). [DOI] [PMC free article] [PubMed]
- 44.Jiang, B., Yu, B., Zhang, X., Liu, M. & Yang, D. A 15N CPMG relaxation dispersion experiment more resistant to resonance offset and pulse imperfection. J. Magn. Reson.257, 1–7 (2015). [DOI] [PubMed]
- 45.Yuwen, T. & Kay, L. E. Revisiting 1HN CPMG relaxation dispersion experiments: a simple modification can eliminate large artifacts. J. Biomol. NMR73, 641–650 (2019). [DOI] [PubMed]
- 46.Korzhnev, D. M., Kloiber, K. & Kay, L. E. Multiple-quantum relaxation dispersion NMR spectroscopy probing millisecond time-scale dynamics in proteins: Theory and application. J. Am. Chem. Soc.126, 7320–7329 (2004). [DOI] [PubMed] [Google Scholar]
- 47.Kumar, G. S. et al. Dynamic activation and regulation of the mitogen-activated protein kinase p38. Proc. Natl Acad. Sci. USA115, 4655–4660 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Henzler-Wildman, K. & Kern, D. Dynamic personalities of proteins. Nature450, 964–972 (2007). [DOI] [PubMed] [Google Scholar]
- 49.Seibold, S., Liu, L., Lovell, S. & Bettaile, K. P. Crystal Structure of UDP-N-acetylmuramoylalanine-D-glutamate ligase (MurD) from E. coli in complex with UMA and AMP-PNP. PDB: 9DQW.
- 50.Amaral, M. et al. Protein conformational flexibility modulates kinetics and thermodynamics of drug binding. Nat. Commun.8, 2276 (2017). [DOI] [PMC free article] [PubMed]
- 51.Skinner, S. P. et al. CcpNmr AnalysisAssign: a flexible platform for integrated NMR analysis. J. Biomol. NMR66, 111–124 (2016). [DOI] [PMC free article] [PubMed]
- 52.Mureddu, L. & Vuister, G. W. Simple high-resolution NMR spectroscopy as a tool in molecular biology. FEBS J.286, 2035–2042 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lakomek, N. A., Ying, J. & Bax, A. Measurement of 15N relaxation rates in perdeuterated proteins by TROSY-based methods. J. Biomol. NMR53, 209–221 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Farrow, N. A. et al. Backbone Dynamics of a Free and a Phosphopeptide-Complexed Src Homology 2 Domain Studied by 15N NMR Relaxation. Biochemistry33, 5984–6003 (1994). [DOI] [PubMed] [Google Scholar]
- 55.Vranken, W. F. et al. The CCPN data model for NMR spectroscopy: Development of a software pipeline. Proteins: Struct. Funct. Genet.59, 687–696 (2005). [DOI] [PubMed]
- 56.d’Auvergne, E. J. & Gooley, P. R. Optimisation of NMR dynamic models I. Minimisation algorithms and their performance within the model-free and Brownian rotational diffusion spaces. J. Biomol. NMR40, 107–119 (2008). [DOI] [PMC free article] [PubMed]
- 57.d’Auvergne, E. J. & Gooley, P. R. Optimisation of NMR dynamic models II. A new methodology for the dual optimisation of the model-free parameters and the Brownian rotational diffusion tensor. J. Biomol. NMR40, 121–133 (2008). [DOI] [PMC free article] [PubMed]
- 58.Singh, A., Purslow, J. A. & Venditti, V. 15N CPMG relaxation dispersion for the investigation of protein conformational dynamics on the μs-ms timescale. JoVE170, 10.3791/62395 (2021). [DOI] [PMC free article] [PubMed]
- 59.Phillips, J. C. et al. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26, 1781–1802 (2005). [DOI] [PMC free article] [PubMed]
- 60.Best, R. B. et al. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput8, 3257–3273 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Vanommeslaeghe, K. et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput Chem.31, 671–690 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Palmer, A. G. 3rd NMR characterization of the dynamics of biomacromolecules. Chem. Rev.104, 3623–3640 (2004). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Description of Additional Supplementary Files
Data Availability Statement
1HN, 15N chemical shifts of the MurD apo and bound states to support the NMR spectra in Fig. 1b and Fig. 6b can be found in Supplementary Data 1. Numerical data to support the graphical representation of Fig. 2, insets a, c and d, can be found in Supplementary Data 2. Numerical data to support the graphical representation of Fig. 3, insets c, d and e, can be found in Supplementary Data 3. Numerical data to support the graphical representation of Fig. 5, insets i), ii) and iii), can be found in Supplementary Data 4. The initial and final configurations of the MD trajectories of the MurDapo state can be found in Supplementary Data 5 and 6, respectively. The initial and final configurations of the MD trajectories of the MurDATP state can be found in Supplementary Data 7 and 8, respectively. The initial and final configurations of the MD trajectories of the MurDinh state can be found in Supplementary Data 9 and 10, respectively. All relevant data supporting the findings of this study are available upon request from the corresponding authors.