Abstract
Parameter identification of a PEMFC is the process of using optimization approaches to determine the best unknown variables suitable for the development of a precision fuel cell performance forecasting model. Since these variables may not always be mentioned in the manufacturer’s datasheet, identifying them is essential to accurately forecasting and evaluating the fuel cell’s performance. Like many swarm-based algorithms, the Hippopotamus Optimization (HO) algorithm is prone to getting trapped in local optima, which can hinder its ability to identify global optimal solutions. This limitation becomes particularly pronounced in complex, constrained optimization problems. Additionally, the algorithm’s reliance on previous solutions for updating positions often leads to slow convergence. To address these challenges, a modified version of the HO algorithm (MHO) is proposed that integrates two innovative strategies: a novel exploitation mechanism and an Enhanced Solution Quality method. Five distinct optimization techniques; the MHO algorithm, the Grey Wolf Optimizer (GWO), the HO algorithm, the Chimp Optimization Algorithm (ChOA), and the sine cosine algorithm (SCA) are used to calculate the six unknown parameters of a PEMFC. The sum square error (SSE) between the estimated and measured cell voltages is the fitness function that needs to be minimized during optimization, and these six parameters act as choice variables. HO, GWO, SCA, and ChOA came after the MHO algorithm, which produced an SSE of 1.748996055. Because MHO accurately anticipated the performance of the fuel cell, it is suitable for the development of digital twins for fuel-cell applications and control systems for the automobile industry. Furthermore, it was demonstrated that MHO converged faster than the other techniques studied.
Keywords: Modified hippopotamus optimization, Fuel cell, Parameter identification
Subject terms: Engineering, Electrical and electronic engineering
Introduction and related work
Due to the rapid depletion of fossil fuel reserves and the increasing demand for electricity, sustainable energy sources are becoming increasingly important for both large industrial purposes and small-scale power applications1–6. Making use of energy derived from renewable resources, like Wind and solar energy are examples of renewable energy sources that are often dependent on their environment. As a result, fuel cells were created to supplement the existing green energy sources. sources of energy. Historically, fuel cells have been classified into three groups: portable, stationary, and transportation-related7. Automotive fuel cell technology has advanced rapidly. sector because more and more large land vehicles like public buses are utilizing fuel cells. Additionally, stationary fuel cells are increasingly being used in homes and offices8. Stationary fuel cells have multiple applications. Many businesses and researchers have been interested in fuel cells in recent years. The chemical energy produced by the interaction of oxygen and hydrogen, or ambient air, can be quickly converted into electrical energy using fuel cells9. Solid oxide, phonic acid, alkaline, and proton exchange membrane fuel cells are among the many types of fuel cells10. PEMFC fuel cells are the most often used fuel cell type in the automotive sector, despite the fact that each of these fuel cell types serves a distinct purpose11,12.
Despite their benefits, fuel cells (FCs) have drawbacks such limited output voltage and current. To build modules with the requisite voltage and current, series connection of cells is required. Issues including linearly varying ohmic loss, activation loss at low current densities, and concentration polarization loss at high current densities result in a lower output voltage from the open circuit voltage. Accurate quantification of these losses is challenging because of equations with seven unknown factors, only one of which can be measured empirically13–17.
Fuel cells (FCs) are dependable and eco-friendly alternative energy sources that can be used in a variety of applications, such as mobile phone recharging, electric cars, and residential and commercial buildings. They generate clean byproducts and have cheap operating costs, high efficiency, scalability, and silent operation. The low operating temperature, high power densities, quick startup, smaller volume, less weight, and general dependability of PEMFCs make them stand apart18. PEMFCs are used in stationary and portable power sources and are especially well suited for automotive applications19.
Meta-heuristic algorithms are employed by researchers to surmount the obstacles presented by PEMFCs. These algorithms are widely used for obtaining PEMFC parameters because of their simplicity, adaptability, problem independence, gradient-free nature, versatility, and resistance to local optima trapping. The No-Free-Lunch theorem highlights the fact that not all engineering optimization issues can be successfully resolved by any optimizer currently in use. To estimate PEMFC parameters, a variety of algorithms are used, such as the artificial ecosystem optimizer20, seeker optimization algorithm21, harmony search algorithm22, bird mating algorithm23, hybrid bee colony24, particle swarm optimization25, simplified TLBO26, evolution strategy (ES)27, and grey wolf optimizer28.
Additionally, a variety of metaheuristic-based methods for PEMFC parameter estimation have been investigated recently. Adaptive Sparrow Search Algorithm29, Moth-Flame Optimization30, Pathfinder Algorithm31, Levenberg-Marquardt Backpropagation Algorithm32, Hybrid Water Cycle Moth-Flame Optimization33, Modified Monarch Butterfly Optimization34, Gradient Based Optimizer35, Osprey Optimization Algorithm36, Hybrid Artificial Bee Colony Differential Evolution Optimizer37, Improved African Vulture Optimization Algorithm38, rime-ice algorithm39, and Walrus Optimizer40 are a few of these among others. Also, several algorithms such as Improved exponential distribution optimizer41, Dynamic Hunting Leadership42, Enhancing Sand Cat Swarm43.
The main objective and contribution of this effort can be summed up as follows:
The performance of the Modified Hippopotamus Optimization (MHO) method, a contemporary metaheuristic technique, is being investigated in order to address PEMFC problems.
The six PEMFC parameters are computed using the MHO approach.
The sum of square error is the fitness function applied to identification issues.
The proposed MHO method is compared to the Grey Wolf Optimizer (GWO), Hippopotamus optimization (HO), Chimp optimization algorithm (ChOA), and sine cosine algorithm (SCA).
To ensure that all comparator techniques, including the suggested MHO approach, function as intended, Ned Stack PS6, a real PEM fuel cell model, is utilized.
Every method is assessed across thirty distinct runs based on the convergence and robustness statistics.
Additionally, the suggested MHO method is contrasted with other published methods, including the Vortex Search approach with Differential Evolution (VSDE), the Equilibrium Optimizer (EO), the Manta Rays Foraging Optimizer (MRFO), the Neural Network Algorithm (NNA), the Artificial Ecosystem Optimizer (AEO), the Slap Swarm Optimizer (SSO), and the Equilibrium Optimizer (EO).
The following is how this work is structured: Section “Analysis of the PEM fuel cell” discusses PEMFC modeling. In Section “Problem analyzing for estimating PEM fuel cell variables”, the problem formulation for estimating PEMFC parameters is described. In Section “The basic hippopotamus optimization algorithm”, examine the basic hippopotamus optimization algorithm. Analysis is done on the enhanced hippopotamus optimization algorithm, which is described in Section “The proposed MHO algorithm”. The benchmark validation is covered in Section “Benchmark validation”. Section “Results of PEMFC” will address the PEMFC results. The work’s conclusion and future work are found in Section “Conclusions and future work”.
Analysis of the PEM fuel cell
Renewable energy sources are becoming more and more significant for both small-scale power applications and large-scale industrial purposes as a result of the quick depletion of fossil fuel supply and the growing demand for electricity44. Fuel cells were developed as a means of supplementing the existing available green energy sources due to their susceptibility to environmental conditions, even if renewable energy sources are widely used. In the past, fuel cells have come in three varieties: transportable, portable, and fixed45,46.
The polarization curve of a fuel cell running at 80 °C is displayed in Fig. 1. There are three main zones on the polarization curve. These regions are frequently known as activation losses, ohmic losses, and concentration losses47. There is a nonlinear activation zone. Comprehensive information about the electrochemical process taking place inside the cell is provided by the activation zone. The membrane frequently experiences ohmic losses. The final section discusses the mass concentration losses brought on by modifications to the concentration gradient inside the cell48. The total cell voltage is indicated by 
in Eq. (1)49.
Fig. 1.
Losses in Fuel cell.
 |
1 |
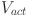stands for activation polarization, 
for ohmic loss, 
for concentration loss, and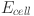 
for open circuit voltage48. It is also evident that the current density affects the output voltage in the ohmic section. As mentioned before, the ionic resistance of the electrolyte also affects the slope. The mass transfer constraints lead the voltage to drop sharply to zero, which results in the concentration loss. Equation (2)44 shows that the amount that the cell’s total output voltage (
) can grow depends on the number of cells (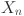
) linked in series.
 |
2 |
Equation (3)44 demonstrates the incorporation of additional factors that account for temperature variations surrounding the cell.
 |
3 |
In this work, the initials r, F, and z stand for the ideal gas constant, faraday, and the number of moving electrons equal to two. The temperature (T) of the cell is shown along with the partial pressures of hydrogen (
) and oxygen (
). Equations (4) and (5) provide a quantitative representation of the various partial pressure parameters39,40.
 |
4 |
 |
5 |
and 
stand for anodic and cathodic relative humidity, respectively. At the inlet, the anode pressure is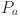 
, and at the cathode, it is 
. While the current is icell, the cell’s area is recorded as A. Equation (6) expresses the direct link between temperature T and the water vapour saturation parameter, 
. Consequently, the activation losses are calculated using Eq. (7). CO2 is the symbol for the oxygen concentration, which is calculated using Eq. (8). The parametric coefficients 
are semi-empirical. Equation (9) can be used to calculate the ohmic losses46.
 |
6 |
 |
7 |
 |
8 |
 |
9 |
The symbols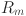 
and 
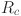stand for ionic and electrical resistance, respectively. The membrane parametric coefficient is found using Eq. (11) and the electronic resistance, which is assigned to the least changes with respect to the current and voltage, is calculated using Eq. (10)46. Equation (12) is used to quantitatively compute the concentration polarization45. The parametric coefficient, sometimes referred to as the diffusion parameter, is represented by 
, the actual current density by 
, and the maximum current density by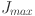 
 |
10 |
 |
11 |
 |
12 |
Problem analyzing for estimating PEM fuel cell variables
It is necessary to compute the six model parameters 
for developing a mathematical computational model for PEMFCs. These events often affect the accuracy of the established IV curve. The model parameters can be deduced from the measured data by using the SSE as an objective function for both the measured and estimated datasets.
The objective function and the variable boundaries are the two primary components of optimization algorithms. The choice variables’ limitations are displayed in Table 1. The primary objective function is the sum of square error (SSE). The following formula is used to examine the SSE:
 |
13 |
Table 1.
| Variables | Upper constraint | Lower constraint |
|---|---|---|
|
0.0022 | 0.0043 |
|
− 1.19969 | − 0.8532 |
|
|
0 | 0.2 |
|
0.000034 | 0.000098 |
|
23 | 13 |
|
− 0.00026 | − 0.0000954 |
where 
, is the measured voltage, N is the number of data reading.
The basic hippopotamus optimization algorithm
As in Fig. 2 [https://pixabay.com/photos/hippo-hippopotamus-bathing-group-5916630/; https://pixabay.com/photos/hippo-hippopotamus-animal-look-515027/], the hippopotamus (Hippopotamus amphibious) is a large, semi-aquatic mammal with a significant impact on its ecosystem. As a megaherbivore, it plays a crucial role in shaping its environment by creating diverse habitats and altering the landscape. Native to sub-Saharan Africa, hippopotamuses are typically found in regions abundant with water bodies and grazing lands49. They exhibit a range of defensive behaviors, including intimidating vocalizations and aggressive displays, to deter predators. Despite these defenses, hippopotamuses will quickly retreat to water for protection when faced with persistent threats or a sense of vulnerability50.
Fig. 2.
Hippopotamus behaviors in nature. [a)https://pixabay.com/photos/hippo-hippopotamus-bathing-group-5916630/; b) https://pixabay.com/photos/hippo-hippopotamus-animal-look-515027/]
Amiri et al.51 introduced the Hippopotamus Optimization (HO) algorithm, a novel swarm-based metaheuristic inspired by the natural behaviors of hippopotamuses. This algorithm simulates the hippopotamuses’ behaviors, including their positioning in river, defensive strategies against threats, and techniques for evading predators51. It is conceptually structured around a trinary-phase model that updates positions based on river and pond dynamics, defensive actions, and predator evasion, each described mathematically. The subsequent subsections provide a detailed explanation of the mathematical models incorporated into the HO algorithm.
Phase 1: initialization
The HO algorithm starts by randomly creating an initial set of candidate solutions. This initialization process is mathematically described by Eq. (14). Over several iterations, the algorithm seeks to approximate the optimal solution by identifying the best candidate among the generated solutions52.
 |
14 |
where represents the number of candidate solutions, Dim is the dimension of the problem, and 
denotes the j-th position of the i-th solution. A set of potential solutions, 
was randomly selected and determined using equation below51.
 |
15 |
where 
and 
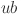denote the lower and upper bounds of the variables, respectively, and 
represents a random value within the range [0, 1].
Phase 2: position update in the pond or river
Hippopotamus groups consist of several adult females, calves, and multiple adult males organized hierarchically, with a dominant male at the top. Dominance is established through continuous assessments of interactions within the group. These groups maintain strong spatial cohesion, with the dominant male responsible for the protection of the herd and its territory, while females are positioned on the periphery. Upon reaching maturity, male offspring are expelled from the group and must subsequently establish their dominance either by attracting females or by competing with resident males. The mathematical model that represents the spatial distribution of male hippopotamuses within their aquatic habitat is described by the following equation51.
 |
16 |
where 
denotes the position of the male, 
indicates the position of the dominant hippopotamus, 
is a random number between 0 and 1, and 
is an integer value of either 1 or 2.
The majority of young hippopotamuses maintain close proximity to their mothers. However, driven by curiosity, some individuals may occasionally stray from the herd or become separated from their maternal group. Therefore, 
Upon separation from the maternal unit, the spatial positioning of a female or immature hippopotamus within the herd is determined as follows51.
 |
17 |
When an immature hippopotamus maintains a proximity to its mother while also remaining within or near the herd, the spatial positioning of the female or immature individual within the group is calculated as follows51:
 |
18 |
Upon separation from the herd, the spatial positioning of the female or immature hippopotamus is calculated as follows51:
 |
19 |
where 
is an integer that can be either 1 or 2, 
represents the mean values of some randomly chosen hippopotamuses, with an equal chance of including the currently considered hippopotamus. Additionally, 
and 
are random numbers between 0 and 1. Furthermore,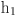 
and 
are either numbers or vectors randomly selected from five predefined scenarios, as indicated in the equation below51.
 |
20 |
where 
, 
, 
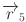, and 
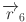are random vectors with values between 0 and 1, 
is a random number between 0 and 1, and 
and 
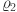are random integers that can be either 0 or 1.
During the optimization process, this phase is divided into two stages, with a focus on incorporating its appearance in later iterations to prevent local optima. Equation (21) governs the transition between these stages51.
 |
21 |
where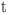 
represents the current iteration, and 
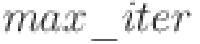denotes the maximum number of iterations.
Phase 3: hippopotamus defense against predator
Hippopotamus herds primarily serve as a defensive strategy. The combined size and mass of the group act as a deterrent to potential predators. Nevertheless, young and more vulnerable members are at increased risk from Nile crocodiles, lions, and spotted hyenas. Hippos generally protect themselves by confronting the predator aggressively and making loud vocalizations. At times, they may even advance toward the predator to strengthen their deterrence. Alternatively, a less aggressive defense involves facing the predator while minimizing movement, thereby signaling their territorial claim. These defensive behaviors can be represented mathematically as follows51:
 |
22 |
 |
23 |
where represents the position of a hippopotamus facing the predator,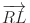 
is a vector of random numbers following a Lévy distribution that simulates Lévy flight movement, 
is a uniformly distributed random number between 1 and 1.5, 
is a uniformly distributed random number between 2 and 4, 
is a uniform random number ranging from -1 to 1, 
is a uniform random number between 2 and 3, and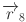 
is a random vector with dimensions 
. Additionally, 
denotes the distance from the i-th hippopotamus to the predator, as detailed below48.
 |
24 |
where 
denotes the position of the predator in the search space, mathematically expressed as follows48.
 |
25 |
where 
denotes a random vector with values ranging from 0 to 1.
Phase 4: hippopotamus escaping from the predator
When faced with multiple predators or when defensive tactics fail to repel a single attacker, hippos adopt an evasive approach. They typically retreat to nearby bodies of water, such as lakes or ponds, as their primary predators, including spotted lions and hyenas, generally avoid aquatic environments. By moving to water, hippos can quickly secure a safe location. This evasive behavior is incorporated into Phase Three of the HO algorithm to improve local search exploitation. To model this behavior computationally, a random location is generated near the current positions of the hippopotamuses. This behavior can be mathematically represented as follows51:
For 
 |
26 |
where represents the position of the hippopotamus searching for the nearest safe location, 
denotes random numbers generated between 0 and 1, 
, 
, and 
is a randomly chosen number or vector from one of the three scenarios detailed below51.
 |
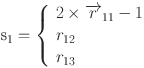27 |
where 
is a random vector with values between 0 and 1, while 
is a random number following a normal distribution, and 
represents random numbers generated between 0 and 1.
At the end of each iteration of the HO, every member of the population is updated according to Phases 2 to 4. This iterative refinement of the population, as described by Eqs. 16–27, persists until the algorithm concludes. The procedural details of the HO algorithm are showed in Algorithm 1.
Algorithm 1.
HO algorithm steps
The proposed MHO algorithm
Like many swarm-based algorithms, the HO algorithm is prone to getting trapped in local optima, which can hinder its ability to identify global optimal solutions. This limitation becomes particularly pronounced in complex, constrained optimization problems. Additionally, the algorithm’s reliance on previous solutions for updating positions often leads to slow convergence. To address these challenges, a modified version of the HO algorithm (MHO) is proposed that integrates two innovative strategies: a novel exploitation mechanism and an Enhanced Solution Quality (ESQ) method. These enhancements aim to significantly improve the algorithm’s performance by yielding superior solutions compared to the original HO. The following subsections provide detailed explanations of these proposed strategies.
New exploitation strategy
As explained in the previous section, Eq. (25) defines the exploitation phase of the HO algorithm, enabling effective convergence toward optimal solutions. However, relying solely on local boundaries during this phase can overly restrict the search space, especially in later iterations, leading to premature convergence and potentially suboptimal outcomes. This issue becomes more pronounced when the current best solution is near a local optimum. Additionally, the single update mechanism in Eq. (25) limits the algorithm’s adaptability to various optimization challenges. To improve HO’s exploitation capabilities and speed up convergence, a new exploitation strategy is introduced, described as follows:
 |
28 |
where 
denotes a randomly chosen position vector from the current population. Meanwhile, 
is a control randomization parameter that produces a variable ranging between positive and negative values. This mechanism ensures a thorough exploration of the search space and helps prevent the algorithm from getting stuck in sub-optimal solutions. The parameter is defined as follows:
 |
29 |
where 
refers to random numbers generated within the interval from 0 to 1.
ESQ strategy
Ahmadianfar et al.53 proposed a non-metaphorical optimization algorithm called RUN, which directly tackles the optimization process using the fourth-order Runge–Kutta method. This algorithm efficiently balances exploration and exploitation by incorporating random elements53. To maintain ongoing improvement and avoid premature convergence, RUN employs the ESQ strategy. Unlike the traditional HO algorithm, which struggles with limited local search diversity and premature convergence, this study improves HO by incorporating the ESQ strategy. This enhancement ensures that each solution moves to a better position before the next iteration, fostering exploration and preventing entrapment in local optima. The strategy is mathematically expressed as follows53:
 |
30 |
where 
is a random value that enhances diversity and 
is an integer that can be 1, 0, or − 1. T = he remaining variables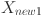 
, 
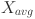, and 
are defined as follows53:
 |
31 |
 |
32 |
 |
33 |
where 
is a random value ranging from 0 to 1 and 
is a random number calculated as 
. However, the fitness value of the newly generated solution 
might not be as high as that of the original, unenhanced solution. To leverage this new solution effectively and increase the chances of finding a better solution, an alternative method for generating a new solution, 
is proposed53:
 |
34 |
where 
represents the solution obtained using the Runge−Kutta search method while 
is a random value calculated as 
.
Framework of MHO algorithm
To clarify the MHO framework, its pseudo-code is presented in Algorithm 2.
Algorithm 2.
MHO algorithm steps
Computational complexity
Computational complexity is crucial for assessing algorithm performance. This section examines the time and space complexity of the proposed MHO.
Time complexity
The computational complexity of MHO can be assessed by breaking down the complexities of its individual components. The runtime of an optimization algorithm can be estimated by analyzing its structure and computational requirements. The time complexity of the original HO is expressed as 
, where N. denotes the population size, D is the problem dimension and T represents the maximum number of iterations, a key termination criterion. For the proposed MHO, the new exploitation strategy is integrated into HO without increasing the overall complexity, while the ESQ strategy is applied at the end of each iteration, adds an additional O(TND). complexity.
By combining these components, MHO achieves an overall time complexity of 
. These additional strategies increase the complexity compared to the original HO’s 
, but they significantly improve exploration and convergence with minimal computational overhead.
Space complexity
In computer science, computational space complexity refers to the amount of memory required to execute an algorithm. For MHO, memory usage is primarily determined by the number of dimensions D and the population size N, both defined during the initialization phase. Consequently, the space complexity of MHO is 
.
Benchmark validation
This section evaluates the effectiveness of the MHO algorithm in addressing global optimization problems through rigorous benchmarking. To validate its performance before real-world application, the algorithm was evaluated using the 20-dimensional CEC’2020 test suite54. A comparative analysis was conducted with three advanced optimization algorithms, including the standard HO. Performance metrics were assessed using statistical measures such as best, worst, mean, standard deviation, ranking, and the Friedman test55. To further underscore MHO’s superiority, additional analyses were performed using Wilcoxon tests56, convergence analysis, and box plots. The comprehensive results provide robust evidence of MHO’s exceptional performance and its competitive edge in the field of global optimization.
Benchmark description
A thorough experimental evaluation was carried out using the CEC’2020 benchmark suite, which is widely used for testing various optimization challenges. This suite consists of ten functions, each designed to address different aspects of optimization problems. Table 2 details the specifications for each function, including their dimensionality, search space boundaries, and optimal values. To increase the complexity of the problems, the functions were rotated and translated. The benchmark suite includes four types of functions: unimodal, multimodal, hybrid, and composite. Unimodal functions are used to assess exploitation capabilities, while multimodal functions evaluate exploration performance. Hybrid functions are designed to test the algorithm’s ability to balance exploitation and exploration, and composite functions measure accuracy and robustness. For a clearer visualization of the function landscapes, partial plots of these functions are shown in Fig. 3.
Table 2.
CEC’2020 benchmark details.
| F | Name of function | Type | D | Range |
|
|---|---|---|---|---|---|
| 1 | Shifted and Rotated Bent Cigar | Unimodal | 20 | [− 100, 100] | 100 |
| 2 | Shifted and Rotated Schwefel’s | Multimodal | 20 | [− 100, 100] | 1100 |
| 3 | Shifted and Rotated Lunacek bi− Rastrigin | Multimodal | 20 | [− 100, 100] | 700 |
| 4 | Expanded Rosenbrock’s plus Griewangk’s | Multimodal | 20 | [− 100, 100] | 1900 |
| 5 | Hybrid 1 (N = 3) | Hybrid | 20 | [− 100, 100] | 1700 |
| 6 | Hybrid 2 (N = 4) | Hybrid | 20 | [− 100, 100] | 1600 |
| 7 | Hybrid 3 (N = 5) | Hybrid | 20 | [− 100, 100] | 2100 |
| 8 | Composition 1 (N = 3) | Composite | 20 | [− 100, 100] | 2200 |
| 9 | Composition 2 (N = 4) | Composite | 20 | [− 100, 100] | 2400 |
| 10 | Composition 3 (N = 5) | Composite | 20 | [− 100, 100] | 2500 |
Fig. 3.
3D view of some randomly selected CEC’2020 benchmark functions57.
Parameter setting
To thoroughly evaluate the MHO algorithm, a comparative analysis was carried out using the CEC’2020 benchmark suite. MHO was compared with the Chimp Optimization Algorithm (ChOA)57, Sine Cosine Algorithm (SCA)58, Grey Wolf Optimizer59, and the standard HO51. Table 3 provides the parameter settings for all algorithms. Each algorithm was run independently 30 times, with a maximum of 1000 iterations and a population size of 50. Statistical metrics, including the best, worst, mean, standard deviation, and rank, were calculated for each algorithm. To further evaluate MHO’s performance, both the Friedman and Wilcoxon signed rank tests were conducted. All experiments were executed in MATLAB R2023 on a Windows 11 system with a Core i7 3.10 GHz processor and 32 GB of RAM.
Table 3.
Parameters of algorithms.
| Algorithm | Parameters values |
|---|---|
| ChOA | m = chaotic |
| SCA | A = 2 |
| GWO | a = Linear decreasing from 2 to 0 |
| HO | Parameter-less |
| MHO | Parameter-less |
Statistical results
This subsection provides a statistical analysis of MHO and its competitors using the CEC’2020 benchmark functions. Table 4 summarizes the performance metrics for all algorithms across these functions, with bold values highlighting the best results. MHO achieved the top performance in most functions, demonstrating its effectiveness across diverse problem types. Additionally, MHO consistently obtained the highest average fitness values on several functions, emphasizing its superior performance. The Worst metric, which assesses robustness, showcased MHO’s exceptional capability to handle challenging conditions.
Table 4.
Comparison of MHO and its competitors in solving the CEC’2020 functions.
| F | Index | ChOA | SCA | GWO | HO | MHO | |
|---|---|---|---|---|---|---|---|
| 1 | Best | 5.0598E+09 | 4.1400E+09 | 2.0644E+04 | 3.4965E+03 | 1.0091E+02 | |
| Worst | 2.3585E+10 | 9.1168E+09 | 6.9449E+08 | 1.5122E+04 | 1.1855E+04 | ||
| Mean | 1.3571E+10 | 6.2138E+09 | 1.4107E+08 | 8.9337E+03 | 2.7353E+03 | ||
| Std | 3.9977E+09 | 1.2085E+09 | 2.3160E+08 | 3.2415E+03 | 3.6538E+03 | ||
| Rank | 5 | 4 | 3 | 2 | 1 | ||
| 2 | Best | 4.5584E+03 | 4.5814E+03 | 1.5615E+03 | 2.2833E+03 | 1.5755E+03 | |
| Worst | 6.0476E+03 | 5.4812E+03 | 5.2322E+03 | 4.3261E+03 | 3.8437E+03 | ||
| Mean | 5.3777E+03 | 5.0442E+03 | 2.5547E+03 | 3.1978E+03 | 2.5634E+03 | ||
| Std | 3.9644E+02 | 2.7762E+02 | 9.3110E+02 | 4.3712E+02 | 5.2285E+02 | ||
| Rank | 5 | 4 | 1 | 3 | 2 | ||
| 3 | Best | 8.6610E+02 | 8.7541E+02 | 7.4088E+02 | 7.8348E+02 | 7.5253E+02 | |
| Worst | 9.8104E+02 | 9.6900E+02 | 8.6995E+02 | 9.2841E+02 | 8.5856E+02 | ||
| Mean | 9.3347E+02 | 9.2612E+02 | 7.8226E+02 | 8.6850E+02 | 8.0181E+02 | ||
| Std | 2.7314E+01 | 2.0895E+01 | 3.3637E+01 | 2.8603E+01 | 2.1079E+01 | ||
| Rank | 5 | 4 | 1 | 3 | 2 | ||
| 4 | Best | 1.9000E+03 | 1.9000E+03 | 1.9000E+03 | 1.9000E+03 | 1.9000E+03 | |
| Worst | 1.9005E+03 | 1.9085E+03 | 1.9076E+03 | 1.9000E+03 | 1.9000E+03 | ||
| Mean | 1.9000E+03 | 1.9011E+03 | 1.9019E+03 | 1.9000E+03 | 1.9000E+03 | ||
| Std | 9.7433E−02 | 2.4064E+00 | 2.1710E+00 | 0.0000E+00 | 0.0000E+00 | ||
| Rank | 3 | 4 | 5 | 1 | 1 | ||
| 5 | Best | 3.7016E+05 | 1.6609E+05 | 2.2691E+04 | 2.6968E+04 | 1.5095E+04 | |
| Worst | 4.8050E+06 | 3.8055E+06 | 2.5636E+06 | 1.2338E+06 | 4.3414E+05 | ||
| Mean | 1.5107E+06 | 1.5751E+06 | 4.2877E+05 | 3.5863E+05 | 1.8443E+05 | ||
| Std | 1.1308E+06 | 8.1845E+05 | 5.4262E+05 | 3.1612E+05 | 1.2256E+05 | ||
| Rank | 4 | 5 | 3 | 2 | 1 | ||
| 6 | Best | 2.2372E+03 | 2.1171E+03 | 1.6440E+03 | 1.8098E+03 | 1.6025E+03 | |
| Worst | 3.0320E+03 | 2.7968E+03 | 2.3311E+03 | 2.8349E+03 | 1.8990E+03 | ||
| Mean | 2.6317E+03 | 2.4260E+03 | 1.8112E+03 | 2.2427E+03 | 1.6910E+03 | ||
| Std | 2.1114E+02 | 1.7030E+02 | 1.3357E+02 | 2.5477E+02 | 9.2027E+01 | ||
| Rank | 5 | 4 | 2 | 3 | 1 | ||
| 7 | Best | 1.4613E+05 | 8.4367E+04 | 1.3841E+04 | 3.4859E+03 | 2.7699E+03 | |
| Worst | 4.2596E+05 | 1.0821E+06 | 8.2005E+05 | 5.8030E+04 | 3.3278E+04 | ||
| Mean | 2.8909E+05 | 4.2327E+05 | 1.3030E+05 | 2.5209E+04 | 1.1500E+04 | ||
| Std | 8.4095E+04 | 2.3488E+05 | 1.4711E+05 | 1.8320E+04 | 8.5603E+03 | ||
| Rank | 3 | 5 | 4 | 2 | 1 | ||
| 8 | Best | 6.2535E+03 | 2.6800E+03 | 2.3083E+03 | 2.3006E+03 | 2.3000E+03 | |
| Worst | 7.2913E+03 | 7.0432E+03 | 6.6160E+03 | 5.4182E+03 | 2.3026E+03 | ||
| Mean | 6.8472E+03 | 4.4434E+03 | 2.6871E+03 | 2.4938E+03 | 2.3009E+03 | ||
| Std | 2.5529E+02 | 1.7906E+03 | 9.4406E+02 | 7.3152E+02 | 7.8814E−01 | ||
| Rank | 5 | 4 | 3 | 2 | 1 | ||
| 9 | Best | 2.9943E+03 | 2.9557E+03 | 2.8164E+03 | 2.8803E+03 | 2.8386E+03 | |
| Worst | 3.1430E+03 | 3.0371E+03 | 2.9420E+03 | 3.0987E+03 | 2.9096E+03 | ||
| Mean | 3.0620E+03 | 2.9959E+03 | 2.8591E+03 | 2.9888E+03 | 2.8698E+03 | ||
| Std | 4.1431E+01 | 2.2000E+01 | 3.7659E+01 | 6.5122E+01 | 1.9177E+01 | ||
| Rank | 5 | 4 | 1 | 3 | 2 | ||
| 10 | Best | 3.0683E+03 | 3.0664E+03 | 2.9140E+03 | 2.9458E+03 | 2.9043E+03 | |
| Worst | 4.1874E+03 | 3.2273E+03 | 3.0214E+03 | 3.0719E+03 | 3.0084E + 03 | ||
| Mean | 3.4752E+03 | 3.1477E+03 | 2.9655E+03 | 3.0045E+03 | 2.9648E+03 | ||
| Std | 3.3848E+02 | 4.5588E+01 | 3.4745E+01 | 2.8925E+01 | 3.3276E+01 | ||
| Rank | 5 | 4 | 2 | 3 | 1 | ||
| Mean rank | 4.5 | 4.2 | 2.5 | 2.4 | 1.3 | ||
| Final rank | 5 | 4 | 3 | 2 | 1 | ||
Bold values represent the best results
To statistically validate MHO’s overall performance, the non-parametric Friedman test was performed. This test, suitable for various data distributions, was appropriate for this analysis. The results, shown in the final rows of Table 4, confirm that MHO ranks superior to other algorithms. These results strongly support the conclusion that the enhancements made to the HO algorithm have significantly improved its ability to find global optima.
Figure 4 displays a radar chart that compares MHO’s performance with that of other algorithms across the ten CEC’2020 benchmark functions. The smaller enclosed area on MHO’s radar chart visually underscores its superior performance across a range of optimization challenges, illustrating MHO’s outstanding optimization capabilities and stability. MHO consistently delivers high-quality solutions through efficient and precise search methods, regardless of the problem’s complexity.
Fig. 4.
Radar chart for different methods.
Wilcoxon rank test
Although the results from the CEC’2020 test functions suggest that MHO is superior to some extent, the stochastic nature of metaheuristic algorithms requires a more thorough statistical analysis to definitively determine significant differences between algorithms. To statistically compare MHO with other algorithms on the CEC’2020 test functions in 20 dimensions, the Wilcoxon rank-sum test is employed. This method is commonly used for evaluating improved optimization algorithms and is applied here with a significance level of p less than 0.05. Table 5 shows the results of the Wilcoxon rank-sum test comparing MHO with benchmark algorithms. A p-value below 0.05 indicates that MHO significantly outperforms the respective algorithm, whereas a p-value of 1.00 suggests no notable difference. Instances of NaN values indicate minimal performance variation. As depicted in Table 5, MHO demonstrates significant superiority over ChOA and SCA across all functions (F1–F10), indicating a highly significant difference. Compared to GWO, MHO also shows consistent superiority in 6 out of 10 CEC2020 functions. For HO, MHO exhibits significant outperformance across all CEC2020 functions, with F4 showing a NaN value indicating that there is no significant difference. The findings consistently reveal a statistically significant difference between MHO and other algorithms over CEC’2020 functions, supporting the claim that MHO operates differently than its counterparts and providing valuable insights into its comparative effectiveness.
Table 5.
p-value of Wilcoxon sum test between MHO and its competitors.
| F | ChOA versus MHO | SCA versus MHO | GWO versus MHO | HO versus MHO |
|---|---|---|---|---|
| 1 | 1.5099E−11 | 1.5099E−11 | 1.5099E−11 | 1.0979E−07 |
| 2 | 1.5099E−11 | 1.5099E−11 | 1.9579E−01 | 7.6458E−06 |
| 3 | 1.5099E−11 | 1.5099E−11 | 9.9808E−01 | 5.8687E−10 |
| 4 | 1.6157E−07 | 9.6661E−11 | 2.2868E−12 | NaN |
| 5 | 2.2522E−11 | 8.0661E−11 | 7.9782E−02 | 1.6937E−02 |
| 6 | 1.5099E−11 | 1.5099E−11 | 3.5994E−05 | 2.4876E−11 |
| 7 | 1.5099E−11 | 1.5099E−11 | 2.0998E−10 | 1.1329E−03 |
| 8 | 1.5099E−11 | 1.5099E−11 | 1.5099E−11 | 4.4414E−06 |
| 9 | 1.5099E−11 | 1.5099E−11 | 1.5099E−11 | 4.4414E−06 |
| 10 | 1.5099E−11 | 1.5099E−11 | 8.6499E−01 | 8.7396E−06 |
Convergence behavior
A convergence analysis was conducted to compare MHO with several similar algorithms. Figure 5 presents the convergence curves of ChOA, SCA, GWO, and the original HO, benchmarked against the proposed MHO on the 20-dimensional CEC’2020 test functions. The convergence curves clearly show that MHO achieves superior convergence speed in the early stages, reflecting its strong exploration capabilities. In most test functions, MHO quickly identifies optimal solutions, surpassing other algorithms that frequently get stuck in local optima. MHO’s ability to escape local solutions and maintain high solution quality highlights its effectiveness. These findings collectively demonstrate MHO’s notable advantage in rapidly achieving high-quality solutions while effectively balancing local and global search dimensions.
Fig. 5.
Convergence curves for the proposed MHO and its competitors.
Boxplot behavior
Boxplot analysis is a valuable method for visualizing data distribution, especially in cases with numerous local minima. To offer a detailed view of the results, boxplots were used to divide the data into quartiles. These plots effectively depict the data distribution, showing minimum and maximum values with whiskers and the upper and lower quartiles with the box’s extent. A narrower boxplot signifies greater consistency in the data. Figure 6 displays boxplot comparisons of MHO with other algorithms across various test functions. For functions F4 and F8, MHO consistently performed better, as indicated by the red line in the boxplot, which represents the best mean value at each iteration. Additionally, MHO showed a more concentrated and compact distribution of the best mean values across most test scenarios, highlighting its exceptional performance, consistency, and stability. These results emphasize MHO’s strong performance and its effectiveness for a diverse range of optimization problems.
Fig. 6.
Boxplots for the proposed MHO and its competitors.
Complexity analysis results
To evaluate the time complexity of mHO and other leading algorithms following the CEC’2020 benchmark specifications, we measured their performance on problems with dimensionalities of 5, 10, and 20. Three key parameters related to computational cost were considered: T0, T1, and 
. Specifically, T0 denotes the execution time of the CEC’2020 test framework itself. T1 measures the time required to perform 1000 iterations of the D-dimensional benchmark function F1. The parameter represents the average time needed for 1,000 iterations of the same function, calculated as the mean over five independent T2 measurements 
.
The time complexity of each algorithm was assessed using T0, T1, , and the derived ratio 
. To ensure consistency and fairness, all algorithms were run under the same conditions: processing one individual at a time, without employing parallel computing or vectorized operations. All experiments were implemented in MATLAB with a uniform coding style. The baseline runtime T0 was determined according to the following formula54:
 |
35 |
where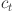 
set to 1,000,000. Table 6 presents the results of the time complexity comparison among the seven algorithms. As reported in the table, MHO is among the more complex approaches. However, comparing to standard HO, the proposed MHO method maintains computational efficiency comparable to baseline algorithm ho, without introducing significant overhead.
Table 6.
Time complexity results.
| Dimension | Algorithm | T0 | T1 |
|
(-T1)/T0 |
|---|---|---|---|---|---|
| 5Dim | ChOA | 0.21569 | 1.64789 | 1.520675 | 6.11955 |
| SCA | 0.21569 | 0.27679 | 0.287646 | 0.99566 | |
| GWO | 0.21569 | 0.59702 | 0.393009 | 2.37501 | |
| HO | 0.21569 | 7.95192 | 8.412286 | 28.45571 | |
| MHO | 0.21569 | 8.09638 | 10.42826 | 27.10952 | |
| 10Dim | ChOA | 0.21569 | 2.79010 | 2.785286 | 10.15063 |
| SCA | 0.21569 | 0.36750 | 0.419195 | 1.28467 | |
| GWO | 0.21569 | 0.49380 | 0.568015 | 1.72142 | |
| HO | 0.21569 | 10.57700 | 9.987828 | 39.05099 | |
| MHO | 0.21569 | 12.91720 | 10.09473 | 49.79410 | |
| 20Dim | ChOA | 0.21569 | 5.85755 | 5.28721 | 21.87054 |
| SCA | 0.21569 | 0.59978 | 0.46183 | 2.31899 | |
| GWO | 0.21569 | 0.86748 | 0.63811 | 3.38384 | |
| HO | 0.21569 | 13.30732 | 10.71843 | 50.97916 | |
| MHO | 0.21569 | 14.80698 | 11.79887 | 56.85167 |
Thorough performance evaluations of the MHO algorithm show that it excels in convergence speed, stability, robustness, solution accuracy compared to current methods. When compared with four other algorithms, MHO reveals considerable advantages, proving to be a highly effective tool for tackling contemporary benchmark problems. Its strong optimization capabilities make it a versatile solution applicable to a broad spectrum of problems, including both constrained and unconstrained engineering challenges.
Results of PEMFC
Using the MHO algorithm, the ideal variables of a Nedstack PS6 have been determined. Other methods including the (HO)51, Chimp Optimization Algorithm (ChOA)57, Sine Cosine Algorithm (SCA)58, and Grey Wolf Optimizer (GWO)59 are contrasted with the suggested MHO method. Nedstack PS6 experimental data have been used to gauge each algorithm’s accuracy and dependability. Table 7 shows the detected variables at the optimal SSE for PEMFC. According to this table, the MHO algorithm yields the best SSE with a value of 1.74899605528212. ChOA, GWO, SCA, and HO follow in order of decreasing SSE. Tables 8, 9, 10, 11 and 12 provide the estimated variables for MHO, HO, GWO, SCA, and ChOA, respectively, based on 30 runs of each method. Table 13 provides clarification on the estimated voltage values for all methods at their best run in comparison to the experimental value. After each algorithm has been executed thirty times independently, it is evaluated. The metrics used to assess each algorithm are accuracy and reliability. For each approach presented in terms of reliability, the standard deviation of the SSE value and the lowest SSE value related to the algorithm’s accuracy are stated. More information on the statistical analysis of PEMFC for all active algorithms is given in Table 14. The suggested MHO technique achieves the maximum accuracy according to these statistics, followed by ChOA, GWO, SCA, and HO.
Table 7.
The parameters identified from PEMFC at the best objective function.
| MHO | HO | GWO | SCA | ChOA | |
|---|---|---|---|---|---|
|
− 0.628826226 | − 1.19978 | − 1.143744026 | − 0.8532 | − 1.19978 |
|
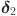
0.002003524 | 0.003377986 | 0.003552655 | 0.002600317 | 0.003574609 |
|
5.64505E−05 | 0.000034 | 5.78515E−05 | 5.13458E−05 | 4.77642E−05 |
|
− 9.30123E−05 | − 0.0000954 | − 0.0000954 | − 0.0000954 | − 0.0000954 |
|
13.01777796 | 13 | 13 | 13 | 13 |
|
0.004362536 | 0.001602276 | 0.001912334 | 0.001766411 | 0.001930513 |
Table 8.
Decision variables based on MHO method over Thirty run.
|
|
|
|
|
|
|
|---|---|---|---|---|---|
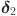
| − 0.900941142 | 0.002495033 | 3.40E−05 | − 9.54E−05 | 13.6344998 | 0.011590059 |
| − 0.856934285 | 0.002367046 | 3.42E−05 | − 9.53E−05 | 12.9885056 | 0.001343505 |
| − 0.852765542 | 0.002355816 | 3.42E−05 | − 9.53E−05 | 12.99021477 | 0.001832291 |
| − 0.852488338 | 0.002391433 | 3.68E−05 | − 9.53E−05 | 13.19009691 | 0.004489737 |
| − 0.852415106 | 0.002658033 | 5.56E−05 | − 9.52E−05 | 12.97741339 | 0.001211783 |
| − 0.914008235 | 0.002669864 | 4.36E−05 | − 9.53E−05 | 13.03699472 | 0.002474961 |
| − 0.853410763 | 0.002351792 | 3.38E−05 | − 9.50E−05 | 12.98723344 | 0.002482045 |
| − 0.858454583 | 0.002746473 | 6.05E−05 | − 9.53E−05 | 12.99166578 | 0.001880456 |
| − 0.628826226 | 0.002003524 | 5.65E−05 | − 9.30E−05 | 13.01777796 | 0.004362536 |
| − 0.918616529 | 0.002656199 | 4.17E−05 | − 9.54E−05 | 13.95205734 | 0.016102352 |
| − 1.169165497 | 0.003288658 | 3.40E−05 | − 9.53E−05 | 13.11798777 | 0.003902238 |
| − 0.852717497 | 0.002411717 | 3.82E−05 | − 9.53E−05 | 13.05892317 | 0.003012878 |
| − 0.853560811 | 0.002361318 | 3.45E−05 | − 9.53E−05 | 12.99084577 | 0.001817175 |
| − 0.891618655 | 0.002625802 | 4.51E−05 | − 9.53E−05 | 12.99147127 | 0.001871001 |
| − 0.83951319 | 0.002523224 | 4.88E−05 | − 9.48E−05 | 12.87988812 | 0.001159176 |
| − 0.946919596 | 0.00316278 | 7.13E−05 | − 9.53E−05 | 13.04321011 | 0.00249958 |
| − 0.847369774 | 0.002343748 | 3.46E−05 | − 9.51E−05 | 12.94191982 | 0.001193604 |
| − 0.880309694 | 0.002607034 | 4.62E−05 | − 9.53E−05 | 12.98735588 | 0.001324907 |
| − 0.970199531 | 0.003094719 | 6.17E−05 | − 9.53E−05 | 12.98900457 | 0.001429792 |
| − 0.840210389 | 0.002329354 | 3.51E−05 | − 9.49E−05 | 13.93781448 | 0.016468385 |
| − 0.892461444 | 0.002513127 | 3.71E−05 | − 9.48E−05 | 13.00087136 | 0.002820209 |
| − 0.966021635 | 0.002994866 | 5.56E−05 | − 9.55E−05 | 12.99689819 | 0.000965885 |
| − 0.876189733 | 0.002420983 | 3.40E−05 | − 9.53E−05 | 12.98554685 | 0.001653564 |
| − 0.916811454 | 0.002920728 | 6.06E−05 | − 9.53E−05 | 12.99687729 | 0.001591734 |
| − 0.775195376 | 0.00213628 | 3.53E−05 | − 9.16E−05 | 12.92421159 | 0.006106023 |
| − 1.103290579 | 0.003092878 | 3.40E−05 | − 9.53E−05 | 12.98975636 | 0.001736253 |
| − 0.852637037 | 0.002425995 | 3.92E−05 | − 9.53E−05 | 12.99142221 | 0.001871034 |
| − 0.993294508 | 0.003168938 | 6.22E−05 | − 9.53E−05 | 12.9875147 | 0.001442203 |
| − 1.033305392 | 0.003325473 | 6.48E−05 | − 9.53E−05 | 13.00768937 | 0.002210085 |
| − 0.962963226 | 0.002683872 | 3.44E−05 | − 9.53E−05 | 12.98939338 | 0.001592661 |
Table 9.
Decision variables based on HO method over Thirty run.
|
|
|
|
|
|
|
|---|---|---|---|---|---|
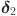
| − 0.8532 | 0.002350452 | 3.40E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.003493236 | 4.23E−05 | − 9.54E−05 | 13 | 5.88E−05 |
| − 0.8532 | 0.002517538 | 4.55E−05 | − 9.54E−05 | 13.0997332 | 0.003257109 |
| − 1.19978 | 0.003375271 | 3.40E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.003376547 | 3.40E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.003925687 | 7.26E−05 | − 9.54E−05 | 13 | 0 |
| − 0.899759288 | 0.003211548 | 8.47E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.00337683 | 3.40E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.004039213 | 8.04E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.0043 | 9.80E−05 | − 9.70E−05 | 13 | 0.002964917 |
| − 1.120739681 | 0.003141388 | 3.40E−05 | − 9.54E−05 | 13 | 2.15E−05 |
| − 1.19978 | 0.00338174 | 3.44E−05 | − 9.54E−05 | 13 | 4.32E−05 |
| − 0.888488476 | 0.002798315 | 5.81E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.003376124 | 3.40E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.003375432 | 3.40E−05 | − 9.54E−05 | 13 | 0.000330936 |
| − 1.09864807 | 0.003083041 | 3.40E−05 | − 9.54E−05 | 13 | 0.004316925 |
| − 1.177143006 | 0.003791393 | 6.79E−05 | − 9.54E−05 | 13 | 0 |
| − 1.018690954 | 0.003231468 | 6.14E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.004289184 | 9.80E−05 | − 9.54E−05 | 13 | 0 |
| − 0.8532 | 0.00294234 | 7.55E−05 | − 9.54E−05 | 13 | 8.55E−05 |
| − 0.902264822 | 0.002496156 | 3.40E−05 | − 9.54E−05 | 13 | 5.87E−05 |
| − 1.16158477 | 0.00417419 | 9.80E−05 | − 9.54E−05 | 13.30376615 | 0.003783873 |
| − 1.19978 | 0.003375838 | 3.40E−05 | − 9.54E−05 | 13 | 6.88E−05 |
| − 1.19978 | 0.003376219 | 3.40E−05 | − 9.54E−05 | 13.03028579 | 0.000279202 |
| − 1.19978 | 0.003572777 | 4.79E−05 | − 9.54E−05 | 13 | 0 |
| − 0.8532 | 0.002635463 | 5.42E−05 | − 9.54E−05 | 13 | 0 |
| − 1.19978 | 0.003377986 | 3.40E−05 | − 9.54E−05 | 13 | 0.001602276 |
| − 1.173636124 | 0.003298045 | 3.40E−05 | − 9.54E−05 | 13 | 5.62E−09 |
| − 0.8532 | 0.00256863 | 4.92E−05 | − 9.54E−05 | 13 | 4.04E−07 |
| − 0.887648519 | 0.002906453 | 6.56E−05 | − 9.54E−05 | 13.23596668 | 0.005644496 |
Table 10.
Decision variables based on GWO method over Thirty run.
|
|
|
|
|
|
|
|---|---|---|---|---|---|
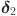
| − 1.19978 | 0.003716525 | 5.77E−05 | − 9.54E−05 | 13.04953802 | 0.002851265 |
| − 0.971747833 | 0.003614934 | 9.79E−05 | − 9.54E−05 | 13.00628474 | 0.002124339 |
| − 1.040043872 | 0.00381499 | 9.80E−05 | − 9.54E−05 | 13 | 8.40E−05 |
| − 1.19978 | 0.004185043 | 9.06E−05 | − 9.54E−05 | 13 | 0.001970895 |
| − 1.143744026 | 0.003552655 | 5.79E−05 | − 9.54E−05 | 13 | 0.001912334 |
| − 1.132748526 | 0.003740901 | 7.33E−05 | − 9.54E−05 | 13.04899825 | 0.002678976 |
| − 1.182943428 | 0.004219348 | 9.67E−05 | − 9.54E−05 | 16.43048109 | 0.042873746 |
| − 0.885594765 | 0.003248114 | 9.00E−05 | − 9.54E−05 | 13.02068345 | 0.002242957 |
| − 1.168460472 | 0.003738238 | 6.58E−05 | − 9.54E−05 | 13 | 0.001705025 |
| − 0.908009173 | 0.003401455 | 9.62E−05 | − 9.54E−05 | 13.03506491 | 0.002465244 |
| − 0.8532 | 0.003262792 | 9.80E−05 | − 9.54E−05 | 13 | 0 |
| − 1.133277677 | 0.003826872 | 7.93E−05 | − 9.54E−05 | 13 | 0.001921543 |
| − 1.007789501 | 0.003691186 | 9.58E−05 | − 9.54E−05 | 13.01597286 | 0.002179375 |
| − 1.063037488 | 0.00337415 | 6.21E−05 | − 9.54E−05 | 13.08274621 | 0.00325926 |
| − 0.8532 | 0.003051926 | 8.31E−05 | − 9.54E−05 | 13 | 0.00063368 |
| − 0.8532 | 0.003215312 | 9.45E−05 | − 9.54E−05 | 13 | 0.001679047 |
| − 1.135662981 | 0.003848918 | 8.03E−05 | − 9.54E−05 | 13.14713616 | 0.004197861 |
| − 1.17562421 | 0.00357296 | 5.27E−05 | − 9.54E−05 | 13.02320967 | 0.002339348 |
| − 1.189708248 | 0.003372284 | 3.57E−05 | − 9.54E−05 | 13.03781036 | 0.002438037 |
| − 1.049821928 | 0.003637599 | 8.33E−05 | − 9.54E−05 | 13.1575743 | 0.00429828 |
| − 0.9340651 | 0.003365078 | 8.82E−05 | − 9.54E−05 | 13.0379443 | 0.002424316 |
| − 0.989647198 | 0.003655536 | 9.70E−05 | − 9.54E−05 | 13.25197832 | 0.00587076 |
| − 0.976294316 | 0.003591587 | 9.54E−05 | − 9.54E−05 | 15.21121026 | 0.031075518 |
| − 1.169131779 | 0.0041364 | 9.35E−05 | − 9.54E−05 | 13 | 0.001918595 |
| − 1.161674729 | 0.004140419 | 9.55E−05 | − 9.54E−05 | 13 | 0.00069601 |
| − 0.917685274 | 0.003368025 | 9.18E−05 | − 9.54E−05 | 13.07694479 | 0.003168036 |
| − 1.014001967 | 0.003709163 | 9.59E−05 | − 9.54E−05 | 13 | 0.000103862 |
| − 1.021074639 | 0.002862617 | 3.49E−05 | − 9.54E−05 | 13.01687118 | 0.00231974 |
| − 0.86660484 | 0.002534937 | 4.39E−05 | − 9.54E−05 | 13.00901338 | 0.002225264 |
| − 0.854123825 | 0.002429456 | 3.91E−05 | − 9.54E−05 | 13.06728847 | 0.003188073 |
Table 11.
Decision variables based on SCA method over Thirty run.
|
|
|
|
|
|
|
|---|---|---|---|---|---|
| − 1.19978 | 0.003649418 | 5.32253E−05 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002351941 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.003262422 | 0.000098 | − 0.0000954 | 13 | 0 |
| − 1.063237103 | 0.003772499 | 9.02508E−05 | − 0.0000954 | 13 | 0 |
| − 0.878980895 | 0.002423562 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003374244 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002350064 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 0.88194252 | 0.002434611 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002823504 | 6.71323E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003720758 | 5.81328E−05 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.003261725 | 0.000098 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002600317 | 5.13458E−05 | − 0.0000954 | 13 | 0.001766411 |
| − 0.8532 | 0.002350334 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002349859 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.049937334 | 0.003640618 | 8.3657E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.004226426 | 9.3906E−05 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002448507 | 4.07381E−05 | − 0.0000954 | 13 | 0.001343108 |
| − 1.19978 | 0.004288558 | 0.000098 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002349603 | 0.000034 | − 9.54537E−05 | 13 | 0 |
| − 0.8532 | 0.002348148 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.183595744 | 0.003483388 | 4.49356E−05 | − 0.0000954 | 13 | 0 |
| − 0.889462387 | 0.003101857 | 7.91838E−05 | − 0.0000954 | 13 | 0 |
| − 0.861314028 | 0.002544019 | 4.57638E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003909207 | 7.1416E−05 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002915189 | 7.36247E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003762051 | 6.12168E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.0043 | 0.000098 | − 9.66949E−05 | 13 | 0.004468184 |
| − 1.19978 | 0.003375522 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003374931 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.003233728 | 9.59943E−05 | − 0.0000954 | 13 | 0 |
Table 12.
Decision variables based on ChOA method over Thirty run.
|
|
|
|
|
|
|
|---|---|---|---|---|---|
| − 1.154099617 | 0.003239904 | 0.000034 | − 0.0000954 | 13 | 9.49691E−06 |
| − 1.19978 | 0.003375665 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.138825261 | 0.003529373 | 5.73079E−05 | − 0.0000954 | 13 | 0.001806753 |
| − 0.8532 | 0.002451203 | 4.11393E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003374897 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 0.869146284 | 0.002396858 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.158076343 | 0.003464954 | 4.88995E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003424073 | 3.7305E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003376945 | 0.000034 | − 0.0000954 | 13 | 5.19421E−08 |
| − 1.19978 | 0.00337518 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002350558 | 0.000034 | − 0.0000954 | 13 | 7.96426E−07 |
| − 1.19978 | 0.003376351 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003574609 | 4.77642E−05 | − 0.0000954 | 13 | 0.001930513 |
| − 1.178115254 | 0.003565769 | 5.18775E−05 | − 0.0000954 | 13 | 5.72136E−07 |
| − 0.998728859 | 0.002781885 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 0.975888638 | 0.002860898 | 4.43299E−05 | − 0.0000954 | 13 | 0 |
| − 0.8532 | 0.002741013 | 6.14203E−05 | − 0.0000954 | 13 | 0 |
| − 0.936658086 | 0.002691541 | 4.06035E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003503253 | 4.29589E−05 | − 0.0000954 | 13 | 0 |
| − 1.02719099 | 0.002865276 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.07360911 | 0.003188348 | 4.70895E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003376798 | 0.000034 | − 0.0000954 | 13 | 1.57566E−09 |
| − 1.19978 | 0.003376321 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003374446 | 0.000034 | − 0.0000954 | 13 | 7.15927E−05 |
| − 1.19978 | 0.003376036 | 0.000034 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003620986 | 5.1217E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.00351259 | 4.36274E−05 | − 0.0000954 | 13 | 0 |
| − 1.090944767 | 0.003773235 | 8.43979E−05 | − 0.0000954 | 13 | 0 |
| − 1.19978 | 0.003375258 | 0.000034 | − 0.0000954 | 13 | 6.99028E−05 |
| − 0.8742215 | 0.002898796 | 6.79866E−05 | − 0.0000954 | 13 | 3.47691E−06 |
Table 13.
Comparison between estimated and measured voltage at the best solution.
| Measured | MHO | HO | GWO | SCA | ChOA |
|---|---|---|---|---|---|
| Estimated | |||||
| 61.64 | 62.19874459 | 62.28914797 | 62.29824013 | 62.28964269 | 62.29863587 |
| 59.57 | 59.71077512 | 59.74609005 | 59.75483913 | 59.74639856 | 59.75522591 |
| 58.94 | 59.00081696 | 59.02233287 | 59.03090848 | 59.02254726 | 59.03129067 |
| 57.54 | 57.48786539 | 57.48397029 | 57.49201756 | 57.48389812 | 57.49238552 |
| 56.8 | 56.72525966 | 56.71086733 | 56.71855552 | 56.71060048 | 56.71891358 |
| 56.13 | 56.06380482 | 56.04161738 | 56.04894081 | 56.04115285 | 56.04928864 |
| 55.23 | 55.18936753 | 55.15871464 | 55.1654798 | 55.1579477 | 55.16581164 |
| 54.66 | 54.65894785 | 54.62414124 | 54.6305265 | 54.62316861 | 54.63084723 |
| 53.61 | 53.68001714 | 53.63936048 | 53.64496645 | 53.63796615 | 53.64526381 |
| 52.86 | 52.99505801 | 52.95160325 | 52.95660671 | 52.94988309 | 52.95688548 |
| 51.91 | 51.49479312 | 51.44849549 | 51.45202736 | 51.44598026 | 51.45225892 |
| 51.22 | 51.08245903 | 51.03609004 | 51.03918318 | 51.03333798 | 51.03940017 |
| 49.66 | 49.47118782 | 49.42709275 | 49.42833957 | 49.42334495 | 49.42849296 |
| 49 | 48.67725745 | 48.63563455 | 48.63589747 | 48.63135673 | 48.63601549 |
| 48.15 | 48.07855387 | 48.03933153 | 48.03882094 | 48.03463731 | 48.03891048 |
| 47.52 | 47.68199403 | 47.64460375 | 47.64356598 | 47.63962587 | 47.64363577 |
| 47.1 | 47.08998965 | 47.05568056 | 47.0538337 | 47.05026755 | 47.05387268 |
| 46.48 | 46.28982504 | 46.26031812 | 46.25733525 | 46.25429456 | 46.25732994 |
| 45.66 | 45.48148081 | 45.45754737 | 45.45336617 | 45.45088028 | 45.45331293 |
| 44.85 | 44.86375906 | 44.84456529 | 44.83943283 | 44.8373877 | 44.83934068 |
| 44.24 | 44.03503643 | 44.02285229 | 44.01639298 | 44.01496313 | 44.01624536 |
| 42.45 | 42.98281355 | 42.9806175 | 42.97238424 | 42.97177784 | 42.9721604 |
| 41.66 | 42.11775661 | 42.12471414 | 42.11494096 | 42.11505013 | 42.11464916 |
| 40.68 | 41.00331835 | 41.02339987 | 41.01152148 | 41.0126099 | 41.01113428 |
| 40.09 | 40.32596869 | 40.35481542 | 40.34158273 | 40.34330169 | 40.34113276 |
| 39.51 | 39.62466573 | 39.6632722 | 39.64857035 | 39.65097381 | 39.6480511 |
| 38.73 | 38.67320986 | 38.72628467 | 38.7094664 | 38.71285674 | 38.7088454 |
| 38.15 | 37.94626596 | 38.01146267 | 37.99291783 | 37.99711391 | 37.99221223 |
| 37.38 | 36.94243179 | 37.02613092 | 37.00501721 | 37.0104131 | 37.00418332 |
Table 14.
Statistical analysis for PEMFC.
| Min | Mean | Max | SD | |
|---|---|---|---|---|
| MHO | 1.748996055 | 1.935972652 | 1.998268903 | 0.040751296 |
| HO | 1.947167448 | 2.040748337 | 2.253767337 | 0.05623442 |
| GWO | 1.945590718 | 1.968682178 | 2.156233458 | 0.046645671 |
| SCA | 1.946286137 | 2.050069248 | 2.374590534 | 0.074358729 |
| ChOA | 1.945575482 | 2.027764754 | 2.061770701 | 0.023681133 |
The behavior of each algorithm is compared with the robustness data of each of the thirty different runs, and the main criterion for classifying the algorithms’ performance is the convergence of the iteration in each run. Figures 7 and 8 illustrate each PEMFC algorithm’s robustness and convergence, respectively. These numbers show the suggested MHO technique’s high level of durability, dependability, and convergence of faster performance.
Fig. 7.
Robustness curves.
Fig. 8.
Convergence curves.
Discussion
The MHO method has been used to determine a Ned stack PS6’s optimum variables. Other approaches including HO, GWO, SCA, and ChOA are contrasted with the suggested MHO method. These approaches are used to solve the same issue in the same setting. Additionally, the suggested MHO methodology is contrasted with approaches from other published research, including the vortex search approach with DE (VSDE), artificial ecosystem optimizer (AEO), neural network algorithm (NNA), equilibrium optimizer (EO), manta rays foraging optimizer (MRFO), and slap swarm optimizer (SSO). The comparative examination of all algorithms is explained in Table 15. The suggested MHO approach gets the best SSE for PEMFC based on the data in Table 15. Figure 9 illustrates the relationship between the observed voltage and the estimated voltage obtained using the MHO approach. Additionally, the voltage’s absolute inaccuracy is shown in this figure. These statistics show how closely the measured results and the identified findings from the suggested MHO approach match.
Table 15.
Comparison of mfho’s optimal fitness function with that of alternative PEMFC algorithms40.
Fig. 9.
Comparison of the PEMFC’s measured and identified voltage using the MHO technique.
Conclusions and future work
The ideal parameter identification procedure for the Nedstack PS6 PEM fuel-cell model has been examined in this research work using a number of contemporary optimization approaches. The five optimization strategies listed below have been given careful thought: The proposed Modified Hippopotamus optimization method is compared with the Grey Wolf Optimizer, Hippopotamus optimization, Chimp optimization algorithm, and sine cosine algorithm. HO produced the highest value, 1.947167448, while the MHO technique produced the lowest result, 1.748996055. The data gathered indicates that when the SSE is utilized as the objective function, the RIME is more successful at forecasting results. It also ensures faster convergence than other metaheuristic algorithms studied, which makes it a feasible solution for global optimization problems unrelated to fuel cell problems. The MHO approach will be applied in the future to resolve further significant, practical optimization issues related to solar energy and power systems. Additionally, approaches from various published publications, including the Equilibrium Optimizer, Manta Rays Foraging Optimizer, Neural Network Algorithm, Artificial Ecosystem Optimizer, Slap Swarm Optimizer, and Vortex Search with DE, are compared to the suggested Modified Hippopotamus optimization method. These six parameters serve as choice variables during optimization, and the fitness function that has to be reduced is the sum square error between the estimated and measured cell voltages. To assess the efficiency and dependability of the Modified Hippopotamus optimization approach in a variety of domains, future research will broaden the study to include different fuel cell models or applications.
Acknowledgements
Authors thank Princess Nourah bint Abdulrahman University Researchers for Supporting Project number (PNURSP2025R409), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Author contributions
Resources: E.A.A., D.S.K.; Conceptualization: E.A.A., A.A.K.I., A.M.E.R., D.S.K., E.H.H., A.N., F.A.H., M.S., A.B.; Original Draft Writing: E A.A.K.I., A.M.E.R., E.H.H., A.N., F.A.H., M.S., A.B. Methodology: E.A.A., A.A.K.I., A.M.E.R., D.S.K., E.H.H., A.N., F.A.H., M.S.; Software: E.A.A., D.S.K., M.S.,A.B.; Validation: E.A.A., D.S.K., M.S.; Investigation: A.A.K.I., A.M.E.R., E.H.H., A.N., F.A.H., M.S.; Data Curation: A.A.K.I., A.M.E.R., E.H.H., A.N., F.A.H., M.S. All authors have read and agreed to the published version of the manuscript.
Data availability
The datasets used and/or analyzed during the current study available from the corresponding author on reason¬able request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Ali, M. N., Mahmoud, K., Lehtonen, M. & Darwish, M. M. F. Promising MPPT methods combining metaheuristic, fuzzy-logic and ANN techniques for grid-connected photovoltaic. Sensors21, 1244 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.AbdElminaam, D. S., Houssein, E. H., Said, M., Oliva, D. & Nabil, A. An efficient heap-based optimizer for parameters identification of modified photovoltaic models. Ain Shams Eng. J.13, 101728 (2022). [Google Scholar]
- 3.Ismaeel, A. A. K., Houssein, E. H., Oliva, D. & Said, M. Gradient-based optimizer for parameter extraction in photovoltaic models. IEEE Access9, 13403–13416 (2021). [Google Scholar]
- 4.Houssein, E. H. et al. Performance of gradient-based optimizer on charging station placement problem. Mathematics9, 2821 (2021). [Google Scholar]
- 5.Abdelminaam, D. S., Said, M. & Houssein, E. H. Turbulent flow of water-based optimization using new objective function for parameter extraction of six photovoltaic models. IEEE Access9, 35382–35398 (2021). [Google Scholar]
- 6.Said, M., Houssein, E. H., Deb, S., Alhussan, A. A. & Ghoniem, R. M. A novel gradient-based optimizer for solving unit commitment problem. IEEE Access10, 18081–18092 (2022). [Google Scholar]
- 7.Yuan, X., Liu, Y. & Bucknall, R. A novel design of a solid oxide fuel cell-based combined cooling, heat and power residential system in the U.K. IEEE Trans. Ind. Appl.57, 805–813 (2021). [Google Scholar]
- 8.Ihonen, J. et al. Operational experiences of PEMFC pilot plant using low grade hydrogen from sodium chlorate production process. Int. J. Hydrog. Energy. 42, 27269–27283 (2017). [Google Scholar]
- 9.Qiu, Y. et al. An intelligent approach for contact pressure optimization of PEM fuel cell gas diffusion layers. Appl. Sci.10, 4194 (2020). [Google Scholar]
- 10.Ahmed, K. et al. Proton exchange membrane hydrogen fuel cell as the grid connected power generator. Energies13, 6679 (2020). [Google Scholar]
- 11.Nikiforow, K., Pennanen, J., Ihonen, J., Uski, S. & Koski, P. Power ramp rate capabilities of a 5 kw proton exchange membrane fuel cell system with discrete ejector control. J. Power Sources381, 30–37 (2018). [Google Scholar]
- 12.Menesy, A. S. et al. Effective parameter extraction of different polymer electrolyte membrane fuel cell stack models using a modified artificial ecosystem optimization algorithm. IEEE Access8, 31892–31909 (2020). [Google Scholar]
- 13.Chavan, S. & Talange, D. Electrical equivalent circuit modeling and parameter estimation for pem fuel cell. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies, i-PACT 2017 1–6 (IEEE, 2017).
- 14.Sedighizadeh, M., Rezazadeh, A., Khoddam, M. & Zarean, N. Parameter optimization for a PEMFC model with particle swarm optimization. Int. J. Eng. Appl. Sci.3, 102–108 (2011). [Google Scholar]
- 15.Forrai, A., Funato, H., Yanagita, Y. & Kato, Y. Fuel-cell parameter estimation and diagnostics. IEEE Trans. Energy Convers.20, 668–675 (2005). [Google Scholar]
- 16.Mo, Z. J., Zhu, X. J., Wei, L. Y. & Cao, G. Y. Parameter optimization for a PEMFC model with a hybrid genetic algorithm. Int. J. Energy Res.30, 585–597 (2006). [Google Scholar]
- 17.Outeiro, M., Chibante, R., Carvalho, A. & de Almeida, A. A new parameter extraction method for accurate modeling of PEM fuel cells. Int. J. Energy Res.33(11), 978–988 (2009). [Google Scholar]
- 18.El-Hay, E. A., El-Hameed, M. & El-Fergany, A. A. Improved performance of Pem fuel cells stack feeding switched reluctance motor using multiobjective dragonfly optimizer. Neural Comput. Appl.31, 6909–6924 (2019). [Google Scholar]
- 19.Sarma, U. & Ganguly, S. Design optimisation for component sizing using multi-objective particle swarm optimisation and control of PEM fuel cellbattery hybrid energy system for locomotive application. IET Electr. Syst. Transport.10 (1), 52–61 (2020). [Google Scholar]
- 20.Rizk-Allah, R. & El-Fergany, A. Artificial ecosystem optimizer for parameters identification of proton exchange membrane fuel cells model. Int. J. Hydrog. EnergyIn46, 37612–37627
- 21.Dai, C., Chen, W., Cheng, Z., Li, Q., Jiang, Z. & Jia, J. Seeker optimization algorithm for global optimization: A case study on optimal modelling of proton exchange membrane fuel cell (PEMFC). Int. J. Electr. Power Energy Syst.33(3), 369–376 (2011). [Google Scholar]
- 22.Askarzadeh, A. & Rezazadeh, A. An innovative global harmony search algorithm for parameter identification of a PEM fuel cell model. IEEE Trans. Industr. Electron.59(9), 3473–3480 (2012). [Google Scholar]
- 23.Askarzadeh, A. Parameter estimation of fuel cell polarization curve using BMO algorithm. Int. J. Hydrog. Energy38(35), 15405–15413 (2013). [Google Scholar]
- 24.Zhang, W., Wang, N. & Yang, S. Hybrid artificial bee colony algorithm for parameter estimation of proton exchange membrane fuel cell. Int. J. Hydrog. Energy38(14), 5796–5806 (2013). [Google Scholar]
- 25.Askarzadeh, A. & Rezazadeh, A. Optimization of PEMFC model parameters with a modified particle swarm optimization. Int. J. Energy Res.35(14), 1258–1265 (2011). [Google Scholar]
- 26.Niu, Q., Zhang, H. & Li, K. An improved TLBO with elite strategy for parameters identification of PEM fuel cell and solar cell models. Int. J. Hydrog. Energy39(8), 3837–3854 (2014). [Google Scholar]
- 27.Restrepo, C., Konjedic, T., Garces, A., Calvete, J. & Giral, R. Identification of a proton-exchange membrane fuel cell’s model parameters by means of an evolution strategy. IEEE Trans. Industr. Inf.11(2), 548–559 (2015). [Google Scholar]
- 28.Ali, M., El-Hameed, M. & Farahat, M. Effective parameters identification for polymer electrolyte membrane fuel cell models using grey wolf optimizer. Renew. Energy111, 455–462 (2017). [Google Scholar]
- 29.Sun, Z. et al. Proton exchange membrane fuel cell model parameter identification based on dynamic differential evolution with collective guidance factor algorithm. Energy216, 119056 (2021). [Google Scholar]
- 30.Messaoud, R. B., Midouni, A. & Hajji, S. Pem fuel cell model parameters extraction based on moth-flame optimization. Chem. Eng. Sci.229, 116100 (2021). [Google Scholar]
- 31.Gouda, E. A., Kotb, M. F. & El-Fergany, A. A. Investigating dynamic performances of fuel cells using pathfinder algorithm. Energy. Conv. Manag.237, 114099 (2021). [Google Scholar]
- 32.Yang, B. et al. Parameter identification of proton exchange membrane fuel cell via levenberg-marquardt backpropagation algorithm. Int. J. Hydrog. Energy46(44), 22998–23012 (2021). [Google Scholar]
- 33.Ben Messaoud, R. Parameters determination of proton exchange membrane fuel cell stack electrical model by employing the hybrid water cycle moth-flame optimization algorithm. Int. J. Energy Res.45 (3), 4694–4708 (2021). [Google Scholar]
- 34.Yuan, Z., Wang, W. & Wang, H. Optimal parameter estimation for PEMFC using modified monarch butterfly optimization. Int. J. Energy Res.44(11), 8427–8441 (2020). [Google Scholar]
- 35.Rezk, H. et al. Optimal parameter Estimation strategy of PEM fuel cell using gradient-based optimizer. Energy239, 122096 (2022). [Google Scholar]
- 36.Yuan, Y., Yang, Q., Ren, J., Mu, X., Wang, Z., Shen, Q. & Zhao, W. Attackdefense strategy assisted osprey optimization algorithm for PEMFC parameters identification. Renew. Energy225, 120211 (2024).
- 37.Hachana, O. & El-Fergany, A. A. Efficient PEM fuel cells parameters identification using hybrid artificial bee colony differential evolution optimizer. Energy250, 123830 (2022). [Google Scholar]
- 38.Chen, Y. & Zhang, G. New parameters identification of proton exchange membrane fuel cell stacks based on an improved version of African Vulture optimization algorithm. Energy Rep.8, 3030–3040 (2022). [Google Scholar]
- 39.Ismaeel, A. A. K., Houssein, E. H., Khafag, D. S., Aldakheel, E. A. & Said, M. Performance of rime -ice algorithm for estimating the PEM fuel cell parameters. Energy Rep.11, 3641–3652 (2024).
- 40.Houssein,, E. H., Samee, N. A., Alabdulhafith, M. & Said M. Extraction of PEM fuel cell parameters using Walrus optimizer. AIMS Math.9 (4), 12726–12750 (2024). [Google Scholar]
- 41.Adegboye, O. R. & Feda, A. K. Improved exponential distribution optimizer: Enhancing global numerical optimization problem solving and optimizing machine learning parameters. Cluster Comput.28, 128. 10.1007/s10586-024-04753-4 (2025). [Google Scholar]
- 42.Adegboye, O. R., Feda, A. K., Ojekemi, O. S., Agyekum, E. B., Elattar, E. E. & Kamel, S. Refinement of dynamic hunting leadership algorithm for enhanced numerical optimization. IEEE Access12, 103271–103298. 10.1109/ACCESS.2024.3427812 (2024 pp).
- 43.Adegboye, O. R. et al. DGS-SCSO: Enhancing sand Cat swarm optimization with dynamic pinhole imaging and golden sine algorithm for improved numerical optimization performance. Sci. Rep.14, 1491. 10.1038/s41598-023-50910-x (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Calasan, M., Aleem, S. H. A., Hasanien, H. M., Alaas, Z. M. & Ali, Z. M. An innovative approach for mathematical modeling and parameter estimation of PEM fuel cells based on iterative Lambert W function. Energy264, 126165 (2022). [Google Scholar]
- 45.Wilberforce, T. et al. Boosting the output power of PEM fuel cells by identifying best-operating conditions. Energy Convers. Manag.270, 116205 (2022). [Google Scholar]
- 46.Rezk, H., Wilberforce, T., Sayed, E. T., Alahmadi, A. N. M. & Olabi, A. G. Finding best operational conditions of PEM fuel cell using adaptive neuro-fuzzy inference system and metaheuristics. Energy Rep.8, 6181–6190 (2022). [Google Scholar]
- 47.Wilberforce, T. et al. Design optimization of proton exchange membrane fuel cell bipolar plate. Energy Convers. Manag.277, 116586 (2023). [Google Scholar]
- 48.Ashraf, H., Abdellatif, S. O., Elkholy, M. M. & El-Fergany, A. A. Honey badger optimizer for extracting the ungiven parameters of PEMFC model: Steady-state assessment. Energy Convers. Manag.258, 115521 (2022). [Google Scholar]
- 49.Lewison, R. L. & Carter, J. Exploring behavior of an unusual megaherbivore: A spatially explicit foraging model of the hippopotamus. Ecol. Model.171(1–2), 127–138 (2004). [Google Scholar]
- 50.Tennant, K. S., Segura, V. D., Morris, M. C., Snyder, K. D., Bocian, D., Maloney, D., & Maple, T. L. Achieving optimal welfare for the nile hippopotamus (Hippopotamus amphibius) in North American zoos and aquariums. Behav. Process.156, 51–57 (2018). [DOI] [PubMed] [Google Scholar]
- 51.Amiri, M. H., Hashjin, N. M., Montazeri, M., Mirjalili, S. & Khodadadi, N. Hippopotamus optimization algorithm: A novel nature-inspired optimization algorithm. Sci. Rep.14(1), 5032 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bouaouda, A. & Sayouti, Y. Hybrid meta-heuristic algorithms for optimal sizing of hybrid renewable energy system: A review of the state-of-the-art. Arch. Comput. Methods Eng.29(6), 4049–4083 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ahmadianfar, I., Heidari, A. A., Gandomi, A. H., Chu, X. & Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl.181, 115079 (2021). [Google Scholar]
- 54.Mohamed, A. W., Hadi, A. A., Mohamed, A. K. & Awad, N. H. Evaluating the performance of adaptive gaining sharing knowledge-based algorithm on CEC 2020 benchmark problems. In 2020 IEEE Congress on Evolutionary Computation (CEC) 1–8 (IEEE, 2020).
- 55.Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc.32(200), 675–701 (1937). [Google Scholar]
- 56.Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics: Methodology and Distribution 196–202 (Springer, New York, NY 1992). [Google Scholar]
- 57.Khishe, M. & Mosavi, M. R. Chimp optimization algorithm. Expert Syst. Appl.149, 113338 (2020). [Google Scholar]
- 58.Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst.96, 120–133 (2016). [Google Scholar]
- 59.Mirjalili, S., Mirjalili, S. M. & Lewis, A. Grey wolf optimizer. Adv. Eng. Softw.69, 46–61 (2014). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analyzed during the current study available from the corresponding author on reason¬able request.