Revealing gait as a murine biomarker of injury, disease, and age with multivariate statistics and machine learning

Abstract

Hundreds of rodent gait studies have been published over the past two decades, according to a PubMed search. Treadmill gait data, for example from the DigiGait system, generates over 30 + spatial and temporal measures. Despite this multi-dimensional data, all but a handful of the published literature on rodent gait has conducted univariate analysis that reveals limited information on the relationships that are characteristic of different gait states. This study conducted rigorous multivariate analysis in the form of sequential feature selection and factor analysis on gait data from a variety of gait deviations (due to injury i.e. peripheral nerve transection and transplantation, disease i.e. IUGR and hyperoxia, and age-related changes) and used machine learning to train a classifier to distinguish among and score different gait states. Treadmill gait data (DigiGait) of three different types of gait deviations were collected. Data were collected from B6 mice using the DigiGait system, with gait measurements taken at standardized treadmill speeds of 10, 17, and 24 cm/s over a period of 3–4 s per observation. Each mouse underwent at least two trials at each speed. Data were collected on B6 mice that were healthy and had various types of gait deficit due to: (a) a peripheral nerve injury model with increasing degrees of damage to the neuromusculoskeletal sequence of gait i.e. nerve transection, total hind limb transplantation, (b) a central nerve injury model of increasing degrees of damage to the motor regions responsible for gait i.e. IUGR, IUGR + hyperoxia, and (c) gait changes due to increasing age. Multivariate factor analysis (using MATLAB’s factoran) and forward feature selection (with ten-fold cross-validation) were conducted to identify those features and factors most descriptive of each gait state for comparison. Various machine learning classifier models were trained with ten-fold cross-validation and evaluated (e.g. random forest, regression, discriminant analysis, support vector machine, and ensemble) in a 70 − 30 training-testing split for their accuracy, precision, recall, and F-score. The highest performing model was used to score each type of gait for direct comparison on a scale of -0.5 to 0.5. The score distributions were plotted on a histogram for direct comparisons of score populations among various gait states. Multivariate feature selection revealed that not all 30 + features were relevant to describing the gait states. Plotting misclassification error (MCE) as a function of number of features included revealed that there was a critical number of features (~ 16) that minimized MCE (0.17 via univariate feature selection vs. 0.12 via multivariate feature selection). Incorporating more than 16 features led MCE to increase linearly indicating overfitting. Relationships among the identified features were understood via factor analysis. The factor analysis results were consistent with the biological differences between the groups (e.g. total hind limb transplantation was distinguishable via features descriptive of the positioning of the paw in relation to the body while nerve transection injury alone was distinguishable via features descriptive of changes to fine motor movements). Across all gait states, there was significant conservation of features and factors. This suggests certain relationships may be fundamental to rodent gait analysis regardless of the gait pathology in question. The highest performing machine learning classifier model (ensemble) was able to distinguish between gait deficits with high performance (F-score, recall, precision, and accuracy all > 0.90). This included the ability to distinguish between peripheral vs. central gait deficit, between individual types of peripheral deficit, between individual types of central deficit, and between younger vs. older animals. Using the classifier to score individual animals and plot the scores by group revealed score distributions that were consistent with biological phenomena. For example, the multivariate gait score trends as a result of increasing central nerve injury were consistent with the trends of white matter volume loss in relevant motor regions of the brain as measured via MRI. Finally, the degrees of separation between multivariate gait scores were consistent with the degree of biological difference between gaits (e.g. central injury had greater separation from healthy vs. peripheral injury; older and younger animals had more moderate, yet still statistically significant, separation in scores vs. any of the injury / disease states did with each other). In conclusion, this study establishes a new methodology to quantify and evaluate gait deviations across a variety of different models. Its novelty is in using multivariate statistics to describe the features and factors that characterize gait states due to injury, disease, and age for use in machine learning model training. This includes statistically describing the differences in gait between diseases with vastly different etiologies of gait deficits (peripheral vs. central). In doing so the methodology’s novelty includes accounting for relationships between groupings of features in model training; something that traditional univariate analysis is unable to do. It used multivariate statistics and machine learning to reveal gait as a quantifiable, preclinical biomarker of injury, disease, and age. It collapsed a multi-dimensional biological phenomena (gait) into a single score by encoding revealed biological relationships allowing for direct, quantifiable comparisons of function as it pertains to ambulation. It revealed how these multivariate gait scores can visualize biologically consistent separation and combined effects. Finally, we demonstrate the application of this methodology to already published univariate study that is representative of the hundreds of univariate treadmill gait analysis published over the last two decades. Thereby, opening the door to a new class of multivariate gait analyses that provides greater insight and value than the current state-of-the art.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-025-02073-0.

Introduction

15% of people experience a gait abnormality by the age of 60¹. That number increases to over 80% over the age of 85. Animal models are valuable for studying conditions and treatments that are difficult to study and experiment with in humans (e.g. new medicines, traumatic nerve injuries, limb replacement, tissue regeneration strategies)². Rodent models, in particular, are the most prevalent pre-clinical model for evaluating gait due to their availability, cost effectiveness, and versatility for quickly assessing the viability of novel interventions across the spectrum of gait deficit^3–7. Ultimately, the gait is a result of careful coordination between the nervous system and the musculoskeletal system. This study applies a novel approach for describing, scoring, and comparing gait across varying states / deficit types by applying multivariate statistics to describe its carefully coordinated components.

There are widely adopted methods for evaluating success when studying nerve injury and repair. These include methods for assessing cellular appearance (histopathologic examination)⁸, nerve conduction (nerve conduction velocity)⁹, nerve-muscle connection (electromyography)¹⁰, sensory function (Hargreaves)¹¹, and motor function (Rotarod, DigitGait, CatWalk, swimming, climbing)^5,12.

The lower extremity’s prime function is to enable locomotion. In human gait analysis, studies have investigated multivariate techniques to describe relationships among measurable features of gait¹³. These relationships help statistically characterize gait phenotypes and are used to select features for measurement, classification, and prediction¹³. Implementing a similar level of statistical rigor to animal gait studies represents a novel problem requiring further refinement and investigation.

In rodents, the study of locomotion via treadmill gait (DigiGait™) or free ambulating (CatWalk™) systems provides high levels of spatial and temporal detail, measuring over 30 + individual spatial or temporal gait parameters^14–18. Analyses of data measured by these systems are largely limited to traditional, univariate, multiple-hypothesis testing or feature selection^19–22. Usually this involves comparing the means of individual output parameters for statistical significance and applying some correction for multiple-hypothesis testing^23,24. Such univariate study enables conclusions that do not account for possible relationships among individual gait parameters unlike multivariate analysis. A machine learning model can also be trained using feature selection techniques that omit the examination of multivariate relationships among features²⁵. Thus, discoveries in rodent models, to date, have been primarily limited to a portion of the interplay that makes up the animal’s overall gait.

These limited, univariate gait studies span a variety of rodent models of gait deficit including those of central (stroke), metabolic (diabetic neuropathy)²⁶, degenerative (ALS)²⁷, traumatic (nerve transection / limb transplantation)²⁸, congenital²⁹, and other etiologies. While these diseases may result in dysfunctional gait, it is unlikely that the spatiotemporal details of their dysfunction are the same. For locomotion, indices such as the Sciatic Function Index (SFI) have been developed via multivariate linear regression models to compare healthy and dysfunctional gait³⁰. However, the SFI is a dimensionless number and does not reveal additional insight into exact relationships among specific spatial and temporal measures³¹. In short, what does it really mean if the SFI index is statistically different between two gait states? How do we describe more than just a “difference” between two states?

A comprehensive description of the rodent’s gait would require a multivariate methodology that can factor relationships among all 30 + measures and prioritize those that contribute to gait phenomena rather than noise. Recent advances in gait analysis have established a precedent for a new generation of multivariate approaches that treat measurable gait parameters not as individual, independent features but rather as related groupings of factors³². Unlike traditional univariate approaches that assess each gait parameter independently, the multivariate analysis developed in our lab and applied in this study simultaneously considers interactions among over 30 spatiotemporal measures³². This approach enables the identification of latent relationships and patterning within the data that are otherwise obscured when evaluating features in isolation. In doing so, multivariate methods not only capture the interdependence among gait components but also reduce dimensionality, mitigate noise, and help in revealing subtle biomechanical signatures associated with specific types of injury, disease, or aging.

We hypothesize that out of all spatiotemporal measures of rodent gait, there exists a discrete subset sufficient to uniquely describe the gait of distinct physiological states. That these subsets may be elucidated via multivariate characterization to reveal relationships among the features that encode and describe the different gait phenotypes in a biologically consistent manner. And finally, that encoding the revealed relationships into the training of a classifier model will enable discrimination between gait states with higher accuracy than models trained with features identified via univariate analysis alone.

Results

Animal model results overview

This study evaluates the utility of a novel multivariate pipeline for rodent gait analysis in a variety of different physiological states: injury, disease, and aging. Results for injury are described below in the Peripheral nerve injury results section. Results for disease are described below in the Central nerve pathology results section.

Peripheral nerve injury results

To evaluate the ability of the multivariate pipeline to describe and compare the effects of injury on gait, a total of 30 surgeries were performed in this study with a high success rate (87%). Detailed results including the operative design, immunohistochemical + sensory evidence of successful nerve re-integration can be found in the supplemental material Fig S1, S8, and S9.

Central nerve pathology results

To evaluate the ability of the multivariate pipeline to describe and compare the effects of disease on gait, a model of increasing disease to motor regions of the brain was used (i.e. IUGR, hyperoxia, and IUGR + hyperoxia). Chang et al. 2018 measured white matter volume in said regions³³. The results show that IUGR leads to statistically significant white matter volume loss in the midbrain and pons. And that IUGR + hyperoxia leads to statistically significant white matter loss in the striatum and pallidum. Both conditions lead to statistically significant white matter loss in the internal capsule. Finally, there is a linear (not often statistically significant) decrease in white matter volume in all motor regions of the brain as a function of increasing disease (i.e. IUGR, hyperoxia, and IUGR + hyperoxia). Those results display clear trends that suggest hyperoxia causes more white matter loss than IUGR alone. And that their combination leads to greater white matter loss than either alone (Fig. 1). Multivariate gait analysis was evaluated for its ability to quantitatively describe and distinguish the effect of increasing white matter loss in motor regions on the end functional outcome (i.e. gait).

Fig. 1.

Motor regions of the brain show clear patterns of white matter loss with increasing degrees of injury. Hyperoxia alone consistently results in more loss than IUGR. The combined effect resulted in the greatest extent of white matter loss. The top half of the figure is the original data from Chang et al. 2018. The bottom half show just the means of that data for comparison recognizing that statistical significance shown in the top is in reference to the means of each group.

Feature selection

Univariate analysis

Peripheral gait deficit

Traditional gait studies conduct univariate analysis, which was done here as a basis for comparison. We first plotted the empirical cumulative distribution function (CDF) of the p-values. The CDF of the p-values visualizes the percentage of feature means, when compared for statistical difference via t-test that lie under the critical value. Applying Bonferroni correction for multiple hypothesis testing determined a critical p-value of 0.001. For example, in comparing pathological gait from limb transplantation to healthy controls, 28% of features had statistical significance Fig S2), which amounts to 9 parameters (Table S1). In comparing pathological gait from nerve transection injury alone, 44% of features had statistical significance (Fig S2), which amounts to 14 parameters (Table S1). Comparing the means of every feature 1:1 with the control and then comparing the set of statistically significant features between the two degrees of gait deficit revealed a high degree of shared features with statistical significance (Table S1). While we could attempt to connect the statistically significant features to biological relevance, via univariate analysis we learn little about how the identified features relate to each other to describe the respective gait states diminishing the value of doing so. Therefore, a methodology to understand how statistically significant features contribute to the complex, coordinated movement of gait (i.e. multivariate statistics).

Central gait deficit

Chang et al. 2018 plotted and reported on three gait measures as a result of each degree of pathology. This is typical of gait studies in the literature and represents the traditional univariate analysis. The study reports a strong linear decrease in %Brake/Stride Time as a function of increasing pathology (IUGR, hyperoxia, and IUGR + hyperoxia) as well as a strong linear increase in %Propel/Stride Time and Ataxia Coefficient. We learn that %Brake/Stride Time and %Propel/Stride Time are both statistically altered as a result of hyperoxia and IUGR + hyperoxia. And that Ataxia Coefficient is statistically increased as a result of IUGR + hyperoxia. While this is informative, it looks at each of these spatiotemporal measures as univariate. Gait is a carefully coordinated, multivariate movement. Again, via univariate analysis we learn little about how the identified features relate to each other to describe the respective gait states. To further illustrate this, univariate analysis of peripheral nerve injury also revealed %Brake/Stride Time and %Propel/Stride Time as statistically significant (among 8 + other features not shared between central vs. peripheral pathology). However, it remains unclear what the significance of this overlap or lack thereof means.

Univariate filter feature selection

To further emphasize the limitation of traditional methods, measuring and plotting misclassification error (MCE) as a function of an increasing number included features is a univariate approach to determining the ideal number of features to include in model training. To illustrate, we compute MCE for a discriminant analysis model between 2 and 32 features and plot MCE for the peripheral nerve injury models accordingly (Fig. 2). Note, in this simple, univariate feature addition approach, using 30 features minimizes MCE. Ultimately, the smallest MCE achieved with this method was 0.17 indicating a potential model accuracy of 83% in discriminating healthy gait from pathological gait due to limb transplantation. However, this is a model trained on one holdout set with likely overfitting from using 30 of the 32 available features. It is likely that this is modeling noise, and it is unclear how much generalizable gait phenomena is being modeled. Thus, multivariate (wrapper) methods for feature selection were explored.

Fig. 2.

Contrasting univariate and multivariate feature selection methods for their ability to minimize misclassification error (MCE) as a function of number of features included in the model. Top: Misclassification error (MCE) as a function of number of features calculated using a pseudo-quadratic discriminant analysis, holdout set, and a simple filter method that does not account for any interactions. The lowest achievable MCE was around 0.16 when including 30 features. Middle and Bottom: Multivariate, forward feature selection with cross-validation to minimize misclassification error when classifying healthy gait from pathological gait was conducted to find the optimal combination of features that minimizes MCE. This approach takes interactions between features into account and uses a pseudoquadratic discriminant analysis. The lowest MCE was (Middle Left) ~ 0.12 using 10–14 features when classifying limb transplantation injury, (Middle Right) ~ 0.12 using 10–14 features when classifying just nerve transection injury, (Bottom Left) ~ 0.01 using 14–15 features when classifying just hyperoxia, and (Bottom Right) ~ 0.02 using 10–12 features when classifying just IUGR. Notice how the MCE has a much more consistent and predictable pattern as features are added in comparison to the univariate, simple filter approach referenced in Top. Figure reproduced from the primary and corresponding authors’ prior published study and with their permission³².

Multivariate wrapper feature selection with cross validation

The univariate approach to filter feature selection described above omits relationships between features and is representative of how most rodent gait studies have evaluated their data. Moreover, choosing features purely based on their ranking in filter selection can result in the modeling of redundant information. For example, features 2 and 8 have a linear correlation coefficient of 1.0. This is because these two features, are by definition, related (%SwingStride = 1 - %StanceStride).

Sequential feature selection is a multivariate approach to selecting a subset of features that works by sequentially adding features in various relationships to the model and monitoring exactly which feature relationships lead to decreases in MCE until it is minimized. When classifying between healthy gait and pathological gait due to limb transplantation, our results show that 10 to 12 features are optimal for minimizing MCE (smallest MCE achieved = 0.12 (Fig. 2). For classifying between healthy and pathological gait due to nerve transection injury, our results show that 16 features achieve the minimum possible cross-validation MCE of 0.10. Note how using feature selection (multivariate) leads to a 5–7% improvement in MCE achieved using ~ 20 fewer features as compared to the simple filter approach above. Most rodent gait analyses utilize univariate feature selection^14–19 and the only studies to use sequential feature selection have been reported from our lab³². Note how MCE increases beyond the critical numbers of features indicating overfitting and supporting the following hypotheses: (a) there is a critical subset of features that more accurately describes healthy versus pathological gait and (b) the subset identified via multivariate characterization more generally describes gait when compared to the subset identified via univariate characterization as evidenced by superior model performance and less overfitting. The selected features are shown in Table S1.

Similar results are seen in response to multivariate feature selection with the nerve injury models (Fig. 2). There is a smooth trend of decreasing MCE, a plateau, and then a linear increase with more features added, indicating overfitting. In the case of central nerve injury, the plateau begins sooner at ~ 5 features (unlike Peripheral Nerve Injury (PNI), which starts at ~ 10 features) and reaches its minima at ~ 15 features (like PNI).

However, when examining the selected parameters (Table S1), it is unclear how they may relate to each other. Despite the compelling classification results from adding multivariate feature selection, the process does not reveal exactly how these features relate to each. A technique like factor analysis is needed to identify precisely which features relate to each other.

Factor analysis

Introducing the concept

Prior gait studies have proposed a multivariate rodent gait model described by groupings of features (i.e. factors) that related to each other to better describe gait as opposed to individual, independent features^32,34. Lambert et al. proposed that the multi-dimensional DigiGait data in rats with olivocerebellar ataxia can be reduced to three uncorrelated groupings of variables, or common factors, termed rhythmicity, thrust, and contact³⁴. Factor analysis allows us to understand how the directly measured features (i.e. the collected data) compose potential latent (or unmeasurable) factors that more directly describe the phenomena of interest. To determine the number of likely factors, the average specific variation and loading were plotted as a function of factor number (Fig S3).

In Fig S3, the red line represents the average specific variation, and the blue line represents the average loading. The results confirm that at 6 latent factors, the loading does not increase, while the specific variation continues to decrease, which indicates overfitting. Maximal loading is viewed using 6 factors, while reaching an inflection point in minimizing specific variation. Thus, 6 factors were used to continue the comparative analysis between the latent factors that characterize pathological gait due to transplantation versus nerve transection injury (Table 1). Similar results were seen when conducting factor analysis of Central Nerve Injury models. Fig S3’s bottom-right two panels show the calculated feature loadings of greater than 0.6 or less than − 0.6, which was identified as a significant feature in the respective factor grouping. Note that Stance is the only feature shared between two factors. Otherwise, the factors are each composed of unique features.

Table 1.

Factor analysis results of various etiologies of gait deficit. Notice key similarities (unbolded) and differences (bolded) between the two datasets. The bottom two rows describe the latent or implied factors that make sense of the various groups of observable measures shown above. These latent factors are an interpretation of the factor groupings shown above. The factor groupings were identified via factor analysis, which quantifies the relationship between individual, measurable features and can be used to identify the most highly grouped features. Table reproduced from the primary and corresponding authors’ prior published study and with their permission³³.

Factor analysis results of peripheral nerve injury models

Table 1 shows the latent factors and the features they comprise for pathological gait due to limb transplantation. Table 1 also shows the latent factors and the features they are composed of for pathological gait due to nerve transection injury. The bolded latent factors in each sub-table (Factor 4 and Factor 6 respectively) are composed of different features between the two groups. The other 5 latent factors are composed of the same (or highly similar) features. The distinction is that pathological gait due to limb transplantation is distinguished by the relationship between the absolute paw angle and midline distance. Pathological gait due to nerve transection injury is distinguished by the relationship between paw area at peak stance in sq. cm, paw area variability at peak stance in sq. cm, and MIN dA/dT. The high degree of overlap of feature groupings between the two pathologies suggests that much of the statistical description of gait in these two sources of traumatic nerve injury is the same with a significant point of difference being factors 4 and 6 respectively (i.e. the two bolded columns) (Table 1).

The factor analysis results suggest that animals with a transplanted limb have more variation in the anatomy of their transplanted paw in relation to the midline of their bodies. They also suggest that animals that received nerve transection injury and reattachment do not demonstrate this same variation. This is consistent with the underlying biology: animals with a total limb transplantation likely have an alteration in the anatomical configuration of their paw related to their midline while animals receiving only nerve transection injury might not. Additionally, the data suggest that animals with exclusively nerve transection injury have a discernible variation in how the contact of their paw relates to their ability to make fine motor movements (i.e. jerks or dA/dT) while animals receiving a total limb transplant are likely to have this masked by gross motor defects related to the extensive musculoskeletal injury that accompanies the nerve injury from the transplant. These results suggest that factor analysis may have value in statistically characterizing otherwise intuitive biological phenomena of specific pathophysiological gait states. This is further expounded on in the discussion section.

Factor analysis results of central nerve injury models

Latent factor description of central nerve disease

Factor 1 of the combined model (IUGR + hyperoxia) showed components of both Factor 1 from IUGR (Propel and %PropelStance) and Factor 1 from hyperoxia (Propel and Stride Frequency). A similar trend was observed in Factor 2 of the combined model and Factor 2 of hyperoxia (Paw Area at Peak Stance in sq. cm, Paw Area Variability at Peak Stance in sq. cm) and Factor 3 of IUGR (Paw Area at Peak Stance in sq. cm, Min dA/dT).

Factor analysis allowed for a deeper understanding of the exact relationships among features in contrast to a simple rank list of features as provided by many feature selection techniques. This level of statistical description is currently lacking from gait studies in animal models. The many insights revealed support the hypothesis that multivariate gait analysis provides a more comprehensive statistical description of individual gait states than univariate analysis. This is further examined in the discussion section.

Training a machine learning classifier to discriminate between gait phenotypes

Gait as a biomarker of injury

Using the features identified via multivariate feature selection and confirmed by factor analysis we assessed four different model architectures (Table 2). Accuracy in distinguishing between healthy gait and pathological gait due to any form of peripheral nerve injury (Table 2a) ranged from 0.75 to 0.91, precision from 0.78 to 0.93, recall from 0.77 to 0.91, and F-Score from 0.77 to 0.92. The ensemble model (i.e. boosted classification trees), had the highest-performing metrics in distinguishing between healthy gait and pathological gait due to any form of injury or disease (PNI or CNI).

Table 2.

Evaluating the performance of 4 different model architectures in distinguishing between healthy and pathological phenotypes of gait. Using the identified features from feature selection + factor analysis 4 different model architectures were evaluated for their accuracy, precision, recall, and F-score in their ability to distinguish (A) healthy gait from gait deficit due to peripheral nerve injury and (B) gait deficit due limb transplantation from gait deficit due to total nerve transection alone. Then using the Ensemble model, (C) various additional pairwise comparisons of Central Gait Deficit were evaluated and (D) additional comparisons of gait deviation due to age or between randomly selected controls. Notice how a more moderate deviation due to aging is observed in D as compared to the performance of distinguishing between disease and injury states (A-C). Table partially reproduced from the primary and corresponding authors’ prior published study and with their permission³³.

Accuracy in distinguishing between types of peripheral nerve injury (i.e., hind-limb transplant vs. total nerve transection) ranged from 0.64 to 0.88, precision from 0.71 to 0.93, recall from 0.69 to 0.88, and F-score from 0.69 to 0.90. The ensemble model again was the highest-performing architecture in distinguishing between different types of peripheral nerve injury.

Values output by the model on the holdout sets across injury, disease, and developmental conditions were graphed as box and whisker plots. A strong statistical difference in output distribution between healthy versus injured animals as well as between pathological states was observed (p < 0.0001) (Fig. 3). Sample confusion matrices from one iteration were calculated and included as well for peripheral and central gait deficits (Figs S4, S5, S6, and S7).

Fig. 3.

Multivariate score distribution comparisons of (left and middle) each disease state to control and of direct comparison between (right) each disease state directly reveals statistically significant separation. (Left) Limb transplanted-gait seems to be slightly farther in separation to healthy gait than (middle) Nerve transection-gait is. The comparison of each disease state to each other (Right) reveals a much smaller separation. All of this suggests that the gait deviations seen from the gradations of peripheral injury are more similar to each other than they are to healthy gait. Note that the multivariate gait score is a dimensionless number and that 0 represents the middle of the plane of separation.

Gait as a biomarker of disease and age

Using the features identified via multivariate feature selection and confirmed by factor analysis the ensemble model was confirmed to perform similarly in classifying between healthy gait and deficient gait due to central deficit caused by developmental disorders of growth and respiration as it performed in classifying PNI. Confusion matrices for all pairwise classifications between types of central deficit are included in the supplementary material. The performance of the model in distinguishing between types of central gait deficit ranged between an accuracy of 0.77–1.00, precision from 0.59 to 1.00, recall from 0.69 to 1.00, and F-score from 0.63 to 1.00 (Table 2C). With all comparisons aside from Hyperoxia vs. IUGR + Hyperoxia performing generally > 0.90 in all performance metrics. The model was used to score and plot each observation in a variety of comparisons (Figs. 4 and 5).

Fig. 4.

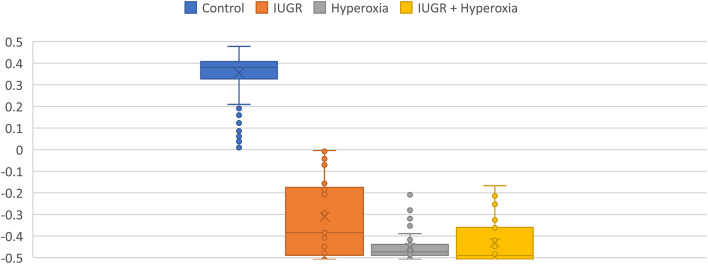
Box and whisker comparisons of each central disease state to control gait via multivariate scoring reveals significant separation of the means. Notice how the combined disease state’s (IUGR + Hyperoxia) distribution appears to resemble characteristics of its individual components (IUGR, Hyperoxia).

Fig. 5.

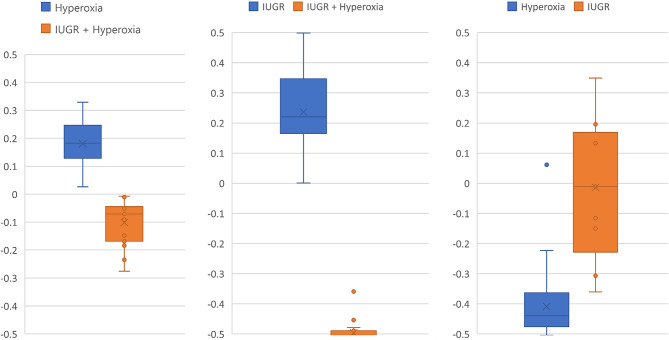
Multivariate score distribution comparisons of (left and middle) each central disease state and the combined and (right) each disease state directly reveals statistically significant separation. (Left) Hyperoxia-gait seems to be closer in separation to the combined score than (middle) IUGR-gait is to the combined. The comparison of each disease state to each other (Right) reveals a shift of the plane of separation strongly towards hyperoxia-gait suggesting its gait had a stronger “pull” on the multivariate scores. All of this suggests that the gait deviations seen in the combined, IUGR + hyperoxia-gait, state are influenced more heavily by hyperoxia than by IUGR.

Scores output by the model on the holdout set were graphed as box and whisker plots. A variety of comparisons were conducted including: (a) all developmental gait deficits vs. control, (b) IUGR vs. control, (c) hyperoxia vs. control, (d) IUGR + hyperoxia vs. control, (e) hyperoxia vs. IUGR + hyperoxia, (f) IUGR vs. IUGR + hyperoxia, (g) hyperoxia vs. IUGR, (h) control vs. control, and (i) younger vs. older (Figs. 4, 5, 6 and 7).

Fig. 6.

Randomly chosen control animals have statistically indistinguishable gait with performance metrics in the 0.50 range (a coin toss).

Fig. 7.

The multivariate pipeline can statistically distinguish gait-related changes due to age with more moderate significance (p = 0.002). Performance metrics are in the 0.75 range (i.e. 50% better than a coin toss).

A strong statistical difference in output distribution between healthy versus injured animals as well as between pathological states was observed (p < 0.001) (Figs. 4 and 5). Between random control groups no statistical difference was seen (p = 0.235). All performance metrics were in the 0.50 range (p > 0.05) (Fig. 6 and Table 2D). Between the younger vs. older group a moderate difference was seen (p < 0.001). All performance metrics were in the 0.70 range (Fig. 7 and Table 2D).

All comparisons showed high statistical significance with certain conditions showing more separation than others. Specifically, hyperoxia and IUGR show less separation than IUGR + hyperoxia compared to any other gait state. The IUGR + hyperoxia scores appear to represent characteristics of the distributions of hyperoxia and IUGR individually (Fig. 5).

Gait as a biomarker of white matter loss in motor regions of the brain

Chang et al. 2018 measured white matter volume in motor regions of the brain as a function of disease state (IUGR, hyperoxia, and IUGR + hyperoxia)³³. Those results display clear trends that suggest hyperoxia causes more white matter loss than IUGR alone. And that their combination leads to greater white matter loss than either alone (Fig. 1). Univariate gait metrics confirm these trends (Fig. 8). Our study reveals further consistency with Chang et al.’s white matter and univariate findings; that multivariate gait metrics display significant separation between healthy and diseased gait states (Fig. 9) with the diseased region of the curve displaying strong linearity (> 0.80) (Fig. 9).

Fig. 8.

Univariate gait metrics show consistency with white matter loss. These are three metrics of the 30 + measured via DigiGait. Notice the strong R² values (> 0.90) in directions that show decreases in braking time, increases in propulsion time, and increases in ataxia as a function of progressively greater disease.

Fig. 9.

Multivariate gait scores are a biomarker of disease states. (Left) strong separation between healthy¹ and diseased^2–4 states. (Right) physiologically consistent separation among disease states. Hyperoxia² and the combined state³ are closer to each other. IUGR on its own has less severe impact. This same trend was seen in the white matter volume data as well as in the univariate gait metrics published by Chang et al. 2018.

Discussion

The goal of this study was to use multivariate statistics to learn about the features, relationships, and factors that are most descriptive of gait in different pathological states. In doing so, we explored the hypothesis that a multivariate characterization of gait will reveal novel relationships between spatiotemporal components specifically in the contexts of (a) peripheral nerve injury, (b) central nerve disease, and (c) normal development. Gait data from DigiGait’s system includes 30 + different spatiotemporal features or outputs. It is important to understand which features are most descriptive of specific pathological states. We called these features primary dimensions and defined them as those features most relevant to describing relationships within the gait data. We hypothesized that these relationships were deterministic of specific phenotypes, which contrasts with features that are not related to describing specific phenotypes and may conversely model noise.

Modeling noise can result in overfitting that detracts from statistical learning of the patterns that describe the phenotype of interest. Feature selection algorithms enable one to test various feature subsets from the original feature set and learn which subset is most descriptive of the underlying phenomena. Feature selection algorithms can be roughly grouped into three categories: filter, wrapper, and embedded methods³⁵. Univariate filter methods select the feature subsets via multiple hypothesis testing without involving a learning algorithm³⁶. Multivariate wrapper methods iteratively evaluate a variety of relationships between features and use the performance of a learning algorithm to evaluate each candidate feature subset³⁷. Embedded methods determine feature importance as part of a model training process³⁸.

In Fig. 2 the wrapper-based, multivariate feature selection resulted in the usage of 10 to 15 select features in the model and thereby decreased the MCE of the model by more than 20%. This result supports the hypothesis that accounting for relationships between components of the gait would allow for more accurate classification between distinct gait phenotypes than univariate studies alone.

This accounting for multivariate relationships is largely absent from the field of animal gait analysis. One study was comparable in its level of statistical description³⁴, coincidentally doing so in a genetic neurodevelopmental model of cerebellar ataxia³⁴. Lambert et al. supported the value of multivariate characterization of gait by conducting feature extraction on highly dimensional gait data from a central nerve injury model of cerebellar ataxia. The authors hypothesized certain indirect, common factors that characterize gait and underlie the more directly measurable features. These common factors included thrust, rhythmicity, and contact area and were directly useful in discriminating between animals with a central lesion vs. those without³⁴. We observed potential patterns in the selected features and hypothesized that pathological gait due to traumatic nerve injury could also be characterized by certain latent factors that are determined by and composed of the selected features.

The level of exploratory statistical description in the prior few paragraphs is largely absent from studies across the field, including some of the latest, that employ gait analysis^22,29,39. Our study contributes a comprehensive, multivariate characterization pipeline for application in the study of any pathologies in which gait is a quantitative translational outcome metric.

When contrasting the latent factors that are statistically meaningful to describing increasing degrees of peripheral gait deficit, we can see specific measures of the paw that are consistent with biological differences in the respective pathologies. For example, limb transplantation injury was better characterized by the relationship of the paw to the midline, which may be due to loss of mechanical integrity and thereby positioning of the limb in relation to the area surrounding the transplant itself. In contrast, the nerve transection injury model was better characterized by fine motor movements of the paw (i.e. MIN dA/dT). This suggests that finer measures are more discernible when there is only nerve injury as compared to nerve + muscle + bone injury (Table 1).

The results from factor analysis showed significant overlap of factors (and their component features) between the two gradations of peripheral nerve injury shared numerous important features. The results also displayed key differences related to fine vs. gross motor movements in each model respectively. When factor analysis was applied to the central nerve injury models effects that were consistent with the biology were also observed. For example, Factor 1 of the combined model (IUGR + hyperoxia) showed components of both Factor 1 from IUGR (Propel and %PropelStance) and Factor 1 from hyperoxia (Propel and Stride Frequency). A similar trend was observed in Factor 2 of the combined model and Factor 2 of hyperoxia (Paw Area at Peak Stance in sq. cm, Paw Area Variability at Peak Stance in sq. cm) and Factor 3 of IUGR (Paw Area at Peak Stance in sq. cm, Min dA/dT).

Factor analysis in this study allowed for a deeper understanding of the exact relationships among features in contrast to a simple rank list of features as provided by many feature selection techniques. This level of statistical description is currently lacking from gait studies in animal models. The many insights revealed support the hypothesis that multivariate gait analysis provides a more comprehensive statistical description of individual gait states than univariate analysis. In the clinic, employing such factor analysis techniques could similarly provide a window into better describing nuances of different patients’ gaits. A recent study contributes evidence toward using gait as a quantitative translational outcome metric for therapeutic development in Angelman syndrome and other genetic neurodevelopmental syndromes²⁹.

The extensive description of our findings is further enriched by an interpretation that underscores the significance of the results within the broader field of preclinical gait analysis. Our results not only demonstrate that critical subsets of gait features can be reliably identified via multivariate techniques, but they also reveal latent factors that mirror the underlying biological mechanisms of locomotion. For example, the separation between pathological and healthy gait states—and between different gradations of injury and disease—is consistent with known biomechanical and neurological differences. This enhanced interpretability suggests that our multivariate scoring system could serve as a robust biomarker, facilitating head-to-head comparisons across diverse experimental models. In turn, these insights pave the way for more nuanced, quantitative assessments in both preclinical studies and potentially in clinical applications, providing a valuable tool for the evaluation of novel therapeutic interventions.

While our multivariate approach offers significant advantages in characterizing complex gait patterns, several limitations warrant discussion. First, potential bias in the feature selection process cannot be entirely ruled out, especially given the correlations inherent among the measured gait parameters and the modest sample sizes characteristic of animal studies. Second, although murine models provide a controlled environment for studying gait alterations, differences in locomotor biomechanics between rodents and humans may limit the direct translational impact of these findings. Future studies should consider validating the selected feature sets with alternative selection algorithms, expanding the datasets, and, where possible, integrating additional model systems or complementary modalities (such as kinetic analysis or imaging) to enhance generalizability and robustness. Addressing these limitations will further refine the methodology and improve its applicability as a tool for both mechanistic studies and preclinical evaluations.

That being said, we explored the hypothesis that characteristic feature relationships of distinct gait phenotypes could be used to train classifiers capable of distinguishing between said phenotypes. The trained classifiers distinguished individual animals for whether their gait was more likely healthy or pathological and discriminated between the two pathologies with high accuracy (Table 2). The highest performing model (ensemble) outputted a distribution of values with highly significant difference in their means (p < 0.0001) (Figs. 3, 4, 5, 6 and 7). The model was built by encoding the features and relationships uncovered to be most important in describing the gait pathologies respectively. In modeling peripheral gait deficit, the plotted multivariate score distributions displayed high statistical separation (p < 0.0001). The ensemble model consistently outperformed individual classifier architectures (e.g., Random Forest, Discriminant Analysis, and Support Vector Machine) as evidenced by its higher accuracy, precision, recall, and F-score across multiple comparisons. This superior performance can be attributed to its inherent ability to integrate and ‘vote’ on predictions made by a set of diverse classifiers, thereby reducing variance and capturing non-linear interdependencies among the gait features more effectively. By leveraging the strengths of multiple base models, the ensemble approach is better suited to address the complexity of the multivariate relationships present in the gait data. Consequently, this results in a more stable and robust classification, ultimately enhancing the model’s capacity to discriminate between subtle differences in gait patterns associated with different injury or disease states.

Additionally, in studies of central gait deficit, consistency between white matter loss and separation of multivariate gait scores can be seen. Diffusion tensor imaging tractography in.

2018 revealed statistically significant losses in white matter volume in motor regions of the brain (Fig. 1)³³. The patterns of loss as a function of disease state were consistent with the decrease in multivariate gait score seen across the same disease states (Fig. 9). Univariate gait data reported in Chang et al. 2018 were also consistent (Fig. 8).

Taken in sum, these data support the idea that the method is sensitive enough to detect more subtle gait changes related to the loss of white matter in motor regions of the brain. To further validate the multivariate approach randomly chosen healthy animals were compared and verified to be statistically indistinguishable from each other. The multivariate approach was also able to resolve more moderately significant separations due to age-related gait changes. This revealed gait as a potential biomarker of age in addition to injury and disease.

Uncovering gait as a biomarker of injury, disease, and age via animal suggests that if provided the spatial and temporal measures of an individual’s steps and sufficient control data, gait deviations could be detected using multivariate statistics and machine learning. The source of these gait deviations could be anything ranging from age, disease, injury, intoxicants, and the list goes on. With this knowledge of fundamental biological phenomena, interesting solutions to important problems arise. For example, one may ask how we may collect sufficient control data of any individual human? Two of the surfaces humans walk the most on are our shoes and the floors in our homes.

In several publications, the premise of collecting gait data within shoes or floor tiles has been supported^40,41. With a control dataset, software developed as a result of the multivariate gait analysis described in this manuscript, paired with smart shoes, socks, or tiles could enable the detection of strokes, age-related gait changes, injuries due to sports, sickness, its onset, intoxicated states, neuropathies, and the recovery processes in any of the above listed etiologies.

Conclusion

This is the first system to multivariately describe and distinguish between gradations of peripheral nerve injury, central nerve disease, and gait deviations due to aging in a murine gait model. The multivariate system for characterizing and scoring gait has revealed gait as a potential biomarker of injury, disease, and development. Using computational statistics, these relationships were taken advantage of to quantify and score something as complex and multi-factorial as gait. Collapsing it down to a single metric that could be plotted and used for comparing fundamentally different gait states head-to-head (e.g. injury, disease, age). The ability of the system to recognize gradations in the progression of injury, disease, or time highlights its statistical resolution and potential.

There are dozens of preclinical microsurgical cores and behavioral phenotyping cores across the country studying dozens of disease models^42,43. A bank of this data would unlock answers to many biological questions. A fundamental question when evaluating novel methods for nerve repair (e.g. materials, biologics, surgical techniques) the biomedical engineer and clinician will both want to know (a) if there’s a difference as a result of the intervention, (b) if there is, in which direction, and (c) to what extent. The multivariate system applied here, enables scientists and engineers to answer that question in a pre-clinical model that accounts for all spatiotemporal measures of the gait. The generalizability of this approach has been demonstrated across patho-physiologies (e.g. central vs. peripheral), etiologies (e.g. disease vs. injury), and developmental ones (e.g. different ages). The implications of gait as a biomarker of age and development in multivariate preclinical biocomputational models opens a field of study to explore. Imagine a study that examined gait, carefully, among a large volume of healthy animals living their lifespan naturally and up to the point of their death. What might we learn? Similar inquiry on human gait data may enable a future where our children’s shoes collect gait data and track their development. The tiles in our homes send daily reports to the mirror we wake up to and give information on one’s body detecting sub-clinical strains and suggesting rehabilitation or performance improvement programs. Our elderly, when home alone, may be monitored for gait deviations indicating potential strokes or falls to alert emergency responders automatically.

Practically, the latest advancement in gait analysis established the precedent for using multivariate statistics to characterize and distinguish between different etiologies of gait deficit^32,34. According to a PubMed search, hundreds of gait studies in animals have been published over the past two decades. We have identified datasets of DigiGait data available at our Behavioral Phenotyping Core from investigators studying additional causes of gait deficit. Academic researchers can do the same by accessing the code available at our GitHub repository and citing this manuscript should any code be used towards future publications (https://github.com/luoyuanlab/gait). Industry professionals must reach out to the corresponding author to make use of the code.

Methods

Experimental design

This study applies a multivariate statistical pipeline to both original data as well as already published data. The goal in doing so is to demonstrate its utility in original research and on already collected data. The datasets collected represent DigiGait treadmill data of B6 mice with a range of injury, disease, and developmental stages. A peripheral nerve injury model was used that represents increasing degrees of damage to the neuromusculoskeletal sequence, namely: (a) healthy animals, (b) animals with nerve injury only (via nerve transection and re-connection), and (c) animals with nerve, muscle, and bone injury (via total hind limb transplantation). A central nerve injury model was used that represents increasing degrees of damage to the motor regions of the brain, namely: (a) healthy animals, (b) animals born from intrauterine growth restriction (IUGR), (c) animals born and exposed to hyperoxia, and (d) animals exposed to both (b) and (c). Finally, data from healthy and younger animals was also compared for the pipeline’s ability to evaluate more subtle differences (e.g. due to natural aging processes).

Animals and experimental groups

Central nerve disease model

Behavioral phenotyping core (BPC) and existing gait deficit data

The mission of the Northwestern University’s Behavioral Phenotyping Core is to “make available a facility to determine the behavioral effects of genetic manipulations, potential pharmaceuticals, aging, and other manipulations upon normal behavior, and the learning and memory capacities of rodents used as model systems”⁴⁴. The BPC also works with PIs to gather pilot data for new applications. Dozens of other BPC’s exist at academic medical centers across the nation, which is apparent via a simple Google search^42,43. To test the hypothesis of the generalizability of the multivariate pipeline developed in this study, NU’s BPC was approached and inquired of any other studies of gait deficit conducted at the institution. Further inquiry led to an investigator who was willing to share her data of gait deficit in models of central nervous injury (Intrauterine Growth Restriction, Intrauterine Hyperoxia)³³.

Central gait deficit data from models of IUGR caused by TXA₂, hyperoxia, and both IUGR + hyperoxia

To illustrate the applicability of the multivariate pipeline on a retrospective set of gait data congenital models of IUGR, hyperoxia, and IUGR + hyperoxia were provided by a collaborator. Following are the summarized details of how IUGR, hyperoxia, or both were induced by the collaborator³³. For IUGR, micro-osmotic pumps (model 1007D, 0.5 mL/h) from Alzet were implanted into gravid C57Bl/6 wild-type mice at 12.5 days post-coitus, corresponding to the beginning of the third trimester of human pregnancy. These pumps were inserted into a subcutaneous pocket in the hip space and contained either the TXA2-analog U-46,619, dissolved in 0.5% ethanol, or 0.5% ethanol alone as the vehicle. The infusion rate was maintained at 2,000 ng/h throughout the remainder of the pregnancy. Pups were delivered spontaneously and weighed at birth. Those born to dams receiving the TXA2 analog and weighing less than 1.266 g (< 10th percentile for sham pup weights) were assigned to the IUGR group. Approximately one-third of the TXA2-analog pups were defined as small-for-gestational age (SGA), mirroring the incidence of human SGA infants born to mothers with uteroplacental insufficiency in IUGR epidemiological studies. Pups weighing more than 1.266 g (> 10th percentile) were assigned to the vehicle group. Litter sizes remained consistent between groups, and all pups were cross-fostered to unmanipulated mouse dams to minimize the surgical effects of pump insertion.

To model hyperoxia, litters of vehicle and IUGR pups were placed in either 75% oxygen (hyperoxia) or 21% oxygen (room air) within 24 h after birth. The hyperoxia exposure was continuous for 14 days within a Plexiglass chamber, with oxygen concentration maintained by an oxygen controller and CO2 levels kept below 0.5%. The chamber temperature did not exceed 23 °C, and humidity was controlled using desiccants. Foster dams were placed with each litter in the hyperoxia chamber and rotated to room air every 24–48 h to prevent excessive oxygen toxicity to the adult animals. After 14 days, the litters were moved to room air until day of life 28 and continued to be fostered until weaning at 21 days. To establish a model of both IUGR and hyperoxia, the procedures described for the individual models were combined.

Peripheral nerve injury models

To demonstrate the value of the multivariate pipeline on an original study, 43 male B6 mice, 8 to 10 weeks old (20 g), were obtained from The Jackson Laboratory (Bar Harbor, ME, USA) and were group-housed. Male mice were used due to their larger size, thereby having easier vascular access.

There were three groups: 17 animals in the negative control group received no treatment. 12 animals in the experimental group received only nerve damage (neurorrhaphy) i.e. a complete nerve transection of the femoral and sciatic nerves with re-coaptation. 14 animals in the second experimental group received a total hind-limb transplant. Animals receiving a procedure received only one procedure on their left hind limb.

The motivation for assessing these three groups was to establish a gradient of increasing neuromuscular damage. In doing so, the goal was to characterize how spatio-temporal gait parameters were altered accordingly. Thereby, investigating how musculoskeletal damage, in addition to nerve injury, alters the statistical characterization compared to just the contribution of nerve injury alone. All experimental procedures were conducted according to an IACUC-approved protocol and were conducted in accordance with the National Research Council’s Guide for the Care and Use of Laboratory Animals. Measures taken to minimize suffering are included in the supplemental material.

Mouse hind-limb transplant model and nerve transection model

The murine hind-limb transplantation was performed using the surgical technique modified from the one previously described by our lab^28,32. Briefly, it involved a total hind-limb transplant. This included reconnection of the sciatic nerve and the femoral neurovascular bundle. It also included connection of the donor femur with the recipients via an intermedullary rod. The experimental details are described further in the supplemental material.

While the total hind limb transplant represented nerve, muscle, and bone injury, a model of sciatic and femoral nerve transection and reconnection were used to represent just nerve injury. Both models involve the transection and reconnection of the femoral and sciatic nerves. Thereby providing a basis for comparing the effect of nerve injury on its own and then alongside the addition of musculoskeletal trauma. The experimental details are described further in the supplemental material.

Developmental model

Gait data from younger vs. older healthy animals

For additional validation and to evaluate the modeling approach’s sensitivity, all healthy individual animals were also grouped into a younger group (83 to 195 days) and an older group (203 to 243 days) and multivariately scored. The multivariate scores were plotted and compared for their statistical separation.

Control model

Gait data from randomly chosen healthy animals

To further validate that any results aren’t due to the multivariate approach modeling noise or some phenomena other than the disease / injury of interest all healthy individual animals were randomly assorted into two groups and multivariately scored. The multivariate scores were plotted and compared for their statistical separation.

Data collection

Digigait procedure

After the respective procedures required for each experimental group, the animals were allowed to recover and reacclimate for two weeks before beginning data collection on the treadmill system. The mice were kept in an animal holding room and acclimated in the Behavioral Phenotyping Core before experiments. Gait was measured using the DigiGait™ Imaging System (Mouse Specifics Inc.) at three different speeds (10, 17, and 24 cm/s) and collected about every two weeks for about nine months. Footprints from a 3–4 s video clip were analyzed for each speed using Digigait™ Analysis version 15. We used the software to quantify 30 + gait indices. Multivariate gait analysis was performed at the conclusion on all data in sum.

Statistical analysis

Dimensionality reduction

All analysis was conducted in MATLAB. Exploratory analysis to reduce and identify the primary dimensions responsible for describing rodent gait was conducted via feature selection and factor analysis techniques. Feature selection was conducted using two contrasting approaches: (a) a traditional univariate analysis with Bonferroni correction and (b) a multivariate, forward sequential feature selection with cross-validation³⁵.

Feature selection

In this study we implement a simple filter by applying univariate criteria separately on each feature with Bonferroni correction. This was done as a baseline to replicate typical (i.e. non-multivariate) analysis of gait performed across the field. This baseline is important for evaluating the hypothesis that multivariate characterization will identify feature sets and feature relationships that better describe gait states and will lead to more accurate classification. We also apply a multivariate, forward sequential feature selection in a wrapper fashion to find important features with the goal of minimizing misclassification error (MCE) of our learning algorithm. This was done to explore the hypothesis that multivariate characterization will reveal relationships that encode and describe the different gait phenotypes in a biologically consistent manner unlike univariate analysis; and that the revealed relationships will enable the training of a classifier model that can discriminate between gait states with higher accuracy than models trained on features identified via univariate analysis. Embedded selection was then applied during model training to further confirm the ideal feature set. During the feature selection procedure we applied 10-fold cross-validation to the training set. We ensured that the same animal was not included in both the training and test sets of each individual fold. While feature selection identified the measured parameters to use in the model it did not describe how the selected parameters may relate to each other.

Factor analysis

To learn more about the exact relationships among features, factor analysis was conducted. Understanding the exact relationships among features is important to exploring the hypotheses that said relationships encode and describe the different gait phenotypes in a biologically consistent manner; and that the revealed relationships will enable the training of a classifier model that can discriminate between gait states with higher accuracy than models trained with features identified via univariate analysis. In the factor analysis model measured variables are dependent upon a smaller number of unobserved or latent factors⁴⁶. The coefficients on these latent factors are called “loadings”. An added component to account for noise called “specific variance” is included. Average specific variance and factor loading as a function of number of latent factors was plotted to determine the number of factors that would be reasonable to assume for analysis. A loading cutoff greater than 0.6 or less than − 0.6 was then used to identify the important features within each factor grouping.

Machine learning pipeline: cross validation, model training, and accuracy calculation

Cross validation

Training and testing sets were defined by randomly picking 80% as training and 20% as testing data. 10 randomly selected training and testing sets were defined to perform 10-fold cross validation. We ensured that the same animal was not included in both the training and test sets within a respective fold.

Model training and performance evaluation

Various classifier model architectures were evaluated using the features identified from the feature selection and dimensional reduction techniques described above. Based on the feature selection results 16 features were chosen to be included in model training. The evaluated architectures included discriminant analyses, random forest, and support vector machine. Regardless of the model type, training was performed using the results of the multivariate feature selection process described above. Outputs of all models were either 0 = dysfunctional gait (surgery) or 1 = healthy gait (control). Average model accuracy, precision, recall, and F-score were measured at the conclusion of the cross-validated model training process. Models trained via multivariate feature selection were compared for their performance with a model trained via univariate feature selection to explore the hypothesis that a classifier model trained on features identified via multivariate analysis can discriminate between gait states with higher accuracy than models trained with features identified via univariate analysis.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Abbreviations

VCA

Vascularized composite allotransplantation

PCA

Principal component analysis

SFI

Sciatic function index

ALS

Amyotrophic lateral sclerosis

IACUC

Institutional animal care and use committee

MCE

Misclassification error

CDF

Cumulative distribution function

PQDA

Pseudo-quadratic discriminant analysis

Author contributions

BAN: Conceptualization, data curation, formal analysis, investigation, methodology, project administration, software, validation, writing – original draft; writing – review & editing. KMK: Conceptualization, investigation, project administration, validation, participated in research design and performance of the research. MJK: Conceptualization, data curation, investigation, methodology, participated in performance of the research and writing of the paper. writing – original draft; writing – review & editing. SH: Conceptualization, investigation, methodology, participated in research design and performance of the research. writing – review & editing. CW: Conceptualization, investigation, methodology, resources, project administration, Participated in research design and performance of the research. writing – original draft; writing – review & editing. JJW: Conceptualization, investigation, participated in research design and performance of the research. JC: Data curation, formal analysis, investigation, methodology, writing – review & editing. MGP: Data curation, formal analysis, participated in conducting data analysis. writing – original draft; writing – review & editing. JAW: Conceptualization, funding acquisition, investigation, project administration, resources, supervision, validation, participated in research design. writing – original draft; writing – review & editing. YL: Conceptualization, investigation, methodology, project administration, supervision, validation, Participated in research design. writing – original draft; writing – review & editing. ZJZ: Conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, Participated in research design. writing – original draft; writing – review & editing.

Funding

Research reported in this publication was supported by the National Institutes of Health under Award Numbers F30DK123985, and T32GM008152 (BAN); CTC Transplant Innovation Endowment grant (110-5442000) (Zhang), DOD Department of the Army: W81XWH2110862 (Zhang), McCormick Foundation/Northwestern Memorial Hospital (Zhang and Wertheim), Julius N. Frankel Foundation via Northwestern Memorial Foundation (Zhang, Han, and Wang); American Heart Association: 20POST35210774 and the Canadian Institute for Health Research: RN409371 - 430628 (Koss); and R01LM013337 (Luo). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Funding sources had no roles in study design, collection, analysis, and interpretation of the data, in the writing of the report, nor in the decision to submit the article for publication. There was no additional external funding received for this study.

Data availability

The datasets generated during and/or analyzed during the current study are publicly available at a data repository and can be found at the following DOI (10.6084/m9.figshare.25546822).

Declarations

Competing interests

The authors declare no competing interests.