Abstract
Enhancing night-time images is crucial for improving the performance of autonomous driving systems, which rely on high-quality visual input for accurate decision-making. This study explores the application of intuitionistic fuzzy generator in combination with T-Norm and T-Conorm operators to enhance low-visibility night-time images. Unlike traditional image processing methods, intuitionistic fuzzy set (IFS) incorporates both the degree of belonging and non-belonging aspects of an image allowing for a more detailed representation of uncertainty in image enhancement. The proposed method analyzes various aggregation operators, out of which Einstein’s T-Norm, Hamacher’s T-Conorm, Weber’s T-Conorm and W-probabilistic T-Conorm operators refine contrast, suppress noise and enhance illumination while preserving critical visual details. Extensive experiments on night-time driving datasets in contrast with existing state-of-the-art methods demonstrate that the recommended approach significantly improves image clarity via standard image quality metrics like SSIM, PSNR and correlation coefficient. Additionally, a sensitivity analysis conducted to assess the robustness and stability of the IFS components and aggregation operators with respect to the parameter  in validating its effectiveness in diverse low-light conditions. The findings indicate that integrating IFS with some particular T-Norm and T-Conorm operations is an innovative strategy to improve the autonomous vehicle’s perception in low-light conditions.
in validating its effectiveness in diverse low-light conditions. The findings indicate that integrating IFS with some particular T-Norm and T-Conorm operations is an innovative strategy to improve the autonomous vehicle’s perception in low-light conditions.
Keywords: Autonomous driving systems, Intuitionistic fuzzy generator, Intuitionistic fuzzy set, T-Norm and T-Conorm operators
Subject terms: Mathematics and computing, Applied mathematics, Computational science, Computer science, Scientific data, Software
Introduction
Recently, researchers have developed ADSs as an emerging technology that diversifies into various applications, such as object detection, tracking, segmentation and identification. An ADS involves the use of various sensors, algorithms and computer technologies to navigate and operate vehicles independently, without the need for human guidance. To develop an ADS, various components, such as cameras, light and radio detection with ranging, ultrasonic sensors, global positioning systems and an odometer are involved in the perceptional phase of the system. The system uses these components to identify and categorize obstacles, road conditions, pedestrians and traffic situations. ADSs are considered innovative results with societal and environmental benefits such as improved fuel economy, reduced traffic congestion and enhanced road safety1. The rapid growth of AI, deep learning and cross-sensor processing drives ADS’s development2.
Images play a crucial role in the ADS for object recognition and segmentation, as they provide visual data that is essential for the system in making accurate decisions and predictions to reduce the traffic accidents caused by human errors3. Furthermore, the integration of advanced image processing algorithms allows the ADS to not only detect obstacles and road conditions but also to differentiate between different types of objects such as vehicles, cyclists and pedestrians. They highly rely on cameras and sensors to perceive these environmental details. LLIE is used to efficiently improve the visual data by significantly improving the brightness, contrast and overall quality of images in dimly lit environments for ADSs. Recently, researchers have been working on making ADS better at seeing things, whereas 4 described a low-light image enhancement (LLIE) method for an ADS that uses deep learning and a multi-scale Retinex-based framework that uses Drive-Retinex-net. Deep neural networks, along with Retinex theory, yield optimized contrast enhancement and noise suppression in their illumination and reflectance components, which significantly improves night-time visibility for ADS. Moreover, the authors in5 designed a task-driven image enhancement network to improve high-level image restoration quality and performance. A network with little memory and a feature identity extraction module made computations simpler while keeping important features for perceptual tasks. Certainly, the authors in6 proposed a LE-net to enhance night-time driving images. LE-net integrates data augmentation, deep learning and attention mechanisms to enhance night-time images efficiently. In7, the authors provided a modified Bright Channel Prior and adaptive gamma correction to enhance visibility with minimal computational cost. It produces the most appropriate, natural-looking images effectively with low processing time and computational cost. Moreover,8 presents an end-to-end Retinex-based illumination that uses a multi-branch architecture and a memory gate mechanism to extract and preserve features at different depth levels. Then, in9, the authors suggested a framework based on convolutional neural networks. It has two parts: one that uses infrared images captured for ADSs to extract features and the other that improves the images. In10, the authors introduced a N-LoLiGan to enhance low-light tunnel images by removing contrast distortion. N-LoLiGan utilizes N-Net which integrates, a generator with a multi-scale input layer and a convolutional block attention module to improve illumination and color retention. Meanwhile,11 designed a real-time lane detection model for ADS during low-light conditions. In this model, zero-reference deep curve estimation++ is used as a LLIE tool to improve low contrast and correct exposure dynamically by predicting a set of luminance entropy curves that iteratively adjust pixel intensities for natural enhancement. Then, the authors in12 introduced a field programmable gate array based LLIE by incorporating Retinex algorithm and coarse grained re-configurable architecture which posses a low latency rate and power efficient solution beneficiary for various real time tasks. Recently,13 presented a real-time LLIE model to improve image visibility during the night which utilizes multi-stage Retinex-based decomposition for illumination enhancement and vision transformer for enhanced feature extraction. Further, adaptive light source-aware enlightenment and illumination-aware exposure-balanced fusion modules were employed to prevent over-enhancement by balancing overall brightness and contrast of the real night-time images. Thereafter, in14 the authors developed a fine grained vehicle type detector in an ADS using EfficientNet for low-light conditions where CLAHE and gamma corrections are utilized to improve the recognition capability. Recently,15 discussed about four major AI-based enhancement techniques: de-blurring, LLIE, de-raining, and dehazing to adverse some significant weather conditions like rain, fog, haze, darkness and motion blur which impacts the performance of ADSs.
Zadeh16 introduced fuzzy logic in 1965, which is excellent at dealing with uncertainty and lack of precision in numerous real-world cases. In image processing, it plays a predominant role while dealing with the vagueness and uncertainty in boundary pixels and spatial relations within the pixel intensities, which allows multiple levels of information representation from pixel-level classification to global scene understanding17,18.
In19, the authors introduced an automated image enhancement technique using a parametric index of fuzziness as an optimization criterion in finding the best S-function for contrast enhancement. Similarly,20 proposed a fuzzy based color image enhancement technique using Gaussian membership function and global contrast intensification operator which preserves original color composition and provides a balanced enhancement. Then,21 explored the potential applications of fuzzy logic in image enhancement and quality analysis due to its superior way of handling uncertainty in image processing inspired by the human way of reasoning. Meanwhile, in22 the authors proposed an automatic ridge-let image enhancement algorithm for road crack detection using fuzzy entropy and divergence which improves the contrast with reducing noise showing a better crack visibility. Certainly, the authors in23 discussed how effectively fuzzy cardinality can be measured and applied to image processing tasks such as color histograms and dominant color detection. The three fuzzy cardinality representations are explored and utilized for computational and linguistic descriptions which making them more robust and human-like.
However, the limitations of fuzzy set theory can be seen in certain cases where a higher level of precision and accuracy is required especially in ADSs to make decisions about navigation and obstacle avoidance based on varying degrees of certainty. Atanassov24 introduced the IFS in 1983 which addresses the uncertainty in a higher perspective, allowing for a more nuanced approach to handling imprecise information. By incorporating both membership and non-membership values, IFS can provide a more comprehensive representation of uncertainty and is successfully applied in various fields, including decision-making, pattern recognition and computer vision. Intuitionistic fuzzy image processing25 emerged to handle vagueness using membership, non-membership and hesitancy functions to better model uncertainty in image analysis. This approach has shown promising results in image segmentation, edge detection and image enhancement tasks such as, in26 proposed an IFS based segmentation approach incorporated with an additional hesitation factor to represent uncertainty in threshold selection and pixel classification.
Meanwhile,27 proposed an image fusion technique using IFS to improve the clarity, contrast and luminance of fused images. It utilizes IFS based entropy as an optimizing parameter for image fusion. The authors in28 introduced an image enhancement technique based on IFS in which hyperbolization is applied to amplify contrast differences between intensity levels. This kind of enhancement improves the visibility of images with weak edges by highlighting regions of interest while preserving image details. Similarly,29,30 proposed a new IFS based enhancement and clustering algorithm by utilizing a novel IFG to enhance low contrast mammogram images and to segment their lesions and tumors. Therefore, IFS-based techniques play a crucial role in improving the quality of medical images for better diagnosis and analysis. Based on these approaches,31–34 proposed a new way of enhancing low light and contrast images and image fusion by using Yager’s generating function35 and Chaira’s generating function29 which is integrated with traditional histogram equalization and contrast limited adaptive histogram equalization techniques. In a similar way,36,37 proposed a LLIE for images and videos using a new NIFG. Recently,38 introduced a LLIE model by using IFG and Retinex theory together resulting in a superior quality of images under low-light and extremely dark environments.
Aggregation operators are essential mathematical tools used to combine multiple input values into a single representative output, particularly in the presence of uncertain, imprecise and contradictory information. In the context of FS and decision-making, aggregation operations like T-Norms and T-Conorms are important because they help combine evaluations from different criteria and options into one overall score. In recent years, various types of aggregation operators have been introduced, such as those in39,40, which establish Aczel–Alsina power aggregation operators in the q-rung Orthopair fuzzy environment for decision-making problems involving complex-valued data, including dam construction site selection and stock market analysis. Similarly,41,42 established power aggregation and Dombi’s T-Norm and T-Conorm operators through the intuitionistic fuzzy rough sets for Dublin’s bike-sharing system and solar cell evaluation to handle uncertainty and imprecision better in the decision making environment. On the other hand, the authors in43,44 represented a novel multi-criteria decision-making framework for analyzing tuberculosis and Zika virus risk factors using Einstein and power aggregation operators in both arithmetic and geometric perspective for type-2 fuzzy sets and its extensions.
Due to their flexibility in integrating information and adaptability to various fuzzy environments, aggregation operators allow more robustness in the modeling of real-world complexities. Even in image processing,45,46 has introduced a medical image enhancement technique for CT scans, X-rays and pathological images in a type-2 fuzzy using the Hamacher’s T-Conorm aggregation operator. This operator combines the upper and lower membership functions of the type-2 fuzzy set, which show enhanced details and preserve important features of the image. Similar work done for MRI images in47 by using a modified type-2 fuzzy set with updating the value 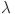 , which is the mean of the highest and lowest intensity of the input MRI image. In image enhancement, aggregation operators are used to integrate fuzzy information, which helps to improve quality of the image. It helps in combining contrast, brightness and edge information to produce an enhanced image.
, which is the mean of the highest and lowest intensity of the input MRI image. In image enhancement, aggregation operators are used to integrate fuzzy information, which helps to improve quality of the image. It helps in combining contrast, brightness and edge information to produce an enhanced image.
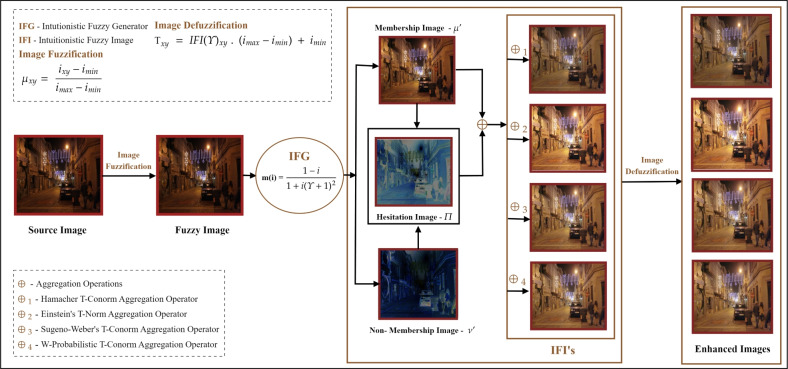
As part of the literature review, different image enhancement algorithms were discussed based on various settings, including those based on machine learning, deep learning, fuzzy logic and IFS. These algorithms can be employed in ADS, medical diagnostics, surveillance and various other applications. This current study represents a new way of enhancing night-time road images for an ADS that integrates the intuitionistic fuzzy generating function with fuzzy aggregation operators such as T-Norms and T-Conorms to suppress noise and represent the uncertainty in pixel intensities far better than traditional enhancement techniques. Figure 1 shows the overall schematic representation of the recommended study. This paper contributes for LLIE of night-time images which has listed as follows:
To introduce a new enhancement model for improving visibility in the night-time images for an ADS to detect obstacles using an intuitionistic fuzzy generator (IFG) associated with fuzzy T-Norm and T-Conorm operations.
To demonstrate its superior performance, this study is compared with some traditional and contemporary enhancement algorithms such as, HE48, SSR49, MSR50, IFI33, IVIFI31, Chithra et. al.36, Ravindar et.al.37.
To elaborate on its efficiency, the proposed method is validated through a comprehensive evaluation using standard image quality metrics like SSIM, PSNR and correlation coefficient.
The remaining paper is structured as follows: Table 1 comprises the abbreviations and acronyms utilized in this research, Section 2 presents the fundamental concepts required for this study, Section 3 outlines the proposed methodology of this research work, Section 4 includes the experimental analysis, and Section 5 provides the conclusion .
Fig. 1.
Overall framework of the proposed study.
Table 1.
List of abbreviations and acronyms.
| S.no | Abbreviation / acronyms | Full Form |
|---|---|---|
| 1. | ADSs | Autonomous driving systems |
| 2. | CLAHE | Contrast-limited adaptive histogram equalization |
| 3. | CT | Computed tomography |
| 4. | HE | Histogram equalization |
| 5. | FS | Fuzzy sets |
| 6. | IFS | Intuitionistic fuzzy sets |
| 7. | IFG | Intuitionistic fuzzy generator |
| 8. | IFI | Intuitionistic fuzzy image |
| 9. | IVIFI | Interval-valued intuitionistic fuzzy image |
| 10. | LLIE | Low-light image enhancement |
| 11. | LE-net | Light enhancement network |
| 12. | LIDAR | Light detection and ranging |
| 13. | MRI | Magenetic resonance imaging |
| 14. | MSE | Mean squared error |
| 15. | MSR | Multi-scale retinex |
| 16. | N-LoLiGan | Novel low-light unsupervised generative adversarial network |
| 17. | PSNR | Peak signal to noise ratio |
| 18. | RADAR | Radio detection and ranging |
| 19. | SOTA | State-of-the-art-techniques |
| 20. | SSIM | Structural similarity index measure |
| 21. | SSR | Single-scale retinex |
| 22. | T-Norm | Triangular Norm |
| 23. | T-Conorm | Triangular Conorm |
Fundamentals
Fuzzy Set
Let  be any universe of discourse, a fuzzy set
be any universe of discourse, a fuzzy set  is a sub-collection of elements from
is a sub-collection of elements from  represented as
represented as  )
) 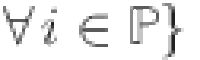 , where
, where  denotes the membership function of i in
denotes the membership function of i in  . The membership function
. The membership function  maps each element to a value in the interval [0, 1] which represents the degree of membership.
maps each element to a value in the interval [0, 1] which represents the degree of membership.
Intuitionistic fuzzy set
Let  be the universe of discourse, an IFS
be the universe of discourse, an IFS  on
on  defined as
defined as  , where
, where 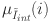 is called as the membership function and
is called as the membership function and  is called as the non-membership function of i in
is called as the non-membership function of i in  . Both
. Both 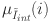 and
and  belongs to the closed interval [0,1] and
belongs to the closed interval [0,1] and 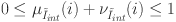 .
.
 is called the hesitation part or intuitionistic index and it is denoted by:
is called the hesitation part or intuitionistic index and it is denoted by:
| 1 |
where, 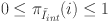 .
.
Similarly, the membership and non-membership functions of an IFS denoted as,
| 2 |
| 3 |
where, 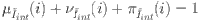 .
.
Central tendency measures
Mean, median and mode represent the central tendency measures51 of an image, which summarize pixel intensity values, providing insights into its overall brightness and contrast by determining its statistical information.
Mean represents the arithmetic average of all pixel intensities within an image. It provides a measure of the overall brightness whereas higher mean signifies a brighter image and a lower mean indicates a darker one. Median is defined as the middle pixel intensity values from an image’s surrounding neighborhood after sorting them in ascending order. It gives a better representation of typical pixel intensity in a noisy image. Mode represents the pixel intensity that appears most frequently in an image which gives insight into the most dominant or recurring intensity value to identify common color, pattern and structure. The mean, median and mode of an input image I with 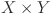 dimension can be written as,
dimension can be written as,
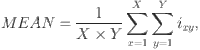 |
4 |
if 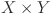 is odd,
is odd,
if 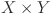 is even,
is even,
| 5 |
Triangular Norms and Conorms
T-Norms (T) and T-Conorm (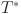 ) are operations that extend the concepts of conjunction and disjunction to the realm of fuzzy logic52. T-Norms and T-Conorms are binary operators defined on the unit interval
) are operations that extend the concepts of conjunction and disjunction to the realm of fuzzy logic52. T-Norms and T-Conorms are binary operators defined on the unit interval 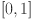 , which are functions
, which are functions 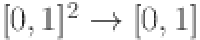 that satisfy commutativity, associativity, monotonicity and possess an identity element.
that satisfy commutativity, associativity, monotonicity and possess an identity element.
Let
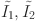 be two fuzzy sets, then
be two fuzzy sets, then  ;
;  .
.Let
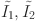 and
and  be three fuzzy sets, then
be three fuzzy sets, then  ;
; 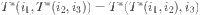 .
.If
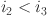 , then
, then 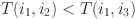 ;
; 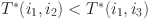 .
.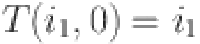 ;
;  .
.

 ,
, 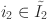 ,
,  .
.
There are several T-Norm and T-Conorm operations in the literature proposed by Yager53, Dombi54, Weber55, Hamacher56 and Wang57.
Yager53 suggested the most demanding and the least interchangeable operations via T-Norm and T-Conorm as  and
and 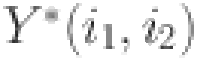 follows.
follows.
| 6 |
| 7 |
Dombi54 has defined the a general class of fuzzy connectives on the basis of the connection between conjunctive and disjunctive to measure the fuzziness using T-Norm 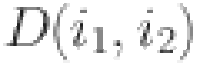 and T-Conorm
and T-Conorm 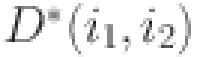 as,
as,
| 8 |
| 9 |
Weber55 suggested a continuous T-Norm and T-Conorm fuzzy operation as follows
| 10 |
| 11 |
Hamacher56 developed a parameterized T-Norm 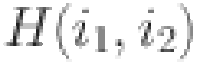 along with its dual T-Conorm
along with its dual T-Conorm 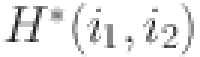 can be denoted as follows,
can be denoted as follows,
| 12 |
| 13 |
To inspect any two membership function among IFSs, Wang57 introduced aggregation operators for Einstein T-Norms and T-Conorms given by  and
and  ,
,
| 14 |
| 15 |
Proposed methodology
A new way of operations introduced on images generated via intuitionistic fuzzy generating functions aggregated based on T-Norm and T-Conorm operators. This process involves (i) fuzzification, (ii) implementation of IFG’s followed by (iii) T-Norm and T-Conorm operations and (iv) estimation of 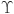 and finally (v) defuzzification to obtain the resultant enhanced images. The overall workflow of the proposed methodology is illustrated in Figure 2, which presents a structured flowchart depicting each step involved in the implementation process.
and finally (v) defuzzification to obtain the resultant enhanced images. The overall workflow of the proposed methodology is illustrated in Figure 2, which presents a structured flowchart depicting each step involved in the implementation process.
Fig. 2.
Flowchart of the proposed study.
Fuzzy image
The images are initially fuzzified using the normalization process which can also be determined as fuzzification whereas the domain of pixel intensities changes from [0,255] to [0,1].
The FI can be formulated in the 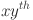 position as,
position as,
| 16 |
where 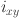 is the respective pixel level values of the original images,
is the respective pixel level values of the original images,  and
and 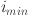 denote the uppermost and lowermost pixel intensity values found in image I.
denote the uppermost and lowermost pixel intensity values found in image I.
Intuitionistic fuzzy generator36
On defining an IFG function for FS’s and IFSs. Any function  is an IFG
is an IFG
| 17 |
For every IFG  , there exist a continuous function h such that
, there exist a continuous function h such that 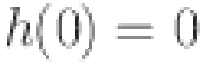 and their fuzzy complementary function can be written as,
and their fuzzy complementary function can be written as,
| 18 |
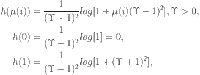 |
19 |
Considering 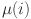 as i for simplicity,
as i for simplicity,
| 20 |
The inverse function can be written as,
| 21 |
from (18), the inverse function (21) can be implemented as follows:
| 22 |
substitute (22) in (21) we get the IFG as,
| 23 |
From (17), the membership function  can be written as,
can be written as,
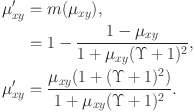 |
24 |
From (23), the non-membership function 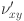 can be written as,
can be written as,
 |
25 |
Substitute (24) and (25) in (1), the hesitancy function 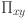 can be written as follows,
can be written as follows,
| 26 |
| 27 |
T-Norm and T-Conorm aggregation
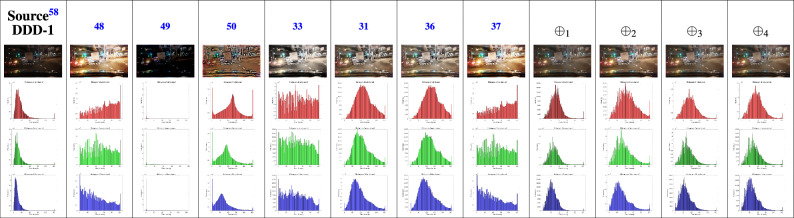
Section 2.4 discusses about different T-Norm and T-Conorm operators from the literature. To find the efficient operator for this analysis of the night-time driving images, they are evaluated by the some T-Norm and T-Conorm operators. Two images from58 are represented in the Figure 3, out of 10 existing operators, Hamacher’s T-Conorm 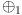 , Einstein’s T-Norm
, Einstein’s T-Norm 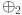 , Weber’s T-Conorm
, Weber’s T-Conorm 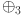 yields superior results in their enhancement.
yields superior results in their enhancement.
Fig. 3.
Images from BDD100k driving data set58 tested among various T-norm and T-conorm operators.
From (13), the Hamacher’s T-Conorm aggregation 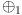 between
between 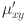 and
and 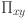 can be written as,
can be written as,
| 28 |
| 29 |
From (14), the Einstein’s T-Norm aggregation 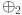 between
between 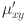 and
and 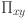 can be written as,
can be written as,
| 30 |
| 31 |
From (11), the Weber’s T-Conorm aggregation 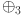 between
between 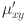 and
and 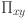 can be written as,
can be written as,
| 32 |
| 33 |
Weighted probabilistic T-Conorm operator
The W-Probabilistic T-Conorm aggregation 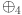 between
between 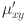 and
and 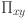 can be written as,
can be written as,
| 34 |
Estimation of ’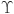 ’
’
The corresponding image’s mode value, which is to be processed, is determined to be the parameter value 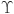 since the mode finds the dominant pixel that occurs in an image and determines its intensity. This current study considers
since the mode finds the dominant pixel that occurs in an image and determines its intensity. This current study considers 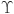 between [0, 1]. Therefore, the fuzzy image’s (16) mode is calculated and applied in the operations and generating functions. The proposed study initiates flexibility in choosing the
between [0, 1]. Therefore, the fuzzy image’s (16) mode is calculated and applied in the operations and generating functions. The proposed study initiates flexibility in choosing the 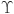 value for every image to be enhanced.
value for every image to be enhanced.
Defuzzification
Defuzzification is the process of transforming a fuzzy set, which represents uncertain or imprecise information, into a desired output. In image processing, it involves converting fuzzy values representing degrees of membership for different elements within an image into precise values. Fuzzy logic systems often handle images by addressing uncertainty and ambiguity through a variety of operations. Defuzzification translates the resulting fuzzy values into a well-defined output, such as specific pixel intensities tailored to the image’s context, after applying these fuzzy operations.
From (16), each pixel in the image T defuzzified as,
| 35 |
Experimental analysis
The experiments were executed using MATLAB (R2023a) with the Image Processing Toolbox. The machine used for the setup is equipped with a Ryzen 5 7520U processor (AMD technology) and Radeon graphics, operating at 2.80 GHz. It runs on Microsoft Windows 11 Home and includes 512GB of SSD storage and 16GB of RAM.
The BDD100K58 driving image data set is utilized for the entire analysis part of this work. Nearly thousands images were evaluated for this study to show how efficient the proposed study performs apart from other SOTA. 20 images were represented as DDD - 1, 2, ..., 20 in the Fig. 4. The results are primarily processed by performing the derived aggregation operations 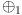 ,
, 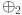 ,
, 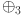 and
and 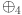 . Each operator yields enhanced image and the resultant 4 images generated by the suggested operators is compared with existing methods in the literature such as,33,34,36,37,48–50. Figures 5, 6, 7, & 8 represents the enhanced version of the images DDD −1, 2, ..., 20 by the Hamacher’s T-Conorm
. Each operator yields enhanced image and the resultant 4 images generated by the suggested operators is compared with existing methods in the literature such as,33,34,36,37,48–50. Figures 5, 6, 7, & 8 represents the enhanced version of the images DDD −1, 2, ..., 20 by the Hamacher’s T-Conorm 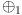 , Einstein’s T-Norm
, Einstein’s T-Norm 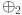 , Weber’s T-Conorm
, Weber’s T-Conorm 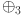 and W-Probabilistic T-Conorm
and W-Probabilistic T-Conorm 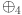 aggregation operators. To evaluate the efficiency of the proposed study, the standard image quality metrics such as SSIM, PSNR and correlation coefficient are utilized here and compared with other existing methods and illustrated in the Table 2.
aggregation operators. To evaluate the efficiency of the proposed study, the standard image quality metrics such as SSIM, PSNR and correlation coefficient are utilized here and compared with other existing methods and illustrated in the Table 2.
Fig. 4.
Source images from BDD100k driving data set.
Fig. 5.
Enhanced images from BDD100k driving data set.
Fig. 6.
Enhanced images from BDD100k driving data set.
Fig. 7.
Enhanced images from BDD100k driving data set.
Fig. 8.
Enhanced images from BDD100k driving data set.
Table 2.
Comparison of SSIM, PSNR and Correlation with proposed and SOTA methods.
| Methods | SSIM 
|
PSNR 
|
Correlation 
|
|---|---|---|---|
| 48 | 0.2228 | 7.0693 | 0.7430 |
| 49 | 0.3088 | 19.8173 | 0.7641 |
| 50 | 0.2416 | 8.7158 | 0.3856 |
| 33 | 0.3090 | 8.2332 | 0.8461 |
| 31 | 0.3244 | 11.0732 | 0.7583 |
| 36 | 0.2699 | 8.8917 | 0.8020 |
| 37 | 0.2228 | 7.0693 | 0.7429 |
 |
0.5967 | 17.8326 | 0.9492 |
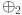 |
0.4497 | 13.2439 | 0.9049 |
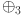 |
0.5432 | 15.9449 | 0.9347 |
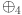 |
0.5414 | 15.8949 | 0.9341 |
’italic’ indicates the highest value.
’bolditalic’ indicates the second highest value.
’underline’ indicates the third highest value.
The texts in Bold indicates the proposed methodologies.
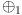 ,
, 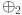 ,
, 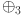 and
and 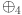 are proposed approaches
are proposed approaches
A histogram is a graphical representation that shows frequency distributions of pixel intensities in an image. It provides a visual summary of how often each intensity value occurs, helping to analyze and understand the image’s characteristics. Figure 9 represents the histograms for the source image DDD-1 along with its comparison methods, such as HE48, SSR49, MSR50, IFI33, IVIFI31, Chithra et al.36, Ravindar et al.37 and the proposed 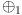 ,
, 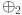 ,
, 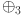 ,
, 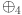 operators generated images via red, green and blue color channels. From this figure, it is visually observed that the histogram pattern of the images generated by operators was similar and amplified compared to other state-of-the-art techniques. The resultant images also present a clear view of the environment, especially at night-time.
operators generated images via red, green and blue color channels. From this figure, it is visually observed that the histogram pattern of the images generated by operators was similar and amplified compared to other state-of-the-art techniques. The resultant images also present a clear view of the environment, especially at night-time.
Fig. 9.
Histogram of image DDD-1 by proposed and state-of-the-art techniques.
Structural similarity index measure
The Structural Similarity Index Measure (SSIM) is a metric for assessing the similarity between two images. It’s specifically crafted to gauge the structural similarity, luminance and contrast details between an original image and a modified version. SSIM finds widespread application in image processing and computer vision, particularly for evaluating the effectiveness of techniques such as image and video compression, denoising and various image enhancement methods. An SSIM score close to 1 indicates high perceptual similarity, while a lower score indicates noticeable degradation.
| 36 |
where 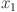 and
and 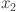 are non-negative constants.
are non-negative constants.
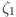 and
and 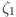 denotes the average gray levels of images I and T.
denotes the average gray levels of images I and T.
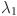 and
and 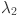 denotes the variance of I and T.
denotes the variance of I and T.
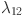 indicates the covariance of I and T respectively.
indicates the covariance of I and T respectively.
In Table 2, the average SSIM values are demonstrated for 1000 images and the proposed study is compared with existing methods such as,33,34,36,37,48–50. By the definition, the images generated by 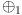 ,
, 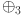 ,
, 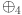 yields average SSIM values of 0.5967, 0.5432, & 0.5414 which is maximum compare to all other methods. It shows that the structural information of the images generated by the proposed study are preserved compared to other existing methods. The average SSIM values are graphically represented in Figure 11a .
yields average SSIM values of 0.5967, 0.5432, & 0.5414 which is maximum compare to all other methods. It shows that the structural information of the images generated by the proposed study are preserved compared to other existing methods. The average SSIM values are graphically represented in Figure 11a .
Fig. 11.
Graphical representation of SSIM, PSNR, Correlation Coefficient.
Peak signal-to-noise ratio
PSNR is a metric used to assess the quality of a reconstructed image by comparing it to the original. Measured in decibels (dB), PSNR is derived from the mean squared error (MSE) between corresponding pixels of the two images. A higher PSNR value indicates closer similarity to the original image, reflecting lower distortion and higher fidelity. This metric is usually applied in image processing and compression to evaluate the performance of algorithms and techniques.
| 37 |
where, MSE stands for mean squared error and implies,
Table 2 represents the average PSNR value of the images from BDD100k58 dataset compared with existing state-of-art-techniques and the proposed study. 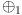 and
and 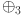 yields the second and third highest PSNR score of 17.8326 & 15.9449 where SSR49 yields the maximum value which is 19.8173. It is visually observed in the Figure 10 that images generated by SSR is too dark compared to the source image itself hence PSNR is showing high values compared to the proposed study. Figure 11bshows the graphical illustration of average PSNR values.
yields the second and third highest PSNR score of 17.8326 & 15.9449 where SSR49 yields the maximum value which is 19.8173. It is visually observed in the Figure 10 that images generated by SSR is too dark compared to the source image itself hence PSNR is showing high values compared to the proposed study. Figure 11bshows the graphical illustration of average PSNR values.
Fig. 10.
Some BD100K images via SOTA methods.
Correlation coefficient
In the field of imaging, the correlation coefficient is a statistical metric employed for evaluating the similarity between two images based on their pixel intensity levels. It gauges the intensity and direction of a linear relationship between two images. It quantifies the degree to which one image’s pixel values correspond to those of another image.
| 38 |
Unlike SSIM, correlation coefficient justifies how closely the pixel values of the enhanced image align with those of the source image. In Table 2, the average correlation coefficient of existing methodologies compared with the proposed study. It shows that the images generated by 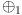 ,
, 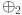 ,
, 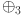 and
and 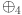 yield maximum average correlation coefficient value greater than 0.9 which denotes that the enhanced images retains the pixel intensity relationships of the source image, suggesting high-quality enhancement. The correlation coefficient values are well illustrated in the Figure 11c.
yield maximum average correlation coefficient value greater than 0.9 which denotes that the enhanced images retains the pixel intensity relationships of the source image, suggesting high-quality enhancement. The correlation coefficient values are well illustrated in the Figure 11c.
The experimental analysis were executed for the images in58 and compared with some existing methodologies, such as33,34,36,37,48–50 by means of some standard image quality metrics like SSIM, PSNR and Correlation coefficient. The proposed methods yields a superior value and the images of 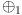 ,
, 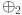 ,
, 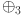 and
and 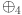 were demonstrated in the Figure 5, 6, 7 and 8. The graphical representation of the image quality metric values is shown in the Figure 11. Images generated by
were demonstrated in the Figure 5, 6, 7 and 8. The graphical representation of the image quality metric values is shown in the Figure 11. Images generated by 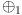 ,
, 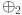 ,
, 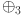 and
and 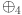 posses superior quality, unlike traditional techniques, this kind of enhancement can be more efficiently utilized by an ADS to improve the visibility of any particular environment to detect obstacles.
posses superior quality, unlike traditional techniques, this kind of enhancement can be more efficiently utilized by an ADS to improve the visibility of any particular environment to detect obstacles.
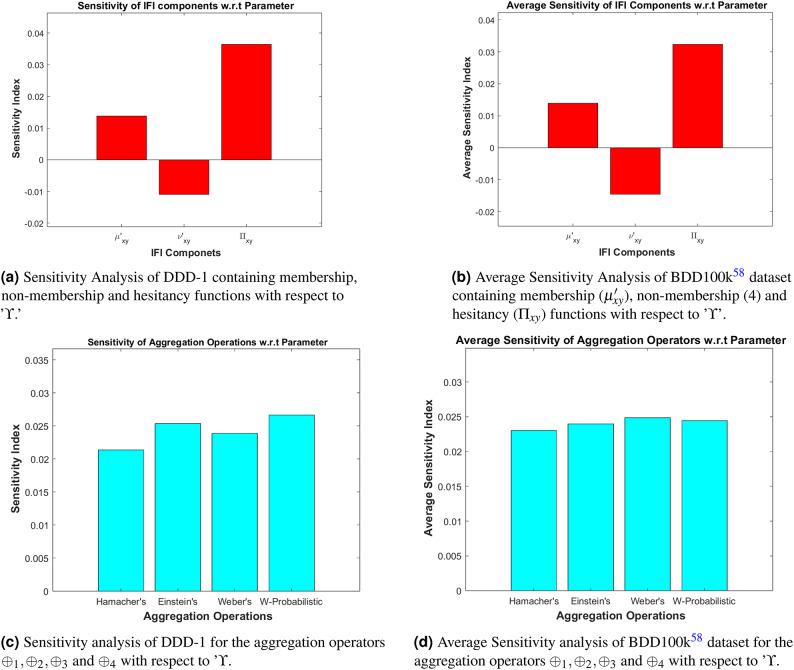
Sensitivity analysis
Sensitivity analysis59 is a technique that determines how variations in input parameters influence the output of a given model. In this enhancement model, 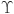 is utilized as the parameter which is associated with improving the visibility of night-time driving images58. By measuring the sensitivity index, one can assess which parameters exert the most influence on the model’s output. A higher sensitivity index indicates that small changes in the parameter lead to significant variations in the output, whereas a lower index suggests greater system stability. In this study, the sensitivity analysis is conducted to analyze the behaviour of
is utilized as the parameter which is associated with improving the visibility of night-time driving images58. By measuring the sensitivity index, one can assess which parameters exert the most influence on the model’s output. A higher sensitivity index indicates that small changes in the parameter lead to significant variations in the output, whereas a lower index suggests greater system stability. In this study, the sensitivity analysis is conducted to analyze the behaviour of 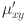 (24),
(24), 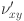 (25), and
(25), and 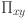 (27) employed in the fuzzy aggregation operators
(27) employed in the fuzzy aggregation operators 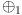 (29),
(29), 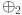 (31),
(31), 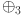 (33), and
(33), and 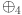 (34) concerning the parameter
(34) concerning the parameter 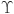 .
.
The sensitivity analysis is conducted in two ways: (i) The sensitivity index has been calculated for the DDD-1 image from Figure 4 for all the functions and operators. 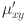 (24),
(24), 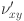 (25),
(25), 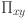 (27),
(27), 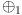 (29),
(29), 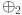 (31),
(31), 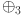 (33), and
(33), and 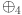 (34). (ii) The average sensitivity index has been calculated for the entire BDD100k58 dataset for all the functions and operators.
(34). (ii) The average sensitivity index has been calculated for the entire BDD100k58 dataset for all the functions and operators. 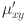 (24),
(24), 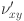 (25),
(25), 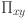 (27),
(27), 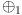 (29),
(29), 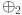 (31),
(31), 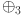 (33), and
(33), and 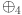 (34). The sensitivity indexes are tabulated in Tables 3 and 4 as follows:
(34). The sensitivity indexes are tabulated in Tables 3 and 4 as follows:
Table 3.
Sensitivity analysis of 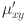 ,
, 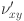 and
and 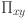 with respect to ’
with respect to ’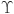 .
.
Membership (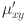 ) ) |
Non-membership (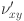 ) ) |
Hesitation (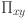 ) ) |
|
|---|---|---|---|
| Sensitivity Index | 0.0138 | − 0.0110 | 0.0365 |
| Average Sensitivity Index | 0.0139 | −0.0145 | 0.0323 |
Table 4.
Sensitivity analysis of  and
and 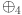 with respect to ’
with respect to ’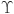 .
.
Hamacher’s 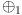
|
Einstein’s 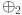
|
Webers’s 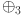
|
W-Probablistic 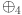
|
|
|---|---|---|---|---|
| Sensitivity Index | 0.0214 | 0.0254 | 0.0239 | 0.0138 |
| Average Sensitivity index | 0.0230 | 0.0240 | 0.0249 | 0.0244 |
In Fig. 12, the overall sensitivity analysis is graphically presented, showcasing the responsiveness of various fuzzy components and aggregation operators to changes in the scalar parameter 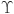 . The sensitivity index calculated reveals the greater robustness and stability of the proposed methodology.
. The sensitivity index calculated reveals the greater robustness and stability of the proposed methodology.
Fig. 12.
Graphical representation of the sensitivity analysis.
Limitations of the proposed methodology
The experimental validation is largely limited to specific night-time driving datasets, which may not capture the full variability encountered in real-life autonomous driving conditions in which it’s generalizability remains uncertain.
The method relies on an IFG reformed by a specific increasing function from the Sugeno class. However, the behavior and enhancement performance of the model are sensitive with respect to the IFG involved.
Utilizing inappropriate increasing or decreasing functions may lead to inconsistent results while computing the membership and non-membership values of the intuitionistic fuzzy image (IFI), affecting the stability and adaptability of the system across different visual inputs.
This method purely works on image enhancement perspective and does not account for multi-modal sensor inputs like LIDAR, RADAR and thermal imaging.
Conclusion
This study demonstrates the effectiveness of intuitionistic fuzzy generating functions combined with T-Norm and T-Conorm operators for enhancing night-time images in autonomous driving systems. By leveraging the ability of intuitionistic fuzzy logic to represent uncertainty more comprehensively, the proposed approach achieves significant improvements in contrast enhancement, noise suppression and illumination correction. Experimental results on night-time driving datasets confirm that our method outperforms conventional enhancement techniques by preserving critical visual details and improving overall image clarity. These findings suggest that integrating intuitionistic fuzzy logic with T-Norm and T-Conorm operations is a significant approach for enhancing autonomous vehicle perception in low-light environments, ultimately contributing to safer and more reliable night-time driving. Further, this method can be embedded into vision modules of autonomous vehicles to enhance image clarity during night-time and low-visibility conditions thereby improving the performance of downstream tasks such as pedestrian tracking, obstacle and lane detection. Beyond ADSs, this approach can be applied to surveillance and security networks to monitor dim-light environments. Future research may focus on real-time implementation like multi-modal sensor fusion and further optimization to enhance its applicability in autonomous navigation systems via hyper-parameter tuning.
Author contributions
M.S. Ragavendirane—Conceptualization, Writing—Original draft preparation, Methodology S. Dhanasekar—Resources, Supervision, Investigation, Validation, Visualization
Funding
Open access funding provided by Vellore Institute of Technology.
Data availability
The data utilized for this study are available at [https://doi.org/10.48550/arXiv.1805.04687]
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Rosenzweig, J. & Bartl, M. A review and analysis of literature on autonomous driving. E-Journal Making-of Innovation 1–57 (2015).
- 2.Zhao, J. et al. Autonomous driving system: A comprehensive survey. Exp. Syst. Appl.242, 122836 (2024). [Google Scholar]
- 3.Barabas, I., Todoruţ, A., Cordoş, N. & Molea, A. Current challenges in autonomous driving. In IOP confer. Series: Mater. Sci. Eng.252, 012096 (2017). [Google Scholar]
- 4.Pham, L.H., Tran, D. N.-N. & Jeon, J.W. Low-light image enhancement for autonomous driving systems using driveretinex-net. In 2020 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia), 1–5 (2020).
- 5.Lee, Y., Jeon, J., Ko, Y., Jeon, B. & Jeon, M. Task-driven deep image enhancement network for autonomous driving in bad weather. In 2021 IEEE International Conference on Robotics and Automation (ICRA), 13746–13753 (2021).
- 6.Li, G., Yang, Y., Qu, X., Cao, D. & Li, K. A deep learning based image enhancement approach for autonomous driving at night. Knowledge-Based Syst.213, 106617 (2021). [Google Scholar]
- 7.Mandal, G., Bhattacharya, D. & De, P. Real-time fast low-light vision enhancement for driver during driving at night. J. Amb. Intell. Human. Comput.13, 789–798 (2022). [Google Scholar]
- 8.Zhao, R., Han, Y. & Zhao, J. End-to-end retinex-based illumination attention low-light enhancement network for autonomous driving at night. Comput. Intell. Neurosci.2022, 4942420 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhong, S., Fu, L. & Zhang, F. Infrared image enhancement using convolutional neural networks for auto-driving. Appl. Sci.13, 12581 (2023). [Google Scholar]
- 10.Wang, J. et al. N-loligan: Unsupervised low-light enhancement gan with an n-net for low-light tunnel images. Digit. Signal Process.143, 104259 (2023). [Google Scholar]
- 11.Liu, Y., Wang, Y. & Li, Q. Lane detection based on real-time semantic segmentation for end-to-end autonomous driving under low-light conditions. Digit. Signal Process.155, 104752 (2024). [Google Scholar]
- 12.Munaf, S., Bharathi, A. & Jayanthi, A. Fpga-based low-light image enhancement using retinex algorithm and coarse-grained reconfigurable architecture. Sci. Reports14, 28770 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mahdizadeh, M., Chen, S. & Ye, P. Illuminating the night: A light source-aware and exposure-balanced low-light enhancement approach for real nighttime scenes. Digital Signal Processing 104999 (2025).
- 14.Ruan, G. et al. Fine-grained vehicle recognition under low light conditions using efficientnet and image enhancement on lidar point cloud data. Sci. Reports15, 4691 (2025). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mo, T., Zheng, S., Chan, W.-Y. & Yang, R. Review of ai image enhancement techniques for in-vehicle vision systems under adverse weather conditions. World Electric Vehicle J.16, 72 (2025). [Google Scholar]
- 16.Zadeh, L.A. Fuzzy sets. Information and Control (1965).
- 17.Bloch, I. Fuzzy sets for image processing and understanding. Fuzzy Sets syst.281, 280–291 (2015). [Google Scholar]
- 18.Haußecker, H. & Tizhoosh, H. R. Fuzzy image processing. In Computer vision and applications 541–576 (Elsevier, 2000). [Google Scholar]
- 19.Vlachos, I. K. & Sergiadis, G. D. Parametric indices of fuzziness for automated image enhancement. Fuzzy Sets Syst.157, 1126–1138 (2006). [Google Scholar]
- 20.Hanmandlu, M. & Jha, D. An optimal fuzzy system for color image enhancement. IEEE Trans. Image Process.15, 2956–2966 (2006). [DOI] [PubMed] [Google Scholar]
- 21.Saenko, A., Polte, G. & Musalimov, V. Image enhancement and image quality analysis using fuzzy logic techniques. In 2012 9th International Conference on Communications (COMM), 95–98 (IEEE, 2012).
- 22.Zhang, D., Qu, S., He, L. & Shi, S. Automatic ridgelet image enhancement algorithm for road crack image based on fuzzy entropy and fuzzy divergence. Opt. Lasers Eng.47, 1216–1225 (2009). [Google Scholar]
- 23.Chamorro-Martínez, J., Sánchez, D., Soto-Hidalgo, J. M. & Martínez-Jiménez, P. M. A discussion on fuzzy cardinality and quantification. some applications in image processing. Fuzzy Sets and Systems257, 85–101 (2014).
- 24.Atanassov, K. T. Intuitionistic fuzzy sets. Fuzzy Sets and Syst.20, 87–96 (1986). [Google Scholar]
- 25.Vlachos, I.K. & Sergiadis, G.D. Intuitionistic fuzzy image processing. Soft Computing in Image Processing: Recent Advances 383–414 (2007).
- 26.Melo-Pinto, P. et al. Image segmentation using atanassov’s intuitionistic fuzzy sets. Exp. Syst. Appl.40, 15–26 (2013). [Google Scholar]
- 27.Balasubramaniam, P. & Ananthi, V. Image fusion using intuitionistic fuzzy sets. Inform. Fusion20, 21–30 (2014). [Google Scholar]
- 28.Deng, H., Sun, X., Liu, M., Ye, C. & Zhou, X. Image enhancement based on intuitionistic fuzzy sets theory. IET Image Process.10, 701–709 (2016). [Google Scholar]
- 29.Chaira, T. Intuitionistic fuzzy approach for enhancement of low contrast mammogram images. Int. J. Imag. Syst. Technol.30, 1162–1172 (2020). [Google Scholar]
- 30.Chaira, T. An intuitionistic fuzzy clustering approach for detection of abnormal regions in mammogram images. J. Digit. Imag.34, 428–439 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jebadass, J. R. & Balasubramaniam, P. Color image enhancement technique based on interval-valued intuitionistic fuzzy set. Inform. Sci.653, 119811 (2024). [Google Scholar]
- 32.Jebadass, J. R. & Balasubramaniam, P. Low contrast enhancement technique for color images using interval-valued intuitionistic fuzzy sets with contrast limited adaptive histogram equalization. Soft Comput.26, 4949–4960 (2022). [Google Scholar]
- 33.Jebadass, J. R. & Balasubramaniam, P. Low light enhancement algorithm for color images using intuitionistic fuzzy sets with histogram equalization. Multimed. Tools Appl.81, 8093–8106 (2022). [Google Scholar]
- 34.Jebadass, J. R. & Balasubramaniam, P. Interval type-2 fuzzy set based block-sbu for image fusion technique. Appl. Soft Comput.143, 110434 (2023). [Google Scholar]
- 35.Yager, R. R. On the measure of fuzziness and negation. ii. lattices. Inform. Control44, 236–260 (1980). [Google Scholar]
- 36.Selvam, C., Jebadass, R. J. J., Sundaram, D. & Shanmugam, L. A novel intuitionistic fuzzy generator for low-contrast color image enhancement technique. Inform. Fusion108, 102365 (2024). [Google Scholar]
- 37.Chinnappan, R.R. & Sundaram, D. A low-light video enhancement approach using novel intuitionistic fuzzy generator. The European Physical Journal Special Topics 1–13 (2024).
- 38.Ragavendirane, M. & Dhanasekar, S. Low-light image enhancement via new intuitionistic fuzzy generator-based retinex approach. IEEE Access (2025).
- 39.Khan, M. R., Ullah, K., Karamti, H., Khan, Q. & Mahmood, T. Multi-attribute group decision-making based on q-rung orthopair fuzzy aczel-alsina power aggregation operators. Eng. Appl. Artific. Intell.126, 106629 (2023). [Google Scholar]
- 40.Khan, M. R. et al. Some aczel-alsina power aggregation operators based on complex q-rung orthopair fuzzy set and their application in multi-attribute group decision-making. IEEE Access11, 115110–115125 (2023). [Google Scholar]
- 41.Khan, M. R., Ullah, K., Khan, Q. & Pamucar, D. Intuitionistic fuzzy dombi aggregation information involving lower and upper approximations. Comput. Appl. Math.44, 1–45 (2025). [Google Scholar]
- 42.Khan, M. R. et al. Evaluating safety in dublin’s bike-sharing system using the concept of intuitionistic fuzzy rough power aggregation operators. Measurement253, 117553 (2025). [Google Scholar]
- 43.Sheela Rani, M. & Dhanasekar, S. Application of type-2 heptagonal fuzzy sets with multiple operators in multi-criteria decision-making for identifying risk factors of zika virus. BMC Infect. Diseas.25, 450 (2025). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sheela, R. M. & Dhanasekar, S. Analyzing risk factors of tuberculosis using type-2 interval-valued trapezoidal fuzzy numbers with einstein aggregation operators extended to mcdm. Heliyon10, e35997 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chaira, T. An improved medical image enhancement scheme using type ii fuzzy set. Appl. Soft Comput.25, 293–308 (2014). [Google Scholar]
- 46.Chandra, N. & Bhardwaj, A. Medical image enhancement using modified type ii fuzzy membership function generated by hamacher t-conorm. Soft Computing 1–22 (2024).
- 47.Wadhwa, A. & Bhardwaj, A. Enhancement of mri images using modified type-2 fuzzy set. Multimedia Tools and Applications 1–16 (2024).
- 48.Krutsch, R. & Tenorio, D. Histogram equalization. Freescale Semiconductor, Document Number AN4318, Application Note30 (2011).
- 49.Choi, D.H., Jang, I.H., Kim, M.H. & Kim, N.C. Color image enhancement using single-scale retinex based on an improved image formation model. In 2008 16th European Signal Processing Conference, 1–5 (IEEE, 2008).
- 50.Petro, A.B., Sbert, C. & Morel, J.-M. Multiscale retinex. Image processing on line 71–88 (2014).
- 51.Khorana, A. et al. Choosing the appropriate measure of central tendency: Mean, median, or mode?. Knee Surgery, Sports Traumatol., Arthroscopy31, 12–15 (2023). [DOI] [PubMed] [Google Scholar]
- 52.Klement, E. P., Mesiar, R. & Pap, E. Triangular norms: Basic notions and properties. In Logical, Algebraic, Analytic and Probabilistic Aspects of Triangular Norms 17–60 (Elsevier, 2005). [Google Scholar]
- 53.Yager, R. R. On a general class of fuzzy connectives. Fuzzy Sets Syst.4, 235–242 (1980). [Google Scholar]
- 54.Dombi, J. A general class of fuzzy operators, the demorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst.8, 149–163 (1982). [Google Scholar]
- 55.Weber, S. Two integrals and some modified versions–critical remarks. Fuzzy Sets and Syst.20, 97–105 (1986). [Google Scholar]
- 56.Oussalah, M. On the use of hamacher’s t-norms family for information aggregation. Inform. Sci.153, 107–154 (2003). [Google Scholar]
- 57.Wang, W. & Liu, X. Intuitionistic fuzzy information aggregation using Einstein operations. IEEE Trans. Fuzzy Syst.20, 923–938 (2012). [Google Scholar]
- 58.Yu, F. et al. Bdd100k: A diverse driving dataset for heterogeneous multitask learning (2020). https://arxiv.org/abs/1805.04687. 1805.04687.
- 59.Karthik, A. & Ghosh, M. Modeling of covid-19 with vaccination and optimal control. The European Physical Journal Special Topics 1–12 (2024).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data utilized for this study are available at [https://doi.org/10.48550/arXiv.1805.04687]