On the calculation of absolute macromolecular binding free energies

Abstract

The standard framework for calculating the absolute binding free energy of a macromolecular association reaction A + B → AB with an association constant K_AB is to equate chemical potentials of the species on the left- and right-hand sides of this reaction and evaluate the chemical potentials from theory. This theory involves (usually hidden) assumptions about what constitutes the bound species, AB, and where the contribution of the solvent appears. We present here an alternative derivation that can be traced back to Bjerrum, in which the expectation value of K_AB is obtained directly through the statistical mechanical method of evaluating its ensemble (Boltzmann-weighted) average. The generalized Bjerrum approach more clearly delineates: (i) the different contributions to binding; (ii) the origin of the much-discussed and somewhat controversial association entropy term; and (iii) where the solvent contribution appears. This approach also allows approximations required for practical evaluation of the binding constant in complex macromolecular systems, to be introduced in a well defined way. We provide an example, with application to test cases that illustrate a range of binding behavior.

The importance to biochemistry of being able to calculate absolute and relative binding affinities from the structures of macromolecular complexes is clear. A large body of literature on the theory, practice, and application exists. See, for example, refs. 1–8 for recent papers that discuss or review the theory and methods. Nevertheless, there is still controversy over some basic theoretical issues. There is agreement that association is accompanied by a loss of translational and rotational (association) entropy but disagreement over the magnitude, whether it varies significantly from system to system or can be approximated by a single value, what theoretical model should be used to estimate it, and how to include solvent effects. This controversy has motivated recent experimental studies using tethered dimerization to estimate translational entropy loss (9, 10). Accurate accounting of the association term is essential for the calculation of absolute binding free energies. Alternatively, if it could be reliably established by experiment or theory that this term is constant for some set of binding reactions, this would greatly simplify the calculation of relative binding free energies for those systems.

The traditional theoretical framework for calculating the absolute binding free energy for the reaction A + B → AB is to equate the chemical potentials of the species on the left- and right-hand sides of this reaction and to evaluate the chemical potentials of the three species, A, B, and AB by using some theory, as described in Hill's classic statistical mechanics treatment of association (11). Recent work describes the extension of this approach to macromolecular association and to ligand–membrane association, along with a detailed discussion of other theoretical issues (1, 2). However, the chemical potential approach is not the only way to approach the problem. We present here an alternative derivation, which can be traced back to Bjerrum, in which the expectation value of the association constant K_AB is obtained directly from ensemble average quantities. Our approach also, like several previous treatments of binding (see, e.g., refs. 1, 12, and 13) emphasizes the advantage of treating the interaction between associating partners by using a potential of mean force. Our goals are: First, to provide a straightforward but rigorous theoretical treatment of binding free energy. Second, to clarify, in response to recent work, the origin of the association entropy term, how it may be calculated or measured, and what the role of the solvent is in this term. Third, to use the theoretical framework to guide the approximations one must inevitably introduce for a computational tractable method for macromolecular association in solvent.

Theory

The “Bjerrum” approach to calculating the absolute binding free energy of a reaction A + B → AB is simply to calculate the expectation value of the equilibrium constant K_AB = [AB]/[A][B] directly from the usual statistical mechanical expression for evaluating the required observables (in this case concentrations) from Boltzmann-weighted averages. Consider one molecule each of A and B in a large volume V of solvent. The same equilibrium constant will be obtained from this system averaged over a sufficiently long time as from a large number of A and B molecules at equilibrium. Without loss of generality, we define the coordinate system by placing A in a fixed orientation at the origin. A particular configuration of this system is then specified by the N solvent atom coordinates, r_V = (r_V1, r_V2 … r_VN), the position and orientation coordinates of B with respect to A, r, and Ω, respectively, and the internal coordinates of A and B and q_A and q_B, respectively. The orientation coordinate is Ω = {φ, ψ, χ), where φ and ψ define an axis in polar coordinates, and χ is the rotation about that axis. Some subset of all possible configurations corresponds to the associated state (AB is present); the rest correspond to the dissociated state (A and B present). The ratio of average concentrations is

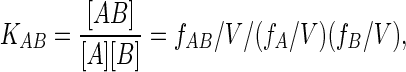where f_i is the fraction of the configurations in which the species i = A, B or AB is present. To evaluate f_i, we define a function H(r, Ω), which is 1 for those positions/orientations of B where it forms a complex with A, and which is 0 otherwise. f_i may now be evaluated from ensemble averages of H(r, Ω):

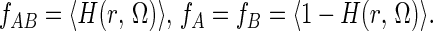Now A and B interact with some potential of mean force (pmf), which depends on their relative position and orientation and which is defined as

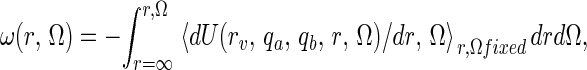where U is potential energy of the whole system. The pmf ω(r, Ω) is the reversible thermodynamic work necessary to bring A and B from a large separation (where ω = 0 by definition) to some separation/orientation (r, Ω). It is an exact quantity obtained from the integration of the Boltzmann-weighted solvent and internal coordinate averaged force between A and B (14). Clearly, the region where ω is significantly negative (<−1 kT) provides one intuitively appealing criterion for defining the bound state, H(r, Ω) = 1. This point is discussed below. In the dilute limit (V → ∞), clearly f_A, f_B → 1, f_AB → 0, but the product f_ABV tends to a limit, equal to the binding constant, of

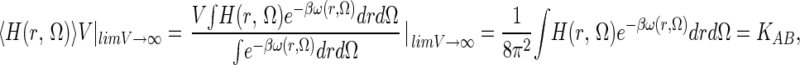where over most of the integration volume ω = 0, the integrand of the denominator is unity, and its integral is just B's rotation/translation (R/T) phase space volume 8π²V. The binding constant in Eq. 4 can be written K_AB = V_BPV/8π², which defines a Boltzmann-weighted phase volume (BPV) as V_BPV = ∫He^−βωdrdΩ with units (length⋅radians)³. K_AB has the units of volume in which concentrations are expressed (usually 1 liter/mol = 1,660 ų/molecule), setting the units for integration length of dr (11.84 Å in this example). It is customary to define the absolute binding free energy as

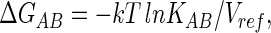where it is understood that this refers to the free energy of binding B from a reference concentration 1/V_ref, although because V_ref is usually omitted in the literature, the choice of reference state must be inferred from the units used for K_AB. Differentiation of Eqs. 4 and 5 by T gives the enthalpy and entropy contributions,

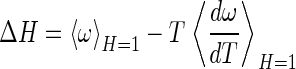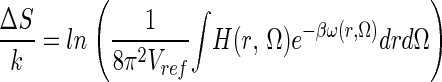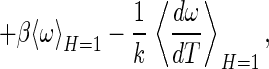where

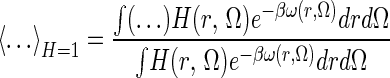indicates an ensemble average over the bound state phase volume. In the bound state, the probability of a particular position/orientation of B is p(r, Ω) = exp(−βω(r, Ω))/V_BPV, whereas in the unbound state, the probability is 1/(8π²V_ref), thus the loss of R/T entropy on binding may be formally defined, by using S = −k ∫p ln p, as

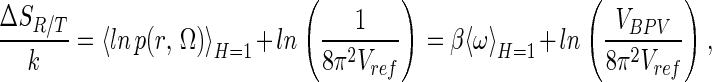which can also be obtained from Eq. 7 by setting the last (solvent/internal entropy) term to zero (see also equation 51 and following discussion of ref. 1).

Eqs. 4, 6, and 7 are exact for dilute solutions. However, direct evaluation of these expressions to sufficient accuracy is likely be impractical for most binding reactions of interest to biochemists, so it is necessary to introduce some approximations for computational tractability. We illustrate one approach, based on the quasiharmonic method (although we emphasize this involves significant approximations, and that other approaches are possible), and consider only cases where the pmf between A and B has a single well defined minimum ω_min. Methods for multiple minima are discussed in detail in recent papers (8, 15). The energy of the AB complex near the minimum can be expanded in a Taylor series and to first order is a harmonic function of displacement in the translational, rotational, and internal coordinates away from this minimum, Δq = (Δq_a, Δq_b, Δr, ΔΩ):

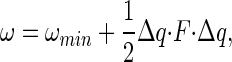where F is the force constant matrix. The quasiharmonic approximation of F is (16, 17)

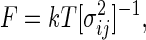where [σ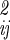]⁻¹ is the inverse of the coordinate fluctuation covariance matrix σ 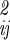= 〈Δq_iΔq_j〉. The configurational integral over these coordinates is then

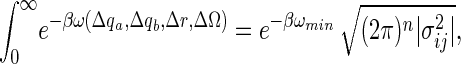where n is the total number of internal, translational, and orientational degrees of freedom, and |σ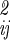| is the determinant of the coordinate fluctuation covariance matrix, σ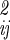. The usefulness of the quasiharmonic method is that even if the fluctuations in q_a, q_b, r, and Ω about the minimum energy structure are not strictly Gaussian (i.e., the energy surface is anharmonic), the integral of the Boltzmann factor is often well approximated by mean squared magnitude of the fluctuations |σ|.

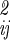Eq. 12 accounts for the correlation between internal, translational, and orientational motions in the off-diagonal terms of σ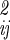. A further reasonable simplification is that different kinds of motions are uncorrelated, so that internal motions of A, B, the three translational motions of B, and the librational motion of B with respect to A are independent, i.e., the corresponding off-diagonal terms in σ 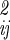are zero. The determinant may then be factored, and substitution of Eq. 12 into Eq. 6 yields

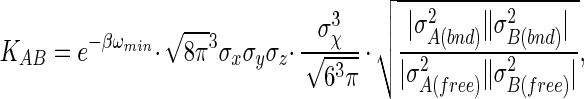where σ_k = x, y, z and σ_χ are the rms fluctuations in position and orientation of B with respect to A in the complex. The contribution from libration of B in the complex is obtained by assuming that it is isotropic (the axis φ/ψ is uniformly oriented in space) and quasiharmonic over small magnitudes of χ, which results in the factor of σ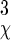/ 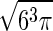(18). Fluctuations in internal coordinates are assumed to be correlated within each molecule but uncorrelated with fluctuations in the position and internal coordinates of the other molecule. Because ω is defined with respect to A and B at large separation, the contributions of internal fluctuations of A and B in the bound (bnd) state are normalized by those in the dissociated (free) state, namely 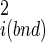|σ|/|σ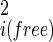|, i = A, B, and contribute only if they change on binding. Because we have used the quasiharmonic approximation to factor out and treat explicitly internal coordinate fluctuation contributions to the pmf, ω_min in Eq. 13 contains just the intermolecular interactions between A and B at the minimum energy conformation, the solvent contributions, plus any internal energy contributions due to the change in the average conformation of A and B on binding. The last three factors in Eq. 13 are the contributions from residual translational motion, residual librational motion, and changes in internal fluctuations, respectively. The Gaussian distribution of r, Ω about the pmf minimum means that the greatest contributions to the integral of H(r, Ω) come from near the minimum, and that contributions further away rapidly decrease because of exponential weighting. Thus little error comes from dropping the restriction of the integral to the region where H(r, Ω) = 1 entailed in the upper integration limit of ∞ in Eq. 12.

The quasiharmonic approximations for the binding enthalpy and entropy are obtained by differentiation of Eq. 13 with respect to T

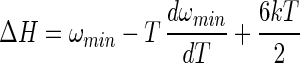and

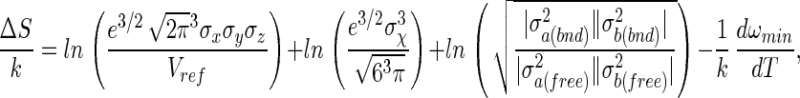where the four terms in Eq. 15 can be identified as the translational, rotational, internal, and solvent contributions to entropy, respectively. The solvent contribution arises from changes in the water configurations, as distinct from the internal and intermolecular configurations of A and B.

Methods

The quasiharmonic approximation of the generalized Bjerrum approach is implemented in an extension of our previous approach to absolute binding free energy calculations (19). Starting from a known complex structure (derived from x-ray crystallography, NMR, or model building), Eq. 13 is evaluated by:

• (i)  Minimization of AB, A, and B by using molecular mechanics, to obtain the structures for the complex at the pmf minimum, ω_min, and the unbound species, respectively.

• (ii)  Determination of the solvation free energies of A, B, and AB by using the Finite Difference Poisson–Boltzmann (FDPB)/surface area method (20) to yield:

  

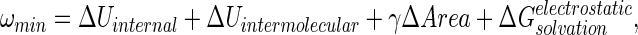
• where ΔU_internal + ΔU_{intermolecular} is obtained from the difference in molecular mechanics potential energy of A and B in the bound and free states, ΔArea is the change in solvent accessible surface area on binding, γ is the apolar hydration surface free energy coefficient, and ΔG 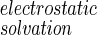is the difference in PB electrostatic solvation free energy between the bound and free molecules. The solvent contribution to the entropy of binding (last term of Eq. 15) arises from the temperature dependence of γ and ΔG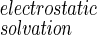, i.e., from the temperature dependence of the hydrophobic strength and the dielectric constant of water, ɛ. Here we do not split the solvation free energy contributions into enthalpic and entropic terms by including the temperature dependence of γ and ɛ, but it would be important to do so when comparing total entropies of binding with experimental data, otherwise the estimation of the translational and rotational contributions would be in serious error.

• (iii)  Molecular dynamics simulations of A, B, and AB followed by analysis of coordinate snapshots to determine σ_X, σ_Y, σ_Z, σ_χ, |σ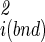| and |σ|.

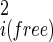Thus the quasiharmonic assumption allows us to replace the evaluation of the pmf over the entire H(r, Ω) = 1 region with a less expensive (but still computationally intensive) evaluation at a single point (ω_min) combined with an estimate of the “width” of the binding well (the rotational and translational entropy terms). We reemphasize the point made by Gilson et al. (1) that without the latter contribution, ω_min, even though it is a free energy, cannot be meaningfully compared to a measured absolute binding free energy. Furthermore, estimation of ω_min by the difference in potential energy between bound and free states is usually a poor estimator of even relative free energies, because it also lacks the solvent and molecular internal entropies.

To illustrate the contribution of the different terms to the binding constant and free energy, we examined four test cases that exhibit a range of binding characteristics: ion–cryptate binding, N-methyl acetamide (NMA) dimerization, antibody FAB fragment–digoxigenin binding, and streptavidin–biotin binding.

Minimization and Molecular Dynamics.

Generation of the NMA structure, model building, minimization, and molecular dynamics were carried out with the InsightII and Discover packages with the consistent valence forcefield (CVFF) (Accelrys, San Diego), except for biotin, for which partial atomic charges were taken from Miyamoto and Kollman (21). The ion–tricyclic cryptate complex Cl⁻SC24 structure was taken from Metz et al. (22). Br⁻SC24 was built by changing the identity of the ion and reminimizing the structure. The structure of the FAB fragment 21-10-digoxigenin complex (23) was taken from entry of the Protein Data Bank (PDB); the structure of the streptavidin–biotin complex was taken from PDB entry (24).

Hydrogens were added and the structures minimized by conjugate gradient with a nonbond cutoff of 12 Å and a dielectric of 1. Molecular dynamics simulations were performed with a time step of 1 fs, nonbonded cutoff of 12 Å, temperature of 298 K, and a distant dependent dielectric of 1R. The distant-dependent dielectric is a rather crude approximation for the energetic effects of solvent, but it is convenient, rapid, and produces reasonable dynamic behavior, which is appropriate because the dynamics is used in our protocol not for solvent energetics but for estimating the amount of internal and intermolecular motion of A and B. Coordinates were saved every 100 steps. To compute |σ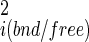|, coordinate snapshots of either A or B in the complex or alone were overlaid by using a rigid body alignment. The mean coordinates and the coordinate fluctuation covariance matrix were then calculated. The matrix was diagonalized using the Housholder method (25) and the eigen values determined. The six lowest values (R/T modes) were generally close to zero, as expected, and were discarded. The determinant of the internal coordinate fluctuations was then computed as the product of the remaining eigen values. To compute σ_X, σ_Y, σ_Z, and σ_χ coordinate snapshots of the complex were overlaid by using rigid body alignment of the largest partner (A). The mean position of B was computed. Then for each aligned snapshot of the complex, the required translation (x, y, z) and rotation (θ, ψ, χ) required to realign B with its average position were computed and the variances calculated. Numerical precisions were estimated from the variance in the final quantities between batches of 0.1-ns simulations.

FDPB/Surface Area.

The procedure for calculating the polar and nonpolar contributions to the solvation energy was taken from previous work (20, 26, 27). Atomic radii were taken from the parse set (20), except for Cl⁻ and Br⁻ radii of 1.94 and 2.09 Å, respectively (28), and digoxigenin, for which consistent valence forcefield (CVFF) radii were used. The nonpolar contribution to solvation was obtained by using γ = 6 cal/mol/Ų. Solvent-accessible surface areas were calculated by using the SURFCV algorithm (29). The polar contribution was calculated by solving the linearized PB equation using a cubic box with 161 grid points on each side, with a box fill of 80%, with a resulting scale, depending on the size of the complex, from 1.5 to 4 grids/Å. The external dielectric constant was either 80 or 1 for solvent and vacuum, respectively. For ion binding to the cryptate SC24, significant polarization of the cryptate ligand groups from the strong ion field is likely. Polarization cannot be included in the CVFF. However, to estimate its effects, we used the local dielectric constant (LDC) model (30) with the FDPB method. In this method, the calculated difference in electrostatic energy of the ion binding to the neutral cryptate in vacuum with a cryptate dielectric of 1 (no Sc24 polarization) and a cryptate dielectric of 2.31 (derived from the polarizability in the LDC model) is used to estimate the effect of polarization. Numerical precision in the solvation calculations was estimated by repeating the calculations with different mappings of the molecules onto the finite difference grid.

Results

The first system studied was the binding of an ion to Sc24, a tricyclic cryptate specific for monovalent anions. Relative binding data are available (31), which show that Cl⁻ binds about 1,000-fold more tightly than Br⁻, and one of the earliest applications of the free energy perturbation (FEP) method was to this system (32). Because there are no rotational and internal fluctuation contributions from the spherical ion, the number of factors contributing to the binding free energy is reduced. The binding is dominated by a strong electrostatic interaction (Table 1), and the stronger binding of Cl⁻ vs. Br⁻ is due to the more favorable intermolecular electrostatic interactions of the former: The smaller Cl⁻ radius permits the liganding groups to approach more closely (defined by the distance of the liganding groups from the ion center, the effective locus of the charge distribution). There are less internal vibrational fluctuations in Sc24 with Cl⁻ bound than Br⁻, a consequence of the stronger intermolecular charge–charge interactions with the smaller ion. Cl⁻ has a greater desolvation penalty. Both these effects reduce the specificity for Cl⁻. However, the relative translational contribution favors the smaller ion because it has slightly more freedom to move in the cage formed by Sc24, because, even though the liganding groups are closer to the center of the Cl⁻ ion there is more space between the van der Waals surface of the ion and the liganding groups. Polarization of the Sc24 liganding NH groups by the strong field of the ion is significant and favors Cl⁻ binding because the liganding groups are closer to the ion. When polarization is included, good agreement with experiment is obtained. We note that in the original FEP study, the polarization effect could not be included, because standard molecular dynamics force fields are not polarizable. However, the FEP simulation also underestimated the relative solvation energies of Cl⁻ vs. Br⁻ as −3.35 kcal/mol. The experimental value is −6.0 kcal/mol (33), close to the value calculated by the FDPB method (Table 1 legend). It seems likely that in the earlier FEP study, these two factors almost canceled each other.

Table 1.

Binding free energy contributions at 298 K, kcal/mol

Contribution	Sc24 (Cl-Br)	NMA	Ab-DXN	BTN-STP
Polar solvation	4.8  ± 0.5	7.9  ± 0.4	16.3  ± 0.5	84.4  ± 1
Nonpolar solvation	0	−0.6  ± 0.1	−4.1  ± 0.1	−3.3  ± 0.1
Total solvation	4.8  ± 0.5	7.3  ± 0.4	12.2  ± 0.5	81.1  ± 1
van der Waals + internal	−4.0	−2.0	−2.3	−44.8
Electrostatic	−6.5	−7.0	−31.5	−62.1
Translation (at 1 M)	−0.7  ± 0.1	2.4  ± 0.1	4.3  ± 0.1	4.3  ± 0.1
Rotation	0	0.8  ± 0.1	5.0  ± 0.1	4.2  ± 0.1
Internal vibration	1.6  ± 0.5	1.0  ± 2	0.0  ± 3	3.5  ± 4
Total nonsolvation	−9.6  ± 0.6	−4.8  ± 2	−24.5  ± 3	−94.9  ± 4
Total ΔG at 1 M	−4.8  ± 0.8	2.5  ± 2.5	−12.3  ± 3	−13.8  ± 5
Measured ΔG at 1 M	−4.2	3.1	−13.9	−18.3

Ab-DXN, antibody FAB fragment–digoxigenin; BTN-STP, biotin–streptavidin.

^*Binding of Cl relative to Br.

^† −5.7 kcal/mol of which comes from the difference in ion hydration free energies.

^‡ Includes −2.8 kcal/mol from polarization of Sc24 by the anion.

^§ Includes a factor of ln(2) for the exchange symmetry of the dimer.

^¶ Data taken from refs. 31, 34, 49, and 50.

Dimerization of NMA in water and other solvents has been measured by Kresheck and Klotz (34), and this system has been analyzed theoretically as a model for hydrogen bonding in proteins (35, 36). This system is an example of binding where both partners are small and rigid, so internal fluctuations should play a small role in the binding energetics. Association is driven by a strong intermolecular electrostatic interaction between the NH and CO groups, opposed to a large extent by desolvation [Table 1; Ben-Tal et al. (35)], leading to weak net binding. As expected, internal fluctuations are only slightly reduced on binding, leading to a small 1 kcal/mol penalty. Unlike this earlier study, we have included an estimate of the R/T penalty on binding. Because the binding is dominated by a single hydrogen bond, effectively a one-point attachment, a large amount of residual rotational motion remains in the complex (Table 2), leading to a very small rotational immobilization penalty of <1 kcal/mol. The translational immobilization is somewhat greater. The sum of all these factors results in weak binding, in reasonable agreement with experiment, considering the small numbers involved and the relative uncertainties.

Table 2.

Summary of translation and rotation contributions to binding at 298 K

Contribution	Cl−Sc24	NMA2	26-10-DXN	BTN-STP
ΔGbind at 1 M	−5.6–6.8	2.5	−12.3	−13.8
σxσyσzÅ3	0.002	1.9	0.08	0.08
σχ (132°)	NA	106°	10°	16°
ΔHtrans + ΔHrot	0.89	1.78	1.78	1.78
−TΔStrans at 1 M	5.6	1.5	3.4	3.4
−TΔSrot	0	<0.1	4.1	3.3
−TΔSassoc at 1 M	5.6	1.5	7.5	6.7

DXN, digoxigenin; BTN-STP, biotin–streptavidin.

^*Expected for isotropic libration.

^† Not applicable for a monoatomic ligand.

The third system we examined was the antibody FAB fragment 26-10-digoxigenin complex, an example of tight binding of a very rigid ligand. The major part of the ligand consists of four fused rings, with only one major conformational degree of freedom: the bond joining the lactone ring substituent at C17. Binding is driven by electrostatic interactions, which are primarily hydrogen bonds with the hydroxyl and lactone oxygens. Because these H-bonds are with neutral protein groups, the electrostatic desolvation is not large, and the net electrostatic interaction is favorable (Table 1). Concomitantly, there are significant penalties for R/T immobilization in this tight-fitting complex. Internal vibrational fluctuation contributions are small, because the ligand is rigid.

The final system we studied was streptavidin–biotin binding, a less rigid ligand than digoxigenin, but one of the tightest protein–ligand associations known and thus a paradigm for high-affinity protein binding. This system has been extensively studied most notably by a combination of molecular dynamics, FDPB/surface area and normal mode analysis (21, 37), a hybrid method developed in part to calculate absolute binding constants. Binding is again driven by a strong intermolecular interaction, worth about −107 kcal/mol. Of this interaction, −62 kcal/mol is electrostatic, which is opposed by +81 kcal/mol of desolvation, so the net electrostatic contribution is unfavorable (Table 1), because of the desolvation of the ureido and carboxylate groups. The binding is driven by the strong nonpolar interactions composed of van der Waals and hydrophobic terms, reflecting the extremely good match of shape and hydrophobic interactions for this complex. Again there are significant penalties for R/T immobilization in this tight-fitting complex, although less than for the more rigid digoxigenin ligand. Biotin has a flexible valeryl carboxylate tail whose mobility is significantly reduced on binding, adding a 2.5-kcal/mol vibrational fluctuation penalty. The general balance of interactions in the Bjerrum model is very similar those found by FEP (21), although we cannot compare the R/T term because it was not separated out in that study. We find a very strong net binding free energy, in agreement with experiment, although the magnitude is somewhat too low. This underestimate may well be because the quasiharmonic method used to evaluate the Bjerrum integral is oversimplified for this system, particularly in representing loss of entropy from bond rotations. Here a method in which snapshots from an extended molecular dynamics simulation are postprocessed using the PB method, permits a larger region of a nonharmonic binding well, e.g., from bond rotomerization, to be explored (38).

Discussion

A concise derivation of a general equation for the binding constant and the enthalpy and entropy components (Eqs. 4, 6, and 7) is one result of this paper. We refer to this as the generalized Bjerrum approach: applied to the association of structureless (spherical) ions and by using a Coulombic potential to approximate ω, it was first used by Bjerrum to derive his well known expression for the ion association constant (39). In this application, the limits of H = 1 are from r = a, the distance of closest approach of the two ions, to r = b, the distance cutoff for ion pairing introduced by Bjerrum. The Bjerrum expression for ion pairing is usually presented without detailed derivation, obscuring its origin in a more exact statistical mechanical expression. It can, however, be generalized, as shown here, to the binding of polyatomic molecules.

Comparison with Chemical Potential-Based Derivation.

Apart from notational differences, our final expressions for binding constant and entropy are almost identical to those derived previously by using the chemical potential approach [equations 49 and 50 of Gilson et al. (1)], except we have dispensed with symmetry numbers, because equivalent positions/orientations are implicitly included in the full integrals over r/Ω, and have omitted the negligible pressure–volume term. Indeed, agreement is expected if both approaches are valid. Eq. 4 is also related to the expression derived previously for membrane association by Ben-Tal et al. by using the chemical potential approach (2), with the differences that for membrane and surface adsorption, the bound molecule is not confined translationally in the plane of the surface, and the appropriate quantity is not an association constant but the surface excess, which is equivalent in the notation used here to Γ = ∫H(e^−βω − 1). However, the derivation of K_AB we present here is shorter and arguably clearer in its assumptions and implications than the standard derivation based on chemical potentials. For example, one simplification is that it involves just configurational (coordinate) integrals of a fixed number of particles. There is no introduction or removal of particles, as implied in the chemical potential approach, with the attendant momentum terms. Although these cancel to leave a mass independent binding constant (as required in the classical approximation), the mass independence is clearer if they are not introduced in the first place. Furthermore, it is easier to see that Eq. 4 is exact in the dilute A/B limit even for nonideal polyelectrolyte solutes such as DNA. This is not so obvious in the chemical potential approach since polyelectrolytes have nonunity activity coefficients even at infinite dilution because of ionic atmosphere effects. Other implications of our approach are discussed in more detail below.

Delineation of the Bound State.

It is clear that a rigorous derivation of the binding free energy requires explicit delineation between the bound and unbound states. For mathematical convenience, we adopt the Heaviside function notation (H = 1/0 delineates bound/unbound states) used previously for gas phase-monoatomic association (12); alternatively, one could specify (rather complicated) integration limits on r/Ω in the integral in Eq. 4. Because one is ultimately comparing to an experimental measurement of K_AB, the ideal situation would be to make H = 1 correspond exactly to those configurations that give the “AB” signal with the experimental probe (spectroscopy, calorimetry, etc.) used to measure the binding constant. In practice, one rarely knows enough about the experimental method to do this. From a computational point of view, one often finesses the issue, as in the quasiharmonic example given here: Most of the contribution to the binding phase volume integral comes near the minimum of the potential well in r, Ω phase space, and the numerical value is rather insensitive to where one cuts off the bound-state integration. Nevertheless, some definition of AB is always involved. This problem does not appear to arise in the usual derivation using chemical potentials, because one assumes there is a distinct AB species as soon as its chemical, μ_AB, is introduced. However, this assumption is misleading, because it merely postpones or hides some definition of what AB is. Also μ_AB is not quite a standard chemical potential, which is the thermodynamic work of insertion into pure solvent at constants T and P: If we insert one “molecule” of AB into water at infinite dilution, it will immediately dissociate, so μ_AB involves some additional constraint to T and P that restricts A + B to exactly the region defining the complex.

Role of Solvent.

A distinction between R/T contributions to binding and the role of the solvent is introduced right from the start. It is inherent in the definition of the complex and the introduction of the potential of mean force between A and B. Although there is some degree of freedom (and care required) in choice of coordinates (40), the R/T coordinates of B are usually defined with respect to either its center of mass and moments of inertia or its centroid and geometric moments (nonmass weighted, used in this work). All solvent effects, including excluded volume, are fully accounted for by the solvent-mediated potential of mean force between A and B. Thus in the Bjerrum derivation, the range of integration for B is 4π²V, where V is the total solution volume. This range is fully consistent with the widely accepted definition of the solute chemical potential as the sum of the thermodynamic work of introducing a solute into a fixed position plus a “liberational” term from solute translation/rotation in the entire solution volume (14, 41). The Bjerrum approach also provides a rigorous definition of solvent and association entropy contributions without appeal to the gas-phase Sackur Tetrode expression for translational entropy (often invoked in the chemical potential type derivations), which has been criticized as unrealistic for binding in solution (4, 42).

Absolute Binding Free Energies.

Calculation of absolute binding constants has been discussed previously by Gilson et al. (1) and others, and it remains a computational challenge. As defined by Eq. 5, it is the free energy change when one molecule of B is taken from a state in which it can rotate and translate freely in a phase volume 8π²V_ref (= 1,660 ų at 1 M) to the bound state, where it undergoes restricted R/T motion under the influence of its solvent mediated intermolecular interactions with A, in the Boltzmann-weighted phase volume (BPV) where H(r, Ω) = 1. Thus, the free energy is the log of a unitless quantity, the volume ratio V_BPV/8π²V_ref. The appearance of V_BPV spells out the requirement for any absolute binding free energy calculation: it must either (i) evaluate a phase volume integral, preferably over the entire bound state, H = 1, but at least over the regions at the bottom of the well that make the most contribution to the integral, (e.g., refs. 13, 43–45, and this work) or (ii) compute a binding free energy relative to some system whose V_BPV is known (46, 47). A computational protocol that uses only the difference in free energy between A, B, and AB at some point(s) in the r, Ω potential well does not give the absolute binding free energy. Such protocols include “single point” FDPB calculations, double disappearance (48), binding energy scoring schemes, and many other empirical binding methods. These methods provide either ω or its equivalent at a single point (usually the minimum) on the ω(r, Ω) surface, or the average ω(r, Ω) for some region about the minimum.

It should also be noted that when “single point” methods are used for relative binding, this is equivalent to the assumption that the shape of the ω(r, Ω) well is the same, and only its depth is changed. This assumption may not work well comparing systems of widely differing affinity, because tighter binding usually implies less residual motion in the complex, i.e., a narrower r, Ω potential well, in which case the integration over the bound phase volume must be evaluated.

Practical Calculation of Binding Free Energies.

For many systems of interest to the biochemist, it would be prohibitive to model the solvent explicitly. In the generalized Bjerrum approach, the pmf provides a natural and well defined way to introduce an implicit or continuum solvent model into the calculations. We have illustrated this by using the FDPB/surface area implicit solvent model for four binding reactions, choosing systems with diverse characteristics: the ligands ranged from a monoatomic ion to a large rigid drug, from very tight to very weak binding, and from electrostatically dominated to apolar dominated. We chose these systems primarily to illustrate the Bjerrum approach and to examine the issue of association entropy, not as a detailed analysis of the most accurate way to do binding free energy computations. Again, we emphasize that there are alternative reasonable approximations to those used here. Nevertheless, the general agreement with experiment is satisfactory enough that we can draw several conclusions about the association entropy. The relevant data from our calculations are summarized in Table 2. First, it is clear that the association entropy contributions vary quite widely (1.5–7.5 kcal/mol at 298 K), depending on the nature and strength of the binding. The upper limit is similar to that for association of the rigid cyclic diglycine molecule (19). The lower limit, for the partially immobilized NMA, is similar to estimates of 1.3 kcal/mol for another partially immobilized case, a lipid in a membrane (2). The translational contribution varies, but it does not simply increase with strength of binding, being largest for the tricyclic cryptate, which completely encapsulates the ion. For this case, the residual motion is about 0.2 Å in the x, y, and z directions, which is small compared to the value of about 0.8 Å for immobilization of a sodium ion in the GA channel (13). The translational part for high-affinity complexes is significantly greater than that estimated from the cratic equation or recent tethering experiments (9, 10) (2.4 and 1.5 kcal/mol at 298 K, respectively). However, we argue that tethering, although undoubtedly producing an enhancement in association rate and complex stabilization, cannot be used to extract an estimate of ΔS_trans for the untethered system. To obtain ΔS_tran, we need to know how much residual motion of B with respect to A there is in the bound state (Eq. 9). This residual motion is determined by the specific interactions between A and B that drive them to form a complex AB with and without the tether and so are subtracted out when the difference in binding entropy or free energy is taken. The contribution of rotational immobilization, which has been omitted in some previous treatments, including the cratic entropy model, is at least as important as translational immobilization, particularly for a ligand that is bound by multiple attachments. Overall, we find that the association entropy penalty is significant for high-affinity complexes but smaller than early estimates in the literature of >14 kcal/mol (at 298 K). How general this conclusion is will be revealed by calculations on other systems. For calculating this and other contributions to the binding free energy, the generalized Bjerrum approach provides a rigorous and self-consistent theoretical basis.

Abbreviations

• FDPB, finite difference Poisson-Boltzmann

• BPV, Boltzmann-weighted phase volume

• pmf, potential of mean force

• FEP, free energy perturbation

• R/T, rotation/translation

• bnd, bound

• NMA, N-methyl acetomide