Molecular recognition of oxygen by protein mimics: Dynamics on the femtosecond to microsecond time scale

Abstract

Molecular recognition by biological macromolecules involves many elementary steps, usually convoluted by diffusion processes. Here we report studies of the dynamics, from the femtosecond to the microsecond time scale, of the different elementary processes involved in the bimolecular recognition of a protein mimic, cobalt picket-fence porphyrin, with varying oxygen concentration at controlled temperatures. Electron transfer, bond breakage, and thermal “on” (recombination) and “off” (dissociation) reactions are the different processes involved. The reaction on-rate is 30 to 60 times smaller than that calculated from standard Smoluchowski theory. Introducing a two-step recognition model, with reversibility being part of both steps, removes the discrepancy and provides consistency for the reported thermodynamics, kinetics, and dynamics. The transient intermediates are configurations defined by the contact between oxygen (diatomic) and the picket-fence porphyrin (macromolecule). This intermediate is critical in the description of the potential energy landscape but, as shown here, both enthalpic and entropic contributions to the free energy are important. In the recognition process, the net entropy decrease is −33 cal mol⁻¹ K⁻¹; ΔH is −13.4 kcal mol⁻¹.

Understanding the process of O₂ binding to hemoglobin and myoglobin is of importance in biological science because these molecules are responsible for the oxygen transportation and storage in mammalian cells. It has been shown by various kinetic studies that the binding process involves movement of oxygen through multiple energy barriers, facilitated by fluctuations in protein structure (1, 2). However, details regarding the origin of each barrier are difficult to determine because of the complex nature of the protein structure. Synthetic model porphyrins are used to mimic the structure and function of the proteins to obtain insights into the correlation between structure and function (3). Picket-fence porphyrin is one of these synthetic models (4). One side of the porphyrin plane is a cage formed by four pivalamido pickets. An attractive property of the picket fence is its high O₂ affinity at room temperature when there is a base attached to its unencumbered side, and the oxygen binding is reversible (4).

Recently, our laboratory reported femtosecond dynamics of cobalt picket-fence porphyrin in benzene (5). From the transient absorption responses, the excited oxygenated picket-fence porphyrin was found to undergo energy relaxation within the porphyrin ring and porphyrin-to-metal electron transfer on the femtosecond scale, followed by reverse electron transfer and release of O₂ within 2 ps. No substantial recombination of O₂ to porphyrin occurred on a time scale up to 20 ns after the excitation, indicating the insignificance of geminate recombination. Because of the limitation of the maximum delay time available with the femtosecond system, the recombination process on longer time scales could not be observed.

Here we report our detailed study, using transient absorption, of O₂ recombination to the picket-fence porphyrin (Fig. 1) in benzene. The O₂–picket-fence complexes (>80%) at room temperature were excited to dissociate the O₂ in picoseconds. The resulting free picket-fence absorption, relative to that of the complexes, was probed with femtosecond pulses, measuring the thermal, ground-state O₂ recombination or association (the “on-rate”) and dissociation (the “off-rate”). The time delay used was up to 5 μs to observe these thermal processes, and we studied the dependence on the temperature and O₂ concentration in the solution. As such these measurements are made with the zero of the time being well defined to avoid inhomogeneous distribution of the initial state. It is the purpose of this paper to report these results and to provide a theoretical framework for understanding the dynamics, kinetics, and thermodynamics of this recognition process.

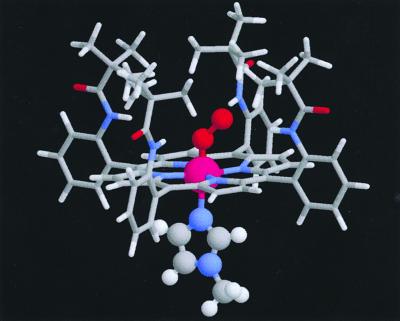
Figure 1.

Molecular structure of the cobalt picket-fence porphyrin with oxygen and the base. The x-ray structure of the analogous iron picket-fence has been determined (16) (see text).

Methodology

Transient Absorption Spectroscopy.

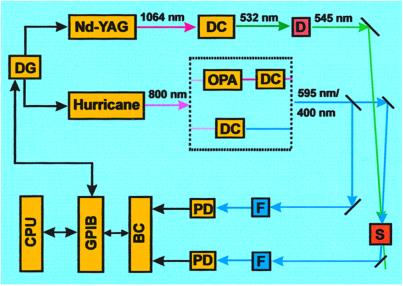
A schematic of the transient absorption experimental setup is shown in Fig. 2. The picosecond pump pulse at 545 nm was from a Nd-YAG (Quantronix 416) pumped dye laser with rhodamine 575 operated at 500 Hz. A Hurricane laser system (Spectra Physics) produces ∼100-fs pulses at 800 nm with 500-Hz repetition rate and 1-mJ pulse energy. Probe pulses were obtained either at 400 nm by directly passing through a BBO (β barium borate) doubling crystal (Casix, Fuzhou, China), or at 595 nm by pumping an optical parametric amplifier (OPA) with the 800-nm pulses and doubling the infrared output of the OPA. The probe pulse train was split into two beams, one passing through the sample and the other going directly to a photodiode as a reference beam, whose energy was used as a measure of probe beam energy before the sample. The time delay between pump and probe pulses was controlled by an electronic delay generator (DG535, Stanford Research Systems, Sunnyvale, CA). The timing jitter was about 20 ns. The two beams were overlapped in the sample by crossing at a small angle (∼1°). Typical pulse energies at the sample, with beam diameters of ∼1 mm, were 0.4 μJ for the pump and 10 nJ for the probe.

Figure 2.

Schematic for nanosecond transient absorption setup. DG, electronic delay generator; Nd-YAG, neodymium-doped yttrium aluminum garnet laser; DC, doubling crystal; D, dye laser; OPA, optical parametric amplifier; S, sample; F, band-pass filter; PD, photodiode; BC, boxcar integrator; GPIB, general purpose interface bus; CPU, computer (central processing unit). For the femtosecond study, see ref. 5.

After passing the sample, the pump and probe beams were separated by a prism and the latter was then focused at a second photodiode, where its energy was measured. To further block the pump beam from entering the photodiode, a band-pass filter (BG 39) was placed in front of the photodiode. The output from the photodiode was gated and integrated by a boxcar integrator before being normalized to the similarly processed reference beam signal. The ratio between normalized transmitted probe energies with the pump beam electronically switched on and off formed the basis of the transient absorption, ΔA, recorded as a function of the time delay between pump and probe pulses. A background recorded with the pump beam physically blocked was subtracted from each transient response to further remove background signals.

Sample Preparation and Materials.

The porphyrin concentration was adjusted to obtain an absorbance of about 0.2 at the Q-band (550 nm) when probing at 595 nm (1-mm cell) or ca. 1.2 (5-mm cell) at the Soret band (410 nm) when probing at 400 nm, using benzene as the solvent. 1-Methylimidazole was then added to the solution to make the base concentration near 10 mM to ensure that most picket-fence porphyrin molecules were five-coordinated (4, 5). Immediately after addition of the base, benzene-saturated gas mixtures of O₂ and Ar were bubbled through the solution for 30 min to achieve the desired oxygen concentration in the solution. The cell was then sealed with a high vacuum valve and ready for transient experiments.

The oxygen molar fraction in the gas mixture was measured by an oxygen analyzer (Mini OX I, MSA Medical Products, Pittsburgh) with ±1% accuracy. The concentration of oxygen in the solution was calculated by using Henry's law with the correction for benzene vapor pressure (95 mmHg at 25°C) (6). The solubility of oxygen at different temperature was calculated by using a known empirical equation with the saturation concentration at 1 atmosphere O₂ and 25°C as 9.1 mM (7). The solution temperature was controlled within ±0.5°C by circulating coolant through the cell jacket with an Endocal Neslab circulating bath. In temperature-dependence studies, transient absorption curves were recorded at five different temperatures at each oxygen concentration before switching to a new sample with a different oxygen concentration. The upper limit of temperature was set at 40°C to avoid any atropisomerization of the porphyrin (8, 9) and the lower limit was set at 10°C to prevent the solution from freezing and to avoid condensation of moisture in the air on the cell windows.

The cobalt picket-fence porphyrin (CoTpivPP, here CoP) was available from previous studies (5, 10), and the purity of the sample was checked by ¹H NMR. Benzene (OmniSolv, EM Science) was passed through a column of aluminum oxide (activated, basic, Brockmann I, Aldrich) before use. 1-Methylimidazole (>99%, redistilled, Aldrich) was used as received. Before being mixed, O₂ (Matheson) was passed sequentially through sodium hydroxide and Drierite columns, and Ar (Matheson) was passed through a Drierite column.

Results and Discussion

Thermal Rates: Oxygen Concentration and Temperature Dependencies.

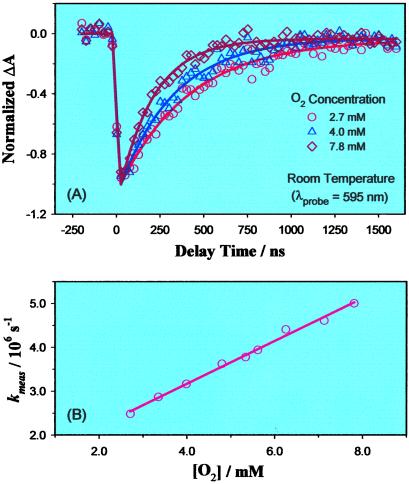
Fig. 3A shows a representative set of transient absorption response on the nanosecond time scale recorded in benzene solutions containing ca. 0.3 mM CoP + 10 mM 1-methylimidazole with various concentrations of O₂ at 25°C. The base concentration was in the range where its influence on the transient response attributable to a second base bound to the porphyrin is negligible (11). For direct comparison with the previous femtosecond study, the pump and the probe wavelengths were initially selected at 545 nm and 595 nm, respectively. Each of the absorbance transients was normalized to its maximum value, which is typically in the range of 1–2 × 10⁻³.

Figure 3.

(A) Normalized transient absorbance of B-CoP in benzene solution containing various concentrations of O₂, recorded at 25°C. Solid curves are single-exponential fits of the corresponding data points. Pump wavelength: 545 nm, probe wavelength: 595 nm. (B) Measured O₂ recombination rate constants as a function of the concentration of O₂, measured at 25°C. The solid line is a linear fit of the data points.

After excitation of the system, the absorbance at 595 nm first decreases and then returns to its original value after nearly microseconds. As in the previous femtosecond study (5), the photobleach at 595 nm is due to photorelease of O₂ from the picket-fence–O₂ complex, B–CoP–O₂, where B stands for the 1-methylimidazole; note that the initial positive absorption (5) near t = 0 is not resolved because of the time resolution used here. The nanosecond time scale recovery is therefore from subsequent recombination of oxygen and the porphyrin. With increasing oxygen concentration, the recovery of transient absorbance to its baseline is faster (Fig. 3A).

These transient responses are well fitted with a single-exponential function, as shown by the solid curves in Fig. 3A. (In some cases a 10⁻⁵ offset, which probably arises from sample photodegradation, is included to best fit the results.) The measured rates, k_meas, at a series of oxygen concentrations, from experiments similar to those shown in Fig. 3A, are plotted in Fig. 3B. It can be seen that k_meas depends linearly on oxygen concentration.

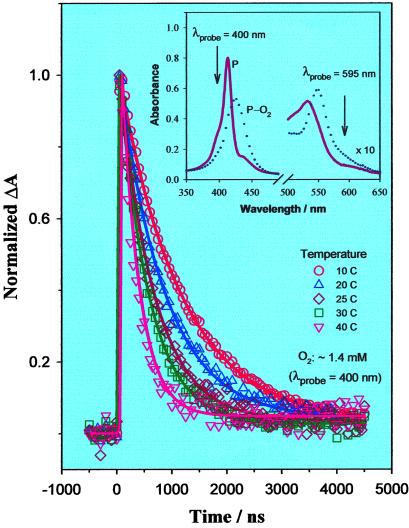
Shown in Fig. 4 is a set of transient responses recorded in benzene with 10 μM picket-fence porphyrin at different temperatures with ca. 1.4 mM oxygen in the solution. Each response is again normalized to its corresponding maximum value, which typically is 1–6 × 10⁻³, depending on the temperature. To improve the signal/noise ratio, for these measurements we probed at 400 nm instead of 595 nm, taking advantage of the larger absorbance difference between deoxygenated and oxygenated porphyrins at this wavelength (Fig. 4 Inset). Different from those in Fig. 3A, the responses of Fig. 4 first increase, followed by decays of a few hundred nanoseconds. This is because the absorbance for deoxygenated porphyrin at 400 nm is larger than that for the corresponding oxygenated species (Fig. 4 Inset). Clearly, with increasing temperature, the decay becomes faster. Similar to the transients of Fig. 3A, the responses are fitted by using single-exponential functions with offsets typically at 10⁻⁵, as demonstrated by the solid curves in Fig. 4.

Figure 4.

Temperature-dependent normalized transient absorbance of B–CoP in benzene containing ∼1.4 mM O₂. The solid curves are single-exponential fits of the corresponding data points. Pump wavelength, 545 nm; probe wavelength, 400 nm. (Inset) Pair of absorption spectra of B–CoP in benzene in the absence (solid curve) and presence (dotted curve) of O₂. The arrows indicate the probe wavelengths used in the transient experiments.

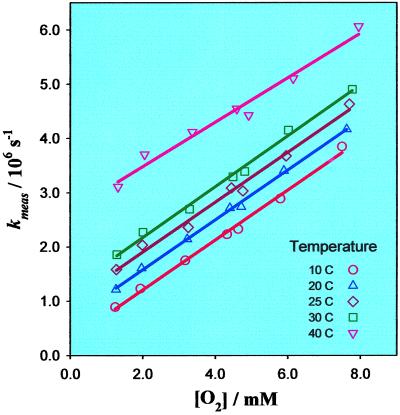
Transient absorption measurements over the same range of temperatures as shown in Fig. 4 were performed with various oxygen concentrations, and the obtained decay rates, k_meas, were plotted against oxygen concentration (Fig. 5). As in Fig. 3B, k_meas for each temperature depends linearly on oxygen concentration, as shown by the plotted fits (solid lines) in Fig. 5.

Figure 5.

Measured oxygen recombination rate constants as a function of oxygen concentration at various temperatures. The lines are linear fits to the corresponding data points.

The Bimolecular Recognition Encounter.

Of special interest here is the understanding of the dynamics—how does the oxygen recombine to the picket-fence porphyrin? Oxygen and carbon monoxide binding to iron heme model compounds such as iron picket-fence porphyrin show biphasic recombination: the picosecond geminate recombination and the nanosecond bimolecular diffusion-controlled association (12–14). The absence of appreciable recovery of the transient absorption at 600 nm in the previous femtosecond study from this laboratory indicates the insignificance of the germinate recombination (5), lending further support to the dominance of the diffusion-controlled process. However, we did observe a small decay contribution, which occurs on tens of picoseconds, indicating that any geminate recombination must be small, a point to which we will return below. We now consider the dynamics of thermal association, recombination, and dissociation processes.

The standard diffusion model: Is it valid?

The standard representation of the observed transient process is the following reaction:

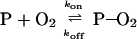1

where P stands for B–CoP, and the on and off steps are taken to be elementary. Under pseudo-first-order reaction conditions—i.e., when oxygen concentration is much greater than that of P, the well-known solution for the concentration of P, [P], after a change from its equilibrium value, [P]_e, caused by the pump pulse at t = 0 is

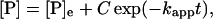2

and similarly,

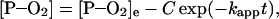3

where the apparent rate, k_app, is given by

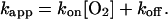4

The absorbance change can then be derived as

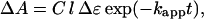5

where Δɛ is the difference in absorption extinction coefficient between deoxygenated and oxygenated porphyrin, l is the effective optical path length determined by the overlap between pump and probe, and C depends on the pump power, quantum yield, etc.

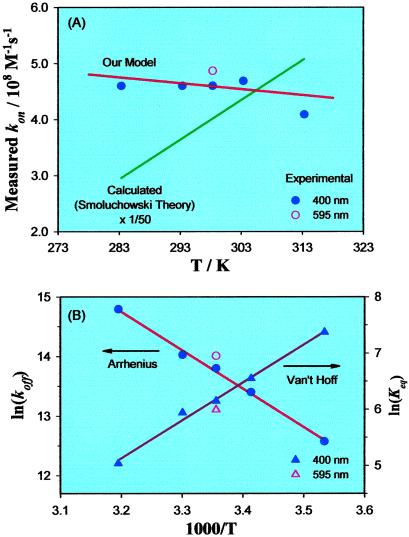
In this model, the transient absorbance signal should exhibit single-exponential behavior with lifetime equal to k_app⁻¹, where k_app, at fixed temperature, varies linearly with oxygen concentration. Our data do indeed display these properties. If, for the moment, we assume the validity of the model, then our k_meas can be equated to k_app in Eq. 4, and the temperature-dependent association and dissociation rate constants, k_on and k_off, are determined from the slopes and intercepts, respectively, of the linear fits in Figs. 3B and 5. These fit parameters are plotted in Fig. 6 for data obtained at room temperature when probing at 695 nm and at five different temperatures with a probe wavelength of 400 nm. It should be emphasized that the obtained k_off is for the thermal dissociation and not for the photodissociation induced by the pump pulse.

Figure 6.

(A) Oxygen association rate constants as a function of temperature. Circles, experimental values; lines, theoretical values calculated for the two models discussed in the text. (B) Arrhenius plot for the dissociation of O₂ from CoP (circles) and van't Hoff plot of the equilibrium constant K_eq = k_on/k_off (triangles). The solid lines are linear fits of the 400-nm data.

The measured k_on values of Fig. 6A are plotted together (note the scaling factor) with k(T) calculated from the classical Smoluchowski theory of diffusion-controlled bimolecular reaction: k = 4πDR, where D is the sum of the diffusion constants for reactants and R is the sum of the radii of reactants (15). (The second line in Fig. 6A will be discussed below.) The radius of porphyrin used for the calculation is 7.4 Å, estimated from the effective molecular volume calculated from x-ray crystallographic data for oxygenated Fe(II) picket-fence porphyrin by assuming the molecule is spherical (16). A radius of 1.47 Å, derived from van der Waals constants (17), was used for O₂. The diffusion constants at different temperatures for oxygen and porphyrin were obtained from the Einstein–Stokes relation [D = k_BT/(6πrη)] with temperature-dependent benzene viscosity (18). As demonstrated in Fig. 6A, the measured values range from about 1/30 to 1/60 the corresponding calculated results. They also show distinctly different temperature-dependent behavior.

The measured k_off values in Fig. 6B (circles) are displayed in the form of an Arrhenius plot. From the linear fit to the data, an activation energy for the dissociation process of 12.8 kcal mol⁻¹ and an activation entropy of 10 cal mol⁻¹ K⁻¹ are derived. The preexponential factor, the product of the entropy term and k_BT/h, is ∼2.6 × 10¹⁵ s⁻¹ at room temperature, over 400 times larger than k_BT/h.

Our two-step model, with reversibility: Recognition and reactivity.

To further explore the abnormal temperature dependence of the association on-rate, we consider a different model that includes two steps and a reaction intermediate. In this model, the two processes are represented by

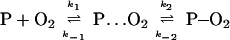6

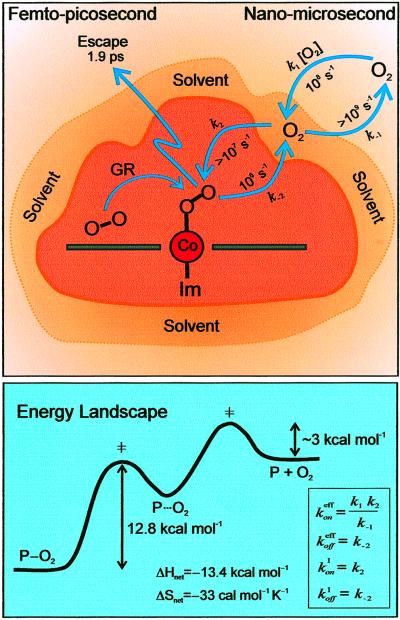
where P⋅⋅⋅O₂ stands for the intermediate, in which the O₂ is associated with the porphyrin structure, but the strong ligand–metal bond has not been formed. A conceptual picture of the structural changes involved is shown at the top of Fig. 7.

Figure 7.

(Upper) A schematic of the structures with rate processes indicated for the initial release of O₂ (left) and for the thermal bimolecular recognition (right). Possible geminate recombination of O₂ to the cobalt center is indicated by GR. (Lower) A cross section of the energy landscape along the dissociation/recombination pathway. Shown in the box are expressions for the effective rates for the overall process (superscript eff) and the thermal passage over the inner barrier (superscript I).

Solution of the rate equations for reaction 6 in the general case yields a biexponential time dependence of the concentration of each species—e.g.,

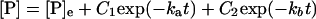7

where

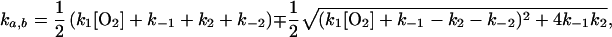and C₁ and C₂ are time-independent constants. Taking k₁ to be the calculated Smoluchowski rate, we found that the limit k₋₁ > k_x for k_x = k₁[O₂], k₂ or k₋₂, is required for consistency with our results (apparent single-exponential time dependence of transient absorption, linear oxygen concentration dependence, k_meas much smaller than diffusion-controlled, a small equilibrium population of the intermediate, and insignificant geminate recombination from the intermediate). Under this condition, the apparent rate constant is the smaller (k_a) of the two rate constants for reaction 6 and can be approximated (to fractional accuracy k_x/k₋₁) as

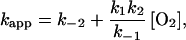8

while the second much faster rate constant, k_b (≅ k₋₁) makes a negligible contribution to the transient absorption.

A comparison between Eqs. 4 and 8 makes it evident that the effective off-rate of the total reaction, k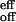, is k₋₂ (rate-limiting step). Thus the activation parameters from the Arrhenius plot of k_off (Fig. 6B) are still valid, but now apply to the passage over the inner barrier of the two-step process (see Fig. 7 Lower). Similarly, the effective on-rates of the reaction are k 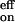= (k₁k₂)/k₋₁.

In this two-step model, the physical basis for the discrepancy between k_on and the Smoluchowski diffusion-controlled rate constant is easily understood, since, for k₋₁ much larger than k₂, most of the diffusion-controlled encounters that lead to the formation of the intermediate do not result in a final bound state. Taking k₁ equal to the Smoluchowski theory calculation of Fig. 6A, a fit of the temperature-dependent on-rate as (k₁k₂)/k₋₁ yields the upper line shown in Fig. 6A. The fit parameters are the activation energy difference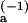 (E − E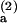) and the difference in entropy change between the k₋₁ and k₂ processes, which are found to be 3.5 kcal mol⁻¹ and 19 cal mol⁻¹ K⁻¹, respectively. The fit determines the ratio k₂/k₋₁, but not the individual k₋₁ and k₂ values, at each temperature.

The anomaly in the on-rate temperature dependence can now be understood. The larger activation energy of the k₋₁ process compensates the activation energies required for the k₁ and k₂ processes, yielding a weakly temperature-dependent k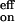. The large entropy increase of the k₋₁ process in which the O₂ is liberated makes k₋₁ larger than k₂, and thus k is smaller than k₁. A model without the reversibility in the second step has been used to explain a biphasic behavior in the Arrhenius plot of the on-rate for oxygen binding to basket-handle and hybrid iron porphyrins in a wide temperature range (from 180 to 320 K) in toluene (19, 20). Without the process described by k₋₂ of reaction 6, we cannot explain the observed dependencies reported here.

Thermodynamics and the equilibrium constant.

It is possible to check the consistency of our derived rates with independent kinetic and thermodynamic measurements. The equilibrium constant [P–O₂]_e/([P]_e[O₂]_e) is K_eq = (k₁k₂)/(k₋₁ k₋₂) for reaction 6 and k_on/k_off for reaction 1. From Eq. 8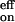, k/k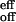 = (k₁k₂)/(k₋₁ k₋₂), so agreement between the ratio of slope to intercept of the k_meas plots and equilibrium constants determined by measuring steady-state absorbance changes with and without oxygen in the system is expected for either model. For example, our values of k_on and k_off at T = 298 K and probing at 400 nm are 4.6 × 10⁸ M⁻¹ s⁻¹ and 1.0 × 10⁶ s⁻¹, respectively. This k_on is about two-thirds of that measured by a similar procedure in toluene solution at room temperature (21), and the k_off is ca. 3 times larger than the reported value. However, the equilibrium constant k_on/k_off in ref. 21 is nearly 3 times larger than equilibrium constants obtained from steady-state measurements in the same work and elsewhere (4). (Note that there is no temperature-dependent study of the rate constants in ref. 21.) Our results give an equilibrium constant K_eq of ca. 460 M⁻¹, in excellent agreement with the value measured in benzene, and similar to that in toluene (540 M⁻¹), from independent thermodynamic studies of the steady-state absorbance with and without oxygen (S.Z. and A.H.Z., unpublished results). Note that the value from the latter measurements in toluene agrees very well with the value of 520 M⁻¹ reported in ref. 4.

Equilibrium constants at the other temperatures studied were obtained from the same independent thermodynamic measurements, and were all close (within 15%) to those obtained from the rates. This agreement further supports the assignment of the transient signals presented here and in the previous femtosecond study to the recombination of O₂ to the picket-fence porphyrin. It also imposes a lower limit on the values of k₋₁ by limiting the size of higher-order corrections to Eq. 8. With k₁ fixed at the Smoluchowski value, we find that our results are consistent with any value of k₋₁ greater than ∼8 × 10⁸ s⁻¹.

From the transient absorption measurements, the reaction thermodynamics can be accessed. Thus the reaction enthalpy and entropy obtained from the van't Hoff plot (Fig. 5B, triangles) of the temperature-dependent equilibrium constants are −13.4 kcal mol⁻¹ and −33 cal mol⁻¹ K⁻¹. As mentioned above, the Arrhenius plot of the measured k_off values in Fig. 6B (circles) gives an activation energy for the dissociation process of ca. 12.8 kcal mol⁻¹ and an activation entropy of ca. 10 cal mol⁻¹ K⁻¹.

Because K_eq = k_on/k_off, the anomalous temperature behavior of k_on in the standard model must also be reflected in an inconsistency between the expectations of that model and the van't Hoff plot. This inconsistency displays itself in the fact that the difference between the activation energy of k_off and the absolute value of the reaction enthalpy from the van't Hoff plot gives an activation energy for k_on in the standard model of −0.6 kcal mol⁻¹, while a fit of the Smoluchowski theory to the Arrhenius equation (ln k₁ vs. 1/T) gives an effective “activation energy” for diffusion in bulk benzene (largely attributable to the exponential temperature dependence of the viscosity) of roughly 2.4 kcal mol⁻¹ (18), a discrepancy of ∼3 kcal mol⁻¹. In the two-step model, on the other hand, this discrepancy arises naturally as the difference in the two barrier heights and is in very satisfactory agreement with the value of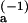 E − E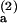 = 3.5 kcal mol⁻¹ obtained from the fit of k(T).

Geometrical restriction.

Because of the buried reaction center of the picket-fence porphyrin, we must also consider the geometrical restriction, steric hindrance, that may contribute to changes in the association on-rate. In the Smoluchowski theory, the reactant molecules are assumed to have uniform reactivity. It has long been recognized that this assumption does not hold in many cases, and extensive theoretical approaches have been proposed to correct for the anisotropic reactivity of reactants (see, e.g., refs. 22–26). In most of these models, the reactive sites are assumed to be on the surface of the molecules (22–24). In the present case O₂ is known to bind, from the encumbered side, to the cobalt center in the pocket formed by the four pickets (16). To a first-order approximation, an encounter formed by O₂ colliding with porphyrin at the area defined by the four pickets can be assumed to be the effective encounter leading to the association.

When this simple model is used, the reaction rate for O₂ binding to picket-fence porphyrin is calculated to be about 1/40 of that estimated from Smoluchowski's theory, a disparity similar to that observed. The temperature dependence is not readily understood on the same geometric basis, however. In the two-step model, the origin of both the reduction in rate and its temperature dependence are clearly defined. Any geometric restriction can be interpreted as an effective barrier for the corresponding processes. The role of geometric constraint may be examined by using molecular dynamic simulations.

Conclusions

Two major focuses of the study reported here are (i) the dynamics of the elementary processes involved over the femtosecond to microsecond time scale, and (ii) the direct measurements of the rates involved in the thermal bimolecular recognition and their temperature and concentration dependencies. The on-rate is k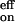 = 4.6 × 10⁸ s⁻¹ M⁻¹, the off-rate is k 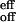= 1 × 10⁶ s⁻¹ at room temperature, whereas the initial O₂ release occurs in 1.9 ps (Fig. 7). The disparity between the experimental and the Smoluchowski diffusion rates suggests an entirely different energy landscape—-a two-step model, with reversibility in both steps, describes the recognition of the macromolecule, most probably nonselectively, and the selective reaction inside the structure. Because the rate for thermal dissociation is slow over a barrier of 12.8 kcal mol⁻¹, the equilibrium shifts toward the formation of ∼80% of O₂ adducts at room temperature, unlike the structure without the pickets; for bare cobalt porphyrin without the picket fence, the activation energy is 4.4 kcal mol⁻¹ (measured in 2-methyltetrahydrofuran without addition of a base) (27). The critical role of the pickets is in hindrance of the dissociation (barrier height effect) and in the selective O₂ binding, which is made with little competition from the solvent or the base at room temperature. The formation of intermediate structure(s) actually facilitates the final recognition on the global energy landscape, which must involve both the diffusion in the solvent and the intramolecular rearrangement of the porphyrin structure. By tuning the temperature, we are able to control the extent of such motions. This two-step mechanism is relevant to macromolecular biological processes of enzymes and DNA/drug recognition. It is remarkable that the process in the initial femtosecond/picosecond O₂ liberation is similar to that observed for the CO/myoglobin system (28). For the O₂/picket-fence system studied here, the nanosecond/microsecond process in solution at room temperature is totally determined by the thermal bimolecular on and off dynamics of recognition.

Abbreviation

CoP

cobalt picket-fence porphyrin