Information theory analysis of patterns of modulation in the advertisement call of the male bullfrog, Rana catesbeiana

Abstract

Male bullfrogs often amplitude modulate the envelopes of the individual notes (croaks) in their multinote advertisement calls. These amplitude modulations change the envelope of the note from smooth and unmodulated to one with varying numbers of modulations. A Markov analysis shows the pattern of change in the envelope to be highly ordered, but not completely so (semi-Markovian). Three simple rules govern the presence or absence of modulations in individual notes. These rules are (1) all calls begin with an unmodulated note; (2) the first note to be modulated will contain only one modulation; and (3) when a change in modulation occurs from one note to the next, it does so with an increase or a decrease of one modulation only. The addition of modulations is correlated with an increase in note duration. Physiologically, the presence of modulations might increase the precision of temporal coding of note periodicities in the central auditory system.

I. INTRODUCTION

Animals use acoustic signals of different form and complexity to communicate such messages as species identification, individual identification, advertisement of social status, advertisement of biological fitness, sexual motivation, and aggressive motivation. Some species have evolved large, complex repertoires to communicate these different messages, while others use a more limited repertoire. A fundamental question in the study of acoustic communication concerns how animals are able to convey multiple, biologically relevant messages with a limited number of signals. The acoustic behavior of anuran amphibians (frogs and toads) has been extensively studied as a model of a communication system consisting of a relatively small repertoire (Wells, 1977; Gerhardt and Huber, 2002). In some species, separate notes in a call communicate distinct messages to different receivers (Narins and Capranica, 1978), while in other species, the same notes may send simultaneous, different messages to different receivers (Capranica, 1965). The incorporation of different messages within a limited repertoire may be achieved by varying the complexity as well as the degree of stereotypy of the signal (Gerhardt and Huber, 2002).

The male bullfrog (Rana catesbeiana) emits a harmonically complex advertisement call that is important for regulating both male–male territorial and male–female attractive interactions (Emlen, 1968; Wiewandt, 1969). The spectral and temporal structure of this vocalization has been described in several publications (Capranica, 1965; Wiewandt, 1969, Bee and Gerhardt, 2001; Bee, 2004; Simmons, 2004). The advertisement call consists of a series of 1–12 individual notes (croaks). The one-note call has been categorized as having a territorial or aggressive function (Capranica, 1965), but the communicative function of the variation in number of notes beyond one has not been definitively established. Each note consists of a number of harmonically related frequencies, extending from about 200 to about 2000 Hz, with a missing or attenuated fundamental frequency around 100 Hz. There is considerable interindividual variability in acoustic properties of individual notes (Bee and Gerhardt, 2001; Bee, 2004). Males may be able to use these differences to discriminate neighbors from strangers, and near neighbors from far neighbors (Davis, 1987; Boatright-Horowitz et al., 2000; Bee and Gerhardt, 2001). Which features female bullfrogs use to choose particular males in a chorus has not been established.

The purpose of this study is to describe and analyze a feature of the male bullfrog’s advertisement call that has not as yet been addressed in the literature. Whereas the envelope, or overall shape, of the individual notes has typically been represented as smooth and unmodulated (Capranica, 1965; Bee and Gerhardt, 2001; Bee, 2004; Simmons, 2004), this is frequently not the case. Rather, males often add extra modulations to the envelopes of the individual notes in their calls. The effect of these extra modulations is to change the shape of the envelope so that visually it contains partial gaps, or repetitive valleys. Human listeners perceive these gaps as slight hesitations or pauses (“stutters”). Using analyses based on information theory (Shannon and Weaver, 1949), we characterize the pattern of change in the envelope of individual notes in the advertisement call. Our data show that modulations are added to individual notes in a highly ordered fashion. The robustness of the pattern suggests that these modulations may serve some communicative function.

II. MATERIALS AND METHODS

A. Field sites

Recordings of the calling activity of male bullfrogs from 1994 (N = 10) and 2003 (N = 10) were used to analyze the presence of modulations in individual notes in their advertisement calls. In July 1994 spontaneous chorusing was recorded at a natural bullfrog breeding pond (80 × 35 m) located in eastern Rhode Island (41°44′34″N, 71°20′14″W); analysis of the vocal interactions between males in this chorus has been published previously (Boatright-Horowitz et al., 2000). Air and water temperatures were measured to an accuracy of 0.5 °C during each recording session and ranged between 21 and 25 °C. Chorus density varied from eight to ten vocalizing males each night.

In June and July 2003, spontaneous chorusing was recorded (as part of a larger experiment, results of which will be presented separately) at three breeding sites in Rhode Island and Massachusetts. The location of the 1994 recordings served as site 1 in the 2003 recording sessions. Chorus density varied between six and eight vocalizing males. Site 2, located in central Massachusetts (42°25′47″N, 71°49′35″W), is a permanent pond approximately 100 m in length and 30 m wide. Chorus density ranged from six to ten vocalizing males. Site 3, located in northwestern Rhode Island (41°45′00″N, 71°45′00″W), is a permanent pond approximately 90 m long and 25 m wide. Chorus density was lower at this site, ranging from three to five calling males per night. Air and water temperatures of the three sites were measured to an accuracy of 0.5 °C and ranged between 17 and 26 °C.

B. Data collection

During 1994, spontaneous chorus activity was recorded on 3 nights between the hours of 22.00 and 00.15 h. Male advertisement calls were recorded using a battery-powered Marantz cassette recorder (model PMD430: frequency response 0.05–14 kHz, ± 3 dB) and a Bionic Ear microphone (frequency response 0.1–14 kHz, ± 3 dB) positioned on a Styrofoam platform placed in the water 1 m from an actively calling male. In 2003, chorus activity was recorded on 10 nights between the hours of 21.00 and 01.00 h using a Midnight Blue MB2000L (frequency response 0.06–15 kHz, ± 3 dB) or Sennheiser ME66 (frequency response 0.05–20 kHz, ± 3 dB) microphone, positioned on a Styrofoam platform about 1 m from individual frogs, and recorded onto the Marantz cassette recorder. Recording sessions lasted between 30 min and 3 h depending on the activity of the chorus. Individual males within each chorus were identified through field notes and visual and auditory inspection of each individual’s calls. Such identification is possible due to the small amount of variation in fundamental and dominant frequencies within an individual’s calls, whereas significant variability can be detected between the calls of individual frogs (Bee and Gerhardt, 2001). In addition, calling males maintained relatively fixed territorial positions during a single night’s chorus and were easily identified by spatial location.

C. Data analysis

Spontaneous vocalizations were converted to 44.1-kHz, 16-bit WAV-format sound files using cooledit 2000. Figure 1 is an oscillogram of an advertisement call recorded during the summer of 1994. This particular call consist of six individual notes. The first note has a smooth, unmodulated envelope, while the envelopes of the other five notes contain modulations. For each call, the numbers of notes and the number of modulations within each note were determined in cooledit by visual and auditory inspection. The frequency of modulation, the fundamental frequency, and the frequency spectrum of each note were analyzed by a custom-written matlab v 6.5 (MathWorks, Natick, MA) script. Duration of individual notes was measured using cooledit (1-ms resolution) and analyzed using spss v. 11.5 statistical packages.

FIG. 1.

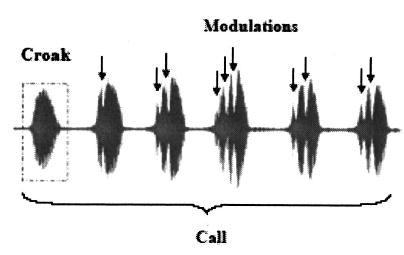
Oscillogram of a male bullfrog’s call recorded at site 1 in 1994. This particular call is made up of six individual notes or croaks. Arrows point to modulations or gaps seen in individual notes. The first note contains no modulations; notes two through six contain 1, 2, 3, 2, and 2 modulations, respectively. Time-domain waveform was exported from cooledit 2000.

To analyze any pattern in the incorporation of modulations within notes, all advertisement calls with no modulations in any notes were eliminated. Calls whose individual notes could not be completely analyzed due to overlap by calls of neighboring males or interference by nonbiological sources of noise were eliminated as well. The remaining calls were analyzed using uncert, a program that examines serial dependencies in sequences of events using Markov chain analysis (Hailman and Hailman, 1993). The program calculates frequencies and probabilities of occurrence of a series of events, the frequencies and probabilities of transition from one event to another, and the uncertainties associated with the events and their transitions. These analyses can be used to evaluate the organizational complexity of, for example, a signal repertoire (McGowan et al., 1999). In our data set, the sequence of events is the number of modulations within consecutive notes in a call. The hypothesis tested is that the number of modulations changes in a systematic way from note to note.

The diversity in the series of events is represented by an uncertainty value, a logarithmic measure (Hailman and Hailman, 1993) based on communication theory (Shannon and Weaver, 1949). To find the maximum amount of uncertainty in a data set, the following formula is applied: U_m = log₂ K, where U_m measures the diversity of events within a sample, log₂ is the logarithm to the base 2, and K denotes the number of different kinds of events involved. Consider, for example, an animal’s repertoire consisting of just one kind of event. The maximum uncertainty would be calculated as U_m = log₂(1) = 0. This makes intuitive sense, because with only one event in a repertoire, there would be absolutely no uncertainty as to what kind of event would follow. Zero-order uncertainty (U₀) is a measure of the probabilities of each of the kinds of events and thus the complexity of the repertoire. Within each data set of events, each individual event (i) has its own frequency of occurrence (F_i). The total number of events of all kinds is the sum of the total frequencies (N). This means that the probability that event i (or P_i) will occur equals the frequency of i (or F_i) divided by the total frequencies of all events (N). If all events are equally probable, U₀ = U_m. First-order uncertainty (U₁) measures the dependencies between first and second events, and second-order uncertainties (U₂) measure the transitional probabilities between event pairs and third events in sequences (Hailman and Hailman, 1993). Although higher measures of uncertainties exist, our data do not exhibit the complexity that would warrant application of them.

III. RESULTS

A. General patterns

A total of 5567 bullfrog calls was collected from 17 recording sessions. Of these calls, 2599 consisted of single-and multinote calls that contained no modulations. Within the remaining 2968 calls, 432 could not be completely analyzed due to interference or call overlap and were eliminated from further analysis. This left a total of 2536 calls made up of 13 081 individual notes that were further analyzed for any pattern in the presence of modulations. Results of analysis of these calls listed according to date and sampling site are shown in Table I.

TABLE I.

Bullfrog advertisement calls collected during 1994 and 2003 by date and site. The number of calls, number of calls with modulations (mods), and number of one-note calls are indicated for each recording session. More than 80% of the modulated calls conform to the two patterns identified.

				% Conformation to pattern		One-note calls
Date	Site no.	Total calls	Calls with mods	“begins with 1 mod”	“+ or − 1 mod”	Total	% with mods
7/02/94	1	406	155	87.1	99.9	196	0
7/02/94	1	307	116	92.2	98.3	165	0
7/03/94	1	299	137	92.0	99.3	123	0
7/08/94	1	290	171	81.9	91.2	165	0
6/24/03	1	249	67	94.0	100	28	0
6/25/03	1	505	245	89.4	98.0	71	0
6/26/03	1	495	228	92.6	98.7	32	0
6/27/03	1	435	180	85.6	94.4	105	0
6/28/03	1	280	102	92.2	96.1	92	0
6/29/03	2	321	232	96.1	97.4	15	0
6/30/03	2	335	231	99.1	99.6	30	0
7/06/03	1	562	230	89.6	98.3	127	0
7/07/03	1	366	142	86.6	97.2	96	0
7/08/03	2	184	81	93.8	98.8	36	0
7/10/03	3	116	58	100	96.6	30	0
7/13/03	1	254	89	85.4	93.3	84	0
7/14/03	3	163	72	97.2	100	60	0

All single-note calls (N = 1455) had unmodulated envelopes. On any recording night, between 27%–72% of all calls (mean 30.4%) contained at least one note with modulations. Between 81.9%–100% of calls that contained any notes with modulations began with one unmodulated note. The mean percent of calls conforming to this “addition of modulations begins with 1 modulation” rule was 91.46% ± 5.1%. When the number of modulations increased or decreased between successive notes within a call, it did so by just one modulation in 91.2%–100% of the calls. A mean of 97.5% ± 2.5% of calls followed the “modulation increases or decreases by one” rule.

The number of modulations overall varied from 1 to 6 in separate calls, with modulation frequencies all below 12 Hz. One animal produced 5 notes with 7, 8, or 9 modulations, but this occurred so rarely that these notes were excluded from analyses with uncert.

B. Uncertainty analyses

The data set was categorized into seven different kinds of events based on the number of modulations (0 to 6) observed in call notes. Based upon the analysis performed by uncert, Table II reveals the frequencies and probabilities of the occurrences of each of the seven kinds of events. Maximum uncertainty (U_m) as computed on seven events is 2.81 bits/event and zero-order uncertainty (U₀) is 2.03 bits/event. A bit is a contraction of computer language’s “binary digit” and is considered the basic unit of information. What this means is that the number of bits is the power to which the number 2 must be raised in order to give the number of equiprobable messages in a signal or a system (Lewis and Gower, 1980). Table III shows a matrix depicting the frequencies of the events as they transition either to the following event or as a repetition of themselves. To obtain a Markovian chain analysis, the frequencies in Table III were converted to probabilities to give a clearer picture of the pattern of insertion of modulations. Based upon those probabilities, U₁ is calculated as 1.31 bits/events, and U₂ as 1.27 bits/event.

TABLE II.

Zero-order analysis. Frequencies and probabilities of occurrence of seven kinds of events as calculated from uncert.

Event	Frequency	Probability
0	4411	0.3372
1	3613	0.2762
2	3401	0.2600
3	1338	0.1023
4	285	0.0218
5	29	0.0022
6	4	0.0003

TABLE III.

First-order analysis. Frequencies (and probabilities) of transition from preceding to following events

	Following event
Preceding event	0	1	2	3	4	5	6
0	1791 (0.4168)	2274 (0.5294)	220 (0.0512)	9 (0.0021)	2 (0.0005)	0 (0.00)	0 (0.00)
1	100 (0.0378)	1033 (0.3899)	1482 (0.5590)	32 (0.0121)	1 (0.0004)	0 (0.00)	0 (0.00)
2	10 (0.0043)	290 (0.1234)	1419 (0.6038)	624 (0.2655)	7 (0.0030)	0 (0.00)	0 (0.00)
3	5 (0.0050)	16 (0.0160)	274 (0.2740)	577 (0.5770)	128 (0.1280)	0 (0.00)	0 (0.00)
4	0 (0.00)	0 (0.00)	5 (0.0200)	95 (0.3800)	131 (0.5240)	19 (0.0760)	0 (0.00)
5	0 (0.00)	0 (0.00)	1 (0.0357)	1 (0.0357)	16 (0.5714)	8 (0.2857)	2 (0.0714)
6	0 (0.00)	0 (0.00)	0 (0.00)	0 (0.00)	0 (0.00)	2 (0.5000)	2 (0.5000)

Individual graphs for each event are shown in Fig. 2. For each of the graphs, the initial state (S) is identified by the number in the upper-right corner. The probability of the next event is illustrated for each of the seven possibilities (0 through 6). For example, the event state S-0 is followed by a repetition of itself with a probability of 0.42, by S-1 with a probability of 0.53, and by S-2 with a probability of 0.05. Event state S-1 is followed by S-0 with a probability of 0.04, by a repetition of itself by 0.39, by S-2 with a probability of 0.56, and by S-3 with a probability of 0.01. Inspection of the individual graphs shows the increased probabilities of an event being followed by itself, by the preceding event, or by the following event. This pattern is precisely predicted by the “number of modulations increases or decreases by one” rule.

FIG. 2.

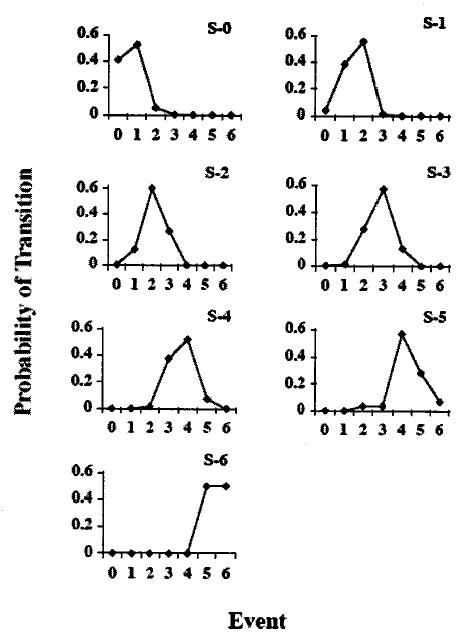
Probabilities of transition from each of the seven kinds of events (S-0 to S-6, upper right corner in each graph) to each of the events (0 through 6 on x axis). For example, a note containing zero modulations (upper-left graph) is followed by another note with no modulations with a probability of 0.42, by a note with one modulation with a probability of 0.53, by a note with two modulations with a probability of 0.002, by a note with 4 modulations with a probability of 0.0005, and by a note with 5 or 6 modulations with a probability of 0.

This pattern of transition can be graphically represented through the use of kinematic graphing. Kinematic graphs represent the temporal or sequential ordering of events. Because a system can only be in one state at a time, each state must exclude all other states. In addition, the states must be discrete and easily discriminated from one another (Sustare, 1978). The present data follow these rules perfectly. A male bullfrog can produce only one event state (a single note) at one time, and each event state within its call is discernible from all others (zero through 6 modulations in individual notes). In our kinematic diagram (Fig. 3), circles are used to represent individual events. Events are categorized and labeled according to the number of modulations contained within a note, beginning with S-0 (unmodulated), S-1 (one modulation), S-2 (two modulations), and so forth up to and including S-6 (six modulations). Each time one state ends and is followed by another state, a transition is said to occur. When a transition occurs, it is depicted by an arrow between the two state events. The direction of the arrow shows the temporal sequence of the events—always pointing away from the initial state and towards the following state. Recurrent arrows, which point from one state back to itself, represent a temporal repetition of that state. When all arrows are included in the kinematic graph, a complete picture of the behavior of the system results. Beginning with event S-0, 41.7% of the total S-0 events are recurrent (repeating); 52.9% transition to event S-1; 5.1% transition to event S-2; and very small fractions transition to events S-3 and S-4 (0.021% and 0.005%, respectively). Due to the relatively small amounts of information these transitions add to the system, coupled with the attempt to maintain clarity in the diagram, they are not represented by arrows in the kinematic graph. Moving through the graph, the same observations can be made for each of the event states (S-1 through S-6), with the frequencies of transitions emanating from each of the event states totaling 100%.

FIG. 3.

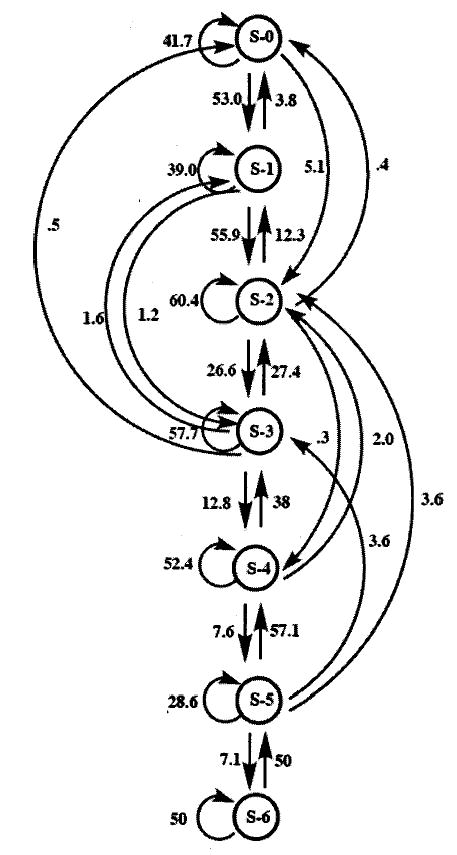
Kinematic diagram of first-order Markov chain analysis. Events are represented by circles (S-0 through S-6, depending upon number of modulations contained within the note). Transitions between events are depicted by arrows pointing away from an initial event and towards a following event. Recurrent arrows represent repetitions of initial events. Probabilities of transitions are found next to arrows.

C. Correlation with other acoustic parameters

The addition of modulations to the envelope of individual notes is correlated with an increase in note duration. This trend is shown in Fig. 4 for an individual male. Data are best fit by a cubic regression (r² = 0.83, P<0.01). Over all males, the relationship between note duration and number of modulations is statistically significant (ρ = 0.63, P<0.001). In contrast, in advertisement calls with no modulated notes, there is no significant relationship (ρ = 0.12) between note duration and its position within the call (that is, later notes do not have longer durations than earlier notes). The change in duration between successive notes thus is related to the insertion of modulations, not to note position.

FIG. 4.

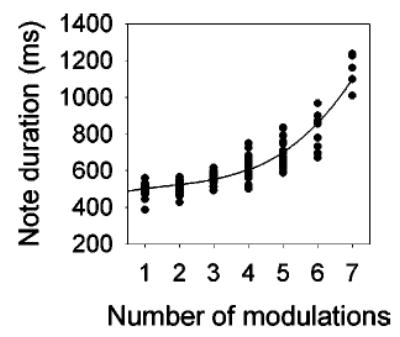
Relationship between note duration and number of modulations per note in the spontaneous vocalizations of one male recorded at site 1 in 1994. The curved line is the best-fitting regression through the data.

Although the insertion of modulations into successive notes followed the patterns described for all males, there was individual variability in the extent to which males added modulations to their calls. Individual variability was determined for the ten males recorded in 1994, during sessions in which each male was recorded for periods of about 3 h. The percent of calls that included any modulations varied from 0% to 100% between individuals. There was no significant relationship (r² = −0.06) between the percent of calls that included modulations and fundamental frequency of unmodulated notes in an individual’s calls. From this analysis, we infer that the insertion of modulations may be related to chorus dynamics or to female choice rather than to male body size (which is correlated with fundamental frequency; Bee and Gerhardt, 2001).

D. Variation over chorus time

The numbers of calls containing modulations in any notes as a percent of total calls for all males from site 1 in 2003 are shown in Fig. 5(A). The percent of calls with modulations is low on the first recording day (which was the first day males were vocally active at that site), rises to a maximum of about 50% on the second day, and levels off around 40% until the end of the calling season at that site. Data from an individual male on one night, recorded at site 1 in 1994, are shown in Fig. 5(B). The number of notes with modulations (regardless of the number) given by this male varies over the entire chorusing bout, with a peak between calls 40 and 50. Notes with modulations are not restricted to either the beginning or the end of the calling bout, but occur throughout and seem to alternate with unmodulated calls.

FIG. 5.

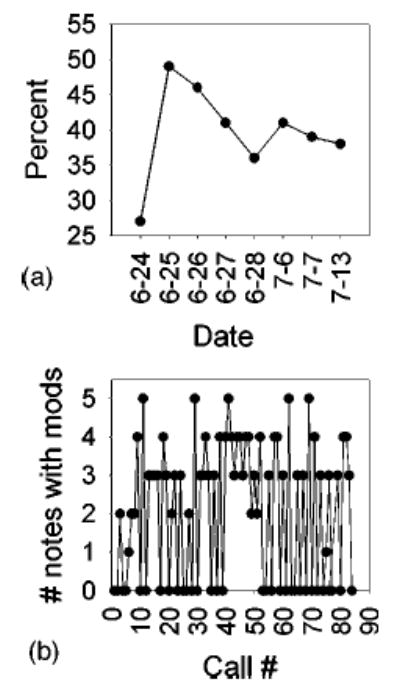
(A) Percent of calls containing any modulations as a function of all calls in the spontaneous vocalizations of male bullfrogs recorded at site 1 in 2003. (B) Number of notes with modulations in the spontaneous calling of one male recorded at site 1 in 1994.

IV. DISCUSSION

Individual notes in the advertisement call of male bullfrogs often contain extra envelope modulations that visually appear as gaps within an individual note and which acoustically to human listeners resemble pauses or “stutters.” There appear to be three simple rules that govern the pattern of incorporation of these modulations within individual notes in an advertisement call. First, all calls begin with an unmodulated note. Second, the first note to contain a modulation contains only one. Third, the number of modulations changes systematically between notes, with an increase or a decrease of one modulation only. Adherence to these rules is exceedingly robust. Of the 2536 calls analyzed, 100% began with a note containing no modulations, 91.5% followed the “modulation begins with one” rule, and 97.5% followed the “plus or minus one modulation” rule. This pattern is consistent between individual males, as well as across choruses and breeding sites. The regularity of the pattern suggests that it serves some biological significance in the communication behavior of the bullfrog.

A. Markov chains, properties, and processes

Markov chain analyses were developed as a way of determining if events that occur in sequence are independent of one another. A crucial feature of these analyses is the concept of uncertainty (or entropy), which is calculated using the number of events that occur in a particular sequence. When such events are completely independent of one another (i.e., the previous event has absolutely no influence on the immediately following event), the data are described as exhibiting the Markov property. At the other end of the spectrum are previously occurring events that absolutely determine the appearance of the following event. These types of data are termed Markov processes. In a Markov process, knowing which event occurs first will completely predict which event will follow. Animal behavior often falls between these two extremes and is therefore labeled semi-Markovian (Fagen and Young, 1978). This simply means that the last event the animal engages in may be a good predictor, albeit not a perfect one, of the next event to follow. Because different sets of data vary in their degree of approach to true Markov processes, information theory (Shannon and Weaver, 1949) can be used to estimate how much uncertainty occurs in a sequence of events, and thus provide an estimate of the amount of redundancy or diversity in a particular data set. This kind of analysis has become a powerful quantitative tool for examining and analyzing animal communication systems in diverse species and across a range of modalities. Information theory has been used to categorize the whistle signals of dolphins (McGowan et al., 1999, 2002) and the call repertoires of Mexican chickadees (Ficken et al., 1993), and to analyze aggressive communications in mantis shrimp (Dingle, 1969) and hermit crabs (Hazlett and Bossert, 1965). It has also been applied to analysis of intermale behavior of grasshoppers (Steinberg and Conant, 1974), the study of brood recognition in Mexican free-tailed bats (Beecher, 1989), and the mutually symbiotic relationship between goby fish and snapping shrimp (Preston, 1978). It is this generality of application that makes information theory so useful in examining the capacity, structure, and organization of animal repertoires.

Uncertainty analyses reveal that the appearance of modulations in bullfrog advertisement calls follows a semi-Markovian, deterministic pattern. This is shown in the sizable drop in uncertainty that occurs between U₀ and U₁, with less of a drop between U₁ and U₂. The drop between U_m and U₀ shows that knowing the relative frequencies of the seven events in the data set has decreased the amount of uncertainty, and the drop from U₀ to U₁ has established the existence of a pattern. The low value of U₁ is consistent with the “plus or minus 1” rule, since knowing how many modulations (x) the first note has strongly implies the next note will contain x, x + 1, or x − 1 modulations. The analyses suggest that information transfer is occurring based upon the ordered frequencies between successive events.

B. Mechanisms of production

Calling is an energetically costly behavior for frogs, with an oxygen demand that exceeds that occurring during forced exercise (Taigen and Wells, 1985). In Hyla, the trunk muscles are specialized for high-power output, but are highly susceptible to fatigue (Girgenrath and Marsh, 1999). It is possible that the pattern of insertion of modulations reported here reflects fatigue of the vocal musculature. For example, the production of modulations in a series of successive notes might indicate that the male was simply running out of breath. Such a fatigue hypothesis implies that bullfrogs would incorporate more modulations in their calls at the end than at the beginning of a nightly chorus, and that the aggregate chorus would show more modulations at the end than near the beginning of the calling season. Our behavioral data do not show such a simple trend.

In Bufo, amplitude modulation of vocalizations is produced by both active (pattern of contraction of the thoracic musculature) and passive (vibration of the arytenoid cartilages) mechanisms (Martin, 1971). Which mechanism best accounts for the pattern of modulation seen here cannot be determined from the present data. One possibility is that the production of longer call notes might passively engage the arytenoid cartilages, thus producing modulations. The positive relationship between note duration and number of modulations supports this hypothesis. Inserting modulations might also allow the male to extend the length of the individual notes in his calls while reducing the amount of air exchange needed. This in turn implies that longer duration notes have a different perceptual significance than shorter duration ones. Male bullfrogs do not respond readily to playbacks of short-duration notes outside the normal range of variability in note duration, but they respond equally vigorously to playbacks of modal duration and long-duration notes, showing patterns of generalization rather than discrimination for this acoustic feature (Simmons, 2004). These data suggest that the insertion of modulations per se might not have a perceptual significance to other males in the chorus. On the other hand, female bullfrogs, like female frogs of other species (Gerhardt and Huber, 2002), may prefer notes with longer rather than shorter durations, and use note duration as an indicator of male quality. This hypothesis has not been tested directly.

C. Physiological relevance of envelope modulation

Envelope periodicity is an important feature mediating vocal interactions in many anuran species (Gerhardt and Huber, 2002). In playback experiments, male bullfrogs respond differentially to synthetic advertisement calls with unmodulated and modulated notes, when these envelope differences are produced by changes in either the phase structure or the harmonic structure of the signal (Hainfeld et al., 1996; Simmons and Bean, 2000). Although these experiments did not explicitly test responses to signals that resemble the modulation pattern described here, they predict that modulation is a salient perceptual cue for these animals. Physiological experiments show that the 100-Hz periodicity of unmodulated synthetic notes and the envelope fluctuations produced by changes in phase structure are encoded in the bullfrog’s eighth nerve by a neural code based on phase-locked discharges (Schwartz and Simmons, 1990; Simmons et al., 2001). This temporal code seems to weaken in the central auditory system, such that, in the auditory midbrain (torus semicircularis, TS), only a relatively small number of neurons respond with phase-locked discharges to modulations in the 90–100-Hz range (Simmons et al., 2000). Yet, strong phase-locked activity continues to occur even in the TS in response to signals with amplitude modulations of 20–50 Hz (Bibikov and Nizamov, 1996; Simmons et al., 2000). The modulated notes described in this study have low-frequency modulations of 12 Hz or less. Although such low frequencies have not been tested in studies of modulation coding in the frog’s auditory midbrain, we predict that these stimuli would produce strong phase locking, thus retaining a temporal code for processing of the advertisement call in the central auditory system.