Estimating prokaryotic diversity and its limits

Abstract

The absolute diversity of prokaryotes is widely held to be unknown and unknowable at any scale in any environment. However, it is not necessary to count every species in a community to estimate the number of different taxa therein. It is sufficient to estimate the area under the species abundance curve for that environment. Log-normal species abundance curves are thought to characterize communities, such as bacteria, which exhibit highly dynamic and random growth. Thus, we are able to show that the diversity of prokaryotic communities may be related to the ratio of two measurable variables: the total number of individuals in the community and the abundance of the most abundant members of that community. We assume that either the least abundant species has an abundance of 1 or Preston's canonical hypothesis is valid. Consequently, we can estimate the bacterial diversity on a small scale (oceans 160 per ml; soil 6,400–38,000 per g; sewage works 70 per ml). We are also able to speculate about diversity at a larger scale, thus the entire bacterial diversity of the sea may be unlikely to exceed 2 × 10⁶, while a ton of soil could contain 4 × 10⁶ different taxa. These are preliminary estimates that may change as we gain a greater understanding of the nature of prokaryotic species abundance curves. Nevertheless, it is evident that local and global prokaryotic diversity can be understood through species abundance curves and purely experimental approaches to solving this conundrum will be fruitless.

The ability to measure bacterial diversity is a prerequisite for the systematic study of bacterial biogeography and community assembly. It is therefore central to the ecology of surface waters, the oceans and soils, waste treatment, agriculture, and global elemental cycles. However, the experimental definition of bacterial diversity has never been undertaken for any naturally occurring bacterial community anywhere, and the extent of prokaryotic diversity is widely held to be beyond practical calculation (1).

Our understanding of bacterial biogeography and community assembly is correspondingly vague, anecdotal, and controversial. For example, the global distribution of some aquatic protozoa has been used to assert that the entire microbial world is composed of a small number of ubiquitous organisms (2, 3), whereas the apparently endemic distribution of some bacteria has been used to suggest the opposite (4, 5). Perhaps more importantly, the inability to estimate diversity inhibits microbial ecologists from using or testing established theories of biogeography and community assembly, even though the complex nature of the microbial world means that microbial ecology is severely constrained by a lack of theory.

However, to estimate the extent of microbial diversity, it is not necessary to count every single species or taxa in a sample. It is sufficient to simply estimate the area under the bacterial species abundance curve for that environment. There is insufficient experimental evidence to support a particular parametric description of this curve. However, MacArthur (6) and later May (7) deduced that the highly dynamic and random growth that is thought to be characteristic of prokaryotes would lead to a lognormal species abundance curve. Subsequent work by statistical mathematicians, also assuming random growth, has confirmed this finding in exponential and logistic growth scenarios (8, 9).

On this basis, we are able to show how relatively easy to measure variables can be used to define bacterial diversity. The work does not presuppose a particular definition of a species, merely the existence of credible criteria for distinguishing between different organisms. For the purpose of this paper, this means a meaningful difference in the sequence of the 16S RNA gene. We use the term taxa as a shorthand for groups of bacteria that can be distinguished on that basis.

Relating Prokaryotic Diversity to Things We Can Measure

In log-normal communities S(N), the number of taxa that contain N individuals is traditionally (7) given by

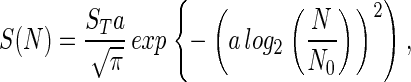where a is an inverse measure of the width of the distribution whose standard deviation is σ²: a = (2ln2σ²)^−1/2_; S_T is the total number of taxa, and N₀ is the modal abundance. S_T corresponds to the area under S(N) and is therefore a measure of the extent of diversity. The use of log₂ in Eq. 1 is a convention that stems from the original work in this area (10, 11).

Ideally, the parameters S_T, a, and N₀ would be estimated from a representative sample of measured species abundance data by using a statistical technique such as the method of moments or least squares analysis. However, the quantification of individual populations of bacteria in the environment is remarkably difficult. The experimental definition of S(N) for most values of N is impossible, or at least very difficult and time consuming, to determine. Therefore, an alternative method of parameterizing Eq. 1 is required that relies on properties of the population that can be easily identified. A method is developed here that uses two such properties: N_max and N_T. N_max is the number of individuals in the most abundant species, which can be relatively easily measured or inferred. N_T is the total number of individuals in the community. This can be confidently measured in microbial communities, as it is the total microscopic count.

Theoretically, N_T is defined by the integral

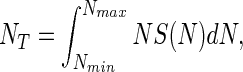where N_min is the number of individuals in the least abundant species. The function NS(N) (Fig. 1) is usually referred to as the individuals curve (7). If it is assumed that the log-normal species abundance curve is not truncated and therefore is symmetric about N₀, then it can be shown that,

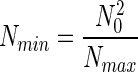and that, consequently, Eq. 2 becomes,

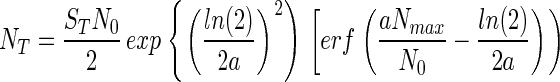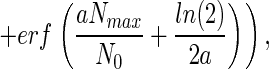where erf( ) represents the error function.

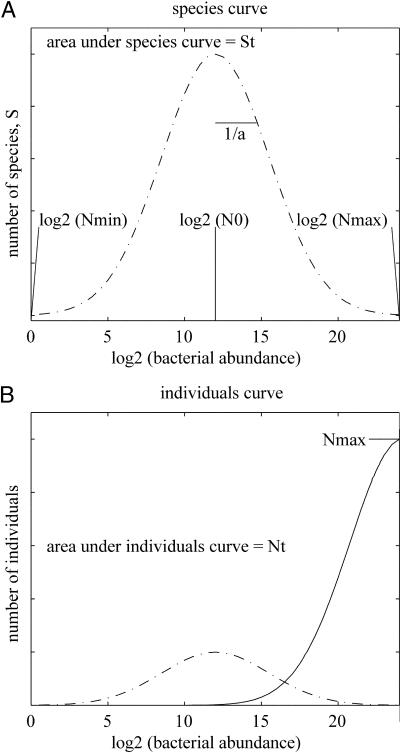
Fig 1.

Species abundance and individual abundance. (A) The lognormal species abundance curve. The x axis shows log₂(N), where N is bacterial abundance; the number of individuals within a species. The y axis shows the number of species, S, occurring at any abundance (N). N_max (x axis) is the number of individuals in most abundant species, N_min (x axis) is the number of individuals in the least abundant species, and N₀ (x axis) is the modal species abundance. The total diversity, S_T, is the area under the species abundance curve. The width of the species curve is inversely proportional to the spread parameter a. Here, one species with 2²⁴ ( = 1.6 × 10⁷) individuals occurs at N_max and one species with 2⁰ (=1) individuals occurs at N_min. (B) The individuals curve (solid) is found by multiplying abundance, N, by S, the number of species at that abundance (dots and dashes as in A not to scale). The total number of individuals in the sample is N_T, which corresponds the area under the individuals curve. N_max is the number of individuals in the most abundant species. Both N_max and N_T can be easily measured. This example obeys Preston's canonical hypothesis which states that the peak of the individuals curve coincides with N_max. This fixes the value of a. A and B show that most species occur with very low abundance, so direct empirical measurement of diversity is impractical.

Ultimately the aim is to find an expression that defines S_T in terms of N_max and N_T rather than a and N_0. N₀ can be removed from Eq. 4 by assuming that only one species will occur with N_max individuals, which means that S(N_max) = 1. Therefore_, from Eq. 1,

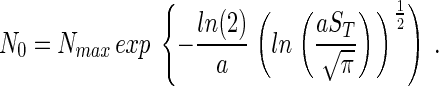Substituting Eq. 5 into Eq. 4 gives

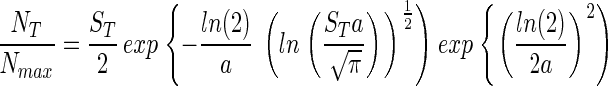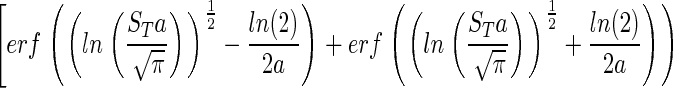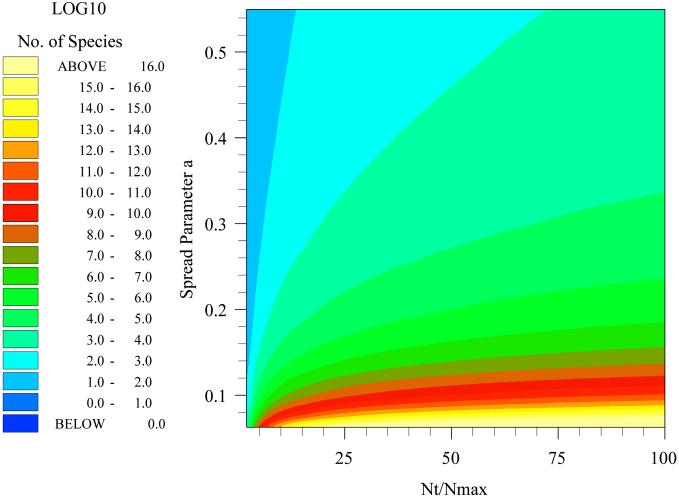
This rather complicated equation essentially states that N_T/N_max is a function of a and S_T. Thus, we can estimate S_T for any community, large or small, in which we can define a, N_T and N_max. This equation may be solved numerically (Fig. 2) to describe the relationship between the spread a and S_T the number of species or distinct taxa (displayed as log₁₀ in Fig. 2). We propose two methods for the estimation of a. However, first we wish to discuss the measurement of N_T/N_max.

Fig 2.

Relating species diversity to things we can measure. The figure shows how the number of species (color) varies with spread parameter, a, and the ratio of the total number of individuals (N_T) to the number of individuals in the most abundant single species (N_max).

The Measurement and Utility of N_T/N_max.

There are few reliable data on the relative abundance of even the most abundant representatives of microbial communities at either large or small scale. The quantitative fluorescent in situ hybridization (FISH) is perhaps the most appropriate method for considering data at a small scale. In the absence of such data the relative abundance of sequences in a clone library offers the best available information on relative abundance. Unfortunately, reports of relative abundance in clone libraries are nearly always based on one sample. Therefore we cannot, at present, incorporate the underlying sample to sample variation into our work. However, there is at least one paper (12) that suggests that the variation between clone libraries derived from the same environment is modest (coefficient of variation of 5–11%). If and when FISH data are extensively used in conjunction with our approach, it will be possible, necessary, and appropriate to take errors in measurement into account.

The reciprocal of the N_T/N_max ratio has already been proposed as a diversity index in its own right (13). May (7) found this index to be conceptually and computationally agreeable. It is therefore interesting and pleasing to note that a ranking of environments on the basis of ratio N_T/N_max (discussed below) shows soil > seawater > activated sludge. This is consistent with what experimentalists know about diversity in these environments.

Determining a by Using Preston's Canonical Hypothesis.

Preston (10, 11) has hypothesized specific relationships between the individuals curve and the species abundance curve known as Preston's canonical distribution. The theoretical explanation for the canonical hypothesis (14) is based on the random division and subdivision of resources. This theory assumes a degree of ecological and evolutionary homogeneity that may not be found in bacterial communities. However, by the same token, Preston's hypothesis may very well apply to ecologically and evolutionarily homogenous components of the bacterial community; for example the ammonia oxidizing bacteria (AOB).

Preston's hypothesis states that the peak of the individuals curve coincides with N_max, the number of individuals in the most abundant species. It follows (7) that

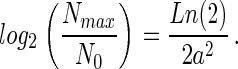By using the previous assumption that S(N_max) = 1 this expression may be inserted into Eq. 1 to give an expression relating S_T to a:

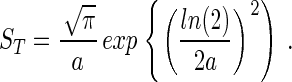Combining Eqs. 6 and 8 yields a function that relates N_T to N_max and a,

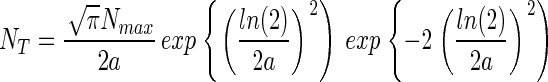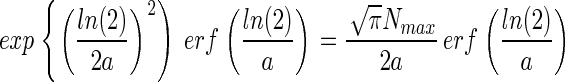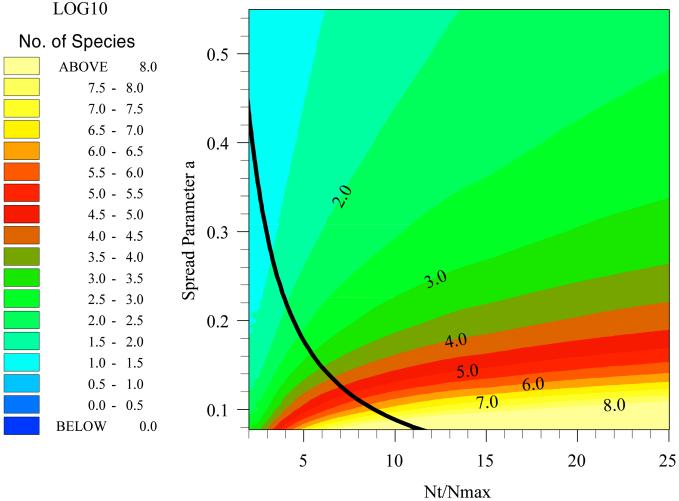
Thus, if N_T and N_max are known then Eq. 9 can be solved numerically for a and, subsequently, S_T can be estimated from Eq. 8. Fig. 3 shows that when the canonical hypothesis applies the diversity (displayed as log₁₀), estimated in this way, is extremely sensitive to N_T/N_max values.

Fig 3.

Estimating the spread parameter, a, by using Preston's canonical hypothesis. The color shows the number of species as spread parameter a and N_T/N_max vary. Preston's hypothesis states that the peak of the individuals curve coincides with N_max, the number of individuals in the most abundant species. This fixes the spread parameter, a, at a value that is shown by the solid line. Thus, where Preston's hypothesis is true, the total number of species for any value of N_T/N_max should lie along the solid black line.

Calculating Diversity by Using the Canonical Hypothesis

We are thus in a position to use the published clone libraries to estimate the diversity of those functional groups that appear to fulfill the condition of homogeneity. A clone library of AOB in the Arctic Ocean (15) had an N_T/N_max value of just 1.7. On this basis, it appears that AOB diversity of the entire Arctic Ocean could be as low as 6. This is not significantly greater than the estimated AOB diversity of some sewage works (16) and a great deal less than the AOB diversity in a small volume of soil (17).

There is some evidence of globally abundant AOB taxa; for example, the same AOB sequences have been found to be abundant in the Mediterranean Sea (18) and the Arctic Ocean (15); analogous observations have been made for sewage works (19). We can show that this does not necessarily mean that global AOB diversity is very low. For even if a single ubiquitous taxon comprised 15% of all of the AOB, the global diversity would be 10⁴.

This approach may be applied to other flora and fauna with even more confidence than bacteria because more is known about the distribution of such organisms and many have been shown to be canonical. Thus, this method could find a role in the rapid assessment of the diversity that is urgently required in the many threatened hyperdiverse communities around the world (1).

Determining a by Assuming N_min.

The second method for estimating the spread, a, is by knowing, or assuming, the value of N_min, the abundance of the least abundant species. By using Eq. 1, Eq. 3 and the assumption that S(N_min) = 1, S_T can be expressed in terms of a, N_min, and N_max,

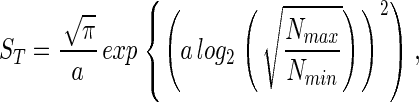and consequently, Eq. 5 can be rewritten,

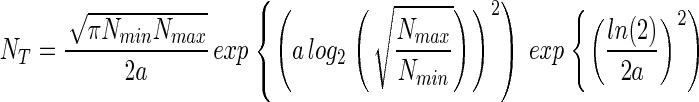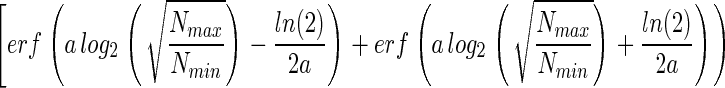Therefore, a knowledge of N_min, N_max, and N_T allows Eq. 11 to be solved numerically for a and, subsequently, S_T to be estimated with Eq. 10.

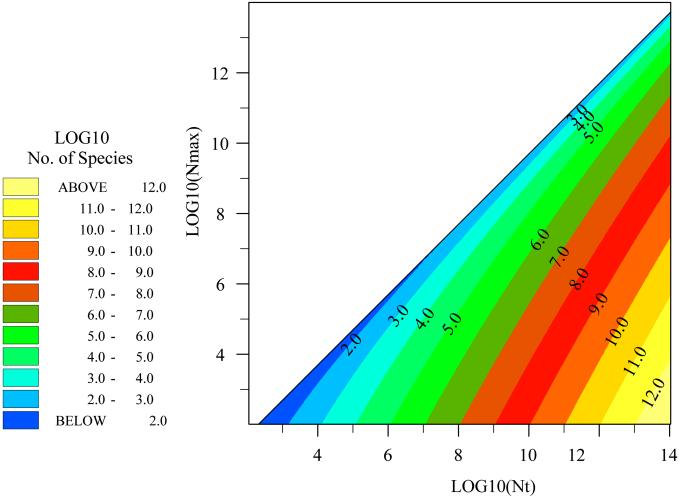
We propose that in small samples N_min will usually be 1 (Fig. 4). We reason that a small sample containing a large number of individuals (e.g., soil, seawater) will contain a large number of species. A slightly larger sample with a slightly larger number of individuals will have a slightly larger number of species. The smallest possible increase would be 1 species occurring at a density of 1. This may be an oversimplification, however, N_min values are likely to be small in small samples (N_T of about 10⁹ individuals). S_T estimates will not be sensitive to small deviations from the N_min assumption.

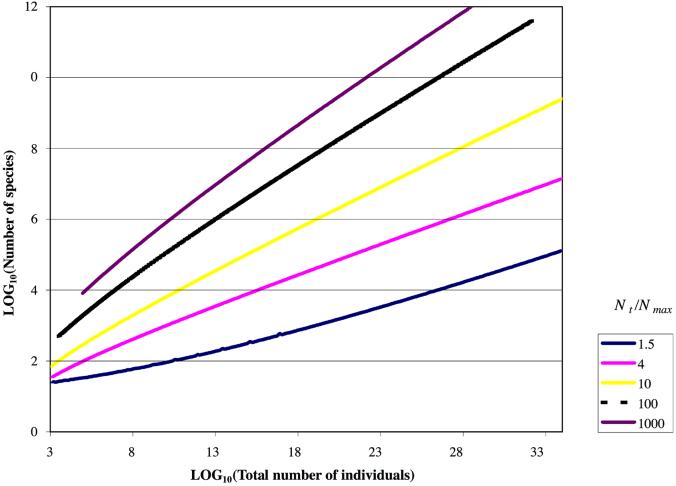
Fig 4.

S_T estimated by assuming the value of N_min, the abundance of the least abundant species is 1.

Calculating Diversity at a Small Scale Assuming N_min = 1

The species diversities predicted assuming N_min = 1 are realistic (displayed as log₁₀ in Figs. 4 and 5) and may be crudely compared with the published data and observations. Clone abundance information for the Sargasso Sea (20) suggest an N_T/N_max ratio of 4, and N_T is known to be about 10⁶ per ml, which suggests an S_T value of about 163 taxa for a milliliter of seawater. The same reasoning for a gram of soil (N_T/N_max of at least 10; N_T value of 10¹⁰; ref. 21) suggests an S_T value of about 6,300 taxa; a figure consistent with the value proposed by Torsvik (22) in her classic experiments on DNA/DNA hybridization kinetics in soil. Dykhuizen (23) reinterpreted Torsviks work, suggesting that the N_T/N_max was in fact between 100 and 1,000 and estimating the diversity of 30 grams of soil to be between 40,000 and over 500,000. Dykhuizen's proposed N_T/N_max values would permit diversities of between 10⁵ and 10⁶ in 100 g of soil. Thus, we are able to show that Dykhuizen's proposals are not only plausible, but probably inevitable unless the ratios he suggests are very wrong or the N_min value in the soil is very high indeed. These estimates for soil include spores and resting cells. These cells have a growth rate of just below zero. Because the average net growth rate in a soil must also be around zero (otherwise the numbers of individuals in a soil would increase inexorably) spores will clearly fall within a plausible random distribution of growth rates.

Fig 5.

The maximum possible diversity for differing numbers of individuals and different N_T/N_max ratios (under the assumption that N_min = 1). A ratio of 1,000–100 might apply to soils and sediments, whereas a ratio of 4 might apply to the sea or a lake. To crudely estimate the diversity of communities where N_min = >1 subtract the proposed N_min value from the known N_T value.

It follows that all clone libraries will underestimate diversity. For example, one of the most extensive published clone libraries is that of Godon (24), who found 133 bacterial taxa. Chao's (25) correction suggests a diversity of at least 223–320 taxa in a single sample taken from an anaerobic digester. Given an N_T/N_max ratio of 20 and an N_T value of 10⁹ (anaerobic digesters have about 10⁹ bacteria per ml and the most abundant clone accounted for 5% of all clones) our approach suggests a diversity an order of magnitude greater than this (just over 9,000). Presumably, even Chao's correction cannot compensate for gross underestimates. Although bias in the PCR, favoring rarer organisms and thus higher ratios, has been reported, the level of bias observed is modest (26) and cannot account for the discrepancy. Our FISH-based studies in wastewater treatment (activated sludge), suggest a ratio of just 1.5 (R. J. Davenport, M. Milner, and T.P.C., unpublished data) implying a diversity of about 70 taxa in a milliliter of activated sludge.

Calculating Maximum Possible Diversity at a Large Scale by Assuming N_min = 1

With care, the N_min = 1 approach may be used to speculate intelligently (under the assumption of lognormality) about the maximum possible value of S_T for very large areas and volumes. To do this we retain the assumption that N_min = 1, employ known or estimated values for the relative abundance of the most abundant individual, and expand the total number of individuals to suit our purpose (Fig. 5). For example, there are about 10²⁹ individual bacteria in the sea (27), two-thirds of which are Bacteria and one-third of which are reported to be Archaea (28). There is evidence of a single very abundant bacterial taxon (20) accounting for perhaps 25% of the planktonic marine bacteria, suggesting that there are less than 2 × 10⁶ bacterial taxa in the sea. On the other hand the global archaeal ratios have been reported recently (28) to be about 2, implying a maximum global planktonic marine archaea diversity of about 20,000 taxa. A lake with about 10¹⁵ individuals would have a diversity of not more than 8,000 taxa if it had an N_T/N_max ratio of 4. More prosaically, we have shown sewage works (activated sludge) to have ratios of about 1.5–2 (1 taxon is 50–65% of biomass), which implies, at most, about 500 individual taxa.

Can Local Diversity Constitute Global Diversity?

We can also shed light on the idea that global bacterial diversity is made up of a relatively small number of ubiquitous taxa. One way to tackle this question is to ask if all of the relevant diversity in the world had to fit it into one small component of an environment: how much diversity would there be, and would the required minimum abundance be so high as to preclude the possibility of speciation and extinction? The answer appears to depend on the environment and the taxonomic group. If the entire bacterial diversity of the seas could be accommodated (still with a ratio of 4) in just 1,000 m³ of sea (10¹⁵ individuals) the global diversity would be just 8,000 distinct taxa. The least abundant taxon would have 10⁸ representatives (not many by bacterial standards), which would (if evenly spread around the sea) give a mean concentration of 1 per 10 cubic kilometers. As the sea is a mixed environment, this might be construed as being everywhere.

If the entire bacterial diversity of the soil could be accommodated in a single ton of soil (also 10¹⁵ individuals) with a ratio of 100, the global diversity would be around 4 × 10⁶; this is not a small number. It would imply a minimum global diversity of about 4.5 × 10⁶ (assuming there are about 10²⁹ individual bacteria in the soil; ref. 27) which would mean, on average, one individual of the least abundant species for every 27 km². The atmosphere is thought to have an N_T value of 10¹⁹, which is sufficient to accommodate 4 × 10⁶ taxa (at a ratio of 100); however, the abundance of the rarest organisms would be very low indeed (40). The difference between soil and water perhaps explains why some marine and freshwater scientists believe in the ubiquity of all microbial taxa (2, 3), whereas those that study soils do not (4, 5). Interestingly, the minimum abundance values cited in our examples appear to be modest and do not appear (intuitively) to preclude speciation or extinction; i.e., a new species could attain these densities and an established species at these densities could disappear. Though, obviously, these questions might be complicated by how widely the organisms were distributed.

Alternative Distributions

We are aware of the importance of the underlying distribution. There are many distributions to choose from and new distributions are being proposed all of the time (29, 30). In the absence of sound empirical evidence it is essential therefore to choose a distribution on a rational theoretical basis. At present, the available theoretical evidence points strongly to a lognormal distribution (6–9). We would caution against anyone taking a “pick and mix” approach and choosing the distribution that would give the answer that they want. It will be far more productive to concentrate on the central intellectual question: what is the distribution?

We hope that this work represents a first step in the process in answering that question. Hubbell (30) suggests that there is a family of distributions from the lognormal through the log series to the geometric series and that the competing forces of speciation and invasion govern this distribution. Thus, the next step might be to get an experimental handle on invasion and speciation. A corollary of this view would be that the phylogenetic level at which a prokaryotic group is characterized would have an effect on the distribution. One is more likely to observe a rare species than a rare family, thus a species abundance curve might be lognormal, but a family or order abundance curve might not.

Concluding Comments

Our estimates are hampered by a lack of data on the abundance of even the most abundant organisms in the environment. However, we are confident that more quantitative data will become available in the near future. This in turn will allow us to refine our extrapolations. In particular, measuring the numbers of the second, third, and fourth (and so on) most abundant taxa, and adapting the method described here appropriately, could substantially improve our “quick and dirty” estimates (although not our underlying assumptions). Ultimately, this line of experimentation would lead to a proper description of a bacterial species abundance curve, and thus confirm (or disprove) our central assumption. In practice, this will be very difficult and probably very expensive; therefore, such an investigation should not be undertaken without a thorough mathematical exploration of the likely answer.

The differences between soil and planktonic environments are perhaps related to the lack of structure and resource (31) in the latter. However, it is not clear why the marine Archeal diversity appears to be so much lower than the Bacterial diversity, are the former subject to greater extinction or inherently less likely to speciate? We do not understand what the relationship is between the huge reservoir of diversity found in the soil and the diversity of the sea and lakes; do the former invade the latter? Moreover, an understanding of the real nature of, and mechanisms underlying, local and global N_min values will be central to an understanding of the extent of microbial diversity.

The deductions in this paper are based on theoretical indications of lognormality. This may turn out to be only an approximate description of reality (29, 30). Some may choose to disregard this sort of work because of this uncertainty. However, this is the counsel of despair. For we have clearly shown that the nature of bacterial species abundance curves is the central issue in the description of prokaryotic diversity and that simply counting species is an essentially endless task. The strategy exposed in this paper may be easily adapted for alternative distributions if or when compelling evidence is found to support their application to the prokaryotic world. For example, Hubbell's (30) work would require different distributions to be used for metapopulations (e.g., the entire sea) and subsamples. Microbial ecology, which drives the ecology of the planet, urgently requires approximate theoretical and experimental descriptions of the whole to complement the trend to ever more perfect experimental descriptions of the parts.

Abbreviations

• FISH, fluorescent in situ hybridization

• AOB, ammonia oxidizing bacteria