Waddington's canalization revisited: Developmental stability and evolution

Abstract

Most species maintain abundant genetic variation and experience a range of environmental conditions, yet phenotypic variation is low. That is, development is robust to changes in genotype and environment. It has been claimed that this robustness, termed canalization, evolves because of long-term natural selection for optimal phenotypes. We show that the developmental process, here modeled as a network of interacting transcriptional regulators, constrains the genetic system to produce canalization, even without selection toward an optimum. The extent of canalization, measured as the insensitivity to mutation of a network's equilibrium state, depends on the complexity of the network, such that more highly connected networks evolve to be more canalized. We argue that canalization may be an inevitable consequence of complex developmental–genetic processes and thus requires no explanation in terms of evolution to suppress phenotypic variation.

Waddington developed the concept of canalization to explain the “very general observation… that the wild type of an organism, that is to say, the form which occurs in Nature under the influence of natural selection, is much less variable in appearance than the majority of the mutant races” (1). Corroborating Waddington's observation are a number of experiments demonstrating increased phenotypic variance under extreme genetic or environmental perturbation (2–6). A key insight of Waddington was that the constancy of wild-type phenotypes in the face of genetic and environmental perturbations is best viewed as a buffering of the developmental process. That is, Waddington argued that the evolutionist's traditional focus on the genetic (i.e., hereditary) system must be supplemented by a focus on the epigenetic (i.e., developmental) system (7, 8). Waddington's favored view, evident in the above quotation, is that buffering of the epigenetic system evolves as a result of natural selection, in particular selection toward an intermediate optimum, i.e., stabilizing selection. Naively stated, this conclusion appears self-evident: as long as genetic variation exists, any mechanism that dampens the effects of that variation on the phenotype is expected to be favored by stabilizing selection. It is not surprising, therefore, that most attempts to model mathematically the evolution of canalization begin with Waddington's assumption of stabilizing selection (9–15). As we will see below, the implementation of this assumption can confound the action of natural selection with the process of development, thereby obscuring the role other forces may play in producing a canalized genetic system.

Despite the experimental and theoretical groundwork laid by Waddington, the mechanisms and evolutionary causes and effects of canalization remain elusive. However, in the current era of sophisticated developmental genetics and genome-scale functional analysis, canalization has begun to receive increased attention, both as a potentially solvable puzzle and as a framework for understanding the evolution of complex genomes. For example, Rutherford and Lindquist (6) recently uncovered vast genetic variation by compromising the function of Drosophila Hsp90, a stress-induced chaperone protein that confers stability on a variety of signal-transduction proteins. They conclude that Hsp90 serves as an evolutionary “capacitor,” buffering genetic and environmental variation except under extreme conditions, at which point the expressed variation becomes available for natural selection. This interpretation parallels the link drawn by Waddington between canalization and the inheritance of environment-induced phenotypic variation, or “genetic assimilation” (16), and provides a developmental–genetic mechanism for the breakdown of epigenetic buffering under extreme perturbation. Another perspective on canalization is now offered by the outpouring of genomic sequence and expression data in model organisms. For example, A. Wagner (17) analyzed jointly gene-sequence and gene-expression data on a genome-wide scale in yeast and concluded that robustness of the wild type to mutations is due not to genetic redundancy but to epistatic interactions between unrelated genes. Relying on previous theoretical results, he concluded that this robustness evolved as a response to stabilizing selection.

Mathematical modeling of canalization has also advanced recently. Not surprisingly, most reports consider stabilizing selection as the most pertinent evolutionary force. Gavrilets and Hastings (10) modeled a situation in which genotypes produce phenotypes with different degrees of sensitivity to microenvironmental variation (“developmental noise”) and showed that under stabilizing selection, canalization evolves. A. Wagner (13) explicitly modeled the developmental process along with the evolutionary process and reported the evolution of canalization under stabilizing selection (see more detailed discussion below). G. P. Wagner et al. (14) introduced a population–genetic modeling framework and concluded that canalization against environmental variation increases with increasing intensity of stabilizing selection, whereas canalization against mutation increases only up to a point, above which stabilizing selection too effectively purges the population of genetic variation, a prerequisite for selection for genetic canalization. They pointed out, however, the possibility that selection for environmental canalization may produce genetic canalization as a by-product. An example of a mechanistic basis for such a link is provided by Ancel and Fontana (15), who modeled the secondary structure of RNA as a phenotype subject both to microenvironmental variation and to optimizing selection. They found that selection for environmental insensitivity eventually leads to a halt in further evolution, as the phenotype becomes concomitantly canalized to mutation. Rice (12) favored a more abstract approach, focusing on a generalized mapping of genotype to phenotype. He used a geometrical representation of a “phenotype landscape,” in which epistatic interactions among genes are manifest as local curvatures of the phenotype surface. Canalization evolves under stabilizing selection, except under a scenario in which an already canalized population is subjected to a new phenotypic optimum, at which point “decanalization” may occur temporarily. Such an occurrence may be related to the process of genetic assimilation. Eshel and Matessi (9) presented an analytic model of genetic assimilation in which individuals randomly experience environments favoring different phenotypic optima, and in which genotypes differ in their sensitivities to different environments. They concluded that natural selection produces a genetic system that is canalized to produce the phenotype optimal in the most frequently experienced environment. Pál and Miklós (11) reached similar conclusions to those of Rice (12) and Eshel and Matessi (9). Kawecki (18) considered a different type of environmental variation, in which the selective regime is the same for all members of a population in a given generation but fluctuates from generation to generation. Under certain rates of fluctuation and strengths of selection, canalization is favored.

Demonstrating that stabilizing selection is sufficient to evolve genetic canalization does not demonstrate its necessity, nor does it illuminate the mechanism of buffering [except notably in the case of Ancel and Fontana (15)]. Indeed, it has been proposed (14, 15, 19) that buffering of genotypic differences may be a by-product of selection for environmental buffering. This is a potential explanation of why key developmental traits, presumably under strong selective pressure, may be canalized against mutations, despite the implications of G. P. Wagner et al.'s (14) population–genetic model. To explore the possibility that genetic canalization may be a by-product of other selective forces, we favor an evolutionary model that explicitly incorporates the developmental process as well as the population–genetic one. Our starting point is the model of A. Wagner (13), who treats development as the interaction of a network of transcriptional regulatory genes, phenotype as the equilibrium state of this network, and fitness as a function of the distance between an individual's equilibrium state and the optimum state. We developed a generalization of A. Wagner's (13) model that is both more biologically realistic and flexible and includes the original model as a special case (see Methods). Furthermore, this generalization allows us to perform evolutionary simulations and to measure the phenotypic sensitivity of a genotype to mutation when selection for an optimum phenotype is absent.

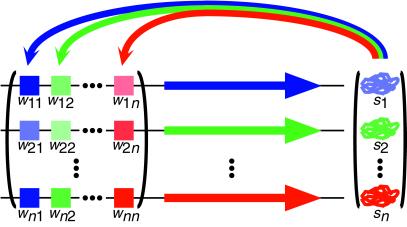
Evolution in the model consists of three phases: mating, development, and selection. Mating and selection are modeled in accord with traditional population–genetic approaches. Development is not typically included in population–genetic models, so we briefly explain its representation in the model (see Methods for details). As shown in Fig. 1, one can represent a network of transcriptional regulators by a state vector containing the concentration of each gene product and a matrix, the entries of which represent the effects of each gene product on the expression of each gene. Entries may be either positive (activating) or negative (repressing) and may differ in magnitude. Zero elements in the matrix represent the absence of interaction between the given gene product and gene. The developmental process is then fully described by a set of nonlinear coupled difference equations. A. Wagner (13) draws an analogy between the rows of the interaction matrix and the enhancer regions of the genes in the network (see Fig. 1) and further justifies the biological realism of this type of model by reference to data from actual genetic networks. An important assumption in the model, also justified by A. Wagner (13), is that functional genetic networks will reach a stable equilibrium gene-expression state, and that unstable networks reflect, in a sense, the failure of development. Thus, in his model and ours, development itself enforces a kind of selection, because we require that the network of regulatory interactions produce a stable equilibrium gene-expression state (its “phenotype”), whose distance to an optimum state can then be measured during the selection phase. Throughout this paper, the term “developmental stability” connotes the achievement of an equilibrium gene-expression state and is distinguished from “canalization,” which connotes phenotypic (or developmental) insensitivity to mutation, as well as from “stabilizing selection,” which connotes selection for a particular optimum gene-expression pattern. For the present analysis, we do not consider limit cycles as stable equilibria, although it is possible to do so (20), and it may be interesting to see whether networks that produce stable oscillations differ qualitatively in their evolution from those that converge to a fixed point.

Fig 1.

Representation of a gene regulation network. Each gene (horizontal arrow) is regulated by the products of the other genes, via upstream enhancer elements (boxes). Strength and direction of regulation (depicted as different color saturation levels) are a function of both the regulatory element and the abundance of its corresponding gene product. Genotype is represented as the matrix, W, of regulatory interactions, and phenotype is the vector, Ŝ, of gene-product levels at equilibrium (see Methods).

We report here the results of numerical simulations of our model of an evolving developmental–genetic system. We demonstrate an important, perhaps primary, role for the developmental process itself in creating canalization, in that insensitivity to mutation evolves even when stabilizing selection is absent. We go on to demonstrate that the complexity of the network is a key factor in this evolutionary process, in that networks with a greater proportion of connections evolve greater insensitivity to mutation. We conclude by discussing the implications of our results and the prospects for future theoretical and experimental investigations of canalization.

Methods

Following A. Wagner (13), we consider a finite population of M randomly mating individuals, each modeled as an interaction network of N genes. As shown in Fig. 1, these interactions are represented by a N × N matrix, W, whose elements, w_ij, denote the effect on gene i of the product of gene j. An individual's genotype is defined by its w_ij, which are drawn independently from the standard Normal distribution. (Although the W matrix encapsulates such epigenetic features as protein–DNA-binding affinities and transcriptional activation or repression strengths, it is properly considered a “genotype,” in that these features can in principle be mapped to specific nucleotide sequences in the enhancer regions of the network genes. For the purposes of this model, we do not consider mutations in the sequences that code for the gene products, i.e., mutations that simultaneously affect the interaction of a given gene product with all of its target enhancer elements.) The fraction, c, of nonzero entries in the W matrix is a parameter of the model and reflects the complexity of the regulatory network. Each network is a dynamical system, with state vector S(t) := (s₁(t), … , s_N(t)) representing the expression levels of each gene at time t. For the present study, we assume that mRNA transcripts and their corresponding protein products are directly proportional in concentration (i.e., there is no posttranscriptional regulation), so S(t) can be considered as either transcript or protein concentrations. The dynamics of S(t) are modeled by the set of nonlinear coupled difference equations

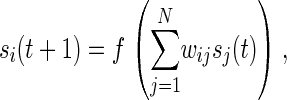where f(x) = 2/(1 + e^−ax) − 1 is a sigmoidal function in which a controls the rate of change from a state of repression to one of activation. The initial state, Ŝ(0), is constant for each simulation and is set by randomly choosing each s_i = −1 or +1. We define development as the process of iterating Eq. 1 a fixed number of times or until equilibrium. The equilibrium steady state, Ŝ, is reached when a measure analogous to a variance,

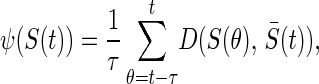is smaller than ε = 10⁻⁴, where D(S^U,S^V) = ∑(s − s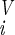)²/(4N) lies in the interval [0 .. 1], and where S̄(t) is the average of expression levels in the time interval (t − τ, … , t). When the equilibrium criterion is satisfied, Ŝ= S̄(t). The number of iterations until equilibrium is termed the path length; if the system does not reach steady state within 100 iterations, it is considered unstable. Note that the activation function and Hamming distance used by A. Wagner (13) are a special case of f(x) and D(S^U,S^V), respectively, at the limit a → ∞. Unless otherwise stated, N = 10, M = 500, a = 100, and τ = 10. A range of a values was tested, with no qualitative effect on the results (not shown).

All M individuals in the starting population are identical and are a copy of a randomly generated founder individual. We require the founder to have a steady state, which we then define as the optimum phenotype, S^OPT. Fitness is defined as

where σ determines selection strength. Individuals that do not reach developmental equilibrium are assigned fitness 0. Note this departure from the model of A. Wagner (13), who assigns such individuals fitness e^−(1/σ).

Subsequent generations are produced by random pairing of individuals. Reproduction assumes segregation (i.e., offspring are created by randomly selecting rows of the W interaction matrix from each parent with equal probability), followed by mutation (replacement with an independent random number from the standard Normal distribution) of each nonzero entry with probability 0.1/(cN²). This makes the per “genome” mutation rate independent of c, so we do not bias highly connected networks to evolve faster. Note also this particular mutation rate ensures that on average fewer than 0.47% of individuals experience multiple mutations. An offspring is chosen to be included as a member of the population if it (i) reaches developmental equilibrium, and (ii) has fitness greater than a random number generated from the Uniform distribution on the interval [0 .. 1]. In our simulations, evolution proceeds for 400 generations.

Sensitivity to mutation, inversely related to canalization, is estimated by perturbing an individual's W matrix and measuring the distance between a reference phenotype and the perturbed phenotypes. In the presence of stabilizing selection, the reference phenotype is S^OPT; in the absence of stabilizing selection, it is the unperturbed individual's Ŝ. We define perturbation as the mutation of exactly one nonzero w_ij element by replacing it with an independently drawn random number from the standard Normal distribution. For some perturbed matrices, ψ(S(t)) > ɛ, ∀t ≤ 100. For the data presented in Figs. 2 and 4, these developmentally unstable individuals are assigned Ŝ = S̄(100). This assignment may bias the sensitivity measure, as the proportion of developmentally unstable perturbed individuals decreases during evolution; thus, in a separate analysis, we excluded these unstable individuals (see Results and Discussion). Each individual's sensitivity is averaged over 10 perturbations, and the reported results are averaged over the 500 individuals in the population, for a total of 5,000 perturbations.

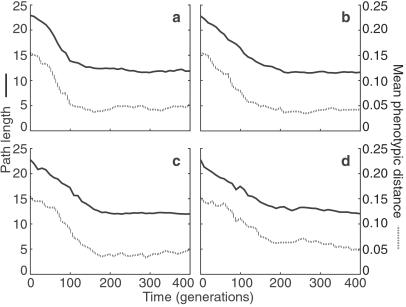
Fig 2.

Typical time course of path length to developmental equilibrium (solid line) and of sensitivity to mutation (mean phenotypic distance of each individual in the population to phenotypes produced by single mutations of its genotype, broken line). The same founder individual evolves under strong stabilizing selection, σ = 0.1 (a), intermediate stabilizing selection, σ = 1 (b), and no stabilizing selection, σ ≈ ∞ (c and d). Populations are either random mating (a–c) or random mating without fertility selection (d) (see text).

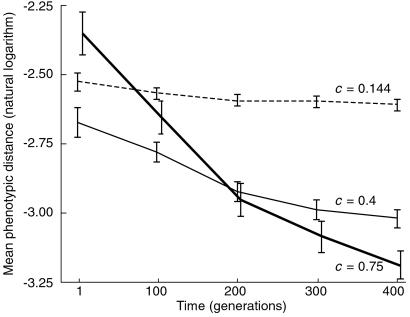
Fig 4.

Effect of network complexity on sensitivity to mutation. Three sets of 100 simulations were performed, with different average proportions of nonzero regulatory interactions: c = 0.75 (thick solid line), 0.4 (thin solid line), and 0.144 (broken line). Sensitivity to mutation was determined every 100 generations. Log-transformed values were analyzed, as untransformed data departed significantly from normality, whereas transformed data did not (Lilliefors tests). Plotted are mean sensitivities, expressed as mean phenotypic distances on perturbation; error bars are ±1 SEM. Two-way ANOVA on the transformed data yields p ≈ 0 for each main effect (c and time) as well as their interaction. Nonparametric Kruskal–Wallis tests on untransformed data confirm these strong effects.

Results and Discussion

Evolution of Canalization with Different Strengths of Stabilizing Selection.

Following A. Wagner (13), we investigate two key properties of evolving regulatory networks. First, we characterize the development of each individual by its path length, that is, how quickly the gene-expression pattern reaches equilibrium. Second, we measure the degree to which mutation of individual genotypes affects their equilibrium gene-expression states, that is, the degree to which they are canalized. Fig. 2a, showing a typical result under fairly strong stabilizing selection, demonstrates that these properties evolve in concert: within a small number of generations, phenotypic sensitivity to mutation decreases dramatically, as does the path length to equilibrium. A. Wagner (13) shows that, even in randomly generated regulatory networks before evolution, path length and mutational sensitivity are correlated. This is a first indication of how development and canalization are intertwined.

When the strength of stabilizing selection is reduced, both path length and mutational sensitivity still decrease, and the time scale of this decrease is not noticeably changed from the scenario of stronger selection (Fig. 2b). This observation led us to hypothesize that the evolved robustness to mutation was not because of stabilizing selection but was instead because of the requirement for development of a stable gene-expression pattern. The structure of the model creates a kind of fertility selection, by which mating pairs that tend to produce a greater frequency of stably developing progeny contribute more to the succeeding generation. The hypothesis is supported by the observation that path length and mutational sensitivity decrease even when the strength of stabilizing selection is reduced to zero (Fig. 2c), at which point considerable phenotypic drift occurs (compare Fig. 3 a–c). That is, when any genotype is acceptable so long as it produces a stable equilibrium phenotype, robustness to mutation still evolves.

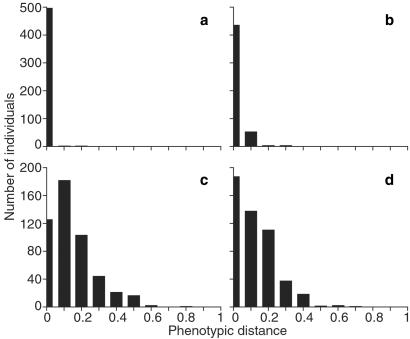
Fig 3.

Effect of stabilizing selection on phenotypic variation. (a–d) Histograms of the phenotypic distances between the population's founding individual and each of the 500 members of the final population. Data are from the respective simulations in Fig. 2.

One is led to wonder whether the evolution of canalization under no stabilizing selection on the gene-expression pattern is an artifact of the modeling framework or whether it represents a finding of real biological significance. We argue that the latter is true on a number of counts. To begin, we acknowledge that it is difficult to envision a scenario in nature in which the stability of a developmental module is required, but the phenotype produced by that module is not subject to selection. One situation in which this condition may hold is when a species colonizes a new territory with virtually unlimited resources, so selection is only for those that develop to reproduce. Furthermore, even if such a scenario does not pertain, the conceptual decomposition of stabilizing selection—into selection for an optimum and selection for developmental stability—is important. Thus, even in scenarios in which members of a population are subject to selection for an optimum, the evolution of canalization may proceed because of the underlying selection for stability of the developmental outcome. Our results suggest that this underlying selection can occur very fast. Because others have argued that the evolution of canalization under stabilizing selection may be slow (9, 13), developmental stability may therefore be the dominant force in the evolution of canalization.

We can go one step further to argue the primacy of developmental stability as a factor in the evolution of canalization. We repeat the evolutionary simulation under no stabilizing selection, this time also removing the fertility selection because of the requirement for developmental equilibrium. We do this by allowing each randomly chosen mating pair to produce progeny until they generate one that reaches developmental equilibrium. Thus, the only selection remaining is that unstable genotypes are discarded and stable ones are retained. Still, canalization evolves (Fig. 2d) as phenotypic drift occurs (Fig. 3d).

Influence of Network Complexity on the Evolution of Canalization.

The evolution of canalization without both stabilizing and fertility selection suggests a profound connection between the stability of development and sensitivity to mutation. Repeated selection of developmentally stable genotypes leads fairly quickly to increased robustness to mutation. We thus conclude that the study of developmental networks, both actual and theoretical, will yield insights into the evolution of phenotypic robustness (21, 22). The complexity of gene interactions promises to feature prominently in investigations along these lines. To test the dependence of our results on the interconnectedness among the genes in the modeled regulatory network, we consider the effect of changing the proportion of nonzero interactions for a fixed number of genes. A. Wagner (13) finds that a greater degree of insensitivity to mutation evolves, under stabilizing selection, in networks with higher connectivity. We show in Fig. 4 that this relationship holds even when selection for an optimum is absent. After 400 generations, networks with c = 0.75 (an average of 75% nonzero connections) have significantly lower sensitivity to mutation than networks with c = 0.4, which in turn have significantly lower sensitivity than networks with c = 0.144. Interestingly, before undergoing evolution, randomly generated c = 0.75 networks do not have, on average, low sensitivity to mutation. However, these networks respond the most to repeated selection for stable development (Fig. 4). One manifestation of this repeated selection is that mutations in the evolved networks are less likely than mutations in the before-evolution networks to lead to developmental instability. For example, in c = 0.75 networks, the proportions of mutations that do not disrupt developmental stability, before and after 400 generations of evolution are, respectively, 0.73 and 0.95, a statistically significant difference (p ≈ 0, one-way ANOVA on arcsin-transformed data). However, we conclude that the higher sensitivity to mutation of the networks before evolution is not because of the greater proportion of mutations that cause developmental instability. Removing these unstable individuals from the analysis, although lowering measured sensitivities at all time points, does not alter their significant downward trend (p = 0.0001, one-way ANOVA on log-transformed data).

The demonstration here of a dependency on network connectivity of the capacity to evolve canalization is similar to an observation made by Frank (23), who used large simple Boolean networks under a two-stage selection regime. Our results suggest that phenotypic selection is not required for the emergence of this property of highly connected networks. Frank (23) concludes, in agreement with Kauffman (22) and with Zuckerkandl (24), who cite different reasons, that networks of intermediate connectivity should be favored by selection. Under selection, highly connected (e.g., c = 0.75) networks may evolve effectively lower connectivity, by selecting w_ij elements near 0. If true, this limits the evolution of canalization, unless these near-zero elements can still serve to stabilize the phenotype.

A Shift in Perspective on Canalization.

We have found that selection for developmental stability is sufficient to evolve canalization rapidly. It is fair to question how general this conclusion is. Clearly, inferences from models are only as good as the models themselves, and every model is necessarily a simplification of reality. As justified both by A. Wagner (13) and in this paper, our model has appealing features of biological realism. However, extensions do suggest themselves and deserve future study. One area of interest is the mutational process. The influence of mutation rate can be explored, as well as the effect of introducing a correlation between the interaction constants of a present allele and its mutated descendant (25). One could also allow new connections to form, either by choosing a pair of formerly noninteracting genes or by introducing gene duplications and allowing paralogs to diverge. Mutations of the gene-product coding sequences can also be considered, by introducing correlated changes into the interaction constants for all targets of the given gene product. Recombination, another factor influencing the rate and course of evolution, may also merit attention. A. Wagner (13) observed no appreciable difference in his results when he replaced free recombination among loci with complete linkage. However, as posited by Stearns (26), the frequent creation of new allelic combinations may be an important challenge to developmental–genetic stability, thereby affecting the evolution of canalization. Stearns (26) provides a potential resolution of this contradiction, by postulating the existence of “nonlinearities that stabilize expression, evolved or not,” an intuition that clearly resonates with our results. Other possible directions include the investigation of the effect of different selection regimes and of variation in environmental conditions. Finally, our results suggest that an important direction will be to explore the structure of actual, well characterized developmental-genetic networks (21) in the context of the relationship between canalization and network topology.

The challenge now, both theoretically and experimentally, is to confirm or refute the existence of a deep connection between developmental–genetic complexity and insensitivity to mutation. If borne out by future studies, this observed connection would necessarily displace stabilizing selection as the default explanation for canalization. Moreover, it may ultimately explain why buffering of key developmental traits is so universal (1), why mutational sensitivity appears uncorrelated with fitness sensitivity (27, 28), and why canalization appears to evolve in a few generations in selection experiments (29–32). It also highlights the importance of studying effectors of developmental stability, e.g., Hsp90 and other chaperone proteins, to understand evolutionary stability (6). At the same time, we side with Dickinson and Seger (33) to caution against assigning purpose to Hsp90's role in modulating “evolvability” for, as our results suggest, this may be an inevitable consequence of its developmental function.

The requirement for developmental stability may be pervasive, generating canalization of a wide range of traits. Of course, stabilizing selection may yet, over the long term, fine tune levels of mutational sensitivity, perhaps even being ultimately responsible for differences in the degree of canalization between some phenotypic traits. We suggest, however, that unless stabilizing selection is explicitly demonstrated to be the driving force in the evolution of canalization of a particular trait, it should no longer be assumed to be so. For example, A. Wagner (17) shows that in yeast, the lack of phenotypic effect of a large proportion of knockout mutations is due not to genetic redundancy but instead to epistatic interactions between unrelated genes. He argues, without direct evidence, that these interactions have evolved under stabilizing selection to become a canalized system. Our results imply that this conclusion may not be justified, as selection for developmental stability, independent of selection for particular phenotypes, is sufficient to evolve insensitivity to mutation. Just as Kacser and Burns (34) demonstrate that dominance is an emergent property of genes involved in metabolism, we show that canalization is an emergent property of developmentally stable gene networks.