Somatic stem cells and the kinetics of mutagenesis and carcinogenesis

Abstract

There is now strong experimental evidence that epithelial stem cells arrange their sister chromatids at mitosis such that the same template DNA strands stay together through successive divisions; DNA labeled with tritiated thymidine in infancy is still present in the stem cells of adult mice even though these cells are incorporating (and later losing) bromodeoxyuridine [Potten, C. S., Owen, G., Booth, D. & Booth, C. (2002) J. Cell Sci.115, 2381–2388]. But a cell that preserves “immortal strands” will avoid the accumulation of replication errors only if it inhibits those pathways for DNA repair that involve potentially error-prone resynthesis of damaged strands, and this appears to be a property of intestinal stem cells because they are extremely sensitive to the lethal effects of agents that damage DNA. It seems that the combination, in the stem cell, of immortal strands and the choice of death rather than error-prone repair makes epithelial stem cell systems resistant to short exposures to DNA-damaging agents, because the stem cell accumulates few if any errors, and any errors made by the daughters are destined to be discarded. This paper discusses these issues and shows that they lead to a model that explains the strange kinetics of mutagenesis and carcinogenesis in adult mammalian tissues. Coincidentally, the model also can explain why cancers arise even though the spontaneous mutation rate of differentiated mammalian cells is not high enough to generate the multiple mutations needed to form a cancer and why loss of nucleotide-excision repair does not significantly increase the frequency of the common internal cancers.

The continually renewing tissues of multicellular animals are made up of separate families of multiplying cells, each family being confined to a limited space, effectively closed at one end and open at the other. Because the cells are multiplying, the cells nearest to the open end are being discarded continually, and thus the only cells to last for any length of time are the “stem” cells that lie next to the closed end. As long as self-renewing tissues remain organized in this way, their stem cells are therefore the only cells that survive from one year to the next. Thus, we might expect to find that stem cells are protected, as far as possible, against the accumulation of mutations.

As was pointed out some time ago (1), the retention of the same, immortal strand for each chromosome through successive stem-cell divisions would ensure that any error made during DNA duplication in S phase does not stay with the stem cell but will pass to a nonstem daughter cell at either the next division or the one after. To avoid accumulating mutations in the immortal strands caused by errors during DNA repair, those forms of repair that involve strand exchange or local resynthesis of damaged strands would have to be inhibited. This, too, seems to be a property of stem cells and their immediate descendants, because they have been found to be highly sensitive to the lethal effects of physical and chemical mutagens (2, 3) and to avoid certain forms of DNA repair (4).

The average stem cell may therefore be virtually immutable, but her progeny multiply exponentially and therefore cannot avoid accumulating replication errors. Thus the production of a mutant clone may require two events: the stem cell must be killed, and the daughter cell that acts as its replacement has to have acquired the mutation. For example, where there are 256 exponentially multiplying cells that divide twice a day and are being replenished continually by the divisions of a single stem cell, none of these 256 cells will ever be separated from the stem cell by more than eight divisions, and the replication errors made in those eight divisions are destined, of course, to be discarded. But in the absence of a functioning stem cell every one of the 256 cells, after 30 days, would bear the replication errors accumulated during 60 divisions; only when a stem cell has been recreated from one of these cells can the system return to its original protected state at which two steps are needed to create any additional mutations.

It is not clear what epigenetic changes have to occur in a daughter cell if it is to take the place of a killed stem cell, but there are reasons for thinking that promotion of a daughter cell to stem-cell status cannot occur as long as the system is being subjected to even a low level of DNA damage. The evidence for this last conjecture is given in the two main sections of this paper.

To recapitulate, the model being presented here is as follows.

• (i)  If left undisturbed, stem cells accumulate few mutations, first because they are defective in DNA repair and tend to die if they suffer DNA damage, and second because they conserve immortal strands and therefore do not accumulate replication errors.

• (ii)  Most of the mutant clones in epithelia arose because a stem cell died and was replaced by a mutant daughter. To produce a permanently mutant clone, two events therefore are necessary: the existing stem cell has to be killed, and the mutation must have occurred in the lineage of the daughter that takes its place.

• (iii)  The immediate descendants of a stem cell are growing exponentially, and thus, unlike the stem cell, they cannot avoid accumulating spontaneous errors of replication. This rather than mutagenesis driven by DNA damage is postulated to be their main route for acquiring changes in sequence.

• (iv)  During continuous exposure to a DNA-damaging agent, no daughter cell can complete the steps needed to convert it into an immutable stem cell. Thus the probability that any given epithelial clone is mutant will be proportional to (a) the probability that at some point its stem cell was killed, and this will be proportional to the dose rate of the DNA-damaging agent and the duration of exposure, and (b) the probability that the replacing daughter has acquired a replication error, and this will be proportional simply to the time or the number of daughter cell divisions that have occurred since the stem cell was killed.

The following is a more precise description of the hypothesis. During continuous exposure to a DNA-damaging agent, the number of stem cells killed at each instant of time (dt) should be directly proportional to dose rate (D), i.e., equal to k × D × dt. If a stem cell is killed at time t and exposure to the agent is continued to time T, the chance that its daughters have acquired a particular rare mutation, A, will be effectively proportional to T − t, i.e., equal to k_a × (T − t). Thus, the total number of mutant clones at time T will be

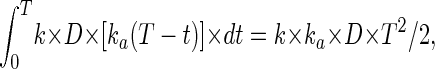where k is the rate constant for cell killing (per unit dose of mutagen), and k_a is the rate constant (per unit of time) for accumulation of the A mutation in the immediate descendants of killed stem cells. Thus the number of mutant clones should be proportional to the first power of dose and to the square of time. As soon as exposure is terminated, one of the daughters can become the new stem cell, but inevitably it will carry the mutations accumulated, since the stem cell died, and thus the frequency of mutant clones will remain constant from then on.

By the same reasoning, in the simplest case the frequency of clones bearing a particular set of N mutations, A, B, … . N would be

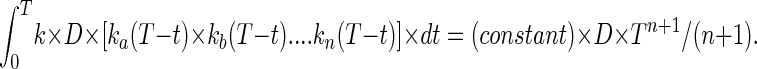Thus the frequency of multiply mutant clones should be proportional to the first power of dose and to the (n + 1)th power of time.

The Kinetics of Mutagenesis in Stem Cell-Derived Populations.

The rules governing the behavior of somatic stem cells are understood best for the small intestine, where the stem cells lie at the bottom of cylindrical infoldings of the epithelium, the “intestinal crypts.” The walls of these crypts contain a multiplying population of cells on their way to being discarded into the contents of the gut, and ≈40 of these cells are capable of replacing a killed stem cell (5). In the small intestine of the mouse there are roughly 1 million crypts, and each of these produces several hundred cells every day (6).

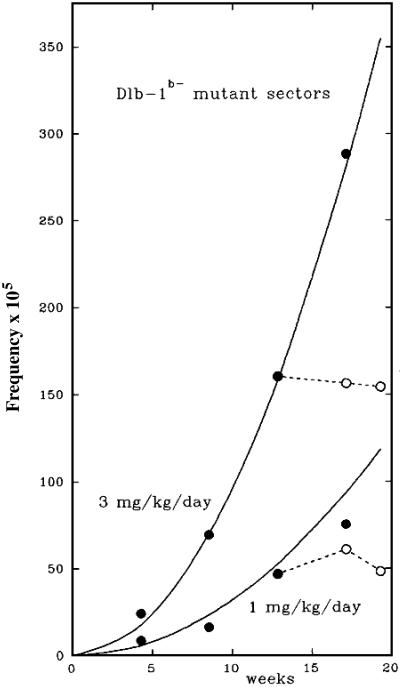
The production of mutant clones has been followed in the crypts of mice exposed for many weeks to a daily i.p. injection of the mutagen N-ethyl-N-nitrosourea (ENU) (Fig. 1; ref. 7). The experiment used mice bearing one copy of the gene (Dlb-1^b) that determines the presence of a stainable cell-surface lectin-binding site. When this gene has been inactivated in a stem cell (or in its immediate progeny), a mutant clone arises that can be seen as an unstained patch of cells.

Fig 1.

The accumulation of mutant clones in the wall of the small intestine of mice that received a daily i.p. injection of either 1 or 3 mg/kg ENU (7). The mice carried one copy of Dlb-1^b, which codes for a stainable cell-surface lectin, and that allowed microscopic measurement of the frequency of unstainable, mutant sectors (clones) in the epithelium. The points show the observed frequency of mutant sectors during treatment (filled circles) and after treatment ceased (open circles). The curves show the expected values if the frequency of sectors equals 3.3 × 10⁻⁶ × (mg/kg ENU) × (weeks)². To allow for the time between mutation in a cell and the appearance of a visible clone of mutant descendants, the points were displaced 4 days to the left (7). The raw data for this figure were kindly provided by John Heddle (York University, Toronto).

Fig. 1 shows that the number of unstainable Dlb-1^b− sectors, although at all times proportional to dose rate, rose as the square of the duration of exposure until exposure ceased, after which the number remained constant. In other words, during exposure each daily increment in mutant sectors was proportional not only to the daily dose but also to the duration of exposure up to that time. These observations gave rise to the conjecture, mentioned earlier, that killed stem cells cannot be replaced until there have been a few clear days, free of further DNA damage. Indeed, after a month's exposure to daily doses of ENU, the mutability of crypts has been observed to return to its initial state after 30 days in the absence of ENU (L. Cosentino and J. Heddle, personal communication).

During continuous exposure to ENU, the rate of accumulation of mutant clones will depend on (i) the rate of killing of stem cells and (ii) the time-dependent or division-dependent mutation rate of the cells that are having to act as substitutes for killed stem cells. Neither of these rates is known, but we can arrive at a lower limit for the mutation rate of the stem-cell substitutes. After exposure to 3 mg/day of ENU for 15 weeks, the rate of production of Dlb-1^b− mutant sectors had reached 30 × 10⁻⁵ per week, and there was no sign that the rate of increase was slowing down. If, for example, 10% of the stem cells had been killed after 15 weeks' exposure and the immediate progeny of these killed stem cells were dividing twice a day (6), they must be producing Dbl-1^b− mutations at the rate of 2 × 10⁻⁴ per division, which is in the range of the rates observed in the genes of certain cancer cells that are deficient in DNA repair (8). If fewer than 10% of the stem cells have been killed, the rate must be even greater. But, of course, normally as long as the stem cells are not being killed, these mutant cells do not accumulate because they are being discarded continually.

The Kinetics of Carcinogenesis.

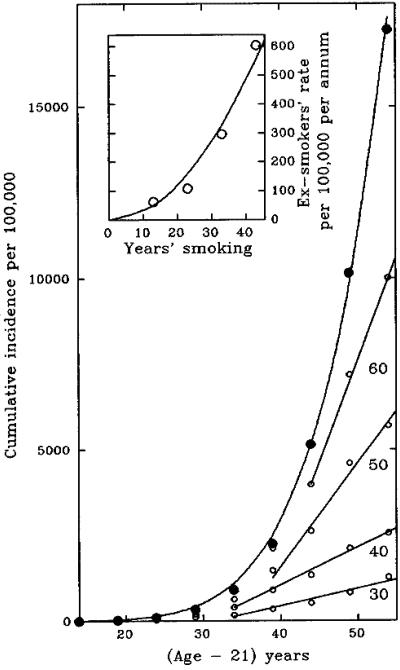
Like the production of Dlb-1^b− mutant sectors, the incidence of cancer in experimental animals continuously exposed to carcinogens commonly increases as the first power of dose and a higher power of time. This is true for a wide variety of carcinogens and for many different tissues (9, 10). The best studied example of human carcinogenesis is smoking-induced lung cancer, and here too the frequency of cancer is roughly proportional to the first or possibly second power of dose rate D (cigarettes per day) and to the sixth power of the duration of smoking (11, 12). Fig. 2 shows the observed cumulative incidence of lung cancer in smokers in relation to duration of smoking (age − 21) on the assumption that smokers start smoking when they are 17 and that on average 4 years elapse between the creation of a cell with the requisite changes and the emergence of a detectable cancer.

Fig 2.

Lung cancer in male smokers (12). The points in the main graph show the cumulative incidence of lung cancer (per 100,000) in relation to age (filled circles), and the curve shows the expected values if cumulative incidence per 100,000 equals 7.1 × 10⁻⁷ × (years − 21)⁶; the open circles show the cumulative incidence per 100,000 smokers who stopped smoking at 30, 40, 50, or 60 years old, less the cumulative incidence in people who never smoked. (Inset) The final annual incidence (rate of increase in cumulative incidence) per 100,000 ex-smokers (open circles) in relation to their duration of smoking; the curve shows the expected values if the final annual incidence in ex-smokers equals 0.3 × (duration of smoking)², assuming that people start smoking at the age of 17. The raw data for this figure were kindly provided by Sarah Darby.

Although the relation between dose and time is exactly what would be expected for the production of clones bearing five mutations, there is one conspicuous difference from the result described in the previous section. The production of new Dlb-1^b− mutant sectors ceased on termination of exposure to the mutagen, whereas the cumulative incidence of lung cancers continues to increase in people who have stopped smoking, albeit more slowly than if they had continued to smoke. According to the present model, we would have expected the cumulative incidence to remain constant once the cells cease to undergo DNA damage, the killed stem cells can be replaced, and the system can return to its original low rate of spontaneous mutation. Thus there are two features that have to be explained: the fact that cumulative incidence continues to increase and the fact that, as the figure shows, the cumulative incidence in ex-smokers eventually settles on a steady linear increase (i.e., the annual incidence in ex-smokers becomes constant).

We see from Fig. 2 Inset that the final annual incidence (the first derivative of cumulative incidence) in ex-smokers is roughly proportional to the square of their duration of smoking, suggesting that this, like the frequency of Dlb-1^b clones in Fig. 1, could represent the frequency of clones bearing one particular class of mutation. The obvious candidate is p53, because (a) continuous high levels of P53 force cells in vitro to preserve immortal strands (J. Sherley, personal communication), (b) in the absence of P53 the progeny of stem cells lose their extreme sensitivity to radiation (13) and, being killed less readily, presumably will be mutated more readily, and (c) mutations in p53 are found in more than 50% of lung cancers (14).

The fact that the final increase in cumulative incidence in ex-smokers is linear (i.e., the final annual incidence is constant) could be simply a matter of the frequency of the different steps in the making of a cancer. Some of the affected pathways may involve many genes and therefore represent a large target, and these changes after a few years may cease to be rate-limiting in cells bearing mutations in p53. If, however, one of the necessary changes is rare, perhaps because it is a particular change a particular codon in a gene such as ras (15), this usually will be the final, rate-limiting step and the cause of the final constant annual incidence. Of course, these added elements offered as an explanation for the lung cancers in ex-smokers bring in too many independent parameters to be taken very seriously, but at least they show that the obscure relation between duration of smoking and incidence of cancer in smokers and ex-smokers can be explained in terms of the known properties of somatic stem cells.

Discussion

At first sight, it may seem strange that inhibition of DNA repair in certain cells can be a protective mechanism for multicellular organisms. Yet it is obvious that if you had to choose which cell should take on the duties of a stem cell, you would prefer one that, being alive, showed that it had not experienced any damage rather than one that might have experienced damage and then tried to repair the damage. Thus it is an understandable strategy that stem cells should be defective in certain forms of DNA repair.

Conservation of immortal strands was observed first in embryonic cells (16), and its main role may be in the opportunities it provides for strand-specific control of differentiation. But the present analysis is limited to showing that strand conservation in somatic stem cells gives us a simple explanation for the strange relation between dose and time in the production of mutant clones, in particular the production of cancer. Many mathematical models have been applied to the kinetics of carcinogenesis. The model developed here is biological rather than mathematical, in that biology dictated the mathematics rather than the more usual procedure in which the mathematics is set up to fit the data and then some meaning, wherever possible, is attached to each of the independent parameters. The present model uses simply the number of steps needed to make a cancer plus the inevitable rate constants relating cell killing and mutation to dose and time. It explains how cancer incidence can be proportional to the first power of dose and a much higher power of time. The observed sensitivity of stem cells to killing by DNA-damaging agents suggests that they do not carry out several forms of DNA repair, which could explain the previously inexplicable observation that loss of the nucleotide-excision repair pathway has no obvious effect on the incidence of most kinds of cancer (17, 18). Last, the lack of DNA repair in stem cells and their progeny could explain how cancers bearing multiple mutations are much more common than would be expected from the mutation rate of most human cells in culture (19).

The assumption that carcinogenesis is driven by cell killing could explain why the mutations found in most kinds of cancer do not point to any particular class of mutagen, but there are some exceptions. G-to-T transversions in p53 are more common in the lung cancers of smokers than in those of nonsmokers, which suggests that some of the sequence changes were caused by mutagenesis by polyaromatic hydrocarbons rather than to spontaneous errors of replication (14). If, for example, a third of all of the mutations in heavy smokers were caused by direct mutagenesis by cigarette smoke, a 2-fold reduction in their cigarette consumption would reduce the incidence of cells with mutations in five critical genes ≈3-fold [(1 + 0.5)/(0.5 + 0.5/2⁵) = 2.9], and at that point cumulative cancer incidence would become proportional to somewhere between the first and second power of dose.

Overall, the model is obviously too simple. Many types of cancer commonly go through a preliminary precancerous stage of clonal expansion, which would have a large effect on the relationship between incidence and age if the final cancers are arising in these expanded populations rather than in the underlying stem cells. Many instances are known where the process for producing an experimental cancer can be divided into several stages (for example, the action of a mutagenic “initiator” followed at some later time by prolonged exposure to one or more nonmutagenic “promoters” to stimulate cell proliferation). Some human cancers have a complex relationship with age, going through a maximum and then declining or changing at a certain age from a steeply exponential to a slow linear increase. Finally, certain programs of cell replacement are known to operate by using hierarchies of stem cells; for example, the stem cells responsible for making the structures associated with each hair lie in a separate region from which a single stem cell emerges very rarely, takes over the responsibility for hair growth for a limited period, and then is discarded (20). Although, therefore, it may not be reasonable to expect any simple model to be applicable to all forms of cancer, the hypothesis that cancer can be driven by killing stem cells rather than by direct mutagenesis could explain many of the mysteries of carcinogenesis.

Abbreviations

• ENU, N-ethyl-N-nitrosourea