In vivo quantification of localized neuronal activation and inhibition in the rat brain using a dedicated high temporal-resolution β⁺-sensitive microprobe

Abstract

Understanding brain disorders, the neural processes implicated in cognitive functions and their alterations in neurodegenerative pathologies, or testing new therapies for these diseases would benefit greatly from combined use of an increasing number of rodent models and neuroimaging methods specifically adapted to the rodent brain. Besides magnetic resonance (MR) imaging and functional MR, positron-emission tomography (PET) remains a unique methodology to study in vivo brain processes. However, current high spatial-resolution tomographs suffer from several technical limitations such as high cost, low sensitivity, and the need of restraining the animal during image acquisition. We have developed a β⁺-sensitive high temporal-resolution system that overcomes these problems and allows the in vivo quantification of cerebral biochemical processes in rodents. This β-MICROPROBE is an in situ technique involving the insertion of a fine probe into brain tissue in a way very similar to that used for microdialysis and cell electrode recordings. In this respect, it provides information on molecular interactions and pathways, which is complementary to that produced by these technologies as well as other modalities such as MR or fluorescence imaging. This study describes two experiments that provide a proof of concept to substantiate the potential of this technique and demonstrate the feasibility of quantifying brain activation or metabolic depression in individual living rats with 2-[¹⁸F]fluoro-2-deoxy-d-glucose and standard compartmental modeling techniques. Furthermore, it was possible to identify correctly the origin of variations in glucose consumption at the hexokinase level, which demonstrate the strength of the method and its adequacy for in vivo quantitative metabolic studies in small animals.

Alterations in local cerebral metabolic rate of glucose (lCMRglc) have been reported in several human brain conditions such as psychiatric disorders or neurodegenerative diseases. Understanding the cellular mechanisms involved in these diseases and the development of new therapeutic strategies will advance more rapidly through the use of animal models. The quantitation of metabolic rates in the rodent brain was achieved initially by using the 2-deoxy-d-[¹⁴C]glucose autoradiographic method (1). Although efficient, this technique requires the sacrifice of several animals to obtain each time point and thus can provide only ex vivo, averaged kinetic constants calculated from values obtained from various animals. As an alternative, positron-emission tomography (PET), an imaging technology designed to use compounds labeled with positron-emitting radioisotopes to image and measure biochemical processes in vivo, has been adapted to use in small animals. The implementation of several high spatial-resolution PET scanners within the last several years (2–9) has enabled the adaptation of the 2-deoxy-d-[¹⁴C]glucose method to in vivo imaging of small animals by using 2-[¹⁸F]fluoro-2-deoxy-d-glucose (FDG) as a tracer. However, such PET scanners require high counting statistics for image reconstruction that strongly reduce the possibility of performing high temporal-resolution measurements.

PET cannot provide direct chemical analysis of reaction products in tissue and in many instances uses labeled compounds such as FDG to trace a reduced number of steps in a biochemical process such that kinetic analysis can be used to estimate the reaction rates. Such applications require high temporal-resolution PET measurements of tissue radioactivity over time and the time course of the radiolabeled tracer concentration in plasma. These data then can be analyzed in a compartmental model describing the transport and biochemical reactions that the radiotracer undergoes to yield a quantitative estimate of the local biochemical process. If for pharmacokinetic experiments using a single tracer injection a coarse temporal resolution is acceptable at the end of the experiment, the use of complex modeling approaches involving multiple-injection protocols requires a high temporal sampling of regional brain kinetics (sampling rate <30 s) that is not readily compatible with the performance of current small-animal PET scanners, especially at the end of the experiment when radioactive signals become low because of radioisotope decay and biological washout. The development of a new generation of small-animal PET scanners and dedicated software should overcome part of this limitation, but both remain at present under progress (10). As a complementary approach to PET imaging, we developed a radiosensitive implantable microprobe to record locally radioactive concentrations with a high temporal resolution (1 s) compatible with the use of compartmental modeling. This β-MICROPROBE is an in situ technique involving the insertion of a fine probe into the brain tissue in a way very similar to that currently used for microdialysis or cell electrode recordings. In the present study, we used two successive experimental approaches in which patterns of neuronal activation and mitochondrial energy impairment are involved to provide a proof of concept to substantiate the β-MICROPROBE's potential and demonstrate that it can be used to determine accurately the kinetic rates for each individual animal and therefore estimate interindividual variation by using a three-compartment/four-rate constant model (1, 11, 12). First, local metabolic decreases observed after local mitochondrial blockade were investigated in individual rat striata after unilateral intrastriatal injection of the mitochondrial complex II inhibitor, malonate. Second, the ability of the probe to measure modest increases (5–10%) in somatosensory cortex metabolic rates in response to physiological sensory stimulation was evaluated in the well established whisker-stimulation model (13, 14). In addition, the present studies show that in comparison with small-animal PET imaging, the β-MICROPROBE allows absolute quantitative studies of local cerebral kinetics and, by using compartmental modeling approaches, the determination of kinetic rate constants for any radiolabeled positron-emitting probe. Furthermore, the direct recording of the activity in the tissue means that it is more sensitive than tomographic techniques because of the statistical demands of the reconstruction processes inherent to the PET technique. Finally, the method could be developed to study the conscious animal, undertake repeated measurements, and follow tracer uptake in the same tissue over hours and days, a methodological advance that would appeal to a very wide audience of experimental animal-based scientists who already use in situ monitoring but cannot manage in vivo imaging techniques.

Materials and Methods

β-MICROPROBE Principle.

The β-MICROPROBE is a local radioactivity counter that takes advantage of the limited range of β particles within biological tissues to define the localized detection volume (a sphere of ≈0.8-mm radius centered on the probe tip for ¹⁸F; ref. 15). The probes are composed of a 1-mm diameter, 1-mm-long β-radiosensitive tip made of scintillating plastic fiber (BICRON, Newbury, OH) attached to a 1-mm diameter, 6-mm-long optical-fiber light guide. Previous work showed that the use of plastic scintillators allow one to neglect the signal from 511 keV annihilation γ for brain studies (15), because this low-density material presents a low detection efficiency for γ rays while providing a good detection efficiency for β particles. The light pulses generated by β particles crossing the scintillator are guided to a single photon photodetector (Hamamatsu R7400, Hamamatsu Photonics, Hamamatsu City, Japan) that delivers a count rate directly proportional to the concentration of FDG in the analyzed volume. Although the cutting of the sensitive tip of the probe is realized under a microscope, its length may vary slightly from one probe to another, resulting in a small difference in probe sensitivity. Therefore, the probe sensitivities were calibrated before experiments with 10 ml of a homogeneous aqueous solution of FDG of known activity. The measured sensitivities of 0.22 and 0.25 counts⋅kBq⁻¹⋅ml⁻¹ for the two probes, respectively, were used to perform quantitative analysis.

Animal Preparation and FDG Scanning Procedure.

The experiments were conducted on male Sprague–Dawley rats (Iffa Credo, L'Arbresle, France) weighing 280–340 g. Anesthesia was induced with 5% isoflurane in a gas mixture of O₂/N₂O (30:70%) and maintained with 1.5–2.5% isoflurane during the entire surgical procedure. Catheters were placed in both femoral veins and arteries, and a tracheotomy was performed for mechanical ventilation (rodent ventilator 683, Harvard Apparatus). The animals were mounted in a stereotactic frame, and a craniotomy was performed for the insertion of a microprobe into the right and left somatosensory cortical areas (whisker-stimulation paradigm/interaural axis, −1 mm, lateral ±6 mm; ref. 16) or into the right and left striatum (malonate lesion paradigm/anterior, −0.5 mm bregma, lateral ±3 mm, ventral −5 mm from dura mater).

Isoflurane was discontinued 30 min after α-chloralose bolus injection (60 mg/kg, i.p.) and maintenance (40 mg/kg/h, i.p. as a cyclodextrin complex).

FDG was prepared routinely in the laboratory with a specific activity of at least 1,000 Ci/mmol (1 Ci = 37 GBq) at the time of synthesis. One hour after completing the surgical procedure, α-chloralose-anaesthetized rats received FDG in a volume of 1 ml of sterile saline (rate, 1 ml/min). Acquisition of local radioactivity count rates began 10 min before tracer injection to evaluate environmental background (≈5 cps) and continued for 120 min with a temporal resolution of 1 s. Mean background noise was subtracted from the raw data, and radioactive-decay correction for ¹⁸F (t_1/2 = 1.829 h) was applied to obtain quantitative time-activity curves. In the whisker-stimulation paradigm (see below), a second FDG injection was performed immediately after initiation of the whisker stimulation.

Timed arterial blood samples were collected continuously for the first 2.5 min after each FDG administration (0.683 ± 0.139 mCi, mean ± SD) and then at increasing intervals up to 60 min after each injection. Additional periodic arterial blood samples were used to measure P_aCO₂, P_aO₂, pH, hematocrit, and plasma glucose concentration. Body temperature was monitored rectally and maintained by means of a thermoregulated blanket.

Whisker-Stimulation Paradigm.

Unilateral whisker stimulation consisted of mechanically stimulating the whiskers by using a homemade electromagnetic device (13). Stimulation (3–4 Hz) included repeated front and back flexion of vibrissa and started concomitantly with the injection of FDG and lasted during the 60 min after the second FDG injection (0.614 ± 0.120 mCi, mean ± SD).

Cerebral Blood-Flow Measurement Using Laser-Doppler Flowmetry.

Cerebral blood flow was measured by laser-Doppler flowmetry (laser blood-flow monitor MBF3D, Moor Instruments, Axminster, U.K.) to ensure effectiveness of the stimulation paradigm and to adjust the placement of β⁺-MICROPROBES. Laser-Doppler flowmetry probes were positioned at the surface of the dura and away to large pial vessels to obtain low and stable values. Probe position and reactivity of the preparation were tested by determining the cerebrovascular responsiveness to changes in inhalated isoflurane concentration. When a suitable location is determined, coordinates are registered to place the β-MICROPROBE at the same stereotactic site.

Unilateral Striatal Malonate Lesion.

Malonate (Sigma–Aldrich) was dissolved to 3 M in PBS, and the pH was adjusted to 7.3–7.4 with HCl. By using a 10-μl Hamilton syringe, unilateral lesions were performed by injections of malonate (1 μl) into the right striatum (0.5 mm anterior to bregma, −3 mm lateral to the midline, and −5 mm ventral from the dura). The neurotoxin was injected over 4 min, after which the needle was left in place for another 5 min. The rats then were taken away from the stereotactic frame and prepared as described earlier (see Animal Preparation and FDG Scanning Procedure). Three hours after malonate injection, the rats were returned to stereotactic apparatus, and the probes were positioned in each striatum followed by an injection of FDG (0.718 ± 0.320 mCi, mean ± SD). The remainder of the experimental procedure was identical to the vibrissae-stimulation paradigm.

Autoradiography.

Animals were anesthetized terminally (thiopental, 120 mg/kg), and brains were removed and frozen in isopentane (−30°C). Serial coronal sections (20 μm) were cut and autoradiographic analysis performed by using a Microimager analyzer (Biospace Mesures, Paris). Sections were stained for Nissl to determine the probe track, and the section from 1 mm anterior to 1 mm posterior was used for the region of interest activated during electrical stimulation.

Histochemistry.

For histochemical evaluation, a set of cryostat-cut sections was used for Cresyl violet staining and terminal deoxynucleotidyltransferase-mediated UTP end labeling reaction (for details see ref. 17). Quantification of terminal deoxynucleotidyltransferase-mediated UTP end labeling reaction-positive nuclei on 20-μm sections was performed in the dorsolateral striatum of malonate-treated animals. Brain sections were observed and recorded with a Zeiss Axioskop microscope connected to an image acquisition and analysis system (IMSTAR).

Semiquantitative measurement of succinate dehydrogenase inhibition was performed as described (18). The images of each section were acquired with CYTOSTAR (IMSTAR) and quantified as reported (18).

Data Analysis.

To optimize the computation efficiency, time-activity curves were resampled before the modeling step. Measures were averaged over varying time intervals (18 × 10 s, 9 × 60 s, and 16 × 210 s) for 60 min.

A classical compartmental model with three compartments was used for the determination of the FDG-transport rate constants of the neighboring cerebral tissue. It consists of the concentration of FDG in plasma and tissue and FDG-6-P in tissue. Because the kinetics were measured over 2 h, this model includes the expression for the reaction of hydrolysis from FDG-6-P to FDG in tissue (19). These four constants were identified as K₁, k₂, k₃, and k₄.

The kinetics obtained during the stimulation experiments were processed with a double-injection modeling approach, which consists of estimating two independent sets of four parameters: one for the period of rest (0–60 min) and one for the period of activation (60–120 min). This method rests on the assumption that the parameter values change rapidly at the beginning of the activation, which is supported by Bonvento et al. (14), who reported a local flow increase within 3 s in a study by using the same activation paradigm.

To estimate accurately the value of k₄, we verified in preliminary experiments that the k₄ estimate over the first 60 min is a good approximation of the “reference value” obtained with the total 120-min kinetic. The very low level of statistical noise in the kinetics also helps in assessing reliable k₄ estimates within this relatively short period (60 min).

The sets of (K₁, k₂, k₃, and k₄) parameters were fitted by minimization of a weighted least-squares cost function and a Marquardt algorithm. An estimation of the standard errors was performed based on the use of a sensitivity analysis and the covariance matrix (20).

Results

β-MICROPROBE Detection of Striatal Metabolic Inhibition Induced by Striatal Energy Impairment.

To determine whether the β-MICROPROBE could detect decreased neuronal activity in the rat brain, FDG uptake in rats that had undergone unilateral intrastriatal malonate injection was evaluated. Malonate is a reversible succinate dehydrogenase inhibitor that, when administered intraparenchymally, induces a selective mitochondrial complex II deficiency. In the rat, this experimental situation models the metabolic impairment preceding neurodegeneration in Huntington's disease.

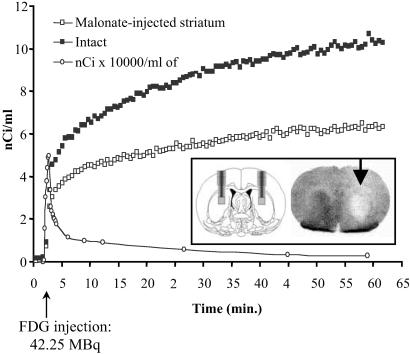
In the present study, α-chloralose-anaesthetized rats were injected with malonate in the right striatum and monitored with probes implanted bilaterally in each striatum 3 h postinjection. This observation time was selected according to previous studies that demonstrated that, 3 h postinjection, malonate causes a pure decrement in neuronal metabolic activity (selective decrease in succinate dehydrogenase, complex II activity) associated with neither cell degeneration nor DNA fragmentation observed 24 h postinjection. Intrastriatal β-MICROPROBE recordings show that metabolic activity was reduced significantly in the malonate-injected side relative to the uninjected side at all time points. By 40 min after tracer injection, FDG uptake decreased by 30% in the injected striatum as compared with the uninjected striatum. A representative example of FDG activity in the striatum and plasma (corresponding to rat 3 of Table 3) is shown in Fig. 1.

Table 3.

Rate constants determined with a 4K model in the somatosensory cortex after FDG injection

	Animal no.	State	K1	k2	k3	k4	lCMRglc, mmol/100 ml per min
Ipsilateral cortex	1	Rest/activation	0.284/0.207	0.262/0.178	0.073/0.067	0.019/0.022	78.39/71.70
	2	Rest/activation	0.235/0.220	0.087/0.094	0.010/0.016	0.000/0.022	32.71/30.86
	3	Rest/activation	0.313/0.366	0.153/0.126	0.042/0.040	0.001/0.000	85.39/111.71
	4	Rest/activation	0.273/0.287	0.273/0.319	0.065/0.094	0.015/0.020	61.25/76.21
	5	Rest/activation	0.284/0.267	0.237/0.249	0.042/0.066	0.015/0.015	54.15/70.86
P value			NS	NS	NS	NS	NS
Contralateral cortex	1	Rest/activation	0.451/0.283	0.249/0.205	0.046/0.081	0.011/0.020	89.08/101.52
	2	Rest/activation	0.299/0.293	0.078/0.085	0.009/0.015	0.000/0.006	41.76/59.33
	3	Rest/activation	0.284/0.425	0.128/0.176	0.028/0.047	0.000/0.017	64.57/113.46
	4	Rest/activation	0.346/0.391	0.262/0.307	0.059/0.084	0.011/0.017	74.19/98.00
	5	Rest/activation	0.352/0.344	0.167/0.190	0.017/0.039	0.001/0.012	41.19/74.21
P value			NS	NS

NS, nonsignificant;

^*, P < 0.02.

Fig 1.

Malonate effect on metabolic activity in the striatum of an anaesthetized rat. Five rats were injected with malonate (1 μl, 3 M) into the right striatum, and glucose consumption was measured 3 h later. The FDG uptake dramatically decreased in the injected striatum after malonate injection, whereas no detectable cell damage was noticed by using terminal deoxynucleotidyltransferase-mediated UTP end labeling reaction; however, autoradiographic analysis revealed a hypometabolism in the same order of magnitude as measured with the β-MICROPROBE. (Inset) Probe positioning and FDG autoradiography.

Compartmental analysis of β-MICROPROBE recordings using the individual plasma-activity curve as an input function (Table 1) and a standard three-compartment/four-rate constant tracer kinetic model extending the original method of Sokoloff et al. (1) shows that the decrease in FDG striatal uptake observed in the malonate-injected striatum compared with the intact contralateral striatum is caused by a selective decrease in k₃ (P < 0.02, paired t test, n = 5), with no significant changes of K₁, k₂, or k₄.

Table 1.

Rate constants determined with a 4K model after malonate administration in the right striatum

	Animal no.	K1	k2	k3	k4	lCMRglc, mmol/100 ml per min
Left striatum	1	0.5069	0.4031	0.09878	0.0141	97.00
	2	0.2941	0.1986	0.0583	0.0004	74.19
	3	0.2777	0.1297	0.0461	0.0011	85.60
	4	0.2368	0.1392	0.0521	ND	75.24
	5	0.2691	0.2062	0.1189	0.0325	95.69
Right striatum	1	0.4711	0.3183	0.07644	0.0054	88.69
	2	0.2641	0.2057	0.0526	0.0004	59.73
	3	0.1678	0.1173	0.0311	0.0007	41.38
	4	0.2379	0.1273	0.0360	ND	61.19
	5	0.2853	0.1993	0.0862	0.0312	83.75
P value		NS	NS	**	NS

^*, P < 0.05; **, P < 0.02 right vs. left striatum; NS, nonsignificant; ND, not determined.

lCMRglc were calculated from the operational equation of Sokoloff et al. (1, 11, 12) (K₁ × k₃/k₂ × k₃) × Cp/LC, where Cp represents the arterial plasma glucose concentration measured in each experiment with a lumped constant (LC) fixed at 0.60. lCMRglc calculated from K₁, k₂, and k₃ values identified by the compartmental analysis showed that the average cerebral glucose utilization in the intact striatum was 85.6 compared with 66.9 μmol/100 ml per min in the malonate-injected striatum, representing a significant 21.7% decrease in metabolic activity (Table 1). Postmortem immunohistochemical in situ quantification of succinate dehydrogenase activity in each individual rat demonstrated a marked decrease in succinate dehydrogenase activity very similar to the change in glucose consumption, with no obvious neuronal degeneration as determined by Nissl staining and terminal deoxynucleotidyltransferase-mediated UTP end labeling reaction labeling. The absence of cell loss or DNA fragmentation in the malonate-injected striatum indicates that the reduction in glucose consumption reflects a decrease in neuronal activity and not the loss of neurons within the injected striatum, which is in line with the selective decrement in k₃ (which represents the rate constant for intracellular phosphorylation of FDG by the hexokinase) and the lack of changes in the normal K₁ and k₂ values observed in both hemispheres. The latter indicates that the carrier-mediated blood-to-brain transport of FDG is still operating fully 3 h post-malonate injection. Finally, the lack of change in the k₄ constant indicates that the decrease in FDG striatal uptake is not caused by increased deoxyglucose-6-phosphatase activity, which remains in the normal range of values.

β-MICROPROBE Recordings of Basal Cortical Metabolic Rates and Absolute Quantitation of Neuronal Activation Induced by Unilateral Whisker Stimulation.

The above studies demonstrate that β-MICROPROBE recordings have sufficient temporal resolution for the quantitative assessment of decreased neuronal metabolic activity in living rats. To assess whether β-MICROPROBE recordings can also detect increases in metabolic activity, we studied FDG uptake in the somatosensory cortex of rats before and during mechanical unilateral stimulation of the whiskers. To maintain physiological parameters as constant as possible throughout the experimental procedure, animals were anaesthetized with α-chloralose (induction and maintenance, see Materials and Methods for detailed procedure). Table 2 demonstrates that all physiological variables monitored (pH, P_aCO₂, P_aO₂, mean arterial blood pressure, heart rate, hematocrit, plasma glucose, and body temperature) remained within the normal range before, during, and after whisker stimulation, which comprised up to 130 min of FDG uptake. It is noteworthy that the only change noted during vibrissal stimulation in the contralateral relative to the ipsilateral somatosensory cortex was a 10–15% increase in cerebral blood flow recorded by laser-Doppler flowmetry. This increase is of the same order of magnitude of changes reported in the literature (14).

Table 2.

Physiological parameters before and during whiskers stimulation

Physiological variables (mean ± SD)	Rest	Activation
Heart rate, beats per min	355  ± 5	348  ± 28
Mean arterial blood pressure, mmHg	127  ± 8	117.5  ± 12.5
PaCO2, mmHg	33  ± 3	33  ± 2
PaO2, mmHg	159  ± 25	149  ± 29
pH	7.43  ± 0.05	7.43  ± 0.03
Body temperature, °C	37.1  ± 0.13	37.1  ± 0.08
Hematocrit, %	NM	47  ± 2
Glucose, g/l	1.32  ± 0.08	1.36  ± 0.10

NM, not measured.

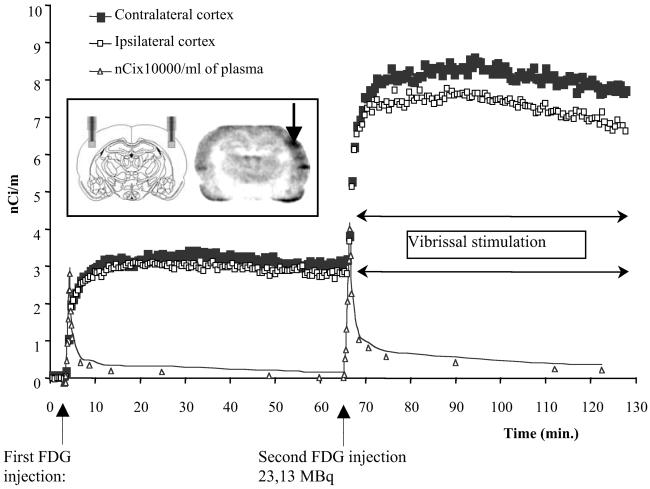
With two probes located bilaterally in the somatosensory cortex, rats received a first i.v. injection of FDG, and cortical uptake of the radiotracer was studied for 65 min (resting condition). Then, the vibrissae were unilaterally stimulated continuously followed by a second i.v. injection of FDG. Cortical radiotracer uptake was monitored for an additional 65-min period. β-MICROPROBE recordings of the somatosensory cortices FDG activity show remarkably similar metabolic activities in both sides under rest conditions, whereas FDG uptake increased on average by 10% in the contralateral relative to the ipsilateral cortex under vibrissal stimulation, consistent with neuronal activation. A representative example of cortical FDG uptake and plasma-activity curves (corresponding to rat 2 of Table 3) is shown in Fig. 2. These cortical β-MICROPROBE measurements of FDG uptake compare well with the results obtained by Sokoloff et al. (1) in the rat under rest condition.

Fig 2.

Decay-corrected time-activity curve showing FDG uptake in rat 2 (Table 3) in rest condition and during vibrissal stimulation. This rat was stimulated unilaterally by continuously stroking the whiskers on the left side. The stimulation was initiated simultaneously with the injection of the second bolus dose of FDG. As shown on the autoradiographic image, the whisker-stroking markedly increased FDG uptake on the contralateral somatosensory cortex compared with the ipsilateral cortex. (Inset) Probe positioning and FDG autoradiography.

We performed a compartmental analysis of FDG cortical kinetics on the β-MICROPROBE measurements by using the plasma-activity curves as the input function in the model. Because total radioactivity concentrations declined significantly from 40 to 65 min in the rat somatosensory cortex, we used a three-compartment/four-rate constant model to fit the experimental data, assuming that a significant dephosphorylation of FDG-6-P (rate constant k₄ in the model) would occur in rats after 40 min of FDG uptake.

Quantitative analysis of FDG cortical uptake under resting conditions yielded very similar values for K₁, k₂, k₃, and k₄ values in both cortices. Calculated values of K₁, k₂, and k₃ are comparable to those published previously for the sensory-motor cortex of the normal conscious rat, which were: K₁ = 0.193 ± 0.037 min⁻¹, k₂ = 0.208 ± 0.112 min⁻¹, and k₃ = 0.049 ± 0.035 min⁻¹ (1). In the activation condition, microprobe recordings show that the increase in FDG uptake observed in the somatosensory cortex contralateral to the stimulation is caused by to a marked increase in the k₃ constant (P < 0.02, paired t test, +67% compared with resting condition; phosphorylation of the FDG by hexokinase), a significant increase (P < 0.01, paired t test, 2-fold increase relative to the ipsilateral cortex) in the k₄ rate constant (dephosphorylation rate of the FDG-6-P), and no significant changes of K₁ and k₂ rate constants (blood-to-brain transfer of FDG). The above data demonstrate that the increase in cortical FDG uptake observed in the contralateral hemisphere after vibrissal stimulation reflects an actual increase in metabolic activity.

lCMRglc calculated from K₁, k₂, and k₃ values identified by the compartmental analysis showed that the average cerebral glucose utilization in the nonactivated cortex was 72.3 compared with 89.3 μmol/100 ml per min in the activated somatosensory cortex, representing a significant 43.7% increase (P < 0.02, paired t test) in local glucose utilization (Table 3).

Postmortem autoradiography performed in two of the rats demonstrated a clear increase in radiotracer uptake in the somatosensory cortex contralateral to the stimulated vibrissae and the minimal trauma caused by the placement of the probe (Fig. 2).

Discussion

The present report demonstrates the ability of a β⁺-sensitive implantable detector to quantitatively assess neuronal depression or activation in the rat brain. In the current study, we used FDG as a validated radiotracer of cerebral metabolic activity.

Absolute Quantification of Glucose Metabolism in α-Chloralose-Anaesthetized Rats.

The present FDG studies demonstrate that the sensitivity and temporal (≈1 s) and spatial resolution (0.8 mm with ¹⁸F-radiolabeled tracers) of the β-MICROPROBE system permits the quantitative assessment of even modest changes in regional metabolic activity in individual rats.

As determined here, the local glucose metabolic rate was 72.3 μmol/100 ml per min for the somatosensory cortex under rest condition and 85.6 μmol/100 ml per min for the striatum. The lCMRglc value determined by the β-MICROPROBE for the somatosensory cortex is comparable to the values obtained by using 2-deoxy-d-[¹⁴C]glucose autoradiography: 67 ± 2 μmol/100 ml per min under thiopental sodium anesthesia and 118 ± 3 μmol/100 ml per min in the conscious-restrained state (1). The lCMRglc in striatum derived from the β-MICROPROBE measurements is similar to that estimated with FDG autoradiography (21) and somewhat higher to that determined by using FDG micro-PET, for which partial volume effects lead to underestimation of lCMRglc as reported by Moore et al. (22).

An important potential application of the technique is the possibility to adapt the detector to chronic studies in freely moving and operating animals, which would allow combining behavioral experiments and simultaneous radiotracer measurements that are not possible by using small-animal PET imagers that require anesthesia or at least constraint and immobilization of the animal at the time of measurement. Such an experiment implies two major constraints: the use of a rotating collector set on the top of the rodent cage on which a photodetection module will be plugged (this component, currently used for in vivo electrophysiological experiments, will enable the rat to move almost unrestrained while the experiment is performed) and chronic arterial catheters on rats, which will allow one to inject the radiotracer and take blood samples. In addition, to minimize tissue damage caused by probe implantation, we have examined the effects of chronic implantation of 500-μm diameter probes, which permit longitudinal studies of neurodegenerative or plastic processes in freely behaving rodents, thus avoiding the well described effects of anesthesia on local blood flow, energetic metabolism (23–25), or radiotracer binding (26–28).

Temporal-Resolution and Kinetics Modeling.

The high temporal resolution (typically 1 s) of the β-MICROPROBE used in combination with compartmental tracer kinetic analysis allows the quantitative determination of biological rate constants from cerebral radioactivity kinetics. The strength of this method is illustrated by the two applications described here, which show that both increases and decreases in FDG uptake observed in the physiological models used are caused by selective variations in glucose consumption at the hexokinase level (k₃ rate constant) and not by alterations in blood-to-brain transfer of FDG (K₁ and k₂ rate constants). These observations are very informative, because an increase in cerebral blood flow is associated with vibrissae stimulation and could have accounted at least partly for the increased cortical uptake. Similarly, in the malonate experiment, physical leakage of the blood–brain barrier could have occurred because of the progressive neuronal degeneration, and that could have altered radiotracer availability. It is noteworthy that rate-constant values extracted from the compartmental analysis of microprobe recordings are consistent with those reported in the literature using various different methods (1, 11, 12), further confirming the validity of the β-MICROPROBE approach.

Combination with Other in Vivo Techniques.

For metabolic, pharmacological or behavioral experiments in living animals, the simultaneous use of various techniques can be of great interest to assess physiological parameters in real time in individual animals. The technical constraints of small-animal PET imaging require the development of dedicated instrumentation to be used with in vivo techniques, particularly those requiring high magnetic field (29). In contrast, the microprobe can be used readily with MRI or NMR spectroscopy, because the detector is insensitive to high magnetic fields. In the case of pharmacological studies, similar coupling of microprobe recording experiments with the microdialysis technique could increase accessibility of many investigators to combined β-radiotracer measurement with microdialysis studies in the rodent's brain as an alternative to the use of large animals (30, 31). Some preliminary studies combining both methods already have been carried out successfully on anaesthetized rats and have shown some promising results (32).

Conclusion

The β-MICROPROBE provides an effective tool for the assessment of metabolic changes on small animals in vivo. In addition to measuring metabolic changes, the probe is suited also for pharmacokinetic studies (33) and takes advantages of ¹⁸F- or ¹¹C-radiolabeled molecules currently available for PET imaging. In many brain-imaging studies the objective is to obtain time-activity curves for radiotracer local concentration in brain region often selected ahead of time. The miniaturized local radioactivity counter takes advantage of this with an excellent temporal resolution for reasonable injected activities (typically 1 mCi or less), compared with that of current imaging tomographs that require, for the time being, minutes between each data point because of the need for high counting statistics for image reconstruction, especially when considering the end of the kinetic curve. The high temporal resolution of the β-MICROPROBE enables accurate measurements of dynamic molecular changes and compartmental tracer kinetic modeling, which lead to an improved understanding of the physiological phenomenon underlying macroscopic parameters changes. Finally, this work demonstrates that β-MICROPROBE recordings can provide absolute quantitative values of lCMRglc by using the classical FDG model. The high temporal resolution makes it possible to extract reliable kinetic rate constants K₁, k₂, k₃, and k₄ from FDG kinetics in each individual animal, thus allowing the detection of neuronal activity changes and offering the opportunity to study interindividual metabolic variations. In conclusion, the technical simplicity and insensitivity to magnetic fields allow easy coupling of the β-MICROPROBE with other in vivo techniques, a major interest not only for metabolic measurements but also for pharmacokinetics studies.

Abbreviations

• lCMRglc, local cerebral metabolic rate of glucose

• PET, positron-emission tomography

• FDG, 2-[¹⁸F]fluoro-2-deoxy-d-glucose