Abstract
In the event of a smallpox bioterrorist attack in a large U.S. city, the interim response policy is to isolate symptomatic cases, trace and vaccinate their contacts, quarantine febrile contacts, but vaccinate more broadly if the outbreak cannot be contained by these measures. We embed this traced vaccination policy in a smallpox disease transmission model to estimate the number of cases and deaths that would result from an attack in a large urban area. Comparing the results to mass vaccination from the moment an attack is recognized, we find that mass vaccination results in both far fewer deaths and much faster epidemic eradication over a wide range of disease and intervention policy parameters, including those believed most likely, and that mass vaccination similarly outperforms the existing policy of starting with traced vaccination and switching to mass vaccination only if required.
Although smallpox was eradicated in 1979 by the World Health Organization campaign (1), it remains a feared bioterrorist threat (2). In the aftermath of the September 11 terrorist attacks, the U.S. is stockpiling 286 million doses of smallpox vaccine (3). The Centers for Disease Control and Prevention (CDC) interim response plan (4) calls for targeted vaccination and quarantine: symptomatic smallpox cases would be isolated, contacts of cases vaccinated, asymptomatic contacts monitored but not isolated, and febrile contacts quarantined for 5 days. These guidelines also recommend a broader vaccination strategy if the initial number of cases or outbreak locations is “sufficiently large,” or if new cases fail to decline after two or more generations of cases have developed from those initially identified, or 30% of vaccine stores have been used. An expert panel has also recommended a targeted vaccination strategy (ref. 5; http://www.bt.cdc.gov/DocumentsApp/Smallpox/RPG/index.asp).
Model.
To assess the CDC guidelines (and possible alternatives), we embed their key features in a disease transmission model of a smallpox attack in a large urban center. The model incorporates four stages of infection (1, 6), each exponentially distributed in duration with mean r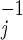 days spent in stage j = 1, 2, 3, or 4: (1) asymptomatic, noninfectious and vaccine-sensitive; (2) asymptomatic, noninfectious, and vaccine-insensitive; (3) asymptomatic and infectious; and (4) symptomatic and isolated. In our model, the transition from stage 3 to stage 4 reflects response operations in addition to disease progression. When an infected recognizes his or her symptoms, which may occur some time after the symptoms first appear, (s)he seeks medical help and is immediately isolated. A fraction δ of symptomatic cases die of disease, whereas the remaining fraction eventually recover (and are immune to reinfection).
days spent in stage j = 1, 2, 3, or 4: (1) asymptomatic, noninfectious and vaccine-sensitive; (2) asymptomatic, noninfectious, and vaccine-insensitive; (3) asymptomatic and infectious; and (4) symptomatic and isolated. In our model, the transition from stage 3 to stage 4 reflects response operations in addition to disease progression. When an infected recognizes his or her symptoms, which may occur some time after the symptoms first appear, (s)he seeks medical help and is immediately isolated. A fraction δ of symptomatic cases die of disease, whereas the remaining fraction eventually recover (and are immune to reinfection).
Disease transmission derives from free (or homogeneous) mixing among available susceptibles and asymptomatic infectious individuals in the population. Although we recognize that free mixing is not an accurate depiction of actual population interactions, free mixing usually leads to larger epidemics than nonrandom mixing would admit (7). Given the potentially disastrous consequences of a smallpox attack, we ask whether proposed control strategies can control such “worst-case” outbreaks. Surely strategies that contain smallpox epidemics under the free mixing assumption will also work under mixing patterns less favorable to the spread of disease. In this sense, our approach is to plan for the worst but hope for the best.
Absent intervention, each infectious individual generates an average of R0 = βS0(0)/r3 infections early in the epidemic (8), where S0(0) is the number of susceptibles immediately after an attack at time t = 0, and β is the effective disease transmission rate per person per unit time. Although the transmission rate is likely to decrease after the attack is detected and announced, we use a single value of R0 throughout the epidemic that represents the postdetection scenario. Because the total number of deaths is highly dependent on the number of infected persons when the emergency response is initiated, an increase in the detection delay (discussed below) or the predetection R0 has an effect similar to increasing the initial attack size—an effect we investigate later.
Newly detected symptomatic infections become “index cases,” isolated to prevent further transmission. Index cases are interviewed to generate a list of c persons with whom they have had potentially infectious contacts in the recent past, but only a fraction p of true contacts (and hence only a fraction p of infectees) are named and located via contact tracing. The model correctly places infected contacts found in their appropriate stage of disease while accounting for the probability that such persons were already traced from a prior index, and thus avoids double counting. This crucial aspect of our analysis differs from previous contact tracing models (9, 10) and reveals a “race to trace:” even if a contact is identified immediately on detection of the infecting index case, the time from infection of the contact to detection of the index (and tracing of the contact) can exceed the time during which the infected contact remains sensitive to the vaccine. Contact vaccination in such a circumstance is both ineffective (the infection is not prevented) and inefficient (vaccine is wasted). Contact tracing can control a smallpox outbreak only if the race to trace is repeatedly won.
Susceptible and asymptomatic infected persons located via contact tracing enter a tracing/vaccination queue serviced by n vaccinators who can each process (locate and vaccinate) μ persons per day on average. Only susceptibles and stage 1 infected individuals can be protected via the vaccine, which is effective with probabilities ν0 and ν1, respectively. Unsuccessfully vaccinated persons return to the freely mixing population either as susceptibles or infecteds in the appropriate stage of disease. On vaccination, a fraction h of individuals in stage 3 of infection are found to be febrile and are quarantined for α−1 days on average. A fraction f of vaccinations result in fatalities. Mathematically, this model is described by the 17 ordinary differential equations discussed further in the Appendix.
We focus on two strategies: traced vaccination (TV), described in the last paragraph, and mass vaccination (MV), where the entire population simultaneously enters the vaccination queue. The CDC policy, which can be viewed as TV followed by a switch to MV if the former is unable to contain the epidemic, will also be assessed. We also consider preattack vaccination. To allow for detection and ramp up, TV and MV are initiated in our model when 10% of the initial number of infected people have exhibited symptoms.
Parameter Values.
Table 1 contains the parameter values for our base case. About half of these values are taken from classic references (e.g., ref. 1). The infection rate β was chosen so that R0 = 3, which is near the lower range of 3.5–6 estimated in ref. 9 (although we will vary R0 in sensitivity analyses discussed below). We assume a large attack of 1,000 initial cases in a population of 10 million persons in our base case but vary the attack size between 1 and 100,000 in our sensitivity analyses below. To estimate the number of vaccinators that could be requisitioned in an emergency, we focus on public health nurses. A Health Resources and Services Administration survey (11) reports that 0.78% of the U.S. population is used in nursing, whereas 18.3% of used nurses work in public or community health. Applying these percentages to N = 10 million and dividing by 3 to produce round-the-clock 8-hr shifts yields 4,758, which we have rounded to 5,000. Vaccinators trace and vaccinate the contacts named by index cases. In our model, it takes T and V time units, respectively, to trace and vaccinate a named contact. Hence, μ−1 = T + V for TV and μ−1 = V for MV. We assume T = 3V, recognizing that the time required to locate contacts is much greater than the time required for vaccination (12), and V−1 = 200 per day based on the 1947 mass vaccination of New York City (2). When we were in doubt regarding the values of some parameter values (e.g., p and h), we erred on the side favoring TV.
Table 1.
Parameter values for the model
| Parameter | Description | Value | Reference |
|---|---|---|---|
| β | Infection rate | 10−7 person−1⋅day−1 | See text |
| c | Names generated per index | 50 | 1, 9 |
| p | Fraction of infectees named by index | 0.5 | See text |
| N | Population size | 107 | See text |
| r1 | Disease stage 1 rate | (3 days)−1 | 1 |
| r2 | Disease stage 2 rate | (8 days)−1 | 1 |
| r3 | Disease stage 3 rate | (3 days)−1 | 1 |
| r4 | Disease stage 4 rate | (12 days)−1 | 1 |
| n | Number of vaccinators | 5000 | 11 |
| μ | Service rate | 50/day (TV), 200/day (MV) | 12 |
| h | Fraction febrile in stage 3 | 0.9 | See text |
| α | Quarantine rate | (5 days)−1 | 4 |
| v0 | Vaccine efficacy, stage 0 | 0.975 | 13, 14 |
| v1 | Vaccine efficacy, stage 1 | 0.975 | 13, 14 |
| δ | Smallpox death rate | 0.3 | 1 |
| f | Vaccination fatality rate | 10−6 | 1 |
I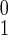 (0) (0) |
Initial number infected | 103 | See text |
Base Case Results.
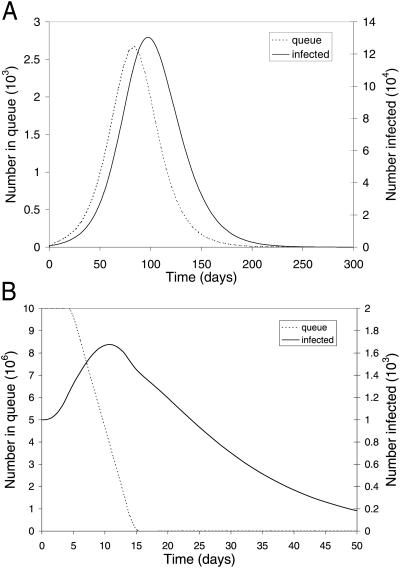
Fig. 1 depicts the population dynamics of TV and MV, both initiated on day 5, for our base case parameter values (Table 1). TV leads to 367,000 cases and 110,000 deaths over 350 days (Fig. 1A), even though tracing and vaccination resources are ample (that is, the maximum queue length in Fig. 1A is less than the total number of available health workers) and requires 59,000 isolation units for symptomatic cases (but only 750 for febrile quarantine). MV takes only 10 days to complete, leads to 1,830 cases and 560 deaths over 115 days (Fig. 1B), and requires only 690 isolation units for symptomatic cases (60 for febrile quarantine). The effect of quarantining febriles in Fig. 1 is to reduce the number of TV deaths from 112,000 to 110,000 and the number of MV deaths from 585 to 560.
Fig 1.
Population dynamics of a smallpox attack with the basic reproductive ratio R0 = 3. The number of infected people, regardless of disease stage, and the number of people, whether susceptible or asymptomatically infected, waiting in the vaccination queue during the aftermath of a smallpox attack. The (A) TV policy and the (B) MV policy are both initiated 5 days after an initial attack of size 1,000 in a population of 107.
Sensitivity Analysis and Preattack Vaccination.
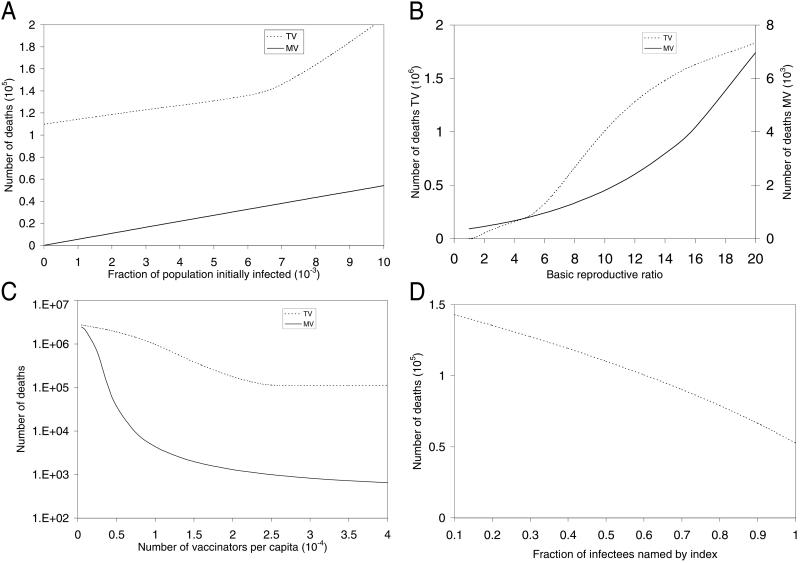
A sensitivity analysis comparing the number of deaths incurred under TV and MV was performed for the three model parameters that possess the most uncertainty (Fig. 2 A–C). TV is more sensitive than MV to the size of the initial attack (Fig. 2A), and R0 (Fig. 2B). Although deaths decline as the number of vaccinators increases for both TV and MV (Fig. 2C, which uses a log scale), the number of deaths under TV is independent of the number of vaccinators when the latter exceeds about 2,670, which is the maximum length of the vaccination queue throughout the course of the epidemic in Fig. 1A. The TV deaths vs. R0 curve has two kinks in Fig. 2B: the curve increases at R0 = 1.36, which is the largest value of R0 for which TV can contain the spread of disease, and further steepens at R0 = 5, when the vaccination queue becomes congested. The TV policy is also sensitive to three other TV parameters: the fraction of infectees named by an index (Fig. 2D), the ratio of tracing time to vaccination time, and the number of names generated per index (not shown).
Fig 2.
Sensitivity analysis for uncertain model parameters. The number of deaths under TV and MV versus (A) the fraction of the population initially infected, (B) the basic reproductive ratio R0, and (C) the number of vaccinators per capita, keeping the total population size fixed at 107. The number of deaths under TV versus (D) the fraction of infectees named by an index.
Under either TV or MV, there may be a number of people who either cannot be located or who should not be vaccinated (e.g., people who have eczema, are pregnant, or are immunosuppressed). Because prevaccination screening will likely preclude the vaccination of the great majority of immunosuppressed people, we assess this effect under MV by reducing the vaccine efficacy. As an illustration, even if the vaccine efficacy is decreased from 0.975 to 0.9, the number of deaths increases only from 560 to 700 in our base case because, although one million persons remain susceptible by day 15, R0 essentially drops from 3 to 0.3 (because only 10% of the population is unvaccinated), well below the epidemic threshold. Because TV traces over 80% of the population in the base case, complications due to vaccinating the immunosuppressed will be similar for TV and MV. Also, MV eradicates the epidemic much quicker than TV, making the quarantine of unvaccinated immunosuppresseds a viable alternative under MV.
Similarly, the effect of preattack vaccination (15) can be inferred from our model. Vaccinating a fraction θ of the population before an attack implies that initially a fraction θ(1 − f)ν0 would be immune, a fraction θ(1 − f)(1 − ν0) would be susceptible and unsuccessfully vaccinated, a fraction 1 − θ would be susceptible and untraced, and a tiny fraction θf would die of vaccine complications, where ν0 is the vaccine efficacy for susceptibles (ν0 = 0.975 in our base case). A slightly conservative (i.e., over-) estimate of the postattack fatalities using either TV or MV follows by reducing R0 to R0(1 − θν0) in our model. Consequently, the effect of preattack vaccination, which reduces the gap between TV and MV, can be gleaned from Fig. 2B and Fig. 3 (described below). For example, if 40% of the population undergoes preattack vaccination, R0 effectively falls from 3 to 1.83, and the number of deaths under TV and MV are 40,000 and 440, respectively.
Fig 3.
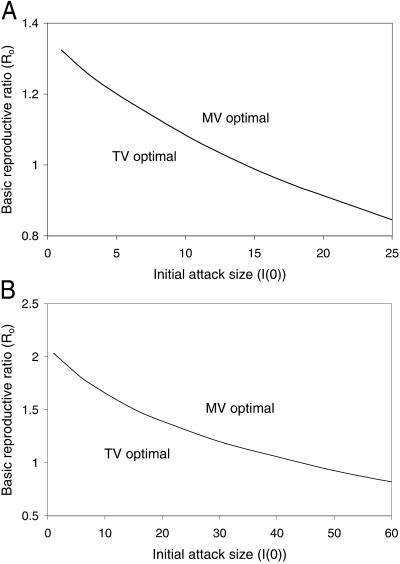
Breakeven curves for the number of deaths under TV versus MV, as a function of the basic reproductive ratio R0 and the number of people initially infected I (0). (A) An index names half of his or her contacts, and (B) an index successfully names all contacts. All other parameters are fixed at their base level (Table 1).
Comparing TV, MV, and the Interim CDC Policy.
Fig. 3 shows breakeven curves, where the total number of deaths from TV and MV are equal, in terms of the initial attack size and R0. For the base case in which index cases name half of their contacts (Fig. 3A), even if only several people are exposed in the initial attack, MV generates less deaths than TV if R0 > 1.3, which is well below most estimates for smallpox R0 (9). Similarly, with the optimistic assumption that index cases successfully name all contacts (Fig. 3B), MV results in fewer deaths than TV if R0 > 2. Highly asymmetric consequences lurk behind Fig. 3: in the region where TV is favored, the number of deaths under each strategy is quite small, whereas in the region where MV is favored, TV may generate many thousands of deaths over a number of months. Moreover, if the MV vs. TV decision ever has to be made, the value of R0 will not be known more precisely than at present, and an accurate estimate of the initial attack size may not be available (ref. 16; http://www.hopkins-biodefense.org/lessons.html). Hence, a decision maker concerned with minimizing the number of deaths in the face of this uncertainty should choose TV only if (s)he is quite certain that R0 and the initial attack size fall in the TV-favorable region of Fig. 3.
We model the CDC guidelines by switching from TV to MV 28 days (i.e., two generations, where Σ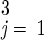 r
r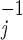 = 14 days) after the start of TV (e.g., on day 33 in the base case). Doing so leads to 4,680 deaths and 15,570 cases over 165 days in the base case, whereas the epidemic peaks at 38 days with 11,400 persons infected. The cost of waiting to switch from TV to MV is very high—4,120 incremental deaths in our base case compared with responding with MV from the start. Consider a strategy that has two decision points: on day 5, the TV vs. MV decision is made with imprecise information about R0 and the initial attack size, and (as in the CDC plan) on day 33 there exists an option to switch from TV to MV after R0 and the initial attack size have been observed. In this setting, it would be optimal to initiate TV on day 5 only if the decision maker were very confident that R0 and the initial attack size are very small.
= 14 days) after the start of TV (e.g., on day 33 in the base case). Doing so leads to 4,680 deaths and 15,570 cases over 165 days in the base case, whereas the epidemic peaks at 38 days with 11,400 persons infected. The cost of waiting to switch from TV to MV is very high—4,120 incremental deaths in our base case compared with responding with MV from the start. Consider a strategy that has two decision points: on day 5, the TV vs. MV decision is made with imprecise information about R0 and the initial attack size, and (as in the CDC plan) on day 33 there exists an option to switch from TV to MV after R0 and the initial attack size have been observed. In this setting, it would be optimal to initiate TV on day 5 only if the decision maker were very confident that R0 and the initial attack size are very small.
Discussion
The CDC policy is fashioned after the famed “surveillance-containment” policy widely credited with the elimination of smallpox worldwide (1, 4). Our results are not inconsistent with the historical claims for surveillance containment, for in many of the smallpox outbreaks the World Health Organization controlled, the estimated initial number of infections was low (1, 6), prior vaccination and recovered cases had already rendered a high degree of herd immunity, effectively reducing R0 (8), and contact tracing was very accurate (high p) because of the physical layout of affected villages and the relative isolation of their inhabitants from other areas of settlement (1). The parameters describing many historical smallpox outbreaks would thus favor TV over MV, as suggested by Fig. 3B. By the same token, our breakeven curves (Fig. 3) are not inconsistent with the mass smallpox vaccination of New York City residents in 1947 in response to eight cases (2), because a large city has millions of highly mobile residents and visitors that render contact tracing difficult (low p), and because the U.S. populace may not tolerate the length of time required for TV to eradicate a small outbreak.
In summary, compared with MV, TV slows the overall vaccination rate, which lengthens the time until herd immunity is reached. As a consequence, the infection continues to spread, potentially increasing the tracing/vaccination burden to the point at which significant congestion occurs. Such queuing delays further reduce the effectiveness of vaccination, for contacts are less likely to be in the vaccine-sensitive stage 1 of disease by the time they are found. Worded differently, congestion makes losing the race to trace more likely. This combination of inefficient and ineffective vaccination could also lead to quarantine overrides (because of insufficient quarantine capacity) as the number of infections continues to spread.
Conclusion
We have formulated a mathematical model that, to our knowledge, is the first to capture two crucial and interrelated features for comparing TV and MV: a detailed analysis of the race to trace and the queuing caused by limited tracing and vaccination resources. Our results show that over a wide range of scenarios, MV leads to many fewer deaths than TV. Moreover, the cost in both deaths and time of delaying the switch to MV—as suggested by the interim CDC policy—is very high, particularly in light of the public clamoring for vaccination and the mass panic that would likely ensue in the event of an attack. For these reasons, given our current states of knowledge and response capabilities [e.g., there is no widely accepted screening test for smallpox (5)], we believe that unless preattack vaccination is used to significantly increase herd immunity in the population, serious consideration should be given to replacing the existing CDC policy by MV in the event of a smallpox attack in a large urban center.
Acknowledgments
We thank Ellis McKenzie of the Fogarty International Center, National Institutes of Health, for initiating this project. This work was supported by the Societal Institute for the Mathematical Sciences, via Grant DA-09351 from the National Institute on Drug Abuse (E.H.K.) and a grant from the Singapore–Massachusetts Institute of Technology Alliance (L.M.W.).
Abbreviations
CDC, Centers for Disease Control
TV, traced vaccination
MV, mass vaccination
Appendix
Throughout, the subscript j denotes stage of infection, whereas the superscript ℓ denotes whether a person has yet to be traced (ℓ = 0) or has already been traced and vaccinated (ℓ = 1). All parameters used are defined in Table 1. The state variables are: Sℓ = number of type ℓ susceptibles; I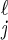 = number of type ℓ infected persons in disease stage j (j = 1, 2, 3, 4); Qj = number in tracing/vaccination queue at disease stage j (j = 0 means susceptibles); H = number in febrile quarantine; Z = number immune (from vaccination) or recovered from smallpox; D = number dead. We also denote the total number of freely mixing infectious individuals as I3 = I
= number of type ℓ infected persons in disease stage j (j = 1, 2, 3, 4); Qj = number in tracing/vaccination queue at disease stage j (j = 0 means susceptibles); H = number in febrile quarantine; Z = number immune (from vaccination) or recovered from smallpox; D = number dead. We also denote the total number of freely mixing infectious individuals as I3 = I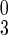 + Q3 + I
+ Q3 + I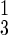 , and the total number of persons in the tracing/vaccination queues as Q = Σ
, and the total number of persons in the tracing/vaccination queues as Q = Σ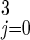 Qj. Finally, define τ to be the time interval between the smallpox attack and the initiation of intervention. Whereas in the text the attack occurs at time t = 0 and the response begins at time t = τ (5 days in our base case), to ease the presentation in the equations below, we let the attack occur at time t = −τ and the response begin at time t = 0. These assumptions lead to the following ordinary differential equations.
Qj. Finally, define τ to be the time interval between the smallpox attack and the initiation of intervention. Whereas in the text the attack occurs at time t = 0 and the response begins at time t = τ (5 days in our base case), to ease the presentation in the equations below, we let the attack occur at time t = −τ and the response begin at time t = 0. These assumptions lead to the following ordinary differential equations.
Untraced States.
Disease transmission occurs in accord with the usual mass action law, whereas disease progression occurs with stage-dependent constant hazard rates. Previously untraced contacts who are named by their true index of infection and found are traced by their appropriate stage of disease accounting for their (random) time of infection by the index {[pλj(t)] terms in Eqs. 2 and 3}. In contrast, those previously untraced contacts who are susceptible, or infected but named by someone other than their true index of infection, trace proportionately over all untraced individuals {[c − pR0(t)] terms in Eqs. 1–3; both functions R0(t) and λj(t) will be explained further shortly}. Note that no tracing occurs before time t = 0.
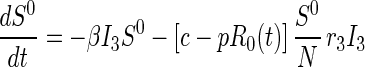 |
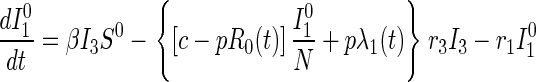 |
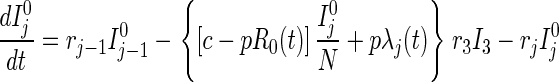 |
for j=2, 3 [3]
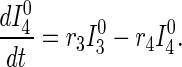 |
Queueing States.
Until t = 0, there is no tracing and hence no queuing. Once t > 0, note that because only n tracers/vaccinators are available, the total flow out of the queuing states can never exceed nμ per day. If the system becomes congested (more than n persons are in the queue), then those in queue in disease stage j receive service at rate nμQj/Q, that is, the service provided is proportional to the relative numbers in queue. This explains the min(1, n/Q) in Eqs. 5–7. Disease transmission and progression continue unabated among those in the queue.
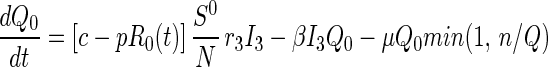 |
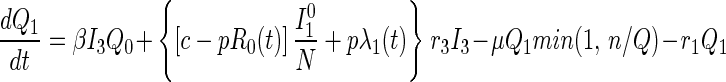 |
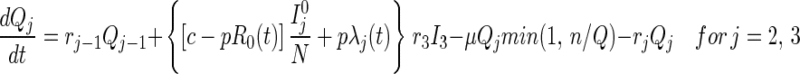 |
Stage 3 Quarantine (Holding) State.
Under CDC policy, in addition to symptomatic cases, only febrile individuals are subject to quarantine. We assume that a fraction h of infectious (stage 3) individuals are identified as febrile and are remanded to quarantine of mean duration α−1 days at the time they are processed in the vaccination queue (except for vaccine fatalities), which leads to
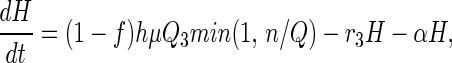 |
as quarantined individuals do not contribute to disease transmission but continue to progress to smallpox.
Traced but Unsuccessfully Vaccinated States.
All unsuccessfully vaccinated individuals (except those in quarantine or vaccine fatalities) freely mix in the population, contributing to disease transmission, while disease progression occurs in the usual way.
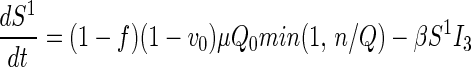 |
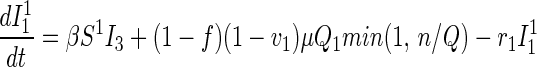 |
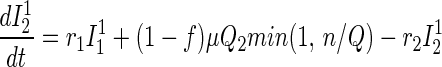 |
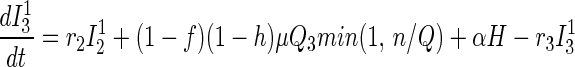 |
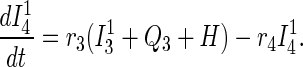 |
Immune/Recovered and Death States.
Successful vaccinations occur with probability ν0 and ν1 for susceptibles and those in stage 1 disease, respectively, whereas the fraction 1 − δ of those who progress to symptomatic smallpox eventually recover (on average r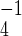 days after development of symptoms) and remain immune. However, the fraction δ of those who develop smallpox die of the disease, whereas the fraction f of all those vaccinated die of vaccine-related complications.
days after development of symptoms) and remain immune. However, the fraction δ of those who develop smallpox die of the disease, whereas the fraction f of all those vaccinated die of vaccine-related complications.
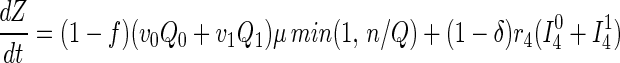 |
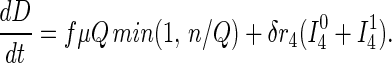 |
The Functions R0(t) and λj (t).
When a newly symptomatic smallpox case is discovered at time t, she will have infected on average R0(t) persons over her duration of infectiousness, where
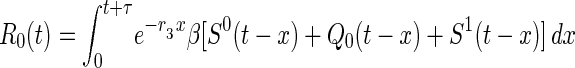 |
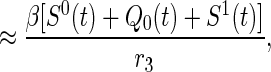 |
with the quasistationary approximation (i.e., the epidemic is viewed as fixed on a short time scale) following from the fact that persons are infectious for only 3 days on average, which is very short relative to the duration of the overall epidemic. Note that R0(0) = βS0(0)/r3 = R0, as defined in the text. Of the R0(t) persons previously infected by an index detected at time t, some will already have been named at random by other index cases even though no transmission occurred. The rate with which anyone in the population is randomly traced at time u ≥ 0 is given by
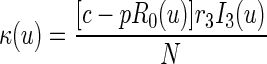 |
[κ(u) = 0 otherwise]. Therefore, the expected number of untraced contacts previously infected by an index detected at time t who are in disease stage j when the index is detected is equal to
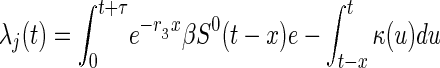 |
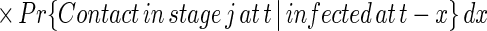 |
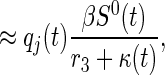 |
where qj(t) is (approximately) the conditional probability that a contact of an index detected at time t is in stage j of disease given that the contact has not been traced by time t, and equals
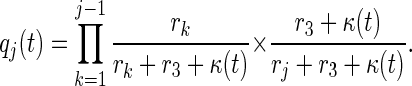 |
The justification for the approximation in Eqs. 18 and 19 is the same quasistationary argument used in Eq. 16.
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Fenner F., Henderson, D. A., Arita, I., Jezek, Z. & Ladnyi, I. D., (1988) Smallpox and Its Eradication (World Health Organization, Geneva).
- 2.Henderson D. A. (1999) Science 283, 1279-1282. [DOI] [PubMed] [Google Scholar]
- 3.Check E. (2001) Nature (London) 414, 677. [DOI] [PubMed] [Google Scholar]
- 4.Centers for Disease Control, (2001) CDC Interim Smallpox Response Plan and Guidelines (Centers for Disease Control, Atlanta, GA), Draft 2.0.
- 5.Henderson D. A. (1999) J. Am. Med. Assoc. 281, 2127-2137. [Google Scholar]
- 6.Meltzer M. I., Damon, I., LeDuc, J. W. & Millar, J. D. (2001) Emerg. Infect. Dis. 7, 959-969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kaplan E. H. (1991) Math. Biosci. 105, 97-109. [DOI] [PubMed] [Google Scholar]
- 8.Anderson R. M. & May, R. M., (1991) Infectious Diseases of Humans (Oxford Univ. Press, Oxford).
- 9.Gani R. & Leach, S. (2001) Nature (London) 414, 748-751. [DOI] [PubMed] [Google Scholar]
- 10.Müller J., Kretzschmar, M. & Dietz, K. (2000) Math. Biosci. 164, 39-64. [DOI] [PubMed] [Google Scholar]
- 11.Division of Nursing, Bureau of Health Professions, Health Resources and Services Administration, (2001) The Registered Nurse Population (Health Resources and Services Administration, Washington, DC).
- 12.Macke B. A., Hennessy, M., McFarlane, M. M. & Bliss, M. J. (1998) Sex. Transm. Dis. 25, 561-568. [DOI] [PubMed] [Google Scholar]
- 13.Mack T. M. (1972) J. Infect. Dis. 125, 161-169. [DOI] [PubMed] [Google Scholar]
- 14.Mack T. M., Thomas, D. B. & Khan, M. M. (1972) Am. J. Epidemiol. 95, 157-168. [DOI] [PubMed] [Google Scholar]
- 15.Bicknell W. J. (2002) N. Engl. J. Med. 346, 1323-1325. [DOI] [PubMed] [Google Scholar]
- 16.O'Toole T. & Inglesby, T., (2001) Shining Light on Dark Winter (Johns Hopkins Center for Civilian Biodefense Strategies, Baltimore).