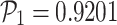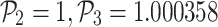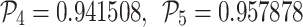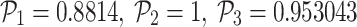Abstract
The following paper presents a new analytical framework for the optimization of player positioning, a methodology with significant practical implications. The method implements the multi-objective optimization by ratio analysis with full multiplicative form (MULTIMOORA) in a decision-making context in which several non-commensurable performance variables have to be combined. The application of Dombi operationalizes the framework by prioritizing weighted aggregation operators coupled with circular q-rung orthopair fuzzy sets (Cq-ROFSs). The Cq-ROFSs allow multidimensional representation of uncertainty, and allow dynamic actions upon the fuzzy parameter q, such that both intuitionistic fuzzy sets and Pythagorean fuzzy sets are subsets. Two Dombi prioritized operators on Cq-ROFSs are thereby devised a Cq-ROFSs Dombi prioritized weighted averaging operator (Cq-ROFSDPWA) and a Cq-ROFSs Dombi prioritized weighted geometric operator (Cq-ROFSDPWG). Results from empirical experiments are reported that demonstrate the performance of the resulting methodology, highlighting its practical relevance. The fundamental properties of these operators are also examined. The proposed aggregation operators are applied within the MULTIMOORA technique to assess their effectiveness. Numerical examples demonstrate that the methods yield logical and consistent results across different decision-making scenarios. Comparative analyses further highlight the advantages of the Cq-ROFSDPWA and Cq-ROFSDPWG operators over existing approaches.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-025-18795-0.
Keywords: Circular q-rung orthopair fuzzy information; Dombi t-norm, and t-conorm; Decision analysis process with MULTIMOORA method; Optimizing player positioning
Subject terms: Engineering, Mathematics and computing
Introduction
One crucial component of decision sciences is Multi attribute decision-making (MADM), a procedure that can produce ranking outcomes for finite options based on the attribute values of many alternatives1. C. Shit and G. Ghorai proposed Dombi aggregation operators under Fermatean fuzzy information for MADM. Shit et al., developed a harmonic aggregation operator for trapezoidal picture fuzzy MADM problems2. C. Shit and G. Ghorai applied Aczel-Alsina aggregation with hesitant fuzzy sets to select the best educational brand3. Nowadays, MADM is widely used in numerous sectors because it is related to the development of organizations and social decision-making in all its dimensions4. Trying to better, effectively, and correctly convey the attribute value is a key issue in real-world decision-making processes5. The expression of attribute values of alternatives by exact values is insufficient in the real world due to the vagueness of decision-making contexts and an array of decision-making challenges as well. Zadeh6 created the FS theory to address these kinds of problems. FS is made up of the truth grade phrase and the recommendation to resume at the unit interval. However, there are several circumstances where the idea of FS is ineffective. For instance, the FS theory cannot deal with information presented to a person in the form of truth and falsity grades. The way Atanassov7 attempted to overcome the limitations of the classical fuzzy sets was to combine the non-membership degree (MD) in a proposition and the measure of membership degree (MD) therein by formulating the intuitionistic Fuzzy Set (IFS) framework. Due to its limitation, whereby the total power of these two parameters lies in the unit interval, IFS assumes a versatile and effective tool in the process of making decisions about complex and suspicious data. The IFS model has thus been used in a wide range of fields by many researchers7. C. Shit and G. Ghorai used interval-valued picture fuzzy VIKOR to select charging methods for public stations8.
Despite its benefits, the IFS model also exhibits problems whereby the provided values of truth and falsehood sum to more than one. To solve this constraint, Yager7 proposed an amendment to the IFS rule, stating that the squared addition of the truth and falsehood coefficients should have its square sum within the [0, 1] interval. This led to the development of the Pythagorean Fuzzy Set (PyFS). Comparative analysis of evidence that PyFS is superior to IFS when it comes to dealing with complex and uncertain data in the decision-making context. Various researchers in many fields, therefore, have embraced the PyFS concept9. Based on PyFS, Yager10 later studied the circumstances under which PyFS can be interpreted as a q-rung orthopair Fuzzy Set (q-ROFS), that the q-power of any mental form of truth and falsehood is no greater than one. The thus-named q-ROFS framework has drawn a lot of interest because of the flexibility that the q-parameter offers to it, allowing it to be used to diagnose deficiencies in many different applications11–13.
More recently, the circular IFS mode came about, which limits its drawing to the domain below the intuitionistic fuzzy interpretation triangle14. To increase the representational scope of such a construct, a new extension has been proposed, that of the circular q-rung orthopair fuzzy sets (Cq-ROFS), extending the uncertainty domain to outside the intuitionistic fuzzy interpretation triangle, though being circumscribed therein by the circle. There are many connections and operations, especially mathematical operations, for Cq-ROFS15–17.
Karande and Chakraborty18 investigated using the conventional Multi-objective optimization based on the ratio analysis (MOORA) approach. Baležentis et al.10 employed the MULTIMOORA approach and IFSs for performance management in another investigation. The study’s suggested methodology has been expanded to include other aggregation strategies. Multiple decision-making issue techniques have been extended to IFSs. Aggregation operators are a crucial component in numerous attribute issues (AO). Xu19 presented fundamental aggregation operators for IFSs. Based on IFSs, Xu and Yager20 created fundamental geometric operators. Using t-norm and t-conorms, formulated aggregation operators such as the Hamacher approach based on interval-valued IFSs21. Hussain and Pamucar22 presented novel aggregation operators using rough sets. A series of Schweizer-Sklar mathematical approaches developed by Hussain et al.23. Jaleel24 investigated some reliable agricultural robotics under the system of bipolar fuzzy theory. Advanced decision analysis and database management systems were established in25. Hussain et al.26 evaluated the performance of Dombi’s mathematical approaches using interval-valued spherical fuzzy theory. Mahmood et al.27 put forward the theory of an innovative approach to the spherical fuzzy context. Hussain et al.28 deliberated on some new approaches to the Aczel Alsina operations. The advanced technology of the electric motor car was developed by Hussain et al.29. Alcantud et al.30 discussed a novel approach to temporal intuitionistic fuzzy theory. Hwang et al.31 investigated new similarity measures using Sugeno integral operators. Farid et al.32 A new technique for waste management was discussed, utilizing the q-rung orthopair fuzzy context. Alreshidi et al.33 combined two theories of similarity and entropy measures for deriving new approaches. Bui et al.34 proposed a decision-making problem using the properties of similarity measures. However, Archimedean and Einstein operators can also be applied to solve issues involving numerous attributes35,36.
Often, decision support systems require considering a wide range of criteria that affect the selection of available options37,16. Furthermore, it is difficult to describe how to select the best solutions given the expert’s ambiguity about how to express the linkages between the data that have been gathered. These issues also occur in sports when players or coaches have a wide range of options to choose from while planning a team for a tournament or conducting training. This work suggests an objective fuzzy inference system based on fuzzy logic to evaluate players in team sports using football as an example. For offensive positions, a multi-criteria model based on the characteristics of the MULTIMOORA method has been developed to evaluate players based on their match facts. This method works well for assigning player skill ratings, as the study has shown. The unique qualities of the MULTIMOORA technology led to its selection.
This study has taken a novel method in light of the previously mentioned thorough investigations and literature review. Prioritized aggregation is associated with the Dombi operator. A more comprehensive process based on the q-ROFVs decision matrix is introduced. Moreover, the benefits and capabilities of employing this approach can be summed up in the following ways:
Decision-makers are aware that in actual MADM issues, each characteristic has a distinct priority level. Thus, in the present investigation, priority AO is used to indicate various priority levels. Experts or different techniques can be used to calculate the weight values, and an individual’s desired order of priority can be used to identify the priority order. As a result, the criteria’s weighting and priority order are not required to coincide.
The decision makers’ evaluations appear as an additional wide range by Cq-ROFVs.
A variety of Dombi aggregation operators (AOs) are formulated using the theory of Cq-ROF information and prioritized aggregation operators.
The MULTIMOORA method is an effective optimization technique for the MADM method under the system of Cq-ROF context.
A MADM approach is explored using newly introduced operators, which are supported by certain numerical examples.
The comparison analysis and the impact of the parameters are also examined to assess the reliability and knowledge of the operators under investigation.
The structure of this framework is illustrated in the following ways: In Sect. 2, we examine the concept of Cq-ROFSs and their operational norms. There is also an extensive examination of the Dombi operators. In Sect. 3, we employ the Dombi prioritized weighted aggregation operators and describe their characteristics. In Sect. 4, the specified operators are used with the MULTIMOORA technique. In Sect. 5, the specified operators and their uses are demonstrated using a numerical example. Additionally, comparisons of the suggested models were made for various parameters. The suggested techniques were also contrasted with those of previous research. The final section discusses Future research and the suggested framework’s benefits.
Preliminaries
To understand basic concepts and fundamental roles, we provide an overview of some notions of q-ROFS and Dombi operations.
Q-rung orthopair fuzzy set (q-ROFs)
The theory of q-ROFS was developed by Yager10 in 2016. We also explored the notion of PFSs38 and Fermatean fuzzy sets (FFSs)39.
Definition 110
A mathematical shape of q-ROFS  is given by:
is given by:
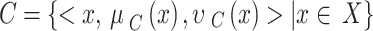 |
1 |
Where 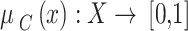 and
and 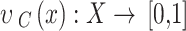 indicate the MD and NMD, respectively, subject to a condition:
indicate the MD and NMD, respectively, subject to a condition: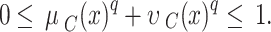 Moreover, the hesitance value is denoted by
Moreover, the hesitance value is denoted by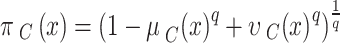 and the pair
and the pair is known as a q-rung orthopair fuzzy value.
is known as a q-rung orthopair fuzzy value.
Definition 210
Consider three q-ROFVs 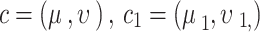 and
and 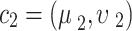 . Then, basic operations are given as follows:
. Then, basic operations are given as follows:
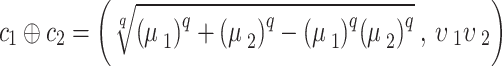
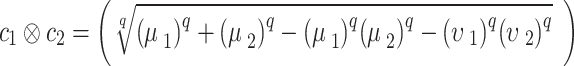
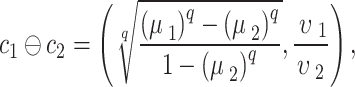 if
if 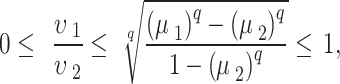 otherwise
otherwise  ;
;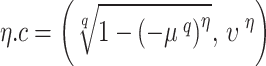 , for
, for 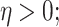 .
.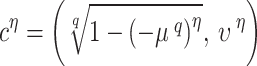 , for
, for 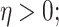 .
.
Definition 340
Consider a q-ROFV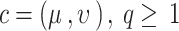 . Then, some expressions of score values and accuracy values are given as follows:
. Then, some expressions of score values and accuracy values are given as follows:
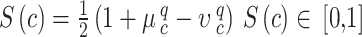 |
2 |
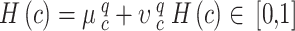 |
3 |
Here, we discussed a comparison of two different q-ROFVs 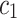 and
and 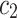 as follows:
as follows:
If  then
then 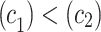 ; if
; if 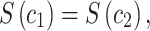 then
then 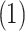
 then
then 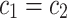 ;
; 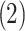 if
if  , then
, then 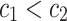 .
.
Dombi operations
This subsection presents some dominant expressions of Dombi t-norm and t-conorm.
Definition 441
Consider two positive real numbers 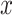 and
and 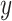 . Then, the Dombi TN and TCN are characterized as follows:
. Then, the Dombi TN and TCN are characterized as follows:
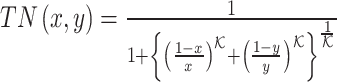 |
4 |
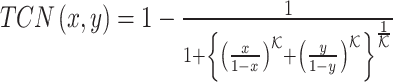 |
5 |
We have discussed the flexible operations of Dombi TN and TCN operations in the context of q-ROFVs.
Definition 542
Consider two q-ROFVs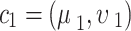 and
and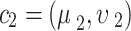 with
with 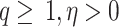 . Then, we have:
. Then, we have:
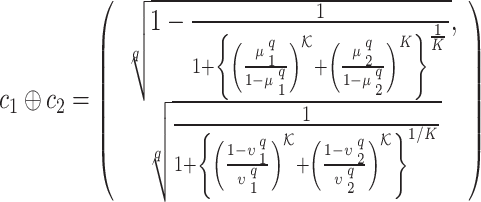 |
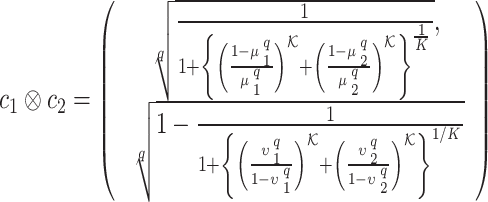 |
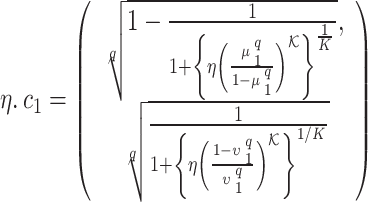 |
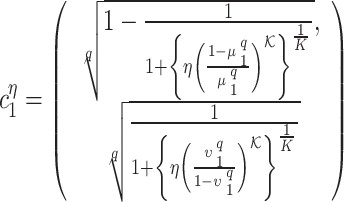 |
Definition 643
Consider a collection of preferences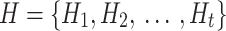 with the linear ordering
with the linear ordering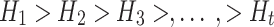 . So, we denote higher priority with
. So, we denote higher priority with  such as
such as 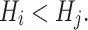 However, the power average operators are given by:
However, the power average operators are given by:
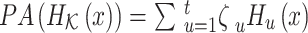 |
6 |
As,
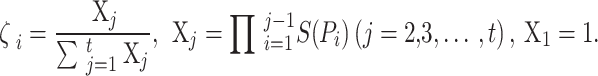 |
Definition 744
The mathematical shape of C-IFS  in
in 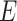 is given by:
is given by:
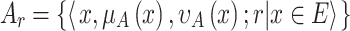 |
As 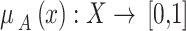 and
and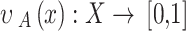 indicate the MD and NMD with an addition value of the radius of the circle
indicate the MD and NMD with an addition value of the radius of the circle 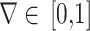 among MD and NMD. Furthermore, the C-IFS must satisfy the condition
among MD and NMD. Furthermore, the C-IFS must satisfy the condition 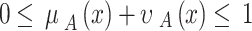 .
.
Moreover, the hesitancy degree of 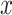 in
in  is expressed as:
is expressed as: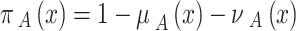 .
.
Definition 844
The mathematical shape of Cq-ROFS 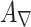 in
in 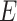 is given by:
is given by:
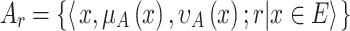 |
As 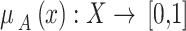 and
and indicate the MD and NMD with an addition value of the radius of the circle
indicate the MD and NMD with an addition value of the radius of the circle 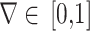 among MD and NMD. Furthermore, the Cq-ROFSmust satisfy the condition
among MD and NMD. Furthermore, the Cq-ROFSmust satisfy the condition 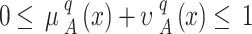 .
.
Moreover, the hesitancy degree of 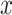 in
in 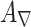 is expressed as:
is expressed as: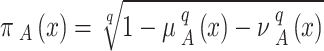 . The circular q-rung orthopair fuzzy value (Cq-ROFV) is denoted by
. The circular q-rung orthopair fuzzy value (Cq-ROFV) is denoted by 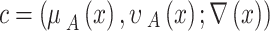 .
.
Cq-rung orthopair fuzzy Dombi prioritized aggregation operators
This section formulates some flexible operations of Dombi TN and TCN insight into the Cq-rung orthopair fuzzy context.
Definition 9
Consider are two Cq-ROFVs with
are two Cq-ROFVs with . Then, we have the following operations:
. Then, we have the following operations:
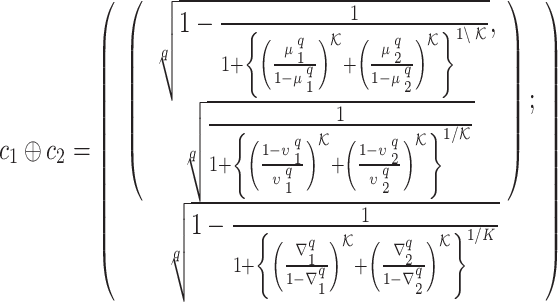 |
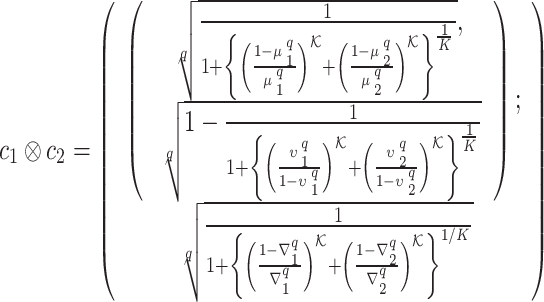 |
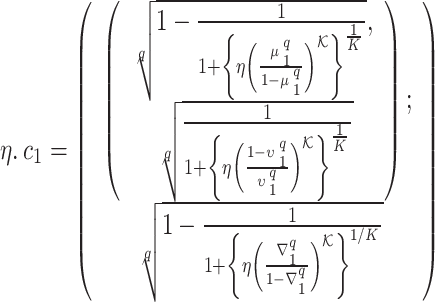 |
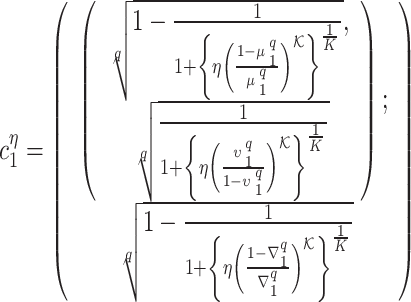 |
Cq-rung orthopair fuzzy Dombi prioritized weighted averaging aggregation operators
This subsection presents a series of new mathematical approaches of the Cq-ROFDPA and Cq-ROFDPWA operators with some feasible properties.
Definition 10
Let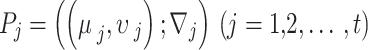 be the collection of Cq-ROFVs. The Cq-ROFDPA operator is expressed as follows:
be the collection of Cq-ROFVs. The Cq-ROFDPA operator is expressed as follows:
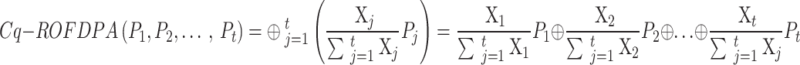 |
Where 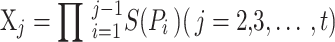 and
and 
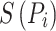 is the value of the score function.
is the value of the score function.
Theorem 1
Let a collection of Cq-ROFVs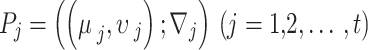 . Then fused value by using the Cq-ROFDPA operator is also a Cq-ROFV and we have:
. Then fused value by using the Cq-ROFDPA operator is also a Cq-ROFV and we have:
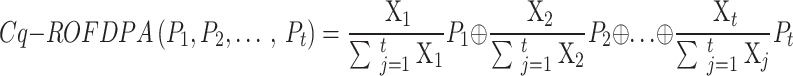
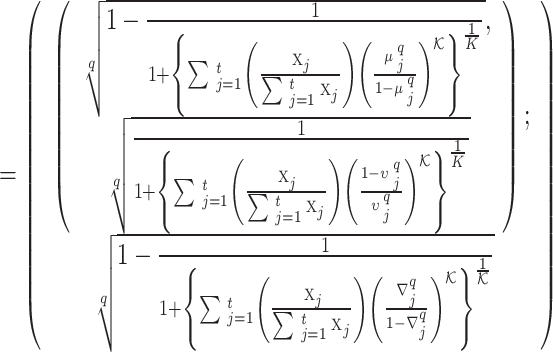 |
7 |
Where 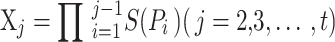 and
and 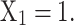
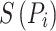 is the value of the score function.
is the value of the score function.
Proof See Appendix A.
Theorem 2
Let 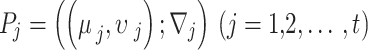 be the collection of Cq-ROFVs. Where
be the collection of Cq-ROFVs. Where 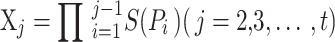 and for
and for 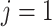 ,
, 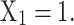
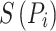 is the value of the score function. If
is the value of the score function. If 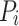 are all equal. Then
are all equal. Then  for all
for all 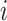 . We prove the following statement.
. We prove the following statement.
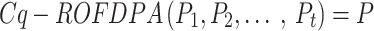 |
Proof See Appendix B.
Theorem 3
Let 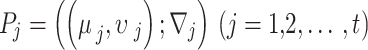 be the collection of Cq-ROFVs. Then,
be the collection of Cq-ROFVs. Then,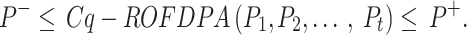
Proof See Appendix C.
Theorem 4
Let 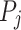 and
and 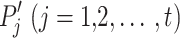 be two collections of Cq-ROFVs. If
be two collections of Cq-ROFVs. If 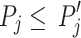 for all
for all  , where
, where 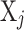
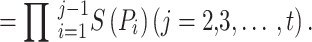
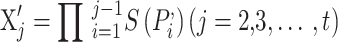 and
and 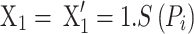 and
and 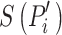 are values score function
are values score function 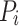 and
and 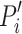 respectively. Then,
respectively. Then, 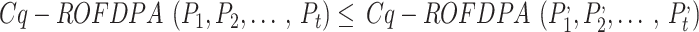 .
.
Proof See Appendix D.
Definition 11
Let 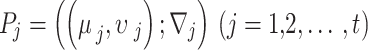 be the collection of Cq-ROFVs.
be the collection of Cq-ROFVs. 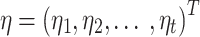 such that
such that 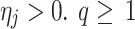 and
and 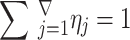 Cq-ROFDPWA operator defined
Cq-ROFDPWA operator defined
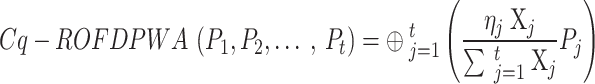 |
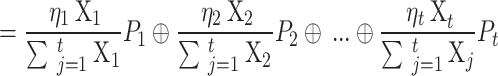 |
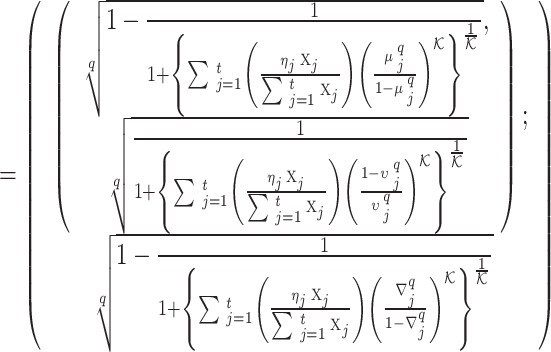 |
8 |
.
where 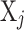
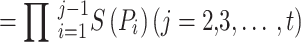 and
and 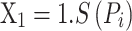 is the value of the score function.
is the value of the score function.
Cq-rung orthopair fuzzy Dombi prioritized weighted geometric aggregation operators
This section formulated an innovative approach of the Cq-ROFDPG and Cq-ROFDPWG operators under the system of Cq-ROF information.
Definition 12
Let 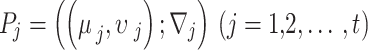 be the collection of Cq-ROFVs.
be the collection of Cq-ROFVs.  operator defined as
operator defined as
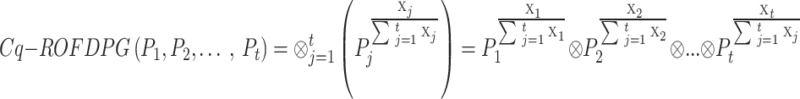 |
where 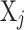
 and
and 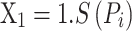 is the value of the score function.
is the value of the score function.
Theorem 5
Let a collection of Cq-ROFVs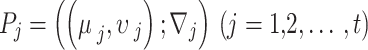 . Then the fused value by using the Cq-ROFDPG operator is also a Cq-ROFV and we have:
. Then the fused value by using the Cq-ROFDPG operator is also a Cq-ROFV and we have:
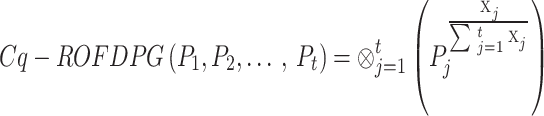 |
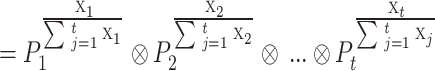 |
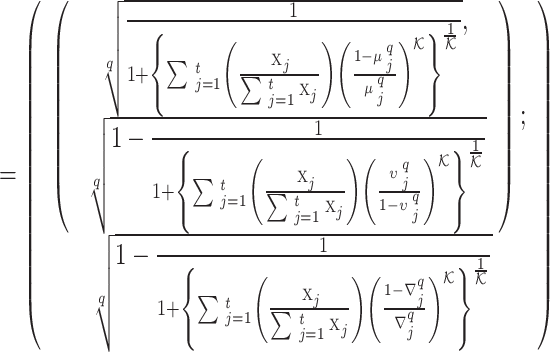 |
9 |
where 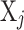
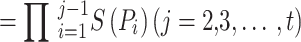 and
and 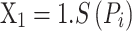 is the value of the score function.
is the value of the score function.
Proof See Appendix E.
Theorem 6
Let 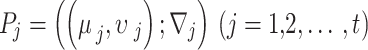 be the collection of Cq-ROFVs. Where
be the collection of Cq-ROFVs. Where 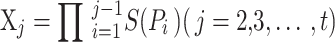 and for
and for 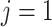 ,
, 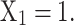
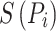 is the value of the score function. If
is the value of the score function. If  are all equal. As
are all equal. As  for all
for all 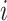 .
.
Then 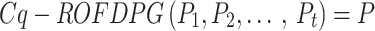 .
.
Proof is similar to the proof of theorem 2.
Theorem 7
Let 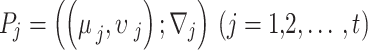 be the collection of Cq-ROFVs. Then,
be the collection of Cq-ROFVs. Then,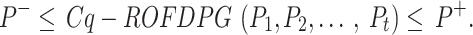
Proof is similar to the proof of theorem 2.
Theorem 8
Let  and
and 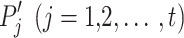 be two collections of Cq-ROFVs. If
be two collections of Cq-ROFVs. If 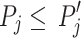 , For all
, For all 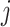 , where
, where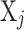
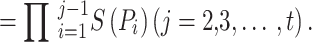
 and
and 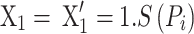 and
and 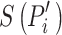 are value score function
are value score function  and
and 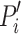 respectively. Then,
respectively. Then, 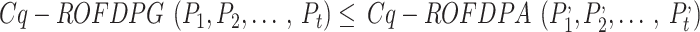 .
.
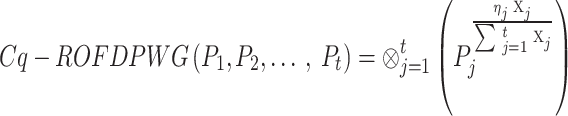 |
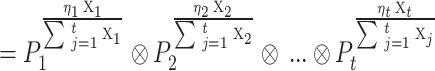 |
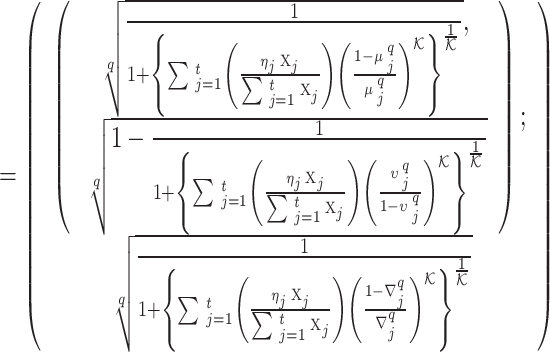 |
10 |
Proof is similar to the proof of Theorem 2.
MADM method based on the investigated operators
This section presents the decision algorithm for the derived mathematical approaches of the Cq-ROFDPWA and Cq-ROFDPWG operators. An advanced technique of the MULTIMORA method is used to evaluate some flexible optimal options by combining the theory of criteria and different alternatives. To serve this purpose, consider a set of alternatives. 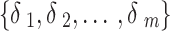 and a collection of attributes
and a collection of attributes 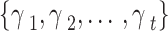 with weight vectors
with weight vectors  that satisfies
that satisfies 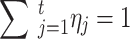 and
and 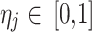 . Furthermore, decision-makers assume Cq-ROF information in different alternatives and attributes, which are listed in the decision matrix
. Furthermore, decision-makers assume Cq-ROF information in different alternatives and attributes, which are listed in the decision matrix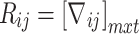 . To aggregate given information about different preferences, we use the following algorithm of the MULTIMOORA method and derive mathematical terminologies under the system of Cq-ROF environment.
. To aggregate given information about different preferences, we use the following algorithm of the MULTIMOORA method and derive mathematical terminologies under the system of Cq-ROF environment.
Step 1. Problem formulation
First, the decision maker arranges various attributes and information associated with each alternative or individual in a decision matrix 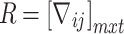 .
.
Step 2. Normalization of Cq-ROF decision matrix
Mostly, attribute information has two types: benefit attributes (B) and cost type attributes (C). If there is more than one type of attribute information, then we have to normalize the given information using the following expression:
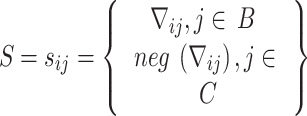 |
11 |
Step 3. MULTIMOORA ratio system calculation
Investigate the ratio system for the MULTIMOORA method using the derived approaches of the Cq-ROFDPWA operator based on Cq-ROF information:
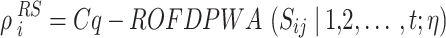 |
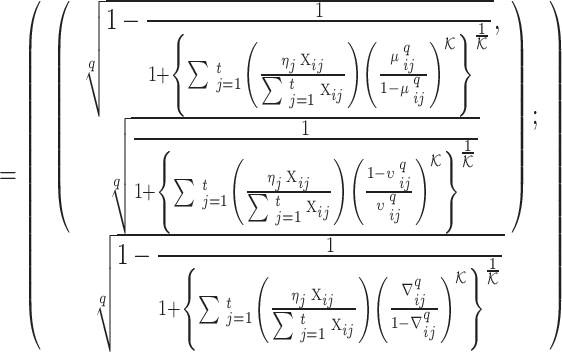 |
12 |
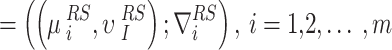 |
Utilize the following expression to investigate single-term information associated with each alternative:
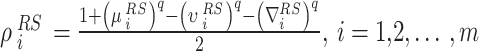 |
13 |
Here, crisp values are normalized using the following expression:
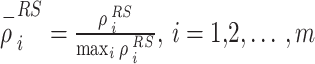 |
14 |
Where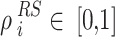 .
.
Step 4. Reference point analysis
Using the theory of the Chebyshev distance formula, compute different reference points for each alternative or individual as follows:
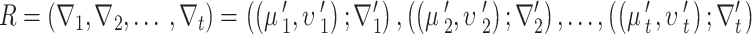 |
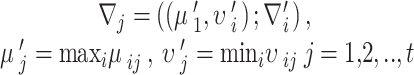 |
15 |
If an ideal solution has maximum membership degrees 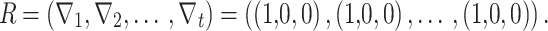 Here, we compute the Hamming distance among two different Cq-ROFVs using the following expression: Let
Here, we compute the Hamming distance among two different Cq-ROFVs using the following expression: Let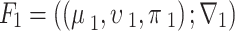 and
and 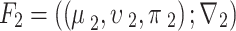 be two Cq-ROFVs.
be two Cq-ROFVs.
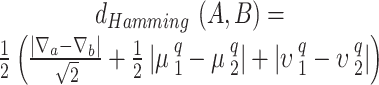 |
16 |
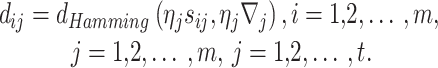 |
17 |
Additionally, compute the maximum Chebyshev distance using the investigated reference point for each alternative or individual:
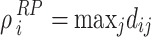 |
Since computed reference point is a non-compensatory technique. The lower value of the reference point 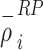 has higher efficiency. Next, we will find out the normalized score.
has higher efficiency. Next, we will find out the normalized score.
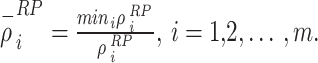 |
18 |
Where is the highest utility value 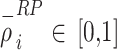 .
.
Step 5. Multiplicative utility function evaluation
Compute the multiplicative utility function using the derived approaches of the Cq-ROFDPWG operator with the degree of weights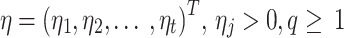 criteria.
criteria.
The following expression computes the utility function:
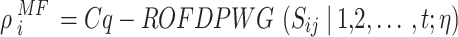 |
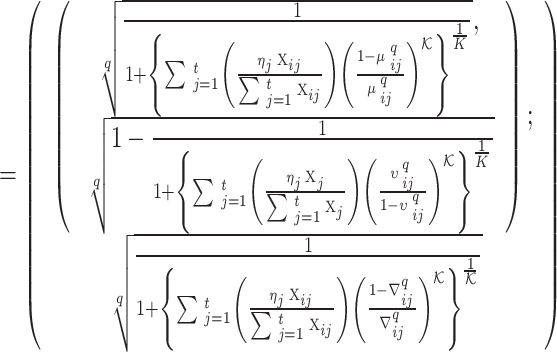 |
19 |
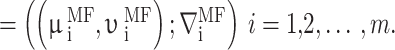 |
20 |
Utilize the score function to compute the single-term results using the following expression:
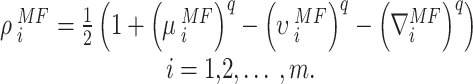 |
21 |
Then crisp values are normalized.
 |
22 |
The maximum value of the computed results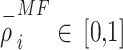 .
.
Step 6. Ranking and final decision
Finally, to evaluate the rank of the alternative, we apply the Dominance theory seen in the three Moora45.
Figure 1 shows the flowchart of the MULTIMOORA method.
Fig. 1.
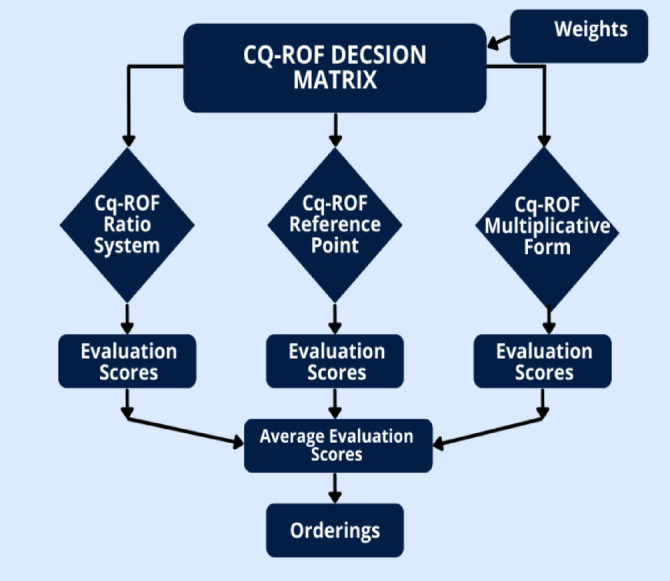
A framework of the MULTIMOORA methodology.
Application
In the context of a football match, one of the most critical factors determining whether a team will emerge victorious is the composition of its players or the positioning of each player within the team that corresponds with the skills he possesses. Generally, the method of selection is performed individually, with the trainer’s estimations serving as the basis for the procedure. In this manner, it is not feasible to determine the value of a structure or team that possesses a particular player foundation. The authors of this research developed a decision support system. The purpose of this system is to provide the coach with guidance in determining which players are the most suitable to fill a particular position within the team structure. The ability of an individual to analyze the ball is a skill that is tested throughout the game of football. There are a lot of individuals all over the world who enjoy playing and watching football. Engaging in the activity of watching or playing football can serve as an effective way of relieving stress brought on by various responsibilities at the workplace, on campus, and beyond. This practice can also be used to strengthen familial connections, which is another potential benefit.
Those who are passionate about football frequently have particular players, organizations, and national teams. Without a doubt, a club’s goal is to win in several different competitions. Many factors contribute to the success of a team, including the lineup of the players, the vision of the head coach, the selection of structures, the distinct capabilities of all players, and other key elements. The club meets all of these responsibilities through the implementation of routine training activities that are meticulously organized, beginning with fundamental drills and involving participation in teamwork. In general, a player is regarded as outstanding if they can play in multiple positions, or more specifically, if they can play in various roles. Because of this limitation, a player can rotate in any circumstance at any time according to the plan that the coach established. Sanata Dharma University (USD FC) is a participant in the football tournaments that the Yogyakarta City PSSI branch organization conducts. In 2015, USD FC was recognized for this distinction. Although the team aims to achieve the First distinction, it faces challenges, including players who are often late and workout routines that conflict with their academic commitments. The growth of the players is impeded as a result of these challenges, and it is difficult for coaches to evaluate and report the players’ performance accurately. There is also a common issue that arises among players who practice regularly and players who practice infrequently. Some players who regularly attend practice sessions are left out when it is time to play for the team in matches, which can make their teammates jealous.
The numerous barriers mentioned above result in the player’s evaluation data becoming extensive, which can confuse the coach when determining the most suitable player positions and alternative positions based on the capabilities of the players. In the example below, we will examine how the coach can easily assess which players are qualified for specific positions and which players, given their abilities, would be better suited for other positions. Figure 2 illustrates the original positioning numbering Scheme used in football player positioning.
Fig. 2.

Schematic illustration of the traditional soccer position numbering system (1–11) on a standard field. Numbers represent standard player positions in a classic formation. Figure created by the authors using artificial intelligence.
Numerical example
This section provides real-world examples to illustrate the exactness and continuity of the suggested techniques. Every real-world example is displayed using the MULTIMOORA-Cq-ROF approach. For this example, the impact of the Dombi parameter  and
and 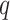 parameters is also examined. We evaluate the findings in light of previous research in the field. The proposed operators were studied in MULTIMOORA-Cq-ROF Pythagorean fuzzy numbers.
parameters is also examined. We evaluate the findings in light of previous research in the field. The proposed operators were studied in MULTIMOORA-Cq-ROF Pythagorean fuzzy numbers.
Example 1
The purpose of this is to establish the ideal positioning for five football players 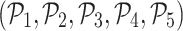 or the attacking position at attacking center middle fielder, depending on four essential attributes. These attributes are important for measuring the general efficiency and role played by all players in the squad. We thoroughly examine the abilities and versatility of players for various positions on the playing field. According to the following four attributes are as follows:
or the attacking position at attacking center middle fielder, depending on four essential attributes. These attributes are important for measuring the general efficiency and role played by all players in the squad. We thoroughly examine the abilities and versatility of players for various positions on the playing field. According to the following four attributes are as follows: 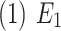 is the Technical skills;
is the Technical skills; 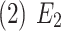 is the Physical Fitness;
is the Physical Fitness; 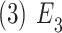 is the Tactical Awareness;
is the Tactical Awareness; 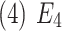 is Teamwork. Here, we attempt to discover the ideal positions for each player. This procedure is crucial for boosting team effectiveness, increasing player performance, and developing future game planning. By an organized analysis and weighting technique, we give an extensive foundation enabling responsible decision-making in player positioning. A panel of experts, including the head coach, deputy instructors, and the team athletics psychiatrist, was assembled to analyze the players. The panel followed a systematic decision-making process to guarantee certain the assessment was extensive and impartial. The specification of the Prioritization relation attributes is as follows:
is Teamwork. Here, we attempt to discover the ideal positions for each player. This procedure is crucial for boosting team effectiveness, increasing player performance, and developing future game planning. By an organized analysis and weighting technique, we give an extensive foundation enabling responsible decision-making in player positioning. A panel of experts, including the head coach, deputy instructors, and the team athletics psychiatrist, was assembled to analyze the players. The panel followed a systematic decision-making process to guarantee certain the assessment was extensive and impartial. The specification of the Prioritization relation attributes is as follows: 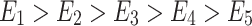 . The decision maker assigns some specific degree of weight to the criteria associated to each alternative
. The decision maker assigns some specific degree of weight to the criteria associated to each alternative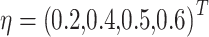 . Table 1 shows the decision matrix of the Cq-ROF information. An expert assesses each option in this decision matrix based on the standards in the PFN’s situation. An example is shown for
. Table 1 shows the decision matrix of the Cq-ROF information. An expert assesses each option in this decision matrix based on the standards in the PFN’s situation. An example is shown for 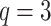 and
and 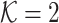 in the phases that follow. Additionally, the Prioritized matrix for
in the phases that follow. Additionally, the Prioritized matrix for 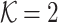 and
and 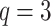 is determined in this way.
is determined in this way.
 |
Table 1.
Decision matrix with circular pythagorean fuzzy numbers.
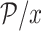
|
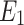
|

|
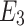
|

|
|---|---|---|---|---|
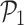
|
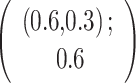
|
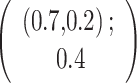
|
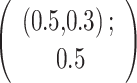
|
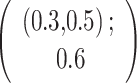
|
|
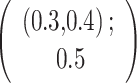
|
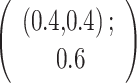
|
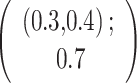
|
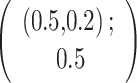
|
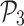
|
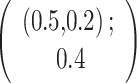
|
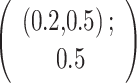
|
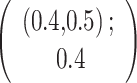
|

|
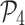
|
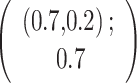
|
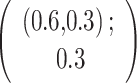
|
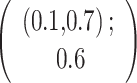
|
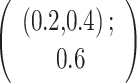
|

|
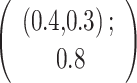
|
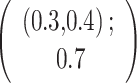
|
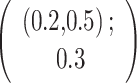
|
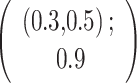
|
Phase (1) identification of the attributes is of the same type, so there is no need for a normalization process.
Phase (2) In this phase, the ratio system for MULTIMOORA-Cq-ROFS is operated on using the Cq-ROFDWA operator. The weight vector of the attributes is 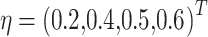 Such that
Such that 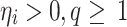 .
.
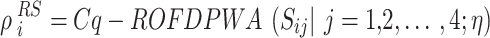 |
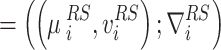 |
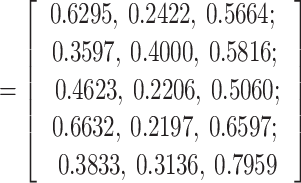 |
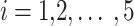 |
(The outcomes of the aggregation process is 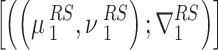 ,
, 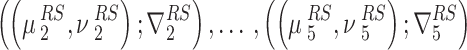 .
.
Phase (3) Investigate the score function using the information of phase 2.
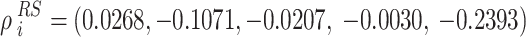 |
The values of the crisp are normalized.
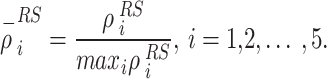 |
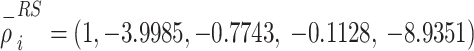 |
For MULTIMOORA-Cq-ROFS the rank result of the ratio system 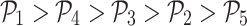 .
.
For all possibilities, the Chebyshev distance is computed and the reference point is established.
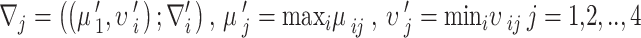 |
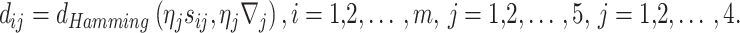 |
Moreover, the maximum Chebyshev distance from the reference point is also calculated for every alternative.
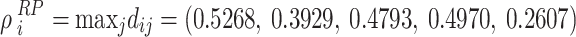 |
The process used as a reference point is non-compensatory. Thus, the lesser 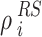 value has a larger utility. However, normalized utility scores can be computed in the following stage.
value has a larger utility. However, normalized utility scores can be computed in the following stage.
Phase (4) Here, we computed normalized utility scores using the following expressions:
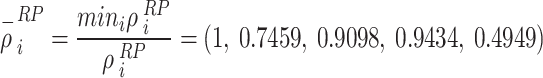 |
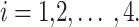 |
Investigate the rank of alternatives using the MULTIMOORA method and Cq-ROF information as follows: 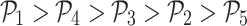
Phase (5) In this phase, the multiplicative utility function for MULTIMOORA-Cq-ROFS is treated with the Cq-ROFDPWG operator. Some weight is assigned to each attribute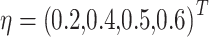 such that
such that  .
.
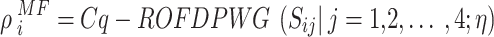 3
3
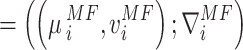 |
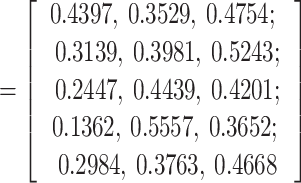 |
 |
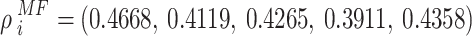 |
The crisp information is normalized as follows:
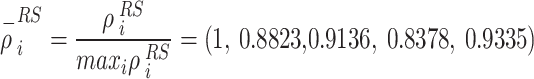 |
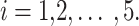 |
Phase (6) For MULTIMOORA-Cq-ROFS, the rank result of the multiplicative utility function: 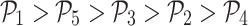 of are utilized the concept of dominance is used to rank as occurring due to the combination of MOORA and multiplicative form Table 2 provides the MUTIMOORA ranking for
of are utilized the concept of dominance is used to rank as occurring due to the combination of MOORA and multiplicative form Table 2 provides the MUTIMOORA ranking for 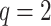 and
and 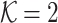 . The first possibility seems to be the most excellent option. From the MULTIMOORA structure, the is
. The first possibility seems to be the most excellent option. From the MULTIMOORA structure, the is 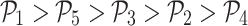 .
.
Table 2.
MULTIMOORA results according to dominance theory (PyFNs).
| Ratio system | Reference point | Multiplicative form | MULTIMOORA | |
|---|---|---|---|---|
|
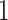
|
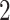
|
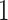
|
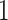
|
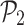
|
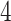
|
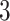
|
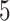
|
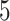
|
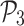
|
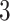
|
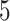
|
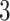
|
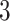
|
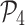
|
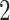
|
|
|
|
|
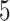
|
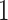
|
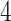
|
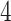
|
Such a prioritized approach to weighted aggregation operators, which was implemented to incorporate Dombi, can drastically enhance the accuracy of decisions about player positioning by providing an alternative aggregation structure capable of dynamically adapting to various dimensions of importance given to performances. By varying the parameter of Dombi, decision-makers can model the relative importance of criteria such as speed, stamina, tactical awareness, and technical skills. This allows for more specific, consistent, and flexible assessments, and thus players are placed in an optimal position in relation to the strategic goals of the teams.
Impact of different parameters 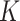 and
and 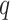 on the MULTIMOORA method based on Cq-ROF and CPYF information
on the MULTIMOORA method based on Cq-ROF and CPYF information
For instance, exceptional examples are compared for 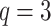 and
and 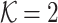 . These particular examples were picked to illustrate doubts better and to compare with alternative approaches, uncertainties can only be expressed in an intuitionistic if
. These particular examples were picked to illustrate doubts better and to compare with alternative approaches, uncertainties can only be expressed in an intuitionistic if  . The data is more comprehensive, though. The Pythagorean fuzzy set expresses the uncertainty if
. The data is more comprehensive, though. The Pythagorean fuzzy set expresses the uncertainty if 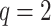 . Furthermore, PyFNs already make up the data. However,
. Furthermore, PyFNs already make up the data. However,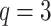 was used as an example since Cq-ROF studies examined MADM difficulties from a broader perspective, it is also known that the score values get closer to one another as the
was used as an example since Cq-ROF studies examined MADM difficulties from a broader perspective, it is also known that the score values get closer to one another as the  values increase.
values increase.
Let’s analyze how 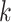 and
and 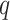 parameters affect the suggested techniques. Table 4 presents the rankings derived from the parameter effects results on MULTIMOORA-Cq-ROF. There is no aggregating mechanism utilized in the reference point method. It just varies based on
parameters affect the suggested techniques. Table 4 presents the rankings derived from the parameter effects results on MULTIMOORA-Cq-ROF. There is no aggregating mechanism utilized in the reference point method. It just varies based on 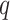 values. Consequently, Table 3 provides a reference point method based on
values. Consequently, Table 3 provides a reference point method based on  values. The impact of the
values. The impact of the 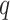 and
and 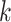 parameters on the MULTIMOORA-Cq-ROF structure are displayed in Tables 3 and 4. Table 3 illustrates that the optimal choice remains constant based on the
parameters on the MULTIMOORA-Cq-ROF structure are displayed in Tables 3 and 4. Table 3 illustrates that the optimal choice remains constant based on the 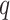 values. As the q values rise, the score values get closer to one another. Consequently, the highest limit of
values. As the q values rise, the score values get closer to one another. Consequently, the highest limit of 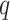 is
is 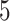 . The best player at the position of attacking middle field, according to the MULTIMOORA result, is
. The best player at the position of attacking middle field, according to the MULTIMOORA result, is 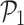 , which was obtained by applying prioritized aggregation with Dombi TN. For
, which was obtained by applying prioritized aggregation with Dombi TN. For 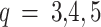 and
and 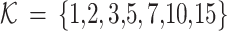 values, regardless of the aggregating operators employed. Based on the observed data, the ranking shows that
values, regardless of the aggregating operators employed. Based on the observed data, the ranking shows that 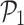 is the best player in the attacking midfield position. At
is the best player in the attacking midfield position. At 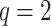 , the positions of players
, the positions of players 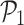 and
and 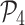 are quite close to each other at
are quite close to each other at 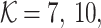 and
and 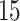 . Still, this closeness does not impact the overall results of the MULTIMOORA method, which continues to rank the player
. Still, this closeness does not impact the overall results of the MULTIMOORA method, which continues to rank the player 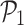 As the most preferred choice, the method demonstrates its consistency and robustness in evaluating player performance under varying parameter scenarios.
As the most preferred choice, the method demonstrates its consistency and robustness in evaluating player performance under varying parameter scenarios.
Table 4.
Impact of different parameters on the MULTIMOORA method.
| q-parameter | k values | Ratio system | Multiplicative form | MULTIMOORA method |
|---|---|---|---|---|
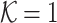
|
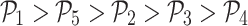
|
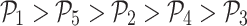
|
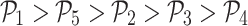
|
|
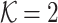
|
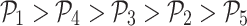
|

|
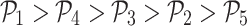
|
|
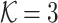
|

|
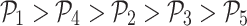
|
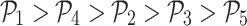
|
|
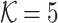
|
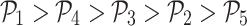
|
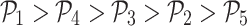
|
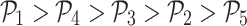
|
|
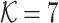
|

|
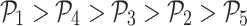
|
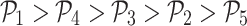
|
|
|
|
|
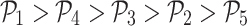
|
|
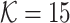
|
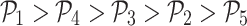
|
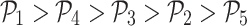
|
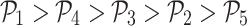
|
|
| q = 3 |
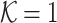
|
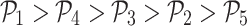
|
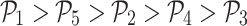
|
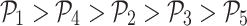
|
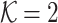
|
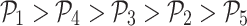
|
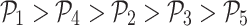
|
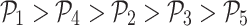
|
|
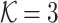
|

|
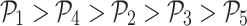
|
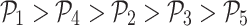
|
|
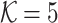
|
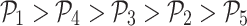
|
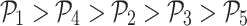
|
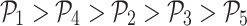
|
|
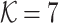
|
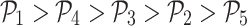
|
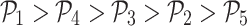
|
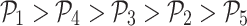
|
|
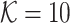
|
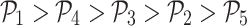
|
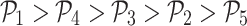
|
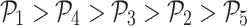
|
|
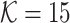
|
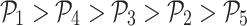
|
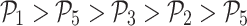
|
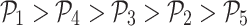
|
|
| q = 4 |
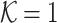
|
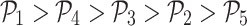
|
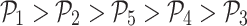
|
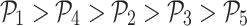
|
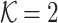
|
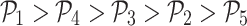
|
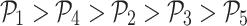
|
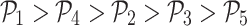
|
|
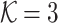
|
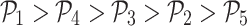
|
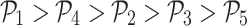
|
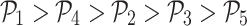
|
|
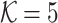
|
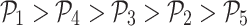
|
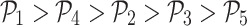
|
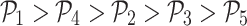
|
|
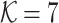
|
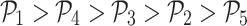
|
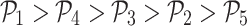
|
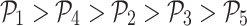
|
|
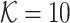
|
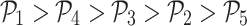
|
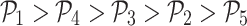
|
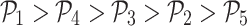
|
|
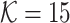
|
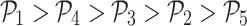
|
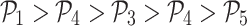
|

|
|
| q = 5 |
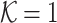
|
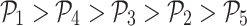
|
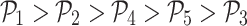
|
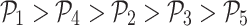
|
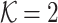
|
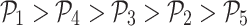
|
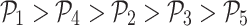
|
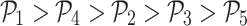
|
|
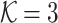
|
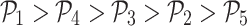
|
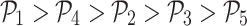
|
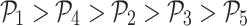
|
|
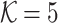
|
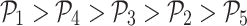
|
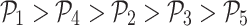
|
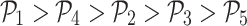
|
|
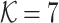
|
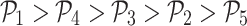
|
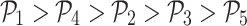
|
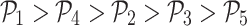
|
|
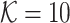
|
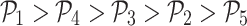
|
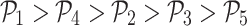
|
|
|
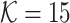
|
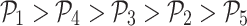
|
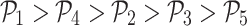
|
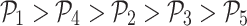
|
Table 3.
Reference point rankings for MULTIMOORA-Cq-ROF PyFNs.
| q-parameters utility score | Reference point | |
|---|---|---|
| q = 2 |
|
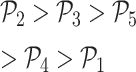 . . |
| q = 3 |
|
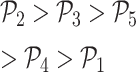 . . |
| q = 4 |
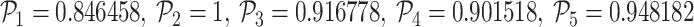
|
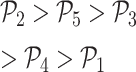 . . |
| q = 5 |
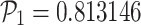 , , 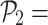 1, 1, 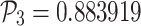 , , 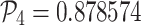 , , 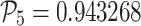
|
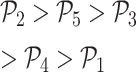 . . |
Comparative analysis
This section explores the impact of excluding the circular radius information in the decision-making process by comparing Cq-ROFDPWA and Cq-ROFDPWG operators with q-ROFDPWA and q-ROFDPWG operators. Initially, the decision matrix is aggregated using the Cq-ROFDPWA and Cq-ROFDPWG operators. Cq-ROFDPWA and Cq-ROFDPWG scores are comparatively steady because of the existence of the circular part. In contrast, deleting the radius component and then re-aggregating the resultant data using q-ROFDPWA and q-ROFDPWG leads to a significant increase in the variability of the scores. Particularly, q-ROFDPWA has greater average values, but q-ROFDPWG shows higher shifts, both positive and negative differences, with Cq-based alternatives increasing notably. This is reflective of the stability that the radius component creates; the neglect of which creates increased variances, particularly in the geometric aggregation. An observation of these aggregate techniques reveals that by removing the radius, the smoothing effect is reduced by the weighted averaging operator, and the sensitivity of the geometric operator is increased, especially in q-ROFDPWG, which has remarkably noticeable fluctuations. The derived rankings confirm the significance of the radius element; the formulations with Cq provide more uniform and consistent results as compared to the q-based formulations, which, due to the absence of radius, enhance the variations. This demonstrates the significant role of the radius term in balancing and stabilizing aggregation results, particularly in player evaluation and movement analysis. The empirical assessment discussed in the manuscript proves that the proposed Cq-based operators not only provide mathematically stable aggregation outcomes but also lead to attractive practical benefits. They serve as consistent and continuous player evaluation, significantly enhancing tactical decision-making and real-time positioning optimization. This enhancement is particularly notable when compared to singular, usually q-ROF-based approaches.
We can analyze aggregated results and the ranking of alternatives listed in Tables 5 and 6. Figure 3 displays an analysis of four different aggregation operators: q-ROFDPWA, Cq-ROFDPWG, q-ROFDPWG, and q-ROFDPWS, along with alternatives 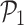 to
to 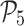 . It is important to note that q-ROFDPWA recorded the highest performance scores on more than one occasion, whereas the results of Cq-ROFDPWG and q-ROFDPWG were in the middle yet quite consistent, thus signifying different operation styles on the part of the operators.
. It is important to note that q-ROFDPWA recorded the highest performance scores on more than one occasion, whereas the results of Cq-ROFDPWG and q-ROFDPWG were in the middle yet quite consistent, thus signifying different operation styles on the part of the operators.
Table 5.
Score values corresponding to each alternative.
| q-ROFDPWA | q-ROFDPWG |
|---|---|
| 0.6182 | 0.5146 |
| 0.4941 | 0.4848 |
| 0.5430 | 0.4622 |
| 0.6326 | 0.4099 |
| 0.5074 | 0.4748 |
Table 6.
Ranking of alternatives.
| Ranked Results | |
|---|---|
| q-ROFDPWA |
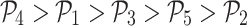
|
| q-ROFDPWG |
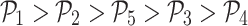
|
Fig. 3.

Diagram of Computed Results Using the Cq-ROFDPWA, Cq-ROFDPWG, q-ROFDPWA, and q-ROFDPWG Operators.
Conclusion
This article presents an innovative approach to the system of Cq-ROF information and some exceptional cases. These approaches are utilized to resolve real-life applications and decision algorithms of the MULTIMOORA method based on the Cq-ROF context. The following are the outcomes of the investigation on developing a decision support system for evaluating football players’ positions: The MULTIMOORA approach has been effectively applied in the construction of the Decision Support System for Positioning Players in a Football Team. This technique can identify a player’s optimal position in addition to other positions. The coach can get help from the Decision Support System for determining the Position of Football Players utilizing the MULTIMOORA approach in deciding a player’s position based on their abilities. The findings of the manual calculation and the MULTIMOORA method’s computation for this player’s position in the application are identical.
The MULTIMOORA framework, equipped with Dombi prioritized weighted aggregation operators, and the Cq-ROFS constraints in player positioning optimization on a soccer field, represents a notable methodological contribution. However, some limitations are to be discussed. The first is that the procedure is computational since even in its present form, the need to compute the circular radii, as well as the parameters which can be varied in the operators defined by Dombi, adds a significant degree of complexity to the processing act, which is a considerable difficulty considering that it will be necessary to estimate many players at once. Furthermore, although an understandable intention to develop the model with the general set-up of player placement is evident, its direct, reality-based application in other sports and situational position responsibilities may require methodological adjustments to accommodate the contingency of sports-based features, tactical privileges, and, accordingly, performance levels. Future studies must therefore aim to refine the calculations involved and generally test the effectiveness of the technique in a wide range of sporting settings, which will lead to a more practical application of the method.
In the future, we will expand our developed research work into various fuzzy environments and real-life applications of artificial intelligence, machine learning, social and environmental sciences, medical diagnosis, pattern recognition, and waste management. We can also apply our derived theories to various optimization techniques, such as the TOPSIS method, MARCOS method, EDAS method, and AHP method.
Supplementary Information
Below is the link to the electronic supplementary material.
Author contributions
Asma Farhad and Kifayat Ullah participated in the conceptualization and composition of the manuscript. Dragan Pamucar oversaw the research and offered essential improvements. Zeeshan Ali contributed to data analysis and the final evaluation of the text. All authors reviewed and endorsed the final version of the manuscript.
Data availability
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
AI declaration statement
The soccer field diagram in this article was generated using an artificial intelligence tool (OpenAI, 2024) under the direct guidance of the authors. No copyrighted or third-party images were used. The figure is fully original and created solely for this scientific publication.Acknowledgement: This work was supported in part by the National Science and Technology Council, Taiwan, under Grant NSTC 114-2410-H-224-001 and internal number 114-1011.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Kifayat Ullah, Email: kifayat.khan.dr@gmail.com.
Dragan Pamucar, Email: pamucar.dragan@sze.hu.
References
- 1.Hussain, S. Enhancing web security through complex cubic q-Rung orthopair fuzzy information. Spectr. Oper. Res.3 (1), 153–182. 10.31181/sor31202641 (2026). [Google Scholar]
- 2.Shit, C. & Ghorai, G. Multiple attribute decision-making based on different types of Dombi aggregation operators under fermatean fuzzy information. Soft Comput.25 (22), 13869–13880. 10.1007/s00500-021-06252-9 (2021). [Google Scholar]
- 3.Shit, C., Ghorai, G., Xin, Q. & Gulzar, M. Harmonic aggregation operator with trapezoidal picture fuzzy numbers and its application in a Multiple-Attribute Decision-Making problem. Symmetry10.3390/sym14010135 (2022). [Google Scholar]
- 4.Shit, C. & Ghorai, G. A novel Aczel-Alsina aggregation operators based multi-criteria group decision making approach under hesitant fuzzy set for the selection of best brand in educational institution. Eng. Appl. Artif. Intell.158 (111464). 10.1016/j.engappai.2025.111464 (2025).
- 5.Ijaz, F., Azeem, M. & Ali, J. Dynamic aggregation operators for selection of optimal communication system in the rescue department under complex q-rung orthopair fuzzy environment. Spectr. Decis. Mak. Appl.10.31181/sdmap31202646 (2026). [Google Scholar]
- 6.Zadeh, L. A. Fuzzy sets. Inf. Control. 8 (3), 338–353. 10.1016/S0019-9958(65)90241-X (1965). [Google Scholar]
- 7.Atanassov, K. T. Intuitionistic fuzzy sets. Fuzzy Sets Syst.20 (1), 87–96. 10.1016/S0165-0114(86)80034-3 (1986). [Google Scholar]
- 8.Atanassov, K. T. Interval valued intuitionistic fuzzy sets. In Intuitionistic Fuzzy Sets: Theory and Applications (ed K. T. Atanassov) Studies in Fuzziness and Soft Computing., Heidelberg: Physica-Verlag HD10.1007/978-3-7908-1870-3_2 (1999).
- 9.Peng, X. & Yang, Y. Some results for pythagorean fuzzy sets. Int. J. Intell. Syst.30 (11), 1133–1160 (2015). [Google Scholar]
- 10.Yager, R. R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst.25 (5), 1222–1230 (2016). [Google Scholar]
- 11.Liu, P. Multiple attribute group decision making method based on interval-valued intuitionistic fuzzy power Heronian aggregation operators. Comput. Ind. Eng.108, 199–212 (2017). [Google Scholar]
- 12.Gao, H., Ran, L., Wei, G., Wei, C. & Wu, J. VIKOR method for MAGDM based on q-rung interval-valued orthopair fuzzy information and its application to supplier selection of medical consumption products. Int. J. Environ. Res. Public Health. 17 (2), 525 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Riaz, M., Çagman, N., Wali, N. & Mushtaq, A. Certain properties of soft multi-set topology with applications in multi-criteria decision making. Decis. Making: Appl. Manage. Eng.3 (2), 70–96 (2020). [Google Scholar]
- 14.Petchimuthu, S., Palpandi, B., Rajakumar, K. & M, F. B. Sustainable urban development: q-Rung orthopair fuzzy MCDM with generalized power prioritized Yager aggregation. Spectr. Oper. Res.3 (1), 275–309. 10.31181/sor31202649 (2026). [Google Scholar]
- 15.Pratama, D., Yusoff, B., Abdullah, L. & Kilicman, A. The generalized circular intuitionistic fuzzy set and its operations. AIMS Math.8 (11), 26758–26781 (2023). [Google Scholar]
- 16.Ali, Z. Fairly aggregation operators based on complex p, q-Rung orthopair fuzzy sets and their application in Decision-Making problems. Spectr. Oper. Res.10.31181/sor21202514 (2025). [Google Scholar]
- 17.Petchimuthu, S., M, F. B., Mahendiran, C. & Premala, T. Power and energy transformation: Multi-Criteria Decision-Making utilizing complex q-Rung picture fuzzy generalized power prioritized Yager operators. Spectr. Oper. Res.10.31181/sor21202525 (2025). [Google Scholar]
- 18.Karande, P. & Chakraborty, S. Application of multi-objective optimization on the basis of ratio analysis (MOORA) method for materials selection. Mater. Design. 37, 317–324. 10.1016/j.matdes.2012.01.013 (2012). [Google Scholar]
- 19.Xu, Z. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst.15 (6), 1179–1187 (2007). [Google Scholar]
- 20.Xu, Z. & Yager, R. R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen Syst. 35 (4), 417–433. 10.1080/03081070600574353 (2006). [Google Scholar]
- 21.Liu, P. Some Hamacher aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making. IEEE Trans. Fuzzy Syst.22 (1), 83–97 (2013). [Google Scholar]
- 22.Hussain, A. & Pamucar, D. Multi-attribute group Decision-Making based on pythagorean fuzzy rough set and novel Schweizer-Sklar T-norm and T-conorm. J. Innovative Res. Math. Comput. Sci.1 (2), 1–17 (2022). [Google Scholar]
- 23.Hussain, A., Latif, S. & Ullah, K. A novel approach of picture fuzzy sets with unknown degree of weights based on Schweizer-Sklar aggregation operators. J. Innovative Res. Math. Comput. Sci.1 (2), 18–39 (2022). [Google Scholar]
- 24.Jaleel, A. WASPAS technique utilized for agricultural robotics system based on Dombi aggregation operators under bipolar complex fuzzy soft information. J. Innovative Res. Math. Comput. Sci.1 (2), 67–95 (2022). [Google Scholar]
- 25.ur Rehman, U. Selection of database management system by using Multi-Attribute Decision-Making approach based on probability complex fuzzy aggregation operators. J. Innovative Res. Math. Comput. Sci.2 (1), 1–16 (2023). [Google Scholar]
- 26.Hussain, A., Bari, M. & Javed, W. Performance of the multi attributed Decision-Making process with Interval-Valued spherical fuzzy Dombi aggregation operators. J. Innovative Res. Math. Comput. Sci.1 (1), (2022).
- 27.Mahmood, T., Ullah, K., Khan, Q. & Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Applic. 31 (11), 7041–7053. 10.1007/s00521-018-3521-2 (2019). [Google Scholar]
- 28.Hussain, A., Ullah, K., Alshahrani, M. N., Yang, M. S. & Pamucar, D. Novel Aczel–Alsina operators for pythagorean fuzzy sets with application in Multi-Attribute decision making. Symmetry10.3390/sym14050940 (2022). [Google Scholar]
- 29.Hussain, A., Ullah, K., Senapati, T. & Moslem, S. Complex spherical fuzzy aczel Alsina aggregation operators and their application in assessment of electric cars. Heliyon9 (7). 10.1016/j.heliyon.2023.e18100 (2023). e18100. [DOI] [PMC free article] [PubMed]
- 30.Alcantud, J. C. R., Khameneh, A. Z. & Kilicman, A. Aggregation of infinite chains of intuitionistic fuzzy sets and their application to choices with Temporal intuitionistic fuzzy information. Inf. Sci.514, 106–117. 10.1016/j.ins.2019.12.008 (2020). [Google Scholar]
- 31.Hwang, C. M., Yang, M. S., Hung, W. L. & Lee, M. G. A similarity measure of intuitionistic fuzzy sets based on the Sugeno integral with its application to pattern recognition. Inf. Sci.189, 93–109 (2012). [Google Scholar]
- 32.Farid, H. M. A., Dabic-Miletic, S., Riaz, M., Simic, V. & Pamucar, D. Prioritization of sustainable approaches for smart waste management of automotive fuel cells of road freight vehicles using the q-rung orthopair fuzzy CRITIC-EDAS method. Inf. Sci.661, 120162. 10.1016/j.ins.2024.120162 (2024). [Google Scholar]
- 33.Alreshidi, N. A., Shah, Z. & Khan, M. J. Similarity and entropy measures for circular intuitionistic fuzzy sets. Eng. Appl. Artif. Intell.131, 107786 (2024). [Google Scholar]
- 34.Bui, Q. T., Ngo, M. P., Snasel, V., Pedrycz, W. & Vo, B. Information measures based on similarity under neutrosophic fuzzy environment and multi-criteria decision problems. Eng. Appl. Artif. Intell.122, 106026 (2023). [Google Scholar]
- 35.Xia, M., Xu, Z. & Zhu, B. Some issues on intuitionistic fuzzy aggregation operators based on archimedean t-conorm and t-norm. Knowl. Based Syst.31, 78–88 (2012). [Google Scholar]
- 36.Zhao, X. & Wei, G. Some intuitionistic fuzzy Einstein hybrid aggregation operators and their application to multiple attribute decision making. Knowl. Based Syst.37, 472–479 (2013). [Google Scholar]
- 37.Petchimuthu, S., Palpandi, B., M, F. B. & P. P, and Sustainable urban innovation and resilience: artificial intelligence and q-Rung orthopair fuzzy expologarithmic framework. Spectr. Decis. Mak. Appl.10.31181/sdmap21202526 (2025). [Google Scholar]
- 38.Yager, R. R. Pythagorean fuzzy subsets.In 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS). 57–61. (IEEE, 2013).
- 39.Senapati, T. & Yager, R. R. Some new operations over fermatean fuzzy numbers and application of fermatean fuzzy WPM in multiple criteria decision making. Informatica30 (2), 391–412 (2019). [Google Scholar]
- 40.Aydemir, S. B. & Yilmaz Gündüz, S. Extension of multi-Moora method with some q-rung orthopair fuzzy Dombi prioritized weighted aggregation operators for multi-attribute decision making. Soft. Comput.24 (24), 18545–18563 (2020). [Google Scholar]
- 41.Dombi, J. A general class of fuzzy operators, the DeMorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst.8 (2), 149–163 (1982). [Google Scholar]
- 42.Jana, C., Muhiuddin, G. & Pal, M. Some Dombi aggregation of Q-rung orthopair fuzzy numbers in multiple-attribute decision making. Int. J. Intell. Syst.34 (12), 3220–3240 (2019). [Google Scholar]
- 43.Yager, R. R. Prioritized aggregation operators. Int. J. Approximate Reasoning. 48 (1), 263–274. 10.1016/j.ijar.2007.08.009 (2008). [Google Scholar]
- 44.Xu, C. & Wen, Y. New measure of circular intuitionistic fuzzy sets and its application in decision making. MATH8 (10), 24053–24074. 10.3934/math.20231226 (2023). [Google Scholar]
- 45.Brauers, W. K. M. & Zavadskas, E. K. Multimoora optimization used to decide on a bank loan to buy property. Technological Economic Dev. Econ.10.3846/13928619.2011.560632 (2011). [Google Scholar]
- 46.Shit, C. & Ghorai, G. Charging method selection of a public charging station using an Interval-Valued picture fuzzy bidirectional projection based on VIKOR method with unknown attribute weights. Information10.3390/info16020094 (2025). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.