Delay-induced stochastic oscillations in gene regulation

Abstract

The small number of reactant molecules involved in gene regulation can lead to significant fluctuations in intracellular mRNA and protein concentrations, and there have been numerous recent studies devoted to the consequences of such noise at the regulatory level. Theoretical and computational work on stochastic gene expression has tended to focus on instantaneous transcriptional and translational events, whereas the role of realistic delay times in these stochastic processes has received little attention. Here, we explore the combined effects of time delay and intrinsic noise on gene regulation. Beginning with a set of biochemical reactions, some of which are delayed, we deduce a truncated master equation for the reactive system and derive an analytical expression for the correlation function and power spectrum. We develop a generalized Gillespie algorithm that accounts for the non-Markovian properties of random biochemical events with delay and compare our analytical findings with simulations. We show how time delay in gene expression can cause a system to be oscillatory even when its deterministic counterpart exhibits no oscillations. We demonstrate how such delay-induced instabilities can compromise the ability of a negative feedback loop to reduce the deleterious effects of noise. Given the prevalence of negative feedback in gene regulation, our findings may lead to new insights related to expression variability at the whole-genome scale.

There is considerable experimental evidence that noise can play a major role in gene regulation (1–10). These fluctuations can arise from either intrinsic sources, which are related to the small numbers of reactant biomolecules, or extrinsic sources, which are attributable to a noisy cellular environment. Although the importance of fluctuations in gene regulation was stressed >30 years ago (11), recent experimental advances have renewed interest in the stochastic modeling of the biochemical reactions that underlie gene regulatory networks (12–16). The most typical approaches are the utilization of the Gillespie algorithms (17–20), the direct analysis of the master equation, or the development of simplified descriptions based on the Fokker–Planck or Langevin equations (see ref. 21 for a review). A common thread in many of these approaches has been to consider intrinsic noise as the dominant source of variability in gene expression.

One major difficulty often encountered in the analysis of gene regulatory networks is the vast separation of time scales between what are typically the fast reactions (dimerization, protein–DNA binding/unbinding) and the slow reactions (transcription, translation, degradation). There have been many studies devoted to the development of reduced descriptions of these systems using the idea of quasiequilibrium for the fast processes compared with the slow dynamics (cf. ref. 22 and references therein). These approaches have thus far implicitly assumed that all of the reactions (fast and slow) are Markovian processes obeying Poissonian statistics. In this regard, it is important to note that the transcriptional and translational processes are not just slow but also are compound multistage reactions involving the sequential assembly of long molecules. Thus, by virtue of the central limit theorem, these processes should obey Gaussian statistics with a certain characteristic mean delay time. When delays in biochemical reactions are small compared with other significant time scales characterizing the genetic system, one can safely ignore them in simulations. Furthermore, time delays usually do not affect the quasiequilibrium behavior of gene regulatory networks and mean values of corresponding observables, and the conventional stochastic models without delays work properly here (for a review, see ref. 23). However, if indeed the time delays are of the order of other processes or longer, and the feedback loops associated with these delays are strong, taking the delays into account can be crucial for description of transient processes. This finding implies that when delay times are significant, both analytical and numerical modeling should take into account the non-Markovian nature of gene regulation.

The fact that delayed-induced stochastic oscillations can occur during transcriptional regulation is supported by recent studies of circadian oscillations in Neurospora, Drosophila, and others. It is widely accepted now that these oscillations are caused by delays in certain elements of gene regulation networks [see recent experimental (24, 25) and modeling (26–29) studies]. It is plausible that the role of time delays in circadian rhythms has come to light because the delays in the corresponding reactions are particularly long (several hours) in comparison with other characteristic times of the system. It would be logical to suppose that shorter delays present in other systems also can have a significant impact on dynamics; however, they may be more difficult to detect with currently available experimental methods.

The behavior of stochastic delay-differential equations (SDDEs) has been extensively studied, and various approximation techniques have been developed and utilized (30–35). For example, delayed differential equations have been reduced to coupled map lattices and perturbed by white noise, demonstrating how the phase space density reaches a limit cycle in the asymptotic regime (30). The stability of the moment equations for linear SDDEs has been explored to elucidate the oscillatory properties of the first and second moments (31), and the master equation approach has been applied to a delayed random walker in an effort to demonstrate the effects of delay in an analytically tractable system (32, 33). The limit of short delay time has been used to show how a univariate nondelayed stochastic differential equation can be used to approximate the original system (34), and, more recently, a noise-driven bistable system with delayed feedback was reduced to a two-state model with delayed transition rates to demonstrate the phenomenon of coherence resonance (35). These important studies have provided many valuable insights, yet little work has been directed toward realistic delay times coupled with intrinsic noise in the context of gene regulation.

In the present work, we develop methodologies for the analysis and simulation of delayed biochemical reactions that describe gene regulation. Specifically, we establish a theoretical approach for reducing and solving master equations that describe gene expression in the presence of both delayed degradation and negative feedback, respectively. We augment the original Gillespie simulation technique to account for the non-Markovian aspects of delay and compare the simulation results with our analysis.

Finally, given the prevalence of negative feedback in gene regulation (36), our findings may lead to insights related to the recently observed oscillatory behavior in numerous transcripts at the whole-genome scale (37).

Delayed Protein Degradation

Formulation.

To elucidate our approach, we begin with a model that is relatively simple yet maintains a high degree of biological relevance. Protein degradation often occurs through a sequence of events that are mediated by a complex proteolytic pathway (38), and it is thus natural to assume a delay time that takes into account the cellular degradation machinery. In modeling the process, we use the standard biochemical rate approach and first write the chemical reactions describing protein production and degradation

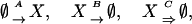[1]

where A and B are the nondelayed rates of protein production and degradation, and C is the rate of the delayed degradation reaction (indicated by the wide arrow). This reaction represents the initiation of the protein degradation machine, which ultimately degrades the protein at a time τ after initiation. To isolate the effects of the time delay, we simplified the system by lumping transcription and translation into a single process. One can easily generalize to include the multistage processes of transcription and translation, and our findings with respect to delay will be general. This type of delayed degradation comprises one of the simplest forms of delay, and it is well known that it can lead to periodic oscillations. Regarding the parameter values, we can use recent findings on the Neurospora crassa circadian clock circuit (see refs. 28 and 29), in which FRQ protein is produced at a rate of ≈1.5 nM/h and degrades after multiple phosphorylation steps at the rate of ≈1 h^-1. These multiple phosphorylation steps can significantly delay the degradation. In addition to this delayed degradation, normal dilution leads to a nondelayed degradation with a rate of ≈0.3 h^-1. Similar elements with comparable production and degradation levels can be found in the Drosophila circadian oscillator circuit (28).

Deterministic Description.

The deterministic dynamics of this system in the rate approximation are described by the following linear delay-differential equation:

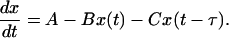[2]

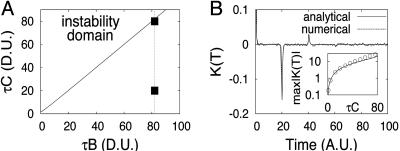
This system has one fixed point x^* = A/(B + C), whose stability determines the transition to oscillations. By finding the eigenvalues of this linear system, we obtain the neutral curve for the Hopf bifurcation (see Fig. 1A) in the plane (τB, τC). For large τ, this curve is nearly the straight line τB = τC, and at B = 0 the critical value for C is given by C = π/2τ. In the unstable domain, the amplitude of the oscillations grows indefinitely without saturation. However, in the “real” system with a discrete number of molecules, saturation is provided by the fact that the number of proteins cannot become negative.

Fig. 1.

Analysis of the delayed protein degradation model. (A) Neutral curve of the Hopf bifurcation (solid line). The dashed line depicts the cross-section of parameter space that corresponds to B Inset.(B) Comparison of correlation functions obtained analytically (solid line) and numerically (dashed line). Fixed parameters are τ = 20, A = 100, B = 4.1, and C = 1. Inset shows the height of the secondary negative peak of the correlation function of τC in dimensionless units (D.U.).

Stochastic Description.

Now we account for the fact that chemical reactions (1) occur randomly in time according to their respective rates. Because the number of molecules involved in intracellular biochemical reactions is typically not large, random fluctuations are important, and a stochastic approach should be used to describe the behavior of such a system. Thus, in this work we concentrate our attention on intrinsic noise only. It is worth mentioning, however, that in many cases extrinsic sources of noise can dominate over intrinsic ones. In such cases the extrinsic noise can be modeled with additional stochastic reactions without any feedback from the “internal” degrees of freedom. These reactions can be included in the general scheme described below, but the corresponding master equation would become significantly more complicated.

Nondelayed stochastic reactions usually exhibit Poissonian statistics, with an exponential decay of their autocorrelation functions, but time delay leads to significant differences in the stochastic properties of the system. Specifically, we will focus on the structure of the autocorrelation function and power spectrum for the number of proteins for the single-gene system with delayed degradation. Dynamical processes occurring in genetic networks operate over a broad range of time scales, and the natural representation of these different processes can be given by a power spectrum. In particular, in certain cases the periodic component of protein fluctuations caused by time-delayed reactions can be masked by broadband stochastic fluctuations. However, power spectra of these fluctuations demonstrate the presence of these periodic or quasiperiodic oscillations quite clearly.

Let us denote by P(n, t) the probability of having n monomers at time t. Then the master equation for the time evolution of the probability P(n, t) can be written as

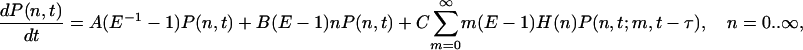[3]

where E is the unitary shift operator, EP(n, t) = P(n + 1, t), P(n, t; m, t - τ) is the joint probability of having n molecules at time t and m molecules at time t - τ, and H(n) is the Heaviside function [H(0) = 0, H(n > 0) = 1]. The latter is added to account for the fact that the delayed degradation reaction cannot occur if the number of species at time t is zero.

This set of equations is not closed because the one-point probability distribution is determined by the two-point probability distributions on the right-hand side of the equation. We make the assumption that the time delay τ is large compared with the other characteristic times of the system, so the events at time t and t - τ are effectively decoupled. Under this approximation, we can write

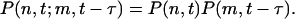[4]

This assumption can be supported, for example, by recent results on circadian oscillations in Neurospora and other organisms. The total delay in that systems can lead to oscillations with a period as large as tens of hours, and stochastic events separated by such time spans become effectively decoupled. In other cases, however, the delay time can be of order or smaller than other characteristic times. Extrinsic processes that are much slower than the time-delayed reactions can be taken into account as adiabatic change of parameters, and the theory developed here would still apply. If, however, there are significant cell processes operating on the time scales of the order of time delay, one has to resort to numerical simulations.

In fact, large τ is a necessary but not a sufficient condition for this theory to hold. We will see below that strong delayed feedback leads to significant correlations over long periods of time, and an additional condition for the applicability of Eq. 4 is to have relatively weak feedback. Adopting this approximation, we obtain

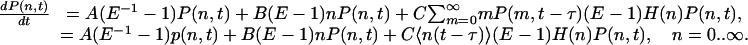[5]

Exploiting the same approximation, we can write the autocorrelation function in the following form (see Supporting Text, which is published as supporting information on the PNAS web site):

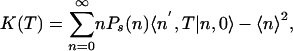where P_s(n) is the stationary probability and 〈n′, T|n, 0〉 is the conditional mean number of proteins at time T, given it was n at time 0. By using the generating function method, we can calculate the stationary probability distribution and the conditional mean from the master equation (5) and arrive at the autocorrelation function (see Supporting Text for details of this calculation)

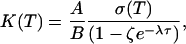[6]

where 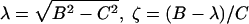, and

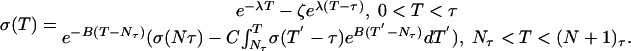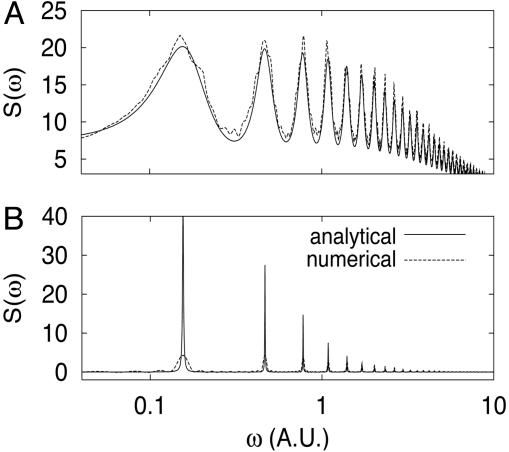
This solution is defined if B > C, i.e., below the deterministic Hopf bifurcation. It has a form of a sequence of peaks of alternating polarity with decaying heights (Fig. 1B). By using Eq. 6 we can calculate the power spectrum S(ω) (cf. ref. 35)

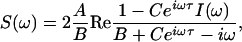[7]

where

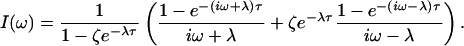The main difference between the deterministic and stochastic approaches manifests itself in Fig. 2, where the power spectra for the latter are plotted in accordance with Eq. 7. One can see that the stochastic model predicts quasiregular oscillations in the parameter range where the deterministic model shows a stable steady state. Thus, it is evident that the coupling between noise and delay leads to the oscillatory behavior, whereas each element separately does not.

Fig. 2.

Comparison of power spectra S(ω) obtained analytically (solid line) and numerically (dashed line) for the delayed protein degradation model (Eq. 1) with τ = 20, A = 100, B = 4.1, and two values of C indicated by filled squares in Fig. 1 A, C = 1 (A) and 4 (B). Insets show the same comparison for the correlation functions normalized by the variance. The frequency ω and time are plotted in arbitrary units (A.U.).

Stochastic Simulations: Modified Gillespie Method

To test the validity of our approximations and analytical results, we performed numerical simulations of the original system of stochastic chemical reactions (1). Here we introduce modifications to the direct Gillespie (DG) algorithm (17), which allow us to incorporate delayed reactions. Suppose the system consists of N components X_i, which react through M elementary reaction channels R_μ. According to the DG algorithm, time is advanced from one elementary reaction to the next. At every “stop” one determines the time of the next reaction and which reaction it will be. For Markovian processes, the distribution of times until the next reaction is exponential

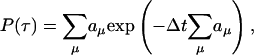[8]

where a_μ = c_μh_μ is the propensity of channel R_μ. The choice of the next reaction is made based upon the discrete distribution,

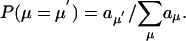[9]

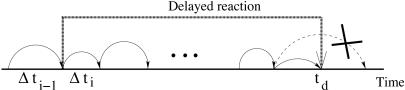
When some of the channels are non-Markovian, it is necessary to modify the original version of the DG algorithm as follows. At each stop we perform the same selection of the next reaction time according to the distributions in Eqs. 8 and 9. If the next reaction time is chosen to be t^* but the selected reaction is delayed, it is placed in a stack, so it will actually be completed at time t^* + τ. If, however, the chosen reaction is Markovian, the time of the next reaction t^* is compared with the times of the previously scheduled delayed reactions. If none of those scheduled reactions are to occur before t^*, the time is advanced to t^*, the numbers of molecules are updated according to the chosen nondelayed reaction, and the process repeats. If, however, there is a delayed reaction scheduled for completion at t_d < t^*, the last selection is ignored, time advances to t_d, the scheduled delayed reaction is performed, and the selection process repeats. The formal steps for the algorithm execution are as follows (see Fig. 3 for the illustration):

Fig. 3.

Illustration to the modified Gillespie algorithm for normal and delayed reactions.

1. Input values for initial state X = (X₁,..., X_N), set time t = 0 and reaction counter i = 1.

2. Compute propensities of M reactions a_μ, μ = 1,..., M.

3. Generate uniform random numbers u₁, u₂ ∈ [0, 1]

4. Compute the time interval until the next reaction Δt_i = -ln u₁/Σ_μa_μ.

5. Check whether there are delayed reactions scheduled within time interval [t, t + Δt_i]. If YES, then steps 2–4 are ignored, time t advances to the time t_d of the next scheduled delayed reaction, X states are updated according to the delayed reaction channel, and counter is increased i = i + 1. Proceed to step 2. If NO, go to step 6.

6. Find the channel of the next reaction μ, namely take μ to be the integer for which 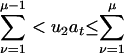, where 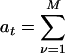is the total propensity.

7. If the selected reaction μ is not delayed, update X according to the R_μ, update time t = t + Δt_i and increase counter i = i + 1. If the selected reaction is delayed, update is postponed until time t_d = t + τ. Go to step 2.

We note that stochastic variations of the delay time itself can be an additional source of genetic noise. Our numerical algorithm can easily incorporate these fluctuations; however, in the present work for simplicity we assume that τ is constant.

The comparison for the power spectra and correlation functions obtained analytically and numerically is shown in Figs. 1B and 2 for τ = 20. The chosen delay time is large compared with the characteristic equilibration time B^-1 ≈ 0.25, which is necessary to justify the master Eq. 5. The first peak of the power spectrum in both figures corresponds to the frequency ω = 2π/2τ ≈ 0.157.

When the system is far away from the Hopf bifurcation, the influence of the delay term is relatively weak, and the analytical and numerical curves are in excellent agreement (Figs. 1B and 2A). In Fig. 1B Inset we plot the height of the secondary peak located near τ = 20 as a function of the parameter τC. Near the Hopf bifurcation (Fig. 2B), the agreement between our analytical approach and the simulations becomes worse because the processes at times t and t - τ become strongly correlated (the secondary peak of the correlation function is large).

Negative Feedback with Delayed Production

In this section we apply our approach to a system that represents one of the most common motifs in gene regulation (36, 39). Namely, we consider single-gene protein synthesis with negative feedback. The dynamics of this system have been analyzed deterministically (40) and stochastically (21), and experimental findings have demonstrated how negative feedback can dampen the effects of noise (3). Here we generalize this system by allowing for the finite delay time necessary for protein transcription and translation. We postulate that the chemical state of the operator site 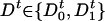determines the production of protein at time t + τ. If the operator at time t is unoccupied (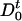), then the protein may be produced at time t + τ with probability A per unit time. Otherwise, if the operator is occupied (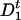), the production at time t + τ is blocked. The transitions between operator states, denoted as D₀ (unoccupied) and D₁ (occupied), occur with rates k₁, k_-1, can be written as

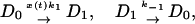[10]

where x(t) represents the number of proteins at time t. The protein production and degradation reactions can be written as

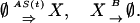[11]

Here S(t) = 1 for unoccupied operator state D₀ and 0 for occupied state D₁. Thus, the reactions have negative feedback through the first reaction rate in Eq. 11.

Deterministic Description.

We introduce continuous variables x(t) for the average number of proteins and s(t) for the average number of unoccupied operator sites at time t. For a single gene circuit, s(t) ≤ 1, and the number of occupied sites is 1 - s(t). Exploiting the typically large separation of time scales between protein–DNA binding rates and the production/degradation rates, the deterministic rate equations for reactions 10 and 11 can be written as

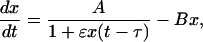[12]

where ε = k₁/k_-1. This system has only a single positive stationary solution, which is always stable, so the system does not possess bifurcations (see Supporting Text).

Stochastic Description.

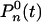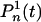We introduce two probabilities, and , for the number of proteins to be equal to n at time t, and for the state of the operator at time t - τ to be 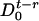or 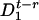, respectively. Then the master equations for the reactions in Eqs. 10 and 11 have the form

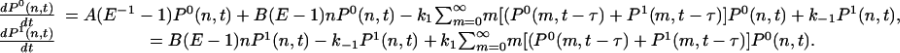[13]

We have again made the assumption that the processes at times t and t - τ are weakly correlated, and to first approximation the two-point probability distribution function factorizes, P(n, t; m, t - τ) ≈ P(n, t)P(m, t - τ). To calculate the correlation function, we again use generating functions (see Supporting Text)

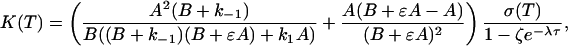[14]

with the same notations as in Eq. 6.

Comparison of Analytical and Numerical Results.

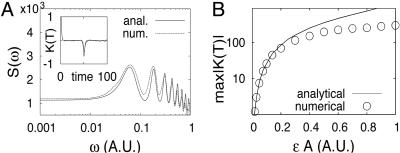
We performed DG simulations of the stochastic model for the single-gene negative feedback system. Comparison between our analytical and numerical findings is depicted through the power spectra and correlation functions in Fig. 4A. The first peak of the power spectra corresponds to the frequency ω = 2π/2τ ≈ 0.063. We note that the heights of the analytical and numerical peaks (Fig. 4B) agree well for small εA but diverge as the parameter that controls the delay term (εA) grows. This result is to be expected, because the condition of applicability of our approximation was rapid decay of correlations, which corresponds to small ε.

Fig. 4.

Analysis of the negative feedback model. (A) Comparison of power spectra and correlation functions (Inset) obtained analytically (solid line) and numerically (dashed line). A = 100, k₁/k_-1 = 0.002, τ = 50, B = 1. (B) The height of the secondary peak of the correlation function as a function of εA; other parameters are the same as in A.

Negative Feedback with Dimerization

Most transcription factors form higher-order multimers before regulating their target genes. Thus, a natural generalization of the previous model is to account for protein homodimers that down-regulate monomer production. Suppose that the protein can exist both in the form of isolated monomers X and dimers X₂ with the dimerization reactions given by

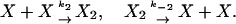[15]

Incorporating these new reactions, the reactions of the previous section (Eq. 10) should be rewritten as

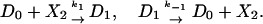[16]

Production–degradation reactions are given by

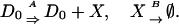[17]

As before, protein production occurs with a time lag τ and can only occur if the operator is unoccupied at time t.

Deterministic Description.

Assuming that the production and degradation of proteins are slow compared with dimerization and protein–DNA reactions, we can eliminate the fast variables and reduce the system of deterministic rate equations to just one equation for the number of monomers x₁ (D.V., unpublished data).

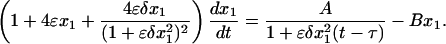[18]

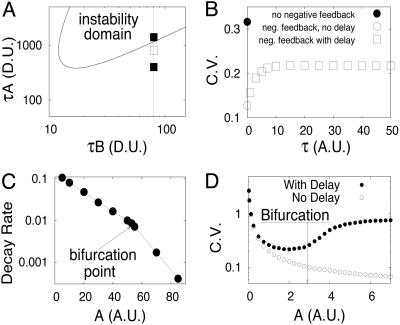
Protein dimerization plays an important role in the system dynamics. In comparison with the model of the previous section (Eq. 12), the delay term in Eq. 18 is quadratic. It can be shown that the system can now possess a Hopf bifurcation for sufficiently strong negative feedback. The neutral curve is plotted in Fig. 5A, where the oscillatory instability domain is above the curve.

Fig. 5.

Analysis of the negative feedback model with dimerization. (A) Neutral curve of the Hopf bifurcation for negative feedback model with dimerization (Eqs. 15, 16, 17) The fixed parameters are ε = 0.1, δ = 0.2. (B) Coefficient of variation as a function of delay time τ for A = 40 (indicated by the open square in A). (C) Decay rate of secondary peaks of the correlation function as a function of A.(D) CV as a function of production rate A. The fixed parameters are B = 4, k₁ = 100, k_-1 = 1,000, k₂ = 200, k_-2 = 1,000.

Stochastic Simulations.

We performed a series of numerical simulations of Eqs. 15, 16, 17 based on the modified DG method for the parameters shown in Fig. 5A along the dashed vertical line. Although the linear analysis within the deterministic model predicts the onset of oscillations above the point A^* = 57.85, no such clear boundary appears to occur in the stochastic model. In Fig. 5B, we plot the coefficient of variation 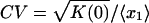vs. delay time τ for A = 40. This quantity characterizes the relative magnitude of the fluctuations in the system. Three cases can be identified here. If there is no negative feedback, i.e., ε = 0, then the noise effect is maximal (filled circle in Fig. 5B). Negative feedback leads to a sharp decrease of fluctuations (open circle, τ = 0). If the feedback is delayed, the fluctuations are enhanced because the delay makes the system more sensitive to disturbances and thus works against the premise that negative feedback dampens fluctuations.

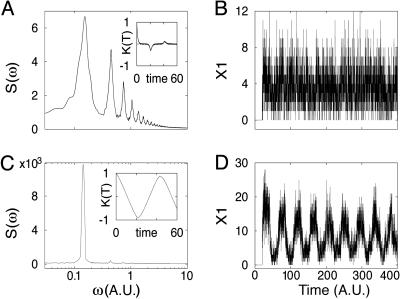
The power spectrum, correlation function, and the time series for two particular parameter sets are shown in Fig. 6. One can see that even far below the Hopf bifurcation (Fig. 6 A and B), the correlation function has a remarkably narrow peak, indicating that some periodicity in the stochastic signal exists (Fig. 6A Inset). The first peak of the power spectrum corresponds to the frequency ω = 2π/2τ ≈ 0.159 (τ = 20). As the system approaches the bifurcation point A^*, the peaks become wider and higher. Above the bifurcation the power spectrum and correlation function are depicted in Fig. 6C. They correspond to periodic oscillations above the bifurcation threshold with a period slightly higher than 2τ (Fig. 6D).

Fig. 6.

Power spectra and correlation functions (A and C) and sample trajectories (B and D) obtained in stochastic simulations with τ = 20 and the values of B, k₁, k_-1, k₂, k_-2 the same as in Fig. 5 for two values of production rate: A = 20 (below Hopf bifurcation) (A and B) and A = 70 (above Hopf bifurcation) (C and D).

At first glance, one might expect that within the stochastic approach the bifurcation-like transition from the steady state to a limit cycle is not observed, and the point of such a transition cannot be clearly determined. However, Fig. 5C shows that this hypothesis is not the case. If the decay rate of the correlation function peaks as a function of A is plotted on a logarithmic scale, the curve can be approximated well by two lines that intersect at A ≈ 56. Thus, stochastic fluctuations shift the bifurcation point by ≈5 with respect to the deterministic value for A (A^* = 57.85). This result appears particularly important from an experimental point of view, because frequently an experimenter needs to define a bifurcation occurring in a stochastic system. As we have shown, relatively simple manipulations with the autocorrelation function can help in defining this bifurcation.

Fig. 5D illustrates how the coefficient of variation (CV) changes with transcription rate A in two cases: with (open circles) and without (filled circles) time delay in protein production. If in the former case CV decreases monotonically with transcription rate because the number of molecules increases, in the latter case as the system crosses the bifurcation point the CV increases again and tends to some limiting level.

Finally, delayed feedback strongly affects transient behavior of genetic networks. Unlike nondelayed system, the transition to a new fixed point in the delayed system is accompanied by significant stochastic oscillations (see Fig. 7, which is published as supporting information on the PNAS web site).

Discussion

We have developed both deterministic and stochastic models for transcriptional regulation with delayed feedback and have explored these models both analytically and numerically. Problems with delay are generally difficult because of the non-Markovian nature of the dynamics, yet we have demonstrated that the main features of such systems can be understood using relatively simple models. Assuming significant decorrelation on the time scale of gene transcription, we have deduced a truncated master equation of the reactive system and derived analytical expressions for the correlation function and power spectrum. In addition, we have developed a generalization of the Gillespie algorithm that accounts for delay and have demonstrated how numerical simulations can be performed and compared with analytical findings. Within the context of negative autoregulation, which is one of the most commonly occurring regulatory motifs (36), we have shown how oscillations can arise from the coupling of noise and delay.

The likely importance of fluctuations arising from the small number of reactant molecules in gene expression was noted by Stuart and Branscomb in 1971 (11). In this prescient work, analytical techniques were applied to a model for the lac operon to show how fluctuations could play an important role in gene regulation. Owing mainly to the lack of experimental assays capable of resolving fluctuations at the single-cell level, this work went largely unnoticed, and the role of noise in gene expression received little attention until the late 1990s. More recently, the predicted role of intrinsic noise in the context of developmental pathways ignited widespread interest (12), and there have been numerous subsequent experimental studies that empirically demonstrate the importance of such fluctuations (1–10).

As in the case of intrinsic noise, the generic origin of delay implies a high likelihood that it plays an important role in gene regulation (cf. ref. 41 and references therein). It could be a dominant source of large deterministic variability, as in the case of circadian rhythms (26, 27), or it can play a supportive role as a mechanism that amplifies the effects of random fluctuations. Along these lines, it is interesting to note that our model can be used to demonstrate that the “noise signature” of a system dominated by delay can be similar to a system dominated by intrinsic noise (Fig. 5D). This result implies that care must taken in attributing variability to purely stochastic sources, because delay-induced variability can appear empirically similar to fluctuations arising from intrinsic noise.

Pragmatically, models that use delay could be essential in understanding whole-genome regulation, because it is unrealistic to construct models that incorporate the numerous sequences of biochemical reactions that underlie the complexities of transcribing and translating a single gene. Time-delayed reactions have long been utilized as a natural approximation for the modeling of such a complex sequence of events. This reduction comes at a high cost, because analytical and numerical techniques are more difficult, and there has been little work addressing the coupling of intrinsic noise in biochemical reactions with delay. In this regard, our results provide a framework for analyzing and simulating the interplay of noise and delay. Along the same lines, the generalization of the Gillespie algorithm provided in our work should prove highly useful because large-scale simulation techniques that incorporate time delays should lead to new insights in describing the dynamics of complex gene regulatory networks.