Dynamics of sleep-wake cyclicity in developing rats

Abstract

Adult mammals cycle between periods of sleep and wakefulness. Recent assessments of these cycles in humans and other mammals [Lo, C. C., Amaral, L. A. N., Havlin, S., Ivanov, P. Ch., Penzel, T., Peter, J. H. & Stanley, H. E. (2002) Europhys. Lett. 57, 625-631 and Lo, C. C., Chou, T., Penzel, T., Scammell, T. E., Strecker, R. E., Stanley, H. E. & Ivanov, P. Ch. (2004) Proc. Natl. Acad. Sci. 101, 17545-17548] indicate that sleep bout durations exhibit an exponential distribution, whereas wake bout durations exhibit a power-law distribution. Moreover, it was found that wake bout distributions, but not sleep bout distributions, exhibit scale invariance across mammals of different body sizes. Here we test the generalizability of these findings by examining the distributions of sleep and wake bout durations in infant rats between 2 and 21 days of age. In agreement with Lo et al., we find that sleep bout durations exhibit exponential distributions at all ages examined. In contrast, however, wake bout durations also exhibit exponential distributions at the younger ages, with a clear power-law distribution only emerging at the older ages. Further analyses failed to find substantial evidence either of short- or long-term correlations in the data, thus suggesting that the durations of current sleep and wake bouts evolve through time without memory of the durations of preceding bouts. These findings further support the notion that bouts of sleep and wakefulness are regulated independently. Moreover, in light of recent evidence that developmental changes in sleep and wake bouts can be attributed in part to increasing forebrain influences, these findings suggest the possibility of identifying specific neural circuits that modulate the changing complexity of sleep and wake dynamics during development.

As members of a diurnal species, adult humans experience sleep as a prolonged period of rest during the night; however, sleep actually occurs as a series of discrete bouts interrupted by bouts of wakefulness. What is perhaps most striking during the first several months after birth, when circadian influences on behavioral state are not well established, is the brevity of these bouts of sleep and wakefulness (1). In newborn rats at 2 days of age (P2), these cycles are astonishingly rapid: The average bout lengths of nuchal muscle atonia (indicative of sleep) and high nuchal muscle tone (indicative of wakefulness) are only 15 s and 5 s, respectively (2). Over the next week, bout lengths increase significantly as forebrain mechanisms exert increasing modulatory control over brainstem mechanisms controlling sleep and wakefulness (2).

Recently, Lo et al. (3) analyzed the distributions of sleep and wake bouts in human adults. They found that, whereas sleep bouts exhibited an exponential distribution [such that the frequency distribution f(t) of bout durations of duration t was proportional to e^(-t/τ), where τ is the characteristic time scale], wake bouts exhibited a power-law distribution [such that f(t) ≈ t^-α, where α is a characteristic power-law exponent]. In a subsequent report (4), these findings were extended to cats, rats, and mice. From this comparative analysis, Lo and colleagues found that the exponential time scale τ for sleep bout durations increased with body size, thus possibly implicating a constitutional variable (e.g., metabolic rate) in the regulation of sleep bouts. In contrast, the power-law exponent α for wake bout durations did not vary across species.

Although establishing the generalizability of these results by examining more species will be important, data from developing animals could provide additional critical information. In particular, in analyzing the sleep and wake bout durations of P2 and P8 rats, we found that both are better captured by exponential, not power-law, distributions (2). If wake bout durations do not exhibit power-law behavior in early infancy, then such behavior may develop gradually as the neural components of sleep and wakefulness are elaborated. In addition, because the precise nature of these distributions critically shapes the models that we adopt to describe the temporal dynamics of sleep and wakefulness (3), establishing the statistical properties of these bout durations across development becomes important. Therefore, using archival and newly collected data from rats at P2, P8, P10, P14, and P21, we assess here the statistical behavior of sleep and wake bout durations. By demonstrating a pronounced developmental transition in wake bout durations, important new information is provided that can help shape models of sleep-wake behavior and point to specific neural processes responsible for developmental shifts in the statistical properties of sleep-wake behavior.

Methods

All experiments were performed under National Institutes of Health guidelines for the care of animals in research and were approved by the Institutional Animal Care and Use Committee of the University of Iowa.

Subjects. Thirty P2, P8, P10, P14-15 (hereafter P14), and P20-21 (hereafter P21) male and female rats from 29 litters were used. Six subjects were tested at each age. Weights ranged from 6.5-9.1 g at P2, 16.3-20.7 g at P8, 24.3-27.7 g at P10, 32.8-41.1 g at P14, and 49.4-68.5 g at P21. All pups were born to Harlan Sprague-Dawley rats housed in the animal colony at the University of Iowa. The pups were raised in litters that were culled to eight pups within 3 days of birth (day of birth = day 0). Litters and mothers were raised in standard laboratory cages (48 × 20 × 26 cm), in which food and water were available ad libitum. All rats were maintained on a 12-hr light-dark schedule with lights on at 7 a.m.

Recording of Sleep-Wake Behaviors. Some of the data from the P2 and P8 rats (2) and the P14 rats (5) have been published previously. The P10 and P21 data were collected for this study. The methods for recording sleep and wake behavior were similar for all pups reported here. The basic testing method and differences in the treatment of pups of different ages are described below.

Surgery. On the day of testing, a P2, P8, or P10 rat with a visible milkband was removed from the litter, weighed, and anesthetized with isoflurane. Under isoflurane anesthesia, bipolar stainless steel hook electrodes 50 μm in diameter (California Fine Wire, Grover Beach, CA) were inserted bilaterally into the nuchal muscle and secured with collodion. After surgery, the pup recovered for at least 1 h in a humidified incubator maintained at thermoneutrality (i.e., 35°C for P2 and P8 subjects; 32°C for P14-15 subjects). P21 subjects were prepared identically except that they recovered in the testing chamber maintained at thermoneutrality (i.e., 32°C) for at least 30 min.

P14 rats were prepared similarly to the other subjects except that additional electrodes were implanted for the recording of extraocular muscle activity and neocortical electroencephalogram, as described in ref. 5. Bipolar stainless steel hook electrodes were implanted bilaterally into the nuchal muscle and secured with collodion. The subject was placed into the testing chamber, which was maintained at thermoneutrality (i.e., 32°C), for 2-4 h to recover and acclimate.

Procedure. All pups were tested unrestrained during the day inside an electrically shielded double-walled glass chamber (height, 17.0 cm; i.d., 12.5 cm) with a Plexiglas lid. Air temperature inside the chamber was regulated at thermoneutrality for each age using a temperature-controlled water circulator. Access holes in the side and lid of the chamber allowed for passage of air through the chamber as well as for the passage of electrodes. A round platform constructed of polyethylene mesh was fitted inside the chamber and a perforated felt pad was placed on top of the mesh.

Nuchal electromyogram (EMG) electrodes were connected to differential amplifiers (A-M Systems, Carlsborg, WA) and their signals were amplified (×10,000) and filtered (300-5,000 Hz). EMG data were visualized by the experimenter during the test with a data acquisition system (BioPac Systems, Santa Barbara, CA). A microcamera was placed above the chamber lid for monitoring and recording of behavior. EMG and video data were recorded to digital videotape with a data recorder (DV8, WinTron Technologies, Rebersberg, PA).

All subjects acclimated to the testing chamber for at least 30 min before data recording began. For P2, P8, and P10 subjects, data were recorded for 1 h. For P14 and P21 subjects, data were recorded for 2 h and 6 h, respectively.

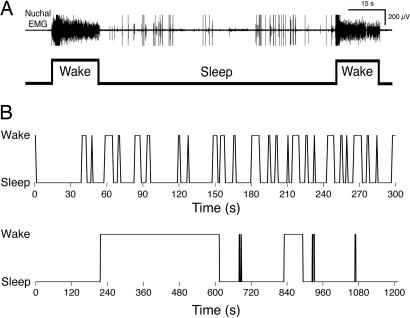
Data Analysis. As described in ref. 2, the EMG signal for each subject was dichotomized into bouts of atonia and high muscle tone (indicative of sleep and wakefulness, respectively). EMG signals were digitized at 1 or 2 kHz with a data acquisition system (BioPac Systems). Digitized signals were summed (when there were two usable EMG signals), integrated, and full-wave rectified. Then the EMG signal was dichotomized into bouts of sleep and wake as follows: The amplitude of five 1-s segments of noise-free, uninterrupted atonia and high-tone periods was measured for each pup and averaged, and the midpoint between the two was calculated. A bout of sleep or wake was defined as a period in which muscle tone was below or above, respectively, the midpoint value for at least 1 s (see Fig. 1A). At least 50 sleep-wake cycles were analyzed from each subject.

Fig. 1.

Illustration of method for deriving sleep and wake bout durations from nuchal EMG record. (A) (Upper) A 2.4-min record in a P8 rat of nuchal EMG showing two brief periods of high muscle tone indicative of wakefulness separated by a longer period of muscle atonia indicative of sleep. (Lower) These dichotomous states are also depicted. (B) Cycling between sleep and wakefulness in a P2 (Upper) and P21 (Lower) rat. Note the different time scales in the two traces.

For the analyses described above, data were imported into statview 5.0 (SAS Institute, Cary, NC) and deltagraph 5.5 (SPSS, Chicago). Survivor distributions were produced from each pup and from pooled data at each age. Data were plotted by using log-log and semilog coordinates, and regression analyses were performed on the data to assess the r² values and, therefore, the degree of fit of the data to power-law and exponential distributions, respectively. ANOVA was used to test for differences across age; for post hoc tests, Fisher's protected least significant difference was used. Paired t tests were used to test for within-age differences. For all tests, the Type 1 error rate (alpha) was set at 0.05. Means are presented with their standard errors.

To examine correlations among neighboring high-tone and atonia intervals, all data sets were truncated (when necessary) to 50 complete cycles of high muscle tone and atonia. Then, for each subject, we computed the following four classes of correlation coefficient: (i) between successive high tone intervals, (ii) between successive atonia intervals, (iii) between each tone interval and its succeeding (adjacent) atonia interval, and (iv) between each tone interval and its preceding (adjacent) atonia interval. With five age groups, six subjects at each age, and four coefficients calculated for each subject, there were a total of 120 comparisons, thus establishing the Type 1 error rate (alpha), after Bonferroni correction, of 1 - (1 - 0.05)^(1/120) = 0.00043.

In some cases, a data set may exhibit significant correlations that manifest only over larger numbers of bout intervals. Therefore, in addition to the short-term correlational analysis described above, a long-term analysis was also performed using the same data. For this analysis, spectra were computed for the high muscle tone and atonia intervals separately (6). Because any long-term cross-correlations between the tone and atonia intervals would appear in the spectra of these intervals individually, we did not calculate these cross spectra.

For each subject, we began by subtracting the sample mean from each interval and dividing by the sample standard deviation. Because individual spectra exhibit large variability, we averaged spectra over all six animals within each age group. The null hypothesis in this case yields a χ² distribution with 12 degrees of freedom. Because there were 25 (i.e., 50/2) values for each averaged spectrum, 5 age groups, and 2 types of intervals (high muscle tone and atonia), the total number of spectral values was 250, thus establishing the Type 1 error rate (alpha), after Bonferroni correction, of 1 - (1 - 0.05)^(1/250) = 0.00021.

Results

Fig. 1 A illustrates the method used here to convert nuchal EMG data to sleep and wake durations. In this 2.4-min record from a P8 rat, two periods of high muscle tone, indicative of wakefulness, are shown, as is one period of muscle atonia, indicative of sleep. (The spikes in the EMG record during sleep indicate myoclonic twitches.) Fig. 1B depicts rapid cycling between sleep and wakefulness over a 300-s period in a P2 rat and the slower cycling over a 1,200-s period in a P21 rat. Each bout of sleep and wakefulness is used to generate mean sleep and wake bout durations and contributes to the production of survivor data (see below).

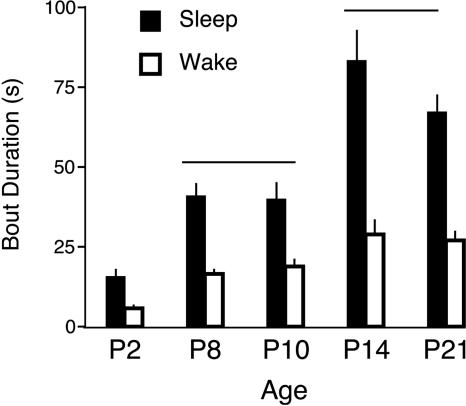
As shown in Fig. 2, mean sleep bout durations increased significantly with age (F_4,25 = 21.2, P < 0.0001), as did mean wake durations (F_4,25 = 12.3, P < 0.0001). Post hoc tests revealed that, for both sleep and wake durations, values at P2 were significantly less than those at P8 and P10 and that values at P8 and P10 were significantly less than those at P14 and P21. Interestingly, despite these developmental changes in both sleep and wake durations, the percentage of time asleep stayed within a narrow range of values (from 67% and 74%) across the ages examined here (F_4,25 = 0.6, not significant).

Fig. 2.

Mean sleep (filled bars) and wake (open bars) bout durations for pups at the five ages examined here. The horizontal lines indicate that, for sleep and wake durations, the values at P2 were significantly lower than those at P8 and P10, which were in turn significantly lower than those at P14 and P21. Data are expressed as means ± SE.

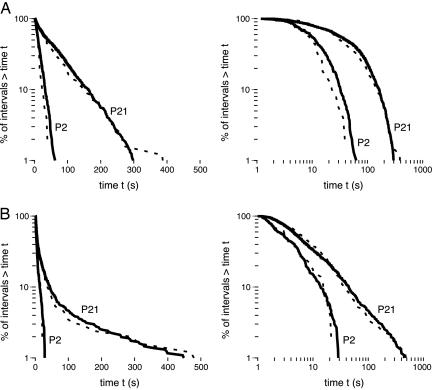
Survivor distributions for data at P2 and P21 are presented in Fig. 3 for pooled data (solid lines) as well as for representative subjects (dotted lines). Survival data that follow an exponential distribution fall on a straight line in a semilog plot (Fig. 3 Left) and those that follow a power-law distribution fall on a straight line in a log-log plot (Fig. 3 Right). For sleep durations, it can be seen that the data for the P2 and P21 rats are best described by an exponential function because they follow a straight line on the semilog plot. This function also describes the data for the wake durations at P2; in contrast, by P21, these data are now linearly distributed on a log-log plot, thus indicating a shift from an exponential distribution at P2 to a power-law distribution at P21.

Fig. 3.

Survivor plots of sleep (A) and wake (B) bout durations for rats at P2 and P21. Each plot was constructed using pooled data at each age (solid lines) and data from one representative pup at each age (dotted lines). (Left) The plots were constructed using semilog coordinates; straight lines on these plots indicate that the data follow an exponential distribution. (Right) The plots were constructed using log-log coordinates; straight lines on these plots indicate that the data follow a power-law distribution.

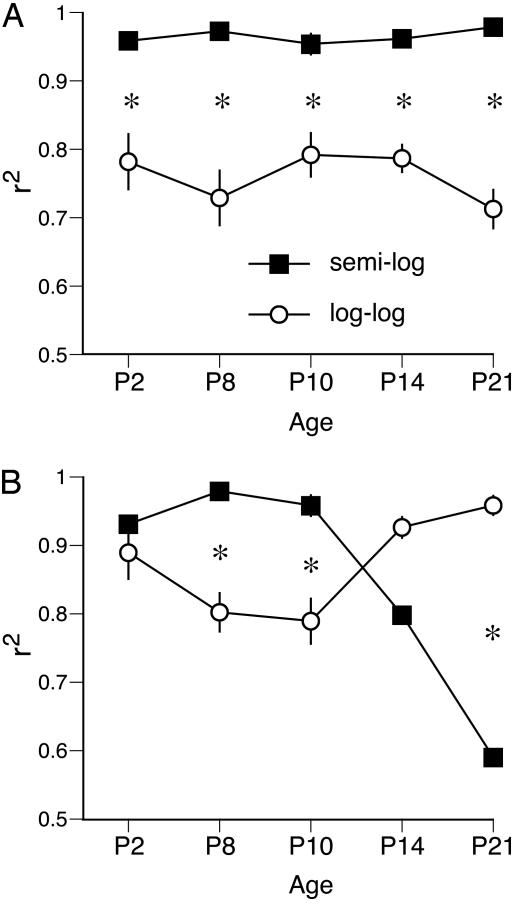
To assess whether the survivor functions of the sleep and wake bout durations are best described as exponential or power-law distributions at each age, regression analyses were performed for each pup when data were plotted using semilog and log-log coordinates. For sleep bout durations (Fig. 4A), ANOVA revealed a significant main effect of distribution (F_1,50 = 180.1, P < 0.0001), but neither the main effect of age (F_4,50 = 0.6) nor the age × distribution interaction (F_4,50 = 1.9) was significant. Paired t tests revealed that an exponential distribution provided a significantly better fit to the data than did a power-law distribution at each of the five ages examined.

Fig. 4.

Values of r² produced using regression analysis of survivor data at five postnatal ages in infant rats. For each individual pup, the degree of fit of the data to power-law and exponential distributions was determined, yielding a value of r² that was then averaged across subjects at each age. (A) Values of r² for sleep bout durations showing that the data are consistently best described by an exponential distribution. (B) Values of r² for wake bout durations showing that the data are best described by an exponential distribution at P8 and P10 and by a power-law distribution at P21. Data are expressed as means ± SE. ^*, significant within-age difference.

Because of the uniform exponential behavior for sleep durations across age, it was possible to document the evolution of the time constant, τ, in the equation f(t) = e^(-t/τ). Values for τ were derived by curve-fitting individual data at each age. (As expected for data that distribute exponentially, the calculation of τ using this method produces values that are close to the mean durations depicted in Fig. 2.) There was a main effect of age on τ (F_4,25 = 36.1, P < 0.0001); at P2, the mean value of τ was 12.1 ± 1.6 s; it increased to 45.4 ± 9.0 s and 45.6 ± 6.5 s at P8 and P10, respectively; it peaked at 96.6 ± 6.9 s at P14 and dipped to 69.5 ± 2.7 s at P21. For their 2- to 3-month-old rats, Lo et al. (4) report a value for τ of 372 s (6.2 min). This quintupling of the value of τ between P21 and 2-3 months of age likely reflects continued developmental change as sleep bouts consolidate further after weaning, especially during the lights-on period in this nocturnal species; it should be noted, however, that methodological differences between the two studies may also account for some of this age-related disparity.

Only at P21 was it valid to compute the value of the characteristic power-law exponent, α. As with τ, values of α were derived by curve-fitting individual data, yielding a mean value of 0.765 ± 0.034. Converting from a survivor function to a probability density function, this value for α becomes 1.765, which compares with a value of 2.3 reported by Lo et al. (4) for 2- to 3-month-old rats. As discussed for τ above, the disparity in the value of α between P21 and 2-3 months of age could reflect a true developmental difference, methodological differences between the two studies, or a combination of the two.

For wake bout durations (Fig. 4B), ANOVA revealed a significant main effect of age (F_4,50 = 6.7, P < 0.0005) but not distribution (F_1,50 = 1.4) and a significant age × distribution interaction (F_4,50 = 32.3, P < 0.0001). The interaction was due to the fact that these durations were increasingly better fit by a power-law distribution between P10 and P21. Indeed, at P8 and P10, paired t tests revealed that an exponential distribution provided a significantly better fit to the data than did a power-law distribution, whereas, by P21, the reverse was true.

Analysis of the short-term correlations in the data for each subject yielded only one significant result (i.e., for the high muscle tone interval autocorrelation for one P21 subject), and only four other correlations approached statistical significance. Furthermore, none of the spectral values computed to detect possible long-term correlations in the data even approached statistical significance.

Discussion

Although sleep studies in adults traditionally rely upon multiple electrographic criteria for defining sleep and wake states, recent work in adult rats indicates that neocortical electroencephalogram measures alone are sufficient to distinguish the primary behavioral states (7). In contrast with adults, the neocortical electroencephalogram in infant rats before the age of P11 does not provide useful information for distinguishing sleep-wake states (8, 9). We have found, however, that nuchal muscle tone alone provides a reliable indicator of sleep and wakefulness in infants (5, 10, 11). Moreover, this single measure of state has been used in week-old rats to identify medullary and mesopontine regions involved in the regulation of sleep and wakefulness (12, 13). Therefore, the sleep-wake durations and transitions reported here using nuchal EMG likely reflect the same neural activity within the brainstem that gives rise to sleep-wake cycles as defined by using electroencephalogram and EMG measures in adults.

A variety of approaches have been adopted to model sleep-wake behavior in infants (14) and adults (15, 16). Only rarely, however, have investigators focused on the fine structure of the bout durations of sleep and wakefulness (17). Such a focus is warranted given that conventional measures of total time asleep and awake must, by necessity, be derived from the accumulation of much smaller bouts of sleep and wakefulness. In other words, an understanding of the dynamics and, therefore, the underlying mechanisms of sleep-wake behavior requires attention to the fine temporal structure of bout activity. On this basis, Lo et al. (3) examined the temporal dynamics of sleep and wake bouts in adult humans. Using conventional electrographic criteria of sleep and wakefulness to categorize behavior in 30-s bins (as in the present study, the different stages of sleep were not considered in their analysis), they demonstrated that sleep bouts follow an exponential distribution, whereas wake bouts follow a power-law distribution. Based on their findings, Lo et al. devised a computational model to capture these statistical properties of sleep and wake durations. In a subsequent report in which the sleep-wake bouts of adult humans, cats, rats, and mice were examined, Lo and colleagues replicated their earlier findings (4). Moreover, they reported that the wake-related power-law exponent (α) was the same across the four species, whereas the sleep-related time constant (τ) increased with increasing body size.

The present findings support the conclusions of Lo and colleagues in some respects but not in others. First, by showing at all ages tested here that sleep bout durations are best described as following an exponential distribution, our results support those of Lo and colleagues and extend them to the neonatal period of an altricial species. This general statistical feature of sleep bout durations remains constant despite significant increases in mean sleep bout duration over this period (see Fig. 2) and, therefore, sizable increases in τ. Thus, τ not only varies across species but across age as well.

Second, we found that wake bout durations early in ontogeny are best described as following an exponential distribution and that it is only after P14 that they begin to follow a power-law distribution. Interestingly, this dramatic transition in the statistical distribution of wake bout durations occurs despite the relatively small increases in mean wake bout duration over this period (see Fig. 2). One implication of this transition from exponential to power-law behavior is that the scale invariance reported by Lo and colleagues (4) for wake bout durations is perhaps only applicable to adult mammals. Moreover, this developmental transition in the statistical distribution of wake bout durations implies that their model, which accurately describes sleep-wake transitions in adults, must be modified to account for the lack of power-law behavior for wake bout durations in early infancy.

Another feature of the model proposed by Lo et al. (3) that is supported here in infants concerns a lack of short-term autocorrelations and cross-correlations for neighboring sleep-wake states (with one minor exception). In addition, our assessment of computed spectral values also indicated a lack of long-term correlations in the data. Taken together, these results suggest that as infants cycle between sleep and wakefulness, there is no memory for the duration of previous intervals. Thus, the available evidence leads us to conclude that transitions between sleep and wakefulness most closely resemble an alternating renewal process (18, 19); at the youngest ages tested here, for which both sleep and wake durations distribute exponentially, the sleep-wake state model further specializes to a two-state Markov process.

The alternating renewal process means that the system resets every time the animal wakes up or goes to sleep; no memory of the past persists beyond these events. However, some memory can exist within intervals, particularly for those that exhibit a power-law distribution. For example, a wake time that has already persisted for a long time is likely to last even longer, producing a relative lack of intermediate-duration wake times. In contrast, for a Markov process (a subset of alternating renewal processes), as with the youngest subjects tested here, the time remaining in any interval is independent of how long it has persisted so far: a total lack of memory.

Recent evidence suggests that the developmental elongation of sleep and wake bout durations during ontogeny (see Fig. 2) reflects increasing forebrain modulation of brainstem neural circuits. For example, transections located between the midbrain and anterior hypothalamus of P8 rats (2), as well as combined lesions of the preoptic area and basal forebrain (E. J. Mohns, K.Æ.K., and M.S.B., unpublished data), cause a reversion to sleep-wake cycles typical at P2. The present results further suggest that this ontogenetic elaboration of brainstem and forebrain neural circuits may also be related to the shift in the statistical distribution of wake bout durations that occurs during that period. For example, the exponential distribution of wake bout durations in early ontogeny may reflect the primary contribution of brainstem neural circuits, whereas the gradual emergence of the power-law distribution may reflect the developing influence of more rostral structures. It must be stressed, however, that the different developmental time courses for increases in bout durations and changes in the statistical distributions of those durations (compare Figs. 2 and 4) may reflect the influences of nonidentical neural processes.

In relating the current findings to developmental changes at the neural level, there are several issues that should not be ignored. For example, the onset of the power-law distribution of wake durations around P14 could be associated with the onset of eye opening and the subsequent development of circadian sleep rhythmicity (20). A link between these two processes would then implicate the developing influence of the suprachiasmatic nucleus and its connectivity with well established hypothalamic and brainstem nuclei involved in the control of sleep and wakefulness (21). Another important issue concerns the postnatal development of sleep homeostasis (22, 23), including sleep pressure and rebound, and its relationship to the findings reported here. Although here we recorded sleep-wake activity for relatively brief periods during the lights-on period, longer-term recordings throughout the day and night and at different ages will be necessary to reveal circadian and homeostatic influences on the statistical properties of sleep-wake bouts.

In summary, the present study and those of Lo and colleagues (3, 4) indicate lawful statistical behavior of sleep and wake bout durations. By focusing on the temporal dynamics of these transitions, we move closer to the actual dynamics that govern this fundamental biological rhythm. The present study demonstrates the additional promise of developmental assessments of sleep and wakefulness for revealing basic biological mechanisms. Thus, by combining temporal precision, across-species comparison, developmental analysis, and assessment of neural substrates, we should be able to make progress toward the development of computational models that fully capture the dynamics and mechanisms of sleep-wake behavior across the life span.