Abstract
Background
The increasingly available multi-omics datasets have posed both new opportunities and challenges to the development of quantitative methods for discovering novel mechanisms in biomedical research. One natural approach to analyzing such datasets is mediation analysis originated from the causal inference literature. Mediation analysis can help unravel the mechanisms through which exposure(s) exert the effect on outcome(s). However, existing methods fail to consider the case where (1) both exposures and mediators are potentially high-dimensional and (2) it is very likely that some important confounding variables are unmeasured or latent; both issues are quite common in practice. To the best of our knowledge, however, no methods have been developed to address these challenges with statistical guarantees.
Methods
In this article, we propose a new method for HIgh-dimensional LAtent-confounding Mediation Analysis (HILAMA) that considers both high-dimensional exposures and mediators, as well as the possible existence of latent confounding variables. HILAMA employs the Decorrelating & Debiasing method to estimate the individual effects of exposures and mediators on the outcome. A column-wise regression strategy with parallel computing is considered to efficiently estimate the exposure-mediator effect matrix. HILAMA then applies the MinScreen procedure to eliminate non-significant pairs, and the Joint-Significance Testing (JST) method to compute p-values for the retained pairs, controlling the False Discovery Rate (FDR) using the Benjamini-Hochberg (BH) procedure.
Results
The proposed method is evaluated through extensive simulation experiments, demonstrating its improved stability in FDR control and superior power in finite sample size compared to existing competitive methods. Furthermore, our method is applied to the proteomics-radiomics data from ADNI, identifying some key proteins and brain regions related to Alzheimer’s disease. These empirical results demonstrate that HILAMA can effectively control FDR and provide valid statistical inference for high dimensional mediation analysis with latent confounding variables under certain assumptions.
Conclusions
HILAMA can effectively control FDR and provide valid statistical inference for high dimensional mediation analysis with latent confounding variables under certain assumptions.
Supplementary Information
The online version contains supplementary material available at 10.1186/s12874-025-02686-z.
Keywords: High-dimensional mediation analysis, Latent confounding, False discovery rate control, Multi-omics, Alzheimer’s disease
Background
The emergence of modern biotechnologies, such as high-throughput omics and multimodal neuroimaging, has led to the rapid accumulation of omics data at various levels, often including information on genomics, epigenomics, transcriptomics, proteomics, radiomics, and clinical records. It then becomes possible to thoroughly study complex diseases such as cancer and Alzheimer’s disease by integrating information from various scales [1, 2]. For example, large collaborative consortia such as Alzheimer’s Disease Neuroimaging Initiative (ADNI) have collected information across all the levels mentioned above to help unravel the causal mechanisms of Alzheimer’s disease [3]. It is thus urgently needed to develop rigorous statistical methods for analyzing such datasets to reliably dissect the causal mechanisms [4–6].
Such a problem falls into the category of causal mediation analysis [7, 8], which can help disentangle the intermediate mechanisms between cause-effect pairs from observational datasets [9–13]. The classical mediation analysis can be traced back to 1930 s [14], and then reverberated in early 1980 s based on regression techniques [8]. Over the following decades, a vast literature has been engendered to put mediation analysis on a more rigorous ground both mathematically and conceptually [15–18]. We refer interested readers to VanderWeele [7] for a textbook-level introduction.
However, methods for mediation analyses with a single or a few exposures and/or mediators often cannot be directly scaled to address high-dimensional omics data. For instance, traditional hypothesis testing methods, such as Joint Significance Test (JST) [19], Sobel’s method [20], and bootstrap method [21], tend to be overly conservative particularly in genome-wide epigenetic studies [22, 23].
In response to the above challenge, recent years have seen a surge in the development of new methods for high-dimensional mediation analysis. These methods aim to explore the biological mechanisms derived from multi-omics data [24, 25]. For instance, some have focused on epigenetic studies or neuroimaging studies with high-dimensional mediators and a continuous outcome [26–30]. They have primarily employed (debiased/de-sparsified) penalized linear regression and multiple testing procedures to formulate their methods. Derkach et al. [31] have tackled a similar problem by considering multiple latent variables as mediators that influence both the high dimensional biomarkers and the outcome [31]. Furthermore, the continuous outcome setting has also been extended in a few recent works to survival outcome settings, alongside high-dimensional mediators [32–34]. Additionally, mediation analysis with high-dimensional continuous mediators has also been further developed to handle compositional microbiome data [35–38]. In a similar vein, Shao et al. [39] investigated high-dimensional exposures with a single mediator in an epigenetic study, utilizing a linear mixed-effect model [39]. All the above studies have contributed to the growing literature on exploring complex biological relationships.
Specifically for neuroimaging data analysis, Zhao et al. [40] recently developed a novel method that deals with multivariate-mediator and multivariate-outcome [40]. However, there have been limited works studying both multivariate exposures and mediators. Zhang [41] considered high-dimensional exposures and mediators through two different procedures; however, they require the mediators to be jointly independent and mainly focus on the mediator selection problem [41]. Zhao et al. [42] developed a novel penalized principal component regression method that replaces the exposures with their principal components in a lower dimension [42]. This approach, however, lacks direct causal interpretation when the exposures are scientifically meaningful. More importantly, most high-dimensional mediation analysis approaches make the untestable assumption of no latent confounding, which is highly problematic in multi-omics biological studies due to the prevalence of non-randomized study designs. If hidden confounding cannot be ruled out, these methods can be biased due to spurious correlations and result in an inflated False Discover Rate (FDR) [43]. Recently, several works have been devoted to tackle this problem in the simpler high-dimensional linear models, which can be viewed equivalently as estimating the total causal effects of the exposures under the Latent Structural Equation Modeling (LSEM) framework [44–47]. Specifically, Sun et al. [48] are the first to address the large-scale hypothesis testing problem in the high-dimensional confounded linear model by proposing the Decorrelating & Debiasing estimator [48]. They achieve FDR control under finite sample sizes by introducing a decorrelating transformation prior to the debiasing step.
Inspired by the aforementioned works on high-dimensional linear regression with latent confounding [44–48], we propose a novel method called HILAMA, which stands for HIgh-dimensional LAtent-confounding Mediation Analysis. In contrast to the focus of Sun et al. [48] on hypothesis testing in confounded linear models, HILAMA extends this framework to mediation analysis, thereby enabling a comprehensive examination of causal pathways in high-dimensional multi-omics contexts. HILAMA addresses two critical challenges in applying mediation analysis (or any causal inference method) to multi-omics studies: (1) accommodating both high-dimensional exposures and mediators, and (2) effectively handling latent confounding. In contrast to competing methods [8, 26, 27, 42, 49], our method maintains control of FDR at the nominal level for multiple direct/indirect effect testing, even in the presence of latent confounders. Now, we briefly sketch the essential components of our method. First, we employ the Decorrelating & Debiasing method [48] to obtain p-values for each individual effects of the exposures and mediators on the outcome. Second, to estimate the effect matrix of exposures on mediators, we employ a column-wise regression strategy, again incorporating the Decorrelating & Debiasing method [48]. To handle large and high-dimensional datasets, we utilize parallel computing in this step. Third, we apply the MinScreen procedure to eliminate non-rejected hypotheses [50], retaining only the K most significant pairs for the final stage of multiple testing. Lastly, we compute p-values for all K pairs using the JST method [19], employing a data-dependent threshold determined by the Benjamini-Hochberg (BH) procedure [51] to maintain FDR at the nominal level  . We conduct extensive simulations to evaluate the finite sample performance of our method, demonstrating effective FDR controls across various sample sizes, compared to most of the other competing methods in the presence of hidden confounding. Finally, we apply HILAMA to a proteomics-radiomics dataset from the ADNI database (adni.loni.usc.edu) and identify key proteins and brain regions associated with learning, memory, and recognition impairments in Alzheimer’s disease and cognitive impairment.
. We conduct extensive simulations to evaluate the finite sample performance of our method, demonstrating effective FDR controls across various sample sizes, compared to most of the other competing methods in the presence of hidden confounding. Finally, we apply HILAMA to a proteomics-radiomics dataset from the ADNI database (adni.loni.usc.edu) and identify key proteins and brain regions associated with learning, memory, and recognition impairments in Alzheimer’s disease and cognitive impairment.
The rest of this article is organized as follows. We first introduce the proposed model HILAMA, under the Linear Structural Equation Models with high-dimensional exposures, high-dimensional mediators, continuous outcome, and latent confounding. In the next part, we evaluate the FDR and Power performance of HILAMA across a wide range of simulations and analyze the indirect effects of high dimensional proteins on cognitive function through high dimensional imaging information of brain regions as mediators, using a proteomics-radiomics data of Alzheimer’s disease from ADNI. Finally, we conclude the paper with a discussion on the limits and other possible extensions.
Methods
Notations and HIgh-dimensional LAtent-confounding Mediation Analysis (HILAMA)
To describe the HILAMA methodology, we first need to briefly review mediation analyses. Mediation analyses are frequently utilized to disentangle the underlying causal mechanism between two sets of variables, the exposures and outcomes, exerted by a third set of variables, the mediators. The overall causal effects can be decomposed into direct effects from exposures to outcomes, bypassing mediators, and indirect effects via mediators. To be more precise, we ground our discussion under the Linear Structural Equation (LSE) framework, that models the causal mechanisms among p-dimensional exposures  , q-dimensional mediators
, q-dimensional mediators  , r-dimensional baseline covariates
, r-dimensional baseline covariates  , a scalar outcome
, a scalar outcome  , and latent confounders
, and latent confounders  (e.g., batch effects, disease subtypes, and lifestyle factors) as follows:
(e.g., batch effects, disease subtypes, and lifestyle factors) as follows:
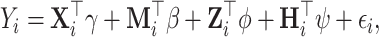 |
1 |
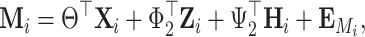 |
2 |
where 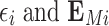 are the noise terms that are independent of
are the noise terms that are independent of  and
and 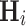 . In the outcome model (1),
. In the outcome model (1),  is the direct effect vector of the exposures
is the direct effect vector of the exposures  on the outcome
on the outcome  , and
, and 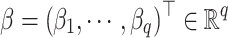 represents the effect vector of the mediators
represents the effect vector of the mediators 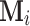 to the outcome
to the outcome  after adjusting for the baseline covariates
after adjusting for the baseline covariates  , and the latent confounders
, and the latent confounders 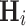 .
. 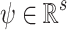 is the parameter vector that relates latent confounders
is the parameter vector that relates latent confounders  to the outcome
to the outcome 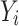 . Here, we allow p and q to be larger than the sample size n, while s is small compared to the p and q. The primary objective of our study is to identify the active direct/indirect effects (
. Here, we allow p and q to be larger than the sample size n, while s is small compared to the p and q. The primary objective of our study is to identify the active direct/indirect effects (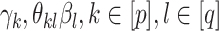 ) from p/pq possible paths, as shown in Fig. 1. Here, [p] represents the set
) from p/pq possible paths, as shown in Fig. 1. Here, [p] represents the set  .
.
Fig. 1.
Causal Diagram considered in this paper.  : exposures of dimension p (protein expression data in our real-data applications);
: exposures of dimension p (protein expression data in our real-data applications);  : mediators of dimension q (imaging data in our real-data applications); Y: a real-valued outcome (clinical outcome or phenome data in our real-data applications);
: mediators of dimension q (imaging data in our real-data applications); Y: a real-valued outcome (clinical outcome or phenome data in our real-data applications); 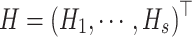 : latent/unmeasured confounders of dimension s (e.g. mis-measured clinical data, epigenetic information, etc.). Here, we omit the observed baseline covariates
: latent/unmeasured confounders of dimension s (e.g. mis-measured clinical data, epigenetic information, etc.). Here, we omit the observed baseline covariates  for the sake of presentation convenience. Solid (red) lines indicate non-null effects, while dotted lines indicate null effects
for the sake of presentation convenience. Solid (red) lines indicate non-null effects, while dotted lines indicate null effects
In the mediator model (2), the matrix  represents the regression coefficients of exposures on mediators and
represents the regression coefficients of exposures on mediators and 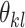 represents the effect of exposure
represents the effect of exposure  on mediator
on mediator 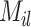 after adjusting for the effect of latent confounders
after adjusting for the effect of latent confounders 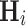 .
. 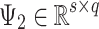 can be interpreted as the confounding effect of the latent confounders
can be interpreted as the confounding effect of the latent confounders 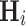 on mediators
on mediators 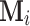 . The mediation model (1) – (2) adopted here is similar to those proposed in [42, 49], which were among the first works to consider both multivariate exposures and mediators. However, we incorporate the latent confounders into our high-dimensional mediation analysis, which is a novel approach in the field. Furthermore, unlike the approach used in [42], our mediation analysis is directly based on
. The mediation model (1) – (2) adopted here is similar to those proposed in [42, 49], which were among the first works to consider both multivariate exposures and mediators. However, we incorporate the latent confounders into our high-dimensional mediation analysis, which is a novel approach in the field. Furthermore, unlike the approach used in [42], our mediation analysis is directly based on  , instead of a transformation
, instead of a transformation 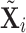 of the original vector
of the original vector  .
.
As mentioned, the causal parameters of interest in mediation analyses are mainly the (average) natural direct and indirect effects. When the ignorability assumption (explained in Supplementary Information) holds [15, 16], the natural direct effect of exposure 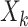 on outcome, denoted by
on outcome, denoted by  , and the natural indirect effect of exposure
, and the natural indirect effect of exposure 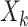 on outcome, denoted by
on outcome, denoted by 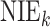 , can be expressed as
, can be expressed as
 |
When 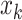 and
and 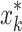 defer by one unit,
defer by one unit, 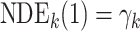 , the regression coefficient between
, the regression coefficient between  and Y in model (1), and
and Y in model (1), and 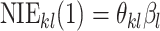 , the product of the regression coefficient between
, the product of the regression coefficient between  and
and  in model (2) and the regression coefficient between
in model (2) and the regression coefficient between  and Y in model (1). For their derivation, see Supplementary Information.
and Y in model (1). For their derivation, see Supplementary Information.
However, in the presence of latent confounders (i.e.  ), neither NDEs nor NIEs are identifiable without making additional assumptions, which are generally based by domain-specific knowledge. To identify the true parameter
), neither NDEs nor NIEs are identifiable without making additional assumptions, which are generally based by domain-specific knowledge. To identify the true parameter  in the confounded linear model (1) and (2), it is necessary to make additional assumptions among the observed variables
in the confounded linear model (1) and (2), it is necessary to make additional assumptions among the observed variables  and the latent confounders
and the latent confounders 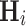 . Based on the aforementioned works [45, 46, 48, 52], a factor model is specified to characterize the relation between
. Based on the aforementioned works [45, 46, 48, 52], a factor model is specified to characterize the relation between  and
and  :
:
 |
3 |
where 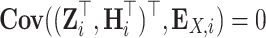 and the random variable
and the random variable 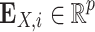 represents the unconfounded components of
represents the unconfounded components of 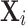 . Moreover, to accurately identify the true signals and effectively remove the confounding effects, we impose a spiked singular value condition on the covariance between the exposures and mediators, as shown in Supplementary Information. Specifically, we require
. Moreover, to accurately identify the true signals and effectively remove the confounding effects, we impose a spiked singular value condition on the covariance between the exposures and mediators, as shown in Supplementary Information. Specifically, we require  , where
, where  and
and 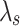 denotes the s-th largest singular values [48]. Our approach is particularly effective in scenarios where the confounding effect is dense, i.e., many observed variables in
denotes the s-th largest singular values [48]. Our approach is particularly effective in scenarios where the confounding effect is dense, i.e., many observed variables in 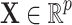 and
and  are simultaneously influenced by the latent confounders
are simultaneously influenced by the latent confounders 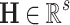 .
.
Our goal is to identify the path-specific indirect effect 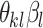 (corresponding to the path
(corresponding to the path  ) from the total
) from the total 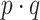 possible paths which corresponds to the following multiple hypothesis testing problem:
possible paths which corresponds to the following multiple hypothesis testing problem:
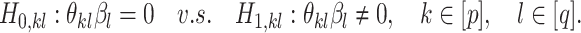 |
4 |
HILAMA procedure
Here, we propose a novel framework called HILAMA to solve the hypothesis testing problem (4) for high-dimensional mediation analysis in the presence of hidden confounding. The framework identifies the true paths with nonzero indirect effects and controls the finite-sample FDR. It involves four major steps as illustrated below (as shown in Fig. 2).
Fig. 2.
Flowchart of HILAMA. First, we regress outcome Y over mediators 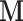 and exposures
and exposures 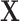 using the Decorrelating & Debiasing approach to obtain the debiased p-values for the parameter
using the Decorrelating & Debiasing approach to obtain the debiased p-values for the parameter 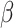 . Second, we similarly perform parallel regression analyses of each mediator
. Second, we similarly perform parallel regression analyses of each mediator 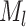 over the exposures
over the exposures 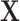 to obtain debiased p-values for the parameter
to obtain debiased p-values for the parameter  . Third, we employ the MinScreen procedure to select a subset of K pairs for subsequent multiple testing. Finally, we calculate p-values for the mediation effect using the JST method and choose a p-value threshold using the BH procedure based on a pre-specified FDR level, where a set of pairs is considered significant if the p-value falls below this threshold
. Third, we employ the MinScreen procedure to select a subset of K pairs for subsequent multiple testing. Finally, we calculate p-values for the mediation effect using the JST method and choose a p-value threshold using the BH procedure based on a pre-specified FDR level, where a set of pairs is considered significant if the p-value falls below this threshold
First, for the outcome model in Eq. (1), we utilize the Decorrelating & Debiasing approach to carry out inference on the regression parameters 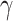 and
and 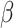 [48]. Specifically, let
[48]. Specifically, let 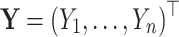 ,
, 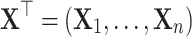 ,
,  ,
, 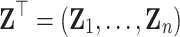 , and
, and 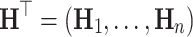 . For simplicity, we first assume the absence of
. For simplicity, we first assume the absence of  . To further avoid notation clutter, we concatenate the exposures and mediators into
. To further avoid notation clutter, we concatenate the exposures and mediators into 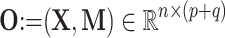 and their coefficients into
and their coefficients into 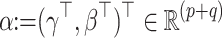 . Equations (1) – (3) can then be reduced to:
. Equations (1) – (3) can then be reduced to:
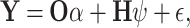 |
5 |
 |
6 |
where 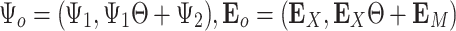 . Since
. Since 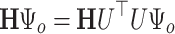 holds for any
holds for any 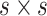 orthogonal matrix
orthogonal matrix  , following the factor analysis literature [52], we further impose–without loss of generality–the identifiability conditions:
, following the factor analysis literature [52], we further impose–without loss of generality–the identifiability conditions:  and
and  is diagonal. If we project
is diagonal. If we project  onto the linear span of
onto the linear span of 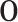 , we have
, we have 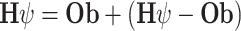 for some
for some 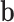 such that
such that 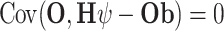 . Consequently, the outcome model (5) can be represented as a linear model with a coefficient different from the truth
. Consequently, the outcome model (5) can be represented as a linear model with a coefficient different from the truth 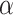 by a bias
by a bias 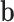 :
:
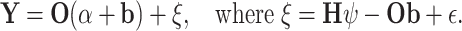 |
7 |
To mitigate the bias 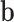 caused by latent confounders
caused by latent confounders 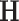 , a decorrelating matrix
, a decorrelating matrix  is left-multiplied to Eqs. (5) and (6), with
is left-multiplied to Eqs. (5) and (6), with 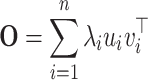 representing the singular value decomposition (SVD) of the design matrix
representing the singular value decomposition (SVD) of the design matrix 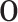 , where
, where  . This decorrelating operation turns the data generating model into:
. This decorrelating operation turns the data generating model into:
 |
8 |
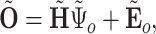 |
9 |
where  . After the transformation, the confounding term
. After the transformation, the confounding term 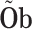 is reduced due to the removal of the top s largest singular values (
is reduced due to the removal of the top s largest singular values ( ). This also results in weaker correlations among the components of
). This also results in weaker correlations among the components of 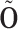 .
.
Remark 1
We provide a heuristic explanation on why multiplying the structural Eqs. (5) and (6) by 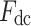 reduces bias. To estimate the latent confounders
reduces bias. To estimate the latent confounders 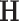 and the loading matrix
and the loading matrix 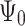 in (6), we apply factor analysis to
in (6), we apply factor analysis to  , yielding:
, yielding:
 |
where  . The orthogonal projection matrix onto the complement of
. The orthogonal projection matrix onto the complement of  is then:
is then:
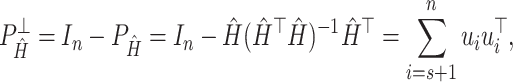 |
which equals 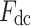 . Left-multiplying by
. Left-multiplying by  projects the data onto the space orthogonal to
projects the data onto the space orthogonal to 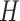 , thereby mitigating the confounding impact of
, thereby mitigating the confounding impact of  on the observed data.
on the observed data.
Based on the transformed data 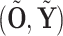 and the assumption that
and the assumption that 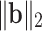 is of small order of magnitude for large covariates under dense confounding [46, 48], the Decorrelating & Debiasing estimator can be derived analogously to the debiased Lasso procedure [53]. This estimator is expressed as follows:
is of small order of magnitude for large covariates under dense confounding [46, 48], the Decorrelating & Debiasing estimator can be derived analogously to the debiased Lasso procedure [53]. This estimator is expressed as follows:
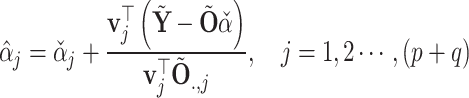 |
10 |
where initial estimation  can be obtained by regressing
can be obtained by regressing  on
on  using Lasso and
using Lasso and 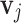 can be obtained as follows
can be obtained as follows
 |
11 |
where 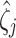 can be the Lasso estimator by regressing
can be the Lasso estimator by regressing 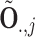 on
on  .
.
When baseline covariates 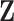 are present, we initially project the observed data onto the orthogonal complement of the span of
are present, we initially project the observed data onto the orthogonal complement of the span of  to eliminate the influence of
to eliminate the influence of 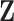 . Specifically, let the projection matrix be
. Specifically, let the projection matrix be  and its orthogonal complement be
and its orthogonal complement be 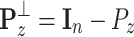 . By left-multiplying Eq. (12) with the projection matrix
. By left-multiplying Eq. (12) with the projection matrix 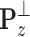 ,
,
 |
12 |
we can eliminate the effect of 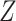 .
.
These estimators, after appropriate rescaling, asymptotically converge to centered Gaussian distributions: 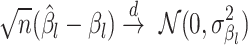 individually under some mild conditions [46, 48]. We denote the corresponding variance estimators as
individually under some mild conditions [46, 48]. We denote the corresponding variance estimators as 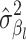 . Then p-values can be computed as follows:
. Then p-values can be computed as follows:
 |
where 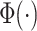 denotes the cumulative distribution function of the standard normal distribution
denotes the cumulative distribution function of the standard normal distribution  .
.
Second, to estimate each column of the parameter matrix  in the multi-response mediation model defined in Eq. (2), we employ a column-wise regression strategy. For each sub-regression problems, we similarly utilize the Decorrelating & Debiasing approach after removing the possible observed baseline covariates
in the multi-response mediation model defined in Eq. (2), we employ a column-wise regression strategy. For each sub-regression problems, we similarly utilize the Decorrelating & Debiasing approach after removing the possible observed baseline covariates 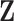 by projection as before. Since the
by projection as before. Since the 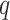 sub-regression problems share the same predictor
sub-regression problems share the same predictor 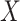 and the calculation of
and the calculation of 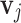 (
(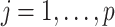 ) solely depends on
) solely depends on  , we first compute
, we first compute 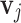 following Eq. (11). This computation is the most time-consuming aspect of obtaining the Decorrelating & Debiasing estimator. Fortunately, we only need to compute this step once. Meanwhile, to address the computational challenges posed by large-scale datasets in multi-omics studies, we leverage parallel computing techniques to accelerate the computation for the
following Eq. (11). This computation is the most time-consuming aspect of obtaining the Decorrelating & Debiasing estimator. Fortunately, we only need to compute this step once. Meanwhile, to address the computational challenges posed by large-scale datasets in multi-omics studies, we leverage parallel computing techniques to accelerate the computation for the 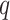 sub-regression problems. This approach enables us to efficiently calculate the point and variance estimators for the coefficients
sub-regression problems. This approach enables us to efficiently calculate the point and variance estimators for the coefficients  (where
(where 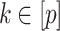 and
and  ), denoted as
), denoted as 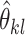 and
and  , respectively. To assess the statistical significance of the coefficient estimates, we calculate the p-values using the formula:
, respectively. To assess the statistical significance of the coefficient estimates, we calculate the p-values using the formula:
 |
Third, we employ the MinScreen procedure to screen the total 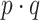 possible causal paths [50]. The screened causal paths by MinScreen are defined as the top K significant paths:
possible causal paths [50]. The screened causal paths by MinScreen are defined as the top K significant paths:  where
where  and
and 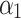 is chosen such that
is chosen such that 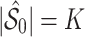 . This preliminary step eliminates the least promising causal paths before calculating the final p-value for
. This preliminary step eliminates the least promising causal paths before calculating the final p-value for 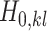 . By doing so, it effectively reduces the computational burden in the subsequent multiple testing phase.
. By doing so, it effectively reduces the computational burden in the subsequent multiple testing phase.
Lastly, we apply the joint significance test (JST), also known as the MaxP test [19], to obtain the p-value for the null hypothesis 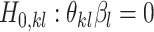 which tests for no indirect effect, for
which tests for no indirect effect, for 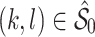 . The p-values for JST are defined as
. The p-values for JST are defined as
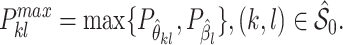 |
We then sort the JST p-values and denote them as  , the notation for order statistics by convention. To protect the FDR at the nominal level
, the notation for order statistics by convention. To protect the FDR at the nominal level 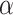 , we find the data-driven p-value rejection threshold
, we find the data-driven p-value rejection threshold 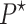 using the BH procedure [51]. The threshold
using the BH procedure [51]. The threshold  is determined as
is determined as
 |
Finally, we define the set containing statistically significant non-zero path-specific effects as  . In this article, we evaluate HILAMA and other competitors by FDR and Power, which are defined as follows:
. In this article, we evaluate HILAMA and other competitors by FDR and Power, which are defined as follows:
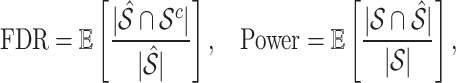 |
where  represents the true non-zero effect path-specific set and
represents the true non-zero effect path-specific set and 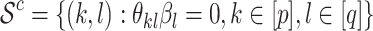 represents the zero effect path-specific set.
represents the zero effect path-specific set.
Simulation studies
Simulation design
In this section, we assess if HILAMA is capable of controlling the FDR with sufficient power across a wide range of simulation settings. The performance is compared against various other approaches. As a baseline benchmark, we employ the univariate Baron & Kenny method (abbreviated as BK) [8] for every possible individual exposure-mediator pair, using the R package  . We also consider methods that only allow a univariate exposure and high-dimensional mediators, including HIMA [26], HDMA [27] and HIMA2 [28]. To compare the results under a nominal level of 0.1, we made minor modifications to the corresponding R packages HIMA and HDMA. We analyzed each individual exposure separately and then aggregated the results. Relevant details are provided in the Supplementary Information. Finally, we compare two penalized methods developed for multiple exposures and mediators. Specifically, for the method “mvregmed” [49], we apply the R package regmed. While for the method developed by Zhao et al. [42] (abbreviated as ZY) [42], we implement their penalized regression algorithm and omit the dimension reduction step for comparison. Here, we only compare the two penalized methods in simulation 2 introduced below due to their slow running time.
. We also consider methods that only allow a univariate exposure and high-dimensional mediators, including HIMA [26], HDMA [27] and HIMA2 [28]. To compare the results under a nominal level of 0.1, we made minor modifications to the corresponding R packages HIMA and HDMA. We analyzed each individual exposure separately and then aggregated the results. Relevant details are provided in the Supplementary Information. Finally, we compare two penalized methods developed for multiple exposures and mediators. Specifically, for the method “mvregmed” [49], we apply the R package regmed. While for the method developed by Zhao et al. [42] (abbreviated as ZY) [42], we implement their penalized regression algorithm and omit the dimension reduction step for comparison. Here, we only compare the two penalized methods in simulation 2 introduced below due to their slow running time.
We first generate the exposure data  according to model (3). The observed baseline covariates
according to model (3). The observed baseline covariates  , latent confounders
, latent confounders 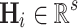 and the elements of
and the elements of  are independently drawn from the standard normal distribution. The unconfounded components
are independently drawn from the standard normal distribution. The unconfounded components 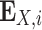 are drawn from
are drawn from  , where
, where  . The parameter
. The parameter 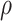 controls the strength of correlation among exposures, and it takes values in the range [0, 1).
controls the strength of correlation among exposures, and it takes values in the range [0, 1).
Similarly, we generate the the mediator data 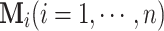 according to model (2). The noise term
according to model (2). The noise term 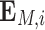 are drawn from
are drawn from  and the confounding effect matrix
and the confounding effect matrix  are drawn from
are drawn from 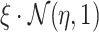 , where
, where  is a Rademacher random variable, i.e.
is a Rademacher random variable, i.e.  . Then, for the signal coefficient matrix
. Then, for the signal coefficient matrix 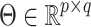 , we randomly choose
, we randomly choose 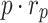 rows having non-zero elements, and choose
rows having non-zero elements, and choose 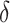 non-zero elements separately in each of these rows, where
non-zero elements separately in each of these rows, where  follows uniform distribution on
follows uniform distribution on 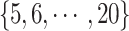 . The non-zero elements in
. The non-zero elements in  follow the distribution
follow the distribution  .
.
Finally, we generate the outcome data  according to model (1). The coefficients
according to model (1). The coefficients  are randomly sampled from a distribution
are randomly sampled from a distribution 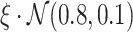 , with a total of
, with a total of 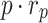 non-zero elements. Similarly, the coefficients
non-zero elements. Similarly, the coefficients 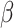 are chosen from the same distribution, with
are chosen from the same distribution, with  non-zero elements. To determine the active location in
non-zero elements. To determine the active location in 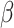 , we define
, we define 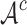 as the set of columns in
as the set of columns in 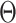 with zero elements (
with zero elements (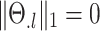 ), and
), and  as the set of columns in
as the set of columns in 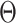 with non-zero elements (
with non-zero elements (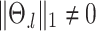 ). From
). From  , we randomly choose
, we randomly choose 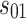 elements with equal probability, where
elements with equal probability, where  . While from
. While from  , we randomly choose
, we randomly choose 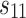 elements with unequal probability, where
elements with unequal probability, where  . The selection probability of
. The selection probability of 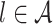 is determined by
is determined by  , which represents the proportion of non-zero elements in column l relative to all non-zero elements in
, which represents the proportion of non-zero elements in column l relative to all non-zero elements in  . The confounding effects
. The confounding effects  are drawn from
are drawn from 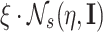 , and the noise terms
, and the noise terms  are drawn from
are drawn from  .
.
For all the simulations below, we fix the sparsity proportions as 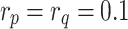 , the dimension of baseline covariates
, the dimension of baseline covariates 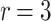 , and latent confounders
, and latent confounders  . Additionally, we set
. Additionally, we set 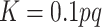 , the nominal FDR level at the
, the nominal FDR level at the  and all the simulation results are averaged over 100 Monte Carlo replications.
and all the simulation results are averaged over 100 Monte Carlo replications.
Simulation results
Simulation 1. In the first simulation, we test the stability of our model under various scenarios. We evaluate the impact of changes in sample size ( ), exposure dimension (
), exposure dimension (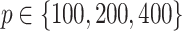 ), mediator dimension (
), mediator dimension (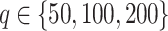 ), correlation size among exposures (
), correlation size among exposures (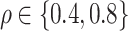 ), and magnitude of latent effects (
), and magnitude of latent effects (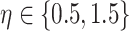 ).
).
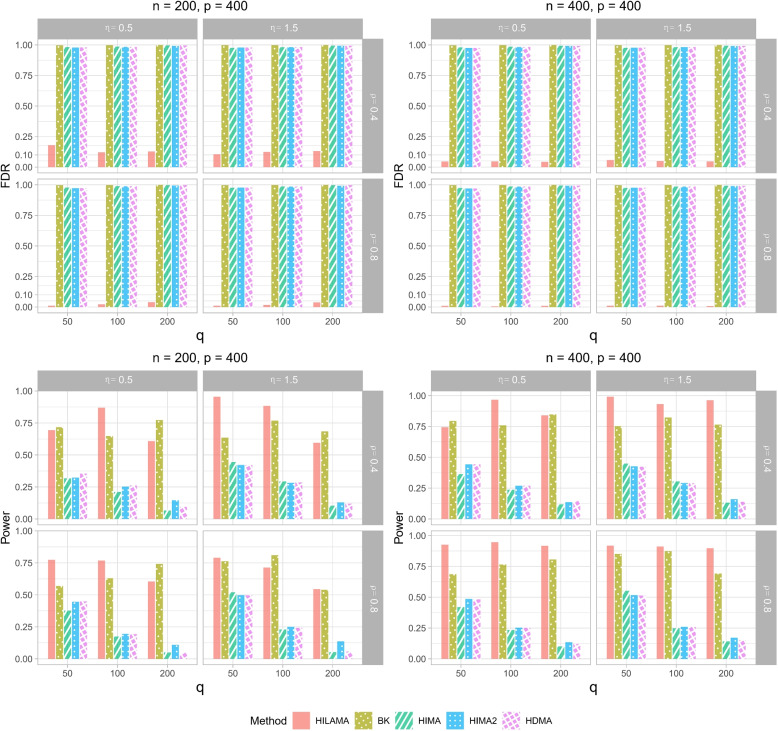
For simplicity, we only present scenarios for 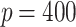 in Fig. 3. For the total 72 different settings, we present the average value of empirical FDR and Power in Supplementary Information. From Fig. 3A, only HILAMA controls the FDR at the nominal level
in Fig. 3. For the total 72 different settings, we present the average value of empirical FDR and Power in Supplementary Information. From Fig. 3A, only HILAMA controls the FDR at the nominal level  in all scenarios, whereas the other three methods all fail to do so. The reasons for their lack of control are due to their failure to correct for the effect of latent confounding, and their inability to accommodate high-dimensional exposure and mediator settings. Turning to the power, by reading Fig. 3B, we can easily see that HILAMA achieves the highest power in larger sample sizes (
in all scenarios, whereas the other three methods all fail to do so. The reasons for their lack of control are due to their failure to correct for the effect of latent confounding, and their inability to accommodate high-dimensional exposure and mediator settings. Turning to the power, by reading Fig. 3B, we can easily see that HILAMA achieves the highest power in larger sample sizes (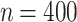 ). However, in smaller sample sizes (
). However, in smaller sample sizes (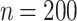 ), the statistical power decreases as correlation coefficient
), the statistical power decreases as correlation coefficient 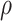 increases. The impact of the aforementioned parameters on the power of HILAMA is generally diminished in larger sample sizes. The powers of the other three methods, on the other hand, are essentially meaningless since their FDRs are all close to 1. Moreover, the point estimates of mediation effects produced by HILAMA exhibit substantially less bias compared to other methods, as measured by
increases. The impact of the aforementioned parameters on the power of HILAMA is generally diminished in larger sample sizes. The powers of the other three methods, on the other hand, are essentially meaningless since their FDRs are all close to 1. Moreover, the point estimates of mediation effects produced by HILAMA exhibit substantially less bias compared to other methods, as measured by 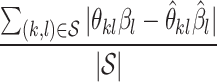 (see Supplementary Information).
(see Supplementary Information).
Fig. 3.
Comparison results of (A) (First row) Empirical False Discovery Rate (FDR) and (B) (Second row) Empirical Power for different methods in Simulation 1. 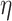 represents latent confounding effect and
represents latent confounding effect and 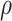 represents the correlation size among exposures. Here we only present
represents the correlation size among exposures. Here we only present  . All results are averaged over 100 replications under the nominal FDR level of 0.1
. All results are averaged over 100 replications under the nominal FDR level of 0.1
Remark 2
As noted by one reviewer, it may be more appropriate to consider scenarios in which methods like HIMA2 perform adequately and to demonstrate how HILAMA performs in that context. To provide a more comprehensive comparison of the advantages and disadvantages of each approach, we considered scenarios including single exposure and those without hidden confounders in the Supplementary Information. In particular, we observe that methods such as HIMA2 can effectively control the FDR and achieve high power only in the absence of hidden confounding; however, they struggle with correlated exposures or hidden confounders. In contrast, HILAMA underperforms in controlling the FDR and exhibits lower power compared to other methods when dealing with a limited number of exposures.
Simulation 2. In the second simulation, we evaluate the impact of latent confounding density on the performance of HILAMA and compare it with the two penalized methods developed for multivariate exposures and mediators, as mentioned earlier. The denseness of latent confounding is measured as the proportion  of zero entries in each row of matrices
of zero entries in each row of matrices 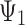 and
and 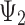 . If
. If  , then
, then 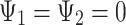 , amounting to no latent confounding; whereas if
, amounting to no latent confounding; whereas if  , all exposures and mediators are confounded by latent confounders, as depicted in simulation 1. Here, we vary only
, all exposures and mediators are confounded by latent confounders, as depicted in simulation 1. Here, we vary only 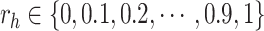 while holding
while holding 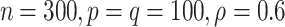 and
and 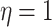 .
.
To compare our p-value based method with the penalized methods mvregmed and ZY, here we assume that the actual number of active pairs is known. We select the top  pairs that control the FDR at the level 0.1 and compare their power. If the FDR cannot be controlled at the 0.1 level, we choose the cut-off point associated with the lowest FDR and calculate the corresponding power.
pairs that control the FDR at the level 0.1 and compare their power. If the FDR cannot be controlled at the 0.1 level, we choose the cut-off point associated with the lowest FDR and calculate the corresponding power.
Figure 4A indicates that both HILAMA and ZY can manage the FDR at the 0.1 level even when some observed variables are confounded by latent confounders. Additionally, HILAMA exhibits the highest power compared to the other two methods across all confounding density setting, as shown in Fig. 4B. However, mvregmed does not effectively control the FDR in certain situations, and its power is relatively low. Furthermore, Fig. 4C demonstrates that HILAMA again has the minimum mean bias compared to the other two competing methods, mvregmed and ZY. Specifically, Fig. 4D shows that although the ZY method achieves good FDR control and power performance, it takes hundreds of times longer to compute than HILAMA, even in this low-dimensional setting.
Fig. 4.
Comparison results of different methods across varied confounding density 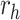 . A Empirical FDR, B Empirical Power, C Mean bias and D Computation time (minutes). All results are averaged over 100 replications. Fix
. A Empirical FDR, B Empirical Power, C Mean bias and D Computation time (minutes). All results are averaged over 100 replications. Fix 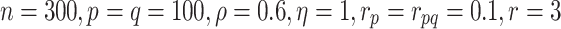 and
and 
Simulation 3. In the third simulation, our aim is to further investigate the impact of signal strength and hidden confounding density on HILAMA. Specifically, we examine the distribution of 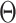 ,
, 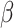 , and
, and  by allowing their non-zero components to follow
by allowing their non-zero components to follow  , where
, where 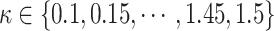 . Additionally, we consider different values for the confounding density
. Additionally, we consider different values for the confounding density 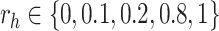 and the exposure dimension
and the exposure dimension  , while maintaining
, while maintaining 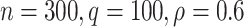 , and
, and 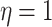 .
.
As depicted by Fig. S3 in Supplementary Information, when the confounding density is small (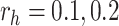 ), HILAMA fails to effectively control the FDR. Conversely, when the confounding density increases (
), HILAMA fails to effectively control the FDR. Conversely, when the confounding density increases ( ), it successfully controls the FDR across all signal strength levels. Notably, even in the absence of hidden confounding, HILAMA exhibits good FDR control. Moreover, as shown in the second column of Fig. S3, the power of HILAMA increases with the signal strength, approaching 1 for all levels of confounding density.
), it successfully controls the FDR across all signal strength levels. Notably, even in the absence of hidden confounding, HILAMA exhibits good FDR control. Moreover, as shown in the second column of Fig. S3, the power of HILAMA increases with the signal strength, approaching 1 for all levels of confounding density.
Data application
In this section, we apply HILAMA to a real multi-omics dataset collected by the ADNI. Before delving into the details, we emphasize that this data analysis should be viewed as at most exploratory rather than confirmatory nature. It is highly likely that the linearity assumption imposed in the Structural Equation Model may not be a good approximation of the reality.
Alzheimer’s disease (AD) is an irreversible and complex neurological disease that affects millions of individuals worldwide. Currently, approximately 6.7 million Americans aged 65 years and older live with AD, and this number is projected to dramatically increase to 13.8 million by the year 2060 [54]. AD is characterized by progressive memory loss and other cognitive impairments resulting from the accumulation of amyloid-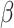 (A
(A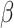 ) and tau proteins in the brain, leading to neurodegenerative symptoms [55]. Specifically, the model of AD pathophysiology outlines a chronological sequence of events in which the formation of A
) and tau proteins in the brain, leading to neurodegenerative symptoms [55]. Specifically, the model of AD pathophysiology outlines a chronological sequence of events in which the formation of A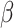 plaques is followed by the deposition of abnormal tau aggregates, subsequent neuronal dysfunction and neurodegeneration, including structural atrophy of cerebral regions such as the hippocampus. Ultimately, this sequence results in cognitive impairment and dementia [56–58]. This model of the temporal sequence of events has been continuously supported by new evidence [59–62].
plaques is followed by the deposition of abnormal tau aggregates, subsequent neuronal dysfunction and neurodegeneration, including structural atrophy of cerebral regions such as the hippocampus. Ultimately, this sequence results in cognitive impairment and dementia [56–58]. This model of the temporal sequence of events has been continuously supported by new evidence [59–62].
Unfortunately, there is currently no effective treatment for AD, underscoring the significance of early diagnosis and comprehending the disease’s pathogenesis. Therefore, it is crucial to develop effective interventions to prevent, slow down, or even cure this disease through biomedical research. With this in mind, the Alzheimer’s Disease Neuroimaging Initiative (ADNI, adni.loni.usc.edu) was established in 2003. Its primary goals are to develop biomarkers for AD, enhance the understanding of its pathophysiology, and improve early detection using various modalities such as magnetic resonance imaging (MRI), positron emission tomography (PET), functional magnetic resonance imaging (fMRI), as well as clinical and neuropsychological assessments.
Here, we utilize the HILAMA approach to examine the connection between proteins in the cerebrospinal fluid (CSF), whole-brain regions, and cognitive behavior. Our aim is to identify critical biological pathways associated with AD by utilizing data from the ADNI database. The CSF proteomics data is acquired using a highly specific and sensitive technique called targeted liquid chromatography multiple reaction monitoring mass spectrometry (LC/MS-MRM), resulting a list of 142 annotated proteins derived from 320 peptides. Additionally, the brain imaging data is obtained through anatomical magnetic resonance imaging (MRI), and volumetric measurements are extracted from 145 brain regions-of-interest (ROI) [63]. To assess the relationship between the aforementioned variables and cognitive function, we consider the composite memory score as the response. This score is measured using the ADNI neuropsychological battery, with higher scores indicating better cognitive function. In our model, we treat the 142 proteins as exposures (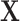 ), the 145 brain regions as mediators (
), the 145 brain regions as mediators ( ), and the memory score as the outcome (
), and the memory score as the outcome (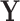 ). For this study, we focus on a total of 287 subjects who have both proteomics and imaging data available. These subjects consist of 86 cognitively normal individuals (CN), 135 patients with mild cognitive impairment (MCI), and 66 AD patients. To account for potential confounding effects, we include covariates such as age, years of education. For more detailed information on these baseline covariates, please refer to Table 1.
). For this study, we focus on a total of 287 subjects who have both proteomics and imaging data available. These subjects consist of 86 cognitively normal individuals (CN), 135 patients with mild cognitive impairment (MCI), and 66 AD patients. To account for potential confounding effects, we include covariates such as age, years of education. For more detailed information on these baseline covariates, please refer to Table 1.
Table 1.
Frequencies and descriptive statistics for demographic and clinical variables in the sample
| Disease status | CN | MCI | AD | Total |
|---|---|---|---|---|
| Number | 86 | 135 | 66 | 287 |
| Memory score | 0.76 ± 0.39 | −0.16 ± 0.43 | −0.79 ± 0.35 | −0.02 ± 0.7 |
| Age | 75.9 ± 5.54 | 74.8 ± 7.35 | 75.1 ± 7.57 | 75.22 ± 6.9 |
| Years of education | 15.6 ± 3.0 | 16 ± 2.96 | 15.1 ± 2.96 | 15.69 ± 2.97 |
Values except in the second line are expressed as mean ± standard deviation
CN Cognitively Normal individuals, MCI Mild Cognitive Impairment individuals, AD Alzheimer’s Disease individuals
Prior to conducting the mediation analysis, we impute some volumetric measures recorded as zero with the corresponding median value in the observed data, and then apply a log-transformation to make the corresponding distribution closer to normal. Subsequently, we standardize the baseline covariates data, protein data and MRI data to have a mean of zero and a standard deviation of one, while only centering the outcome cognitive score to have a mean of zero. In Supplementary Information, we visualize the singular values of the protein and MRI data, allowing us to assess the potential presence of latent confounders in the outcome model and mediator model. By examining Fig. S4., we observe the presence of three and two significantly larger singular values. This finding suggests a distinct spiked structure, indicating the possible presence of latent confounders as depicted in the model (2) and (3).
Following the preprocessing of data, we apply our method to the processed data. However, after implementing the BH procedure, no significant paths are obtained when controlling the FDR at a nominal level of 0.1. In order to obtain meaningful results, we relax the criterion and set the significance threshold for p-values to 0.05 without applying multiple correction. Consequently, we identify 30 significant causal paths, corresponding to 23 proteins and 5 brain regions. In Fig. 5, we visualize the significant causal paths. The estimated path effects, including the 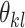 and
and 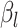 , are presented in the Supplementary Information.
, are presented in the Supplementary Information.
Fig. 5.
The significant causal paths using proteomics-radiomics data. Blue nodes represent the proteins as exposures, green nodes represent the brain regions as mediators and the red node represents the memory score as the outcome. Red lines indicate positive estimates while green lines represent negative estimates. Line thickness corresponds to the effect size. Blue nodes are arranged in two rows for visual clarity and positioning carries no extra information
Our study has identified several brain regions associated with cognitive impairment and AD. Among them, R48 (left hippocampus) plays a crucial role in learning and memory, and is particularly vulnerable to early-stage damage in AD [64]. Importantly, hippocampal atrophy has been universally recognized and validated as the most reliable biomarker for AD [65]. Another crucial region in cognition is R106 (right angular gyrus), which is associated with language, spatial, and memory functions [66, 67]. The aging process leads to structural atrophy in the angular gyrus, which is linked to subjective and mild cognitive impairments, as well as dementia [68, 69]. Additionally, another significant region R142 (right middle frontal gyrus), exhibits a positive correlation between enhanced connectivity within this area and the cognitive decline observed in individuals with mild AD symptoms [70]. Furthermore, heightened connectivity within the middle frontal gyrus may alleviate the consequences of reduced connectivity in other regions of the cognitive control network among AD patients [71]. Furthermore, R205 (left triangular part of the inferior frontal gyrus) and R180 (right planum polare) are also associated with AD and cognitive impairment. However, further investigation is necessary to comprehensively elucidate the roles of these regions in AD pathology and cognitive function.
Several proteins have been identified as potentially critical biomarkers for AD. NPTX2 (Neuronal pentraxin-2) and NPTXR (Neuronal pentraxin receptor) are proteins that bind to glutamate receptors, contributing to synaptic plasticity. Reductions in NPTX2 have been linked to disruptions of the pyramidal neuron-PV interneuron circuit in an AD mouse model [72]. SE6L1 (Seizure 6-like protein) is a potential neuronal substrate of the AD protease BACE1, which is a major drug target in AD [73]. Aberrant function of SE6L1 may lead to movement disorders and neuropsychiatric diseases [74]. Overexpression of the neuropeptide precursor VGF has been found to partially rescue A mediated memory impairment and neuropathology in a mouse model, indicating a protective function against the development and progression of AD [75]. CERU (Ceruloplasmin), a ferrous oxidase enzyme, plays an important role in regulating iron metabolism and redox reactions. Experiments using AD mouse models have shown that ceruloplasmin depletion exacerbates memory impairment, promotes iron accumulation, and restoration of its expression alleviates A
mediated memory impairment and neuropathology in a mouse model, indicating a protective function against the development and progression of AD [75]. CERU (Ceruloplasmin), a ferrous oxidase enzyme, plays an important role in regulating iron metabolism and redox reactions. Experiments using AD mouse models have shown that ceruloplasmin depletion exacerbates memory impairment, promotes iron accumulation, and restoration of its expression alleviates A -induced neuronal damage in the hippocampus [76]. CH3L1 (Chitinase-3-like protein 1) is a biomarker for its ability to detect neuroinflammation and diagnose AD. Elevated levels of CHI3L1 in the CSF can be detected in the early stages of AD, even before the onset of cognitive symptoms [77]. SCG3 (Secretogranin-3), is a member of the granin family involved in neurotransmitter storage and secretion. In vitro studies have highlighted the critical involvement of SCG3 in neuroendocrine regulation, neuronal communication, and neurotransmitter release [78]. NEO1 (Neogenin) is a transmembrane receptor involved in adult neurogenesis. Experimental studies have demonstrated the essential role of neogenin in promoting neurogenesis in the adult hippocampus and preventing depressive-like behavior [79]. APOB (Apolipoprotein B-100) is a recognized risk factor for AD that potentially impact both brain aging and cognitive function. Experimental studies using APOB-100 transgenic mice models have demonstrated that excessive expression of APOB results in memory decline [80]. Moreover, a Mendelian randomization analysis has provide initial evidence suggesting that APOB contributes to an increased risk of developing Alzheimer’s disease [81]. CATA (Catalase) plays a significant role in the intracellular interactions between catalase and amyloid in A
-induced neuronal damage in the hippocampus [76]. CH3L1 (Chitinase-3-like protein 1) is a biomarker for its ability to detect neuroinflammation and diagnose AD. Elevated levels of CHI3L1 in the CSF can be detected in the early stages of AD, even before the onset of cognitive symptoms [77]. SCG3 (Secretogranin-3), is a member of the granin family involved in neurotransmitter storage and secretion. In vitro studies have highlighted the critical involvement of SCG3 in neuroendocrine regulation, neuronal communication, and neurotransmitter release [78]. NEO1 (Neogenin) is a transmembrane receptor involved in adult neurogenesis. Experimental studies have demonstrated the essential role of neogenin in promoting neurogenesis in the adult hippocampus and preventing depressive-like behavior [79]. APOB (Apolipoprotein B-100) is a recognized risk factor for AD that potentially impact both brain aging and cognitive function. Experimental studies using APOB-100 transgenic mice models have demonstrated that excessive expression of APOB results in memory decline [80]. Moreover, a Mendelian randomization analysis has provide initial evidence suggesting that APOB contributes to an increased risk of developing Alzheimer’s disease [81]. CATA (Catalase) plays a significant role in the intracellular interactions between catalase and amyloid in A -induced oxidative stress. This interaction leads to the accumulation of hydrogen peroxide and the onset of oxidative stress conditions in the hippocampus, thereby contributing to the pathogenesis of Alzheimer’s disease [82]. PRDX3 functions as a crucial mitochondrial antioxidant defense enzyme, and its overexpression provides protection against cognitive impairment while reducing the accumulation of A
-induced oxidative stress. This interaction leads to the accumulation of hydrogen peroxide and the onset of oxidative stress conditions in the hippocampus, thereby contributing to the pathogenesis of Alzheimer’s disease [82]. PRDX3 functions as a crucial mitochondrial antioxidant defense enzyme, and its overexpression provides protection against cognitive impairment while reducing the accumulation of A in transgenic mice [83]. Furthermore, its overexpression reduces mitochondrial oxidative stress, attenuates memory impairment induced by hydrogen peroxide and improves cognitive ability in transgenic mice [84]. Recent research has also highlighted the important roles of PRDX3 in neurite outgrowth and the development of AD [85].
in transgenic mice [83]. Furthermore, its overexpression reduces mitochondrial oxidative stress, attenuates memory impairment induced by hydrogen peroxide and improves cognitive ability in transgenic mice [84]. Recent research has also highlighted the important roles of PRDX3 in neurite outgrowth and the development of AD [85].
As suggested by one reviewer, interaction terms between exposures and mediators are common in mediation analysis. To investigate the possibility of these interaction terms, we applied the recently developed model XMInt [86], which focuses on a single exposure and high-dimensional mediators by employing a sequential regularization-based forward selection approach. We selected one protein at a time as the exposure while utilizing the 145 brain regions as mediators. In our analysis, two proteins were identified across four pathways: NPTXR and CERU. We conducted separate analyses for these two proteins to identify potential interaction terms using the XMInt package with the default parameter setting. When NPTXR was used as the exposure, we identified two brain regions, R123 (Left Fusiform Gyrus) and R144 (Right Middle Occipital Gyrus), as mediators, both of which exhibited interactions with the exposure. In contrast, when CERU was used as the exposure, no mediators or interaction terms were identified.
In summary, our study identified several critical brain regions, such as R48, R106 and R142, that are associated with learning, memory, and recognition. Moreover, we have identified several potential biomarkers for AD, such as NPTX2, NPTXR, SE6L1, CERU, VGF, CH3L1, NEO1, SCG3, PRDX3 etc., most of which are not selected by the method ZY [42]. Nonetheless, it is crucial to note that these findings are only suggestive and further experimental validation is warranted to fully understand their contributions to AD pathology and cognitive function.
Discussion
In this paper, we propose HILAMA, a new method for high-dimensional mediation analysis, an important statistical task in the analysis of multi-omics datasets increasingly available in biomedical sciences. HILAMA effectively unravels the causal pathway between high-dimensional exposures and a continuous outcome, in the presence of possibly latent/unmeasured confounders. We validate the practical performance of HILAMA through extensive simulations and by applying it to a real ADNI dataset, which allows for the identification of potential biomarkers for Alzheimer’s disease.
HILAMA features several key advantages over previous methods, designed towards better fitting into real-world multi-omics datasets. First, it is the first method to consider both high-dimensional exposures and high-dimensional mediators in the presence of latent confounders without transforming exposures/mediators into principal components, rendering the analysis results more interpretable. Second, it incorporates a new Decorrelating & Debiasing method [48] to handle latent/unmeasured confounding and improve coefficient estimation, leading to better FDR control. Third, it employs a MinScreen screening procedure [50] to reduce the number of hypotheses being tested, thereby enhancing the statistical power of the tests. Finally, the method is computationally efficient and has implemented parallel computing techniques to handle the ever-increasing size and dimension of modern multi-omics datasets.
To conclude, we point out several venues for future research. First, HILAMA assumes linear models, which is standard practice in multi-omics studies. However, it will be interesting to generalize it to nonlinear/nonparametric models via nonlinear factor analysis [87], autoencoders [88], kernel methods or deep neural networks [89]. Second, HILAMA assumes that the effects of latent/unmeasured confounders on observables are dense. It may be possible to relax this assumption by extending the randomized data-augmentation scheme for total effect to the mediation analysis setting [34]. Third, interaction terms between exposures and mediators are common in mediation analysis, particularly considering multiple exposures and mediators. Incorporating these interaction terms could provide a more nuanced understanding of the relationships involved and enhance the ability of the model to capture certain nonlinear phenomenon. Finally, other methods of dealing with latent confounding can also be incorporated into HILAMA in its future version, such as the approaches [90] that directly leverage the majority rule [91] or the plurality rule [92, 93]. Overall, these future research directions have the potential to expand the capabilities of HILAMA, allowing for more accurate and robust causal inference in multi-omics studies.
Conclusion
The proposed HILAMA method integrates the Decorrelating & Debiasing method and the MinScreen screening procedure, thereby further highlighting its superiority over existing methods, particularly in terms of FDR control and statistical power. It introduces a novel approach for elucidating the causal pathway between high-dimensional exposures and a continuous outcome in the presence of latent/unmeasured confounders, thereby enhancing interpretability, a critical aspect in biomedical research.
Supplementary Information
Supplementary Material 1. Derivations of direct and indirect effects under Latent Structural Equation Modeling. The empirical FDR, power and mean bias for different methods across 72 scenarios in simulation 1 are shown in Fig. S1. Comparison results of empirical FDR and power of different methods under scenarios including single-exposure and those without hidden confounders are shown in Fig. S2. Empirical FDR and power of HILAMA with varied signal strength  , confounding density
, confounding density  and exposure dimension p in simulation 3 are shown in Fig. S3. Singular values of standardized exposure and mediator data after projection are shown in Fig. S4. The summary statistics of the significant paths are shown in Table S1.
and exposure dimension p in simulation 3 are shown in Fig. S3. Singular values of standardized exposure and mediator data after projection are shown in Fig. S4. The summary statistics of the significant paths are shown in Table S1.
Acknowledgements
The authors would like to thank Dr. Yi Zhao at Indiana University School of Medicine for her valuable suggestions on accessing the ADNI data and three anonymous reviewers for helpful comments.
Data used in preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. A complete listing of ADNI investigators can be found at: http://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf.
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
Abbreviations
- ADNI
Alzheimer’s Disease Neuroimaging Initiative
- JST
Joint Significance Test
- FDR
False Discovery Rate
- LSEM
Latent Structural Equation Modeling
- HILAMA
HIgh-dimensional LAtent-confounding Mediation Analysis
- BH
Benjamini-Hochberg
- BK
Baron & Kenny method
- HIMA
High-dimensional Mediation Analysis
- HDMA
High-dimensional De-biased Mediation Analysis
- SIS
Sure Independence Screening
- CSF
Cerebrospinal Fluid
- CN
Cognitively Normal individuals
- MCI
Mild Cognitive Impairment
- AD
Alzheimer’s Disease
Authors’ contributions
X.W., H.L., and L.L. led the conceptualization of the project. Data curation, formal analysis, software development, and visualization were carried out by X.W. The investigation was conducted by X.W. in collaboration with L.L. Funding acquisition, project administration, resources, and supervision were managed jointly by H.L. and L.L. Methodological approaches were devised by X.W., J.Y.L., H.L., and L.L. The original draft preparation involved X.W., H.L., and L.L. Comprehensive review and editing of the manuscript were contributed to by X.W., J.Y.L., S.S.H., Z.L., H.L., and L.L.
Funding
This work was partially supported by the National Science Foundations of China Grants No.12471274 (L.L., X.W.) and No.12090024 (L.L.), the Neil Shen’s SJTU Medical Research Fund (X.W., L.L., H.L.), and the Science and Technology Commission of Shanghai Municipality (STCSM) Grants No.23JS1400700, No.24JS2840200 and No.25JS2850100. The funding bodies played no role in the design of the study and collection, analysis, and interpretation of data and in writing the manuscript.
Data availability
An R package implementing our new method HILAMA is publicly available at https://github.com/Cinbo-Wang/HILAMA. Instructions for generating our simulated data can be found at https://github.com/Cinbo-Wang/Simu_HILAMA, which includes the main R-scripts used to generate the simulation data. The ADNI data were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu) after applying for access and obtaining approval from the ADNI DPC. For more details, see https://ida.loni.usc.edu/explore/jsp/support/support.jsp.
Declarations
Ethics approval and consent to participate
Not applicable
Consent for publication
Not applicable
Competing interests
The authors declare no competing interests.
Footnotes
A complete listing of ADNI investigators can be found in the Acknowledgments.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Xinbo Wang and Junyuan Liu contributed equally to this work.
Contributor Information
Xinbo Wang, Email: cinbo_w@sjtu.edu.cn.
Hui Lu, Email: huilu@sjtu.edu.cn.
Lin Liu, Email: linliu@sjtu.edu.cn.
References
- 1.Subramanian I, Verma S, Kumar S, Jere A, Anamika K. Multi-omics data integration, interpretation, and its application. Bioinform Biol Insights. 2020;14:1177932219899051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kreitmaier P, Katsoula G, Zeggini E. Insights from multi-omics integration in complex disease primary tissues. Trends Genet. 2023;39(1):46–58. [DOI] [PubMed] [Google Scholar]
- 3.Bao J, Chang C, Zhang Q, Saykin AJ, Shen L, Long Q, et al. Integrative analysis of multi-omics and imaging data with incorporation of biological information via structural Bayesian factor analysis. Brief Bioinform. 2023;24(2):bbad073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tanay A, Regev A. Scaling single-cell genomics from phenomenology to mechanism. Nature. 2017;541(7637):331–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lv BM, Quan Y, Zhang HY. Causal inference in microbiome medicine: principles and applications. Trends Microbiol. 2021;29(8):736–46. [DOI] [PubMed] [Google Scholar]
- 6.Corander J, Hanage WP, Pensar J. Causal discovery for the microbiome. Lancet Microbe. 2022;3(11):e881–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.VanderWeele T. Explanation in causal inference: methods for mediation and interaction. Oxford: Oxford University Press; 2015.
- 8.Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J Pers Soc Psychol. 1986;51(6):1173–82. [DOI] [PubMed] [Google Scholar]
- 9.Tobi EW, Slieker RC, Luijk R, Dekkers KF, Stein AD, Xu KM, et al. DNA methylation as a mediator of the association between prenatal adversity and risk factors for metabolic disease in adulthood. Sci Adv. 2018;4(1):eaao4364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu Z, Shen J, Barfield R, Schwartz J, Baccarelli AA, Lin X. Large-scale hypothesis testing for causal mediation effects with applications in genome-wide epigenetic studies. J Am Stat Assoc. 2022;117(537):67–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Clark-Boucher D, Zhou X, Du J, Liu Y, Needham BL, Smith JA, et al. Methods for mediation analysis with high-dimensional DNA methylation data: possible choices and comparisons. PLoS Genet. 2023;19(11):e1011022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yang H, Liu Z, Wang R, Lai EY, Schwartz J, Baccarelli AA, et al. Causal mediation analysis for integrating exposure, genomic, and phenotype data. Annu Rev Stat Appl. 2025;12(1):337–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen M, Nguyen TT, Liu J. High-dimensional confounding in causal mediation: a comparison study of double machine learning and regularized partial correlation network. J Data Sci. 2025;23(3):521–41. [Google Scholar]
- 14.Wright S. The method of path coefficients. Ann Math Stat. 1934;5(3):161–215. [Google Scholar]
- 15.Robins JM, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology. 1992;3(2):143–55. [DOI] [PubMed] [Google Scholar]
- 16.Pearl J. Direct and indirect effects. In: Breese J, Koller D, editors. Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence. San Francisco: Morgan Kaufmann Publishers; 2001. p. 411–20.
- 17.VanderWeele T, Vansteelandt S. Mediation analysis with multiple mediators. Epidemiol Methods. 2014;2(1):95–115. 10.1515/em-2012-0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lindquist MA. Functional causal mediation analysis with an application to brain connectivity. J Am Stat Assoc. 2012;107(500):1297–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychol Methods. 2002;7(1):83–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sobel ME. Identification of causal parameters in randomized studies with mediating variables. J Educ Behav Stat. 2008;33(2):230–51. [Google Scholar]
- 21.MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence limits for the indirect effect: program prodclin. Behav Res Methods. 2007;39(3):384–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Barfield R, Shen J, Just AC, Vokonas PS, Schwartz J, Baccarelli AA, et al. Testing for the indirect effect under the null for genome-wide mediation analyses. Genet Epidemiol. 2017;41(8):824–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huang YT. Genome-wide analyses of sparse mediation effects under composite null hypotheses. Ann Appl Stat. 2019;13(1):60–84. 10.1214/18-AOAS1181. [Google Scholar]
- 24.Zeng P, Shao Z, Zhou X. Statistical methods for mediation analysis in the era of high-throughput genomics: current successes and future challenges. Comput Struct Biotechnol J. 2021;19:3209–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang H, Hou L, Liu L. In: Guan W, editor. A Review of High-Dimensional Mediation Analyses in DNA Methylation Studies. New York: Springer US; 2022. pp. 123–35. 10.1007/978-1-0716-1994-0_10. [DOI] [PMC free article] [PubMed]
- 26.Zhang H, Zheng Y, Zhang Z, Gao T, Joyce B, Yoon G, et al. Estimating and testing high-dimensional mediation effects in epigenetic studies. Bioinformatics. 2016;32(20):3150–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gao Y, Yang H, Fang R, Zhang Y, Goode EL, Cui Y. Testing mediation effects in high-dimensional epigenetic studies. Front Genet. 2019;10:1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Perera C, Zhang H, Zheng Y, Hou L, Qu A, Zheng C, et al. Hima2: high-dimensional mediation analysis and its application in epigenome-wide DNA methylation data. BMC Bioinformatics. 2022;23(1):296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hu W, Chen S, Cai J, Yang Y, Yan H, Chen F. High-dimensional mediation analysis for continuous outcome with confounders using overlap weighting method in observational epigenetic study. BMC Med Res Methodol. 2024;24(1):125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lee H, Chen C, Kochunov P, Hong LE, Chen S. A new multiple-mediator model maximally uncovering the mediation pathway: evaluating the role of neuroimaging measures in age-related cognitive decline. Ann Appl Stat. 2024;18(4):2775–95. [Google Scholar]
- 31.Derkach A, Pfeiffer RM, Chen TH, Sampson JN. High dimensional mediation analysis with latent variables. Biometrics. 2019;75(3):745–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Luo C, Fa B, Yan Y, Wang Y, Zhou Y, Zhang Y, et al. High-dimensional mediation analysis in survival models. PLoS Comput Biol. 2020;16(4):1–15. 10.1371/journal.pcbi.1007768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhang H, Zheng Y, Hou L, Zheng C, Liu L. Mediation analysis for survival data with high-dimensional mediators. Bioinformatics. 2021;37(21):3815–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tian P, Yao M, Huang T, Liu Z. Coxmkf: a knockoff filter for high-dimensional mediation analysis with a survival outcome in epigenetic studies. Bioinformatics. 2022;38(23):5229–35. [DOI] [PubMed] [Google Scholar]
- 35.Zhang J, Wei Z, Chen J. A distance-based approach for testing the mediation effect of the human microbiome. Bioinformatics. 2018;34(11):1875–83. [DOI] [PubMed] [Google Scholar]
- 36.Zhang H, Chen J, Feng Y, Wang C, Li H, Liu L. Mediation effect selection in high-dimensional and compositional microbiome data. Stat Med. 2021;40(4):885–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhang H, Chen J, Li Z, Liu L. Testing for mediation effect with application to human microbiome data. Stat Biosci. 2021;13:313–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wang C, Hu J, Blaser MJ, Li H. Estimating and testing the microbial causal mediation effect with high-dimensional and compositional microbiome data. Bioinformatics. 2020;36(2):347–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Shao Z, Wang T, Zhang M, Jiang Z, Huang S, Zeng P. Iusmmt: survival mediation analysis of gene expression with multiple DNA methylation exposures and its application to cancers of tcga. PLoS Comput Biol. 2021;17(8):1–29. 10.1371/journal.pcbi.1009250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhao Z, Chen C, Adhikari BM, Hong LE, Kochunov P, Chen S. Mediation analysis for high-dimensional mediators and outcomes with an application to multimodal imaging data. Comput Stat Data Anal. 2023;185:107765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhang Q. High-dimensional mediation analysis with applications to causal gene identification. Stat Biosci. 2022;14(3):432–51. [Google Scholar]
- 42.Zhao Y, Li L, Initiative ADN. Multimodal data integration via mediation analysis with high-dimensional exposures and mediators. Hum Brain Mapp. 2022;43(8):2519–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yang F, Wang J, Pierce BL, Chen LS, Aguet F, Ardlie KG, et al. Identifying cis-mediators for trans-eqtls across many human tissues using genomic mediation analysis. Genome Res. 2017;27(11):1859–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chernozhukov V, Hansen C, Liao Y. A lava attack on the recovery of sums of dense and sparse signals. Ann Stat. 2017;45(1):39–76. 10.1214/16-AOS1434. [Google Scholar]
- 45.Ćevid D, Bühlmann P, Meinshausen N. Spectral deconfounding via perturbed sparse linear models. J Mach Learn Res. 2020;21(1):9442–82. [Google Scholar]
- 46.Guo Z, Ćevid D, Bühlmann P. Doubly debiased lasso: high-dimensional inference under hidden confounding. Ann Stat. 2022;50(3):1320–47. 10.1214/21-AOS2152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bing X, Ning Y, Xu Y. Adaptive estimation in multivariate response regression with hidden variables. Ann Stat. 2022;50(2):640–72. 10.1214/21-AOS2059. [Google Scholar]
- 48.Sun Y, Ma L, Xia Y. A decorrelating and debiasing approach to simultaneous inference for high-dimensional confounded models. J Am Stat Assoc. 2024;119(548):2857–68. [Google Scholar]
- 49.Schaid DJ, Dikilitas O, Sinnwell JP, Kullo IJ. Penalized mediation models for multivariate data. Genet Epidemiol. 2022;46(1):32–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Djordjilović V, Page CM, Gran JM, Nøst TH, Sandanger TM, Veierød MB, et al. Global test for high-dimensional mediation: testing groups of potential mediators. Stat Med. 2019;38(18):3346–60. [DOI] [PubMed] [Google Scholar]
- 51.Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Ser B Stat Methodol. 1995;57(1):289–300. [Google Scholar]
- 52.Wang J, Zhao Q, Hastie T, Owen AB. Confounder adjustment in multiple hypothesis testing. Ann Stat. 2017;45(5):1863–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zhang CH, Zhang SS. Confidence intervals for low dimensional parameters in high dimensional linear models. J R Stat Soc Ser B Stat Methodol. 2014;76(1):217–42. [Google Scholar]
- 54.2023 Alzheimer’s disease facts and figures. Alzheimers Dement. 2023;19(4):1598–1695. [DOI] [PubMed]
- 55.Chen M, Xia W. Proteomic profiling of plasma and brain tissue from alzheimer’s disease patients reveals candidate network of plasma biomarkers. J Alzheimers Dis. 2020;76(1):349–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jack CR, Knopman DS, Jagust WJ, Shaw LM, Aisen PS, Weiner MW, et al. Hypothetical model of dynamic biomarkers of the alzheimer’s pathological cascade. Lancet Neurol. 2010;9(1):119–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jack CR, Knopman DS, Jagust WJ, Petersen RC, Weiner MW, Aisen PS, et al. Tracking pathophysiological processes in alzheimer’s disease: an updated hypothetical model of dynamic biomarkers. Lancet Neurol. 2013;12(2):207–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Jack CR Jr, Bennett DA, Blennow K, Carrillo MC, Dunn B, Haeberlein SB, et al. Nia-aa research framework: toward a biological definition of alzheimer’s disease. Alzheimers Dement. 2018;14(4):535–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
59.Mormino E, Kluth J, Madison C, Rabinovici G, Baker S, Miller B, et al. Episodic memory loss is related to hippocampal-mediated
 -amyloid deposition in elderly subjects. Brain. 2009;132(5):1310–23. [DOI] [PMC free article] [PubMed]
-amyloid deposition in elderly subjects. Brain. 2009;132(5):1310–23. [DOI] [PMC free article] [PubMed] - 60.Jack CR, Wiste HJ, Therneau TM, Weigand SD, Knopman DS, Mielke MM, et al. Associations of amyloid, tau, and neurodegeneration biomarker profiles with rates of memory decline among individuals without dementia. JAMA. 2019;321(23):2316–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Guo T, Korman D, Baker SL, Landau SM, Jagust WJ, Initiative ADN, et al. Longitudinal cognitive and biomarker measurements support a unidirectional pathway in alzheimer’s disease pathophysiology. Biol Psychiatry. 2021;89(8):786–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Zhang W, Wang HF, Kuo K, Wang L, Li Y, Yu J, et al. Contribution of alzheimer’s disease pathology to biological and clinical progression: a longitudinal study across two cohorts. Alzheimers Dement. 2023;19(8):3602–12. [DOI] [PubMed] [Google Scholar]
- 63.Doshi J, Erus G, Ou Y, Resnick SM, Gur RC, Gur RE, et al. Muse: multi-atlas region segmentation utilizing ensembles of registration algorithms and parameters, and locally optimal atlas selection. Neuroimage. 2016;127:186–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Nadel L, Hardt O. Update on memory systems and processes. Neuropsychopharmacology. 2011;36(1):251–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Schröder J, Pantel J. Neuroimaging of hippocampal atrophy in early recognition of alzheimer’s disease – a critical appraisal after two decades of research. Psychiatry Res Neuroimaging. 2016;247:71–8. 10.1016/j.pscychresns.2015.08.014. [DOI] [PubMed] [Google Scholar]
- 66.Seghier ML. The angular gyrus: multiple functions and multiple subdivisions. Neuroscientist. 2013;19(1):43–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Humphreys GF, Ralph MAL, Simons JS. A unifying account of angular gyrus contributions to episodic and semantic cognition. Trends Neurosci. 2021;44(6):452–63. [DOI] [PubMed] [Google Scholar]
- 68.Karas G, Sluimer J, Goekoop R, Van Der Flier W, Rombouts S, Vrenken H, et al. Amnestic mild cognitive impairment: structural mr imaging findings predictive of conversion to alzheimer disease. Am J Neuroradiol. 2008;29(5):944–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Jockwitz C, Krämer C, Stumme J, Dellani P, Moebus S, Bittner N, et al. Characterization of the angular gyrus in an older adult population: a multimodal multilevel approach. Brain Struct Funct. 2023;228(1):83–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Sendi MS, Zendehrouh E, Fu Z, Liu J, Du Y, Mormino E, et al. Disrupted dynamic functional network connectivity among cognitive control networks in the progression of alzheimer’s disease. Brain Connect. 2023;13(6):334–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Gaubert S, Raimondo F, Houot M, Corsi MC, Naccache L, Diego Sitt J, et al. Eeg evidence of compensatory mechanisms in preclinical alzheimer’s disease. Brain. 2019;142(7):2096–112. [DOI] [PubMed] [Google Scholar]
- 72.Xiao MF, Xu D, Craig MT, Pelkey KA, Chien CC, Shi Y, et al. NPTX2 and cognitive dysfunction in Alzheimer’s Disease. Elife. 2017;6:e23798. 10.7554/eLife.23798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Pigoni M, Wanngren J, Kuhn PH, Munro KM, Gunnersen JM, Takeshima H, et al. Seizure protein 6 and its homolog seizure 6-like protein are physiological substrates of bace1 in neurons. Mol Neurodegener. 2016;11(1):67. 10.1186/s13024-016-0134-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
74.Ong-Pålsson E, Njavro JR, Wilson Y, Pigoni M, Schmidt A, Müller SA, et al. The
 -secretase substrate seizure 6–like protein (sez6l) controls motor functions in mice. Mol Neurobiol. 2022;59(2):1183–98. 10.1007/s12035-021-02660-y. [DOI] [PMC free article] [PubMed]
-secretase substrate seizure 6–like protein (sez6l) controls motor functions in mice. Mol Neurobiol. 2022;59(2):1183–98. 10.1007/s12035-021-02660-y. [DOI] [PMC free article] [PubMed] - 75.Beckmann ND, Lin WJ, Wang M, Cohain AT, Charney AW, Wang P, et al. Multiscale causal networks identify VGF as a key regulator of Alzheimer’s disease. Nat Commun. 2020;11(1):3942. 10.1038/s41467-020-17405-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Zhao YS, Zhang LH, Yu PP, Gou YJ, Zhao J, You LH, et al. Ceruloplasmin, a potential therapeutic agent for alzheimer’s disease. Antioxid Redox Signal. 2018;28(14):1323–37. [DOI] [PubMed] [Google Scholar]
- 77.Connolly K, Lehoux M, O’Rourke R, Assetta B, Erdemir GA, Elias JA, et al. Potential role of chitinase-3-like protein 1 (chi3l1/ykl-40) in neurodegeneration and alzheimer’s disease. Alzheimers Dement. 2023;19(1):9–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Li F, Tian X, Zhou Y, Zhu L, Wang B, Ding M, et al. Dysregulated expression of secretogranin iii is involved in neurotoxin-induced dopaminergic neuron apoptosis. J Neurosci Res. 2012;90(12):2237–46. [DOI] [PubMed] [Google Scholar]
- 79.Sun D, Sun XD, Zhao L, Lee DH, Hu JX, Tang FL, et al. Neogenin, a regulator of adult hippocampal neurogenesis, prevents depressive-like behavior. Cell Death Dis. 2018;9(1):8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Löffler T, Flunkert S, Havas D, Sántha M, Hutter-Paier B, Steyrer E, et al. Impact of apob-100 expression on cognition and brain pathology in wild-type and happsl mice. Neurobiol Aging. 2013;34(10):2379–88. [DOI] [PubMed] [Google Scholar]
- 81.Martin L, Boutwell BB, Messerlian C, Adams CD. Mendelian randomization reveals apolipoprotein b shortens healthspan and possibly increases risk for alzheimer’s disease. Commun Biol. 2024;7(1):230. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
82.Habib LK, Lee MT, Yang J. Inhibitors of catalase-amyloid interactions protect cells from
 -amyloid-induced oxidative stress and toxicity. J Biol Chem. 2010;285(50):38933–43. [DOI] [PMC free article] [PubMed]
-amyloid-induced oxidative stress and toxicity. J Biol Chem. 2010;285(50):38933–43. [DOI] [PMC free article] [PubMed] -
83.Chen L, Yoo SE, Na R, Liu Y, Ran Q. Cognitive impairment and increased A
 levels induced by paraquat exposure are attenuated by enhanced removal of mitochondrial h2o2. Neurobiol Aging. 2012;33(2):432.e15-432.e26. [DOI] [PubMed]
levels induced by paraquat exposure are attenuated by enhanced removal of mitochondrial h2o2. Neurobiol Aging. 2012;33(2):432.e15-432.e26. [DOI] [PubMed] - 84.Chen L, Na R, Ran Q. Enhanced defense against mitochondrial hydrogen peroxide attenuates age-associated cognition decline. Neurobiol Aging. 2014;35(11):2552–61. [DOI] [PubMed] [Google Scholar]
- 85.Xu B, Gao C, Zhang H, Huang X, Yang X, Yang C, et al. A quantitative proteomic analysis reveals the potential roles of prdx3 in neurite outgrowth in n2a-appswe cells. Biochem Biophys Res Commun. 2022;604:144–50. [DOI] [PubMed] [Google Scholar]
- 86.Li R, Zhu X, Lee S, Initiative ADN. Model selection for exposure-mediator interaction. Data Sci Sci. 2024;3(1):2360892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Amemiya Y, Yalcin I. Nonlinear factor analysis as a statistical method. Stat Sci. 2001;16(3):275–94. [Google Scholar]
- 88.Yang KD, Belyaeva A, Venkatachalapathy S, Damodaran K, Katcoff A, Radhakrishnan A, et al. Multi-domain translation between single-cell imaging and sequencing data using autoencoders. Nat Commun. 2021;12(1):31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Xu S, Liu L, Liu Z. DeepMed: Semiparametric causal mediation analysis with debiased deep learning. Adv Neural Inf Process Syst. 2022;35:28238–51.
- 90.Miao W, Hu W, Ogburn EL, Zhou XH. Identifying effects of multiple treatments in the presence of unmeasured confounding. J Am Stat Assoc. 2023;118(543):1953–67. [Google Scholar]
- 91.Kang H, Zhang A, Cai TT, Small DS. Instrumental variables estimation with some invalid instruments and its application to mendelian randomization. J Am Stat Assoc. 2016;111(513):132–44. [Google Scholar]
- 92.Guo Z, Kang H, Tony Cai T, Small DS. Confidence intervals for causal effects with invalid instruments by using two-stage hard thresholding with voting. J R Stat Soc Ser B Stat Methodol. 2018;80(4):793–815. [Google Scholar]
- 93.Tang D, Kong D, Wang L. The synthetic instrument: From sparse association to sparse causation. 2023. Preprint at https://arxiv.org/abs/2304.01098.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material 1. Derivations of direct and indirect effects under Latent Structural Equation Modeling. The empirical FDR, power and mean bias for different methods across 72 scenarios in simulation 1 are shown in Fig. S1. Comparison results of empirical FDR and power of different methods under scenarios including single-exposure and those without hidden confounders are shown in Fig. S2. Empirical FDR and power of HILAMA with varied signal strength  , confounding density
, confounding density  and exposure dimension p in simulation 3 are shown in Fig. S3. Singular values of standardized exposure and mediator data after projection are shown in Fig. S4. The summary statistics of the significant paths are shown in Table S1.
and exposure dimension p in simulation 3 are shown in Fig. S3. Singular values of standardized exposure and mediator data after projection are shown in Fig. S4. The summary statistics of the significant paths are shown in Table S1.
Data Availability Statement
An R package implementing our new method HILAMA is publicly available at https://github.com/Cinbo-Wang/HILAMA. Instructions for generating our simulated data can be found at https://github.com/Cinbo-Wang/Simu_HILAMA, which includes the main R-scripts used to generate the simulation data. The ADNI data were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu) after applying for access and obtaining approval from the ADNI DPC. For more details, see https://ida.loni.usc.edu/explore/jsp/support/support.jsp.