Conformational dependence of a protein kinase phosphate transfer reaction

Abstract

Atomic motions and energetics for a phosphate transfer reaction catalyzed by the cAMP-dependent protein kinase are calculated by plane-wave density functional theory, starting from structures of proteins crystallized in both the reactant conformation (RC) and the transition-state conformation (TC). In TC, we calculate that the reactants and products are nearly isoenergetic with a 20-kJ/mol barrier, whereas phosphate transfer is unfavorable by 120 kJ/mol in the RC, with an even higher barrier. With the protein in TC, the motions involved in reaction are small, with only P_γ and the catalytic proton moving >0.5 Å. Examination of the structures reveals that in the RC the active site cleft is not completely closed and there is insufficient space for the phosphorylated serine residue in the product state. Together, these observations imply that the phosphate transfer reaction occurs rapidly and reversibly in a particular conformation of the protein, and that the reaction can be gated by changes of a few tenths of an angstrom in the catalytic site.

Protein kinases regulate many biological processes by transferring a phosphate group from adenosine triphosphate (ATP) to the side chains of particular serine, threonine, or tyrosine residues. The bulky, charged phosphate group alters the conformation and function of the target protein (1, 2). Different kinases recognize different primary sequence motifs surrounding the residue to be phosphorylated, in a highly regulated fashion (3–6). Structural studies have revealed several conformational changes, such as closing of the active-site cleft, the packing of the activation loop, and rotation of the C-helix, which are often implicated in controlling the activity of protein kinases (2). The reasons for such control are clear, but no answer has been provided to such questions as these: “How closed is closed?” or “Is this particular conformation of the activation loop `good enough' for phosphorylation to occur?” Quantum chemistry is required to objectively answer these questions.

The extent of conformational heterogeneity in a covalent protein reaction was first quantified in a series of experiments monitoring the temperature-dependent rebinding of CO to myoglobin after flash photolysis (7). Agmon and Hopfield created a concise phenomenological model describing this situation, using transition-state theory to describe the vibrational reaction, and a diffusive coordinate that describes the protein conformation and modulates the reaction barrier to the vibrational transition (8, 9). Moving beyond the phenomenological model requires specifying both the conformational heterogeneity and the sensitivity of the reaction barrier to this heterogeneity. Careful structural analysis (10) and quantum chemistry calculations (11) showed that the reaction barrier heterogeneity is indeed a reasonable consequence of observed structural heterogeneity at the myoglobin active site. A reevaluation of a wide variety of myoglobin data also shows that a distinction between diffusive solvent-controlled conformational motions and Arrhenius transitions that are independent of the solvent dynamics is well supported by experiments (12, 13).

In this work, we explore the conformational sensitivity of the protein kinase reaction in two experimentally determined structures of the cAMP-dependent protein kinase (PKA). One is crystallized with ATP and the protein kinase inhibitor (PKI), which we refer to as the reactant conformation of PKA, or RC (14). The other conformation is obtained by crystallizing with a transition-state analogue, a nonreactive ADP-AlF₃, and a mimic of PKI that is both shorter and has a phosphate-accepting serine instead of an inert alanine at the reactive position (15). We refer to the protein conformation in this case as the transition-state conformation of PKA, or TC. Although the two structures are quite similar, we find qualitatively different energetics of reaction. This finding leads us to conclude that phosphate transfer catalyzed by the protein kinase occurs in a very small region of protein conformational space.

Methods

Initial equilibrium geometries were generated from Protein Data Bank entries 1ATP (RC) and 1L3R (TC), both crystal structures of PKA. Initial guesses for the complete reactant and product structures were obtained by homology-modeling the terminal phosphate of ATP (P_γO₃) and side chains of the serine and catalytic aspartic acid (D-166) into appropriate positions. All atoms that were modeled in this way were allowed to move in subsequent geometry optimization steps. Four different model sizes, containing 82, 88, 244, and 263 atoms, respectively, were constructed. The 82-atom minimal system has been defined by Valiev et al. (16) and includes the Mg₂-triphosphate and its immediate interaction partners, G-52, S-53, K-72, D-166, K-168, N-171, D-184, and the substrate serine residue. Two water molecules from the 1ATP crystal structure are included to complete the sixfold coordination of Mg in the 88-atom system. The 244-atom system contains a significantly larger shell around the reaction center and more of the ATP molecule (including part or all of residues G-52, S-53, F-54, K-72, D-166, L-167, K-168, P-169, E-170, N-171, D-184, F-185, G-186, and the substrate backbone from residues 18–22). The atomic coordinates of backbone carbon and nitrogen atoms for each system were taken directly from the experimental crystal structures. Nonbackbone bond lengths and most angles were derived from amino acid templates to facilitate comparison of energies between structures. Protons were added where needed. Residues were truncated by replacing carbon atoms with protons and adjusting the new C–H bond length accordingly. Atomic coordinates for geometry-optimized reactants and products states for 244- and 82-atom RC and TC calculations, as well as 88-atom TC, are provided in the supporting information, which is published on the PNAS web site.

Atomic interactions are described by the vienna ab-initio simulation package (vasp) density functional theory (DFT) and a plane waves basis (17–20). Ultrasoft pseudopotentials of the Vanderbilt form (21) and a PW91 generalized gradient approximation functional are used. A 270-eV plane-wave cutoff, appropriate for the pseudopotentials, is applied. This cutoff was increased to 300 eV to verify insensitivity of results to choice of basis set. The reaction pathways were computed with periodic images separated by at least an 8-Å vacuum layer. Periodic box sizes of 19 × 21 × 16 ų, 20 × 24 × 21 ų, and 27 × 24 × 23 ų were used for the 82- and 88-atom clusters, 244-atom cluster, and 263-atom structure, respectively.

Reactant and product geometries were calculated by optimizing the geometry of the clusters with a conjugate gradients algorithm. Saddle points connecting these stable geometries were found by using the nudged elastic band (NEB) method (22). In this method, images are generated by linear interpolation between the optimized reactant and product structures, and DFT is used to calculate forces on each atom of each image. The images are then geometry-optimized subject to harmonic forces between the images that force them to be equally spaced along a minimum energy pathway between reactants and products. The climbing image modification to the NEB method (23, 24) was used so that the highest-energy image along the band converges directly to the saddle point, thus increasing the accuracy of the calculated energy barrier with fewer images. Refinements to the barriers for small system changes were computed with the dimer saddle-point finding method (25).

The 82-atom system contains the same 59 unconstrained atoms as Valiev et al. (16), whereas the waters added to make the 88-atom system were allowed to move. The 244-atom system has only 42 moving atoms (the gamma phosphate, Mg1, Mg2, their coordinated water, and the side chains of S-21, D-166, and K-168).

To test the sensitivity of the 244-atom result to system size changes and details of the electrostatic boundary conditions and periodic box size, we added the adenosine ring to make a 263-atom system, and observed changes to the barrier for TC of <15 meV. (Note that 1 eV per molecule ≈ 100 kJ/mol.)

Results

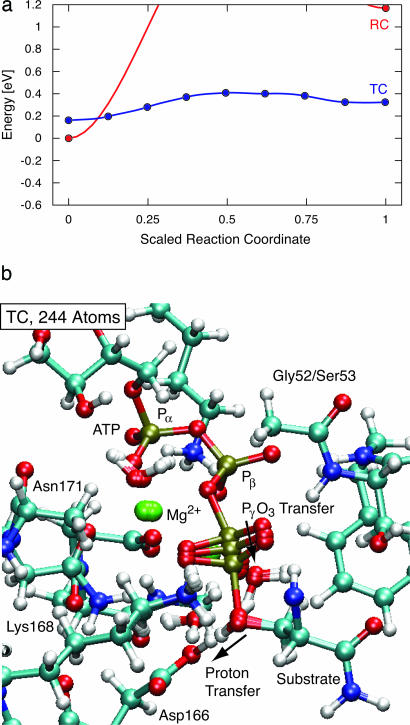
Conformational Dependence. Fig. 1a shows the energetics of the 244-atom systems. The reaction is endothermic in RC by 120 kJ/mol (1.2 eV), whereas in TC, the reaction is nearly isoenergetic with a eV barrier of only 20 kJ/mol (0.2 eV). The reaction pathway of TC, shown in Fig. 1b, shows only small motions during the reaction; only two atoms move >0.5 Å, and the catalytic base moves only 0.07 Å. Apparently, in the TC structure, the atoms around the active site are correctly arranged for both the reactants and products state. In contrast, 1.2 eV endothermicity in RC indicates suboptimal geometries in the product state. The energetics indicate that the protein conformation has adapted to the reactants, providing a strong energy bias against reaction.

Fig. 1.

PKA phosphate transfer energetics depend on protein conformation. (a) Energy along reaction pathway for the 244-atom system in the RC and TC conformers. Reactants (ATP plus protonated serine) are at left. The reaction in RC is extremely unfavorable, whereas the TC conformation allows isoenergetic reactants and products with a barrier of only 12 kJ/mol. (b) Structures for reactants, transition state, and products of calculated phosphate transfer pathway in PKA for a 244-atom TC structure. Note that 1 eV per molecule is 100 kJ/mol.

At the transition state, the P_γO₃ has a planar configuration, halfway between the ADP and the serine. Proton transfer from the serine to the Asp-166 occurs after the phosphate transfer. Transferring the proton to an oxygen atom on the P_γ phosphate was found to be unfavorable by >0.5 eV. These observations are in agreement with previous DFT studies (16).

One possible spurious origin for the low barrier in TC is that the active site has collapsed around the AlF₃, destabilizing both the reactants and products. Fig. 1a shows that the reactants state of TC is only 0.16 eV higher than RC, whereas the product state of TC is 0.85 eV lower than RC. Although the errors contributing to this difference are likely several tenths of an eV, it is remarkable that the ab initio calculation produces reactant energies that are so similar in the two conformations, which are based on two separate crystal structures. It is likely that the TC has significant occupancy in the ensemble of PKA conformations. The use of templates for all rigid degrees of freedom in the two structures may have facilitated comparison of calculated energies between the structures.

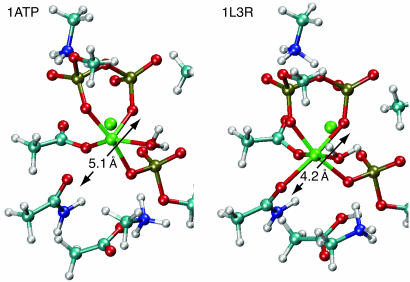
Examination of the reaction pathway geometries reveals two clear reasons for the endothermicity in the TC structure. First, the reaction cleft in RC is ≈1 Å more open in RC than in TC, so the protein is unable to maintain the full octahedral coordination of both magnesium ions throughout the reaction. Fig. 2 shows this distance between the N-171 oxygen and the closest P_β oxygen to be 5.1 Å in the RC conformer. In the TC structure, however, the reaction center is compressed, reducing this distance to 4.2 Å. Lastly, it appears that there is more space for the phosphorylated serine residue in TC than RC.

Fig. 2.

The calculated product states of the 82-atom system are shown for both RC (PDB entry 1ATP) and TC (PDB entry 1L3R). The TC structure has a lower barrier than the RC structure and a favorable product state because in the product and transition states the central Mg atom can remain octahedrally coordinated. In the RC conformer the reaction cleft is opened and the same Mg atom is forced to break one bond, making the reaction unfavorable. The distance between the coordinating oxygen atoms on the Asn-171 and ADP groups, which is a measure of reaction center size, is increased from 4.2 Å in the TC structure to 5.1 Å in the RC structure.

Geometry Constraints. The relatively small set of atoms moving in the calculation shown in Fig. 1 raises a number of questions for both the methodology for calculating and mechanisms of occurrence of phosphate transfer in PKA. One might expect the geometry-optimized reaction pathway to be independent of initial conformation in the limit of the entire protein being allowed to move. Energetic minimization of both RC and TC toward the reactants state, using a classical molecular dynamics potential (which should be reasonable for the reactants state) causes only one-third of the difference in the distance shown in Fig. 2 to disappear, even with no solvent present and every atom in the protein allowed to move during steepest descent followed by conjugate gradient optimization. Although more sophisticated optimizers will undoubtedly help (26), there clearly is an intrinsic roughness to the protein energy landscapes (27).

Table 1 shows motions required for reaction are about half as large in TC as in RC. The Mg²⁺ ions, coordinated water molecules, catalytic base, and lysine all move ≈0.2 Å in TC, and 0.5–1.0 Å in RC. Even the serine residue, which gains a phosphate group, moves only 0.25 Å during the course of reaction. A related observation is that the change in force on the frozen atoms during reaction is about half as large for TC than RC (data not shown).

Table 1. The distances (Å) that particular atoms move in the four reaction pathways.

Atom	82 RC	244 RC	82 TC	244 TC
Mg1	0.63	0.16	0.61	0.10 (0.04)
Mg2	1.07	1.04	0.42	0.25 (0.16)
Pγ	1.65	1.10	1.20	0.89 (0.56)
O1γ	1.20	0.53	0.72	0.35 (0.22)
O2γ	1.43	0.67	0.64	0.33 (0.19)
O3γ	0.99	0.42	0.56	0.49 (0.37)
Ser Oγ	1.43	0.43	1.52	0.27 (0.25)
H	1.24	1.35	1.25	0.53 (0.07)
Asp O	1.12	0.57	0.96	0.07 (0.04)

The distance from the reactants minimum to the transition state is indicated in parenthesis for the 244-atom TC structure.

To directly check the effect of constraint on the results, and guided by knowledge of the forces on frozen atoms, we relieved the constraint on the beta phosphate of ATP. The relative energy of (E_TC–E_RC) went up by 0.35 eV, while the maximum change in force dropped by a factor of ten, and was uniformly distributed across a dozen boundary atoms. The exothermicities of RC and TC changed by <0.1 eV, while optimal geometries differed by ≈0.1 Å, suggesting that the templates used to build the Mg-triphosphate coordination sphere differed from the quantum mechanical potential by ≈0.1 Å in several places.

The conclusion that TC, but not RC, provides a protein conformation in which both the reactants and products geometry of the transferred phosphate residue are unstrained is robust. Furthermore, the motions involved in band formation are only fractions of an angstrom and are confined to a minimal set of atoms.

Dependence on System Size. The computational expense of all-electron quantum chemistry calculations provide a strong incentive to minimize system size. Truncated model calculations must correctly reproduce both constraints on boundary atoms and the electronic structure. We expect that the 244-atom system is approximately correct for both effects.

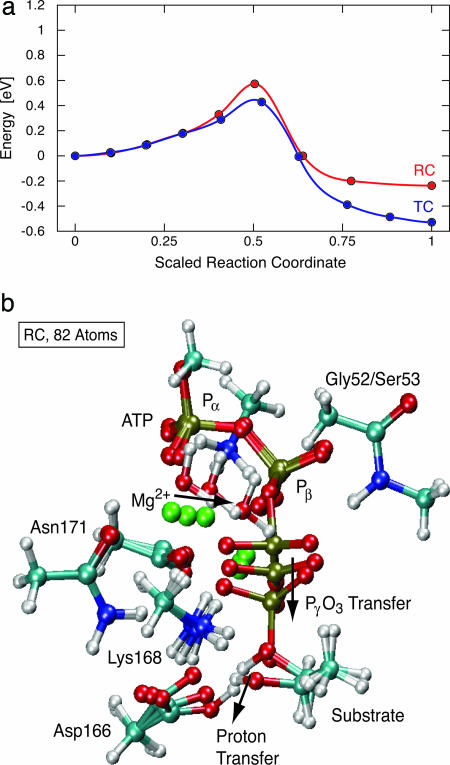
Valiev et al. (16) reported a barrier of 0.5 eV for this reaction, when using either a GGA or B3LYP functional and local basis set on an 82-atom version of the RC structure, with only a pair of atoms fixed at the boundary of each molecular fragment. This result is intermediate between our RC and TC results, and could indicate that computational details provide variability as large as the conformational differences that we cite. To check this possibility, we duplicated their 82-atom system and choice of constraints, and show the results of our calculation in Fig. 3, for both RC and TC. Consistent with their result, we find a 0.5-eV barrier and an exothermicity of 0.2 eV in the RC, indicating a robustness of the result to the various truncation procedures, basis sets, periodic boundary conditions, and functionals used in the calculations.

Fig. 3.

For smaller systems, the reaction energetics do not depend on protein conformation. (a) Energy barrier for the 82-atom system in the RC and TC structures. The TC transition-state analog lowers the reaction barrier and favors the product state. The TC energies are shifted down by 0.4 eV relative to the RC energies to facilitate comparison. Each circle represents an image in the NEB calculation. Adding two water molecules to make the 88-atom system causes the reaction to be endothermic by 0.5 eV (see text). (b) Reaction path for phosphate transfer in PKA with 82 atoms. The three-image sequence is the reactant state, transition state, and product state. The atoms are color-coded. Red is oxygen, light blue is carbon, dark blue is nitrogen, silver is hydrogen, green is magnesium, and gold is phosphorus. At the transition state the phosphate group is planar and the substrate proton has not yet transferred to the Asp-166 catalytic base. Note that 1 eV per molecule is 100 kJ/mol.

This 82-atom result, however, is also insensitive to the starting conformation of the protein, in contrast to the results on the 244-atom systems. This difference implies that the smaller (82-atom) system is not sufficiently constrained to reproduce the restriction of the protein conformation on the active-site chemistry. We tested this by adding two crystallographic water molecules to Mg₁. As a result, the reaction became endothermic by ≈0.5 eV. The 82-atom system is underconstrained and is not large enough to provide accurate energetics of the relative reaction rate of the two systems.

Table 1 shows that the motions of the atoms are much larger in the 82-atom system than in the 244-atom system. Comparison of Figs. 1b and 3b shows a qualitatively larger and more contorted reaction dynamics in the smaller system. Further examination of the 82-atom reaction pathway reveals that atoms are moving that would not be able to in the complete protein system, for example, the Mg²⁺ ions.

A potentially useful observation is that the geometries of reaction in the 82-atom calculation for both conformations are similar to the 244-atom TC calculation. Our limited experience suggests subtle changes in ≈80-atom systems can create significant instability in the results. Such comparisons will require great care but are relatively cheap to compute. This observation suggests that the underconstrained calculations can offer useful clues as to which conformations will favor reaction. Although we do not place great confidence in this number, it is interesting to note that the additional interactions included in the 244-atom system stabilize the reactive conformation (TC) of the protein.

One might expect that, from examination of Fig. 1, once the first shell of ligands to the moving atoms is completed, only groups with a net charge will impact electronic structure. To verify electronic structure convergence, we added the adenosine ring making a 263-atom system, greatly increasing the periodic box size, with minimal difference in energetics and geometries. An energetic offset of 0.4 eV has been subtracted from TC for ease of comparison of the barrier and exothermicity to RC.

Discussion

Molecular dynamics simulation methods have been applied to phosphate transfer in DNA polymerases (28) and protein kinases (29) in a specific effort to understand how the protein conformation influences the reaction rate. We suggest that the transition-state-analog crystal structure (15) provides a much better approximation to the transition-state conformation than is obtainable from molecular dynamics simulation, and that the low-barrier reaction pathway shown in Fig. 1a validates such a statement. We discuss this proposal here, together with ideas needed to compute reaction rates in proteins.

Representative papers considering the reaction dynamics problem in proteins (30–33) are primarily concerned with the complexity of coupling the vibrational transition and solvent motions to the covalent reaction. Because only a few of the unconstrained atoms move in our calculation, it is possible that the dynamics of traversing our minimum energy pathway will occur as a simple and rapid Arrhenius transition. The formalism of Agmon and Hopfield (8, 9) can then be used in combination with an understanding of the energy landscape of hydration and conformational motions (12, 13) to relate the vibrational barrier and prefactor to an overall reaction rate.

Ref. 29 compares a calculated reaction pathway for the same protein structures by using a QM/MM formalism. This formalism allows for a useful partitioning of energy terms according to the physical origin, such as electrostatic, quantum mechanical, or vibrational. The overall energetics and sensitivity to the protein conformation are somewhat different than our results. They observe a 20-kJ/mol-smaller barrier for TC than RC, with both pathways significantly endothermic (60 and 160 kJ/mol) with even higher barriers. Out of the numerous differences between the calculations (QM system size, boundary conditions, model for the reaction dynamics, and QM functional), we feel constraint on the active site is most relevant.

Taking boundary conditions from crystal structures provides an average overall protein conformations. When this boundary is allowed to move (as in ref. 29), our inability to treat the hydration shell, buried water, ions, protonation states, mobile protons, electronic polarizability, and large-scale motion of the proteins will introduce distortions of this boundary. Some problems improve with larger simulations; others get worse.

The sensitivity of calculated energetics to distortions of a few tenths of an angstrom in boundary atoms of ≈80-atom systems provides a geometric scale to evaluate the stability of QM/MM calculations. This idea is similar in spirit to the near-attack conformation (NAC) of Bruice and coworkers (34) in that local geometry and stereo-chemistry considerations imply specific boundary conditions that will allow the reaction to proceed. The types of motions needed to bring RC to TC, however, cannot be defined as dihedral or bond angles but must include a global motion of the two lobes of the kinase that compress the active site and drive the reactants together. One reason for suggesting the Agmon–Hopfield formalism rather than thermodynamic integration is our expectation, based on experiments (35, 36), that relevant motions will occur on times ranging from picoseconds to microseconds, rather than only the nanoseconds available to thermodynamic integration.

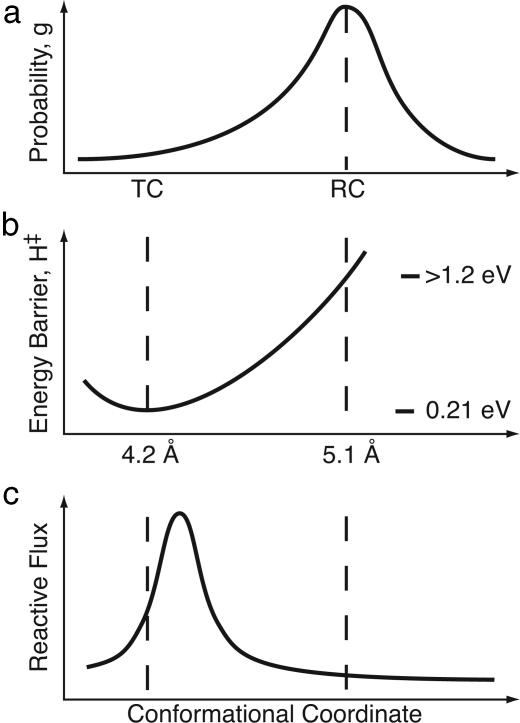
With that said, the most important question is whether Fig. 4 is an appropriate method to decompose the reaction dynamics; a more precise characterization of the conformational ensemble will be required to answer this question.

Fig. 4.

Schematic separation of reaction rate into conformational and vibrational (Arrhenius) coordinates. (a) The distribution of protein conformations, with RC representing an average structure and TC a less-populated member of the distribution. (b) We have calculated an enthalpy barrier for two members of the ensemble, and interpolated between in this figure. (c) Reactive flux as a function of conformation, calculated by using the Agmon–Hopfield formalism described in the text. Note that 1 eV per molecule ≈ 100 kJ/mol.

The current calculations are evaluated in the context of the Agmon–Hopfield model in Fig. 4a, which shows the 1ATP (RC) structure at the peak of a distribution of conformations and 1L3R (TC) at the side. Fig. 4b shows the barrier computed in the two calculations: 150 kJ/mol (1.5 eV) for the reactant conformer, and 15 kJ/mol (0.15 eV) for the transition conformer. Fig. 4c shows the reaction flux across the barrier as a function of protein conformation, simply the product of the probability of a conformation with the rate of reaction for that conformation g(cc)k(cc), where k(cc) = exp[-H(cc)/k_BT].

This model provides an estimate of the distance scale over which the barrier changes can be made by combining the information in Figs. 1, 2, and 4c, which shows that a 0.9-Å shift in the Mg²⁺ position, combined with several other changes of a similar size, shifts the barrier by 120 kJ/mol (1.2 eV). Thus, a reasonable flux is confined to a multidimensional region only ≈0.2-Å-wide! Allostery is the property by which small molecules or proteins binding distant from the active site can influence activity by changing the protein conformation; the present calculation shows that these conformational changes can be quite subtle.

The exact value of the reaction rate requires knowledge of the conformational occupancy of the low-barrier conformation, which we have not attempted to calculate in this work. There is a need for methods that can explore conformational changes in proteins. In this regard, inspection of the calculation in Fig. 3 can be quite helpful in discovering what conformations to look for when screening an MD simulation to find the correct portion of conformation space.

A recent crystal structure of a Y204A mutation of PKA in complex with a peptide inhibitor (37) supports two aspects of our calculation. First, a mixture of reactants and products can coexist; and second, very few residues move in the course of the phosphate transfer. Yang et al. (37) specifically note the absence of motion in the Mg²⁺ ions, coordinated water, K168, and S53.

Conclusions

Two important lessons can be learned from the present work. First, ≈200 atoms need to be included in a quantum mechanical calculation, both to obtain the correct electronic structure and to maintain enough constraints on the boundary layer of atoms to meaningfully reproduce the effect of protein conformation on reaction rate. Second, the existence of the low barrier pathway calculated directly from an appropriate experimentally derived protein structure suggests that the active site of at least some enzymes functions by aligning the reactants in an appropriate conformation from which catalysis proceeds rapidly. In proteins where it is not possible to obtain TC crystal structures, it is essential to find appropriate methods to explore the variety of protein conformational motions. Because protein motions typically occur on time scales ranging from hundreds of picoseconds to microseconds, it is unlikely that simply embedding the quantum region in a larger classical region will resolve this difficulty.

Is ab initio quantum chemistry now in a position to answer the biologically motivated questions posed in the Introduction? It is clear, at least, that the active-site cleft is not closed far enough in the RC structure. On the other hand, the real power of these techniques will only become evident when it is possible to thoroughly sample conformational motions of proteins and protein complexes. If studies of protein folding are any guide, this day is quickly approaching (38).