The intrinsic hypermutability of antibody heavy and light chain genes decays exponentially

Abstract

Somatic hypermutation, essential for the affinity maturation of antibodies, is restricted to a small segment of DNA. The upstream boundary is sharp and is probably related to transcription initiation. However, for reasons unknown, the hypermutation domain does not encompass the whole transcription unit, notably the C-region exon. Since analysis of the downstream decay of hypermutation is obscured by sequence-dependent hot and cold spots, we describe a strategy to minimize these fluctuations by computing mutations of different sequences located at similar distances from the promoter. We pool large databases of mutated heavy and light chains and analyse the decay of mutation frequencies. We define an intrinsic decay of probability of mutation that is remarkably similar for heavy and light chains, faster than anticipated and consistent with an exponential fit. Indeed, quite apart from hot spots, the intrinsic probability of mutation at CDR1 can be almost twice that of CDR3. The analysis has mechanistic implications for current and future models of hypermutation.

Introduction

The affinity maturation of antibodies is fuelled by a process of somatic hypermutation that is restricted to a very small segment of the total genome (reviewed in Milstein and Neuberger, 1996). The hypermutation target includes the whole coding V-region segment but extends beyond it at both ends. The 5′ end starts rather sharply in both the heavy and the light chain loci (Lebecque and Gearhart, 1990; Rada et al., 1994; Rogerson, 1994). Indeed, in the most extensively studied mouse kappa light chains, a very sharp increase in the mutation frequency can be detected in the leader intron, just upstream of the exon coding for the V segment. The sudden surge in mutation frequency, regardless of DNA sequence, occurs ∼185 bases downstream of the promoter (Rada et al., 1997). The mechanistic reason for this precise location is still uncertain but most likely it is related to the fact that initiation of transcription and initiation of hypermutation are driven by similar promoters. Indeed, hypermutation and transcription may be mechanistically linked (Betz et al., 1994; Peters and Storb, 1996; Goyenechea et al., 1997; Tumas-Brundage and Manser, 1997; Winter et al. 1998; Fukita et al., 1998). It is, however, important to keep in mind that the 5′ boundary, sharp as it is, is not an absolute barrier, because the mutation frequency upstream of the boundary remains above background, even beyond the transcription initiation site (Both et al., 1990; Lebecque and Gearhart, 1990; Rothenfluh et al., 1993; Rada et al., 1994, 1997).

The downstream boundary of the hypermutation target segment, on the other hand, is not as clearly defined. There is no doubt that hypermutation cannot extend far, since the C regions of heavy and light chains are invariant. Occasional mutations in the C region of mouse lambda chains have been reported (Motoyama et al., 1991), but this may be because the J-Cλ intron is unusually short (1.1 and 1.3 kb for lambda 1 and 3, respectively, see DDBJ/EMBL/GenBank X58411, versus 2.5 for kappa, see DDBJ/EMBL/GenBank V00777, and >3.2 kb for heavy chains, see DDBJ/EMBL/GenBank J00440). It has been suggested that the mutation frequency gradually and slowly decays, becoming hardly noticeable beyond 1.5–2 kb (Lebecque and Gearhart, 1990). It is possible that the 3′ decay of mutation is related to the distance from a fixed upstream position (Weber et al., 1991), be it the initiation of transcription or the 5′ boundary. The available information is compatible with this view, but is based on incomplete and small databases and does not address the important issue of the nature of the decay, i.e. the different modes of decay that could accommodate presently available data. For instance an attractive possibility would be a model whereby high mutation frequency is maintained over a given distance (e.g. the VDJ segment) to decay quickly thereafter. Indeed, in a previous study we detected no obvious decay immediately downstream of the J segment of lambda chains (González-Fernández et al., 1994). However, mechanistic models should be constrained by experimentally established decay data, unavailable at present.

In this paper we demonstrate that the accumulation of mutations decreases with the distance at which identical intron or exon sequences are placed relative to the initiation of transcription, both in heavy and light chains. We go on to develop a strategy whereby the analysis of decay is based on an average of the mutation frequencies of unrelated DNA segments, located at equal distance from a fixed upstream point. In this way we reduce the effects of hot/cold spots, thus allowing a better understanding of the intrinsic nature of the downstream hypermutation decay.

Results

Location with respect to the promoter determines the decay in mutation frequency of both heavy and light chain genes

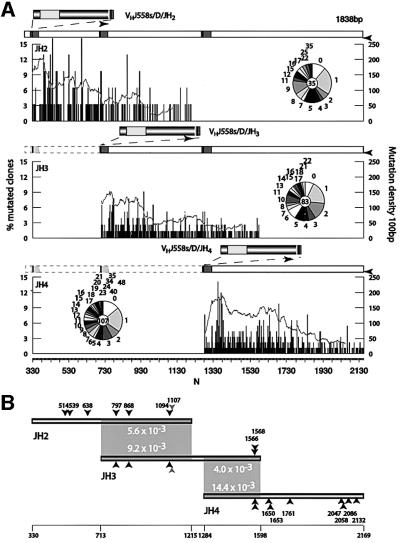
To analyse the decay in heavy chain genes, three sets of sequences were collected from Peyer’s Patches germinal centre B cells. The fragments containing the rearranged VH₄DJ-CH flank were amplified using an upstream primer that recognizes a consensus framework 3 of the VH J558 family members (Jolly et al., 1997) so that the unrearranged allele is not amplified. The products were fractionated by gel electrophoresis to separate the JH₂, JH₃ and JH₄ rearrangements. The DNA from the corresponding bands was then cloned and sequenced. The resulting databases are summarized in Table I. All three sets of sequences have a comparable mutation load, as apparent from the pie chart insets in Figure 1A, which describe the distribution of mutations per clone in the databases.

Table I. Origin of the databases analysed.

	Mutated clones	Length (bp)	No. of mutations	References
Light chains
Lκ V region	224	282	917	Milstein et al. (1998)
Lκ[LiΔ] V region	69	282	297	Rada et al. (1997)
Lκ-Jκ5-Cκ flank	117	1103	762	this paper
Lκ[LiΔ] flank	77	1103	456	this paper
Heavy chains
JH2 flank	31	885	250	this paper
JH3 flank	77	885	493	this paper
JH4 flank	92	885	795	Rada et al. (1998); this paper

Fig. 1. Distribution of mutations in three different JH rearrangements. (A) The histograms represent the distribution of mutations in an 885 bp segment downstream of JH₂, JH₃ and JH₄ rearrangements, presented as the percentage of mutated clones (left axis) with mutations at each position N (horizontal axis). The numbering corresponds to the equivalent position in the germline sequence according to Lebecque and Gearhart (1990) (DDBJ/EMBL/GenBank X53774). The continuous grey line represents mutation density measured as the accumulated percentage of mutated clones for each position in a 100 bp interval (right axis). The schematic diagram on top of each graph represents to scale the relative position of the segments analysed depending on the rearrangement. Black arrowheads indicate the position of the primers used for amplification. Pie chart inserts show the distribution of clones with 0, 1, 2, 3 etc. mutations in each database. The number in the centre indicates the number of sequences analysed. (B) Mutation frequency in homologous intervals in different rearrangements. Shadowed boxes identify the region of identical sequence. The numbers in the boxed area show the mutation frequency in the segment. The differences in mutation frequency are attributable to the relative distance to the initiation of transcription due to the rearrangement. Arrowheads mark polymorphic residues used to identify hybrid artefacts. The light grey arrowheads are a single nucleotide insertion or deletion. The numbering corresponds to the germline sequence as in (A).

The V-D-J recombination event places the flanking intron sequences at different distances from the initiation of transcription. Comparison of the mutations accumulated by flanking fragments downstream of the J segments is revealing. The results are shown in Figure 1A, where the sequences are arranged to overlap homologous segments. It is clear that identical sequences accumulated a higher number of mutations when located at shorter distances from the initiation of translation/transcription. Thus, the segment 713–1215 accumulated 5.6 versus 9.2 mutations/1000 bp in JH₂ and JH₃ rearrangements, respectively, while the segment 1284–1598 accumulated 4.0 versus 14.4 mutations/1000 bp in JH₃ and JH₄ rearrangements, respectively (Figure 1B).

In the case of light chains, data were collected for two transgenes (Table I). Lκ encodes a rearranged VκOx1 light chain (Sharpe et al., 1991) while Lκ[LiΔ] is a shorter variant with a deletion of the leader intron (Rada et al., 1997). Comparison of the mutation density profiles of the two strongly supports the conclusion that distance is the critical parameter of the decay. The only significant difference between the two light chains is that identical sequences are placed at different distances from the transcription initiation site. This does not affect the pattern of mutation, as hot spots remain the same (Figure 2A). In the deletion variant, the identical V segment is 171 bases nearer the initiation of transcription, and the 5′ mutation boundary is located within the V segment. A comparison of identical fragments of the V segments starting at residue 68 (which corresponds to the 5′ mutation boundary of Lκ[LiΔ]; Rada et al., 1997) shows that the deleted form accumulates more mutants than the wild type (19.1 versus 16.3 mutations in 1000 bases; Figure 2B). Yet, when the mutation frequency is computed not by homology of segments but by homology of distances from the transcription initiation, the picture is reversed. Thus, the downstream 931 base interval starting 521 bp from the initiation Met accumulated 6.8 and 4.1 for Lκ and Lκ[LiΔ], respectively. This difference is likely to be due to variations in the location of hot/cold spots in the computed non-homologous fragments. For example, CDR3 is not included in the data starting at 521 of Lκ[LiΔ]. We thus conclude that the rate of mutation of a given base is modulated by its distance from a fixed upstream position.

Fig. 2. Distribution of mutations in transgenic light chains. (A) The histograms show the distribution of mutations as percent of mutated clones (left axis) at each position N. The numbering refers to the initiation Met in the Lκ transgene. The alignment is carried out by sequence homology. The line graphs show the mutation density in 100 bp intervals (right axis). The schematic diagram shows to scale the deletion in Lκ[LiΔ]. The lighter boxes correspond to intronic sequences. (B) A comparison of mutation frequency in an identical sequence interval is indicated by the numbers in the shaded rhomboid. The alignment is carried out by distance to initiation of transcription. The numbering is as in (A).

Bypassing hot-spot biases in the analysis of decay

There are several factors that conspire against a quantitative analysis of the decay. In the first place, large databases are required, especially for the downstream segments, which display a much lower accumulated mutation. More importantly perhaps (as shown above) is that the mutation frequency at each base varies considerably due to the presence of hot and cold spots that, at least in part, are sequence dependent (Betz et al., 1993). For instance, the most mutated bases of the M7VκOx1 gene become almost unmutable when a Ser codon AGC is substituted by TCA (Goyenechea and Milstein, 1996). Indeed, AGC and TCA codons seem to have been preferentially selected in evolution to encode Ser in the complementary determining regions or the invariable segments, respectively (Wagner et al., 1995).

Figures 1 and 2 illustrate how difficult it is to establish with any degree of confidence the shape of the decay, even if (as shown by the wavy profiles of the figures) the computation is carried out by pooling the data of a sliding window of 100 bases. In order to circumvent this problem we pooled mutations by their distances from a fixed point regardless of their homology (synonymous position as opposed to homologous). For instance, in the case of the light chains, we have pooled the data from the two curves of Figure 2. The deletion of the intron displaces, in an arbitrary fashion, hot and cold spots by 171 residues. The pool of the two databases was, therefore, not by sequence homology but by distance from the transcription initiation.

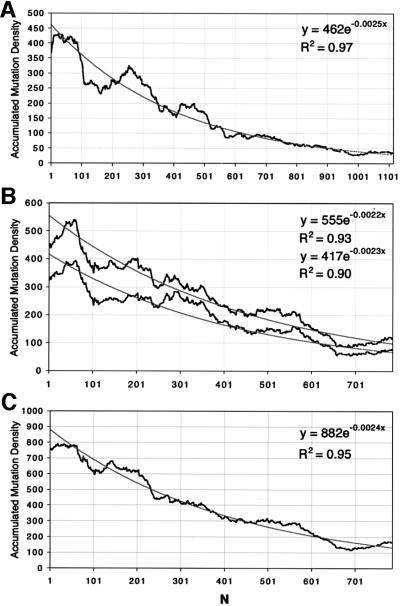
The merged light chain data (accumulated mutations in a sliding window of 100 bases) is shown in Figure 3A. Here, the first 100 residues are the combination of data starting 239 nucleotides downstream of the initiation Met of Lκ and Lκ[LiΔ]. While the plot is still very influenced by the hot and cold segments of the original curves, the shape of the decay is better defined and the curve has a smoother profile. The observed decay in Figure 3A could be approximated to an exponential decay A = A_o.e^–kN, where A is the pooled mutation density independent of sequence environment and A_o is the value at a given distance N from the transcription initiation. In the case of the heavy chain rearrangements, we have combined the data from all three rearrangements and separately the pair JH₄ and JH₂, which are the least affected by potentially hybrid sequences (see Materials and methods). When the pooled data include JH₃, the shape of the decay is not substantially altered (Figure 3B).

Fig. 3. Accumulated mutation density in 100 bp intervals. Details of how the mutation density is calculated are included in Materials and methods. The black line represents pooled mutation density. The grey lines are fitted curves to the experimental data. The insets show the equations and R² values for the exponential fits. (A) Pooled light chains. N = 1 corresponds to position 239 from the initiation Met in the Lκ light chain. (B) Top curves correspond to pooled JH2, three and four rearrangements, while the bottom curves are derived from JH₂ and JH₄ rearrangements. N = 1 corresponds to position 330, 713 and 1284 of JH₂, JH₃ and JH₄, respectively, as in Figure 1A. (C) Pooled mutation density for heavy and light chains. N = 1 corresponds to position 531 of Lκ for the light chains and the same as (B) for heavy chains.

An interesting corollary of our analysis is that we can define better the hypermutation target area as extending to a point where the average mutation frequency decays to <1% of its maximum at the 5′ boundary (A/A_o = 0.01). In the case of the light chain this is predicted to be when N = 1842, and in the case of heavy chains when N = 2093. Thus, heavy and light chains show remarkably similar decays. Indeed, the most important features defining the kinetic decay, namely the fit with an exponential decay and the value of the critical decay constant k, are almost identical. Thus, we felt justified in pooling all sets of data irrespective of their origin, using as the sole restriction the approximate distance from the initiation of transcription. As shown in Figure 3C, the exponential fit to the pooled data is improved. The combined data predicts a fall to <1% of maximum mutation at ∼1920 bases from the 5′ boundary, equivalent to ∼2100 bases from the transcription initiation.

Discussion

In this paper we present an approach to define the nature of the hypermutation decay downstream of the V exon of immunoglobulin genes. First, we confirm that the decrease in the observed mutation frequency at the 3′ end is due to the distance from transcription initiation rather than inherent properties of the genes (Weber et al., 1991). In order to neutralize the problems created by hot and cold spots, we pool data of mutations taken from similar or identical heavy or light chain sequences that are located at different distances from transcription initiation. We then test this approach in a refined analysis of the mode of decay.

The approach is based on the postulate that the probability of mutation of any given residue depends on two factors, namely the environment of the residue in question (hot/cold spots) and a superimposed inherent mutability that decays with the distance from the 5′ hypermutation boundary. One way to dissociate these two factors is to randomize the sequence so that the cumulative mutation will be independent of the environment of each residue. Unfortunately, this is not a practical proposition. However, if different sequences are compared, a certain degree of randomization can be achieved, provided that extreme hot or cold spots do not occur at identical distances from the initiation of hypermutation. Due to the mutational bias introduced by evolutionary forces (Chang and Casali, 1994; Wagner et al., 1995; Dorner et al., 1997; Cowell et al., 1999), a comparison of different heavy or light chains is not likely to randomize events. Indeed all CDRs with an accumulation of hot spots occur at similar distances in all light and heavy chains. This problem can be partially avoided in our case by pooling mutations of different sequences or even identical sequences that differ in the distances from a fixed point.

Our approach thus attempts to describe the decay in the probability that a given base will mutate as a function of its distance from the 5′ hypermutation boundary, regardless of its local sequence environment. The measured decay in average mutation density is assumed to reflect the decay in mutational probability along the hypermutation segment. The observed decay pattern was monotonic, well described by an exponential decay. Thus, putative models predicting a sigmoid decay with a consistently high probability of mutation over the whole of the V-J segment followed by a fast decay further downstream would not be compatible with our results. It has been suggested that there are two phases of hypermutation: the first introducing the AGCT-like hot-spot bias and the second, absent in MSH2 KO mice, introducing the TA-like bias (Rada et al., 1998). It is possible that the intrinsic decay refers largely to the first phase, although at present we are unable to dissect the contribution of the two to the decay.

We have previously defined the 5′ boundary as a small segment where the mutation frequency increases considerably. We speculated that while the boundary could coincide with the transition from transcription initiation to elongation, it was also possible that hypermutation was active, but hindered, within the DNA segment covered by the initiation complex (Rada et al., 1997). Be it as it may, we do not know how many bases of DNA are involved in the transition from low to maximum mutation rate. Therefore, within the whole of this study we have chosen to avoid boundary effects by excluding the segment immediately downstream of the boundary.

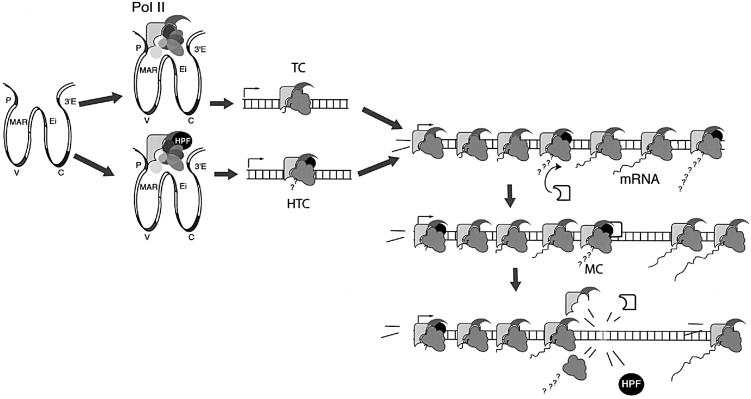
Several models have been proposed to explain how hypermutation works (Brenner and Milstein, 1966; Neuberger and Milstein, 1995; Storb, 1996; Weill and Reynaud, 1996; Steele et al., 1997; Cascalho et al., 1998; Diaz and Flajnik, 1998; Winter et al., 1998; Harris et al., 1999; Bross et al., 2000) and it is not our intention to analyse all of them in the light of our results. However, some comments are in order. Generally speaking, the nature of the decay has not been an integral part of the models proposed so far, although this feature is important in some of them (e.g. Steele et al., 1997; Winter et al., 1998). There is a class of models that rely on the formation of a hypermutation promoter complex (HPC) somehow associated with transcription initiation or transcription elongation (Storb, 1996; Goyenechea et al., 1997). We will now consider a model for the decay based on the assumption that HPC slides along the DNA with a finite probability of initiating the events leading to the hypermutation process at nucleotide position N, and in so doing becoming inactive. A newly formed HPC is required to start the process at the 5′ end (Figure 4). We will assume further that the probability (p) of the event leading to mutation/inactivation of the HPC is equal for any value of N (only valid if hot/cold spots are ignored), regardless of whether or not a previous HPC had interacted at N, with or without eliciting a mutation. Let A now denote the maximum number of consecutive HPCs that start moving along the hypermutating segment and A_N the number of HPCs not likely to initiate an event at N. Let q = 1 – p denote the probability of any HPC not initiating an event at a particular N. Then:

Fig. 4. A model for hypermutation decay. The model is dependent on a hypermutation targeting complex (HTC) sliding along the DNA and at any point, for instance by interaction with a mutator complex (MC), initiating a process leading to error-prone repair. When this happens HTC becomes inactive (for example it ‘falls apart’, as indicated in the figure). The decay would be exclusively due to the requirement of loading the complex at one end and its spontaneous or induced inactivation following the interaction with MC anywhere along the DNA. Loading of a hypermutation promoting factor (HPF) at the initiation of transcription site provides a simple mechanism for defining hypermutation clonality (Goyenechea et al., 1997) and the target area of hypermutation. Indeed, HPF could use RNA pol II as a carrier to slide along the DNA, transforming the transcription complex into a hypermutation complex. This is in line with current views of RNA pol II as not just an RNA synthetase, but the engine of a complex machinery involved in controlling transcription, capping, polyadenylation and splicing, recruiting repair and remodelling chromatin configuration (Cramer et al., 1999; Orphanides and Reinberg, 2000; Shatkin and Manley, 2000).

                            N = 1 → A₁ = A.q

                            N = 2 → A₂ = A₁.q = A.q²

                        A_N = A.q^N (1)

which describes an exponential decay. In our case we have used a constant k that can be connected with q by the conversion:

                                    q = e^–k(2)

so that equation (1) becomes:

                                A_N = A.e^–kN (3)

The best exponential fit of the experimental results was with k ∼0.0024. Thus, from equation (2): q = e^–0.0024 ≈ 0.9976 and p = 0.0024.

Thus, in this model, which ignores hot and cold spots, the probability that HPC initiates a putative hypermutation event at any nucleotide position is 0.0024 over the whole hypermutating segment. In practice and for individual sequences, the environment of each residue will affect this value. With this formula it is easy to calculate the intrinsic probability of mutations occurring anywhere under the assumption that the maximum probability is at the 5′ boundary. For example, the 1/2 probability decay would occur at N_1/2 = ln2/0.0024, ∼290 bases from the 5′ boundary in the leader intron of kappa chains. This is a surprisingly low figure since in normal heavy or light chains it is before the end of the V segment. It suggests that evolution has selected a decay mechanism that predominantly targets the beginning of the V segment, including CDR1. It also provides at least part of a rationale as to why hot spots in CDR1 are ‘hotter’ than canonical hot spots further downstream. At 2 kb from the boundary, the probability of mutation drops to <1%, approximating to the experimental background.

It is important to note that this model is valid for a variety of hypothetical properties of HPC and for the reasons for stopping and becoming inactive. For example, HPC does not need to be capable of transcription, and it could move along the DNA just as a transcription complex does, but in the absence of RNA synthesis. Indeed, there are published data suggesting that hypermutation can proceed in the absence of transcription (Reynaud et al., 2001). Most importantly, there is no need to invoke previous damage to DNA or ‘gratuitous stops’ as a result of stalling induced by a mutation factor (Storb, 1996). We propose an alternative possibility, which was hinted at in our previous model (Goyenechea et al., 1997). This involves a probabilistic breakdown of the complex, either by spontaneous kinetic dissociation or by interaction with a nuclear factor or complex that recognizes HPC. Such hypothetical interaction could introduce the nicks or strand breaks that are thought to precede error-prone corrections (Brenner and Milstein, 1966; Lo et al., 1997; Sale and Neuberger, 1998; Bross et al., 2000; Papavasiliou and Schatz, 2000).

The results shown here demonstrate that the decay of both heavy and light chains is very similar, indicating that the same mechanism applies to both. There are, however, differences due to a larger accumulation of mutations in the heavy chains. These could arise because transgenes accumulate fewer mutations than endogenous genes and/or, on average, light chain genes accumulate a lower number of mutations than heavy chains. Leaving aside this difference, the kinetics and the constants that define the rate of hypermutation decay are remarkably similar. Indeed, the value of k in the exponential decay model is practically identical for both chains and, therefore, the half probability point is almost identical.

It is becoming increasingly clear that hypermutation is a complex event that involves a large number of factors, some of them totally unexpected (Muramatsu et al., 2000). However, the identification of all of the factors involved is insufficient. Understanding the assembly of large complexes and their decay is essential to the understanding of the whole process. Our approach to the study of the decay kinetics of hypermutation is only a small step towards that goal.

Materials and methods

Mice

Transgenic mice carrying a modified kappa light chain Lκ and Lκ[LiΔ] have been described previously (Sharpe et al., 1991; Rada et al., 1997) and were bred in our barrier unit against F1 (C57B/6×CBA). At least two to three individual mice were used per line. For the heavy chain data three individual mice (mixed background C57B/6 and CBA) and a pool of six C57B/6 mice were used.

Peyer’s patches germinal centre B cells [CD45R(B220)⁺ PNA^high] were isolated by fluorescence-activated cell sorting (MoFlow; Cytomation Inc.) after staining with anti CD45R-RPE (Gibco-BRL) and PNA-FITC (Sigma), and genomic DNA was extracted.

Light chains

The flanking Jκ5-Cκ region of the transgene was amplified using primers 5′-TTAGTGGATCCGTTCCTATCACTG-3′ (intron region 5′ to HindIII site) and 5′-ACTTATGAATTCCAGCAGTGGAGTAGTAACCCACTCACG-3′ (overlapping the junction of VκOx1 to Jκ5). PCR conditions were 31 cycles of 93°C (40 s), 55°C (40 s) and 72°C (3 min 40 s), with an extra 5 min extension time at 72°C using Pfu polymerase (Stratagene). PCR products were restricted, gel purified and cloned into EcoRI–BamH1 restricted M13mp18.

For the heavy chain data, JH₂, JH₃ and JH₄ rearrangements of the V_HJ558 family were amplified as previously described (Jolly et al., 1997) using a consensus V_HJ558 family framework 3 forward primer, 5′-GGAATTCGCCTGACATCTGAGGACTCTGC-3′, J_H-C_H back primer, 5′-GACTAGTCCTCTCCAGTTTCGGCTGAATCC-3′, and Expand^™ High fidelity PCR System (Roche), employing six cycles of 93°C (40 s), 64–55°C (touch down annealing) (40 s) and 4 min extension times at 72°C, followed by a further 30 cycles but with extensions at 55°C. Amplified DNA was restricted with EcoRI and SpeI, the correct size band was gel purified and cloned into M13mp19 EcoRI–XbaI or TA-cloned into pCR 2.1 TOPO vector (Invitrogen).

Sequencing

Light chain sequencing primers were –40 M13 primer, 5′-TCTCCC ACCGCGGCGTCTAGATCTCAATAACTACTC-3′ and 5′- CAAGGA CTCGTTCCTACAG-3′, and for the heavy chain were –21 M13 primer, 5′-GTTTCTCTGAGGTGAGGCTG-3′, 5′-GGGCTGTAGTTGGAG ATT-3′, 5′-ACCAACTTAAGAGTAAAAGC-3′ and M13 reverse primer.

All sequencing was carried out using Bigdye^™ terminator cycle sequencing (PE Applied Biosystems) on an ABI377. Sequences were aligned and analysed using Pregap4 and Gap4 software (Bonfield et al., 1995).

For the heavy chain data we eliminated all clonally related sequences by comparing the CDR3 region. Polymorphic changes in the J-C intron were removed. All numbering refers to the sequence reported in Lebecque and Gearhart (1990) (DDBJ/EMBL/GenBank X53774).

In the light chain data, removing clones that shared more than three identical mutations eliminated clonally related sequences. Several mutations had occurred in the transgenes prior to integration, which confirmed the approximate number of copies (3) in the Lκ[LiΔ] mice (line 9) and the equal mutational targeting of all transgene copies. These transgene copy marks were also excluded from the mutation data.

Data processing

The light chain data were derived from two independent PCR amplifications, one encompassing the V region and the second from the rearranged Jκ5 segment of the transgene. In the case of the Lκ transgene data, a compilation of data from the line was used for the V region (Milstein et al., 1998). The mutation accumulated in the Lκ transgene has been documented before (González-Fernández and Milstein, 1993; Yélamos et al., 1995). The mice used for the flanking region analysis were of similar age and housed in the same animal facility. In the case of the Lκ[LiΔ] line, DNA from the same donor mice was used in both V region and flank PCR reactions.

In order to integrate data from different amplifications, the calculations used the percentage of mutated clones with a mutation at each position. This type of analysis reflects the relative probability of mutation of each position.

The mutation density in the 100 base pair interval starting at each position [D_(N)] was calculated according to the following formula:

                                        D_(N) = Σ_N^{N + 99} M_(N)

where N is the nucleotide position and M_(N) the percentage of clones with mutations at that position.

We tried to minimize the impact of hybrid PCR clones that are very strongly dependent on the processivity of the polymerase and the length of the transcript (Eckert and Kunkel, 1991). In the case of Lκ[LiΔ] we could compute the number of hybrid clones, because one of the three Lκ[LiΔ] transgenes was identifiable by minor sequence differences. We found that all of the copies mutated at about the same rate and we could not detect any hybrid sequences. It is to be emphasized that in our analysis, these types of hybrid do not affect the data because we are computing total accumulation of mutations in a given residue of the pool of sequences, regardless of their clonal origin. On the other hand, in heavy chains the downstream primers used could not recognize the individual rearrangements within the same mouse. Hybrid clones created during the PCR amplification depend largely on the length of the cloned fragments and the extent of sequence identity between the fragments. We have minimized this type of artefact by restricting our analysis to a relatively short segment of DNA and determining the frequency of hybrid clones within those segments using polymorphic residues of the C57B6/CBA mice (Figure 1B). In the JH₂ there were 18% of hybrid sequences while in JH₃ the proportion was larger (26%), reflecting the larger segment of homology with the other sequences. Not surprisingly, the hybrid sequences of JH₄ amplifications dropped to 11%. However, the real impact of the crossovers is much lower, because the most common hybrids would arise by crossover with homologous rearrangements and would not affect our calculations for the same reason as discussed for the multiple copies of light chain transgenes. Indeed, in the case of JH₂ most of the hybrids are likely to be within the JH₂ amplifications, because the first half of the sequence has no homology with any of the others.