Quantitative Modeling of Arabidopsis Development^,

Abstract

We present an empirical model of Arabidopsis (Arabidopsis thaliana), intended as a framework for quantitative understanding of plant development. The model simulates and realistically visualizes development of aerial parts of the plant from seedling to maturity. It integrates thousands of measurements, taken from several plants at frequent time intervals. These data are used to infer growth curves, allometric relations, and progression of shapes over time, which are incorporated into the final three-dimensional model. Through the process of model construction, we identify the key attributes required to characterize the development of Arabidopsis plant form over time. The model provides a basis for integrating experimental data and constructing mechanistic models.

Plant development is a dynamic process in which the topology and geometry change over time in a seemingly complex manner. This changing form provides the context of gene action while at the same time being under the control of gene action. To understand this process quantitatively, we first need to identify and measure the key attributes of plant form needed to specify the observed growth pattern. This can be achieved by coupling data acquisition with the construction of a model. The needs of the model guide the process of data acquisition, and the choice of parameters is eventually validated by the final appearance of the model (Bell, 1986).

We present such a model for Arabidopsis (Arabidopsis thaliana), one of the key organisms used in the study of plant biology. Measurements and staging of wild-type Arabidopsis growth have been described previously to provide standards for comparisons with mutants (e.g. Smyth et al., 1990; Groot and Meicenheimer, 2000a, 2002b). Arabidopsis models have previously been constructed by De Visser et al. (2003) for the purpose of simulating a number of flowering mutants, and by Chenu et al. (2004) for the purpose of simulating light acquisition by rosette leaves. We present a more detailed model of the wild-type plant, intended to serve as a stepping stone for the integration of developmental and molecular genetic data, and for the incorporation of developmental mechanisms.

Models of plant development can be implemented using a variety of methods (Prusinkiewicz, 1998). We chose the formalism of l-systems (Lindenmayer, 1968; Prusinkiewicz and Lindenmayer, 1990; Karwowski and Prusinkiewicz, 2003), which provides a programming language for describing the models and a convenient method for visualizing the results as growing three-dimensional structures. According to this formalism, a plant is viewed as a developing assembly of individual units, or modules. These modules are characterized by parameters such as length, width, and age, as well as parameters characterizing shape. A methodology for constructing l-system models based on empirical estimates of such parameters has been introduced by Prusinkiewicz et al. (1994).

Here we adapt this methodology to model a developing Arabidopsis (Landsberg erecta) plant from seedling to maturity. We consider the developmental progression in the size, shape, and position of individual organs from the early stages (approximately 1 mm) to when they attain their final size. This required an integration of data obtained from dissected plants with those obtained using nondestructive methods. The shapes of organs were measured at different stages of development and interpolated to simulate plant growth in continuous time. The model provides an insight into the number and nature of the parameters needed to capture the properties of a growing structure. In addition, the approach highlights some growth patterns, such as the relationship between phyllotactic angle and plastochron.

RESULTS

Plant Nomenclature and Architecture

A plant shoot can be considered as a series of metamers (m), each comprising three modules: an axillary meristem, subtending leaf (if present), and supporting internode. In the main axis of the measured plants, one cotyledon was defined as m0, the other as m1, and the metamers above this were numbered sequentially m2, m3,…mi. Metamers on lateral branches were labeled first according to the identity of the parental metamer and then numbered sequentially from the base of the lateral, starting at 0. The structure of Arabidopsis is shown in Figure 1. The leaf insertion angle is the angle between the stem and the leaf axis, and the branching angle is the angle between the main stem and the first internode of the lateral branch.

Figure 1.

Schematic diagram of Arabidopsis (not to scale). Metamers of the main axis and on some of the lateral branches are labeled. The branching angle (β) and leaf insertion angle (α) are shown for m8 and m9, respectively.

General Approach

A comprehensive account of growth requires a description of how the dimensions and shape of each module change over time. Changes in dimensions were described for each module by measuring one feature, such as length or width, at various time points. This provided a scaling factor that could be plotted against time. In addition, the shape of each structure was quantified at various stages using several approaches.

To obtain a continuous description of growth, functions were fitted to the observed scaling factors and shapes. The resulting parameter values then provided the information required to reconstruct the plant and visualize its development over time.

Main Stem

Internodes

The most convenient scaling factor for internodes was length. Internode lengths of five measured plants were incorporated. The first eight metamers showed very little internode elongation, forming a rosette of leaves. For the purposes of the descriptive model, the length of these metamers was considered to be zero. Metamers from m9 onward showed elongation (bolting), allowing m9 to be defined as the bolting metamer (Fig. 1). Internode lengths for m9 to m15 were measured at daily intervals from when each internode was visible (about 1 mm) to when it stopped growing.

The resulting data for one plant plotted against time (measured in hours from sowing [hfs]) are shown in Figure 2A. The same data plotted on a logarithmic scale indicated that the rate of growth was exponential during early phases and then declined (Fig. 2B). Many growth processes of plants follow such sigmodal pattern; we achieved the best fit (r² > 0.9) using the sigmoidal Boltzmann function supported by the Origin software. This function has the form:

where A is the final (maximal) size, t_m is the time when the organ attains half of its maximal size (corresponding to the inflection point in linear plots), and k controls the relative elemental growth rate, also known as the specific growth rate (Richards and Kavanagh, 1945; Hejnowicz and Romberger, 1984; Fig. 2, C and D).

Figure 2.

Internode length (int l) plotted against time on a linear scale (A) and on a logarithmic scale (B). The Boltzmann function on a linear scale (C) and on a logarithmic scale (D). All lengths are in millimeters.

The internode data from five plants was fitted with Boltzmann functions, allowing averages for each of the parameters (A, t_m, and k) to be estimated for m9 to m15. The growth rate in internode length during the exponential phase of growth was similar for all metamers (k = 0.06 ± 0.007 h⁻¹; Fig. 2B). This corresponds to a doubling time of 11.3 ± 1.2 h (doubling time = ln 2/k). The maximum internode length was about 64 ± 6 mm for m9, 39 ± 18 mm for m10, and about 10.6 ± 1.6 mm for flower-bearing metamers (m11 onward).

Internode shape could be captured by length-to-width ratio, as internodes are approximately cylindrical. Log-log plots of width against length for each internode gave a reasonable fit to a straight line (r² > 0.9), indicating that the ratio of the relative rates of growth in length and width was approximately constant (an allometric relationship). The mean slope of such plots was 0.2 ± 0.08, indicating that all internodes from m9 onward grew about 5 times faster in length than width.

Leaves

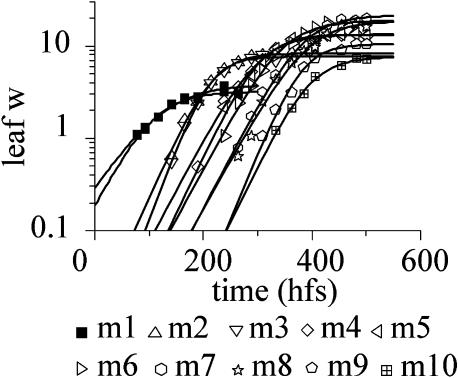
There were typically 11 leaves on the main axis of each plant (i.e. leaf number = 11). These comprised two cotyledons (m0 and m1), seven rosette leaves (m2–m8), and two cauline leaves (m9 and m10; Fig. 1). Flower-bearing metamers (m11 onward) did not have subtending leaves. The most convenient scaling factor for leaf growth was width, as this could be readily measured from images of plants photographed from above. Measurements were taken at the point of maximum width from when each leaf was about 1 mm wide to when it attained its final size. As with internode length, the data on leaf width could be fitted with the Boltzmann function (Fig. 3). Parameters were averaged over five plants.

Figure 3.

Leaf width (leaf w) of the main-stem metamers plotted against time (hfs) and fitted with the Boltzmann function.

The growth rate in leaf width during the exponential phase was similar for m2 to m10 (k = 0.03 ± 0.007 h⁻¹, corresponding to a doubling time of about 23 h). The maximum leaf width, A, was about 8 mm for m2 and m3, gradually increased to about 23 mm for m8, and then decreased with formation of the cauline leaves to about 14 mm for m9 and 9 mm for m10.

Leaf shapes at various developmental stages were obtained from dissected plants. Leaves of each metamer were removed when they were at a width of approximately 1 mm, 3 mm, 6 mm, and the final leaf width (Fig. 4A). To capture their shape, curves (B-splines with endpoint interpolation) were manually fitted to the outside edge of the left half of the leaf outlines using eight points (e.g. Fig. 4B). This provided reference shapes at discrete time points throughout the growth of the leaf. Shapes between these time points were then derived by linear interpolation (see modeling section below).

Figure 4.

A, Four dissected leaves at widths of 1 mm, 3 mm, 6 mm, and the maximum leaf width for each metamer normalized by height. B, The mature leaf of m5, with an eight-point B-spline fitted to its outline, and the resulting outline curve.

Lateral Branches

Internodes

The axillary buds of metamers m4 to m10 on the main stem grew out to form lateral branches. The m4 branch formed two leaves at its base, followed by several leaves separated by visible internodes. The bolting metamer for this branch was therefore referred to as m4-2. Bolting metamers for other branches were typically m5-2, m6-1, m7-0, m8-0, m9-0, and m10-0. Internode length was taken to be zero up to the bolting metamer.

For each lateral branch, internode lengths for leaf-bearing metamers formed after the bolting metamer were measured daily. The measurements were plotted against time and fitted with the Boltzmann function. The growth rates during the exponential phase of growth were similar to each other and to those of the main stem (k = approximately 0.065 ± 0.02h⁻¹, compared to k = approximately 0.06 ± 0.007 h⁻¹ for the main stem). The maximum internode length, A, was progressively smaller for consecutive metamers along each branch (data not shown).

Internode shape for lateral branches was assessed using a log-log plot of internode width against internode length for all metamers on each branch. As with the main stem, internode length grew about 5 times faster than width (mean ratio = 0.2 ± 0.08).

Leaves

The number of leaves on each lateral branch was found to decrease from six at the base of the plant (m4 branch) to one at the top of the plant (m10). Each consecutive branch typically had one leaf less than its predecessor.

Leaf widths for each metamer of the lateral branches were measured daily, plotted against time, and fitted with the Boltzmann function (data not shown). The maximum leaf width decreased with increased metamer number along each branch, and the specific growth rate was similar to that of the main stem (k = 0.02 ± 0.005).

The final shape of each leaf on each lateral branch was estimated from dissected plants (Fig. 5). Eight-point splines were fitted to the outline of flattened mature leaves, as for the leaves on the main axis (Fig. 4).

Figure 5.

Mature leaf shapes of the m4 to m10 lateral branches. Rows refer to leaves from the same branch of index n, while columns refer to leaves at the same position along each branch. Thus, the leaf in the bottom left corner is the first leaf of branch m4 (i.e. m4-0).

Flowers

Main Stem

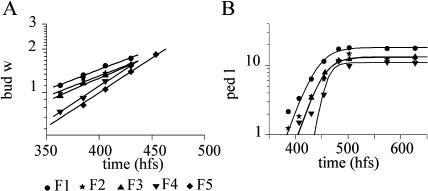
All flowers were considered to develop with a similar developmental time line following their initiation. The first five flowers of the main stem (m11–m15) from five plants were photographed daily and measurements taken from the images. During early stages (before flower opening), bud width was chosen as a convenient scaling factor as it increased exponentially with time (k = 0.004 ± 0.0002 h⁻¹; Fig. 6A). After flower opening, bud width did not change very much and therefore ceased to be a useful scaling factor.

Figure 6.

Flower measurements from a single plant taken at daily intervals and plotted against time (hfs). A, Bud width fitted with an exponential function. B, Pedicel length fitted with the Boltzmann function.

For later stages of flower development, pedicel length was used as a scaling factor. Changes in pedicel length could be measured from just before flower opening, when the pedicels were a few millimeters long (Fig. 6B). The Boltzmann function was found to fit pedicel length growth from 4 mm onward.

The scaling factors chosen for the organs were sepal width, petal width, anther width, pedicel length, stamen filament length, and carpel length. Each of these scaling factors was determined from photographs of dissected flowers that had previously had their width and pedicel length measured. This allowed time points to be assigned for individual flower organ measurements. For convenience these were displayed aligned to the time course of the first flower (Fig. 7). Measurements on dissected buds also allowed pedicel length to be estimated for early stages.

Figure 7.

Organ measurements from dissected flowers aligned with the time course of flower 1 using bud width (▪) or pedicel length (□) data. In A to D, data are fitted with the Boltzmann function: A, sepal width (sep w); B, petal width (pet w); C, anther width (ant w); D, carpel length (car l). In E and F, data are fitted with an exponential function during the early phase of growth and the Boltzman function during the later phase. E, Pedicel length (ped l); F, filament length (fil l). The switch point between phases is shown with a black arrow. Time of flower opening is indicated by white arrow.

Data for four of the flower organ scaling factors, sepal width, petal width, anther width, and anther length, could be fitted with the Boltzmann function (Fig. 7, A–D). However, the other two scaling factors, pedicel length and filament length, could not be fitted well with a single function as they exhibited a more complex pattern of growth. This involved an early exponential phase with a relatively low growth rate, followed by a later phase described by a Boltzman function with a higher growth rate.

For pedicel length, the switch from low growth rate (k = approximately 0.005 h⁻¹) to high growth rate (k = approximately 0.06 h⁻¹) occurred at about 20 h before flower opening (Fig. 7E). For stamen filament length, the switch from the low (k = approximately 0.006) to high (k = approximately 0.09) growth rate occurred at about 60 h before flower opening (Fig. 7F).

As a first approximation, the shape of pedicels, stamen filaments, and carpels was considered to be cylindrical and could therefore be captured by length-to-width ratios. Log-log plots of width against length for these organs (data not shown) indicated that the pedicels and carpels grew about twice as fast in length than width, while stamen filaments grew about three times faster in length than width.

Sepal and petal shapes were determined using similar methods to those used for the leaves. Petals and sepals at four different stages of growth were removed from flowers and curves fitted around the outside edge of each organ (Fig. 8). The scaling factor (width) for each dissected organ was also determined, allowing the stages to be assigned time points.

Figure 8.

Petals and sepals dissected and flattened at four stages of development with a spline curve fitted to the left half of the shape.

Lateral Branches

To relate flower development on each lateral branch to that of the main stem, the first flower bud of each lateral branch was photographed at a time when the bud was between 1 to 2 mm wide. By comparing the timing and bud width obtained from these images with the time course of flower development on the main stem (Fig. 6A), the delay in initiation of flowering on lateral branches relative to the main stem could be estimated. This showed that flower formation on the coflorescences, m9 and m10, initiated approximately 70 h after that on the main stem. For metamers below m9, this delay in flower formation on each lateral branch increased progressively, up to approximately 130 h for the m4 lateral branch. In the model, the time course for individual flower development on the lateral branches was considered to be similar to that on the main inflorescence.

Plastochron and Phyllotactic Angle Calculations

The time course of scaling factors for leaf and flower growth was used to estimate the time interval (plastochron) between the development of successive metamers. For metamers bearing leaves (m1–m10), the time at which leaf width attained a particular value (log₁₀ of leaf width in mm = 0.1) was calculated according to the relevant growth function. The difference in this time for successive metamers gave an estimate of the plastochron (Fig. 9, bottom plot, plastochrons m0–m10).

Figure 9.

Average plastochron (▪) and angle (□) between successive metamers plotted against metamer interval. Dotted line shows the golden angle of approximately 137.5°.

For metamers above m10, plastochrons were estimated using three scaling factors: the times at which a particular flower bud width (log₁₀ of bud width in mm = −0.05), pedicel length (3 mm), or internode length (5 mm) were attained. Plastochron values obtained from these different factors were similar to each other (13.6 ± 2.9 h, 10.9 ± 2.6 h, and 9.7 ± 5.3 h, respectively). They were therefore averaged using four flowers from five plants (i.e. a total of approximately 20 flowers) and plotted against metamer number (Fig. 9, bottom plot, plastochrons F1 and beyond). The results show that for the leaf-bearing metamers, plastochron values initially oscillate and then settle at a value of about 27.9 ± 13.5 h for m9 and m10. The interval between the last leaf and the first flower-bearing metamer is of a similar duration (29.1 ± 7.5 h). The subsequent metamers appear with a plastochron of 12 ± 3.1 h.

Early fluctuations were also observed for the divergence (phyllotactic) angles. Angles between successive leaves or flowers of the first 14 metamers were estimated from digital images and averaged over five plants (Fig. 9, top plot). The cotyledons and the first pair of leaves (metamers m1–m5) appear in an approximately decussate arrangement, which gradually changes to spiral phyllotaxy with the divergence angle converging to 138.2°, close to the golden angle of 137.5°. The angles are inversely correlated with plastochron; a large divergence angle is associated with a short plastochron.

Model Description

General Description

A developmental model of Arabidopsis, based on the measurements presented above, was written in the l-system-based modeling language L+C (Karwowski and Prusinkiewicz, 2003). Following the methodology of l-system model construction according to measured architectural data (Prusinkiewicz et al., 1994), the input to the Arabidopsis model consists of a developmental description of individual plant components (modules). The model includes four basic module types: apices, internodes, leaves, and flowers. Each flower is further decomposed into modules representing its individual parts: the pedicel, the carpel, as well as the sepals, petals, and stamens, when present. The simulation program assembles these components into a growing three-dimensional structure of the whole plant. At the beginning of the simulation, this structure consists of a single apex. As the simulation proceeds, the apex creates the main plant axis as a sequence of internodes with the associated lateral apices and optional leaves. The lateral apices may produce lateral axes or flowers, as depicted in the plant map (Fig. 1).

Labeling of Apices

It follows from the developmental nature of the model that the axes and their individual metamers are produced by the apices. Each apex A is associated with three indices o, n, and i, where o is the order of the axis to which the apex belongs (o = 0 for the main axis, 1 for the lateral branches), n (only meaningful for lateral axes) is the position of the parental metamer that supports the axis, and i is the current position of the apex along its axis.

The initial apex has the identity A(0,0,0). The index i is incremented by one every time the apex creates a metamer; thus, the identity of the main apex after it has produced i metamers is A(0,0,i). The lateral apex created by the main apex A(0,0,i) has identity A(1,i,0); that is, o is set to 1, n is set to the value of i of the parental apex, and i is set to zero. These indices are used to number the metamers the apex creates consistently with the numbering scheme shown in Figure 1. For example, apex A(1,7,2) creates metamer m7-2.

Generation and Structure of Metamers

During development, the main apex A(0,0,i) produces metamer mi, and has its state updated to A(0,0,i+1). The metamers can be of vegetative or flowering type. A vegetative metamer mi consists of a leaf-supporting internode I_L(0,0,i), a leaf L(0,0,i), and a lateral apex A(1,i,0). A flowering metamer mi consists of a flower-supporting internode I_F(0,0,i), and a flower F(0,0,i). Lateral apices A(1,n,i) produce metamers mn-i in an analogous manner. The position of the first flowering metamer within axis (o,n) is identified by parameter Rm[o,n], associated with that axis.

Implementing Module Growth

Module growth is simulated according to experimentally determined parameter values, such as constants for Boltzmann growth curves, reference shape data, allometric constants, and divergence angles. For leaves and leaf-supporting internodes, a module's indices are used to access the data specific to this module.

Flower components and flower-supporting internodes are treated collectively rather than individually; all modules of the same type are simulated according to a shared data set, taking into account different initiation times of the modules. The initiation time of the first flower and its supporting internode on the main axis is specified explicitly in the data set. Parameter Rd[o,n] associated with each lateral axis specifies the delay in the initiation time of its first flower relative to that of the main axis. Successive flowers along each axis are further delayed by a fixed plastochron.

Curving of plant axes, as well as elevation angles and downward bending of the leaves, have been estimated according to the appearance of Arabidopsis plants.

Interpolating Shapes

The shape of internodes, pedicels, stamen filaments, and carpels was approximated using cylinders characterized by length and width (diameter). At each simulated time, the scaling factor (anther width, pedicel length, stamen filament length, and carpel length) was estimated from time-course curves (Fig. 7), and the remaining parameter was estimated using allometric relations.

The shapes of leaves, petals, and sepals were obtained by interpolating their B-spline organ contours. The leaves were considered individually, using a separate set of contours for each metamer, whereas the petals and sepals were treated summarily, using the same set of contours for all flowers. When the organs were measured, each contour was associated with the organ's width, serving as the scaling factor. At each simulated time, the width of the organ was estimated from time-course curves (in the same manner as the scaling factors for the cylindrical organs). This width was compared to the widths of the sampled organs to find the closest organ that was narrower and the closest that was wider. The control points of the associated contours were then linearly interpolated to estimate organ shape at the current width, and an organ of that shape was drawn at the organ's width. If the organ was narrower than the narrowest or wider than the widest measured organ, a single contour was scaled to the desired width.

Model Visualization

A comparison of sample developmental stages of Arabidopsis plant with the model is shown in Figure 10. Images of the model represent direct output of the modeling program, as observed during the simulation of development. The comparison indicates that the model captures the architecture of a growing Arabidopsis plant faithfully. Discrepancies are due primarily to the fact that the model represents an average plant, combining the data from several measured plants, whereas the photographs obviously represent individual plants. Furthermore, the model does not reproduce the nutation of stems, which strongly affects their shape at any time, and details of plant organs (venation and trichomes).

Figure 10.

Comparison of sample Arabidopsis plants (A, C, E) with the model (B, D, F). A and B, at 264 hfs; C and D, at 417 hfs; E and F, at 491 hfs. Scale bar = 1 cm.

DISCUSSION

We have constructed a three-dimensional spatio-temporal model of Arabidopsis shoots, calibrated to experimental data. The model simulates and realistically visualizes the development of the plant (main axis and first-order branches), with the individual organs described from early stages (approximately 1 mm in size) to maturity. The model integrates a large amount of experimental data, including sizes and shapes of individual organs (internodes, leaves, and flower organs) measured at frequent time intervals.

Construction of a model operating in continuous time created the problem of interpolating the experimental data. In the case of scalar measurements, such as lengths or widths, this interpolation was accomplished by fitting growth curves to the data. In addition, allometric relations were used to correlate the length and width of some organs (internodes, pedicels, stamens, and carpels) and thus reduced the number of independent variables in the model.

The interpolation of leaf and petal shapes was more difficult. It was addressed by approximating organ contours using spline curves and interpolating positions of their control points over time.

Another problem arose from the destructive nature of measurements made in the early stages of organ development. This was addressed by correlating size data obtained in a nondestructive manner with the shape data obtained by dissecting plants at specific developmental stages.

Our model represents in an integrated manner several aspects of Arabidopsis development and morphology. At the architectural level, these include the correlated fluctuation in divergence angle (Medford et al., 1992; Callos and Medford, 1994) and plastochron during early Arabidopsis growth, the basipetal sequence of the switch to flowering in lateral branches, and the gradual changes in the number of cauline leaves supported by consecutive branches. At the organ level, our model captures variation of leaf shapes in space (along the stem and in lateral branches) and over time.

Our model is constructed according to the values of measured parameters averaged over several plants. Since we also know the variances, it is tempting to select model parameters according to the measured distributions (mean values and standard errors) in an attempt to capture the variability of Arabidopsis form. Nevertheless, although incorporation of stochastic variation into the model is technically simple, it is questionable how meaningful the resulting simulations would be, since in reality parameter values are likely to be correlated, and our model does not reflect these correlations.

In addition to providing a reference for the kinetics of Arabidopsis development, this descriptive model may also serve as a stepping stone for constructing future mechanistic models, with the aim of better understanding plant development in genetic, physiological, ecological, and evolutionary terms. In these applications, the descriptive model will provide a framework into which mechanistic components can easily be plugged. For example, the descriptive model makes use of the measured divergence angles for leaves and lateral inflorescences subtended by them. The observed inverse correlation between divergence angle and plastochron suggests that the timing and positioning of primordia are interdependent; primordia that are initiated close together in time are positioned far apart in space. This may reflect the dynamics of a spacing mechanism in which formation of a primordium is influenced by where and when other primordia have formed (Douady and Couder, 1996). A mechanistic component might thus be built into the model to generate the observed values of plastochrons and divergence angles according to a phyllotactic mechanism. Such a mechanism should also be consistent with molecular data (Reinhardt et al., 2003). Similarly, the basipetal pattern of the switch to flowering in lateral branches, which is currently reenacted according to experimental data, might be generated by simulating an auxin-related mechanism of apical dominance (Thimann and Skoog, 1934; Booker et al., 2003). The development of inflorescences could be controlled by a model component that simulates interaction between crucial genes, such as LFY, TFL1, and AP1 (Schultz and Haughn, 1993; Ratcliffe et al., 1999). The substitution of mechanistic components for the descriptive components of this model may thus provide a path for a manageable, incremental development of mechanistic models of the whole plant. Such models may help us understand in causal terms phenomena that depend on the integration of many functional and structural components, such as developmental responses of plants to environmental conditions and evolutionary responses to selective pressures.

Conclusion

We have presented a descriptive developmental model of Arabidopsis shoots. The model integrates a large amount of experimental data pertinent to the geometry and the timing of development of Arabidopsis plants. Consequently, the model can be used as a reference for the kinetics of Arabidopsis development. In addition, the model can act as a stepping stone for constructing future mechanistic models, with the aim of better understanding plant development in genetic, physiological, ecological, and evolutionary terms.

MATERIALS AND METHODS

Data Acquisition

Arabidopsis (Arabidopsis thaliana) Landsberg erecta seeds were sown in plugs and thinned out to one seedling per plug on germination. The plants were grown under continuous light at 25°C. After germination, five seedlings were selected for continuous monitoring of growth. These five plants (calibration plants) were photographed daily to obtain measurements of the metamers of the main axis and lateral branches. To obtain leaf and flower organ shapes, sample plants from the same population were taken each day and dissected. The removed leaves and flower organs were flattened between glass plates and photographed.

Photographs were taken with a Nikon Coolpix 995 digital camera and the growth measurements were obtained from the digital images with the aid of a program written in Matlab. Shapes of leaves, sepals, and petals were determined using an interactive curve editor. The user manipulated eight control vertices of a cubic B-spline with endpoint interpolation to match accurately an organ's border in an overlaid image. Continuous measurements of internodes, leaves, pedicels, and carpels at each time point were fitted with functions describing their growth using Origin Version 7 (OriginLab).

Modeling

Simulations were executed using program lpfg, which is incorporated into plant-modeling packages l-studio (for Windows) and vlab (for Linux), distributed by the University of Calgary (Prusinkiewicz, 2004). The model was specified in the L+C language (Karwowski and Prusinkiewicz, 2003). The simulations results are visualized as a three-dimensional plant structure, which can be interactively viewed from different angles and animated to illustrate the developmental processes.

For leaves and leaf-supporting internodes, a module's indices are used to access the data specific to this module. These data are read from a file in the AMAPmod format (Godin and Guédon, 2000), which organizes the listing of module parameters according to the topological position of each module within the branching structure. The entry specific to each leaf also includes a reference to the file that lists the sequence of reference shapes for that leaf. In contrast to leaves, all flowers shared a common data set.