Dynamics of the acetylcholine receptor pore at the gating transition state

Abstract

Neuromuscular acetylcholine receptors (AChRs) are ion channels that alternatively adopt stable conformations that either allow (open) or prohibit (closed) ionic conduction. We probed the dynamics of pore (M2) residues at the diliganded gating transition state by using single-channel kinetic and rate-equilibrium free energy relationship (Φ-value) analyses of mutant AChRs. The mutations were at the equatorial (9′) position of the α, β, and ε subunits (n = 15) or at sites between the equator and the extracellular domain in the α-subunit (n = 8). We also studied AChRs having only one of the two α-subunits mutated. The results indicate that the α-subunit, like the δ-subunit, has a region of flexure near the middle of M2, that the two α-subunits experience distinct energy barriers to gating at the equator (but not elsewhere), and that the collective subunit motions at the equator are asymmetric during the AChR gating isomerization.

The acetylcholine receptor (AChR) is an allosteric protein that couples a change in affinity for ligands at the two transmitter binding sites with a change in conductance of its pore (1–3). To understand the mechanism of AChR gating, it is important to illuminate the complex molecular motions that link the stable closed (C) and open (O) conformations. The pore-lining, M2 segment has long been recognized as a critical structure in AChR gating (4). In particular, the equatorial 9′ position (see Fig. 1A) is a highly conserved Leu (in all five subunits) that forms a flexible region (a “kink”) in the otherwise helical segment (5–7). It has been suggested that the equatorial region of M2 serves as the main barrier to ion permeation in the closed-channel conformation (5, 8), whereas substituted-Cys-accessibility studies place the “gate” closer to the cytoplasmic limit of M2 (9). Mutations at the M2 9′ position have been shown to left-shift the whole-cell dose–response curve and cause a substantial increase in open channel lifetimes (10–13) and also affect desensitization (11, 14). However, the effects of these 9′ mutations on gating have not been analyzed at the level of equilibrium and rate constants.

Fig. 1.

Kinetic analyses of α9′ double mutants. (A) Locations of residues in the α_ε-subunit [Protein Data Bank ID code 2bg9 (28)]. Top to bottom: W149 is at the transmitter binding site, and S269(27′), V259(17′), and L251(9′) are in the M2 segment. The arrow (30 Å) marks approximately the membrane and the pore. (B) Continuous, low-time resolution view of currents from AChRs having a L9′T mutation in both α-subunits (inward current, down). Boxed cluster is shown at higher time resolution in C.(C) Clusters of openings from AChRs having different 9′ mutations in both α subunits. The WT residue (Leu) is boxed. (D) REFER plots for the α9′ double-mutant series. The solid line/filled symbols pertain to a membrane potential of –100 mV, and the dashed line/open symbols pertain to a membrane potential of +60 mV (see Fig. 7).

There is a spatial gradient in the extent to which AChR mutations that change the gating equilibrium constant alter the opening vs. the closing rate constant (15, 16). The closing rate constant is increasingly affected as one proceeds down the length of the protein, from the transmitter binding sites to the cytoplasmic limit of the transmembrane domain. Further, residues appear to be organized into contiguous domains within which all members have a similar behavior with regard to the effect of mutations on the opening vs. the closing rate constant (17). In some cases, these domains overlap secondary structural elements (e.g., helices), whereas in other cases such a direct correlation between function and structure is not apparent. The boundaries between these domains appear to be discrete (18).

For a two-state reaction, the extent to which a perturbation alters the forward vs. the backward rate constant is parameterized by Φ, a fraction between 0 and 1 that is the correlation between the log of the forward rate constant and the log of the equilibrium constant for a series of point mutations. Φ quantifies the extent to which the perturbed site resembles energetically (with respect to its sensitivity to the perturbation) the product in the transition state ensemble (TSE) of the reaction. For example, if the perturbed site has a change in TSE energy that is equal to that of the O conformation, then the closing rate constant will not change and Φ = 1. Insofar as energy is a reflection of structure, and assuming a single transition state (18), fractional Φ-values imply the existence of intermediate structures in which the contacts that exist at the reaction's end states, C and O, are incompletely formed (19).

Further interpretation of Φ-values requires assumptions about the underlying reaction mechanism. Although the events that constitute AChR gating are not known, many features can be rationalized by a scheme in which a small number of rigid-body domains sequentially undergo two-state structural transitions (20). These features include the two-state kinetic behavior in patch-clamp recordings (21), the presence of discrete domains within which residues all have the same Φ-value (17), the approximately longitudinal organization of the Φ-values (15, 18), and an apparent upper limit to the channel-opening rate constant of ≈1 μs^–1 (22). Recently, it was shown that with such a reaction scheme there is a relationship between Φ and the position of the perturbed reaction within the chain, with higher Φ-values arising from the perturbation of earlier steps in the sequence (23). Thus, Φ reveals the temporal order of conformational change assuming that (i) there is a single TSE, (ii) domain motions are two-state and completely coupled, and (iii) perturbations change only the depth of a single well in the TSE. More complicated mechanisms, for example, in which the domains fluctuate semi-independently, where domains adopt more than two conformations, or where mutations alter multiple wells and barriers of the TSE, could obviate the inference of a temporal sequence from Φ-values.

Φ-Value analyses of many sites in the AChR suggest that the C → O gating conformational change occurs as a coarse-grained, Brownian conformational “wave,” with groups of residues in the extracellular domain moving in advance of those in the membrane domain (15–17). Analysis of δ-subunit M2 mutants showed that residues in the extracellular half of this segment have a Φ-value of ≈0.3, whereas those in the intracellular half (including 9′) have a Φ-value of ≈0.0, with a break point near the middle of the segment (18). Here, we use single-channel kinetic analyses, combined with Φ-value analyses, to probe the gating dynamics of 23 different AChR constructs having mutations in the upper half of the M2 segment of the α-subunit, and the equatorial, 9′ residues of the α, β, and ε subunits.

Methods

Mutagenesis and Expression. Mutations to mouse AChR subunit cDNAs were engineered by using the QuikChange Site-Directed Mutagenesis Kit (Stratagene). Human embryonic kidney fibroblast cells (HEK 293) were transiently transfected by using calcium phosphate with 4.0 μg of total cDNA per 35-mm culture dish, applied for 10–12 h. The subunit ratio was 2:1:1:1 (α:β:δ:ε) plus 0.5 μg of GFP.

Electrophysiology. Cell-attached patch recordings began ≈24 h after transfection (cell-attached, 22–24°C). The bath and pipette contained 137 mM NaCl, 0.9 mM CaCl₂, 2.7 mM KCl, 1.5 mM KH₂PO₄, 0.5 mM MgCl₂, and 8.1 mM Na₂HPO₄ (pH 7.3). Only the pipette solution contained agonist. Except where noted, cells were held at a pipette potential of +85 mV (estimated membrane potential, –100 mV). Single-channel currents were low-pass filtered at 20 kHz and digitized at 50 kHz (SCB-68, National Instruments, Austin, TX).

Most of the mutations increased the gating equilibrium constant; thus, we used the low-efficacy agonist choline at a saturating concentration (20 mM) to estimate the gating rate constants (21, 24). At this concentration the estimated inverse association rate is less than the imposed “dead time” (see below); hence, essentially all events can be attributed to fully liganded AChRs.

Kinetic Analyses. All kinetic analyses were carried out by using qub software (www.qub.buffalo.edu). At 20 mM choline, openings occur in clusters with gaps between clusters reflecting epochs during which all of the AChRs in the patch are desensitized. Clusters of one-channel openings were selected after invoking a critical closed-interval duration (t_crit) of 50 ms. The selected currents were further low-pass filtered to 12 kHz and were idealized by using the segmental k-means algorithm (25) with a C ⇄ O model (starting rates = 10 s^–1).

The opening (β) and apparent closing (α_B) rate constants were estimated (92 patches from 27 different constructs) from the idealized interval durations by using a maximum-interval likelihood algorithm (26) after imposing a dead time of 33–75 μs. With the exceptions described below, intervals within clusters were mono-exponentially distributed, and rate constants were estimated directly by using a two-state, C ⇄ O model (starting rates = 100 s^–1). In some cases, a second closed state was added to account for a short-lived desensitized state (27). Intracluster intervals from the 9′ (αL251) mutants M, C, T, and A had one open and three shut components (see Fig. 2). The fastest shut component was absent from hybrid clusters in 6 of 28 patches even though it was always apparent in the double-mutant clusters from these same patches. We used a model with two or three uncoupled C states and one O state to estimate the rate constants.

Fig. 2.

Kinetic analyses of α17′ double-mutants. (A) Example clusters of α17′ double mutants activated by a saturating concentration of choline (20 mM). Open is downward. The WT residue (Val) is boxed. All mutations increased the cluster open probability by increasing the opening rate constant and decreasing the closing rate constant (Table 1). The kinetics for the small side chains (G, A, and S) appear by eye to be faster than the others, which we attribute to a catalytic effect (15, 18). (B) REFER plot for the α17′ mutant series. The Φ-value for the whole series is of 0.63 ± 0.18 (solid line). Eliminating the G, A, and S data points does not change significantly the Φ-value (0.61 ± 0.04; dashed line).

In WT AChRs, 20 mM choline is greater than the equilibrium dissociation constant for fast, open-channel block by this agonist (K_B) (21). Consequently, the apparent single-channel current amplitude (i_B) is reduced, and the apparent closing rate constant (α_B) is decreased compared with low choline concentrations where block is negligible. The α-subunit M2 17′ and 27′ residues do not face the permeation pathway (28). For these mutants we assumed that K_B was the same as the WT, and Φ-values were estimated from the slope of a plot of log β vs. log(β/α_B). The α-subunit M2 9′ mutants, however, had different K_B values (see below). To correct for channel block in these mutants, we measured the intrinsic current amplitude (i₀) using a choline concentration (200 μM) where channel block is insignificant. AChRs close relatively slowly when blocked; thus, the block-free closing rate constant (α) is α_B(i₀/i_B), and Φ-values were estimated from a plot of log β vs. log(β/α).

Hybrid AChRs. Cells were cotransfected with both WT and mutant α-subunit cDNAs in 5:1 ratio, together with WT β-, ε-, and δ-subunit and GFP cDNAs. A mixture of AChRs was expressed having zero, one, or two mutant α-subunits (plus WT non-α subunits). For the 27′ mutants, these populations were distinguished on the cluster mean open probability (P_o) (Fig. 1B). For the 9′ mutants, recordings at 20 mM choline showed four distinct populations that were distinguished by their current amplitudes (see Fig. 4B), whereas currents elicited by 200 μM choline exhibited only a single current amplitude (i₀). The multiple amplitudes at 20 mM choline arose from different K_B values for the four types of AChR construct: WT, double-mutant, and two different hybrids (α_ε or α_δ mutated). Clusters were segregated into separate populations by using the segmental k-means algorithm with only P_o (27′) or current amplitude (i_B; 9′) as the discrimination criterion. Clusters with mean values of >1 SD from the population mean were discarded. For each 9′ mutant, a K_B value (mM) was calculated from the relationship: i_B = i₀/(1 + 20 mM/K_B) (Table 1).

Fig. 4.

Kinetic analyses of α9′ hybrids. (A) Clusters of openings from AChRs having two, one, or zero α9′ mutation (s). For each mutation, within a single patch there are four cluster populations having distinct kinetics and current amplitudes. The intermediate two populations reflect AChRs that are hybrids, having a point mutation in either α_ε or α_δ.(B) Current amplitude histogram for one patch (αL9′T). The hybrids each have distinct amplitudes because of differential equilibrium channel-block by the agonist (Table 1). (C) REFER plots for the hybrid populations. The WT side chain (Leu) is boxed. At the αM2–9′ position each hybrid has a distinct Φ-value, indicating that the two α-subunits have progressed to different extents at the transition state of the gating reaction.

Table 1. Gating rate and equilibrium constants.

Construct	Opening rate constant β, S-1	Closing rate constant αB, S-1	Corrected α, S-1	iO, pA	iB, pA	KB, mM	Gating equilibrium constant, Θ, uncorrected/corrected	Θ ratio, mut/WT	N
WT	121	834	2,583	7.0	2.3	9.5	0.15/0.05	1	4
α9′AHyb 2	566	29.2	91.8	8.2	2.6	9.3	19.4/6.2	124	4
α9′AHyb 1	131	14.9	64.1	8.2	1.9	6.1	8.8/2.0	40	4
α9′TDbl	472	17.7	31.8	7.0	3.9	25.2	26.7/14.8	296	3
α9′THyb 2	310	202	420	7.0	3.4	18.6	1.5/0.74	14.8	6
α9′THyb 1	134	59.1	155	7.0	2.7	12.3	2.3/0.86	17.2	6
α9′TOut	569	83.7	—	—	—	—	6.8	—	3
α9′MDbl	414	47.7	118	7.2	3.0	14.3	8.7/3.5	70	3
α9′MHyb 2	232	231	664	7.2	2.5	10.6	1.0/0.35	7.0	4
α9′MHyb 1	121	73.3	245	7.2	2.2	8.5	1.7/0.49	9.8	4
α9′MOut	332	289	—	—	—	—	1.1	—	1
α9′CDbl	339	47	136	7.8	2.7	10.6	7.2/2.5	50	3
α9′COut	359	150	—	—	—	—	2.4	—	3
α9′VDbl	69	930	3,408	6.6	1.8	7.5	0.07/0.02	0.4	2
α9′IDbl	147	1247	3,897	5.0	1.6	9.4	0.12/0.04	0.8	4
α17′ADbl	1,291	687	—	—	—	—	1.9	12.7	4
α17′DDbl	1,683	149	—	—	—	—	11.3	75.3	6
α17′GDbl	1,357	1,105	—	—	—	—	1.2	8	3
α17′SDbl	2,041	814	—	—	—	—	2.5	16.7	4
α17′TDbl	202	404	—	—	—	—	0.5	3.3	2
α17′YDbl	1,109	164	—	—	—	—	6.8	45.3	3
α27′IDbl	2,396	139	—	—	—	—	17.2	115	4
α27′IHyb	627	401	—	—	—	—	1.6	10.7	4
ε9′A	563	53	232	7.0	1.6	5.9	10.6/2.4	48	3
ε9′M	337	81.7	318	7.0	1.8	6.9	4.1/1.1	22	2
β9′M	547	111	472	6.8	1.6	6.3	4.9/1.2	24	1
β9′N	622	86	356	6.5	1.6	7.2	7.2/1.7	34	2

The rate constants were obtained from single-channel currents elicited by 20 mM choline. The apparent closing rate constant, α_B, is slower than the value at low choline concentrations because of channel block by the agonist. i_O and i_B are the open-channel current amplitudes at 200 μM choline (negligible channel block) and 20 mM choline, respectively. K_B denotes the calculated value of the equilibrium dissociation constant for channel block by choline at — 100 mV (see Methods). For the Ala double mutant, K_B was 16.6 mM. The subscript “Out” refers to parameters measured at a depolarized membrane potential (+60 mV; see Fig. 7). A closing rate constant corrected for channel-block (α) was calculated for all 9′ constructs (see Methods). The rate constants are means, and N is the number of patches.

Results and Discussion

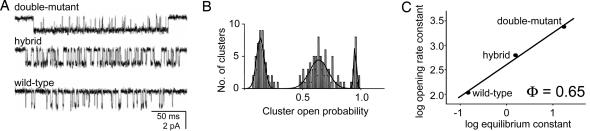
α-Subunit Equator. Fig. 1B shows continuous single-channel currents (elicited by 20 mM choline) from AChRs having the mutation L9′Tinboth α-subunits. The channel-opening rate constant for this doubly mutated construct was 472 s^–1, and the channel-closing rate constant was 32 s^–1, compared with 121 and 2,583 s^–1, respectively, for WT AChRs. The diliganded gating equilibrium constant (Θ), which is the ratio of the opening/closing rate constants, is 296-fold larger in αL9′T compared with the WT, with this change being caused mainly by an 81-fold decrease in the closing rate constant.

Fig. 1C shows example clusters of openings from AChRs having different side-chain substitutions at the 9′ position of both α subunits. The Val and Ile substitutions result in WT-like gating behaviors, whereas the Met and Cys substitutions increased Θ but to a lesser extent than Thr. We were unable to measure the gating rate constants for the α9′ Ala double mutant because of the presence of subcurrents. When the gating rate constants for the entire mutant series were recast as a rate-equilibrium free energy relationship (REFER) (Fig. 1D), the plot was approximately linear with a slope (Φ-value) of 0.26 ± 0.04. If we assume that AChR gating is a sequence of coupled reactions, the small Φ-value for the α9′ mutant series suggests that, on average, the two α-subunit equatorial residues move relatively late, approximately with the δ-subunit 12′ residue (Φ ≈ 0.28) (18).

We used choline as the agonist because the channel-opening rate constant with acetylcholine is too fast to be measured reliably. Φ-Values for unliganded gating are ≈1 everywhere (29), which raises the possibility that the nature of the ligand at the binding site can influence the measured Φ-values. However, it has been shown for a position in αM4 that the diliganded gating Φ-values are similar for AChRs activated by choline or by acetylcholine (16). It should be kept in mind that all of the Φ-values in this work pertain to fully liganded AChRs having choline at the transmitter binding sites.

Some of the mutants (M, C, T, and A) had more than one shut component within clusters, which made the identification of the gating rate constants ambiguous. In WT diliganded AChRs, depolarization decreases the gating equilibrium constant (≈e-fold/100 mV) mainly by increasing the channel closing rate constant (15, 30). We compared the gating rate constant estimates of the αL9′T double mutant at two membrane potentials, –100 and +60 mV. The predominant, gating C ⇄ O transition in this construct had a similar voltage-sensitivity (see Fig. 7, which is published as supporting information on the PNAS web site) and Φ-value (Fig. 1D) as the WT. A similar pattern was seen for the M and C double mutants.

α-Subunit 17′ and 27′. The gating rate constants were estimated for AChRs having mutations at the 17′ and 27′ positions of M2, in both α-subunits. These positions are in the upper half of M2, between the equator and the extracellular domain (Fig. 1A). At α17′ (Fig. 2), all of the mutations increased the cluster open probability by both increasing the opening rate constant and decreasing the closing rate constant (Table 1). The REFER plot for the entire α17′ mutant series yielded a Φ-value of 0.63 ± 0.18 (solid line, Fig. 2B).

The REFER plot for α17′ had more scatter than the plot for α9′. Although some of this scatter is statistical, inspection of the currents suggested that both the opening and closing rate constants for the small side-chain mutants at 17′ were faster than for the other substitutions. We attribute the scatter in the α17′ REFER to a “catalytic” effect of the G, A, and S side chains, as has been described previously for specific mutations of other AChR positions (15, 17, 18). Eliminating the three small side-chain values from the α17′ REFER analysis did not change significantly the Φ-value (0.61 ± 0.04; dashed line, Fig. 2B).

The α27′ residue is in the M2–M3 linker and makes intimate contact with residue V46 in loop 2 of the extracellular domain (Fig. 1A) (28). Previously, analyses of three α27′ mutants, including a mutation (Ile) that causes a slow channel congenital myasthenic syndrome (31), yielded a Φ-value of 0.69 for this position (32). We repeated the analysis of the αS27′I double-mutant and found a Φ-value of 0.65 ± 0.06 (Fig. 3B).

Fig. 3.

Kinetic analyses of α27′ double-mutants and hybrid. (A) Clusters of openings from AChRs having a Ser → Ile mutation at the α-subunit M2 27′ position (α269). Within a single patch there are three kinetically distinct cluster populations. (B) The cluster open probability distribution has three components that reflect the activity of AChRs having two (double-mutant), one (hybrid), and zero (WT) mutations. (C) REFER plot for α27′. The two α27′ positions make equal energetic contributions to and have progressed to the same extent at the transition state of the gating reaction (Φ = 0.65 ± 0.06).

The similarity of the Φ-values at α17′ and α27′ suggests that these two residues have progressed, on average, approximately to the same extent at the overall gating transition state. However, the difference in Φ-values between the 17′ and 9′ positions in αM2, 0.37 Φ-units, is significant (18). This difference in Φ is similar in magnitude to that between the 12′ and 9′ residues in δM2 (18).

The Φ-values we have measured for the α-subunit M2 domain (27′, 17′, and 9′) are consistent with the overall, approximately longitudinal gradient in Φ-values for AChR gating. The value of ≈0.64 for the upper half of αM2 is less than that for the base of the extracellular domain [Φ ≈ 0.81 (17)] but larger than that for the αM2 equator (Φ≈ 0.26). If Φ-values reflect the sequential position within a reaction chain, then these results are consistent with the notion that gating occurs as a reversible, Brownian conformational wave that links the affinity change at the transmitter binding sites with the conductance change in the pore. We hypothesize that the sequence of α-subunit motions during channel opening is as follows: [transmitter binding sites/loop 5] ⇄ [loop 7/loop 2] ⇄ [upper M2] ⇄ [M4] ⇄ [M2 equator] (see Movie 1, which is published as supporting information on the PNAS web site).

The results also support the hypothesis that the gating domains act as rigid bodies that have discrete boundaries. The Φ-values for 27′ and 17′ are similar, and we speculate that these residues, along with the nine intervening residues in this helical segment, move synchronously during gating. This finding implies that the upper half of αM2 moves as a rigid body, as does the upper half of δM2 and the entire αM4 segment. Moreover, there is a sharp difference in the Φ-values for αS269 (0.65) and αV46 [0.81 (17)], even though these two residues appear to be closely apposed (28). The difference in Φ-values between α17′-9′ and δ12′-10′ (18) further suggests that the boundaries between these gating domains are discrete (see Fig. 6A) and that the structures between the boundaries are regions of flexure.

Fig. 6.

Structural correlates of the Φ-values. (A) Longitudinal projection of the AChR showing four gating domains in the α_δ- and δ-subunits. The domains are color-coded by Φ-value: orange, ≈0.8; yellow, ≈0.65; red, ≈0.35; blue, ≈0.0. There is a longitudinal gradient in Φ-value, with residues organized into domains that appear to have distinct boundaries. For all domains, Φ-values of the residues at the boundaries (e.g., 2′ and 10′ in δM2) have been determined experimentally. (B) Symmetry of α-subunit Φ-values in hybrid constructs. Top to bottom: αD97 [loop 5; Φ = 0.93 (34)], αS269 (M2–27′, Φ = 0.65), αC418 [M4–10′, Φ = 0.50 (16)], and αL251 (M2–9′; Φ = 0.32 and 0.02). Early in the gating reaction the α-subunit gating motions are synchronous (green) but are asynchronous at the equator of M2 (red and blue). (C) Cross section of the pore at the equator showing the 9′ residues of all subunits (Leu) and the 12′ residue of the δ-subunit (Ala). The red atoms (Φ≈ 0.35) move in advance of the blue atoms (Φ≈ 0) in the diliganded AChR gating reaction. [Protein Data Bank ID code 2bg9 (28); pymol (http://pymol.sourceforge.net)].

Hybrid Analyses. To probe independently the movements of each α-subunit, we measured the gating rate constants of hybrid AChRs, which are constructs having only one mutated α-subunit. Two results to consider regarding the symmetry of the two α-subunits in the gating reaction are the relative magnitudes of the effect of a mutation on the energies of the ground states (the fold changes in Θ) and on the change in energy of the transition state (the Φ-values). For the α27′ position (Ile mutation), there was only one hybrid population that had a cluster P_o that was intermediate between that of the WT and the double mutant (Fig. 3). The ≈10.7-fold increase in Θ for this hybrid relative to the WT was equal to the square root of the 115-fold increase for the double mutant relative to the WT. In addition, the hybrid Φ-value was similar to that for the double mutant. This pattern indicates that the two α27′ residues make equal energetic contributions to, and move synchronously in, the gating reaction. A similar pattern has been reported for an equatorial, M4 residue of the α-subunit (16).

We next studied hybrid constructs of the α9′ position (Fig. 4). Two kinetically distinct hybrid populations were apparent for Met, Thr, and Ala mutations of the αL9′ position. These populations were readily identified in the single-channel record because a point mutation of either α9′ residue differentially altered the equilibrium constant for channel block by choline (K_B) and produced a distinct apparent open channel current amplitude (i_B; Table 1).

For constructs with the same side chain in both α-subunits, K_B was Thr > Ala > Met > Cys > Leu (range, 25.2–9.5 mM). In both of the hybrid populations (where the companion α9′ side chain was Leu), this order was Thr > Met > Ala, with K_B being slightly higher in the hybrid population, which we hypothesize to have a mutated α_ε 9′ residue (see below). This result suggests that there is a small degree of asymmetry in the energy of interaction between choline (in the pore) and each of the two α9′ side chains, although further experiments are required to ascertain the extents to which the rate constants for choline association and blocked-channel closing are influenced by the mutations.

The fold-changes in Θ for the Met and Thr 9′ hybrid constructs (Table 1) were roughly similar in both α-subunits and were approximately equal to that predicted by equal-and-independent energetic contributions to gating. Interestingly, although both hybrid classes altered Θ mainly by slowing the closing rate constant, they did so to different extents. REFER analyses (Fig. 4C) showed that each hybrid class had a distinct Φ-value, 0.32 ± 0.01 or 0.02 ± 0.02. Assuming a sequential gating mechanism, this result suggests that the two α9′ residues move asynchronously during the diliganded gating reaction.

Previous analyses of hybrid constructs showed that in the vicinity of the transmitter binding site there is a ≈5-fold difference in the change in Θ for mutations at each of the two α-subunits (33, 34), whereas the equatorial residues (10′) of αM4 make equal contributions to the gating equilibrium constant (16). This difference in symmetry makes sense because the ground-state environments of the two α-subunits are likely to be different at the transmitter binding sites (which are at an interface with either the ε or δ subunit) but are similar at M4 (facing the lipid; ref. 35). Our observation that the two αM2 9′ and 27′ residues make nearly equal contributions toward Θ suggests that the local ground-state environments in these regions of the protein are, for the most part, symmetric between the two α-subunits with regard to gating. This observation is consistent with previous experiments showing that M2 9′ mutations act independently and symmetrically to shift the macroscopic current EC₅₀ (11, 12).

With regard to Φ-values, analyses of hybrids with a mutation in the extracellular domain (Φ = 0.93; ref. 34), M4 (Φ = 0.54; ref. 16), and at the 27′ position of M2 (Fig. 3) show that at these positions the two α-subunits have approximately the same Φ-value. Surprisingly, this symmetry is broken at the αM2 9′ position (Fig. 4). Thus, the two α-subunit gating motions appear to progress in parallel for residues that move early in the reaction (Φ ≥ 0.5) but become desynchronized by the time they reach the equator of M2 (see Fig. 6B).

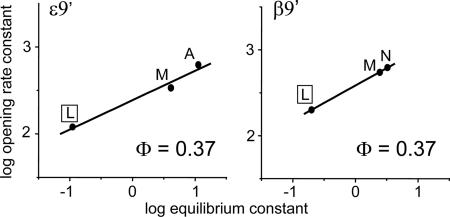
In a final set of experiments we measured the gating rate constants for point mutations of the 9′ position in the ε and β subunits (Fig. 5). The Φ-values for these two subunits were both 0.37 (±0.06 and ±0.01, respectively). The 9′ position in the δ-subunit was previously shown to have a Φ-value of 0.03 (18).

Fig. 5.

REFERs for ε- and β-subunit equatorial (9′) residues. The WT side chain (Leu) is boxed. These positions have the same Φ-value, which suggests that they have progressed to the same extent at the transition state of the diliganded gating reaction. One α-subunit and the upper half of δM2 have similar Φ-values (≈0.32 and 0.34, respectively), whereas the other α-subunit has a Φ-value of 0.02.

We cannot unambiguously associate the different Φ-values with the α-subunit that is between the δ and ε subunits (α_δ) or the one that is between the β and ε subunits (α_ε), but we note that at 9′ one of the α-subunits has progressed approximately to the same extent as the ε and β subunits. We therefore speculate that the order of subunit movement at the M2 equator is α_ε ≈ ε ≈ β > α_δ ≈ δ (Fig. 6C).

Conclusions

Our results do not directly address the controversial issue of the location of the channel gate. However, they reveal that the equatorial M2 region of the AChR plays a critical role in the gating mechanism. First, the difference in Φ-values between 17′ and 9′ in the α-subunit indicates that this region of the AChR is flexible, as previously suggested by structural (5), affinity-labeling (7), computational (36), and kinetic (18) experiments. Second, assuming a sequential reaction mechanism, the results suggest that the motion of the upper half of αM2 precedes that of αM4 but that this order is reversed at the equator. This finding suggests that the middle of M2 serves as an energy barrier (a “speed bump”) to both α-subunit movements that generates a radial component to the otherwise longitudinal gating conformational wave. Third, the loss of synchrony between the two α-subunits at 9′ indicates that this energy barrier is different for each α-subunit, causing one to move before the other. Although we cannot distinguish whether this energy difference arises from differences in the structures of the stable C and O states or is manifest only at the transition state, the approximate symmetry of the hybrid mutant effects on Θ suggests that this difference is not a ground-state effect. Finally, the difference in the two α-subunit gating trajectories appears to organize the equatorial residues so that (α_εεβ)9′ move approximately as a coherent unit, followed by the (α_δδ) 9′ subunits. This finding suggests that the collective subunit motions in this region of the protein are asymmetric during the gating isomerization.

Our knowledge of the AChR membrane domain gating dynamics is still incomplete because Φ-values for other positions in the β- and ε-subunits as well as for M1, M3, and the lower half of M2 in the α-subunits have yet to be measured. Nonetheless, the experiments indicate that the equatorial region of M2 is a dynamic, flexible, and asymmetric junction that constitutes a key barrier of the TSE and that governs the propagation of gating conformational changes through the AChR.