Dynamic effects of antibody-dependent enhancement on the fitness of viruses

Abstract

Antibody-dependent enhancement (ADE), a phenomenon in which viral replication is increased rather than decreased by immune sera, has been observed in vitro for a large number of viruses of public health importance, including flaviviruses, coronaviruses, and retroviruses. The most striking in vivo example of ADE in humans is dengue hemorrhagic fever, a disease in which ADE is thought to increase the severity of clinical manifestations of dengue virus infection by increasing virus replication. We examine the epidemiological impact of ADE on the prevalence and persistence of viral serotypes. Using a dynamical system model of n cocirculating dengue serotypes, we find that ADE may provide a competitive advantage to those serotypes that undergo enhancement compared with those that do not, and that this advantage increases with increasing numbers of cocirculating serotypes. Paradoxically, there are limits to the selective advantage provided by increasing levels of ADE, because greater levels of enhancement induce large amplitude oscillations in incidence of all dengue virus infections, threatening the persistence of both the enhanced and nonenhanced serotypes. Although the models presented here are specifically designed for dengue, our results are applicable to any epidemiological system in which partial immunity increases pathogen replication rates. Our results suggest that enhancement is most advantageous in settings where multiple serotypes circulate and where a large host population is available to support pathogen persistence during the deep troughs of ADE-induced large amplitude oscillations of virus replication.

An estimated 50-100 million people are afflicted by dengue fever each year (1). Two to five hundred thousand of these cases occur as the severe, life-threatening form of the disease, dengue hemorrhagic fever (DHF) (2). The factors that lead to severe disease are debated, with both viral factors and host immune status thought to contribute (3). Evidence shows that preexisting heterotypic immunity is a strong risk factor for the development of DHF (4-6). Several nonmutually exclusive mechanisms have been proposed to explain how sequential dengue infections might cause severe disease, including abnormal T cell activation and cytokine release or apoptosis (7, 8). However, the leading hypothesis is that DHF is associated with a phenomenon called antibody-dependent enhancement (ADE) of dengue virus replication. A non-neutralizing antibody from previous heterotypic dengue infection has been shown to enhance the growth of virus in vitro (9) and in vivo in nonhuman primates (10). Additionally, the presence of transplacentally acquired maternal dengue antibodies has been associated with DHF in infants (4). Higher viremia has been observed in individuals experiencing their second dengue infection than those undergoing primary infection, although one other study was inconclusive (11, 12). There is also evidence that viral strains vary in virulence (13). It is most likely that both viral factors and immune status are important in determining the severity of disease. Epidemics in the Americas demonstrate that both viral factors and host immune states play clear roles in disease severity. Secondary infections of dengue serotype 2 have been associated with severe disease in several settings in the Americas, but only for viruses of Southeast Asian origin, not those of American origin (14-16). Because ADE appears to be a characteristic of some dengue viruses and not others, the present work seeks to explore the particular dynamic mechanisms and settings that make ADE an advantageous strategy.

Although the model we present is specific to dengue, the results are applicable to any microbial agent affected by immune enhancement. ADE has been observed in vitro for other families of pathogens, including retroviruses and coronaviruses (17-19). Accordingly, ADE is a concern in the development of vaccines against HIV and severe acute respiratory syndrome as well as dengue (17, 20).

ADE of dengue viruses was first observed in Southeast Asia (21), and all four serotypes of dengue have circulated in Southeast Asia for at least 50 years (22). The association of DHF with secondary infection and ADE has been observed in Southeast Asia for many years as well (21). We hypothesize that the large urban centers of Southeast Asia where multiple serotypes of dengue circulate at high levels of transmission provide the most advantageous environment for the emergence of ADE. In a previous study, we observed spatial-temporal traveling waves in the incidence of DHF that emanated from Bangkok and spread radially throughout the country (23). In that work, we hypothesized that Bangkok acts as a pacemaker for the surrounding region because all four serotypes are maintained there, providing a source of periodic reintroductions of particular serotypes to the surrounding region. In this study, we take steps toward addressing these hypotheses by studying the dynamics of dengue circulation in a single population. We develop a model of the dynamics of dengue transmission in the presence of ADE. We model the cocirculation of four serotypes as occurs in nature and, more generally, n serotypes to study the effect of ADE in systems of varying numbers of cocirculating serotypes. We use this model to determine the impact of ADE on competition between serotypes and on the persistence of multiple serotypes in a single population.

We speculate that ADE confers a fitness advantage on enhanced viruses, and that there is ongoing natural selection for such strains. We hold that it will be important to disease control efforts to understand the processes, such as ADE, that affect the evolution and pathogenicity of dengue viruses. Although new serotypes have been reported prematurely in the literature (24), no new serotypes beyond the four known have emerged. We explore the consequences of emergence of new dengue serotypes by comparing the dynamics of model systems with two to six serotypes.

Mathematical models describing the transmission of dengue viruses appeared in the literature as early as 1970 (25). Models have focused on several different aspects of transmission; simulating the abundance of the mosquito vector and its effect upon transmission (26), the effect of ADE on transmission dynamics (27), and the effect of seasonality on transmission dynamics (28). Research groups have explored the effects of ADE on the dynamics of dengue transmission by using several different approaches (25, 27, 29, 30). Feng (29) examined the effect of ADE in a two-serotype model via the inclusion of a parameter that increased the susceptibility of those individuals who had previously been exposed to one serotype. Kawaguchi (30) examined the impact of increased mortality of secondary dengue infections upon competition and coexistence of two serotypes. Ferguson et al. (27) used a slightly different approach to examine the effect of ADE on the dynamics of dengue transmission in a two-serotype model. In their compartmental model, the authors assume that ADE increases the viral load of those individuals experiencing a second, heterotypic infection (27). Thus, secondary infections act to increase the force of infection (the per capita rate of infection) of the second infecting serotype. Evidence that ADE acts to increase viral loads of those undergoing secondary infection (11) suggests that this formulation more accurately reflects the biology of dengue infection than the formulation by Feng (29). Because individuals experiencing a secondary infection have higher viral loads, there is a higher probability that a blood meal taken by a mosquito from such an individual would have sufficient levels of virus to pass infection on to another individual. This observation, that secondary infections increase viral loads, directly supports a theory that preexisting immunity increases the transmissibility of secondary infections. In contrast, to date, there is no clinical or epidemiological evidence that preexisting heterotypic immunity increases susceptibility to infection.

Materials and Methods

Our model is based on the standard Susceptible, Infectious, and Recovered epidemiologic model. The model builds on previous work that has addressed the interaction of multiple serotypes of a disease within a population (31, 32). We have generalized the two-serotype dengue model developed by Ferguson et al. (27) to n dengue serotypes (n = 2 to 6). The dynamics of n serotypes circulating in a single population of constant size are given by

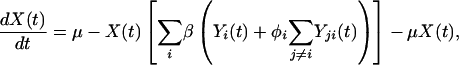[1]

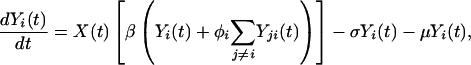[2]

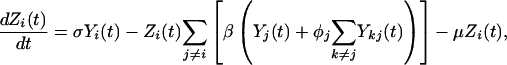[3]

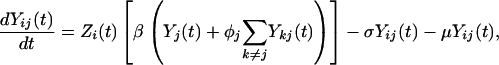[4]

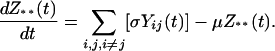[5]

(Note: All summations are from 1 to n, subject to restrictions below the summation symbol.) X(t) is the fraction of the population susceptible to all n serotypes, Y_i(t) is the fraction currently infectious with serotype i, Z_i(t) is the fraction recovered from infection with serotype i, Y_ij(t) is the fraction currently infectious with serotype j having previously been infected by serotype i, and Z_**(t) is the fraction that has recovered from two infections of dengue. Individuals are assumed to be immune to all serotypes of dengue after two sequential infections because tertiary infections are reported very rarely (22). The total number of compartments for a system of n serotypes is given by n² + n + 2. We assume that primary infection with any single dengue serotype confers lifelong homotypic immunity but no immunity to other serotypes. ADE is assumed to increase the transmissibility of secondary infections of serotype i by a factor labeled the ADE factor, φ_i. For model simplicity, the transmission coefficient, β, is assumed to be equal for each serotype. The base value for the transmission coefficient was derived from estimates of the basic reproductive rate, R₀, for dengue in Thailand (33). The force of infection for serotype i, the per capita rate of acquisition of infection, is assumed to be proportional to the total fraction infectious with serotype i but with the secondary infections weighted by the enhancement factor, φ_i (27). An ADE factor of 1 corresponds to no enhancement, whereas an ADE factor of 2 means that secondary infections contribute twice as much as primary infections to the force of infection. The values of parameters in the model and the references used appear in Table 1. For model simplicity, we assume that the population is constant with a birth rate, μ, exactly equal to the death rate. We assume that mortality rates in our population are independent of disease status. We believe this assumption is a reasonable because of the low case fatality rate of DHF (≈0.01) and the much lower fatality rate of dengue infection (≈0.0001) in Thailand (34). The work of Kawaguchi and Rohani (30, 35) suggests that the dynamics of dengue are significantly impacted by dengue-induced mortality only at much higher levels of mortality than are observed. The rate of recovery, given by σ, is assumed to be equal for primary and secondary infections. The ADE factor is varied in our model runs from 1 to 5.

Table 1. Parameter values used in this model.

Parameter	Value	Ref.
β, transmission coefficient, year-1	400	33
μ, I/host life span, year-1	0.02	27
σ, recovery rate, year-1	100	27
φi, ADE factor of serotype i	1-5	-

Results

Introduction of an Enhanced Strain. We have chosen to represent ADE as a characteristic of an entire serotype for most of the model results presented below rather than allowing the ADE factor to vary among strains within a serotype. Although this assumption simplifies the model results, it is more probable that ADE would emerge in a particular viral strain within a serotype. We hypothesize that if ADE were to emerge as a characteristic of one viral strain, it would competitively displace all other viral strains within a serotype. To address this hypothesis, we adapted the modeling framework described above to simulate multiple viral strains within one serotype. For simplicity, we constructed a model of two serotypes, one serotype consisting of just one viral strain and the other serotype consisting of two viral strains. The two strains within a serotype conferred perfect immunity to each other upon infection. The two strains differed only in the degree of ADE they underwent, one having an ADE factor of 1, the other an ADE factor of 2. In this model, we have confirmed that the enhanced strain competitively displaces the nonenhanced strain within its serotype. However, competition between strains of diverse levels of enhancement and other viral characteristics (e.g., transmissibility of nonenhanced infection) should be studied in the future. In this paper, we assume that each strain within a serotype experiences an identical level of ADE.

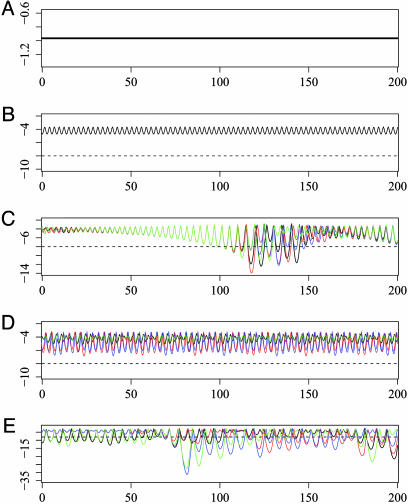
General Description of Model Behavior. We determined the behavior of our systems while changing the ADE factor for all serotypes at once (denoted φ_all), and for changing the value of the ADE factor for just one serotype (without loss of generality choosing φ₁ to vary) while holding the ADE factor equal to 1 for all other serotypes. At different values of φ_all and φ₁, the behavior of the solutions changes dramatically. Fig. 1 presents example time series of the simulations for different values of φ_all in a four-serotype model. Shown in the solution time series are the total infectious fractions for each of the four serotypes. These solutions exhibit fixed point behavior (where each disease state settles to a constant fraction of the population) (A), stable oscillations (B), synchronized, unstable oscillations with interspersed chaotic desynchronization (C), synchronized pairs of serotypes that exhibit a nonzero phase angle with respect to one another (D), and completely desynchronized, chaotic behavior (E). Note that although we have assumed equal base transmission rates for each of the serotypes, the prevalence of each serotype is not equal at all times. A general trend in these results is for increasingly large oscillations with increasing enhancement.

Fig. 1.

Example time series from simulation with φ_i equal for all i. (A) φ_all = 1.5. (B) φ_all = 1.88. (C) φ_all = 2.1. (D) φ_all = 2.7. (E) φ_all = 3.2. Log (base 10) axes are used for the vertical axes. The horizontal axis is time in years for each of the plots. Four series are shown in each plot displaying the total infectious compartments for each serotype colored red, green, blue, and black (all four compartments are identical in A and B). A threshold value of 1 × 10^-8 used to define extinction in Fig. 5 is indicated by the dotted horizontal line (data not shown in A).

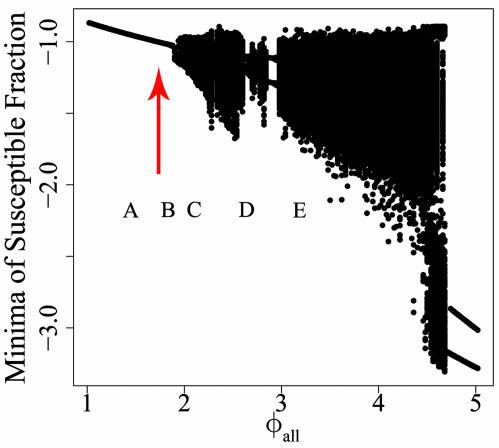
We present a more complete characterization of the behavior of these systems as φ_all is varied in Fig. 2. Fig. 2 presents a bifurcation diagram showing the behavior of the susceptible fraction in the four-serotype system as φ_all is changed. Plotted in the figure are the local minima of the susceptible fraction of the population over 100 years of simulations for 20 separate random initial conditions at varying levels of φ_all. Steady-state solutions are represented by a single point. Oscillatory solutions are represented by a single point only if the same local minimum is reached in each cycle. Points on the horizontal axis for which there are multiple points on the vertical axis indicate values of φ_all for which multiple local minima occur over the 100-year interval. Simulations in which the ADE factor is varied for just one serotype, with the remaining serotypes having ADE fixed at 1 (data not shown) and the data above show there is a trend for oscillations to have increasing amplitude as either φ_all or φ₁ increases.

Fig. 2.

Behavior of the susceptible fraction of the dengue four-serotype model for various values of φ_all, the ADE factor for each serotype. Shown are the local minima of the susceptible fraction (log base 10) occurring over 100 years for 20 runs at each setting of φ_all. The first 5,000 years of numerical integrations were discarded to avoid transient behavior before recording local minima for 100 years. The location of the Hopf bifurcation is indicated by the red arrow.

Selective Advantage of ADE. It is intuitively appealing to view ADE as an adaptive strategy for viruses that grants increased transmissibility in the presence of high levels of population immunity. We quantitatively measure the effect of ADE on the prevalence of a serotype undergoing enhancement by comparing the serotype's equilibrium prevalence at various levels of enhancement in a system of n circulating serotypes. Fig. 3 presents the equilibrium prevalence of serotype 1 (serotype 1 is arbitrarily chosen as the enhanced serotype) at levels of φ₁ varying from 1 (no enhancement) to 2 in settings of 2, 3, 4, 5, and 6 cocirculating serotypes. We set φ_i = 1 for i ≠ 1. Then we consider the effect of serotype 1 gaining ADE. For large values of φ₁, the solutions oscillate (discussed in subsequent sections). However, for reasonably small changes in φ₁ (φ₁ < 2), the equilibrium point is stable. As expected, we find that the equilibrium prevalence of serotype 1 increases as φ₁ increases. During the initial increase in stable equilibria, the slope of the increase depends on the number of cocirculating serotypes. For every unit increase in φ₁, the increase in prevalence that occurs is greater in systems with greater numbers of cocirculating serotypes (Fig. 3). Solving for the equilibrium point of Eqs. 1, 2, 3, 4, 5, we performed an asymptotic expansion for the primary infectives of serotype 1 when φ₁ = 1 + ε and φ_i = 1 for i ≠ 1, where ε is a small parameter and the mortality terms of Eqs. 1, 2, 3, 4, 5 were omitted for simplicity. As a function of the number of serotypes, the fraction of the population with primary infection of serotype 1 is

[6]

The slope of this fraction as a function of ε increases as n increases. Thus, we find that ADE has more impact when there are more serotypes circulating, because of the larger pool of individuals who have been exposed to one heterotypic serotype. Similarly, we find that the impact of ADE is greater in systems in which the force of infection of the nonenhanced serotypes was higher (data not shown), another factor that increases the proportion of individuals who have experienced infection by one heterotypic serotype.

Fig. 3.

Fraction primary infectious with serotype 1 in a system of 2-6 serotypes versus the ADE factor of serotype 1, φ₁, within range 1 to 2. In this range of the ADE factor, each of the systems of n serotypes settles to a stable, fixed point. Shown is the dependence of the steady-state value of the primary infectious compartment of the enhanced serotype on φ₁. Results for each of the n serotype systems are color-coded according to Inset.

Onset of Oscillations. Ferguson et al. (27) demonstrated that the inclusion of ADE in models of two dengue serotypes induces cycles in incidence. We also find oscillations in incidence in each of the n serotype models. As the ADE factor increases, these models undergo a Hopf bifurcation. At this point (indicated by the red arrow in Fig. 2) the behavior of the equilibrium solutions of these models changes from steady states to limit cycles. The point at which these systems undergo the bifurcation in φ_i varies as a function of the number of serotypes. In our models in which the ADE factor is equal for all serotypes, we find that the value of φ_all at which oscillations begin declines from ≈2.7 for systems of only two serotypes to ≈1.7 for a system of six serotypes. The Hopf branch for each of the n serotype systems begins with oscillations of period ≈3 years. Interestingly, the period of the oscillations at the onset does not vary significantly with the number of serotypes. Also, these Hopf branches are stable for only a small range of φ_all to the right of the bifurcation point. Another bifurcation leads to chaos-like oscillations as indicated by the Lyapunov exponents (41).

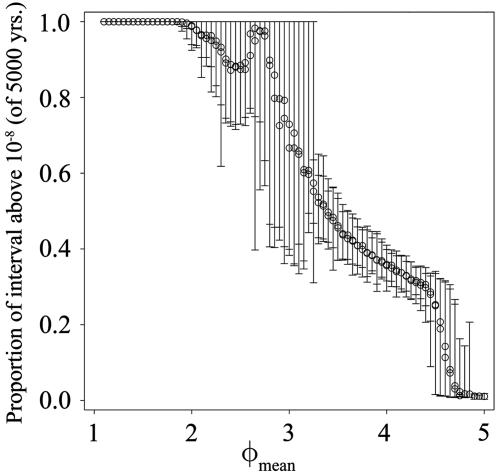
Threats of ADE to Persistence. As the ADE factor increases, the oscillations that these systems experience increase in amplitude. As these oscillations increase in amplitude, the minimum prevalence of the dengue viruses in the troughs between epidemics decreases. Oscillations with very low minima are assumed to threaten persistence. Our continuous system of ordinary differential equations does not allow for fadeout. However, we characterized the persistence of viruses in any given model formulation by calculating the time interval for which the prevalence of a particular dengue serotype was above a chosen small fraction (1 × 10^-8). This fraction was selected to be one order of magnitude below the fraction corresponding to one individual in a population the size of Bangkok (1 × 10⁷). This threshold is represented by the dashed lines in Fig. 1. Fig. 4 presents the proportion of the interval spent above this threshold as a function of φ_all. At each value of φ_all, the mean and range of 50 solutions is shown. The largest ranges occur when several coexisting stable solutions exist. As a general trend, as φ_all increases, the proportion of the solutions above this threshold decreases. There is, however, one region, from 2.6 to 2.7, where increases in φ_all result in increases in the proportion of the interval spent above threshold. This region corresponds to a loss of synchrony across all serotypes. Before φ_all = 2.6, the behavior of solutions includes large regions of synchrony between the incidence of each serotype interspersed with chaotic regions with reduced synchrony (I.B.S., unpublished data). During the regions of synchrony, the four serotypes exploit the susceptible fraction at synchronized time points, driving the susceptible component to a very low fraction. Our intuition is that this reduction in the susceptible fraction results in deeper troughs in the incidence of all four serotypes. After φ_all = 2.6, the system experiences a reduction in overall synchrony among the four serotypes, with only certain subsets of the serotypes (two or three serotypes) synchronized for large time periods. A similar decrease in the proportion of solutions that lie above the threshold of 1 × 10^-8 is observed while increasing the ADE factor of just one serotype in the four serotype system (data not shown).

Fig. 4.

Persistence of dengue serotype 1 as a function of φ_all. At each value of φ_all, the proportion of the simulated interval of 5,000 years above 1 × 10^-8 is presented. The first 5,000 years of each model run were discarded to minimize the effect of transient behaviors. Shown are means (circles) and ranges of 50 simulations (from randomly perturbed initial conditions). The red arrow indicates the location of the Hopf bifurcation. The letters A-E indicate the settings of φ_all used for the time series appearing in the corresponding lettered part of Fig. 1.

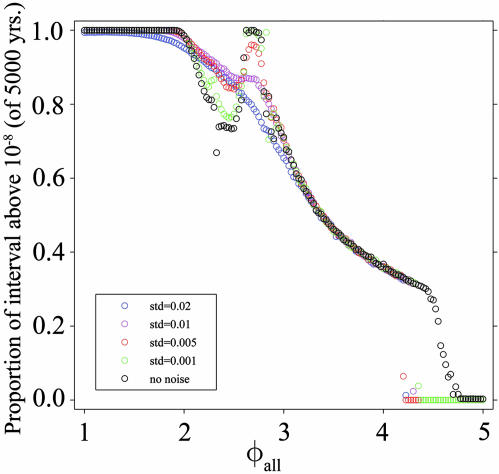
We also addressed the robustness of our results to asymmetry in the amount of enhancement experienced by each serotype. We recalculated the proportion of time above the threshold shown in Fig. 4 as a function of φ_i = φ_mean + ε_i where φ_mean indicates a contribution to all φ_i that is systematically varied as φ_all is in Fig. 4. These results are shown in Fig. 5. Unlike Fig. 4, here the φ_i vary because of the contribution of ε_i, a normal, random variable with mean zero. Fig. 5 presents the mean and range of the proportion above threshold as a function of φ_mean where ε_i has a standard deviation of 0.1. The results of these runs are qualitatively similar to the results where the ADE factor is identical for all serotypes.

Fig. 5.

Persistence of dengue serotype 1 as a function of φ_mean. In these runs, the ADE factor for each serotype is φ_i = φ_mean + ε_i where ε_i is a normal random variable with mean zero and standard deviation 0.1. At each value of φ_mean, the mean and range of the proportion of the simulated interval of 5,000 years above 1 × 10^-8 for 50 simulations is presented.

We find that the range of φ_all > 1 that does not induce oscillations reduces as the number of cocirculating serotypes increases. This result suggests that the range of φ_all that does not have significant regions of reduced persistence decreases with increasing numbers of cocirculating serotypes. Characterization of the persistence of dengue in these other n serotype systems should be considered for future study.

The Effect of Including Stochastic Noise. We have developed a stochastic formulation of our system to explore the effect of randomness on our results. We add to each of our disease state compartments a noise term that is proportional to the variable. In Eqs. 1, 2, 3, 4, 5 above, we add a random noise vector, η, multiplied by the corresponding variables (i.e., for each variable V_i, we add a term η_iV_i to the equation for dV_i/dt). This noise term represents continuous multiplicative white noise, because the vector η consists of normally distributed random variables with mean zero. Using this system, we recalculated the persistence measurements from Fig. 4 as we varied the standard deviation of the noise from 0.001 to 0.02. Results are show in Fig. 6. Numerical integration of the stochastic formulation of these models yields qualitatively similar results to the deterministic formulation. For small standard deviations, the general trend is that the proportion above the threshold for a given φ_all increases. This trend is expected because the noise breaks the synchrony of the solutions, avoiding the lowest fractions in the large oscillations. As the standard deviation increases, the persistence curve smoothes to a monotonic decrease of proportion above threshold vs. ADE.

Fig. 6.

Persistence of dengue serotype 1 in the four-serotype stochastic model as a function of φ_all. At each value of φ_all, the mean of the proportion of the simulated interval of 5,000 years above 1 × 10^-8 for 50 simulations is presented. The black symbols present the results with no noise included. The colored symbols present the resultant behavior from including multiplicative noise of various standard deviations (ranging from 0.001 of the population for each compartment to 0.02).

Discussion

We have described an evolutionary tradeoff between the advantage that ADE grants dengue viruses in the form of increased transmissability and the disadvantages of ADE due to an increased probability of extinction at high levels of enhancement. Other researchers have described a similar tradeoff between short-term reproductive rates and long-term persistence for pathogens in general (36, 37). Those authors hypothesize that high reproductive rates are advantageous for short-term competition, but high transmission induces boom-bust cycles that threaten persistence. These cycles reflect the classic dynamical overshoot of pathogens overexhausting the pool of susceptibles resulting in population crash (36). We have observed a similar phenomenon. In the case of ADE, there is an additional resource that may be overused: the pool of individuals susceptible to secondary infections. Our results suggest that there is a dynamic fitness landscape for dengue viruses by using enhancement. ADE initially provides an advantage to viruses in a population with substantial immunity. However, as enhancement provides substantial advantage, the enhanced strains overcompete with other serotypes and exhaust the pool of individuals susceptible to secondary infections. The loss of this resource causes large-amplitude cycles for the enhanced serotype and eliminates the advantage gained by ADE (because there are very few secondary infections). We note that the onset of these oscillations occurs very quickly with respect to changes in ADE. Because ADE is incompletely understood, it is difficult to speculate on how enhanced virus replication might evolve over time (i.e., continuously in small increments or in discrete jumps). Regardless of the exact mechanism, our results suggest that there are dynamical limitations to the extent to which this strategy can be exploited. Our results also indicate that there is an optimal level of enhancement for dengue viruses, the highest level of enhancement that does not induce large amplitude cycles (In our present model, this value implies that secondary infections would not be more than approximately two to three times as transmissible as primary infections).

Phylogenetic analysis of dengue viruses in several locales suggest that the viruses undergo repeated genetic bottlenecks (38, 39). During these bottlenecks, diverse populations of dengue viruses experience dramatic declines in population numbers. After these bottlenecks, a much less diverse population of viruses remains. Seasonal fluctuations of mosquito populations have been suggested as a mechanism for these population bottlenecks (39). The dynamic cycles our models exhibit offer an alternative mechanism for these population bottlenecks.

We have generalized the work of previous researchers (27) to address n serotypes of dengue (n = 2-6), including the case of four cocirculating serotypes observed in many regions of the world, and have examined the effects of ADE on persistence of dengue viruses. With the addition of serotypes to our model systems (over the two addressed by previous research), the Hopf bifurcation occurs at smaller ADE values. Following from observations of our four-serotype system, we expect an earlier onset of large-amplitude cycles in systems with more serotypes. Thus, enhancement may provide a mechanism that limits the number of serotypes that can cocirculate in any particular setting.

There are several limitations to the approach we have taken. Although we have addressed the impact of stochasticity in our models, we have not modeled the extinction process explicitly. The behavior of a stochastic, discrete individual model of this system may exhibit different behavior. Our future work will focus on validating the observations we have made in a stochastic system with discrete individuals and more carefully analyzing the temporal progression of extinctions. We have not included costs of enhancement or tradeoffs between having enhancement and other traits affecting transmission or other characteristics. We expect there to be biological tradeoffs that are not explicitly modeled here. Additionally, for simplicity, we have not included seasonality in our models nor short-term cross-immunity between serotypes (40).

The extent to which dengue virus replication is enhanced in humans is not fully understood nor has it been carefully quantified. We have shown here that the exact ADE value has important implications for setting the prevalence and incidence of serotypes and competition between serotypes. Because severe disease (DHF) is associated with secondary infections, ADE, and increased replication, epidemiological limits on virus survival may also serve as clinical limits to disease severity. These results suggest that there should be renewed attention on measuring immune enhancement of virus replication in vitro and in vivo.