Atomic and Electronic Properties of Doped CsPbBr₃ Perovskite: An Ab Initio Study

Abstract

Lead halide perovskites have emerged as promising materials for a broad range of applications, including optoelectronic devices and solar cells. Nevertheless, their practical utilization is constrained by the physical properties of their constituent atoms. To address these limitations, it is essential to tailor the atomic and electronic structures of lead halide perovskites to meet specific functional requirements. Doping is explored in this work as a strategy to tailor the electronic structure of CsPbBr₃ perovskites. Various elements are considered as dopants at different crystallographic sites. The stability of doped CsPbBr₃ (generic form ABX₃) correlates primarily with the ionic radius of dopants at the A-site, and with both ionic radius and electronegativity at the B- and X-sites. Among the different doping sites, B-site substitution leads to the most pronounced changes in the electronic structure. The emergence of defect states and the variation in band gap are attributed to electronic effects from the atomic energy levels of dopants and geometric effects from their ionic radii. Defect states become less prominent at lower doping concentrations. Overall, electronic effects are found to play a more dominant role than geometric effects in shaping the band structure. Additionally, externally applied strain can further modulate the band gap of doped CsPbBr₃. This study provides insight into rational dopant selection for tuning the electronic properties of CsPbBr₃ for targeted applications. Potential applications include solar cells, light-emitting devices, lasers, and photodetectors, where doping enhances entropic stability, broadens absorption, and increases quantum yield.

Introduction

The broad range of applications of organic and organic–inorganic lead-halide perovskites has spurred significant efforts to investigate their fundamental properties. These materials have been used in devices such as light-emitting diodes, , photodetectors, , lasers, , and solar cells, , among others. Understanding their fundamental propertiesincluding the band gap, carrier effective masses, dielectric function, spin–orbit-coupling-induced (SOC-induced) band splitting, and Kane energyis essential for predicting basic optical characteristics such as the exciton binding energy, radiative lifetime, and photoluminescence (PL). ,

The atomic and electronic structures of perovskites are temperature-dependent. As the temperature rises, these materials often undergo structural phase transitions, typically evolving from orthorhombic to tetragonal and finally to cubic phases. , To broaden the scope of perovskite-based applications, for example, by extending the range of the absorption or emission spectra, it is necessary to tailor their electronic structures. One of the most effective strategies for achieving this is through compositional modification via doping. In a perovskite with the general formula ABX₃, doping involves substituting atoms at the A, B, or X sites with alternative elements. In particular, heterovalent doping has been proposed as a means to enhance electrical conductivity and carrier mobility by introducing excess electron or hole carriers. , The change of electronic structure via doping also leads to a change in their optical properties. − Compared to double perovskites with the formula A₂BB′X₆, , doped perovskites exhibit higher absorption efficiency and photoluminescence quantum yield (PLQY), enhanced defect tolerance, low-cost fabrication, and tunable band gaps, making them particularly suitable for optoelectronic and solar cell applications. −

Substitution at the A-site has been proposed as a strategy to enhance the stability of perovskites, leading to higher PLQY and a reduction in surface defects. ,− For example, the substitution of Cs with Rb has been shown to improve structural stability by reducing Br vacancies, owing to lattice distortion that increases orbital coupling between Pb and Br.

Replacing Pb (at the B-site) is highly desirable because of its toxicity, provided that the optical performance is preserved or improved. Substitution at the B-site with elements such as Al, Ba, Ga, Mn, Ni, and Sn has been demonstrated to enhance PLQY, − increase emission lifetime, , improve power-conversion efficiency, raise the optical absorption coefficient, enhance stability, ,, and reduce surface defects.

Moreover, doping with certain elements (e.g., Ni as in ref ) can influence both radiative and nonradiative recombination pathways by passivating preexisting defects, such as vacancies. Nevertheless, prior theoretical investigations have indicated that substitution at the B-site is generally more challenging.

Atoms at the B- and X-sites play a critical role in determining the electronic and optical properties of perovskites, as they directly contribute to the valence-band maximum (VBM) and the conduction-band minimum (CBM). − For instance, the band gap has been shown to increase with the electronegativity of the B- and X-site atoms. Furthermore, both the band gap and the effective masses of charge carriers tend to decrease with increased orbital overlap, which can be achieved by doping with atoms that enlarge the Goldschmidt tolerance factormaking the structure more cubicor by selecting dopants with larger ionic radii at the X-site and smaller ionic radii at the A-site.

Doping with certain elements can lead to undesirable effects, such as a reduction in the emissive lifetime due to carrier trapping by defect states. For instance, doping with Sr²⁺ reduces the average PL lifetime from 200 ns to approximately 60 ns. Similarly, Bi³⁺ doping results in emission quenching by introducing trapping and scattering centers originating from defect states. In addition, intrinsic defects such as vacancies are generally detrimental to optoelectronic performance. Therefore, a comprehensive understanding of intrinsic defect formation and behavior is essential for improving device performance, as it enables the development of strategies to mitigate or eliminate these defects.

Many factors influence the phenomena observed in experiments, emphasizing the importance of theoretical studies for elucidating the underlying mechanisms. Establishing clear relationships between experimental observations and the atomic as well as electronic structures of perovskites provides critical physical insight. Although numerous theoretical works have investigated the effects of doping in perovskites, comprehensive studies at the atomic level remain limited. The objective of the present work is 2-fold. First, we aim to provide guidelines for tailoring the composition of halide perovskites toward specific applications by considering fundamental atomic properties (e.g., electronegativity and atomic radius) and their consequences for structural and electronic characteristics (e.g., bond lengths, lattice volume, band gap, dielectric response). Second, we seek to deepen the understanding of how atomic configurations govern electronic structure, thereby bridging experimental observations with theoretical insights.

In this work, we conduct a systematic investigation of the doping effects in CsPbBr₃, considering a variety of dopants (including vacancies) at different crystallographic sites. We analyze the atomic properties, such as the formation energies of various dopants and their preferred configurations. The resulting electronic properties are examined through calculated band structures and densities of states (DOS). Additionally, we explore the influence of externally applied strain on the band structure of doped perovskites. Through this comprehensive study, we develop a general understanding of how different dopants impact both the atomic and electronic structures of CsPbBr₃, offering insights that may be extended to other perovskite materials.

Computational Methods

Owing to computational limitations in evaluating the large number of dopants considered, only a single dopant is introduced into a 2 × 2 × 2 supercell of CsPbBr₃ (containing 40 atoms) as an example (Figure ). This corresponds to doping concentrations of 12.5% for the A- and B-sites and 4.17% for the X-site. A variety of elements are considered as dopants: Na, K, and Rb for substitution at the A-site; Ag, Al, Ba, Bi, Ga, Mn, Na, Nb, Ni, and Sn at the B-site; and F, Cl, and I at the X-site. In addition, vacancy defects are modeled with 12.5% concentrations for Cs and Pb vacancies, and 4.17% for Br vacancies.

1.

Unit cell of doped CsPbBr₃ perovskite at site (a) A (b) B (c) X. Cs, Pb, Br and dopant atoms are shown in green, gray, brown and red colors, respectively.

The Vienna Ab initio Simulation Package (VASP) − is employed for all calculations. The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional is used within the framework of the projector augmented-wave (PAW) method. , A k-point sampling grid of 4 × 4 × 4 is used for structural relaxation, while a denser grid of 10 × 10 × 10 is applied in the calculation of the density of states (DOS). For lower doping concentrations, 4 × 4 × 4 supercells (320 atoms) are employed, along with a 2 × 2 × 2 k-point mesh. These configurations correspond to doping concentrations of 1.56% at the A- and B-sites, and 0.52% at the X-site. The force convergence criterion for structural relaxation is set to 0.02 eV/atom, and the electronic minimization is performed until the total energy difference is less than 10^–8 eV. Spin–orbit coupling (SOC) is included in all electronic structure calculations. It should be noted that all calculated band gaps are underestimated owing to the known limitations of the PBE functional. The atomic structures are visualized using VESTA, and the effective (unfolded) band structures are plotted using the VaspBandUnfolding code.

Owing to the excess charge remaining after substituting Pb²⁺ with monovalent ions (e.g., Ag and Na) or trivalent ions (e.g., Al, Bi, Ga, and Nb), the resulting doped perovskites are not charge-neutral. Therefore, a modified formation-energy expression for charged dopants is adopted −

$$E_{\mathrm{F}}=E_{\mathrm{T}}(Z{:\mathrm{C}\mathrm{s}\mathrm{P}\mathrm{b}\mathrm{B}\mathrm{r}}_3)-E_{\mathrm{T}}({\mathrm{C}\mathrm{s}\mathrm{P}\mathrm{b}\mathrm{B}\mathrm{r}}_3)+m{\mu }_Y-n{\mu }_Z+q(E_{\mathrm{V}\mathrm{B}\mathrm{M}}+{\mu }_{\mathrm{e}})+E_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$$ 1

where E _T denotes the total energy of the doped system (Z:CsPbBr₃) or pristine material (CsPbBr₃); μ _Z and μ _Y are the chemical potentials of the added (Z) and removed (Y) atoms, respectively, in their elemental bulk forms; and n is the number of atoms of type Z replacing m atoms of type Y at the A-, B-, or X-sites. E _VBM refers to the VBM of pristine CsPbBr₃, and μ_e is the chemical potential of electrons (i.e., the Fermi level of undoped CsPbBr₃ in this case), which can be varied within the band gap and treated as a tunable parameter. E _corr is a correction term accounting for the finite-size effects and spurious electrostatic interactions of charged defects in supercell calculations (E _corr of various doped CsPbBr₃ are shown in Table S1). The formation energies of charged dopants are computed using the Spinney package.

Results and Discussion

Lattice Parameters in Different Doped CsPbBr₃

Table presents various lattice parameters and formation energies for different doped CsPbBr₃ systems. The Goldschmidt tolerance factor t is widely used as a preliminary indicator of structural stability

$$t=\frac{r_{\mathrm{A}}+r_{\mathrm{X}}}{\sqrt{2}(r_{\mathrm{B}}+r_{\mathrm{X}})}$$ 2

where r denotes the ionic radius of the atoms at the A, B, or X sites. The structure is considered thermodynamically stable if t lies between 0.8 and 1.0. , Within this range, the ions fit well into the cubic structure, minimizing strain energy. Most of the dopants examined in this work meet this criterion, with the notable exception of a Cs vacancy (V_Cs), which yields a smaller tolerance factor of t = 0.768. Additionally, the doped materials are found to satisfy the empirical bond-length relation ${\mathrm{R̅}}_{\mathrm{A}-\mathrm{X}}\approx \sqrt{2}{\mathrm{R̅}}_{\mathrm{B}-\mathrm{X}}$ , , where ${\mathrm{R̅}}_{\mathrm{A}-\mathrm{X}}$ and ${\mathrm{R̅}}_{\mathrm{B}-\mathrm{X}}$ denote the average bond lengths between atoms at the A (or B) and X sites, respectively. However, based on Table , the thermodynamic stability of a given dopant does not appear to correlate directly with the Goldschmidt tolerance factor. For instance, the Pb vacancy (V_Pb) exhibits a relatively high tolerance factor of t = 0.855 but also possesses a high formation energy of 5.12 eV. Other factors, such as configurational entropy, have also been shown to enhance the stability of halide perovskites. , Therefore, the tolerance factor alone is not sufficient to fully indicate structural stability.

1. Summary of Calculated Lattice Parameters for Various Doped CsPbBr₃ Structures, Including Magnetic Moment (M), Lattice Constant (a), Average Bond Lengths (Cs–Br, Pb–Br, Cs–Pb), Volume Change After Doping (ΔV), Goldschmidt Tolerance Factor (t), and Doping Formation Energy (E _F)­ .

compound	M (μB)	a (Å)	Cs–Br	Pb–Br	Cs–Pb	ΔV (%)	t	E F (eV)
CsPbBr3	0.000	5.992	4.237	2.996	5.189	0.00	0.815
Na (A)	0.000	5.985	4.241	2.993	5.185	–0.34	0.797	1.73
K (A)	0.000	5.985	4.239	2.993	5.184	–0.34	0.807	0.63
Rb (A)	0.000	5.986	4.235	2.993	5.184	–0.29	0.811	0.41
VCs (A)	0.000	5.953	4.182	2.981	5.158	–1.96	0.768	3.82
Ag1+ (B)	0.000	5.927	4.194	2.974	5.169	–3.23	0.816	2.66
Al3+ (B)	0.000	5.936	4.200	3.014	5.153	–2.80	0.837	1.76
Ba (B)	0.000	6.050	4.279	3.013	5.226	2.94	0.810	–3.09
Bi3+ (B)	0.000	5.997	4.241	3.002	5.192	0.26	0.820	1.88
Ga3+ (B)	0.000	5.936	4.198	2.987	5.154	–2.76	0.834	2.10
Mn (B)	4.400	5.930	4.194	2.994	5.154	–3.09	0.829	–7.64
Na1+ (B)	0.000	5.940	4.207	2.972	5.193	–2.55	0.820	0.35
Nb3+ (B)	1.885	5.941	4.202	3.002	5.152	–2.54	0.830	2.87
Ni (B)	1.380	5.915	4.186	2.998	5.152	–3.80	0.831	3.00
Sn (B)	0.000	5.980	4.229	2.995	5.179	–0.58	0.820	0.61
VPb (B)	0.000	5.927	4.204	2.956	5.200	–3.23	0.855	5.12
F (X)	0.000	5.983	4.211	3.011	5.179	–1.69	0.816	–1.61
Cl (X)	0.000	5.995	4.229	2.994	5.180	–0.53	0.815	–0.20
I (X)	0.000	5.991	4.247	3.000	5.205	0.90	0.815	0.38
IBr	0.000	5.967	4.142	3.010	5.183	–0.67	0.812	–0.01
VBr (X)	0.000	6.015	4.234	3.000	5.198	0.37	0.818	3.32

^aDoping site positions are indicated in parentheses: (A) for site A, (B) for site B, and (X) for site X. Defects include Cs, Pb, and Br vacancies (V_Cs, V_Pb, V_Br), and Br interstitials (I_Br). Doping concentrations are 12.5% for sites A and B, and 4.17% for site X.

The volume of doped CsPbBr₃ (within a 2 × 2 × 2 supercell) primarily depends on the distance between Cs and Br atoms, exhibiting an approximately linear relationship according to our calculations, as shown in Figure S1. For substitutions at the A-site, the formation energy increases with the resulting volume change, indicating that the formation energy is influenced by the ionic radius of the dopant occupying the A-site. The volume of doped CsPbBr₃ is also correlated with the distance between the Pb atom and the substituted atom at the B-site (Figure S2). However, unlike the case of A-site substitution, the formation energy does not show a clear dependence on the volume in the case of B-site doping. Interestingly, substitution with certain elements such as Mn, Nb, and Ni at the B-site induces a net magnetic moment in the doped CsPbBr₃, as summarized in Table . This observation is consistent with previous DFT calculations for Mn, and Ni. It should be noted that the PBE functional employed in this work affects the hybridization between atomic orbitals and underestimates the localization of the d orbitals in transition metals, resulting in reduced magnetic moments for CsPbBr₃ doped with Mn, Ni, and Nb. For X-site substitutions, the formation energy tends to become more negative (indicating higher stability) with increasing electronegativity of the substituted atom. Specifically, the electronegativity trend follows F > Cl > I.

Na, the only element considered substituting at both A- and B-sites, shows a preference for replacing Pb (E _F = 0.35 eV) over Cs (E _F = 1.73 eV), consistent with previous theoretical work. This preference may be attributed to the reduction in bond lengths between Br and both Cs and Pb atoms. Substitution of Pb by Na introduces excess charge into the CsPbBr₃ lattice. Na doping offers several benefits, including a reduction in Br vacancies, , enhancement of PLQY, , and improved stability under various environmental conditions. , The substitution site preference is influenced by the valence state and atomic radius of the alkali metal dopant, as well as the chemical potentials governed by the synthesis conditions.

Br vacancies (V_Br) and Br interstitial doping result in volume expansion and compression, respectively. In contrast, both Pb vacancies (V_Pb) and Cs vacancies (V_Cs) lead to volume contraction. This behavior aligns with the redistribution of electronic charge around Pb atoms: charge depletion occurs in the presence of Cs and Pb vacancies, while Br vacancies result in charge accumulation. Among these, V_Br is more likely to form (E _F = 3.32 eV) than V_Cs (E _F = 3.82 eV) and V_Pb (E _F = 5.12 eV). The presence of V_Cs has been shown to cause local lattice distortions and reduce the photoluminescence (PL) lifetime. Mitigation strategies, such as adjusting the dosage of the Cs⁺ precursor, can suppress the formation of V_Cs.

For dopants exhibiting a net magnetic moment (e.g., Mn and Nb), the structure becomes more stable at higher doping concentrations. In practice, the likelihood of successfully forming doped CsPbBr₃ also depends on experimental parameters, such as temperature, incident flux, and precursor ratios, which influence the local chemical potentials of the constituent atoms. Additionally, the kinetic processes occurring during synthesis play a critical role. ,

In addition, a clusterized dopant distribution is calculated to be more favorable for substitution at the A-site with elements from the same group as Cs in the periodic table. Substitutions at the B-site and X-site are more complex, as the dopant distributions are influenced by factors such as atomic radius and electronegativity. At the B-site, a clusterized dopant distribution is more favorable for dopants such as Ag, Bi, and Na, whereas an isolated distribution is preferred for Al, Ba, Ga, Mn, Nb, Ni, and Sn. At the X-site, clustering is favored for F and I, while Cl tends to adopt an isolated distribution. For vacancy defects, Cs vacancies are more likely to form in clusters, whereas Pb and Br vacancies tend to form in an isolated manner.

Electronic Properties in Different Doped CsPbBr₃

Regardless of whether a dopant can be stably incorporated into CsPbBr₃, it is informative to examine how these dopants influence the electronic band structure. The effective (unfolded) band structures of pristine and doped CsPbBr₃ are shown in Figures and , with the corresponding band gaps summarized in Table S2. In this work, we focus only on the relative changes in the band gap of doped CsPbBr₃ compared to pristine CsPbBr₃. This choice is motivated by the well-known underestimation of band gaps obtained using the PBE functional. For instance, the experimental band gap of pristine CsPbBr₃ is 2.3 eV, , whereas our calculations yield 1.78 eV without SOC and 0.64 eV with SOC, consistent with previous theoretical reports. ,,

2.

(a) Band structure and (b) partial density of states of pristine CsPbBr₃.

3.

Effective band structures of various doped CsPbBr₃ within 2 × 2 × 2 supercells: (a) Na_0.125Cs_0.875PbBr₃, (b) K_0.125Cs_0.875PbBr₃, (c) Rb_0.125Cs_0.875PbBr₃, (d) 12.5% Cs vacancy, (e) CsNa_0.125Pb_0.875Br₃, (f) CsBa_0.125Pb_0.875Br₃, (g) CsGa_0.125Pb_0.875Br₃, (h) 12.5% Pb vacancy, (i) CsPbF_0.042Br_0.958, (j) CsPbCl_0.042Br_0.958, (k) CsPbI_0.042Br_0.958, and (l) 4.17% Br vacancy. The Fermi energy is aligned to 0 eV, and spin–orbit coupling is included in all calculations.

For dopants substituting Cs at the A-site, as shown in Figure a–d, elements such as K, Na, and Rblocated in the same group (column) as Cs in the periodic tabledo not significantly alter the overall characteristics of the band structure compared to pristine CsPbBr₃. The trend of decreasing band gap with increasing ionic radius of the A-site dopant, when considering the SOC effect (see Table S2), is consistent with the results reported in ref This behavior can be attributed to the fact that the electronic states of Cs and its group-equivalent dopants contribute minimally to the VBM and CBM, as illustrated in Figures and S4. From a structural perspective, the bond distances between Cs and neighboring atoms (i.e., Pb and Br) are larger than those between Pb and Br (see Table ), further supporting the minimal impact of A-site dopants on the electronic band structure.

Substitution at the B-site leads to more pronounced changes in the band structure, except in the case of Sn, which belongs to the same group as Pb in the periodic table (see Figures and S3). In particular, the presence of defect states results in a metallic character (i.e., zero band gap) for Ga-substitution at the B-site [Figure g]. Similar defect states are observed for other dopants, though their orbital origins vary. For example, the defect states arise from d orbitals in the case of Ni [Figure S5f] and Nb [Figure S5i], and from p orbitals in the case of Bi [Figure S5g]. As shown in the plots of the partial density of states (PDOS) in Figure S5f–i, these dopants significantly alter the density of states near the VBM and CBM. In Figure , it is evident that the influence of these defect states becomes less pronounced at lower doping concentrations (1.56%). This trend aligns with previous theoretical work, which demonstrated that Nb-doped CsPbBr₃ can exhibit either metallic or semiconducting behavior depending on the doping concentration [see Figure c,g].

4.

Comparison of effective band structures of B-site-doped CsPbBr₃ at different substitution concentrations: (a) CsBi_0.125Pb_0.875Br₃, (b) CsMn_0.125Pb_0.875Br₃, (c) CsNb_0.125Pb_0.875Br₃, (d) CsNi_0.125Pb_0.875Br₃, (e) CsBi_0.016Pb_0.984Br₃, (f) CsMn_0.016Pb_0.984Br₃, (g) CsNb_0.016Pb_0.984Br₃, (h) CsNi_0.016Pb_0.984Br₃. The Fermi energy is aligned to 0 eV and spin–orbit coupling is not included.

The origin of these defect states is illustrated in Figure S7, based on the atomic energy levels of the dopant and host atoms. The in-gap defect states observed in the band structures of charged dopants (i.e., those with valency 1⁺ or 3⁺) arise from dopant atomic energy levels that lie within the energy range spanned by the Br 4p and Pb 6p orbitals, which primarily contribute to the VBM and CBM in pristine CsPbBr₃. It is worth noting that although the Ga 4s orbital lies outside this energy range in the isolated atom, it still gives rise to in-gap defect states due to significant changes in the band structure after doping. These changes result in a downward shift of the Ga 4s orbital energy, placing it within the gap.

Changes in the band gap (see Table S2 for values without spin–orbit coupling) are influenced not only by the appearance of in-gap defect states, but also by the alignment of dopant atomic energy levels relative to the Pb 6p and Br 4p orbitals. For example, dopants such as Mn and Ni at the B-site have energy levels close to those of Pb orbitals, while dopants such as Al, Bi, and Sn at the B-site, and F, Cl, and I at the X-site, possess orbital characters similar to the VBM or CBM, which also affect the band edges.

The incorporation of monovalent dopants (1⁺ ions), such as Na and Ag (which have one fewer valence electron than Pb²⁺) leads to a downward shift for the Fermi energy to a lower energy relative to pristine CsPbBr₃. In these doped CsPbBr₃, the states above the shifted Fermi energy 0 eV (which resemble the VBM of pristine CsPbBr₃) are unoccupied. A similar observation was reported in previous experimental work on Ag-doped CsPbBr₃, where strong p-type character was observed. In contrast, trivalent dopants (3⁺ ions), such as Al, Bi, and Nb (which have one more valence electron than Pb²⁺), induce an upward shift of the Fermi energy relative to pristine CsPbBr₃, bringing the CBM of pristine CsPbBr₃ closer to 0 eV. Depending on the orbital composition of the dopant, the states near 0 eV originate from different orbitals: s orbitals for Al [Figure S5j], p orbitals for Bi [Figure S5g], and d orbitals for Nb [Figure S5i].

For charge-neutral dopants such as Ba and Mn, the orbital contributions near 0 eV differ: in Ba-doped CsPbBr₃, they stem from the s and p orbitals of Pb (Figure S5d), while in Mn-doped CsPbBr₃, they originate from Mn d orbitals (Figure S5e). PLQY enhancement in Mn-doped CsPbBr₃ has been attributed to d–d transitions in Mn²⁺, facilitated by energy transfer from excitons. , Kanoun and Goumri-Said. also reported other advantages of Mn doping, such as suppression of defect states and increased carrier effective masses. The latter is consistent with the localized nature of Mn d orbitals observed in the PDOS [Figure S5e]. These findings suggest that doping with elements possessing d orbitals may be an effective strategy for modulating carrier effective masses in perovskite materials. The corresponding PDOS for various B-site doped CsPbBr₃ systems are shown in Figure S5.

For substitution at the X-site, the band structures of CsPbBr₃ doped with F, Cl, and I remain largely similar to that of pristine CsPbBr₃, as these dopants belong to the same group as Br in the periodic table [Figure i–k]. In contrast, doping Br at an interstitial site induces defect states near 0 eV [Figure S3h]. These defect states primarily originate from the p orbitals of the interstitial Br atom [Figure S6d], consistent with the orbital character of the VBM in pristine CsPbBr₃. Notably, the energy position of these defect states can shift slightly upward or downward, depending on the precise interstitial location of the Br atom.

As shown in Figure d,h,l, vacancies of Cs and Pb exhibit opposite effects on the band structure compared to Br vacancies. Specifically, Cs and Pb vacancies shift the Fermi energy (0 eV) downward, while Br vacancies shift the Fermi energy (0 eV) upward relative to pristine CsPbBr₃. This behavior arises from the electron count imbalance: Cs and Pb vacancies result in a deficiency of valence electrons, making it difficult to fully occupy the original VBM; conversely, Br vacancies introduce extra electrons that partially fill the CBM.

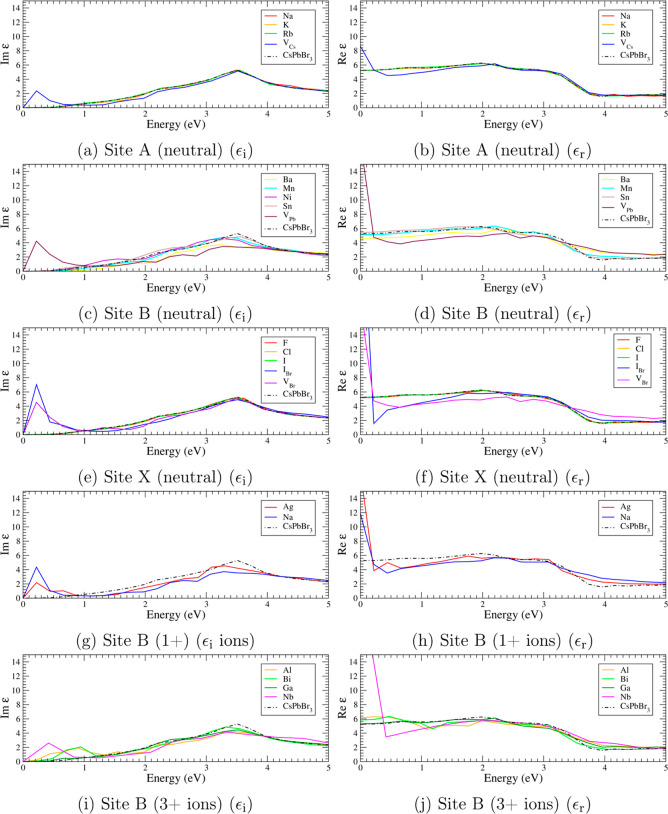
The emergence of defect states induces significant modifications in the dielectric function. Figure presents the dielectric functions of various doped CsPbBr₃ systems. Charge-neutral dopants at the A- and X-sites generally induce minimal changes [Figure a,b,e,f]. In contrast, B-site doping typically causes a shift of the peaks around 3.5 eV toward lower energies [Figure c,d]. Charged dopants result in more pronounced modifications to the dielectric functions, including the emergence of peaks below 1 eV [Figure g,i] and noticeable changes in the magnitude of the dielectric response [Figure h,j].

5.

Dielectric functions of doped perovskites within 2 × 2 × 2 supercells. Imaginary dielectric functions ϵ_i of defects at site (a) A (charged-neutral), (c) B (charged-neutral), (e) X (charged-neutral), (g) B (1+ ions), (i) B (3+ ions). Real dielectric functions ϵ_r of defects at site (b) A (charged-neutral) (d) B (charged-neutral), (f) X (charged-neutral), (h) B (1+ ions), (j) B (3+ ions).

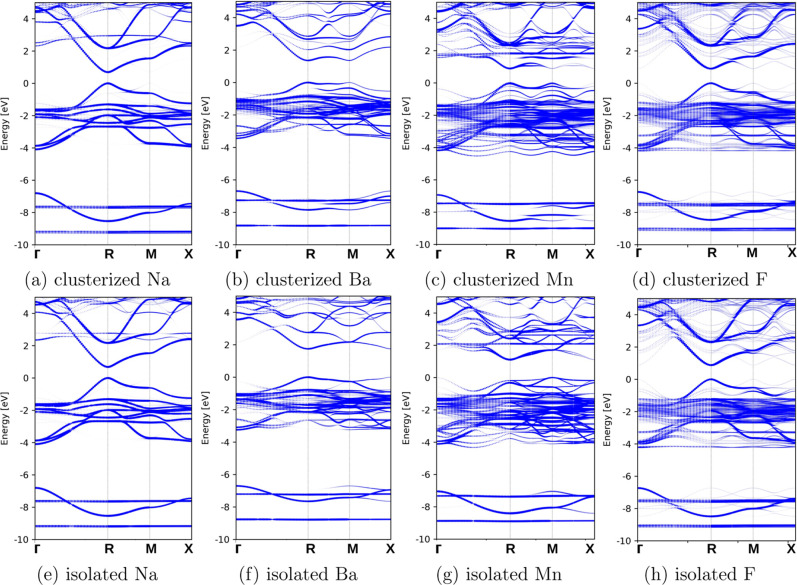
On the other hand, the influence of dopant distribution on the band structure can also be investigated. In this case, the doping concentration is increased to 25.0% for substitutions at the A- and B-sites, and 8.3% for substitutions at the X-site, corresponding to two dopants introduced into a 2 × 2 × 2 supercell. As shown in Figure , the dopant distributions of Na and F at the A- and X-sites, respectively, do not significantly alter the overall characteristics of the band structures [Figure a,d,e,h]. For substitutions at the A- and X-sites, the resulting band gap of doped CsPbBr₃ is generally larger when the dopants are arranged in a clusterized configuration. In contrast, for substitutions at the B-site, isolated dopant distributions (Table S3) tend to produce wider band gaps compared to their clusterized counterparts [Figure b,c,f,g]. For doped CsPbBr₃ exhibiting a net magnetic moment, the magnetic moment increases only slightly in clusterized dopant distributions compared to isolated ones. The magnetic moment and the nature of ferromagnetic or antiferromagnetic couplings in clusterized distributions may vary depending on the choice of transition metal dopants or the doping concentration.

6.

Comparison of effective band structures of doped CsPbBr₃ with different dopant distributions, calculated using 2 × 2 × 2 supercells. (a) Na_0.250Cs_0.750PbBr₃ with a clusterized dopant distribution; (b) CsBa_0.250Pb_0.750Br₃ with a clusterized dopant distribution; (c) CsMn_0.250Pb_0.750Br₃ with a clusterized dopant distribution; (d) CsPbF_0.084Br_0.916 with a clusterized dopant distribution; (e) Na_0.250Cs_0.750PbBr₃ with an isolated dopant distribution; (f) CsBa_0.250Pb_0.750Br₃ with an isolated dopant distribution; (g) CsMn_0.250Pb_0.750Br₃ with an isolated dopant distribution; (h) CsPbF_0.084Br_0.916 with an isolated dopant distribution. The Fermi energy is aligned to 0 eV in all panels, and spin–orbit coupling is included.

Since dopant distribution also affects the band structure, the optoelectronic properties, which are determined by electronic parameters such as the band gap, effective mass, and Kane parameter (describing the interaction between valence and conduction bands), can vary with different dopant configurations. Clustered dopant distributions are predicted to have larger effects, such as enhanced orbital overlap and the formation of impurity bands, because strengthened dopant interactions induce more significant changes in the electronic structure. For example, the PLQY of CsPbBr₃ nearly doubles due to quantum cutting when Yb atoms occupy neighboring B-site positions. −

The change in band structure depends primarily on electronic effects rather than geometrical ones. Na_0.125Cs_0.875PbBr₃, CsBa_0.125Pb_0.875Br₃, and CsPbI_0.042Br_0.958 lead to volume changes of −0.34%, +2.94%, and +0.90%, respectively, compared to pristine CsPbBr₃. The corresponding band gaps are modified to E _g = 0.694, 1.096, and 0.664 eV, in contrast to E _g ≈ 0.637 eV for pristine CsPbBr₃. When external strain is applied in the reverse direction of the volume change, the band gap does not return to its original value. Instead, it shifts to 0.728, 0.834, and 0.570 eV, respectively. The corresponding band structures under external strain are shown in Figure . The direction of applied strain successfully restores the band gap for substitution with Ba (at the B-site) and I (at the X-site), but not for substitutions with Na (at the A-site). In general, the band gap of a doped perovskite increases under tensile strain and decreases under compressive strain (see Figure S8), in agreement with previous theoretical studies. This behavior arises because compressive and tensile strains, respectively, increase and decrease the orbital overlap and hybridization in the VBM and CBM, thereby altering the band gap.

7.

Effective band structures of doped CsPbBr₃ perovskites within 2 × 2 × 2 supercells under externally applied strain. (a) Na_0.125Cs_0.875PbBr₃ under 0.34% tensile strain; (b) CsBa_0.125Pb_0.875Br₃ under 2.94% compressive strain; (c) CsPbI_0.042Br_0.958 under 0.90% compressive strain. The Fermi energy is aligned to 0 eV in all panels, and spin–orbit coupling is included.

Conclusion

In this work, we investigate the atomic and electronic structures of various doped CsPbBr₃ perovskites. The thermodynamic stability of dopants is influenced by both their electronegativity and ionic radius, particularly for B- and X-site substitutions. The unit cell volume increases when atoms are removed from the X site, but decreases for removal at the A or B sites or for interstitial doping at X. A tendency toward dopant cluster formation is observed only for A-site substitutions. While A-site doping has little effect on the band structure, dopants at B and X sites can induce significant changes, including the emergence of defect states, modifications to the band gap, effective mass, and dielectric functions. Additionally, the dopant distribution and externally applied strain can further modulate the electronic structure of doped CsPbBr₃.

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.5c07761.

• Volume versus average Cs–Br distance; volume versus average Pb-dopant distance at the B-site; effective band structures of various doped CsPbBr₃ systems; partial density of states (PDOS) of selected doped configurations; atomic energy levels of various elements in PAW–PBE pseudopotentials; band structures under applied external strain; tabulated values of E _corr for different charged dopants; tabulated values of band gap for various dopants with and without SOC; and band gap for different dopant distributions (PDF)

†.

Department of Physics, National University of Singapore, 2 Science Drive 3, Singapore 117542, Singapore

The authors declare no competing financial interest.