Doppler effect tailoring: extra-red shift of structured light

Abstract

Doppler effect is a universal phenomenon that describes the frequency shift of waves when interacting with moving targets. Recent studies suggest that the spatial structures of light beams would provide a modification of the group and phase velocities of optical fields, raising the question of how spatial confinement on optical fields affects Doppler shifts of structured beams. In this work, we propose and demonstrate the concept of Doppler effect tailoring, i.e., the transverse structure of optical fields naturally causes an extra red shift on the original Doppler shift, which we call the structure-shearing Doppler effect (SDE). Theoretical analyses suggest that the SDE observed in the experiment is actually a universal effect on both light waves and photons and it is predicted to exist beyond optics in any non-planar electromagnetic and sound waves. The SDE may provide new insights into the Doppler effect for astronomical observations, laser cooling, and light-matter-interaction within hollow waveguides or cavities. Technically, a homodyne-free Doppler velocimeter is developed based on the SDE, facilitating a single probe beam without external reference enabling the system resistant to environmental disturbance. Regarding application prospects, the implementation is of great significance for leveraging structured beams in motion sensing in engineering.

The structure-shearing Doppler effect is proposed to reveal extra red shifts induced by transverse structure of optical fields. It enables a homodyne-free velocimeter and offers opportunities in motion sensing and light-matter interactions.

Introduction

The Doppler effect is a well-known fundamental physical phenomenon that describes the frequency shift induced by the interaction between waves and moving objects. The conventional Doppler effect was named by the Austrian physicist Doppler, who noticed that the received frequency of waves would change when the source is moving forward or backward from the observer. The Doppler effect is of great interest to astronomers and engineers. In astronomy, the relative velocity of a star can be measured by observing the wavelength shift of the star glowing¹. The applications of the Doppler effect on velocity measurements have exploded since the laser was employed to develop the laser Doppler velocimeter (LDV) by Yeh and Cummins². The LDVs take advantage of non-contact and high resolution for being applied in a variety of scenarios, such as blood velocity imaging³, flow monitoring⁴, wind lidar⁵, and vibrometry⁶. The concept of the conventional Doppler effect is shown in Fig. 1a, where a fundamental Gaussian beam, which is approximately regarded as a plane-phase wave when ignoring the divergence, is illuminated normally onto the object, and then the Doppler shift is observed from the reflected beam. The interpretation of the Doppler effect could be given in terms of both the wave and particle properties of light. From the perspective of a wave, the frequency of a light wave is defined as the rate of phase change with time, i.e., $f=\partial \Phi /\partial t/2\pi$. Considering that the optical path of the reflected light would change $\delta =2vt$ when a mirror is moving along the z axis, the resultant phase change $\Delta \Phi =k_z\cdot \delta$ would give rise to the Doppler shift $\Delta f_v=2f_{0}v/c$, where $f_0$ is the original frequency of the wave and $c$ the speed of light in vacuum, assuming that the plane wave travels along the z axis and thus the longitudinal component of wavevector $k_z$ is equal to the global $k_0$. From the perspective of a photon, the frequency of a photon is related to its energy $\epsilon$, i.e., $f=\epsilon /h$, where h is the Planck constant. With the reversal of linear momentum during interaction with a moving mirror, the impulse of $2\hslash k_z$ would lead to energy transferring between the photon and the mirror of $\Delta \epsilon =2\hslash k_{z}v$, where $\hslash =h/2\pi$, and the calculated Doppler shift is the same as that of the wave. Note that both the phase changing of waves or the energy changing of photons here are related to the $k_z$.

Fig. 1. Comparison between the conventional Doppler effect and the structured beam-induced Doppler effects.

a Conventional linear Doppler effect, where a planar phase beam is normally incident on a moving object and the Doppler shift is related to the linear velocity of the object and the phase velocity of the beam. b Rotational Doppler effect (RDE), where a vortex beam with angular wavevector is illuminated onto a spinning object, and the rotational Doppler shift is dependent upon the angular velocity of the object and topological charge of the beam’s orbital angular momentum (OAM). c Structure-shearing Doppler effect (SDE), where a Bessel beam with radial wavevector shines on a moving object and the observed Doppler shift would get an extra redshift compared with (a) due to the superluminal phase velocity of the beam.

As a developed form of the conventional Doppler effect, the rotational Doppler effect (RDE) has been studied when considering the spin angular momentum (SAM) and orbital angular momentum (OAM) of light. The RDE is first observed with SAM by spinning the circular polarization⁷, and it was called the angular analog of the conventional linear Doppler effect⁸. Later, Allen et al. predicted theoretically that the RDE could also be induced by light-carrying OAM⁹, and then it was revealed experimentally with mm-wave¹⁰. The RDE has attracted wide attention in the last decade since it was shown to have great application prospects in angular motion detection¹¹. The developed rotational Doppler velocimetry (RDV) based on RDE has been applied for measuring the rotational speed of various targets, including rough surfaces^11–15, structured objects^16–19, fluids^20–22, and microparticles^23–25. Physically, the RDE is induced by the interaction between the lateral movements and the angular momentum of fields. The concept of RDE based on OAM is shown in Fig. 1b, where the optical vortex, such as Laguerre-Gaussian (LG) beam, is incident on a spinning rough surface or spiral waveplate along the spin axis, and then the rotational Doppler shift can be extracted from the scattered beam with mode filtering. The azimuthal phase gradient of vortex beams twists the initial wavevector $k_0$, giving rise to an azimuthal component $k_{\phi }$ to interact with the angular velocities. The small twisted angle of $k_0$ from the beam axis is related to the OAM of the beam, i.e., $\gamma =\ell /k_{0}r$, where $r$ is the radial location in the beam²⁶. The RDE can be derived from the conventional linear Doppler effect with scalar product between $k_{\phi }$ and the transverse linear velocity of the angular motion, i.e., $\Delta f_{\Omega }={\overrightarrow{k}}_{\phi }\cdot {\overrightarrow{v}}_{\perp }/2\pi =\ell \Omega /2\pi$. The RDE is dependent upon the mode changing during the interacting process with a rotating element that could provide a modulation on OAM²⁷. The physical properties of RDE have recently been extensively studied in both acoustics^28–30 and optics^31–34. A unique property of the RDE is that it is not related to the longitudinal characteristics of light beams, such as wavelength and $k_z$, but to the angular phase inhomogeneity in the transverse plane, i.e., the azimuthal phase gradient. With the study of physical dimensions of structured beams, the RDE has also been developed into its vectorial type, i.e., the vectorial Doppler effect (VDE)^35,36. Taking advantage of the degree of freedom (DoF) of spatial polarization, the VDE enables the vectorial information acquisition of angular velocities.

The spatially structured beams have been developed as a powerful toolbox with tremendous application prospects over the years^37–39. Particularly, the structured beams have shown exotic propagation properties. In the quantum realm, Giovannini’s experiment suggests that the spatial confinement of photons would slow down the propagation speed of the light⁴⁰. Such a phenomenon is then called the structured slowing effect to describe the decreased group velocity of structured beams, and subsequent studies have demonstrated the subluminal group velocity of numerous structured beams, including Bessel-Gaussian (BG) beams^40–42, LG beams^43–45, twisted photons^46,47, and optical speckles⁴⁸. In a free-space configuration, similar to a hollow waveguide, the relationship between phase and group velocities is given as $v_{\varphi }{v}_g=c^2$ ⁴⁹. This means that the overall phase of the structured beams would travel faster than the speed of light c in vacuum. It would induce the structured lagging propagation phase by spatially spreading the k-spectrum⁵⁰, which is similar to the Gouy phase that appears when LG beams transmit through the beam waist⁵¹. From the expression of the Doppler shift, we notice that the superluminal phase velocity of structured beams may cause a modification of the conventional Doppler effect. In this work, we show that the transverse structure of optical fields naturally causes an extra redshift on the original Doppler shift and propose the structure-shearing Doppler effect (SDE) to describe the Doppler effect tailoring by structured beams. The theoretical model of SDE is given through the k-spectrum analysis under paraxial approximation, where the SDE is determined by the transverse wavevector $k_{\perp }$ of spatially structured beams. Technically, we provide a homodyne-free Doppler velocimeter based on the SDE, which is the first configuration using a single probe beam alone without the reference with respect to the state-of-the-art Doppler velocimeters.

Results

Concept of the SDE

The comparison between the conventional Doppler effect and the structured beam-induced Doppler effects is shown in Fig. 1. For the conventional Doppler effect, as shown in Fig. 1a, when a planar phase beam is incident on a moving object along the direction of linear velocity, one can observe the Doppler shift from the planar phase component in the scattered beam as $\Delta f_v=2f_{0}v/c$. The term planar phase here refers to $k_z=k_0$ or, in other words, $k_{\perp }=0$, and the corresponding beam is generally approximated to a Gaussian beam with finite energy, and such a component in scattered speckles can be extracted by locally detecting the center of its k-spectrum or by mode matching with a single-mode fiber (SMF). The Doppler shift is related to both the linear velocity of the object and the phase velocity of the beam, which in this case is equal to light speed c in vacuum. The Doppler effect has been revealed in other forms with the study of structured beams. Typically, for a vortex beam with angular wavevector, as shown in Fig. 1b, its interaction with a spinning rough surface would give rise to the RDE³², i.e., $\Delta f_{\Omega }=\ell \Omega /2\pi$, where the rotational Doppler shift is dependent upon the angular velocity of the object ($\Omega$) and the topological charge change of the beam’s OAM ($\ell$).

Here, a further consideration is how the transverse wavevector of structured beams affects the original Doppler effect. When sculpting a light beam by a transverse phase gradient, the transverse spatial confinement would lead to divergence or convergence of the field. Such a process, from the perspective of wavevector space, appears as k-spectrum spreading from the center to a certain range, and thus the nonzero transverse component produces a modification to the axial component, namely $⟨k_z⟩=\sqrt{k_0^2-⟨k_{\perp }^2⟩}$, where $⟨.⟩$ denotes the statistical expectation over the k-spectrum. From the definition of phase velocity $v_{\varphi }=c\cdot k_0/k_z$, it can be extended to $v_{\varphi }=c\cdot k_0/⟨k_z⟩$ for describing the spatially average phase velocity of structured beams. Correspondingly, the mean Doppler shift of a structured beam interacting with a moving mirror is given as $\Delta f_{SDE}=2f_{0}v/v_{\varphi }$, where $v_{\varphi }=c{\left(1-⟨k_{\perp }^2⟩/2k_0^2\right)}^{-1}$ (note that a 1-order Taylor approximation is used here). Since the $⟨k_{\perp }^2⟩$ here takes a positive value, the spatially average phase velocity of structured beams is predicted to be greater than c, and this would result in the mean Doppler shift being smaller than the original. This means that any structured beam with a spreading k-spectrum would experience extra red shifts in the Doppler effect, and we call this phenomenon the SDE.

Here we consider the structured beam with a ring-shaped k-spectrum as a representative case, i.e., the Bessel beam in real space⁵². In cylindrical coordinates, the transverse wavevector of a Bessel beam is characterized by a single-valued radial component $k_r$. The radial wavevector $k_r$ defines a conical distribution around the propagation axis, and the associated cone angle is given by $\alpha =k_r/k_0$ under small-angle approximation. For the case of SDE that a Bessel beam shines on a moving object, as shown in Fig. 1c, one can obtain the SDE with structure-shearing Doppler shift from the reflected Bessel beam as

$$\Delta f_{SDE}=\frac{2f_{0}v}{c}\left(1-\frac{{\alpha }^2}{2}\right).$$ 1

From Eq. 1, the structure-shearing Doppler shift comprises two components, i.e., a base component, corresponding to the conventional Doppler shift, and a modified component, given by an additional redshift associated with the cone angle in the wavevector domain. Similar to the RDE, the SDE also exhibits spatial-mode dependence. Note that Eq. (1) is derived by regarding that the object is mirrorlike and thus the $k_z$ is reversed during reflection, and the observed α remains. When the object is a rough surface, the structure-shearing Doppler shift can be extracted by radial mode filtering on the scattered beam, and in particular, the fundamental Gaussian mode can be easily obtained through coupling into an SMF, in which case the Doppler shift in Eq. (1) should be divided by 2.

The SDE framework reveals that the resulting Doppler shift is determined by the transverse wavevectors, which may include contributions from the angular wavevectors. This behavior can be illustrated using higher-order Bessel beams, which possess both radial and angular phase gradients. Through Fourier transformation, ideal higher-order Bessel beams can be mapped to perfect optical vortices⁵³, featuring a ring-shaped amplitude profile with fixed radius and an azimuthal phase structure defined by OAM. This implies that ideal higher-order Bessel beams with different OAM share the same range of k-spectrum, and thus, induce identical Doppler shifts under the SDE. However, in practical optical systems, where the beam energy and aperture are finite, the twisted phase arising from the OAM would introduce additional beam divergence⁵⁴. For example, higher-order Bessel beams are commonly created by passing an LG beam through an axicon⁵⁵. In this process, the k-spectrum range would slightly increase with the OAM, analogous to the increase in beam waist of LG beams with higher OAM orders. In the context of this study, the divergence contribution from the angular phase gradient remains small compared to the radial cone angle and can therefore be reasonably neglected. The SDE is a universal phenomenon applicable to any wave with a non-planar spatial structure. We employ the Bessel beam as an example here, primarily due to its well-defined and significant $k_r$, enabling clear observation and analysis of the Doppler shift. In more general cases, such as optical speckles characterized by randomly-distributed k-spectrum⁴⁸, the inhomogeneous distribution of $k_{\perp }$ results in a broadened Doppler spectrum, which is no longer single-valued but instead spread across a frequency range. Notably, this broadened spectrum lies entirely on the red side of the conventional Doppler shift. The global shift of the broadened spectrum can be quantitatively characterized by the statistical average of $k_x^2+k_y^2$, analyzed in Cartesian coordinates.

The SDE can be detected from beat signal by engineering the k-spectrum of the probe beam, and based on this, the concept of homodyne-free structural Doppler velocimetry (SDV) is proposed, as shown in Fig. 2. In conventional Doppler velocimetry, a reference beam is usually required for implementing homodyne interference with probe beam because the photodetector (PD) is lack of response at optical frequency, but the path difference results in poor resistance to environmental disturbance. In contrast, the SDV, using structured beams as the probe, such as the superposed Bessel beams with different cone angles, enables a single probe beam without an external reference. The wavevector-cone of the probe beam is shown in Fig. 2a. From Eq. (1), when illuminated by a superposed Bessel beam with cone angles ${\alpha }_1$ and ${\alpha }_2$, the beat frequency observed in the beam reflected from a moving mirror is given by

$$\mid \Delta f_{SDE}\mid =f_0\cdot \frac{\mid \left({\alpha }_1^2-{\alpha }_2^2\right)v\mid }{c}.$$ 2

Fig. 2. Concept of homodyne-free structural Doppler velocimeter (SDV) based on the SDE.

A structured beam by k-spectrum engineering with two different cone angles k_r/k₀ is used to probe the moving mirror and the velocity information is extracted directly from the Doppler shift in reflected signal beam, enabling a single probe beam without external reference. a Wavevector-cone of the probe beam, which consists of two cones with distinct cone angles. b When the probe beam is a superposition of Bessel beams with different cone angles but identical OAM, the reflected SDE signal beam exhibits temporal flickering. The SDE signal beam can be detected by locally collecting the central region. c When the probe beam comprises two Bessel beams with both different cone angles and OAM, the reflected SDE signal beam exhibits dynamic rotation over time. The SDE signal beam can be measured either through local detection, by partially collecting light within an off-axis region, or through mode-filtering detection, by detecting the overlap between the SDE signal beam and an original state of the probe beam, which is implemented via spatial filtering with single-mode detection. d Detected Doppler signals from which the SDE beat frequency is extracted via Fourier analysis. The signals would exhibit consistent beat characteristics across various detection configurations in b, c.

It suggests that the beat frequency provides a linear response to the velocity, and the response rate is proportional to the squared variance of the cone angles. In particular, different spatial components could induce different frequency shifts in SDE, and thus the reflected beam from the moving mirror would exhibit spatiotemporal properties, i.e., the dynamic evolution of the spatial pattern over time. For the superposition of two spatial components, it can be visualized by Poincaré sphere analog⁵⁶, where the location mapped on the sphere would move along the equator, and the corresponding time-varying structure propagation lagging phase difference⁵⁰ induces the Doppler signal (see Supplementary Note 1 for more details).

When the probe beam is a superposed Bessel beam with two different cone angles but identical OAM, as shown in Fig. 2b, the resulting SDE signal beam appears in the form of Newton rings and the inner region turns between light and dark, with the flickering frequency determined by Eq. (2). In this case, the SDE signal beam can be detected by directly collecting the global beam, or by local detection with collecting light in a central region to improve the signal-noise-radio (SNR). In contrast, when the two Bessel components carry different OAM orders, as shown in Fig. 2c, the SDE signal beam behaves as the petal-like profile that is rotating at the angular change rate of $\Omega =2\pi f_{0}v\Delta {\alpha }^2/c\Delta \ell$, where $\Delta {\alpha }^2={\alpha }_1^2-{\alpha }_2^2$ and $\Delta \ell ={\ell }_1-{\ell }_2$. The SDE-induced rotating beam acts like the optical Ferries wheel⁵⁷ caused by the frequency shift between two OAM modes. Note that since the Doppler signal beam has rotational symmetry of $\Delta \ell$, the detected beat frequency is amplified by a factor of $\Delta \ell$ relative to the beam rotating rate, and thus, after canceling out $\Delta \ell$, the resultant observed beat frequency is topologically charge independent (see Supplementary Note 2 for more details). Two detection strategies are applicable for such SDE signal beams, namely local detection and mode-filtering detection (see Supplementary Note 3 for detailed implementation). The local detection involves partially collecting a portion of the beam using a center-placed slit or an off-axis aperture, while the mode-filtering detection measures the overlap between the SDE signal beam and the original state of the probe beam, using phase-mask demodulation followed by spatial filtering and single-mode detection. In various detection scenarios of Fig. 2b, c, the time-varying signals can be processed via the Fourier transform, and the frequency of the peak in the Fourier spectrum conforms to Eq. (2), showing a linear relationship that enables the determination of the moving speed.

Experimental observation of the SDE

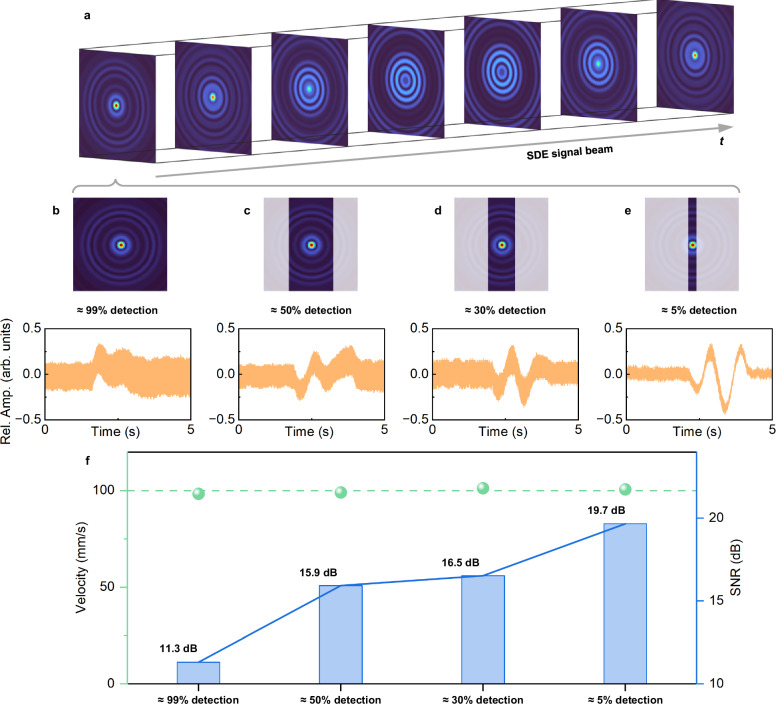
As a straightforward demonstration, the SDE can be observed using a probe beam formed by the superposition of two 0-order Bessel beams with distinct radial wavevectors, without carrying OAM. Details of the experimental implementation are introduced in Methods. In the first demonstration, the probe beam is shaped with α₁ = 0.00205 and α₂ = 0.003, and the moving velocity is set to 10 cm/s. The resulting SDE signal beam exhibits Newton-ring-like interfering fringes with a central dominant spot surrounded by concentric side-lobe rings, flickering over time, as shown in Fig. 3a. Note that, unlike uniform flickering across the entire beam, the flickering here is divided into two regions due to the inhomogeneous initial phase of the central spot and outer rings. Specifically, certain side-lobe rings increase in intensity while the central spot and other side-lobe rings simultaneously decrease, although all regions flicker at the same beat frequency. The SDE beat frequency can be extracted directly by detecting the near-global intensity variation of the entire SDE signal beam, as shown in Fig. 3b. However, analogous to Rayleigh fading, the globally detected Doppler signal contains two anti-phase components at the same frequency, which partially cancel each other and reduce the SNR. As a result, the experimentally observed signal (bottom of Fig. 3b) shows a relatively low peak-to-peak amplitude and an SNR of only 11.3 dB. As a comparison, as shown in Fig. 3c–e, a slit with duty ratios of 50%, 30%, and 5% respectively, is placed before the detector to partially collect the SDE signal beam. The experimental results reveal that restricting the detection region significantly enhances the peak-to-peak amplitude of the Doppler signal. As summarized in Fig. 3f, while the measured velocity remains accurate across all cases, the SNR improves markedly from 11.3 dB to 19.7 dB when a narrow slit isolates the central dominant region. This improvement occurs because the slit could filter out anti-phase signal components from different regions, thereby reducing destructive interference in the detection. This strategy, by placing a slit or aperture to spatially restrict the detection region, is referred to as local detection in the following demonstrations and is adopted in the experiments to enhance SNR.

Fig. 3. Detection of SDE signal beams with radial wavevector difference.

In the experiment, the probe beam is formed by superposing two 0-order Bessel beams with α₁ = 0.00205 and α₂ = 0.003, and the moving velocity is set to 10 cm/s. a Dynamic flickering of the SDE signal beam. b Detection of SDE signal beam by collecting the near-entire beam. c–e Detection of SDE signal beam by partially collecting the beam using slits with duty ratios of 50%, 30%, and 5%, respectively. f Measured velocity and SNR for each detection case in (b–e).

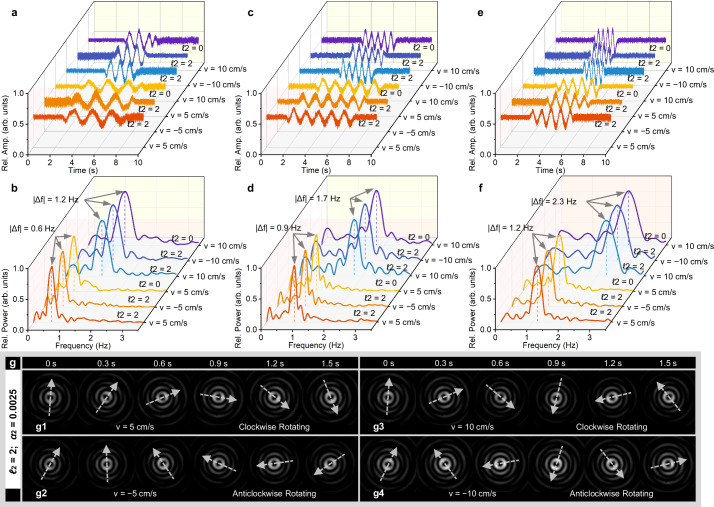
With the probe beam composed of the superposed Gaussian and Bessel beams, the SDE can be observed from the dynamic evolution of the reflected beam and the locally detected beat signals. In this demonstration, the reflected beam from a moving mirror is monitored by a charge-coupled device (CCD) and detected by a PD after a slit. The factors of radial and angular phase gradient are represented by α₁, ℓ₁ (α₂, ℓ₂) for the two spatial components, in which the Gaussian component with a large beam waist is approximately a plane phase and thus α₁ = 0, ℓ₁ = 0. The results collected by the PD under the Bessel component with α₂ = 0.0025 are shown in Fig. 4a. It can be seen that intensity fluctuation occurs in the detected signal when the mirror is moving, and the period of the envelope is related to the velocity. The signals retain similar features of fluctuation when the direction of velocity is reversed or the OAM of the Bessel component is changed. By performing a fast Fourier transform (FFT), the Fourier amplitude spectra of the signals are shown in Fig. 4b. In each Fourier spectrum, there is a prominent Doppler peak that shifts with the magnitude of velocity. The peak frequency is 0.6 Hz at 5 cm/s and doubled at 10 cm/s, and the theoretical values predicted by Eq. (2) are 0.0587 Hz and 1.175 Hz, respectively. When the velocity is reversed, the temporal signals show time-reversal symmetry but are mapped to the same Fourier amplitude spectra because the negative frequency axis takes an absolute value. By comparing the Doppler peak under Bessel component with (ℓ₂ = 2) and without (ℓ₂ = 0) OAM, in which the measured peak frequencies are the same, it suggests that the observed SDE is independent of the angular phase.

Fig. 4. Experimental demonstration of the SDE with local detection.

The probe beam is composed of a superposition of Gaussian (α₁ = 0, ℓ₁ = 0) and Bessel (α₂, ℓ₂) beams. a, c, e The time-varying Doppler signals collected with the Bessel beam at different cone angles, including a α₂ = 0.0025, c α₂ = 0.0030619, e α₂ = 0.0035355. The signals are detected by a photodetector (PD) placed behind a slit. b, d, f The Fourier amplitude spectra corresponding to a, c, e, respectively. g frames of reflected Doppler signal beams captured by a charge-coupled device (CCD).

The typical result for SDE-induced dynamic evolution of the beam is observed by CCD, as shown in Fig. 4g, where the Bessel component carries α₂ = 0.0025, ℓ₂ = 2. The dynamic visualization of the frames and the corresponding Doppler signal acquisition are detailed in Supplementary Video 1. One can see from the frames that the Doppler signal beam rotates clockwise when the direction of velocity is positive, and it is altered to anticlockwise when the velocity is reversed. As in Eq. (1), the blue or redshift of the SDE is related to the direction of motion. Note that the direction is hard to distinguish directly using the locally detected SDE signal due to the time-reversal symmetry, but it can be resolved by global observation. The rate at which the beam is rotating is proportional to the moving velocity during interaction. The greater frequency shift difference from the SDE drives more extrinsic angular momentum in the rotating beam.

For the Bessel component of larger cone angles, the measured results are shown in Fig. 4c, e, where (c) takes α₂ = 0.0030619 and (e) takes α₂ = 0.0035355. The corresponding Fourier amplitude spectra are shown in Fig. 4d, f, where in Fig. 4d, the measured peak frequency is 0.9 Hz at 5 cm/s and 1.7 Hz at 10 cm/s, and the theoretical predictions are 0.881 Hz and 1.762 Hz, respectively, and in Fig. 4f, the measured peak frequency is 1.2 Hz at 5 cm/s and 2.3 Hz at 10 cm/s and the theoretical predictions are 1.175 Hz and 2.350 Hz, respectively. It can be seen that with the enlargement of the radial phase gradient, the extra Doppler shift induced by SDE increases. This means that the extent of SDE can be controlled by designing the radial range of k-spectrum. Due to the limited displacement of the moving mirror in data collection, the effectively processed signal is restricted in a rectangular window function, resulting in a certain width of the Doppler peak in the spectrum of the FFT and its overall profile of the sinc function.

In addition to local detection, when the probe beam involves two different OAM components, the SDE signal beams can also be detected via a mode-filtering technique. Unlike local detection, which captures the beat frequency of two modes by monitoring the localized evolution of interference fringes, mode-filtering detection is a non-local method that measures the overlap between the instantaneous states of the SDE signal beam and the original, unshifted state of the probe beam. In the demonstration of mode-filtering detection of the SDE, the probe beam is composed of a superposition of two higher-order Bessel beams with α₁ = 0.0014697, ℓ₁ = − 3, and α₂ = 0.0035242, ℓ₂ = 3. A mirror moving at 10 cm/s introduces a theoretical beat frequency of 1.92 Hz, as calculated from Eq. 2. The resulting SDE signal beam exhibits a sequence of temporally rotating, petal-like patterns, as illustrated in Fig. 5a. A phase mask, corresponding to the superposed OAM components of the probe beam, is used to demodulate the angular phase components of the SDE signal beam. A coaxial circular aperture is employed to restrict the demodulation region to the inner ring of the beam. The demodulated beams are subsequently Fourier transformed by a lens, and the mode overlap is visualized in the far-field pattern. The time-varying intensity signal is obtained by monitoring the single-mode region of the far-field patterns, as shown in Fig. 5b, and the corresponding Fourier frequency spectrum, displayed in Fig. 5c, reveals a peak at 1.9 Hz, which agrees well with the theoretical prediction. More details for discussing the local detection and mode-filtering detection of the SDE are provided in Supplementary Note 3.

Fig. 5. Experimental detection of the SDE with mode-filtering.

The probe beam is composed of two higher-order Bessel beams (α₁ = 0.0014697, ℓ₁ = − 3, and α₂ = 0. 0035242, ℓ₂ = 3). a Process of mode-filtering detection. The SDE signal beams are demodulated with a phase mask combined with a coaxial aperture. The overlap between the SDE signal beams and the predefined angular mode is revealed in the demodulated far-field patterns. b The time-varying Doppler signals obtained from the single-mode region in each frame of the demodulated far-field patterns. c The Fourier amplitude spectrum corresponding to b.

Detection of velocity with the SDV

The SDV is developed based on SDE to demonstrate the detection of moving velocity, where the probe beam is a superposed Gaussian and higher-order Bessel beam. The SDE beat frequencies at different velocities are measured with a Bessel component carrying ℓ = 2 and various α. As shown in Fig. 6, each data point is carried out by five measurements, and the theoretical lines are predicted by Eq. (2). The velocity can be obtained from the measured beat frequency by using the linear relationship, the slope of which is related to the square of $\alpha$. The operating responsivity of the SDV is ${\alpha }^2/\lambda$, meaning that it works more sensitively with a larger $\alpha$. Nevertheless, considering that the diffraction-free distance of a Bessel beam is approximately $w_0/\alpha$, an enough large $\alpha$ would limit the propagation range in SDE signal collection, and thus the preferences of the parameter in SDV require a trade-off. Since only the absolute value of the frequency can be extracted from the intensity signal detected by a PD, the direction of velocity is ambiguous from the Doppler beat frequency. As a solution, we monitor the reflected Doppler signal beams using a CCD to assist in distinguishing the direction of movement. The typical results of dynamic rotation in Fig. 6 are shown in Supplementary Video 2. The beam rotates anticlockwise when the motion is forward, and it rotates clockwise when the motion is backward. As a result, in the SDV, the magnitude of velocity can be obtained from locally detected signals, and the direction can be determined by monitoring the rotation of the Doppler signal beams.

Fig. 6. Linear response of the SDV.

The probe beam is a superposed Gaussian and higher-order Bessel (ℓ = 2) beam. The beat frequency is obtained from the SDE signal detected locally by a PD, and the corresponding Doppler signal beams with dynamic rotation are visualized in Supplementary Video 2. Each data point is measured five times. The lines are theoretical predictions for the Bessel beam with different α. The anticlockwise and clockwise arrows correspond to the direction of dynamic rotation of Doppler signal beams.

The SDE beat frequency is then measured under various velocities and different radial and angular structure parameters, as shown in Fig. 7. By using the probe beam superposed by Gaussian and Bessel beams, the beat frequency measured under the Bessel component with fixed radial phase as α = 0.0035355 and different angular phase is shown in Fig. 7a. It can be seen that the response of beat frequency relative to velocity is the same for different ℓ, which indicates that the linear response of SDV is independent of the angular structure parameter. The typical Doppler signal beams monitored by the CCD corresponding to Fig. 7a are shown in Supplementary Video 3. For the case ℓ = 0, the intensity of the central region of the beam is flickering over time, and for ℓ > 0, it is rotating anticlockwise at the negative velocities and clockwise at the positive velocities. Note that the two-dimensional (2D) rotation is a vector signal and thus the direction of velocity can be distinguished by the orientation of the beam rotating. At the same beat frequency, the Doppler signal beam is rotating slower when ℓ is greater, the characteristic of which is consistent with the RDE, i.e., the rotating rate is inversely to ℓ under the same Doppler shift. The beat frequency measured by using superposed two Bessel components is shown in Fig. 7b, and the corresponding typical Doppler signal beams are shown in Supplementary Video 4. By fitting the measured values to the theoretical lines, the slope of the fitted lines is proportional to the squared variance of the radial cone angles. The detected beat frequency is independent of the angular topological charge, but the property of the dynamic evolution of the Doppler signal beams is affected by the angular phase structure.

Fig. 7. Measured SDE beat frequency via various velocities and structure parameters.

a The probe beam is superposed by Gaussian and Bessel beams, where the Bessel component carries α = 0.0035355. b The probe beam is superposed by two Bessel beams. The beat frequency is measured by local detection using a PD, and the corresponding Doppler signal beams are visualized in Supplementary Videos 3 and 4. The arrows stand for the direction of dynamic rotation of the Doppler signal beams.

Multimode probing of the SDE

The SDE is then demonstrated considering the probe beam with multiple structured modes, including both the radial and angular phase structures. Figure 8 shows the Fourier spectra of collected time-varying intensity signals when the probe beam is superposed by a Gaussian beam (α₁ = 0, ℓ₁ = 0) and two higher-order Bessel beams (ℓ₂ = 1, ℓ₃ = 2, and α₂, α₃), where α₂ = α₃ = 0.0035 for Fig. 8a, α₂ = α₃ = 0.003 for Fig. 8b, and α₂ = 0.003, α₃ = 0.0035 for Fig. 8c. The velocity of the moving mirror is set to 5 cm/s. Generally, a maximum of n(n-1)/2 Doppler peaks can be detected from a signal containing n components of Doppler shift. As in Fig. 8c, 3 Doppler peaks are observed when the probe beam contains 3 mode components. The radial phase gradients of these 3 modes are different, corresponding to 3 discrete regions of separate $\mid k_r\mid$ in k-spectrum, which cause 3 different shifts in the SDE. In the other cases, where the probe beam also contains 3 mode components but is mapped to 2 radial regions in its k-spectrum, as shown in Fig. 8a, b, only one Doppler peak can be found. Among the Doppler peaks, the frequency at 1.2 Hz is related to α = 0.0035, 0.8 Hz to α = 0.003, and 0.3 Hz to the difference between them. It suggests that the SDE can be analyzed and controlled by radial intensity distribution of the k-spectrum, and the frequency shift is not affected by the phase modulation on the ring structure. The resulting SDE shifts are discrete rather than mixed when multiple radial structures are present in the k-spectrum. The dynamic evolution of multimode beams induced by the SDE is shown in Supplementary Video 5. The Doppler signal beam with multiple SDE shifts exhibits complex evolution, such as flickering and rotating simultaneously, or shape deformation over time.

Fig. 8. Demonstration of the SDE with multimode probing.

The probe beam is superposed by a Gaussian beam and two Bessel beams, where the structure parameters are a α₂ = α₃ = 0.0035, ℓ₂ = 1, ℓ₃ = 2, b α₂ = α₃ = 0.003, ℓ₂ = 1, ℓ₃ = 2, c α₂ = 0.003, α₃ = 0.0035, ℓ₂ = 1, ℓ₃ = 2. The velocity is set to 5 cm/s. The frequency spectra are obtained by using the fast Fourier transform of locally detected Doppler signals, and the corresponding Doppler signal beams are visualized in Supplementary Videos 5.

Discussion

Our results demonstrate a general form of the Doppler effect induced by spatially structured beams, namely the SDE. Over the past decade, studies on the Doppler effect with structured beams mainly focus on the angular phase dimension of the optical fields, with the resulting RDE revealing the interaction between OAM and angular motion. In contrast, the SDE offers a new perspective by linking the Doppler shift to the distribution of the beam’s k-spectrum. Physically, the SDE can be interpreted as a modification of the conventional Doppler effect, wherein the transverse confinement of fields naturally causes an extra redshift beyond that predicted by the classical formulation of Doppler shift. The SDE is applicable to both the structured light waves and photons since it is universal that the longitudinal wavevector would get a reduction when the k-space of the field is not localized at the center, and beyond light, the effect may be applied to any wave, including sound waves. Our work highlights that the conventional Doppler effect should be modified to the SDE in any practical optical system, considering that a beam of finite size spreads due to diffraction. For collimated Gaussian beams with a large beam waist, the divergence in the Rayleigh distance is small, and thus the SDE within the range can be approximately equal to the conventional one. The SDE becomes prominent when the beam exhibits substantial k-spectrum spreading, as in the case of Bessel beams with a well-defined $k_r$. Alternatively, it can also be studied by controlling the convergence or divergence of the sub-wavelets. For example, the transverse Doppler shift has been detected in non-collimated Gaussian beams⁵⁸, in which case the SDE would arise with longitudinal motion.

For the light beam superposed by multiple angular and radial phase structures, the SDE can cause the spatiotemporal coupling on the Doppler signal beams. Our results show that the Doppler signal beam rotates over time when the field carries two spatial modes with different angular topological charges and radial cone angles. The intrinsic OAM of such a dynamic rotating beam induced by the SDE is constant compared with the initial⁵⁹, but the frequency difference of the spatial modes will lead to extrinsic OAM of the energy flow^60,61. In the study of RDE, the rotating beam can be driven by the time-varying geometric phase triggered by a rotating Dove prism. As a comparison, in the SDE, a similar dynamic characteristic is generated by another mechanism, namely the longitudinal torque acting on the structured phase without any lateral interaction. It suggests that there might be a certain connection between the RDE and SDE.

By tailoring the angular phase distribution within each ring-shaped region of a beam’s k-spectrum, one could engineer structured light fields that exhibit complex longitudinal propagation dynamics⁶², such as frozen waves⁶³, longitudinally twisted beams^64,65, and OAM-evolving beams⁶⁶, resulting in unique spatial structures that evolve in the longitudinal direction z. With the SDE, this longitudinal spatial evolution can be mapped onto the temporal domain, enabling a form of spatiotemporal coupling, in which the transverse space (x,y) is linked to time (t). The complicated space-time (ST) wave packets are usually sculpted by synthesizing frequency comb lines or broadband sources, with the mode at each frequency shaped with a specific phase structure or modulated with a particular k-spectrum^67–69. For example, the diffraction-free ST light sheets are created by establishing the correlation between the transverse wavevector and the angular frequency on the surface of the light cone⁷⁰, and the ST wave packets carrying dynamically changing OAM are generated by mapping combinations of OAM modes with different weights to multiple frequencies⁷¹. The modulation methods of ST wave packets inspire us to utilize the SDE to customize the desired beams with dynamic evolution, in which the k-spectrum of the probe beam is designed to form a Doppler frequency comb with the structure of discrete rings or lines (corresponding to different transverse wavevectors $\mid k_r\mid$ or $k_x$, $k_y$), each with specific phase structures to provide spatiotemporal coupling. As a prospect, such property of the SDE can be applied to image the molecular dynamics^72,73 by monitoring the spatiotemporal fields from interaction.

In terms of applications, we have developed a homodyne-free SDV based on the SDE for velocity measurements. The conventional LDV systems typically rely on dual-beam optical arrangements, where either two separate beams travel along distinct paths to interact with the moving object, or a reference beam at the original frequency is optically mixed with the Doppler-shifted signal beam. The two beams are combined on a PD to perform optical homodyning, yielding a beat frequency that brings the Doppler signal into a measurable frequency range for signal processing⁷⁴. However, such dual-beam and reference-based configurations often suffer from instability in complex and dynamic environments, such as in the presence of atmospheric turbulence, mechanical vibrations, or underwater operation, due to the susceptibility of the separate optical paths to differential phase disturbances. As a comparison, the proposed SDV system applies a single structured probe beam comprising two spatial modes with distinct transverse wavevectors but coaxial propagation, thereby eliminating the need for a separate reference beam and dual-path interference. This homodyne-free configuration offers improved robustness and alignment simplicity, making it especially suitable for deployment in challenging environments such as obstacles existing in the probing path. More details about the comparison between the SDV and LDV can be found in Supplementary Note 4, and the additional experimental results demonstrating the enhanced performance of SDV are presented in Fig. S4 of Supplementary Information. Note that previous studies have reported the use of structured beams for LDVs^75–77, where the structured beams were mainly employed to improve the measurement depth of field or to simplify multi-component velocity detection, but the velocity estimation still relied on the conventional Doppler effect and required a reference beam for heterodyne detection. Furthermore, a key feature of the SDV is its ability to provide a 2D time-varying intensity signal that can project the motion information into the dynamic rotation of the Doppler signal beam for intuitive naked-eye observation, which helps to distinguish the direction of motion without resorting to other techniques. For monitoring the variable motion such as vibration, the SDV allows the linear working region to be enhanced by 6 orders of magnitude over the LDV, which facilitates the wavelength ambiguity eliminating⁷⁸, and a recent study suggests that it can be applied under water⁷⁹.

In conclusion, we have shown the SDE that transverse structuring of the waves results in an extra redshift on the original Doppler shift, and based on it, we have proposed a homodyne-free SDV. Physically, the SDE is a universal phenomenon of optical waves and photons, and as a modification of the conventional Doppler effect, it could then be considered in areas such as Doppler cooling⁸⁰ and astronomy when studying structured beams. In particular, when the probe beam or received scattered beam has a complex k-spectrum structure rather than fundamental, the SDE can provide predictions for the statistical expectation of the observed Doppler shifts. Technically, benefiting from the advantages of structured light, the SDV is a modified configuration compared to the previous LDVs, enabling homodyne-free detection. It has widespread application prospects in industrial measurements, biological diagnosis, and shock physics. Future studies will extend SDE investigations to a broader class of structured beams with distinct k-spectra to further enrich the underlying physics. In addition, the LDV will be applied to rough targets and real objects to assess its robustness under practical scenarios. These efforts will advance the development of SDE and related techniques toward real-world applications.

Methods

Details of the experimental implementation

The experimental setup is shown in Fig. S3 in the Supplementary Information. The Gaussian beam with a waist of 0.38 mm from a laser source at 532 nm is expanded by a beam expander of 6 times. Two lenses (f₁ = 50 mm, f₂ = 100 mm) combined with a pinhole are used to clean the beam and expand it twice further, and thus the illuminating beam to be shaped by spatial light modulator (SLM) is nearly a plane wave. There are two advantages of such an implementation in this experiment. First, the divergence of the Gaussian beam is almost negligible in the system, and secondly, a large illuminating region could provide a greater range to control the waist size for creating the Bessel beam. The polarization of the Gaussian beam is adjusted to x-oriented by the half-wave plate to match the working polarization of the SLM. The hologram pattern uploaded on the SLM is designed by the amplitude-phase modulation method, where the amplitude is a Gaussian profile with a waist of 2.5 mm, and the phase is given by adding a grating phase to the phase distribution of the probe beam. The 4 f system, composed of two lenses (f₃ = f₄ = 400 mm) and an aperture, is used to filter out diffractive orders except the first. The probe beam is then illuminated on a mirror which is mounted on a moving state (Thorlabs DDS300/M). The forward direction of velocity is defined along the beam illumination. The reflected beam is split into two parts by a beam splitter (BS3), one of which is directly observed by a CCD, and the other is partially detected by a PD after being filtered through a slit. The analog signals obtained by the PD are converted to digital by an oscilloscope for signal processing. In the demonstration of mode-filtering detection, an additional SLM and lens are inserted between the BS3 and CCD (not shown in the figure), where the SLM is positioned at the front focal plane of the lens and the CCD is placed at the corresponding back focal plane. The hologram, incorporating both the demodulation phase mask and the coaxial aperture, is uploaded on the additional SLM, where the aperture is achieved by adding a grating onto the phase mask within a circular region.

Author contributions

J.W. and Z.W. developed the concept and conceived the experiment. Z.W. and Z.T. performed the experiment and acquired the experimental data. Z.T. carried out the data analyses. Z.W. wrote the original manuscript. All authors contributed to revising the paper. J.W. finalized the paper. J.W. supervised the project.

Peer review

Peer review information

Nature Communications thanks Zhen-Lai Wang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

All key data supporting the findings of this study are included in the main article and its Supplementary Information. Further datasets are available from the corresponding author upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-025-64913-x.