Areas of Molecules in Membranes Consisting of Mixtures

Abstract

The question has arisen in recent literature: how to partition the total area in simulations of membranes consisting of more than one kind of molecule into average areas for each kind of molecule. Several definitions have been proposed, each of which has arbitrary features. When applied to mixtures of cholesterol and DPPC, these definitions give different results. This note recalls that physical chemistry provides a canonical way to define molecular area, in analogy to the definition of partial-specific volume. Results for partial-specific area are obtained from simulations of DPPC/cholesterol bilayers and compared to the results from the other recent definitions. The partial-specific-area formalism dramatically demonstrates the condensing effect of cholesterol and this leads to the introduction of a specific model that accounts for the area of mixtures of cholesterol and lipid over the entire range of cholesterol concentrations.

INTRODUCTION

For bilayers consisting of a single lipid component, the average area per molecule a is a central quantity because it is the simplest measure of lateral organization (1). Given a simulation of a bilayer consisting of a single lipid, the average area per lipid is obviously just the total simulated area divided by the number of lipids in each monolayer, even though any particular lipid may have more or less than the average area, especially in disordered and fluctuating fluid phases. The thickness of the membrane is a measure of the transverse organization, but there are many thicknesses (e.g., hydrophobic, steric, headgroup, or Luzzati/Gibbs surface) that can be defined. Area A is, of course, related to thickness as two factors of the volume V, so A is also a relevant measure for transverse information, and it has the advantage of being unique. However, the inherent simplicity of area A for homogeneous bilayers is challenged when bilayers consist of heterogeneous mixtures of lipids and/or proteins.

Even with all the detail provided by simulations, it is not obvious how to obtain the average area of each lipid in a mixed bilayer (2,3). As an example, we will consider mixtures of cholesterol and dipalmitoylphosphatidylcholine (DPPC) which were studied by simulations of simplified models more than 10 years ago (4–6) and more recently in detailed molecular dynamics simulations that include explicit water (7–15). We will focus on three articles that simulated several concentrations of cholesterol in DPPC (3,16,17). One of the most easily accessible quantities to monitor in an NPT ensemble is the total area A of a bilayer with N_chol cholesterol molecules and N_DPPC DPPC molecules in each monolayer. One can then define the area per total lipid a(x) as a function of the mole fraction of cholesterol, defined as x ≡ N_chol/(N_DPPC + N_chol),

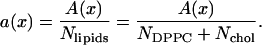(1)

Table 1 and Fig. 1 show that there are some differences between the three simulations, but within statistical error they are rather similar.

TABLE 1.

Areas a(x) per total lipid and cholesterol versus molecular fraction cholesterol x from three sets of simulations

x	Chiu et al. (16)	Hofsäß et al. (17)	Falck et al. (3)	Average
0	0.632	0.635	0.652	0.640
0.04	0.527	—	—	—
0.047	—	—	0.616	—
0.05	—	0.568	—	0.568
0.06	0.518	—	—	—
0.08	0.452	—	—	—
0.10	—	0.553	—	0.530
0.111	0.483	—	—	—
0.125	0.474	—	0.543	—
0.15	—	0.529	—	0.507
0.20	0.462	—	—	0.483
0.203	—	—	0.478	—
0.25	0.439	0.484	—	0.458
0.297	—	—	0.424	—
0.30	—	—	—	0.436
0.333	0.405	—	—	—
0.35	—	—	—	0.422
0.40	—	0.434	—	0.410
0.45	—	—	—	0.398
0.50	0.369	—	0.384	0.385

The data from Hofsäß et al. (17) were taken from the table. The data from Chiu et al. (16) and Falck et al. (3) were estimated from the figures.

FIGURE 1.

Area a(x) per lipid (DPPC and cholesterol) versus cholesterol mole fraction x from three simulations, triangles (16), inverted triangles (17), and squares (3). Solid circles show the average calculated in steps of 0.05 based on linear interpolation.

The goal is to split a(x) into two parts, a_DPPC(x) and a_chol(x). These parts are required to fulfill the relation

(2)

Several different methods have been proposed. Despite the fact that the simulations were performed using similar setups, temperature, and force fields (except that Chiu et al., Ref. 16, applied a surface tension of 80 dyn/cm to their system), the resulting partitionings of the area differ from each other more than the raw data from the simulations.

EXISTING METHODS

The most obvious method assumes that the partitioned areas a_DPPC(x) and a_chol(x) are constants independent of x. Then, the plot of a(x) versus x should be a straight line. In this way, Chiu et al. (16) obtained the results a_DPPC = 0.507 nm² and a_chol = 0.223 nm² for large values of x. However, Fig. 1 suggests that a linear fit is inadequate for small values of x.

Other methods use atomic details to divide the area using Voronoi tessellation. Voronoi tessellation methods come in a variety of types. One type projects the center of mass of each molecule onto a plane and then tessellates the area of the plane, but this has been explicitly criticized for overweighting the area of smaller molecules (2). Instead they chose to tessellate using atoms near the hydrophobic/hydrophilic interface, three atoms for DPPC and one atom for cholesterol. In addition to the issue of how many atoms to use, this method essentially requires an arbitrary decision regarding which slice of area (i.e., at which z level from the bilayer center) is to be used for the tessellation. Although values for cholesterol/DPPC were not specifically given, the areas appear to be similar to those obtained by Chiu et al. (16).

A recent article by Falck et al. (3) shows quite nicely that there is indeed a z-dependence to the molecular areas when examined at an atomic level. Their method uses van der Waals surfaces around the lipid and cholesterol molecules and the leftover area is defined as “free area.” This contrasts with the Voronoi tessellation, which assigns all the area to some molecule, and therefore has no free area. For z values near the cholesterol-ring structure, Fig. 11 from Falck et al. (3) shows a_chol ≈ 0.3 nm² and a_DPPC ≈ 0.4 nm² for x = 0 falling to a_DPPC ≈ 0.3 nm² for x = 0.5, but these are the “bare areas,” none of which includes any free area.

We have reservations regarding the concept of free area (as well as with the corresponding free volume). One would not expect the free area to be largest in the water outside the bilayer, but this is the result shown in Fig. 12 of Falck et al. (3). More generally, free area and free volume will be nonzero for two reasons. First, even a close-packed hard-sphere system will have a free volume corresponding to approximately one-third of the volume (smallest, 26% for a face-centered cubic lattice). Secondly, this lower free-volume limit is only reached at T = 0 for any condensed-matter system. Even in perfect crystals the anharmonicity of the interaction potentials generally lead to thermal expansion, but such expansion does not create any free regions into which other molecules could be inserted. That only occurs in crystals when vacancy defects occur, which is not an appropriate concept for fluids such as water or L_α phase lipid bilayers. We therefore distrust definitions of free areas and volumes that rely only on the bare energetic description of molecules and that ignore the free energy aspect that pertains when T > 0. One motivation for a free-area description lies in its application to diffusion. After careful comparison, Falck et al. (3) conclude that the free-area theory “tends to underestimate the changes in the values of the lateral diffusion coefficients” and that “it seems unnecessary to aim for a quantitative description with such a simple framework.”

A different motivation for examining the variation of properties in the perpendicular direction is that such variations may affect the preference for forming different kinds of structures like bilayers, micelles, or hexagonal phases. Furthermore, it may modulate the free energies of conformational changes in functioning membrane proteins (18). Such variations can, however, be better addressed by the lateral pressure profile perpendicular to the membrane (19), which can be calculated in simulations (20).

A third method for partitioning the area that was suggested by Hofsäß et al. (17) could be clarified and phrased in the following way. The major assumption is that the bilayer can be characterized by a common thickness h(x) that can be expressed in terms of volume and area per lipid as

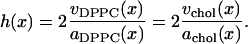(3)

Defining

(4)

and using Eq. 2 yields

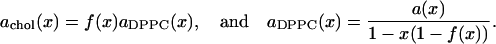(5)

This method transforms the partitioning into one of finding the volume ratio f(x). Volumes are better known than areas and are also known to undergo smaller variations than areas. For example, at the gel-to-fluid phase transition of DMPC, the volume increases by ∼3% (21) whereas the area increases by ∼30%, from 0.47 nm² in the gel phase (22) to 0.61 nm² in the fluid phase (23). Therefore Hofsäß et al. (17) ignored the x dependence in the volume ratio f(x).

We now present an improvement of the volumetric part of the analysis of Hofsäß et al. (17). This may be of some independent interest because volumes of the chemical components in mixtures are important, for example, in estimating electron density and neutron scattering lengths for diffraction experiments. We first define the volume per lipid v(x) by

(6)

(keeping N_DPPC and N_chol defined per monolayer) where the volume of water has been subtracted from the volume V_sim of the simulation cell. Then, just as for the area a(x) in Eq. 2, one requires

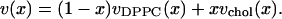(7)

Fig. 2 shows that v(x), unlike a(x) in Fig. 1, is quite linear, so v_DPPC(x) and v_chol(x) are independent of x. The linear regression shown in Fig. 2 gives v_DPPC = 1.220 nm³ and v_chol = 0.541 nm³.

FIGURE 2.

Volume v(x) = (V_sim – N_waterv_water)/(N_DPPC + N_chol) per lipid (DPPC and cholesterol) versus cholesterol mole fraction x. Data from Hofsäß et al. (17).

Returning now to the method of Hofsäß et al. (17) for obtaining areas, the volumetric results in the preceding paragraph give f(x) = 0.443 in Eq. 4, independent of x in Eq. 5. However, because a(x) is not linear and Eq. 5 involves x, a_chol varies from 0.28 nm² for small x to 0.23 nm² for large x. These are slightly different values from the 0.27–0.29 nm² that were reported by Hofsäß et al. (17), where it was assumed that v_chol = 0.593 nm³ based on the crystal unit cell volume.

DEFINITION OF PARTIAL-SPECIFIC AREA

The concept of partial-specific volume has been employed in physical chemistry for many years. It provides a unique definition of molecular volumes based on thermodynamics. The concept is easily extended to partial-specific area, basically by replacing V by A wherever it occurs in the free-volume derivation. Following standard physical chemistry text books (see e.g., Moore, Ref. 24), we define the partial-specific areas a_i for a bilayer consisting of i = 1, …, m types of molecules as

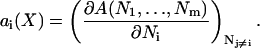(8)

where A is the total area, the N_i values are counted per monolayer, X indicates the set of all m mole fractions x_i, i = 1, …, m of the m components, and the partial derivative is taken with N_j constant for j ≠ i. Because A is a homogeneous function of the N_i variables, it is guaranteed that

(9)

where N ≡ ΣN_i. (This is easily shown by taking the derivative with respect to λ of both sides of A(λN₁, …, λN_m) = λA(N₁, …, N_m).) We apply this formalism to two-component mixtures of DPPC and cholesterol by dividing A(X) in Eq. 9 by N_DPPC + N_chol, which then gives Eq. 2. We note that adding more water does not increase the total area of the membrane for fully hydrated membranes (excess water condition), so the specific area of water is identically zero, and therefore the water component can be ignored in Eq. 2.

Eq. 8 makes it clear that it is necessary to perform simulations for a set of values of x to determine the partial-specific areas a_i(x). Given the total area per molecule a(x) from such a set of simulations, a convenient graphical way to obtain the a_i(x) rewrites Eq. 2 as

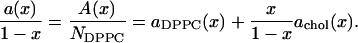(10)

Then, a_chol(x) may be estimated directly as the slope of the tangent in a plot of a(x)/(1 – x) versus x/(1 – x) and a_DPPC(x) is estimated as the intercept of the tangent at x = 0. An alternative way is to introduce the mole fraction(s) and N as new independent variables in Eq. 8. This gives in our two-component case the formulae

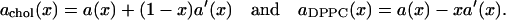(11)

RESULTS FOR MIXTURES OF DPPC AND CHOLESTEROL

The areas per total lipid a(x) versus mole fraction cholesterol x shown in Table 1 and Fig. 1 have been taken from Fig. 2 in Chiu et al. (16), Table 1 in Hofsäß et al. (17), and Fig. 6 in Falck et al. (3). Average values in steps of 0.05 in x for each simulation set were calculated using linear interpolation. The three sets were then averaged and error bars were assigned as standard deviations between the three sets divided by 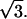These averages are shown in Fig. 1 compared to the individual simulated data sets from which they were derived.

Fig. 3 shows the plot suggested by Eq. 10 that can be used to obtain the specific area of cholesterol from the slope of the local tangent and the area of DPPC from the intercept of this tangent at x = 0. Fig. 3 shows two linear regimes that can be fitted with separate straight lines. For the smallest x the plot gives an area per DPPC of 0.64 nm², consistent with the values for pure DPPC (1) and an area per cholesterol of −0.81 nm². One should, however, note that the three different simulations give quite different specific areas per cholesterol in this region. Using the data in Table 1 for pure DPPC and the lowest cholesterol concentration, a_chol(0) is −2.0 nm² from Chiu et al. (16), −0.71 nm² from Hofsäß et al. (17), and −0.11 nm² from Falck et al. (3). Nevertheless, even if the spread is quite large, due partly to difficulty in evaluating numerical derivatives, it is clear that all simulations give negative values of a_chol(0). For x > 0.3 the average curve gives a_chol = 0.26 nm² and a_DPPC = 0.51 nm², and the difference between the individual simulations is <±0.04 nm². In the intermediate region 0.07 < x < 0.30, the slope is small and positive and it might be tempting to consider a third region with the partial-specific areas a_chol = 0.095 nm² and a_DPPC = 0.58 nm².

FIGURE 3.

The total area A(x) divided by the number of DPPC molecules (i.e., a(x)/(1 – x)) versus x/(1 – x). The three straight lines indicate possible fits for small, large, and intermediate x. The dash-dotted line shows a smooth fit with the function given by Eq. 12.

The simulations were all performed at temperature T = 323K. The experimental phase diagram (Fig. 12 of Vist and Davis, Ref. 25) suggests that this might be a high enough temperature to avoid phase coexistence of so-called liquid-ordered (cholesterol-rich) and liquid-disordered phases. However, when their experimental temperature axis is increased by 4°C to account for deuterated DPPC, there could be the remnant of a transition near x = 0.3. Nevertheless, because the simulations are not run long enough for true phase separation to occur, the appearance of the three distinct regimes shown in Fig. 3 may more likely be artifacts due to simulation uncertainties and numerical processing. As an alternative we have therefore compared the averages in Fig. 1 to a smooth curve. This could be done using many different functional shapes having sufficiently many adjustable parameters. We choose to do it using a four-parameter function

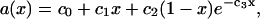(12)

which has a physical justification that will be explained in the Appendix. (We have tried a different functional form that uses an inverse third-order polynomial (also with four parameters), but this makes essentially no difference in the results in this section compared to Eq. 12.) The comparison between the smoothed curve and the raw averages is shown in both Figs. 3 and 4. Fig. 4 also shows the results for partial-specific areas obtained using the derivative method of Eq. 11. The decreasing a_DPPC(x) with increasing x is expected as the mixture becomes more liquid-ordered with increasing cholesterol. The more remarkable result that a_chol is strongly negative for small values of x is consistent with the results obtained using the slope method illustrated by Fig. 3. The only significant difference in these two kinds of results is that any evidence of distinct regimes is automatically extinguished by the smoothing of the average a(x) using Eq. 12.

FIGURE 4.

Solid symbols show average area per lipid a(x) from Table 1 versus cholesterol mole fraction x. The solid curve shows the fit using Eq. 12. The calculated area per DPPC and cholesterol from Eq. 11 are shown as a dashed and a dotted line, respectively. The insert emphasizes negative values of a_chol(x) for small x.

DISCUSSION AND CONCLUSIONS

We first emphasize that the analysis of volumes in Eq. 7 and Fig. 2 gives partial-specific volumes that have reasonable values and are constant as cholesterol mole fraction x is varied. In contrast, the strongly varying partial-specific areas, and especially the strongly negative value of a_chol(x) for small x, appear bizarre at first. It may be noted, however, that even negative partial-specific volumes are well known to occur, for example, for NaOH/water solutions, and this emphasizes the important physical phenomenon of electrostriction. Correspondingly, the negative-specific area of cholesterol is actually a quite insightful result, but it requires a different perspective from the more atomistic perspective employed previously. As is well known, adding one cholesterol molecule to a DPPC bilayer causes the hydrocarbon chains of those DPPC molecules that are in the immediate vicinity of the cholesterol to straighten. Although this could be thought to decrease the average area of the DPPC molecules, this should not decrease the partial-specific area a_DPPC(x). The local perturbation around the cholesterol is not altered by an added DPPC molecule, which simply joins its fully fluid companions in a region that has no cholesterol at small x, and therefore increases A with little recognition of those DPPC molecules that are part of the local perturbation caused by the cholesterol. Therefore, the partial-specific-area formalism includes the local perturbation on the DPPC molecules that are neighbors to the cholesterol as a contribution to a_chol(x), not to a_DPPC. This is, of course, a quite different perspective than the one implicit in the atomic level definitions which try to average over all the DPPC molecules. The result that a_chol(x) becomes strongly negative in the partial-specific-area perspective is a natural indicator of the strength of the well-known condensing effect of cholesterol.

If the perturbation regions around each cholesterol molecule had specific cutoff lengths, then a_DPPC(x) would remain constant at a_DPPC(0) until these regions covered the entire surface. Of course, the perturbations decay smoothly instead of having rigid cutoff lengths, so a_DPPC(x) gradually decreases with increasing x. Nevertheless, Fig. 4 suggests that there remain relatively unperturbed DPPC molecules up to x ≈ 0.1. However, in the high cholesterol regime as x approaches 0.5, a_DPPC(x) approaches 0.50 nm² and a_chol(x) approaches the constant value 0.27 nm². These particular results, derived from the general partial-specific-area approach, suggest a more specific model for mixtures of cholesterol and DPPC that is presented in the Appendix.

The primary motivation for the partial-specific-area approach that we advocate in this article is that it involves none of the arbitrary assumptions that have had to be made in recent atomistic definitions. It is perfectly defined thermodynamically, with a well-founded and historical conceptual framework. It very elegantly displays the well-known condensing effect of cholesterol on lipid bilayers. However, we do not advocate its use exclusively. The other definitions have value for obtaining atomistic perspective, especially into the z variations along the bilayer normal. Nevertheless, we suggest that partial-specific area is the appropriate canonical quantity to report from simulations of mixtures that are performed as a function of mole fractions. It should also be considered for any experiments that are capable of obtaining area a(x).

APPENDIX: A PARTICULAR MODEL FOR AREAS IN CHOLESTEROL/DPPC MIXTURES

Based on the partial-specific areas obtained from the simulations of cholesterol and DPPC, we here suggest a more specific model for this mixture. It must be emphasized that, whereas this model is inspired by the partial-specific-area approach, the assumptions made for this specific model are independent of the general approach which is the primary focus of this article. The first parameter in the model is a constant cholesterol area 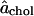for all x; this parameter has been the goal of the atomistic approaches. The second parameter is the area 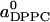for DPPC when x = 0. The third parameter is the amount Δa of area condensation of any DPPC molecule in contact with cholesterol. The fourth parameter is the maximum number n of DPPC molecules that can be condensed by a single cholesterol molecule. The partial-specific area results suggest that, for small x,

(13)

When a(x)/(1 – x) is plotted versus x/(1 – x) as in Fig. 3, the slope at x = 0 gives the partial-specific area of cholesterol. For high cholesterol concentration, all DPPC are in contact with cholesterol and the results for the partial-specific areas suggest that the system behaves more like an ideal mixture with (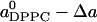) being the area per DPPC and 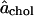the area per cholesterol; that is, for large x,

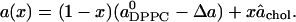(14)

The goal of the model is to provide a single function for all x that includes both these limits. To do this we assume that the cholesterol molecules are randomly distributed and if there is at least one cholesterol within distance d from a phospholipid, then the phospholipid becomes ordered and its area is reduced by Δa. The maximum number of phospholipids, n, that become ordered by a single cholesterol is then given by

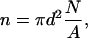(15)

with N/A being the phospholipid area number density. However, this is just the maximum, not the average, because as x increases, an added cholesterol may be within 2d of an already present cholesterol and their “circles of influence” on the phospholipids will overlap. This is taken into account by considering the probability P₀ for not finding any one of the xN cholesterol molecules of the system within a distance of d from a given phospholipid,

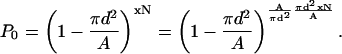(16)

Let N and A go to infinity for fixed non-zero values of the other parameters, and using the fundamental definition of e (the base of the natural logarithm) gives

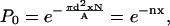(17)

where we have further assumed that n is a constant independent of x. The total area in the model is now

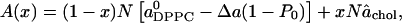(18)

where Δa(1 – P₀) gives the area reduction of each DPPC molecule that is within distance d of a cholesterol. Equations 17 and 18 then give the area per lipid as

(19)

which reduces to Eq. 13 in the small x limit and to Eq. 14 in the large x limit. From these limits we determine the parameters as Δa = 0.14 nm², and n = 7.5. The continuous curves corresponding to these values of the parameters are shown in Figs. 3 and 4, which indicate that this simple model is adequate to fit the simulation data. It is interesting to note that the value of n (which is the most uncertain parameter value with an error of the order ±2) is comparable to the number of nearest-neighbor phospholipids. The value of 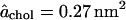is within the range of values that have been obtained from the atomistic approaches described in Existing Methods. Even though the model uses constant 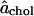and a mole-fraction-dependent decrease in the DPPC area, the cholesterol partial-specific-area a_chol(x) has a negative value of −0.78 nm² at low mole fractions of cholesterol. Therefore, this model encompasses both the partial-specific-area perspective that emphasizes the dramatic condensation effect of cholesterol and the more atomistic perspective that seeks a fixed area for cholesterol.