Detecting Spatial Patterns in Biological Array Experiments

Abstract

Chemical genetic screening and DNA and protein microarrays are among a number of increasingly important and widely used biological research tools that involve large numbers of parallel experiments arranged in a spatial array. It is often difficult to ensure that uniform experimental conditions are present throughout the entire array, and as a result, one often observes systematic spatially correlated errors, especially when array experiments are performed using robots. Here, the authors apply techniques based on the discrete Fourier transform to identify and quantify spatially correlated errors superimposed on a spatially random background. They demonstrate that these techniques are effective in identifying common spatially systematic errors in high-throughput 384-well microplate assay data. In addition, the authors employ a statistical test to allow for automatic detection of such errors. Software tools for using this approach are provided.

INTRODUCTION

There has been tremendous growth in the use of large arrays of simultaneous experiments for chemical and biological research. Chemical genetic screening and DNA and protein microarrays are among a number of increasingly important and widely used techniques that involve large numbers of experiments in a spatial array.^1,2 Such arrays may consist of spots printed on slides or wells in microplates. Each location in an array is usually intended to act as an independent trial under identical conditions. In practice, it is difficult to achieve identical experimental conditions, and one often observes systematic errors that are spatially correlated. For example, microplates often exhibit increased or decreased intensities in wells at edges, in rows, or in “checkerboard” patterns. Spatial errors may cause experimental errors such as misidentifying active compounds as inactive and vice versa. Spatial errors are easy to identify with the naked eye when they are large compared to the signal size or the random background variability, that is, noise. However, patterned errors may be overlooked when patterns are obscured by random error or when there are too many plates or arrays to permit a thorough visual inspection of each one. Here, a simple means of identifying, quantifying, and compensating for systematic errors in array experiments using the discrete Fourier transform (DFT) is presented.³

Array experiments often use automation that contributes to the occurrence of spatially patterned artifacts. Robots are programmed to perform experiments in spatially referenced sequences, such that small variations in equipment performance can cause large systematic errors. For example, when reagents are transferred into microplate wells or when microarray slides are printed, correlated but slight differences between pipette tips, pumps, or pins generate systematic errors. Other types of experimental conditions unrelated to robotics may also vary across spatial dimensions. In microplates, for example, it is common to observe greater evaporation at the edges of a plate and poor gas exchange in the interior of a plate.

MATERIALS AND METHODS

A DFT is a function that decomposes a series of data (signal) into sine waves and expresses the signal in terms of sinusoidal frequency components. The result of the DFT operation is itself called a DFT and is a frequency representation of the data consisting of the amplitude and phase of each frequency component. The DFT contains the same information as the original data in that the original data can be exactly reconstructed given only the DFT. This inverse transform is called the inverse DFT.

The DFT is used in periodogram analysis in which the power density spectrum of a data series is estimated. The power density spectrum shows the energy contained in each frequency component represented in the data. If particular frequencies dominate the original data, the Fourier transform will have large amplitudes at those frequencies. For spatially arrayed data, these frequencies represent spatial periodicities such as peaks and valleys occurring at every other array position, every third position, and so on. Using periodogram analysis, DFTs have been used extensively for locating and removing spatial and temporal signals in image and signal processing. Our software (VisTa) incorporates one of the many freely available software packages for computing the DFT. The periodogram of a particular frequency i is computed from the DFT at frequency i as follows:

$$periodogra{m}_i=\frac{|df{t}_1-\overline{dft}{|}^2}{N}$$

where N is the number of discrete frequencies. For the standard DFT and periodogram, the number of frequencies, N, in the transform equals the number of spatially arrayed experiments or wells. The array average is subtracted from the data so that the data represent the deviations from the average value. The result of this step is that the “zero-frequency” component of the periodogram is zero; otherwise this component could be very large and it does not relate to patterning (variation) in the data. Random, spatially uncorrelated error produces an exponential distribution of amplitudes in the periodogram, whereas spatially systematic error produces amplitude outliers from this distribution. To reproduce a spatial pattern in a test array, anomalously high-amplitude components of the DFT are selected and the inverse DFT is performed on just these overrepresented frequency components. The result is a spatial pattern extracted from the original data. This reconstruction shows which wells have correlated intensity, and their amplitudes indicate the severity of the pattern when compared to the amplitudes in the original data.

Experimental 384-well microplate data are from luminescence-and fluorescence-based assays on cultured cells. These plates contained control experiments in columns 1, 2, 23, and 24. These columns were removed from the data array to leave only the randomly arrayed experiments prior to periodogram analysis. Reconstructed spatial patterns were generated from outliers in the histogram of periodogram amplitudes (see, e.g., Fig. 1B) as identified by visual comparison to random plates.

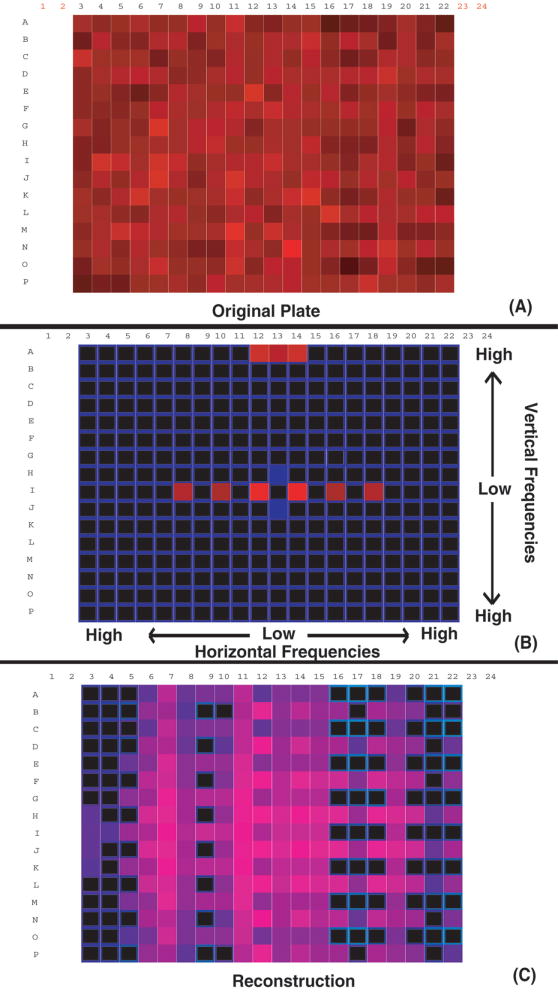
FIG. 1.

Microplate data (A) yield the periodogram (B). Two-dimensional periodograms are traditionally visualized with the zero-frequency components (average of the signal) in the middle. The middle horizontal axis corresponds to horizontal frequencies, and the middle vertical axis corresponds to vertical frequencies. Off-diagonal frequencies are mixtures of both horizontal and vertical frequencies. In this case, the high-amplitude outliers are along the horizontal and vertical frequencies. This pattern is indicative of checkerboarding. Isolating these frequencies and reconstructing data with the inverse transform of just the high-amplitude outlier frequencies yields the pattern in (C), predominantly a checkerboard pattern superimposed on a weaker, larger scale pattern consisting of lowered values in columns 16 to 22.

RESULTS

Analysis of spatial patterns in experimental 384-well plate data

The DFT and periodogram of experimental screening data were generated, the qualitative pattern of spatial patterning was isolated, and the magnitude of the spatial patterning effect was estimated using the techniques described above.

An array of microplate data is shown in Figure 1A. This plate exhibits correlated wells in a checkerboard pattern that is difficult to detect visually. High-frequency components were isolated from the periodogram (Fig. 1B) and used to reconstruct the error pattern (Fig. 1C). The axes of the periodogram in Figure 1B do not indicate array location as in the data arrays in Figures 1A and 1C but rather identify the frequency components of the periodogram as described in the figure caption. Eleven high-amplitude periodogram components were identified as outliers (by inspection) so that the error pattern in Figure 1C is the composite of all 11 of these frequencies in according to their respective amplitudes and phases in the periodogram. The predominant pattern is a checkerboard, but other superimposed patterning is also apparent. The high-frequency components in the upper row of Figure 1B indicate that a pattern exists with the highest possible vertical frequency, that is, alternating low and high intensity in every other well. This is clearly seen in Figure 1C. The horizontal error is a combination of lower frequencies that can also be seen in Figure 1C. The checkerboard component of the pattern was then used to identify the experimental problem, a robotic pipetting error, which caused most of the spatially systematic error.

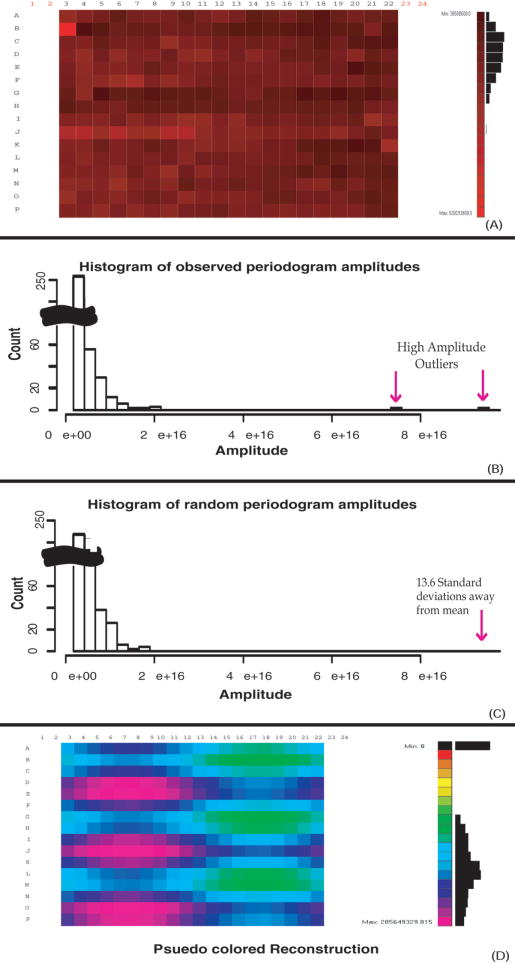
Figure 2 shows a microplate with systematic error and the resulting histogram of the periodogram amplitudes. The histogram of periodogram amplitudes for an uncorrelated random plate is also shown for comparison. The systematic error is clearly seen in the distribution of frequency component amplitudes when compared to a distribution of random data (Figs. 2B and 2C). An inverse transform of just the high-amplitude peaks (Fig. 2D) shows the affected wells and demonstrates the utility of periodogram analysis when spatially systematic error is obscured by a random error of similar magnitude.

FIG. 2.

Microplate with systematic error (A) and a histogram of the corresponding periodogram amplitudes (B). Panel (C) shows a periodogram derived from random uncorrelated data with the same mean and standard deviation as the experimental data. In comparison, the highest amplitude outlier of the periodogram in (B) is 13.6 standard deviations above the mean highest periodogram amplitude generated from a series of 100 random plates, which indicates that the probability of (A) being a random plate is essentially zero. Panel (D) shows the inverse transform of just the indicated high-amplitude outliers from the periodogram, yielding a reconstructed image of the data array containing only the overrepresented patterns.

Quantitating spatial patterning

To quantify the magnitude of spatial patterning in a test array, various criteria may be used to compare the periodogram of the test array to the periodograms of spatially random plates. One such method is presented and demonstrated here.

To identify spatially nonrandom plates, we employ a simple test to determine if the high-amplitude components in the observed periodogram distribution are statistically different from a random noncorrelated distribution. Using this test, it is found that the probability that the largest amplitude frequency component could have been generated by a random signal having the same mean and standard deviation as the observed data. To compute this statistic, a distribution of maximum frequency-component amplitudes is generated for 100 periodograms generated from the random signals. This distribution is observed to be Gaussian, making it simple to determine the probability of finding the observed maximum amplitude. Low probability values (p-values) indicated that the observed periodogram was not random and therefore contains correlated signal. For example, a plate with a p-value of 0.05 indicates that typically, 1 out of every 20 random plates exhibits that plate’s largest amplitude frequency component. Random data generally have p-values around or above 0.5, and plates with p-values of 0.05 have noticeable systematic signal, and p-values lower than this have increasingly pronounced patterns. For example, the highest magnitude outlier from Figure 2B is 13.6 standard deviations away from the average highest amplitude generated from a series of 100 random plates. The corresponding p-value is correspondingly infinitesimally small.

DISCUSSION

Periodogram analysis, widely applied in signal processing for many years, represents a powerful tool for identifying spatial patterns in array data.^4,7 It was found that this type of analysis is capable of detecting many types of spatially systematic errors that occur in 384-well microplates. The method is general in that it can accommodate data with varied array dimensions, average values, and standard deviations. There are several applications of this technique to biological array experiments. For example, it is particularly useful when setting up new array experiments or testing array-processing equipment. Uniform test plates can be produced and analyzed to detect any spatially systematic errors and visualize the error pattern. Such errors are particularly common with robotic systems, and the nature of the pattern can often help identify the source of the error. A second application is quality control for experiments consisting of many arrays. This technique can be used to detect spatially systematic errors that arise in the course of a series of array experiments. Automated spatial error detection could be used to detect errors as soon as they occur and halt the experiment or warn the operator in real time. If spatial patterns do arise during an experiment, the pattern can be visualized to help identify the source of the error.

In our laboratory, periodogram analysis with VisTa was applied over the course of many assays and indicated consistent edge effects in 384-well plate data. These edge biases proved difficult to eliminate from the experiment, leading us to change our plate formatting such that outer wells were no longer used. Our ability to detect this persistent but variable error allowed us to make a substantial improvement in our high-throughput process, leading to higher quality data.

In some cases, periodogram/DFT techniques could be used to actually compensate for spatial errors in affected data. Experimental artifacts, such as the checkerboard pattern seen in a portion of the plate in Figure 2C, could be removed by filtering excess contributions from outliers in the periodogram and reconstructing the data array with the inverse transform. Such an approach is not generally recommended, however, because it could lead to the introduction of new spatial artifacts. The true systematic error is likely to be distributed over multiple frequency components of the periodogram, of which only a small subset might be identified as high-amplitude outliers in the periodogram. Removing the excess contributions of just the highest amplitude frequency components will then not only fail to completely remove spatial artifacts but can introduce new periodic artifacts, even though the overall spatially systematic error is reduced. This data correction technique is probably most appropriate in cases where the spatial error is repeated over many arrays and can thus be most reliably separated from the actual signal.

Identification of spatial artifacts depends on experiments being randomly arranged on the array. If related experiments are arranged in a pattern, it may be difficult or impossible to separate spatial errors from spatial correlations in the experimental signal. For example, in compound screening, many library plates are created with nonrandom selections of compounds so that plates may show spatial correlations simply because similar compounds are arranged together on the plate. Due to the prevalence of spatially correlated errors in automated array experiments, we believe that the identification of such errors should be a high priority in designing these experiments. Thus, it may often be worthwhile to arrange experiments randomly in array experiments even at some cost of simplicity and convenience. In many array experiments, including the examples presented here, a portion of the array is randomly arranged, but other regions of the array contain distinct experiments with a different expected signal, such as negative or positive controls. As demonstrated in the examples above, one may apply spatial analysis to just the random portion of the array.

The periodogram technique is very sensitive to spatial signals and may detect small patterns that, although correlated, are not significant either because they arise frequently just by chance or because they are much smaller than the desired experimental signal. Thus, an important part of adapting this technique to a particular array experiment is to identify the best method for differentiating unacceptable from acceptable pattern types and magnitudes for that particular experiment. The method offered in this article for automated error detection proves useful for common spatial artifacts in our 384-well microplate assays, but alternative methods may differ greatly in their sensitivity to particular spatial errors and might be preferable for different array experiments.

CONCLUSION

Periodogram analysis is a highly effective means of identifying and evaluating types of spatially patterned errors commonly seen in arrayed high-throughput screening experiments. This approach can be used to identify and eliminate spatially systematic errors when setting up manual or automated array experiments, perform automated quality control on array data, and characterize spatial errors in existing data.

The VisTa software created for this study accepts rectangular data arrays of any size. The software, source code, and associated documentation are freely available from the Whitehead Institute.⁸