Skip to main content
PMC home page
BMC Ecology logoLink to BMC Ecology
. 2002 Aug 1;2:8. doi: 10.1186/1472-6785-2-8

A rate equation model of stomatal responses to vapour pressure deficit and drought

D Eamus 1,✉, ST Shanahan 2
PMCID: PMC126274  PMID: 12153703

Abstract

Background

Stomata respond to vapour pressure deficit (D) – when D increases, stomata begin to close. Closure is the result of a decline in guard cell turgor, but the link between D and turgor is poorly understood. We describe a model for stomatal responses to increasing D based upon cellular water relations. The model also incorporates impacts of increasing levels of water stress upon stomatal responses to increasing D.

Results

The model successfully mimics the three phases of stomatal responses to D and also reproduces the impact of increasing plant water deficit upon stomatal responses to increasing D. As water stress developed, stomata regulated transpiration at ever decreasing values of D. Thus, stomatal sensitivity to D increased with increasing water stress. Predictions from the model concerning the impact of changes in cuticular transpiration upon stomatal responses to increasing D are shown to conform to experimental data.

Sensitivity analyses of stomatal responses to various parameters of the model show that leaf thickness, the fraction of leaf volume that is air-space, and the fraction of mesophyll cell wall in contact with air have little impact upon behaviour of the model. In contrast, changes in cuticular conductance and membrane hydraulic conductivity have significant impacts upon model behaviour.

Conclusion

Cuticular transpiration is an important feature of stomatal responses to D and is the cause of the 3 phase response to D. Feed-forward behaviour of stomata does not explain stomatal responses to D as feedback, involving water loss from guard cells, can explain these responses.

Keywords: Stomatal behaviour, VPD, modelled responses, feedback

Background

The response of stomata to changes in atmospheric water content (or more properly the difference in water content between the inside of a leaf and the water content of the boundary layer; or leaf-to air-vapour pressure difference, [1,2] has been the subject of study for several decades [3-6]. It is generally agreed that as leaf-to-air vapour pressure difference (D) increases, stomatal conductance (Gs) declines, linearly or curvi-linearly [7-10]. However, the mechanism by which changes in D result in changes in Gs, remain debated. There is considerable evidence that Gs responds to transpiration rate (E) rather than D per se[11,12,5], although some argue that transpiration rate is not responsible [13], but acts merely as the carrier for the primary messenger, such as abscisic acid or xylem pH or both [1].

The mechanism by which increasing E (resulting from increasing D) can result in declining Gs is similarly debated. A feedback mechanism, whereby reductions in leaf water potential with increased E result in stomatal closure, has been proposed [14] but is unlikely to account for stomatal responses to D [13,15], especially when it is noted that the normal diurnal pattern of leaf water potential and Gs in the field is for the former to decline in the morning as the latter increases [8,16]. A refinement of this mechanism relies upon changes in local gradients of water potential at the mesophyll/epidermis/guard cell scale, rather than whole leaf water potential [10]. High rates of transpiration may result in the generation of localised gradients of water potential that reduce guard cell turgor and hence Gs. One mechanism that has been proposed to account for this is peristomatal transpiration. [17-20]. As D increases, water loss from guard cells increases and guard cell turgor and hence Gs declines. Dewar highlighted the influence of changes in the gradient in water potential between guard cell and subsidiary/epidemal cell [21]. in explaining stomatal behaviour. Such mechanisms have been deemed feedforward [22,23] since E declines as D increases. The role of cuticular transpiration as a determinant of Gs has received gradually increasing support [24,25].

There is increasing evidence to support the view that there are three phases to the stomatal response to E [5,12,25]. Initially, at low values of D, as D increases, Gs is high and E increases (phase C of [12]). At intermediate values of D, as D increases, E remains relatively constant because Gs declines with increasing D (phase A). Finally, at larger values of D, as D increases, stomatal closure is more extreme and E declines with increasing D (phase B).

Water stress reduces maximum Gs [5,6,8,26]. However, water stress also influences the response of stomata to D and E [6,27]. In particular, as water stress develops, stomatal sensitivity to D increases and so-called feed forward responses dominate such that E is reduced for all values of D [5].

The aim of this paper is to report a model that can explain these wide-ranging observations of stomatal behaviour. In particular, we developed a model with the following characteristics:

• Based on known biophysical properties of leaf cells;

• Able to account for the three phase response of stomata to increasing D;

• Able to replicate the impact of water stress upon stomatal responses to D;

• Incorporates known compartments within leaves (for example intercellular airspaces and mesophyll cells).

Initially we have treated time as a parametric variable in order to predict the steady state behaviour of the leaf to changing D. The model is based upon basic biophysical principles and only cell/leaf water relations change in the model. The model consists of a set of five coupled first order differential equations that have been developed from basic principles of water flow in plants.

One of the benefits of only including water relations, is that the dependence of the leaf to water supply can be gauged from model outputs. As will be seen, a large amount of experimentally observed behaviour can be predicted from this model, using water relations.

Results

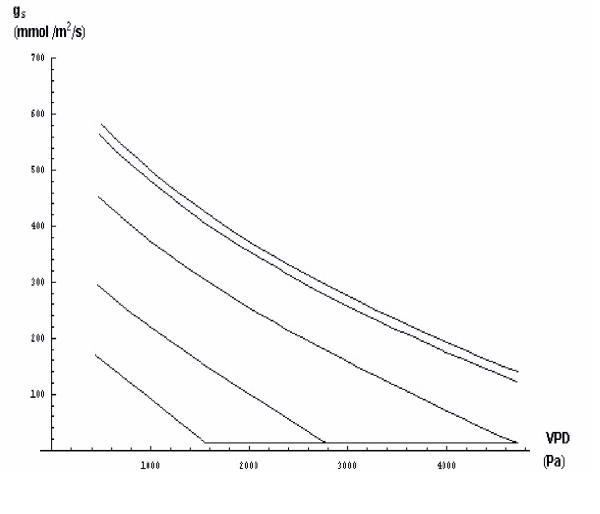
For well watered leaves, when xylem water potential was -0.05 MPa, as D increased, Gs declined curvilinearly (Fig 3). The cause of this decline in Gs was a decline in the volume of the guard cell because water supply to the guard cell became reduced as cuticular transpiration became an increasingly large fraction of total transpiration. As water stress increased, the same pattern of stomatal response to increased D was observed, but the curves were moved downwards (Fig. 3).

Figure 3.

Figure 3

Open in a new tab

The response to stomatal conductance (Gs) to increasing D for unstressed and increasingly stressed leaves. The upper line represents the unstressed leaf, the lowest line represents a leaf with a potential of -2.0 MPa.

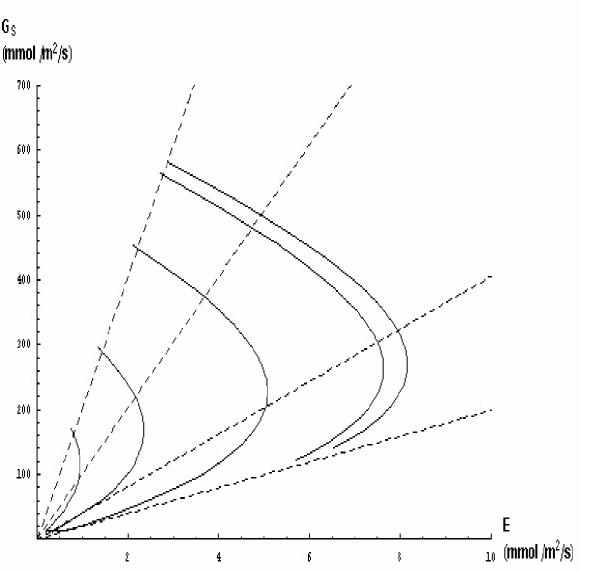
Stomatal responses to E are shown in Fig 4. For well watered leaves, when xylem water potential is -0.05 MPa, as D increased from approximately 0.5 kPa to approximately 5 kPa (this corresponds to the moving from the top of each curve, to the bottom of each curve, in Fig. 4), E increased for small to moderate increases in D (from 0.5 to 2.5 kPa), remained approximately constant for moderate values of D (about 2.5–3.5 kPa) and then E decreased for larger values of D (Fig. 4). Thus, stomata did not regulate E with increasing D when D was low to moderate, but stomata did limit E when D was moderate to large. It is important to note that the values of xylem potential used in Fig. 4 are -0.05, -0.5 -1.0 -1.5 and -2.0 MPa. The upper end of each curve corresponds to ca 0.5 kPa of D. The lower end of each curve corresponds to approximately 5.1 kPa of D (0% RH at 33°C). The dashed lines are lines of constant D.

Figure 4.

Figure 4

Open in a new tab

The relationship between stomatal conductance and transpiration rate as D increases from approximately 0.5 kPa to approximately 5 kPa in steps of approximately 0.5 kPa. The uppermost line is for an unstressed leaf, the lowest line represents a leaf with a xylem water potential of -2.0 MPa. The dashed lines are lines of constant D.

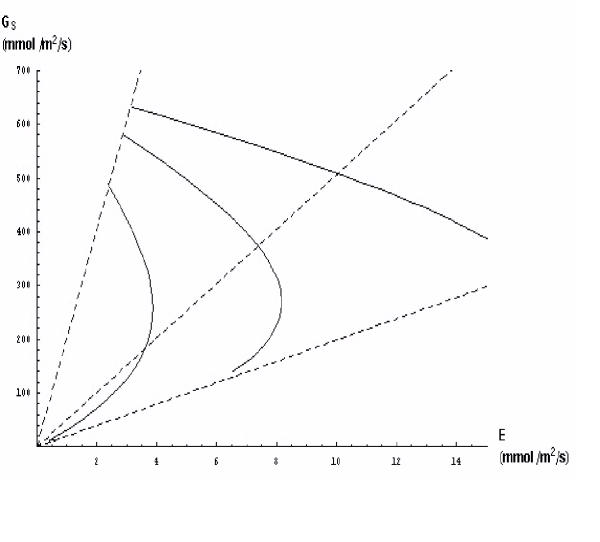
A key prediction can be made from the model, namely the relative importance of cuticular transpiration on sensitivity of Gs to D. We can vary cuticular conductance by varying the 'wax factor'. When the wax factor was halved (ie cuticular conductance increased) the response curves of Gs vs E shifted to the left, but the maximum values of Gs varied only slightly (Fig 5). Consequently, stomatal sensitivity to increasing D had two responses, depending on the magnitude of D. For small values of D, there was minimal change in stomatal sensitivity to increasing D. At high values of D, however, increasing cuticular transpiration by increasing cuticular conductance resulted in an increase in the sensitivity of stomata to D. This can be seen by comparing the slope of the Gs against E curve for large values of D in Figure 5. The dashed lines are lines of constant D.

Figure 5.

Figure 5

Open in a new tab

As the value of the external cuticular wax factor increased (resistance to water flow across the cuticle increased) stomatal sensitivity to increased D declined, as revealed by the decreasing slope of the relationship between conductance and transpiration. Values for the wax factor are 0.5, 1.0 and 2 times the default value for the curves, reading left to right. The dashed lines are lines of constant D.

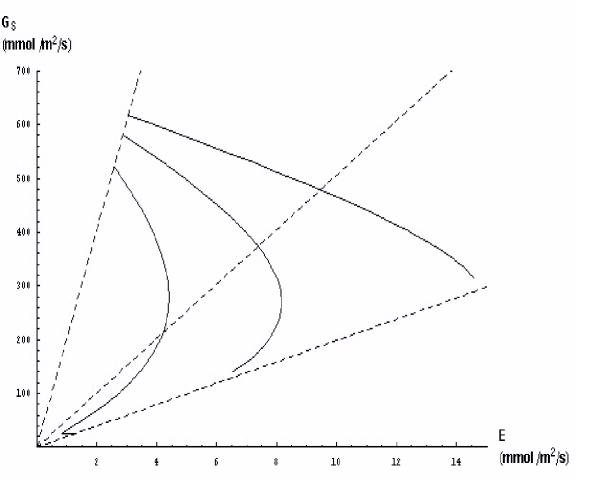
When membrane Lp was halved, the relationship between Gs and E shifted significantly to the left (Figure 6). Interestingly, although maximum Gs did not change, the maximum E was more than halved, compared to the default value of Lp used generally. Indeed, the Gs against E curve tended towards the curve observed when the plant was significantly stressed (Fig. 4). Clearly, reducing Lp resulted in an increase in stomatal sensitivity to E and region C of the three phase curve (see above) was lost, in a similar manner to what was observed when water stress was imposed. The dashed lines are lines of constant D.

Figure 6.

Figure 6

Open in a new tab

As the value of the membrane hydraulic conductivity (Lp) increased (resistance to water flow across the membrane decreased) stomatal sensitivity to increased D declined. Values for Lp are 0.5, 1.0 and 2 times the default value for the curves, reading left to right. Changes in membrane hydraulic conductance influence the maximum value of E and alter stomatal sensitivity to D. The dashed lines are lines of constant D.

Discussion

The parameter values used (stomatal density, stomatal size, xylem water potential as a leaf is water stressed, cuticular conductance, fraction of leaf volume that is air, and hydraulic conductance), are within the ranges of published values. In addition, when using these values, derived relationships, such as the ratio of cuticular to stomatal transpiration when stomata are open, and the proportion of leaf area that is stomatal pore, are also well within published ranges (this may appear obvious, but it is not necessarily so that ratios of two values that are themselves within a range of published values must generate a ratio that is similarly so). Thus, approximately 1.25 % of the leaf surface is stomatal pore and the ratio of cuticular to stomatal transpiration (for open stomata) is about 0.02. For well watered leaves, Gs declined curvilinearly as D increased. Such responses are well-documented [2,9,17,25,30,37,38]. The cause of this decline in Gs was a decline in the volume of the guard cell because water supply to the guard cell became reduced as cuticular transpiration became an increasingly large fraction of total transpiration. As water stress increased, the same pattern of stomatal response to increased D was observed, but tqhe curves were moved downwards. That maximum conductance declines with increasing water stress is well accepted [39].

We observed the three phases of stomatal responses to D [6,12,25,37]. For well watered leaves, as D increased from approximately 0.5 kPa to approximately 5 kPa, E increased for small to moderate increases in D (from 0.5 to 2.5 kPa), remained approximately constant for moderate values of D (about 2.5–3.5 kPa) and then E decreased for larger values of D. Thus, stomata did not regulate E with increasing D when D was low to moderate, but stomata did limit E when D was moderate to large.

As water stress developed in the plant, xylem water potential declined from -0.05 MPa to -2.0 MPa. This reduced maximum Gs (because of the stress function in the model – see Fig. 2). Stomatal behaviour became more and more regulatory as leaf water potential declined. Consequently, at the most severe levels of stress modeled, for almost the whole range of increasing D, E declined, as has been observed previously [5,6,37]. Thus the entire stomatal response to increasing D, for the entire range of D, became confined to the lowest part of the response curve whereby E was reduced at all values of D. Therefore we can conclude that as stress developed, stomata regulated transpiration at ever decreasing values of D – that is, stomatal sensitivity to D increased with increasing levels of water stress. Increased stomatal sensitivity to D with decreasing plant water status has recently been observed [40].

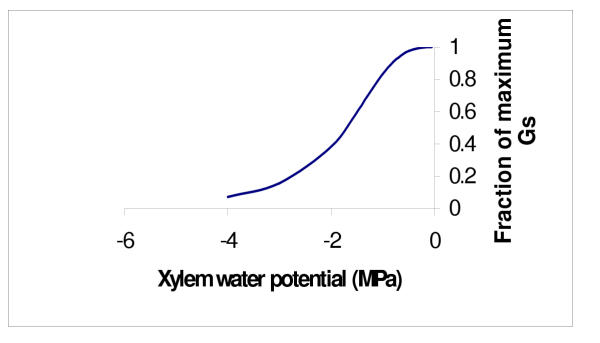
Figure 2.

Figure 2

Open in a new tab

Maximum Gs declines as xylem water potential declines because of the stress function.

How do we interpret the 3 phases of stomatal responses to increasing D and declining leaf water potential? Decreasing the xylem potential of the plant reduced the maximum conductance. Also the "knee" of each curve (maximum transpiration) occurs at lower values of D while plant stress is increasing, further indicating increased sensitivity of stomata to D as plant water status declined [40]. It is important to note that feedback is always operating over the full response curve. As D increases, cuticular transpiration from epidermal and guard cells increase. Guard cells compensate for this increased loss by reducing their volume and hence reducing their aperture relatively more than if there was no cuticular transpiration. It is the presence of this cuticular transpiration and loss into the sub-stomatal cavity that results in the 3-phase (sensu[12]) response of stomata. Thus, at low values of D, stomata are fully open and E increased with increasing D because water loss from the guard cell (both into the sub-stomatal cavity and out to the atmosphere is insufficient to cause stomatal closure. At a critical value of D, increased water loss from the guard cell is sufficient for guard cell turgor and hence aperture to be reduced and E is regulated to an approximately fixed value. For further increases in D, aperture must reduce substantially since cuticular water loss into the surrounding air is a substantial fraction of the total. Consequently E declines with increasing D. These response characteristics have been observed experimentally [5,6].

Feedback control

The model shows that at low values of D, as D increases, E increases. Only at high values of D does increasing D result in E decreasing (the so-called feed-forward behaviour). The model conclusively shows that this behaviour is not feed-forward, but feed-back. At low values of D, E increases with increasing D because the supply of water to the guard cell is sufficient to maintain guard cell volume and hence turgor, despite increasing losses of water from the guard cell through peristomatal transpiration and loss into the sub-stomatal cavity. Because turgor is maintained, stomatal aperture is maintained and hence transpiration increases with increasing D. At this stage, peristomatal transpiration is a very small fraction of total transpiration. However, above a certain value of D, the supply of water to the guard cell becomes insufficient to maintain guard cell volume. It is both peristomatal transpiration and water loss into the sub-stomatal cavity that causes the decline in guard cell volume and hence aperture and hence transpiration. This loss of water from the guard cell therefore feeds back on guard cell volume, and aperture, such as to cause declining aperture at a rate sufficient to cause declining E.

It is important to note that with increasing D the increasing peristomatal transpiration from the guard cell causes the stomata to close further than it would need to if water loss into the sub-stomatal cavity were the only loss pathway from the guard cell. The increasing peristomatal transpiration with increasing D at large values of D cause aperture to decline at a rate sufficient to cause declining E. There is no feed-forward linkage between transpiration through the guard cell to determine aperture. It has been the inability to separate water flux through the aperture from flux from the guard cell that has resulted in the mislabeling of changes in aperture as a feed-forward response.

Predictions of the model

A key prediction can be made from the model, namely the relative importance of cuticular transpiration on sensitivity of Gs to D. We can vary cuticular conductance by varying the 'wax factor'. When the wax factor was halved (ie cuticular conductance increased) the response curves of Gs vs E shifted to the left, but the maximum values of Gs varied only slightly (Fig 5). Consequently, stomatal sensitivity to increasing D had two responses, depending on the magnitude of D. For small values of D, there was minimal change in stomatal sensitivity to increasing D. At high values of D, however, increasing cuticular transpiration by increasing cuticular conductance resulted in an increase in the sensitivity of stomata to D. This can be seen by comparing the slope of the Gs against E curve for large values of D in Figure 5. These results are consistent with the conclusion of Kerstiens [10] who stated that at relatively low D there was an insignificant correlation of stomatal sensitivity and cuticular conductance, but at high VPDs, there was a positive correlation. In addition hexane treated twigs of Douglas fir were more sensitive to D than non-treated branches [41]. Hexane removes part of the cuticular waxes and hence increases cuticular conductance.

Sensitivity analyses

How does model behaviour change if we vary any of the parameters? Several parameter values have been changed by 50 % up and down from the values used to generate the figures. Variation in several parameters had no significant impact upon model behaviour, including leaf thickness, fraction of volume that is air and the proportion of the cell wall that is in contact with air. However, changes in the wax factor (Fig. 5) and membrane hydraulic conductance did have impacts upon model outputs. Changes in the wax factor are discussed above. We now consider changes in membrane hydraulic conductance (Lp).

When Lp was halved, the relationship between Gs and E shifted significantly to the left (Figure 6). Interestingly, although maximum Gs did not change, the maximum E was more than halved, compared to the default value of Lp used above. Indeed, the Gs against E curve tended towards the curve observed when the plant was significantly stressed (Fig. 4). Clearly, reducing Lp resulted in an increase in stomatal sensitivity to E and region C of the three phase curve (see above) was lost, in a similar manner to what was observed when water stress was imposed. There is ample evidence that water stress reduces the conductivity of the soil-plant system [42] and may regulate transpiration rate [43]. From our model, stomatal responses to water stress can be approximately replicated by reducing Lp, suggesting that this may represents a mechanism additional to those previously reported (xylem sap ABA, xylem sap pH) as underlying this response.

Conclusions

In conclusion, we state the following. A simple model of stomatal responses to D was generated based on simple biophysical properties of leaves. This model was able to replicate the three-phase response of stomata to increasing D, and also replicated the impact of water stress upon these responses. Finally, changes in stomatal sensitivity to D as leaf water status changed were also found to replicate published observations. There was no evidence that feed-forward control of stomata occurs. Cuticular transpiration was found to be an important feature underlying stomatal responses to D and causes the 3 phase response of stomata to increasing D. Feed-back behaviour of stomata, through water loss from the guard cells can explain all phases of stomatal responses to D.

Methods

The model – an overview

The model of cell/leaf behaviour makes comprehensive use of Mathematica© software. This is an excellent tool for developing and running the model and displaying results. The rate equations in the model are not empirical. The equations are numerically solved as a function of time. Given a variety of starting conditions, the model quickly moves towards a steady-state solution. (That is, to a point where all time derivatives are zero).

Once steady state is reached, the behaviour of the model to a slowly changing vapour pressure deficit (D) can be found by making D a slowly varying function of time. A set of parametric solutions for various leaf quantities is produced by the model. Variation in D is so slow that at any time the model is in equilibrium for that set of parameters.

Stomatal aperture is taken to be linear with guard cell volume. That guard cell volume and aperture are correlated is fully accepted [3,28]. In the model we set a fraction of maximum guard cell volume at which the stomatal aperture is zero. (The aperture is at maximum size at maximum guard cell volume.) Further, there is little doubt that as water stress develops and xylem water potential declines, maximum stomatal aperture also declines [29-31]. Several mechanisms can be proposed as the link between declining soil water content and declining Gs. These include increased ABA supply to guard cells [31], increased apoplast pH [32] and increased xylem embolism resulting in reduced water supply to the leaf [33]. We link the maximum guard cell volume (and hence aperture) to the xylem water potential in a manner described below, making no assumptions as to the mechanism linking aperture to soil water content.

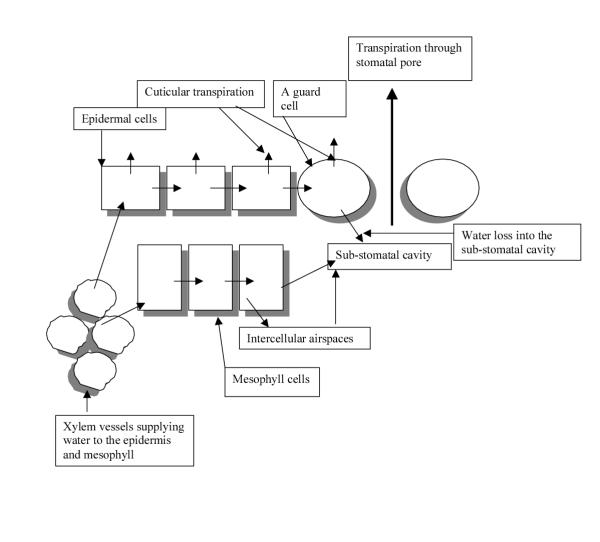
The model leaf is divided into a number of compartments (Fig. 1). These are (a) leaf xylem; (b) chains of mesophyll cells; (c) chains of epidermal cells, including a subsidiary cell; (d) guard cells; (e) intercellular air space; (f) sub-stomatal cavities and (g) the atmosphere outside the leaf. Water supply from the xylem to the rest of the leaf is determined by the gradient in water potential between the xylem and the rest of the leaf. The xylem supplies water (independently) to both the chain of mesophyll cells and the chain of epidermal cells. Mesophyll cells supply water to intercellular air spaces and sub-stomatal cavities. The subsidiary cell supplies water both to the guard cell and the external atmosphere through cuticular transpiration. All epidermal cells supply water to the next cell in the chain and to the external atmosphere through cuticular transpiration. The model assumes that all mesophyll cells are identical, and that all epidermal cells are identical. The number of cells in each type of chain is specified, but this number does not have any significant impact on model outputs. The whole leaf is assumed to be made up of a large number of identical chains. The number of epidermal chains does not need to be specified, since the number of stomata per unit area is specified. The contact area between the guard cell and epidermal cells is defined as a constant.

Figure 1.

Figure 1

Open in a new tab

A schematic diagram of the modelled leaf with compartments and fluxes identified.

Water flows between two points due to the difference in water potential between those points. The direction of flow is not set as a constraint, but by the model reaching equilibrium. It is assumed that the differences in water potential between identical neighbouring cells in any chain are equal. That is, the water potential changes uniformly along a chain, since cells within a chain are assumed to behave identically. Hence only the water potential for the last cell in the chain needs to be specified, and the rate equations for the mesophyll cell potential, or the epidermal cell potential apply to the end cell in the respective chain.

The guard cell and the outside surface of the epidermal cells are covered by a waxy cuticle. The guard cells and epidermal cells lose water directly to the outside environment due to cuticular loss from their outside surface area. The sub-stomatal cavity is assumed to be in diffusive communication with the leaf's intercellular air spaces and internal RH is very close to saturation. See Figure 1 for a schematic diagram of the leaf.

The size of the intercellular air space is specified by the fraction of leaf volume it represents. Since not all the wall area of a mesophyll cell is in contact with this air space, an average fraction of mesophyll wall area that is in contact with the air space is specified (see [6]). Complications arise since most transpirational water flows from the mesophyll cells closest to the sub-stomatal cavity and we assume that RH in the intercellular air space increases with distance from the stomata. To account for this each mesophyll cell is assumed to supply water to 1/NM of the intercellular airspace, where NM is the number of mesophyll cells in the chain. It could be argued that the last mesophyll cell in the chain should be supplying more water then the other cells in the chain, but at present we have no adequate way of estimating this effect. Note that the last cell in the chain has a greater surface area in contact with the air space since it only has a neighbouring cell on one side. From the intercellular air space the water flows to the outside environment through the sub-stomatal cavity and stomatal aperture. The RH of the sub-stomatal cavity at the inside edge of the stomata is the RH that the last mesophyll cell in the chain experiences.

The effect of the wax cuticle on cuticular transpiration is determined by a "wax factor" in the flow equation defining water loss across the cuticle. The resistance to flow across the wall cuticle is substantially (2 * 104) larger than the resistance to flow across a plasmalemma. The value of the wax factor is primarily responsible for determining the amount of cuticular transpiration. The surface area of the stomata in contact with the sub stomatal cavity is also assumed to be covered by a wax cuticle, although the wax factor for flow across this area is allowed to be different from that governing cuticular transpiration. The outside relative humidity is a controlled (but varying) input to the model. In practice, we slowly vary the outside vapour pressure linearly with time, between zero and some set maximum value to generate a set of results.

In practice, for any cell in contact with an air space, either cavity or outside, we define an RH for that cell's wall. In effect, water flows from the symplast of the cell, across the plasmalemma, to the cell wall, and from the cell wall to the airspace (see below). The guard cell wall is especially important since it communicates with four regions (subsidiary cell, guard cell cytoplasm, external atmosphere and sub-stomatal cavity). Water can flow through this wall between the four regions even if stomata are closed.

The only variable that is regulated in this model is the size of the stomatal aperture (the controlled parameter). We have empirically linked (linearly) the size of this aperture to guard cell volume. The flow of water into and out of the guard cell is the only mechanism by which the volume of the guard cell (and hence the aperture) can change. Mechanisms underlying solute accumulation and loss by guard cells are not part of this model but have been the subject of extensive research [34,35]. Stomatal aperture is a maximum when guard cell volume is a maximum, and reduces linearly to zero as guard cell volume reduces to a minimum value (set to 60 % of maximum volume, ie zero aperture is attained when guard cell volume is 60% of the maximum; see [3]). Cell volume can continue to decline when the aperture is shut, since the guard cell may continue to lose water.

Impacts of water stress

The size of guard cells approach a maximum as turgor increases, while the difference in total water potential between the guard cell and subsidiary cell decreases (otherwise guard cells would increase in size without limit). Guard cell volume is prevented from growing too large by specifying a fraction of maximum guard cell volume at which the total potential difference between guard cell and subsidiary cell tends to zero. For an unstressed leaf this fraction is equal to one.

To incorporate the impact of water stress upon stomatal responses to changes in D the fraction of maximum guard cell volume (referred to above) reduces as xylem water potential declines. Hence the maximum possible size of a guard cell (and maximum aperture size) also declines with increasing stress, as observed experimentally [5,6,8]. We do not concern ourselves at this stage with determining the mechanism underlying the link between the declining leaf water status and the reduced maximum size of the guard cell, although a role for chemical signaling is likely.

The model has six coupled rate equations for the volume of the guard cell, the water potential of the mesophyll cells, the water potential of the epidermal cells, the RHs of the cell walls of both the mesophyll and guard cells, and the RH of the sub-stomatal cavity. These six quantities are referred to as state variables. All six equations are similar in form in that the rate of change of the state variable is set to be proportional to either the rate of flow of water into and out of a particular identifiable volume of the leaf, or to the rate of change of the difference in water potential driving the water flows into and out of the volume. That is, the equations have the general form:

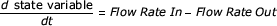Inline graphic (1)

If the areas across which the flow occurs is not known, and we consider cell B in communication with cells A and C in a chain A-B-C

graphic file with name 1472-6785-2-8-i3.gif

Given parametric solutions for the state variables, in terms of the independent variable time, all other necessary quantities can be calculated. For example, water loss from the cavity through the stomatal aperture can be found from the number of stomata, aperture size, the length of the stomata, and the difference in RH across the stomata.

There are a number of parameters in the model which do not depend on time (i.e. constants), including the physical size of all leaf cells except guard cells, the mesophyll wall area, epidermal to guard cell wall area, stomata dimensions etc. All are all given realistic values (detailed in Table 1) derived from the literature. No single study is available that provides all the required parameters for a single species so we have been required to utilise several sources for different species.

Table 1.

The values of the non-time varying parameters

Parameter Range Symbol References
Xylem water potential 0 to -2.0 MPa ΨX [5,6,44]
Subsidiary cell to guard cell water potential difference -0.1 to -0.05 MPa ΔΨSG(t) [45]
Maximum Guard Cell Volume 4.3 × 10-16 m3 Vmax [46]
Maximum Stomatal Aperture 5 × 10-6m Stommax [28,46]
Stomata Density 250 × 106 /m2 σS [38,46]
Subsidiary cell : Guard Cell Contact Surface Area 2.4 × 10-10m2 ASG [40]
Fraction of total leaf volume that is air 50% fv [40]
Leaf Thickness 1 × 10-3m Leafthick Eamus unpbl.
% Mesophyll Cell surface in contact with air 50% fc [40]
Maximum membrane hydraulic conductivity 5 × 10>-14m s-1 Pa-1 LP [47]
Mesophyll cell wall thickness 3 × 10-6 m ΔxMW Eamus unpbl.
Depth of stomatal channel 5 × 10-6 m ΔxGW Eamus unpbl.
Wax Factor Out 2 × 104 WOUT
Wax Factor IN 5 × 103 WIN
Ratio of cuticular to stomatal transpiration when stomata are fully open Ca 0.01 24
Open in a new tab

Water flow through any section of the leaf is driven by the difference in water potential between that section and the two bounding regions. In the air spaces of the leaf, as well as on the surface of all the cell walls, it has been found that RH is a more useful quantity than water potential. This is because the equations for these sections of the leaf have been developed by calculating the rates of change in the number of water molecules per unit volume, and RH is a better measure of this quantity for the vapour state. Water potential is related to RH by the equation:

graphic file with name 1472-6785-2-8-i4.gif

where NA is Avogadro's number, k is Boltzman's constant, T the absolute temperature, and 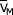Inline graphic the molar volume of water.

The guard cell area in contact with the sub-stomatal cavity or the outside environment, the guard cell wall thickness, and the stomatal aperture are dependent on the volume of the guard cell. We have not let the area of contact (ASG), or thickness of the wall, between the epidermal cell and the guard cell change, even though the total area of the guard cell wall changes. The thickness of the remaining guard cell wall is calculated by assuming the total volume of this guard cell wall remains constant as total cell volume changes. That is, the cell wall becomes thinner as the volume increases. Half of this area is in contact with the atmosphere, the other half with the sub-stomatal cavity. (Both of these are covered by wax.)

The guard cell is assumed to be of the dicotyledenous type, and in this model its volume is assumed to be approximated by a toroid. To account for the actual shape of a stomata we have assumed that the stomata opening is fixed in length (15 × 10-6 m), and is fully closed when the guard cell has 0.6 of its maximum volume, and fully open at the maximum volume. Aperture varies linearly with cell volume between these limits [36]. For stressed leaves the volume of the guard cell, and hence the aperture, never reaches maximum size. To account for the (very) approximately diamond shape of actual stomata openings, we have halved the product of the fixed length and the aperture, and called this the area of the stomatal pore.

The model in full

Subsidiary cell and guard cell water potentials

The rate equation for the subsidiary cell water potential is of the form of equation (1). However, the area of cell wall on either side of an epidermal cell across which water flows into and out of the cell are assumed equal and this area is set equal to the area of contact between the last epidermal cell (the subsidiary cell) in the chain and the guard cell. This assumption "converts" the equation into the form of equation (2) in the steady state. Since water flows from the xylem to the guard cell through this chain, the assumption of equal areas implies that the difference in water potential between the xylem and the guard cell is evenly distributed along the chain of epidermal cells and guard cell. Further, the rate equation for the subsidiary cell water potential has been formulated in terms of the differences in water potential between neighbouring cells, and not the absolute water potentials.

The "potential difference in" term of equation (2) for the subsidiary cell is:

Potential Difference In = ΨX - (NE - 1) ΔΨS - ΨS     (4)

where ΨS is the absolute subsidiary cell water potential, NE is the number of epidermal cells in the chain (including the subsidiary cell), ΨX is the xylem water potential, and ΔΨS is the difference in water potential between subsidiary cell and guard cell, and hence also between neighbouring epidermal cells. The assumption of uniform variation in water potential along the chain ensures that expression (4) simplifies to a single term: ΔΨS (that is, ΨX – ΨS = NE ΔΨS)

The "potential difference out" term of equation (3) for the subsidiary cell is the difference in water potential between the subsidiary cell and the guard cell. This difference in water potential is assumed to have a value that is dependent upon the volume of the guard cell (one of the state variables) and will vary with time as the guard cell volume varies. One other assumption in the model is that there is some volume of guard cell at which this potential difference between guard cell and subsidiary cell would be zero due to increasing guard cell turgor (which increases with guard cell volume as solutes accumulate in the guard cell). This value of cell volume is defined as a fraction of the maximum guard cell size for a totally unstressed plant. This method allows us to vary this fraction with plant stress (as the plant becomes more stressed the guard cells do not increase to the size they would have for an unstressed plant, see below). The potential difference between the subsidiary cell and the guard cell is labelled ΔΨSG(VG(t)), indicating that the difference is dependent on the time varying guard cell volume, VG(t).

The functional form of ΔΨSG(VG(t)) is a matter for further investigation. For this model it has been taken as a function which will produce a constant value of ΔΨSG(VG(t)) when the guard cell has not reached its upper limit on size, while tending rapidly to zero when the guard cell approaches this point. The function is given by the following expression:

graphic file with name 1472-6785-2-8-i6.gif

where:

fM is that fraction of Vmax where the water potential difference goes to zero.

ΔΨSGI is an initial value of the potential difference between the guard cell and the subsidiary cell.

fM has been set to one.

ΔΨSGI can be taken as an "initial" value for the potential difference between the subsidiary cell and guard cell, one that is never actually realised since VG(t) will always have some value less then fM Vmax.

Hence the rate equation for the subsidiary cell water potential becomes:

graphic file with name 1472-6785-2-8-i7.gif

In the steady state, the solution will always be that ΔΨS(t) equals ΔΨSG(VG(t)). When the instantaneous value of ΔΨSG(VG(t)) is found from equation (5), the absolute subsidiary cell water potential, ΨS(t), is determined from expression (4). It is given by:

ΨS(t) = ΨX + NE ΔΨSG (VG (t))     (7)

Similarly, the instantaneous value of the absolute guard cell water potential, ΨG (t), is found by adding ΔΨSG(VG(t)) to the subsidiary cell potential. In the actual program the rate equation for ΨS(t) is solved for numerically, but the result is always as given by equation (7).

Changes in guard cell volume

The rate equation for the volume of the guard cell is of the form of equation (1), where the flow rate is of water into and out of the guard cell. Water flows into the guard cell from the subsidiary cell, and flows out of the guard cell into the guard cell wall. The flows into and out of the guard cell are proportional to the water potential differences between the guard cell and the regions on either side.

The "flow rate in" term is given by the expression:

ASGLP ΔΨSG (VG (t))

where LP is the membrane hydraulic conductivity and ASG is the fixed area between the subsidiary cell and the guard cell. (LP and ASG values are given in Table 1.)

The "flow rate out" term is given by the expression:

graphic file with name 1472-6785-2-8-i8.gif

where:

2AG(t) is the varying area of the guard cell in contact with the sub-stomatal cavity and outside environment (AG(t) each)

RHGwall(t) is the time varying effective RH of this guard cell wall area

Other quantities are as defined in Table 1. Hence the rate equation for the volume of the guard cell is:

graphic file with name 1472-6785-2-8-i9.gif

The sum of ASG and 2AG(t) is the instantaneous total area of the guard cell wall. We have equated this area to the surface area of a toroid whose larger radius is fixed, and whose volume is the instantaneous volume of the guard cell. In effect this means the smaller radius of the toroid increases or decreases with volume. The relation can be expressed as:

graphic file with name 1472-6785-2-8-i10.gif

Equation (10) simply states that the volume change of the guard cell is due to the difference in volume between the flow of water into the cell, and the flow out of the cell. If these two rates are equal, the volume remains constant with time. A more detailed relationship between the guard cell area and its volume is being developed.

Guard cell wall water content

By considering water flow (in terms of the number of molecules) into and out of the cell wall of the guard cell, a rate equation can be developed for the rate of change of the effective RH of this wall. In this equation it is assumed that flow into the wall is due to the difference in water potential between the guard cell cytoplasm and its cell wall. Flow out of the wall is due to the difference in water potential between that of the wall and both the intercellular air space and the outside environment. Flow into each of these areas is reduced by the appropriate wax factor (allowed to be different for each area). These last three water potentials are expressed in terms of RH, using equation (3) where necessary.

The rate equation is of the form of equation (1), with the "flow rate in" term being able to be expressed as:

graphic file with name 1472-6785-2-8-i11.gif

where:

SVP(T) is the saturated vapour pressure of water at temperature T, at standard pressure,

VGwall is the volume of the guard cell wall,

RHGwall(t) is the time dependent RH of the guard cell,

(2AG(t)/VGwall) is the inverse of the cell wall thickness.

The "flow rate out" term is:

graphic file with name 1472-6785-2-8-i12.gif

where:

DW(T) is the vapour diffusion constant for water at temperature T,

RHcav(t) is the time dependent RH of the sub-stomatal cavity.

RHout is the RH of the atmosphere

WIN is the wax factor reducing flow into the sub stomatal cavity

WOUT is the wax factor reducing cuticular flow to the atmosphere.

The complete rate equation for the RH of the guard cell wall volume becomes:

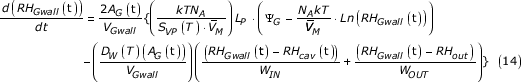
graphic file with name 1472-6785-2-8-i13.gif

Mesophyll cells

For mesophyll cells, water flow into these cells is governed by equations similar to those for the subsidiary cell. However, the surface area and volume of the mesophyll cells are fixed. A fraction of their surface area (fc) is assumed to be in contact with the intercellular spaces, the remainder of the cell is assumed to be in contact with adjacent mesophyll cells. For the last cell in the chain there is only a neighbouring cell on one side, so the fraction in contact with the intercellular space is larger. The time dependent quantity in this system is the mesophyll water potential of this last cell, and assuming the mesophyll cell water potential varies linearly along the chain, the "flow rate in" term of equation (1) for the last cell in the chain can be written as:

graphic file with name 1472-6785-2-8-i14.gif

where

AM is the total area of a single mesophyll cell

NM is the number of mesophyll cells in the chain

ΨMcell(t) is the time varying water potential of the last mesophyll cell in the chain

The "flow rate out term" can be written as:

graphic file with name 1472-6785-2-8-i15.gif

where

RHMwall(t) is the time varying RH of the last mesophyll cell wall

The complete rate equation for the mesophyll water potential becomes:

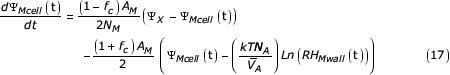
graphic file with name 1472-6785-2-8-i16.gif

Note that when the rate equations are solved for the steady state (time derivatives zero) the common constants in both terms of the right hand side of equation (17) will disappear. (They are important for transient behaviour).

Mesophyll cell wall water content

The next rate equation is for the effective RH of the walls of the last mesophyll cell in the chain. Water flows into this region from a mesophyll cell and then evaporates into the intercellular space. The intercellular space and the sub-stomatal cavity are considered as a single unit for the purpose of the model, but each mesophyll cell supplies water to only part of this volume. The water potential of the cell wall is expressed in terms of its RH. The "flow rate in" term of equation (1) can be written as:

graphic file with name 1472-6785-2-8-i17.gif

where:

ΔxMW is the thickness of the mesophyll cell wall.

The "flow rate out" term of equation (1) can be written as:

graphic file with name 1472-6785-2-8-i18.gif

where:

RHcav(t) is the time varying RH of the intercellular air space and sub stomatal cavity.

The complete rate equation for the RH of the last mesophyll wall becomes:

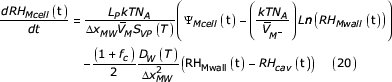
graphic file with name 1472-6785-2-8-i19.gif

Sub-stomatal cavity water vapour content

The rate equation for the last state variable defines the rate of change of the RH in the sub-stomatal cavity. This equation couples the equations for the guard and mesophyll cells since both are in contact with this volume. Water vapour diffuses out of this space through the stomatal aperture to the outside atmosphere. The previous equations apply to single cells, with all individual types of cells being identical with others of their type. This final equation is for that fraction of the whole leaf air space supplied by the last mesophyll cell in all chains, and takes account of all water flow into and out of this space, expressed per square metre of leaf area. The RH of the outside atmosphere is an adjustable parameter in the model; it can be set to a constant value or made a function of time. The "flow rate in" term of equation (1), has two components (last mesophyll cells in all chains and all guard cells) and for this region is:

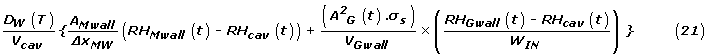
graphic file with name 1472-6785-2-8-i20.gif

where:

σS is the number of stomata per square metre of leaf area

AMwall is the total wall area of all last mesophyll cells interacting with the airspace

Vcav is the total air volume of the leaf, divided by NM.

The "flow rate out" term is:

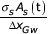Inline graphic (RHcav (t) – RHout)     (22)

where:

AS(t) is the stomata aperture area, a linear function of guard cell volume

RHout is the RH of the atmosphere surrounding the leaf.

Boundary layer effects

One other feature has been incorporated into the model. It is the incorporation of a boundary layer effect into water flow through the stomatal pore. The first approximation of this effect, found by modelling flow through the stomata as flow through a cylinder of diameter d and length l results in a factor being incorporated into the flow equation for flow through the stomatal pore equivalent to:

graphic file with name 1472-6785-2-8-i22.gif

In effect, this means that for narrow long pipes, most of the water vapour concentration difference appears over the length of the pipe. For short wide pipes, only a small concentration difference appears between the ends of the pipe, with the majority of the concentration gradient appearing between either end of the pipe and the region well removed from that pipe end (i.e. a boundary layer). In the model the flow through the pipe (i.e. stomatal pore) is found from the concentration gradient appearing between the ends of the pipe.

Incorporating water stress in the model

The influence of water stress on maximum aperture size is accomplished by making the value fM (which was set to 1 for unstressed plants) a dimensionless function of xylem potential. This function has been chosen by design to be 0.6 + 2/(5 – 2x3), where x is the xylem potential in MPa; the function maps fM into the range of 0.6 for very stressed plants to 1.0 for unstressed plants. This function was chosen because it mimics the observed decline in GS as water stress develops [5,6]. The effect of water stress on maximum GS due to the variation in fM, normalised to the maximum GS for an unstressed leaf, is shown in Figure 2. We concur with Jones that it is D (or E) and soil water potential that control GS, but the direct mechanistic link is through leaf (xylem) water potential [38]. This model does not attempt to incorporate mechanisms by which changes in soil water availability influence Gs; this model does explicitly deal with how changes in D control GS.

Authors' contributions

Author 1 (DE) designed and supervised the experimental work that was undertaken as part of a larger program of work investigating stomatal responses to drought and vapour pressure deficit, as described in Thomas and Eamus (1999). DE also wrote the first draft of this Ms. Author 2 (SS) developed the model, tested the model and assisted in redrafting the Ms.

Contributor Information

D Eamus, Email: derek.eamus@uts.edu.au.

ST Shanahan, Email: steve.shanahan@ntu.edu.au.

References

  1. Grantz DA. Plant responses to atmospheric humidity. Plant, Cell and Environment. 1990;13:667–679. [Google Scholar]
  2. Yong JWH, Wong SC, Farquhar GD. Stomatal responses to changes in vapour pressure difference between leaf and air. Plant, Cell and Environment. 1997;20:1213–1216. doi: 10.1046/j.1365-3040.1997.d01-27.x. [DOI] [Google Scholar]
  3. Raschke K. Movements of stomata. Encyclopedia of Plant Physiology Springer-Verlag, Berlin. 1979;7:15–29. [Google Scholar]
  4. Schulze E-D. Carbon dioxide and water vapour exchange in response to drought in the atmosphere and in the soil. Annual Review of Plant Physiology. 1986;37:247–274. doi: 10.1146/annurev.pp.37.060186.001335. [DOI] [Google Scholar]
  5. Thomas DS, Eamus D. The influence of pre-dawn leaf water potential on stomatal responses to atmospheric water content at constant Ci and on stem hydraulic conductance and foliar ABA concentrations. Journal of Experimental Botany. 1999;50:243–251. doi: 10.1093/jexbot/50.331.243. [DOI] [Google Scholar]
  6. Thomas DS, Eamus D, Bell D. Optimization theory of stomatal behaviour II. Stomatal responses of several tree species of north Australia to changes in light, soil and atmospheric water content and temperature. Journal of Experimental Botany. 1999;50:393–400. [Google Scholar]
  7. Berryman D, Eamus D, Duff GA. Stomatal responses to a range of variables in two tropical tree species grown with CO2. Journal of Experimental Botany. 1994;45:539–546. [Google Scholar]
  8. Prior LD, Eamus D, Duff GA. Seasonal and diurnal patterns of carbon assimilation, stomatal conductance and leaf water potential in Eucalyptus tetrodonta saplings in a wet-dry savanna in northern Australia. Australian Journal of Botany. 1997;45:241–258. [Google Scholar]
  9. Maroco JP, Pereira JS, Chaves MM. Stomatal responses to leaf-to-air vapour pressure deficit in Sahelian species. Australian Journal of Plant Physiology. 1997;24:381–387. [Google Scholar]
  10. Kerstiens G. Cuticular water permeability and its physiological significance. Journal of Experimental Botany. 1996;47:1813–1832. [Google Scholar]
  11. Mott KA, Parkhurst DF. Stomatal responses to humidity in air and helox. Plant, Cell and Environment. 1991;14:509–515. [Google Scholar]
  12. Monteith JL. A reinterpretation of stomatal responses to humidity. Plant, Cell and Environment. 1995;18:357–364. [Google Scholar]
  13. Bunce JA. Does transpiration control stomatal responses to water vapour pressure deficit? Plant, Cell and Environment. 1996;19:131–135. [Google Scholar]
  14. Meidner H, Mansfield TA. Physiology of stomata. McGraw-Hill, London. 1968.
  15. Schulze E-D, Lange OL, Buschbom U, Kappen L, Evenari M. Stomatal responses to changes in humidity in plants growing in the desert. Planta. 1972;108:259–270. doi: 10.1007/BF00384113. [DOI] [PubMed] [Google Scholar]
  16. Eamus D, Cole SC. Diurnal and seasonal comparisons of assimilation, phyllode conductance and water potential of three Acacia and one Eucalyptus species in the wet-dry tropics of Australia. Australian Journal of Botany. 1997;45:275–290. [Google Scholar]
  17. Raschke K. Stomatal action. Annual Review of Plant Physiology. 1975;26:306–340. doi: 10.1146/annurev.pp.26.060175.001521. [DOI] [Google Scholar]
  18. Sheriff DW. Epidermal transpiration and stomatal response to humidity: Some hypotheses explored. Plant, Cell and Environment. 1984;7:669–677. [Google Scholar]
  19. Maier-Maercker U. The role of peristomatal transpiration in the mechanism of stomatal movement. Plant, Cell and Environment. 1983;6:369–380. [Google Scholar]
  20. Dai Z, Edwards GE, Ku MSB. Control of photosynthesis and stomatal conductance in Ricinus communis by leaf to air vapour pressure deficit. Plant Physiology. 1992;99:1426–1434. doi: 10.1104/pp.99.4.1426. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Dewar RC. Interpretation of an empirical model for stomatal conductance in terms of guard cell function. Plant, Cell and Environment. 1995;18:365–372. [Google Scholar]
  22. Hall AE, Kaufman MR. Regulation of water transport in the soil-plant-atmosphere continuum. In: D.M Gates and R.B Schmerl, editor. In "Perspectives of Biophysical Ecology". Springer-Verlag New York; 1975. pp. 187–202. [Google Scholar]
  23. Mott KA, Cardon ZG, Berry JA. Asymmetric patchy stomatal closure for the two surfaces of X. strumarium leaves at low humidity. Plant, Cell and Environment. 1993;16:25–34. [Google Scholar]
  24. Kerstiens G. Stomatal Response to leaf-to-air humidity gradient: a comparison of models. Phys Chem Earth. 1998;23/4:439–442. doi: 10.1016/S0079-1946(98)00050-0. [DOI] [Google Scholar]
  25. Meinzer FC, Andrade JL, Goldstein G, Holbrook NM, Cavelier J, Jackson P. Control of transpiration from the upper canopy of a tropical forest: the role of stomatal, boundary layer and hydraulic architecture components. Plant, Cell and Environment. 1997;20:1242–1252. doi: 10.1046/j.1365-3040.1997.d01-26.x. [DOI] [Google Scholar]
  26. Gollan T, Turner NC, Schulze E-D. The responses of stomata and leaf gas exchange to vapour pressure deficits and soil water content III. In the sclerophyllous woody species Nerium oleander. Oecologia. 1985;65:356–362. doi: 10.1007/BF00378909. [DOI] [PubMed] [Google Scholar]
  27. Turner NC, Schulze E-D, Gollan T. The response of stomata and leaf gas exchange to vapour pressure deficits and water content. I. Species comparisons at high soil water content. Oecologia. 1984;63:338–342. doi: 10.1007/BF00390662. [DOI] [PubMed] [Google Scholar]
  28. Franks PJ. Stomatal closure in dry air. Mechanisms and Ecology. PhD Thesis, Australian National University.
  29. Schulze E-D, Hall AE. Stomatal responses to water loss and CO2 assimilation rates in plants of contrasting environments. In: O L Lange, P Nobel, C B Osmond and H aZiegler, editor. Encyclopedia of Plant Physiology, 12B. Springer-Verlag. Berlin; 1982. pp. 181–230. [Google Scholar]
  30. Prior LD, Eamus D, Duff GA. Seasonal trends in carbon assimilation, stomatal conductance, pre-dawn leaf water potential and growth in Terminalia ferdinandiana, a deciduous tree of northern Australian savannas. Australian Journal of Botany. 1997;45:53–69. [Google Scholar]
  31. Tardieu F, Simonneau T. Variability among species of stomatal control under fluctuating soil water status and evaporative demand: modelling isohydric and anisohydric behaviours. Journal of Experimental Botany. 1998;49:419–432. doi: 10.1093/jexbot/49.suppl_1.419. [DOI] [Google Scholar]
  32. Wilkinson S, Davies WJ. Xylem Sap pH increase: a drought signal received at the apoplastic face of the guard cell that involves the suppression of saturable abscisic acid uptake by the epidermal symplast. Plant Physiology. 1997;113:559–573. doi: 10.1104/pp.113.2.559. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Sperry JS, Pockman WT. Limitation of transpiration by hydraulic conductance and xylem cavitation in Betula occidentalis. Plant, Cell and Environment. 1993;16:279–287. [Google Scholar]
  34. Allen GJ, Amtmann A, Sanders D. Calcium dependent and calcium independent potassium mobilzation channels in Vicia faba guard cell vacuoles. Journal of Experimental Botany. 1998;49:305–318. doi: 10.1093/jexbot/49.suppl_1.305. [DOI] [Google Scholar]
  35. Pei Z-M, Schroeder JI, Schwarz M. Background ion channel activities in Arabidopsis guard cells and review of ion channel regulation by protein phosphorylation events. Journal of Experimental Botany. 1998;49:319–328. doi: 10.1093/jexbot/49.suppl_1.319. [DOI] [Google Scholar]
  36. Raschke K, Dickerson M, Pierce M. In Plant Research. MSU/AEC Plant Research Lab., Michigan State University.; 1972. Mechanics of stomatal response to changes in water potential. pp. 155–157. [Google Scholar]
  37. Jones H. Stomatal control of photosynthesis and transpiration. Journal of Experimental Botany. 1998;49:387–398. doi: 10.1093/jexbot/49.suppl_1.387. [DOI] [Google Scholar]
  38. Fordyce IR, Duff GA, Eamus D. The water relations of Allosyncarpia ternata (Myrtaceae) at contrasting sites in the monsoonal tropics of northern Australia. Australian Journal of Botany. 1997;45:259–274. [Google Scholar]
  39. Reich PB, Hinckley TM. Influence of pre-dawn water potential and soil-to-leaf hydraulic conductance on maximum daily leaf diffusive conductance in two oak species. Functional Ecology. 1989;3:719–726. [Google Scholar]
  40. Thomas DS, Eamus D, Shanahan S. Studies on the influence of season, drought and xylem ABA on stomatal responses to leaf-to-air vapour pressure difference of trees of the Australian wet-dry tropics. Australian Journal of Botany. 2000;48:143–151. doi: 10.1071/BT98090. [DOI] [Google Scholar]
  41. Meinzer FC. The effect of vapour pressure on stomatal control of gas exchange in Douglas fir saplings. Oecologia. 1982;54:236–242. doi: 10.1007/BF00378398. [DOI] [PubMed] [Google Scholar]
  42. Williams M, Malhi Y, Nobre AD, Rastetter EB, Grace J, Pereira MGP. Seasonal variation in net carbon exchange and evapotranspiration in a Brazilian rain forest: a modelling analysis. Plant, Cell and Environment. 1998;21:953–968. doi: 10.1046/j.1365-3040.1998.00339.x. [DOI] [Google Scholar]
  43. Meinzer FC, Goldstein G, Franco AC, Bustamante M, Igler E, Jackson P, Caldas L, Rundel PW. Atmospheric and hydraulic limitations on transpiration in Brazilian Cerrado woody species. Functional Ecology. 1999;13:273–282. doi: 10.1046/j.1365-2435.1999.00313.x. [DOI] [Google Scholar]
  44. Schulze E-D. Soil water deficits and atmospheric humidity as environmental signals. In: J A C Smith and H Griffths, editor. In Water Deficit – plant responses from cell to community. Bios publishers, Oxford; 1993. pp. 129–145. [Google Scholar]
  45. Larcher W. Physiological Plant Ecology. Springer-Verlag, Berlin. 1983.
  46. Eamus D, Wilson JM. The effect of chilling temperatures on the water relations of leaf epidermal cells of Rhoeo discolor. Plant Science Letter. 1984;37:101–106. doi: 10.1016/0304-4211(84)90210-4. [DOI] [Google Scholar]

Articles from BMC Ecology are provided here courtesy of BMC

RESOURCES