Quantifying Transmission of Campylobacter spp. among Broilers

Abstract

Campylobacter species are frequently identified as a cause of human gastroenteritis, often from eating or mishandling contaminated poultry products. Quantitative knowledge of transmission of Campylobacter in broiler flocks is necessary, as this may help to determine the moment of introduction of Campylobacter in broiler flocks more precisely. The aim of this study was to determine the transmission rate parameter in broiler flocks. Four experiments were performed, each with four Campylobacter-inoculated chicks housed with 396 contact chicks per group. Colonization was monitored by regularly testing fecal samples for Campylobacter. A mathematical model was used to quantify the transmission rate, which was determined to be 1.04 new cases per colonized chick per day. This would imply that, for example, in a flock of 20,000 broilers, the prevalence of Campylobacter would increase from 5% to 95% within 6 days after Campylobacter introduction. The model and the estimated transmission rate parameter can be used to develop a suitable sampling scheme to determine transmission in commercial broiler flocks, to estimate whether control measures can reduce the transmission rate, or to estimate when Campylobacter was introduced into a colonized broiler flock on the basis of the time course of transmission in the flock.

Campylobacter species are often identified as bacterial causes of human gastroenteritis throughout the world (2). As an important source of human infections is the mishandling and consumption of contaminated poultry meat (29), a reduction in poultry meat contamination might reduce human exposure and, consequently, the risk of campylobacteriosis.

Several control measures have been implemented to reduce the exposure of humans to Campylobacter spp., either by reducing the incidence of Campylobacter infections in broiler flocks by biosecurity measures at farms or by improving slaughterhouse hygiene. However, these measures are apparently not sufficiently effective, because many broiler flocks still become colonized with Campylobacter spp. (5). Therefore, intervention strategies should be improved or alternatives developed.

Current intervention strategies are based on risk factors identified in field surveys (6, 12, 34). An important disadvantage of these field surveys is that they used associative static models to determine an association between risk factors and the presence of Campylobacter in a flock and were based on qualitative data on the infection status of the flocks at the end of the production period. These studies did not take the dynamic aspects of a Campylobacter infection in a flock into account. Quantitative knowledge of the transmission of Campylobacter is important for the development of control programs for various reasons (8). First, it enables us to determine which measures can reduce transmission, and to what extent (10). Secondly, the transmission rate affects the prevalence of an infection in a population in time, which, in turn, determines the probability of detection. Finally, it may help to determine the moment of introduction of Campylobacter in commercial broiler flocks under field conditions (14, 16, 30). With this knowledge, control measures could focus more on high-risk periods, which might facilitate the maintenance of biosecurity measures at the appropriate level.

Clear quantitative information on Campylobacter transmission is still lacking, although some transmission experiments have been carried out (30, 33). Unfortunately, transmission in these studies was only determined qualitatively. Hartnett et al. (15) analyzed the experiments (30) and did quantify transmission, but their exact method of analysis is unclear. Data from the study of Jacobs-Reitsma (19) were available for further analysis. That group carried out four experiments to determine whether groups of 400 broilers could be colonized after introduction of a few Campylobacter-inoculated seeder birds. This experimental setup, with four seeder birds per group, a high sampling frequency scheme, and relatively large sample sizes, offered the opportunity to quantify transmission. Here, we present the results of a further quantitative analysis of these data (19) and a quantification of the transmission using a mathematical model. These models can be useful in unraveling complex processes at the population level by clarifying some of the factors that determine the speed and scale of transmission of an infectious disease (3, 11, 23). In addition, we show how the transmission parameter could be used to estimate the moment of Campylobacter introduction in the field and how the precision of this estimation is affected by the sampling scheme and sample size.

MATERIALS AND METHODS

Animals.

In four experiments (numbers 1 to 4), the horizontal spread of Campylobacter among broilers (type Ross) was studied. Day-old chicks, used in experiments 1 and 2, were obtained from a Campylobacter-free parent flock of 2,870 birds housed at the Centre for Poultry Research and Information Services “het Spelderholt” (Beekbergen, The Netherlands). This flock was tested for the presence of Campylobacter spp. in 14 pooled samples (four cecal droppings per pooled sample) at day 7 after egg collection. No Campylobacter-positive samples were found after 48 h of culture (method described in reference 17). The chicks used in experiments 3 and 4 originated from a commercial parent flock which was colonized with Campylobacter spp.

Housing.

In each experiment, 400 broilers were accommodated at day of hatch in a separate shed at a density of 20 broilers per m², which is similar to the housing density under commercial conditions. The broilers were fed commercial broiler feed. They were housed on wood shavings, and the drinking water was supplied by means of a nipple drinking system. Before the start of the experiments, samples were taken from water, feed, and wood shavings in the broiler sheds and tested for Campylobacter. The box liners used in the hatchery were tested for Campylobacter as well.

Inoculation.

The Campylobacter strains and inoculation doses are listed in Table 1. Campylobacter coli strain C136 was isolated from a pig farm in March 1990 (16). Campylobacter jejuni strain C356 was isolated in 1990 from broilers (Penner serotype O2) (18) and registered in the CAMPY-NET reference set as number CN076 (14). The strains are stored in glycerol at −80°C and have often been used by the Animal Sciences Group in Lelystad for infection experiments and as reference control strains (9). C. jejuni strain C4021 (experiment 4) originated from the parent flock of the chicks.

TABLE 1.

Challenge strains and inoculation doses

Expt	Campylobacter strain	Penner serotype	Dose (CFU/broiler)
1	C. coli 136	O:46	6.5 × 108
2	C. coli 136	O:46	6.5 × 108
3	C. jejuni 356	O:2	2.6 × 104
4	C. jejuni 4021	Not determined	1.1 × 105

The strains were freshly cultured in heart infusion broth (microaerobically, 37°C, overnight) and diluted in saline to obtain the intended inoculation dose. The actual concentration (CFU/ml) of Campylobacter in the administered suspensions was determined by plating on cephoperazone charcoal deoxycholate agar (CCDA). The complete medium consisted of campylobacter blood-free selective agar base medium (Oxoid CM739) plus CCDA selective supplement SR155.

Experimental design.

In experiments 1 and 2, four chicks per group were orally inoculated with 0.1 ml of the Campylobacter inoculation suspension at day of hatching. In experiments 3 and 4, four chicks per group were orally inoculated with 0.1 ml of the Campylobacter inoculation suspension 1 day after hatching. The inoculated chicks (seeders) were marked on the head with a black spot, were given an identification wing number, and were placed back into their shed. All experiments lasted 42 days. The use of four seeders increases the probability that a large outbreak will occur, allowing transmission to be quantified more accurately (11). The experiment was approved by the Animal Care and Use Committee (license number 44600).

Sampling.

The chicks were sampled at fixed time points (Table 2), starting 1 day after inoculation. In experiments 1 and 2, the four seeders and 50 chicks, chosen at random, were removed from the groups for sampling for Campylobacter by cloacal swabbing. After sampling, the broilers were put back into their groups. In experiments 3 and 4, the seeders were removed from the groups for the time necessary to obtain a fresh (cecal) dropping. A swab was taken from these droppings. Fifty samples of soft, fresh, wet, and homogeneous cecal droppings were collected from the boiler sheds, which were divided into five sectors (1 by 4 m each). Defecation was stimulated by turning on the lights and making a noise, which ensured the samples were fresh. When all samples appeared to be Campylobacter positive, the sample size was reduced in all four experiments to 10 or 12 per group.

TABLE 2.

Number of contact infections in each experiment

Age (days)	No. of Campylobacter-positive broilers
	Expt 1		Expt 2		Expt 3		Expt 4
	Seedersa	Contactsa	Seeders	Contacts	Seeders	Contacts	Seeders	Contacts
2	0	NDb	0	ND
3					0	ND	0	ND
4	3	0/50c	3	0/50	0d	0/50	2	0/50
5	4	0/50	4	0/50	1d	1/50	2	0/50
6					2d	0/50	2	0/50
7	4	9/50	3	8/50	4	0/50	2	0/50
9	4	26/50	4	25/50	4	0/50	3	0/50
11					4	1/50	3	0/50
12	4	48/50	4	45/50
14	4	49/50	4	50/50	ND	38/50	4	20/50
16					ND	47/50	ND	40/50
18					ND	50/50	ND	49/49
23					ND	12/12	ND	12/12
28	ND	10/10	ND	10/10
29					ND	12/12	ND	12/12
35					ND	10/10	ND	10/10
40	ND	10/10	ND	10/10
42	ND	10/10	ND	10/10	ND	20/20	ND	20/20

^aNumber of seeders = 4; number of contacts = 50.

^bND, not determined.

^cNumber positive per number sampled.

^dEnriched samples with two, three, and three positive samples in day 4, day 5, and day 6 seeders in experiment 3, respectively.

Samples were collected with sterile swabs and transported to the laboratory in modified Amies transport medium without charcoal (Probact transport swabs; Technical Service Consultants Ltd., United Kingdom). Swabs were directly streaked on CCDA (Oxoid CM739 plus SR155), incubated microaerobically at 42°C for 2 days, and examined for the presence of Campylobacter. The rest of the material on the swabs was pooled for the seeders and contact birds separately and enriched. In experiments 3 and 4, the samples of the seeders were enriched individually. Enrichment was in CCD broth (Oxoid CM963 plus SR155) microaerobically for 24 h at 42°C. Then, it was streaked on CCDA and incubated microaerobically at 42°C for 24 h and examined for the presence of Campylobacter. To exclude the possibility of infection from another source, the isolates were Penner serotyped as described by Jacobs-Reitsma et al. (18).

Quantification of transmission.

A susceptible-infectious (SI)-type model was used to describe the dynamics of transmission with time (3, 11). In such a model all individuals are considered to be identical and each individual can be in one of two stages: susceptible or infectious. The model then describes the changes in the fraction of individuals in the two states, with s(t) being the proportion of susceptible birds at time t and i(t) the proportion of infectious birds. The SI model assumes that once a bird becomes infected, it will remain infectious during the experimental period (16) and that contacts within the population are random. In addition, both classes S and I are assumed to be homogeneous, and the transmission rate is taken to be constant during the entire infectious period and equal for all infectious broilers.

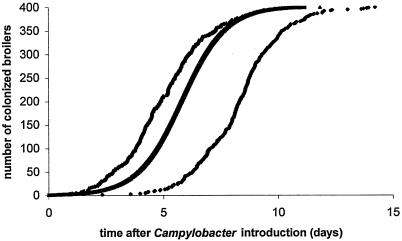
Susceptible birds are assumed to become infected at the rate of βs(t)i(t). The transmission rate parameter β can be defined as the average number of secondary cases caused by one infectious bird per time unit in a susceptible population (11). Although transmission between individuals is inherently a chance process, the dynamics in a large enough population can be approximated by a deterministic differential equation. In the case of the SI model we have the following equation: di(t)/dt = βs(t)i(t), of which the solution is the logistic curve i(t) = ce^βt/(1 + ce^βt), with c = i(0)/[1 -i(0)], i(0) being the proportion of infectious birds at t = 0. The curve is shown in Fig. 1.

FIG. 1.

Simulated course of Campylobacter infection in a population of 400 broilers, starting at t = 0. The middle curve is the deterministic (logistic) curve; the other two are random simulations. As can be seen, the deterministic and stochastic curves are similar, except for a time shift due to random effects in the initial phase of the outbreak.

The logistic i(t) curve led to logistic regression analysis to model the change in i(t) over time. A delay time (τ) was added to the model to account for a possible time shift in the start-up of the epidemic process caused by, for example, the experimental setup, the strains used, the inoculation dose, age, or stochastic effects. This resulted in the following model for the log-odds of i(t):

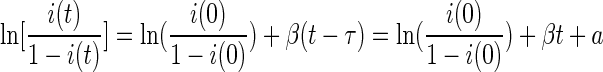The delay time reflects the time between inoculation of the seeders and the time when the first contact birds become infectious. This delay time is different from what is usually called lag phase (25), by which is meant the minimal age of the flock at which infections are observed in the field.

The model was fitted by a standard logistic regression, with ln[i(0)/(1 − i(0)] as offset, t as covariate, and a as intercept. The fit resulted in an estimate for β and for a, from which the delay τ was calculated as τ = −a/β.

Separate models were fitted for each experiment, resulting in four β values and four a values, and shared models were fitted in all possible combinations of these experiments, resulting in common β values for the different experiments. The Akaikes information criterion (7) was used to decide which model had the best fit and to see whether different values of β should be adopted for different (sets of) experiments.

As an example of how β can be used, we investigated the precision with which the moment of Campylobacter introduction can be estimated by regularly sampling the flocks. We simulated 10,000 outbreaks in flocks of 20,000 chicks with β = 1.04 (the estimation result) and starting at time t = 0. Simulations were carried out using the so-called Sellke construction (4): first, for each bird j a value Q_j is drawn from an exponential distribution with mean 1. Then, the epidemic is reconstructed by supposing bird j becomes infected when the cumulative infectiousness β∫₀^ti(u)du reached Q_j, with i(u) being the fraction of infected birds at time u. In this simulation, 10, 20, or 60 birds were sampled every 1, 3, 7, or 14 days, the time of the first sample having been randomly selected from the appropriate uniform distribution, and the number of infected birds at time t was recorded. The resulting proportion of infected birds at each sampling time was then used to carry out a logistic regression analysis, as described above, in which either β was fixed at 1.04 and only a was estimated (and consequently τ) or both β and a were estimated. Because every simulation started at t = 0, the estimated τ is the error made in estimating the time of Campylobacter introduction. Thus, the 10,000 simulations yielded estimation errors for each combination of sample size (10, 20, or 60) and sampling interval (1, 3, 7, or 14 days).

RESULTS

Course of infection.

Campylobacter was not detected in samples of water, feed, box liners, or wood shavings at the start of the experiments. In experiments 1 and 2, contact broilers became Campylobacter positive between days 5 and 7 (Table 2). In experiments 3 and 4, the first contact broilers became Campylobacter positive between days 9 and 11 and between days 11 and 14, respectively. Pooled samples enriched in CCD broth did not become positive before the first bird was positive in the direct culture assay. In experiment 3, between days 4 and 6 more seeders were found to be positive by the enrichment method than by the direct culture method (Table 2), but this did not change the estimate of transmission.

Quantification of transmission.

The logistic regression model was used to estimate β for each experiment separately and to estimate shared β values in all possible combinations. As the simplest model with a single β for all four experiments had one of the lowest Akaikes information criterion scores, there was no evidence that a more complex model was needed. The joint β was estimated at 1.04 per day with a standard error of 0.06, which means that after introduction of Campylobacter in a flock, each broiler will infect on average 1.04 new broilers per day. The estimated intercepts c were −2.57 (standard error [SE], 0.47), −2.77 (SE, 0.48), −6.06 (SE, 0.71), and −7.416 (SE, 0.78) for experiments 1, 2, 3, and 4, respectively. This resulted in estimated delay times of 2.4, 2.7, 5.8, and 7.1 days, respectively.

Because only four birds were initially inoculated, it was hypothesized that the observed delay times, and also the differences between the estimated delay times for the four experiments, were due to chance. Therefore, we tested whether the observed delay times were due to stochastic effects of the transmission process by simulating 10,000 transmission experiments with the stochastic version of the SI model, with β = 1.04, N = 400, and i(0) = 1/400 or 1/100. Simulations were carried out with the Sellke construction (3) as described above. For each simulation, we determined the delay time by comparing the time it took until i(t) = 0.5 with its deterministic expectation. Delay times were obtained for two different initial conditions, namely, four infected chicks, as in the experiment [i(0) = 1/100], and one infected chick, as an example of an extreme case of unsuccessful inoculation [i(0) = 1/400]. The 0.5, 2.5, 5, 50, 95, 97.5, and 99.5 delay time percentiles are shown in Table 3.

TABLE 3.

Expected delay times under two initial conditions: one or four inoculated chicks [I(0) = 1 or 4]^a

I(0)	Expected delay time for percentile
	0.5%	2.5%	5%	50%	95%	97.5%	99.5%
1	−1.69	−1.28	−1.09	0.36	2.89	3.57	5.13
4	−1.08	−0.82	−0.67	0.09	1.05	1.29	1.69

^aThe delay times depend on I(0) and not on population size.

The observed delay times were larger than the upper percentiles of the distributions with I(0) = 4 (four initially inoculated chicks), which was the actual initial condition of the experiments. Only if I(0) = 1 could the delay times of experiments 1 and 2 be explained by chance, but this was not the case for experiments 3 and 4. Therefore, it is likely that a mechanism other than chance was responsible for the observed delay times.

Table 4 shows the 90% intervals of the estimation errors when flocks of 20,000 chicks are regularly sampled to estimate the time of Campylobacter introduction. If β were assumed to be 1.04, then 1-day, 3-day, and 7-day sampling intervals had comparable errors, irrespective of whether 10, 20, or 60 samples were taken. Precision decreased only with a 14-day sampling interval. If there is no information on β, then more intensive sampling would be needed, in order to generate enough data to estimate β. Note that even the most precise estimate of the time of introduction may be wrong by 3 days, due to chance effects at the beginning of the infection chain.

TABLE 4.

Precision of determination of the time of Campylobacter introduction into a flock of 20,000 broilers, with different sample sizes and sampling intervals^a

Sample size	90% interval of estimation error
	β unknownb for sampling interval		β known (β = 1.04) for sampling interval
	1 day	3 days	1 day	3 days	7 days	14 days
10	−2.91, 4.42	−4.49, 3.97b	−1.13, 2.93	−1.31, 3.05	−1.72, 3.25	−3.71, 4.84
20	−2.13, 3.62	−3.04, 4.16b	−1.08, 2.88	−1.19, 2.94	−1.43, 3.11	−3.08, 4.34
60	−1.46, 3.09	−1.97, 3.70	−1.05, 2.87	−1.08, 2.89	−1.17, 2.91	−2.17, 3.68

^aDenoted are the 90% intervals of the estimated introduction times of 10,000 simulated outbreaks starting on day zero.

^bWith β unknown, the introduction time could not be estimated for sampling intervals of 7 or 14 days, in only 69% of the cases with 10 samples every 3 days, and in only 90% of the cases with 20 samples every 3 days.

We also estimated β from the experiments carried out by Stern et al. (33), who kindly provided their original data. They performed experiments with broilers aged between 4 and 42 days. We used the same SI model as above to estimate the transmission rate. The data did not allow an estimate for each age group (too few data), but the overall estimate of β was 1.13 day⁻¹ (SE, 0.04 day⁻¹), which is of the same order of magnitude as our estimate of 1.04 day⁻¹. The Stern data were more suitable than those of Shanker et al. (30), because Stern et al. (33) collected fecal samples more frequently at the start of the infection chain (days 3, 5, and 7).

DISCUSSION

The aim of this study was to quantify the transmission of Campylobacter spp. within broiler flocks. We estimated β from four experiments previously carried out by Jacobs-Reitsma et al. (19). The estimated β value was 1.04 day^-1, which was comparable to the value (β = 1.3 day⁻¹) we calculated using the data of Stern et al. (33), but it was higher than that reported by Hartnett et al. (15) for the data of Shanker et al. (30) (β = 0.1 to 0.3 day⁻¹). However, neither their method nor their assumptions were given explicitly. When we applied our analysis to the same data, the sampling frequency in the initial phase of colonization proved too low to allow for accurate estimation of the transmission rate.

In contrast to what is assumed to occur in the field, that is, that an infection starts with one infected bird, we started the infection with four seeders. We chose this approach to minimize the risk of an unsuccessful experiment due to a failed inoculation and the variability in the infection course, which would make it impossible to accurately quantify transmission. Starting with more than one seeder does not affect the parameter estimate, because the transmission rate is not related to the number of seeders but only depends on the number of infections and susceptible birds present. The parameter is an estimate on an individual broiler level and can be estimated properly, even when the infection starts with more than one infectious bird, but only given that a major outbreak is observed. Choosing four seeders is a compromise between guaranteeing this and staying close to a natural introduction (colonization of one bird).

Mathematical models are important tools for assessing the best means of containing an outbreak, and they help to clarify some of the associations between epidemiological factors (23). However, the assumptions on which a model is based should be examined carefully. The model we used assumed that the birds mixed randomly, which seems reasonable given the observations of Preston and Murphy (26). However, Hartnett et al. (15) interpreted the same data differently and assumed that broilers stay within a cluster and that clusters move. However, since our simpler mathematical model fit the experimental data well, we see no reason to introduce a more complicated model for contact structure.

The overall estimates of β did not differ significantly among experiments 1 to 4, indicating that despite various circumstances the infection processes run a similar course, but the delay time (i.e., time between inoculation of the seeders and the occurrence of the first contact infections) did differ. The delay time for experiments 1 and 2 was approximately 2 days and for experiments 3 and 4 about 5 to 7 days. Stochastic simulations with the SI model indicated that this delay time could not be explained by chance alone. In vitro passage and deep frozen storage of strains might have adversely influenced the initial colonization potential of the strains (22, 27, 30, 32, 35), whereas the colonization potential would be stronger after the strain had adapted to the alimentary tract of broilers, especially the seeders. This phenomenon, however, would be observed in all four experiments, as all strains were treated comparably, and so other explanations should be considered.

In experiments 1 and 2 cloacal swabs were analyzed, which might be a less sensitive method than analyzing cecal droppings, as performed in experiments 3 and 4; however, the correlation between the two methods is reported to be high (13). Since the detection limits were equal for individual birds within each experimental group, this difference does not affect the shape of the epidemic curve (Fig. 1) but shifts it to the left or right. If the exact dynamics of Campylobacter colonization and the detection limits are known, it would be possible to correct for this, but unfortunately this was not the case. The consequence of different detection limits would be that the differences in delay time between experiments 1 and 2 and experiments 3 and 4 are even larger than reported here.

Another possible explanation for the differences in delay times between the experiments is the use of different Campylobacter strains, as it is known from other studies that strains differ in their colonization capacities or transmissibilities (1, 8, 20, 35). This hypothesis might be investigated further. Also, the inoculation doses or the presence of maternal antibodies in the broilers of experiments 3 and 4 might explain the differences in delay time (28). However, all inoculation doses were rather high, and most inoculated chicks started shedding only a few days after inoculation. Therefore, it is not likely that the dose or antibodies caused the time delay in transmission. Thus, although there are several possible explanations, the exact cause of the difference in delay times needs to be investigated further. Because the transmission rate parameter β is not affected by the delay time, this parameter can still be used in further studies to evaluate control measures for their reduction of the transmission of Campylobacter or to determine the within-flock prevalence over time in the field.

As with all laboratory studies, there is the question to what extent findings can be extrapolated to the field situation. However, in this instance, the problem with extrapolation is only relevant for the start of the epidemic, when the first birds become colonized and when the prevalence is still low. In this phase of the epidemic, chance processes play an important role. However, our results suggest that once the infection is spreading, the time taken to go from a prevalence of 5% to 95% will be approximately the same in various situations, allowing extrapolation to the field, which is substantiated with observations in the field (6, 12). Thus, the random mixing model is robust for this phase of an epidemic, and there is no need to use a model with a more complicated contact structure.

A mechanistic model has several advantages: it forces users to identify key parameters, to provide a minimal set of mechanisms necessary to explain the data, and to state underlying biological assumptions. It may also facilitate the generation of new hypotheses (3, 11, 24). We have shown that the mathematical model fit the data of the experiments; we pinpointed the underlying assumptions and created hypotheses for the apparent delay times. Once a suitable model is available, validation of the model for field situations can be performed. Mathematical models have been used extensively to analyze epidemics of infectious diseases (3, 10, 11, 21, 23, 24, 31). The information they generate provides insight into the course of epidemics and can be used in attempts to reduce the incidence of various infectious diseases. Especially in the case of fast-spreading infections like Campylobacter, gathering quantitative information on field infections can be a helpful tool in the evaluation of interventional measures. Knowledge of epidemiological mechanisms and parameters underlying Campylobacter transmission in broiler flocks is important for the evaluation and development of control strategies, because it enables us to determine which measures can reduce transmission and whether the magnitude of the effect is sufficient to reduce transmission or to postpone introduction, which in turn decreases the prevalence in a flock and subsequently the exposure of humans to Campylobacter via contaminated poultry products.