Hairpin folding rates reflect mutations within and remote from the turn region

Abstract

Hairpins play a central role in numerous protein folding and misfolding scenarios. Prior studies of hairpin folding, many conducted with analogs of a sequence from the B1 domain of protein G, suggest that faster folding can be achieved only by optimizing the turn propensity of the reversing loop. Based on studies using dynamic NMR, the native GB1 sequence is a slow folding hairpin 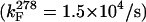. GB1 hairpin analogs spanning a wide range of thermodynamic stabilities 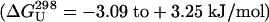were examined. Fold-stabilizing changes in the reversing loop can act either by accelerating folding or retarding unfolding; we present examples of both types. The introduction of an attractive side-chain/side-chain Coulombic interaction at the chain termini further stabilizes this hairpin. The 1.9-fold increase in folding rate constant observed for this change at the chain termini implies that this Coulombic interaction contributes before or at the transition state. This observation is difficult to rationalize by “zipper” folding pathways that require native turn formation as the sole nucleating event; it also suggests that Coulombic interactions should be considered in the design of systems intended to probe the protein folding speed limit.

Protein engineering experiments indicate that β-hairpins appear as transition-state features in numerous folding pathways. Hairpin redesign has resulted in changes in protein-folding mechanisms (1), and hairpin stabilization can accelerate (1–3) or retard (2, 4) protein folding. The protein-folding problem continues to be of high interest for at least three reasons: predicting structures from genome-derived sequences, improving a priori protein-fold design, and enhancing our understanding of the mechanisms of protein misfolding diseases (6, 7). Folding rates have been of particular interest, with more examples of redesigned proteins that fold near the calculated protein-folding speed limit (8) appearing regularly. For β-sheet proteins and β oligomers (as found in amyloid fibrils formed from misfolded protein states), hairpin dynamics play a key role.

Although there is an increasing body of data on hairpin folding dynamics (9–15), with one exception these have not included a set of probing mutations to address specific questions. That exception (14) suggests that loops with a greater turn preference accelerate folding to a much greater extent than the optimization of hydrophobic interactions in the folded state. Other data (12) suggest that the length of the loop connecting the hydrophobic residues that form hairpin-stabilizing cross-strand interactions is reflected in the folding rate. Throughout, hairpin folding has been modeled as a two-state equilibrium. Whether hairpin/coil transitions are 1-μs versus 50-μs events has significant consequences. Peptide helix nucleation is a sub-μs event (10, 16, 17), which allows helix formation to be a preequilibrium event relative to the hydrophobic-collapse stage of protein folding. Can rapid formation of stable hairpins in the unfolded states of nascent proteins serve in a similar fashion? If so, hairpin optimization could be an evolutionary criterion for improving the efficiency of protein folding. Alternatively, is hairpin formation restricted to a transition state role in β-sheet folding?

Essentially all folding rate constants in the 10⁴ to 10⁷/s range have been derived from fluorescence- or IR-monitored temperature jump experiments (12, 13, 18, 19). Two groups have recognized the potential of NMR spectroscopy to probe 10- to 50-μs exchange phenomena (20–22). Raleigh and colleagues (22) extended lineshape analysis to protein-folding transitions with fast exchange on the chemical shift time scale; in a favorable case, rate constants as fast as 2 × 10⁵/s were accessible. We now report that the large structuring shifts observed for hairpin peptides, in combination with an internal referencing method for extracting differential exchange-broadening measures (ΔΔ^ex), allows NMR line broadening methods to quantitate the microsecond time constants needed for studying fast hairpin folding.

The second hairpin of the B1 domain of protein G (GB1p), residues 41–56 (23, 24), was the first hairpin to be examined extensively, and a folding time constant, (k_F)^-1, on the order of 6 μs was reported in 1997 (9). We recently prepared a series of more stable GB1 hairpin analogs with melting temperatures in the 47–85°C range (25). Extensive spectral comparisons with the more stable analogs that retain the identical hydrophobic cluster revealed that GB1p is <30% folded at 25°C. These studies also established that the folding equilibria of these GB1 analogs, like that of the tryptophan zipper peptide (trpzip) analogs (26) studied previously, can be modeled as two-state processes.

Materials and Methods

Materials. Analogs GB1m2 and m3 were available from a previous study (25). GB1p and additional analogs were synthesized on an Applied Biosystem 433A synthesizer by using standard fluorenylmethoxycarbonyl solid-phase peptide synthesis methods and displayed the expected molecular weights by ion-trap MS (see Supporting Text, which is published as supporting information on the PNAS web site). Sequence and purity were verified by ¹H NMR.

NMR Spectroscopy. Samples for 2D spectra consisted of ≈1.5 mM peptide in 20 mM (pH 6–7) phosphate buffer (in 10% or 99.96% D₂O) with 2,2-dimethylsilapentane-5-sulfonic acid as the internal chemical shift reference. All NMR experiments were collected on either Bruker (Billerica, MA) DRX-500 or DMX-750 spectrometers. Peptide H_N and Hα resonances could be assigned through a combination of 2D total correlation spectroscopy and NOESY experiments; the resulting backbone-resonance chemical shift deviations (CSDs) were concordant with the previous correlations (25) of these CSDs with fold population. 1D spectra used for extracting exchange-broadening data, with peptide concentrations 0.8–1.2 mM, were the average of 1,024 scans acquired at a resolution of 32,768 and 16,384 points for the 750- and 500-MHz spectrometers, respectively. As a check for self-association effects, GB1p was also studied at a concentration of 180 μM.

Extracting Folding/Unfolding Rates from Exchange Broadening Data. In a rapid equilibrium between a folded state, F [with lifetime τ_F, τ_F = (k_U)^-1], and an unfolded state ensemble (U, where χ_U is the equilibrium mole fraction of the U state), exchange broadening (Δ^ex) can provide the dynamics of the exchange process when the chemical shift difference between the folded and unfolded state environments (Δν, in Hz) and the equilibrium constant are known. We obtain Δ^ex by comparing the lineshape characteristics of pairs of doublet signals, only one of which has a large Δν. The unfolding rate constants are calculated by Eq. 1 (27).

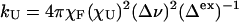[1]

The background theory and methods are detailed in Supporting Text.

Results

The present study is limited to GB1 analogs that retain the central portion of the native strands and thus the native hydrophobic cluster in the folded state. The sequences examined (and that of trpzip4) appear in Table 1 in order of increasing fold stability.

Table 1. Sequences examined.

Sequence	1	6	12	Tm, °C	ΔGU298, kJ/mol
GB1p	GEWTY-DDATKT-FTVTE			<0	—3.09
	(in D2O)			1—10	—2.08
(D7P)-GB1p	GEWTY-DPATKT-FTVTE			26—38	+0.52
	(in D2O)			38—44	+1.59
GB1m2	GEWTY-NPATGK-FTVTE			37—45	+1.53
GB1m3	KKWTY-NPATGK-FTVQE			54—60	+3.25
trpzip4	GEWTW-DDATKT-WTWTE			65—71	+6.6

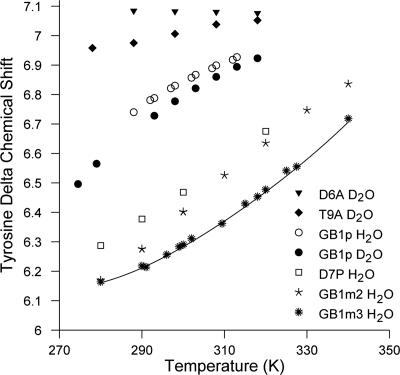
The native hydrophobic cluster contains two chemical shift probes of folding. Kobayashi and coworkers (23, 28–30) have long recognized the value of the Tyr-5–Hδ and Val-14–Hγ_up resonance shifts for measuring the folding equilibrium of GB1 hairpin analogs. In our recent examination of more stable analogs this continued to be the case. The melting temperatures listed in Table 1 include those from all available spectroscopic probes; the 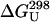values are the average of the values based on the Tyr-Hδ and Val-Hγ_up melting curves. The chemical shift melts for Tyr-Hδ appear in Fig. 1 and are consistent with a common unfolded shift value of ≈7.08 ppm, which is also the accepted random-coil value. For purposes of calculating the equilibrium populations, χ_F and χ_U, we assumed a common, temperature invariant shift of 6.02 ± 0.07 ppm for the folded state. At both 500- and 750-MHz ¹H NMR observation, the resulting structuring shifts are large enough to give measurable signal broadening (Fig. 2 and Fig. 4, which is published as supporting information on the PNAS web site). The corresponding analysis of Val-Hγ_up shift melts (Fig. 5, which is published as supporting information on the PNAS web site) and additional support (congruent melting behavior of multiple chemical shift probes throughout the sequence) for our assumption of two-state folding for GB1 hairpin analogs appear in Supporting Text. In support of our chemical shift assignments for the Tyr-Hδ/Hε and the two Val-Me signals in the folded and unfolded states, we find that the measured exchange broadening for all four probe resonances is proportional to (Δν)².

Fig. 1.

The temperature dependence of the chemical shifts of Tyr-Hδ for the GB1 hairpin analogs examined in this article and reported in the literature. The D6A and T9A mutants of GB1p do not form a measurable hairpin population (29). A fitted line is included for GB1m3, the most folded analog examined.

Fig. 2.

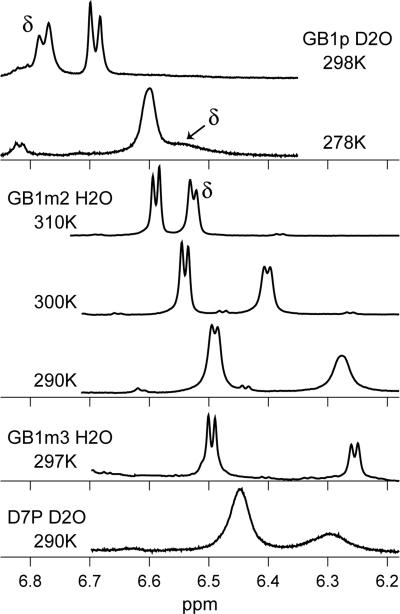
NMR traces demonstrating differential broadening of the Tyr-Hδ versus the less shifted Hε signal; all data were collected at 750 MHz. When the folded fraction exceeds 0.45, Hδ appears upfield of Hε, rather than at its more downfield random-coil position. The peptide analog, temperature, and solvent are shown for each trace. The spectra shown for GB1p are identical to those published in the literature (30).

In our kinetics analyses we compare the line broadening of the Tyr Hδ and Hε signals, deriving the differential broadening (ΔΔ^ex) by comparisons with spectral simulations (Fig. 6, which is published as supporting information on the PNAS web site) for a doublet with an 8.0-Hz coupling constant and varying amounts of added broadening (Δ^total). Representative NMR data for the Tyr-Hδ/Hε pair appear in Fig. 2. The trace shown for GB1m3 corresponds to ΔΔ^ex = 2.6 Hz. The smallest ΔΔ^ex values that were considered significant were on the order of 0.5 Hz for the Tyr signal pair, these afford sub-μs relaxation time constants (τ_ex). Fig. 2 clearly shows the low fold population and slow folding of GB1p. When the same extent of unfolding is observed (for GB1m2) at higher temperatures, the more stable species display less line broadening. Differential broadening parameters for GB1p and its analogs over a range of conditions appear in Table 3, which is published as supporting information on the PNAS web site. We calculate the exchange broadening for Tyr-Hδ exclusively from the NMR data. The scaling factor between 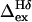and Tyr-Hδ/Hε ΔΔ^ex, [R²/(R² - 1)] with R = (Δν_Hδ)/(Δν_Hε), is measured for each experiment: R is the ratio of the slopes of the δ versus T plots for Hδ and Hε. Folding and unfolding rate constants were derived by using Eq. 1. Both the experimental errors (uncertainty in ΔΔ^ex) and errors associated with the equilibrium constant calculation (the uncertainty in the folded shift value) were propagated through the rate constant calculations. For GB1m2 (and particularly GB1m3) at low temperatures, the error associated with the equilibrium constant and Δν_Hδ dominate. At higher temperatures, the uncertainty in ΔΔ^ex dominates.

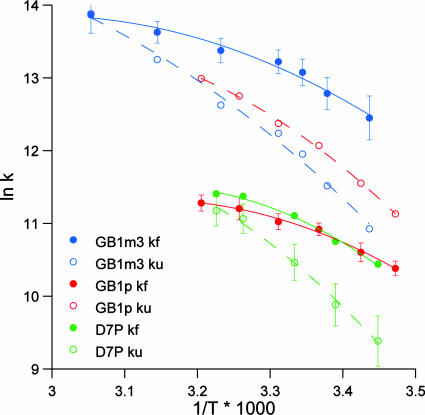
At the low temperature limit (278 K), the GB1p folding rate constant is, for such a small structure motif, remarkably slow (1.46 ± 0.11 × 10⁴/s). Arrhenius plots for the folding and unfolding of three GB1 hairpin sequences appear in Fig. 3. The plots include GB1p (the least stable system) and GB1m3 (the analog with the greatest thermodynamic fold stability). The D7P mutant provides an example of the dramatic effect of a single site mutation. For the D7P mutant, the thermodynamic stability increase is caused exclusively by a decrease in the unfolding rate constant. In contrast, the fold-stabilizing effect associated with the GB1p to the GB1m2 and GB1m3 mutants can be characterized as an acceleration of folding and an increase in the temperature dependence of k_U. In an Arrhenius plot, the latter corresponds to an increase in the energy of activation for unfolding. This expectation is reasonable for a two-state process with little change in the unfolded state energy and a more stable folded state. In the illustrated plots, and for all GB1 analogs examined to date, the Arrhenius plots for k_F are rather shallow and display greater curvature than the corresponding, steeper plots for k_U. Even greater curvature, with an actual decrease in k_F at higher temperatures, has been observed (14) for trpzip4, a particularly stable hairpin of this class. Thus, it is safe to assume that hairpin folding is hydrophobically driven in these peptides, with significant burial of apolar surface area at the transition state. For discussion, we have calculated the folding and unfolding parameters at 298 K (Table 2). Because the data indicate a nonzero ΔCp, the activation enthalpy estimates are based on the instantaneous slopes at 298 K.

Fig. 3.

Representative folding dynamics shown as Arrhenius plots of the folding (filled symbols) and unfolding (open symbols) rate constants: GB1p and GB1m3 in H₂O and the D7P mutant of GB1p in D₂O. Error bars (±1 SD) are shown on the folding plots for GB1p and GB1m3 and the unfolding plot for the D7P mutant. In the case of D7P, points were alternately from 500-MHz (T = 295, 306.5 K) and 750-MHz spectra (T = 290, 300 K). The excellent agreement over this set attests to the absence of broadening caused by oligomer formation.

Table 2. Folding rates and energies of activation for GB1 analogs at 298 K.

		Folding at 298 K		Unfolding at 298 K
Analog, solvent	ΔGU298, kJ/mol	kF, 104/s	Energy of activation, kJ/mol	kU, 104/s	Energy of activation, kJ/mol
GB1p	—3.1	5.5	29	18.2	59
GB1p*	—2.2	6.4	42	16.0	72
D7P*	+1.9	5.9	43	2.9	76
GB1m2	+1.8	21.5	(68)	11.0	(108)
GB1m3	+3.2	41†	50	12.7	84
trpzip4*	+6.6	6.7†	(36)‡	0.43	90

All data are at pH = 6—7 in H₂O unless otherwise indicated. With the exception of trpzip4 (reported at 24°C rather than 25°C) the data are from the present study and derived exclusively from the Tyr⁵-Hδ probe. All trpzip4 data are taken from Du et al. (14). Parenthetic energy of activation values are instances in which the error in rate constants or gaps in the data require extensive interpolation or extrapolation, precluding an accurate determination.

^*Data reported are for D₂O solution

^†At 327 K, the folding rate constant for GB1m3 was 104 × 10⁴/s, the largest value measured. The rate constant for trpzip4 at this temperature is 24 × 10⁴/s [from figure 5 of Du et al. (14)]

^‡This is an extrapolation from 310 K [from figure 5 of Du et al. (14)]

The folding time constant derived for GB1p at 298 K (1/k_F = 17–20 μs) is 3-fold greater than that reported in the literature (9); half of the difference is accounted for by the revision in the applicable equilibrium constant. With the exception of the D7P mutant, the more stable analogs display significantly larger folding rate constants. Our NMR method provided folding rate constants as fast as 10⁶/s (k_ex = 2 × 10⁶/s). In the best case, GB1p (which was examined in duplicate), the rate constant errors are less than ±8% but they increase to ±16% for the fastest folding system (GB1m3). The energy of activation errors are more difficult to assess. In the best cases, the precision is judged to be better than ±10% or 4 kJ/mol (whichever is larger). Even though the extraction of specific rate constants has some intrinsic limitations when k_ex exceeds 6 × 10⁵/s, and obtaining accurate activation enthalpies by this method is problematic, the values in Table 2 do provide a basis for discussing structural effects on hairpin dynamics. The data for trpzip4 are included for comparison.

Discussion

To date there have been very limited data on the relationship between hairpin fold stability and folding dynamics, in large part reflecting the lack of rate determinations for series of hairpin analogs with specific, but limited, mutations. A recent study focused on five trpzip (26) analogs that differ only in the reversing loop (turn) region and included the prior literature data for GB1p in the comparison (14). Du et al. (14) concluded that loop mutations that provide hairpin stabilization do so by accelerating folding, rather than retarding unfolding. The GB1p/trpzip4 dynamics comparison led them to conclude that improvements in the cross-strand hydrophobic cluster do not increase the folding rate constant; rather, they effect decreased unfolding. The latter conclusion remains intact with the present data (Table 2): the enhanced stability associated with incorporating additional indole rings in the hydrophobic cluster results from a 37-fold unfolding rate retardation.

The conclusion regarding loop mutations, however, needs to be modified. In the present series, the D7P mutation is a stabilizing loop mutation and results in a 5.5-fold decrease in the unfolding rate constant. A Pro insertion was also examined by Du et al. (14); replacing an EGNK loop with a hairpin stabilizing, and turn favoring, E-d-Pro-NK loop resulted in a 4-fold increase in the trpzip folding rate constant. This mutation replaces a f lexible glycine with a conformation-restricting d-Pro, which is favored at this site in a type II′ β turn. Du et al. argue that the rate acceleration is caused by the conformational rigidity of d-Pro (which reduces the entropic penalty for turn formation). In a computational folding simulation, the rigidity of a proline at a turn locus has resulted in folding frustration caused by kinetic traps (13). The GB1p to GB1m2 change also represents a stabilizing loop mutation (DDATKT → NPATGK, ΔΔG_U = 4.6 kJ/mol) and includes the D7P mutation. In this case, the predominant effect is an increase (4-fold) in the folding rate constant. Does folding acceleration represent the greater compensating effect of a flexible glycine versus the restrictive proline, even though both are fold stabilizing? The conflicting results for a four-residue versus six-residue loop can be rationalized if the d-Pro-Asn locus reduces the configurational possibilities of the shorter loop to a much greater extent and biases the unfolded state toward conformations that are predisposed to turn and hairpin formation.

The GB1m2 to GB1m3 mutation (ΔΔG_U = 1.4–1.7 kJ/mol) provides a previously unavailable probe of the effects of terminal Coulombic interactions upon dynamics. In this mutation, only the chain ends are altered: (GE—TE) is modified to (KK—QE). Viewed from the perspective of the folded state, this mutation replaces a potentially repulsive Coulombic interaction (the side chains of E2 and E16) with the possibility of additional attractive interactions. The net fold stabilization largely reflects a 1.9-fold increase in the folding rate constant. We suggest that this rate increase requires these Coulombic interactions be present before or at the folding transition state. There are two distinct views of the mechanism of hairpin formation. To be consistent with “zippering” hairpin folding models, with nucleation initiated by turn formation (31, 32), an extremely late transition state with ordering to the ends of the β strands would be required. In an early collapse folding scenario (12, 33, 34), the change in the Coulombic interactions at the chain termini could exert an effect on the loop search required to establish the hydrophobic cluster: chain end repulsion in all of the analogs besides GB1m3 could be a factor in determining the folding rates. Because Coulombic interactions occur over longer distances than attractive van der Waals interactions, these could provide an effective barrier to visiting conformations that can lead to early hydrophobic cluster formation. Likewise, if the hydrophobic cluster forms before full definition of the turn conformation, the attractive interactions between the chain termini of GB1m3 could have the opposite effect, and thus increase the folding rate constant. In any case, the growing database of hairpin folding rates still does not provide a clear-cut distinction between the alternative folding mechanisms. Indeed, the mechanism may change both with loop size and for short loop sequences with unusually strong equilibrium preferences for turn-like conformations.

With the present article, the range of folding time constants for [4:4]-hairpins now spans from 3 to 20 μs; that for [2:2]-hairpin is even larger, from 0.83 (13) to 52 μs (14). In the case of [2:2]-hairpins, it has been established that folding can be accelerated by prior collapse [starting from a cold-denatured state (15)] or cyclization (35). Less is known for the common [3:5]-hairpin motif of proteins. The single peptide model examined by temperature jump methods was a fast-folder [0.8 μs (11)]. The FBP28 WW domain, with a five-residue loop, folds faster than comparable forms with a six-residue loop, and this folding acceleration can be moved to other sequences by loop substitution.† Fast folding may not, however, be a universal feature for these Gly bulge turns. In a study of trpzip analogs with Gly bulge turns, Blandl et al. (36) noted extreme exchange broadening of signals with large structuring shifts. It appears that fast folding requires not only a significant turn propensity but also a proper matching of turn geometry with the specific cross-strand interactions required for hairpin stabilization. To these loop optimization considerations we can now add mutations at the extreme termini of hairpins as another strategy for increasing the rate of hairpin formation. Properly positioned Coulombic attractions may represent an additional design element in protein folding optimization.

The internal referencing method for extracting exchange broadening presented herein extends the reach of dynamic NMR experiments to, and possibly beyond, the μs limit. This method should prove very useful because these NMR experiments are not technically demanding and less subject to instrumental artifacts than laser-induced temperature jump experiments. Their application requires NMR probes that display structuring shifts approaching (or greater than) 1 ppm and is limited to conditions in which the unfolded state is significantly populated (χ_U ≥ 0.1). In addition, the extraction of folding and unfolding rate constants always requires a two-state folding assumption and relies on the equilibrium constant. For miniproteins and peptide models of secondary structure, the latter raises a caveat. Such systems display broad, low enthalpy melting transitions and complete sigmoidal melting curves are rarely available. Although statistical coil norms can be used for the expectation values for the unfolded state, the chemical shifts that represent 100% folding will be, in almost all cases, conjectures rather than firm experimental values. Even when chemical shifts appear to be leveling out at low temperatures for the most stable member of a series of analogs, one cannot eliminate the possibility that such an observation represents a broad inflection point, where the hot and cold denaturation transitions meet, and cannot be equated with >90% folded. This potential source of error typically leads to underestimation of k_F.‡ However, for comparative studies within a series of analogs, so long as the structuring shifts are large and the mutations do not produce any significant change in Δν, linewidth observations over the χ_U = 0.20–0.65 range will give relative folding rate constants suitable for the analysis of the sequence dependence of folding dynamics. We expect that this method will play a prominent role in the studies of the fast-folding limit (8) for proteins.