Cyclic electron transfer in plant leaf

Abstract

The turnover of linear and cyclic electron flows has been determined in fragments of dark-adapted spinach leaf by measuring the kinetics of fluorescence yield and of the transmembrane electrical potential changes under saturating illumination. When Photosystem (PS) II is inhibited, a cyclic electron flow around PSI operates transiently at a rate close to the maximum turnover of photosynthesis. When PSII is active, the cyclic flow operates with a similar rate during the first seconds of illumination. The high efficiency of the cyclic pathway implies that the cyclic and the linear transfer chains are structurally isolated one from the other. We propose that the cyclic pathway operates within a supercomplex including one PSI, one cytochrome bf complex, one plastocyanin, and one ferredoxin. The cyclic process induces the synthesis of ATP needed for the activation of the Benson–Calvin cycle. A fraction of PSI (∼50%), not included in the supercomplexes, participates in the linear pathway. The illumination would induce a dissociation of the supercomplexes that progressively increases the fraction of PSI involved in the linear pathway.

It is widely assumed that the photosynthetic process in algae or plants operates according to two nonmutually exclusive modes: linear and cyclic electron flows. In the linear mode, electrons are transferred from water to the NADP via the three major complexes of the photosynthetic chain, Photosystem (PS) II, cytochrome b₆f (cyt bf), and PSI (1). Little is known, however, about the mechanism of the cyclic process that was first characterized by Arnon (2) in broken chloroplasts. In unicellular algae, a cyclic electron flow operates in anaerobic conditions (3, 4). In higher plants, the occurrence of a cyclic flow in vivo is a subject of controversy (reviewed in refs. 5 and 6). On the basis of a parallel measurement of PSI and PSII yield, Harbinson and Foyer (7) concluded that a cyclic process operates at a significant rate during the induction period but not in steady-state conditions. Heber et al. (8) reported that a decrease of CO₂ concentration stimulates the cyclic flow. At variance, Klughammer and Schreiber (9) conclude that no significant cyclic flow contributes to PSI turnover during the induction period or in the absence of CO₂. It is generally reported that in steady-state conditions in the presence of CO₂, the linear pathway is largely favored with respect to the cyclic flow. Bendall and Manasse (6) concluded that the rate of the cyclic process is no more than 3% of that of the linear pathway.

It is agreed that both PSI and cyt bf complexes are involved in the cyclic flow. Yet, the mechanism of electron transfer between the PSI acceptor side and the cyt bf complex is not clearly identified. It has been proposed that reduced ferredoxin (Fd) or NADP may transfer electrons to plastoquinone (PQ) by way of a membrane-bound Fd PQ-reductase or NADP dehydrogenase (NDH). Plastoquinol (PQH₂) is then reoxidized at the PQH₂-oxidizing site Q_o of the cyt bf complex. This hypothesis involves a membrane protein with functional properties similar to the bacterial or mitochondrial Complex I. Indeed, genes encoding subunits similar to those of Complex I have been identified in the chloroplast genome of higher plants (10). Recent data suggest that Fd PQ-reductase and NDH could be involved in two parallel cyclic pathways (11, 12). However, as pointed out by Sazanov et al. (13), the low concentration of NDH (<0.01 per photosynthetic electron chain) makes its involvement in an efficient cyclic pathway unlikely. Alternatively, electrons may be transferred from PSI to the high-potential cyt b localized on the stromal side of the cyt bf complex. This transfer could involve either Fd alone or an additional stromal enzyme able to bind the cyt bf complex, for instance Fd-NADP-reductase (FNR), which stoichiometrically copurifies with the cyt bf complex (14, 15). It has been proposed that the cyclic electron transfer chain can be organized in supercomplexes that associate PSI, cyt bf, and FNR (reviewed in ref. 16). Indeed, complexes that associate PSI and cyt bf complex have been evidenced with solubilized membranes in upper plants (17) or in Chlamydomonas (18). On the basis of a mathematical modeling of the electron transfer process, Laisk (19) supported the involvement of supercomplexes associating PSI, FNR, and cyt bf complex. There is a general agreement that ∼90% of PSII is localized in the appressed region whereas PSI is localized in the stroma lamellae (20, 21). The cyt bf complex is about equally distributed between these two regions (22). On the basis of a kinetic analysis of fluorescence and oxygen emission, it has been proposed (23, 24) that membrane proteins in the appressed region act as a barrier to the diffusion of PQ, creating isolated domains of various sizes, including an average of 3–4 PSII centers. It excludes the involvement of PQ in the long-range electron transfer between membrane domains. As a major consequence of the restricted diffusion of PQ, the linear electron flow should involve exclusively those cyt bf complexes localized in the appressed region. The connection between the appressed and nonappressed regions would be insured by the long-range diffusion of plastocyanin (PC). Conversely, cyclic electron flow would involve cyt bf complexes included in the nonappressed domain.

In this article we present a kinetic analysis of the linear and cyclic electron flows performed in spinach leaf. Although most of the experiments reported in the literature are performed in light-adapted conditions, the experiments reported here are performed during the induction phase, which follows a period of dark adaptation. We conclude that, in these conditions, the concentration of ATP is limiting and an efficient cyclic process generates the ATP needed for the activation of the Benson–Calvin cycle.

Materials and Methods

Experiments have been performed in fragments of market spinach leaf. When needed, the leaf fragment was infiltrated by depression with water (control), inhibitors, or uncouplers.

Spectrophotometric Measurements.

These measurements were performed with an apparatus similar to that described (25, 26). In Figs. 1–4, 4 experiments have been averaged for each kinetics, which lead to noise level of ΔI/I ∼ 5 × 10⁻⁶. A dye laser pumped by the second harmonic of an Nd Yag laser (695 nm, total duration 6 ns) provided actinic flashes. The light-detecting diodes were protected from scattered actinic light by a BG39 Schott (Mainz, Germany) filter. Continuous actinic illumination was provided by a laser diode SDL (500 mW, emission peak at 690 nm). Membrane potential changes were measured by the difference (518 nm − 546 nm) (27). This difference eliminated minor additional spectral changes and light-scattering changes that were induced by the continuous illumination. Membrane potential changes induced by the single-turnover saturating laser flash were measured in a dark-adapted young spinach leaf infiltrated with water or with 20 μM 3-(3,4-dichloro-phenyl)-1,1-dimethylurea (DCMU) and 1 mM hydroxylamine. The absorption changes were ΔI/I (518 nm − 546 nm) = 4.25 × 10⁻³ and 2.2 × 10⁻³ in the absence and in the presence of PSII inhibitors, respectively. We conclude that PSI and PSII centers are present at a similar concentration. Cyt f redox changes are measured as

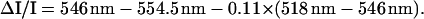The difference (546 nm − 554.5 nm) eliminated the contribution of the C₅₅₀ absorption change (28); the absorption changes associated with the membrane potential [0. 11 × (518 nm − 546 nm)] were subtracted from this difference.

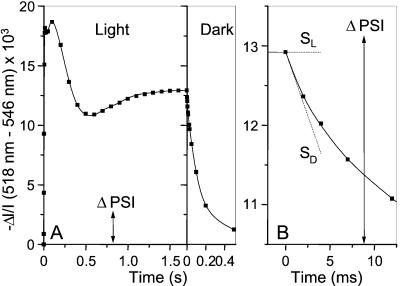
Figure 1.

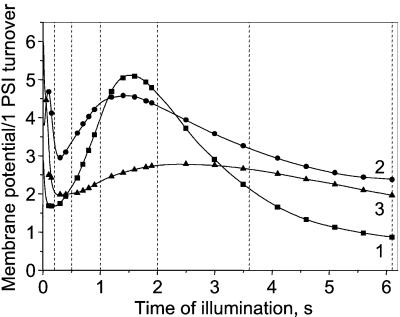
(A) Membrane potential changes induced by a saturating continuous illumination (ki_PSII ∼ 500 s⁻¹, ki_PSI ∼ 2000 s⁻¹). The leaf is submitted to cycles of 1.7 s of light and 6 min of dark. The amplitude of the absorption changes associated with the transfer of one charge across the membrane (one PSI turnover) is ΔI/I = 2.74 × 10⁻³ (arrow). This measurement has been performed under conditions where PSII is inactive (20 μM DCMU + 1 mM hydroxylamine). (B) Enlarged view of the kinetics of membrane potential changes at the time the light is switched off. Dashed lines S_L and S_D, slopes before and after switching off the light. (S_L − S_D) ∼0.32 s⁻¹, expressed in ΔI/I units/s.

Figure 4.

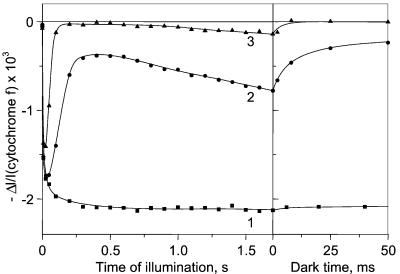
Cyt f redox changes induced by a saturating continuous illumination. The leaf is submitted to cycles of 1.7 s of light and 6 min of dark. Curve 1, 25 μM DCMU; curve 2, control infiltrated with water; curve 3, 2 μM antimycin A.

Fluorescence Measurements.

The actinic beam (green light-emitting diodes HLMP-CM15) was concentrated on ∼20 mm² of the leaf fragment, and the fluorescence was detected from the opposite face of the sample. The time resolution of the method was 30 μs. The estimate (within 10%) of the actinic light intensity was obtained by measuring the fluorescence induction kinetics in the presence of a saturating concentration of DCMU. We measured the time t at which the variable fluorescence yield was ∼2/3 of the variable maximum yield. As shown in ref. 29, an average of 1 photon per PSII center is absorbed at time t, and the PSII photochemical rate constant ki_PSII is thus equal to 1/t.

Results

The following strategy has been developed to determine the rates of the linear (R_linear) and cyclic (R_cyclic) flows. The sum R_ph of the photochemical rates R_PSII + R_{PSI linear} + R_{PSI cyclic} (expressed as the number of turnovers per reaction center and per s) has been measured by the rate of the light-induced formation of the membrane potential (Figs. 1–3). R_PSII is computed from the fluorescence yield measurements (Figs. 5 and 6). After completion of the initial fluorescence rise, the rate of the linear electron flow reaches a quasi steady-state value that is limited by the rate of oxidation of the PSI acceptors by the Benson–Calvin cycle. In these steady-state conditions,

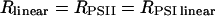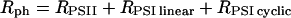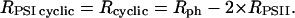Figure 3.

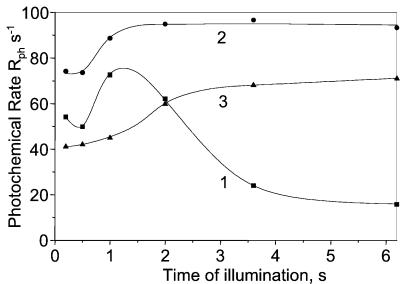
R_ph as a function of the time t of illumination computed from the data of Fig. 2. R_ph is computed by the difference of the slopes measured before and after the light is switched off (as shown in Fig. 1B) at times t indicated by the dashed lines in Fig. 2. Curves 1–3 same conditions as curves 1–3 in Fig. 2.

Figure 5.

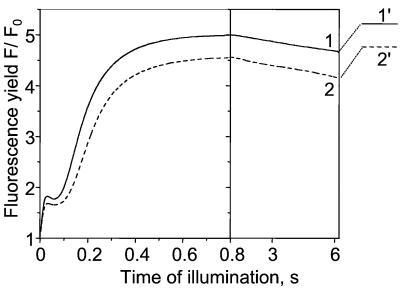
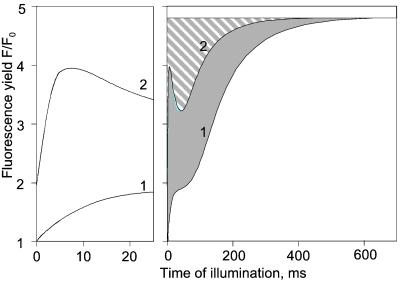
Kinetics of the fluorescence yield F/F₀ in a leaf infiltrated with water. F₀, dark-adapted fluorescence yield. After 6.2-s illumination (ki_PSII ∼84 s⁻¹), a 200-ms pulse of strong light (ki_PSII ∼1600 s⁻¹) that fully reduces Q_A is given. Curve 1, the leaf is dark-adapted for 6 h. Curve 2, the same leaf as for curve 1 is submitted to repetitive cycles (>3) of 6.2 s of light and 7 min of dark. 1′ and 2′, maximum fluorescence yield F_max reached at the end of the 200-ms pulse for curves 1 and 2, respectively.

Figure 6.

Same as Fig. 5, but with a leaf infiltrated with 1.5 μM antimycin A.

Determination of R_ph.

Fig. 1A shows the time course of the membrane potential changes induced by a saturating continuous illumination in a noninfiltrated young leaf submitted to repetitive cycles of 1.7 s of illumination and 6 min of dark (curve 1). During the illumination periods, the membrane potential undergoes complex kinetic changes, which reflect changes in the photochemical rate R_ph, in the rate R_bf of the membrane potential formation by the cyt bf turnover, and in the rate R_leak of ion leaks (either passive or by way of ATPase). The rate of the membrane potential change is R_ph + R_bf − R_leak. When the light is switched off, R_ph immediately falls to zero whereas R_leak and R_bf are unchanged, as discussed in the next paragraph. Thus, R_ph is proportional to the difference (S_L − S_D) between the slopes measured immediately before (S_L) and after (S_D) the light is switched off. In the case shown in Fig. 1B, the light-induced membrane potential reaches a quasi steady-state value, which leads to S_L∼0. R_ph, computed by dividing (S_L − S_D) by the absorption change induced by the transfer of one charge across the membrane, is 0.32/2.74 × 10⁻³ = 117 s⁻¹.

Fig. 2 shows the kinetics of the light-induced membrane potential changes measured with a mature spinach leaf. The time dependence of R_ph is shown Fig. 3. R_ph has been computed for different times of illumination as the difference between the slopes measured before and after the light is switched off following the procedure described in Fig. 1B. In Fig. 2 (curve 1) the leaf is infiltrated with 20 μM DCMU. After ∼1.5-s illumination the membrane potential reaches a peak value of 5.2 that corresponds to ∼130 mV, assuming that a single charge separation induces a membrane potential of ∼25 mV (30). Because no PSII activity is expected in the presence of DCMU, the large membrane potential increase developed between 100-ms and 1.5-s illumination is exclusively associated with PSI turnover and thus reflects an efficient cyclic electron process. In the same time range, R_ph (Fig. 3, curve 1) increases by ∼30% to reach a maximum value of ∼75 s⁻¹, which we ascribe to the cyclic process. Beyond ∼1.5-s illumination, R_ph slowly decreases to a steady-state value of ∼15 s⁻¹. When the leaf is infiltrated with water (curve 2), R_ph reaches a constant value of ∼95 s⁻¹ beyond 2 s of illumination. In the presence of 5 μM antimycin A (curve 3), R_ph increases from 40 s⁻¹ to a steady-state value of ∼71 s⁻¹. Similar results are obtained in the presence of 1.5 and 5 μM antimycin A.

Figure 2.

Membrane potential changes induced by a saturating continuous illumination. The mature leaf is submitted to cycles of 6.2 s of light and 7 min of dark. The membrane potential changes are normalized to that corresponding to a single charge separation ΔI/I = 3.03 × 10⁻³. During the 6.2-s light periods, the light is interrupted for short periods (50 ms) at times indicated by dashed lines (dark transients not shown). Curve 1, 20 μM DCMU. Fluorescence kinetics performed on the same leaf fragment shows that PSII is fully inhibited. Curve 2, control (leaf infiltrated with water). Curve 3, 5 μM antimycin A.

Cyt f Redox Changes.

Fig. 4 shows the kinetics of absorption changes associated with the light-induced redox changes of cyt f. In the presence of DCMU (curve 1) the illumination induces the oxidation of most of cyt f. After switching off the light, cyt f is slowly reduced (t½ ∼40 s, not shown). In the control (curve 2) a large fraction of cyt f (∼37%) is oxidized after 1.7-s illumination. When the light is switched off, a fast reduction phase (t½ ∼4 ms) is observed that we ascribe to the plastoquinol oxidation at site Q_o of the cyt bf complex. Thus, the rate of the membrane potential formation (R_bf) associated with cyt bf turnover decays with the same half time, which justifies the assumption made in the computation of R_ph (see above). In the presence of 2 μM antimycin A (curve 3), the fraction of oxidized cyt f in the light is much lower than in the control. Similar kinetics for cyt f changes are obtained in the presence of 5 μM antimycin A.

Determination of R_PSII and Computation of R_cyclic.

In Fig. 5, the fluorescence induction kinetics has been measured in a leaf infiltrated with water, either dark-adapted (curve 1) or submitted to repetitive light and dark cycles (curve 2), in conditions close to those used in the experiments shown in Figs. 2 and 3, curves 2. The fluorescence yield F_max reached when Q_A is fully reduced is measured by superimposing a 200-ms pulse of saturating light (levels 1′ and 2′). It is worth noting that the F_max level is lower for a leaf submitted to light and dark cycles than for a dark-adapted leaf. This result shows that a small nonphotochemical quenching (31) has developed during the light and dark cycles. As shown in ref. 32, the fluorescence yield F is linearly related to R_PSII during the initial fluorescence rise associated with the PQ pool reduction. Thus, R_PSII is proportional to the difference (F_max − F), normalized to its maximum value (F_max − F₀) reached when Q_A is fully oxidized, where F₀ is the dark-adapted fluorescence yield. We have

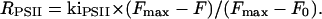After 6.2 s of illumination (curve 2), R_PSII = ∼84 s⁻¹ × 0.16 = ∼13 s⁻¹. From the experiment shown in Fig. 3 (curve 2), one can compute

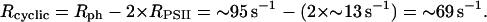Fig. 6 shows the result of a similar experiment but in the presence of 1.5 μM antimycin A. In this condition, (F_max − F)/(F_max − F₀) is only 0.017 either in dark-adapted (curve 1) or preilluminated material (curve 2). Thus,

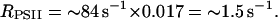And consequently, from the data Fig. 3 (curve 3),

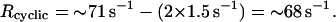Myxothiazol (2 μM) or antimycin A (1.5 μM) induced a similar behavior to that shown in Fig. 6.

Concentration of PSI Secondary Donors.

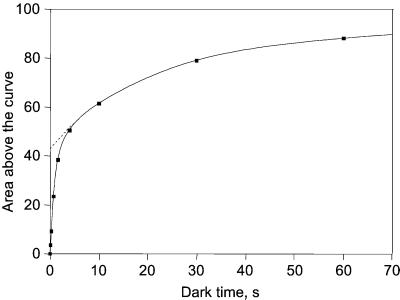
Fig. 7 (curve 1) displays the fluorescence induction curve measured in a noninfiltrated leaf submitted to light (ki_PSII ∼250 s⁻¹) and dark cycles. The plateau observed in the 20–100-ms illumination (as in Figs. 5 and 6) is seen neither in broken chloroplasts nor in plant mutants that lack PSI or cyt bf complex (not shown). It is thus very likely associated with the reduction of a pool of soluble oxidized PSI acceptors. The grayed bound area above curve 1 is proportional to the concentration of all electron carriers oxidized in the dark that are localized between PSII and the rate-limiting step of the Benson–Calvin cycle, including the PQ pool and the PSI acceptors. Curve 2 displays the fluorescence induction measured after a 2-s dark period after the 1.7-s illumination. During this dark period, Q_A is partially reoxidized and the subsequent illumination induces a fluorescence rise as fast as that observed in the presence of DCMU, showing that the PQ pool is still reduced. The fluorescence decrease observed in the 5–50-ms time range reflects the light-induced (PSI) oxidation of PQ. This oxidation is associated with the electron transfer from the PQ pool to PSI acceptors, which have been reoxidized during the 2-s dark period. The concentration of the oxidized carriers localized between PSII and the Benson–Calvin cycle is proportional to the bound area above the second fluorescence induction curve (striped area, curve 2). In Fig. 8, the concentration of these oxidized carriers has been plotted as a function of the dark time between the first and the second light pulses. We ascribe the fast phase (t½ ∼0.6 s) to the oxidation of the PSI acceptors and the slower phase (t½ ∼20 s) to the oxidation of the PQ pool. As expected, the fast phase is not observed with a mutant that lacks cyt bf complex or PSI. The size of the fast pool is ∼0.75 of the slow pool. Assuming that the ratio [PQ]/[Q_A] is ∼6 (i.e., 12 electron equivalents) (23, 24), the number of PSI electron acceptors is ∼9 electron equivalents per photosynthetic chain. Most of these acceptors are very likely Fd and/or NADP, which are washed out during the thylacoid preparation.

Figure 7.

Kinetics of the fluorescence yield F/F₀ in a noninfiltrated leaf. F₀, dark-adapted fluorescence yield. Same leaf as in Fig. 1. Curve 1, the leaf is submitted to repetitive cycles of 1.7 s of light (ki_PSII ∼ 250 s⁻¹) and 6 min of dark. The fluorescence yield is constant between 0.7- and 1.7-s illumination. Curve 2, after a 2-s dark period after the 1.7-s illumination.

Figure 8.

Recovery of the bound area above the fluorescence induction curve (same as striped area, Fig. 7) as a function of the dark period after the 1.7-s illumination. The recovered area has been normalized to the area measured after 6 min of dark.

Discussion

Effect of DCMU.

The photochemical rate transiently reached in the presence of DCMU (∼75 s⁻¹) provides unambiguous proof that a cyclic pathway operates at a rate close to the maximum rate of electron transfer measured in a light-adapted leaf. The number of electrons transferred via the cyclic pathway during the 6.2-s illumination is proportional to the bound area below curve 1, Fig. 3 (∼240). This value is much larger than the number of PSI donors reduced in the dark. It is unlikely that the protein coded by the NDH gene present at low concentration could sustain such an efficient cyclic flow. Moreover, the slow reduction of cyt f in the dark (t½ ∼40 s) excludes that NDH and/or Fd PQ reductase rapidly establishes a thermodynamic equilibrium between the stromal and the luminal compartments.

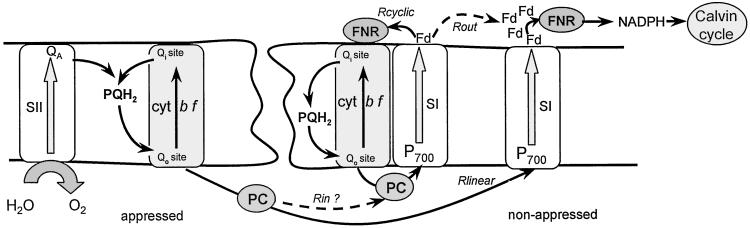
The mere observation of a cyclic electron flow in the absence of PSII activity leads to severe constraint on the mechanism of this process. As the PQ pool is oxidized, the number of reduced PSI donors per chain in the dark is at most 5 (1 Rieske protein, 1 cyt f, 2 PC, and 1 P₇₀₀), a value smaller than the number of oxidized PSI acceptors (∼9 per chain, from Fig. 8). Thus, if all PSI centers were able to transfer electrons to soluble acceptors, the illumination should induce the oxidation of all PSI donors and consequently, the inhibition of the cyclic pathway. Besides, the reduced PSI acceptors are reoxidized by the Benson–Calvin cycle (t½ ∼0.6 s, Fig. 8). As we observed that the cyclic pathway operates with a large efficiency, we must assume that the electrons that appear on the stromal side of PSI involved in the cyclic process are not rapidly transferred to the pool of oxidized PSI soluble acceptors. We favor a model of supercomplex that associates 1 cyt bf complex, 1 PSI, a trapped Fd molecule and, very likely, an FNR (14, 15) (Scheme S1). We propose that within the supercomplex, electrons are transferred from the reduced Fd molecule to the oxidized high-potential cyt b (cyt b_h) localized close to the stromal side of the cyt bf complex. This transfer occurs either directly or by means of the FNR bound to the cyt bf complex. Then, according to the modified Q-cycle process (33), one plastoquinol is oxidized at site Q_o and one PQ is reduced at site Q_i, leading to the reoxidation of cyt b_h and to the transfer of one electron through the membrane. The decrease in the rate of the cyclic pathway we observed beyond 1.5 s (Fig. 3, curve 1) implies the occurrence of a slow leak of electrons between the carriers included in the supercomplex and the pool of PSI acceptors (R_out). As PSII is inhibited, this leak, not compensated by an input of electron (R_in = 0), induces a slow oxidation of P₇₀₀ and the inhibition of the cyclic process. R_cyclic decreases after a larger number of turnovers (>100) showing that R_cyclic >> R_out. This result illustrates the conclusions drawn by Grant and Whatley (34) and Allen (35). These authors proposed that the redox poise of the carriers involved in a cyclic process determines its efficiency and is controlled by the relative rates of electron input (R_in) and output (R_out).

Scheme 1.

Structural and biochemical data show that about half of cyt bf complex is included in the nonappressed region (22). Assuming 1 cyt bf per photosynthetic chain, no more than half of the PSI centers participate to the cyclic flow and the remaining fraction is involved in the linear flow.

Cyclic and Linear Flows in the Absence of Inhibitors.

In a leaf infiltrated with water, the rate of the cyclic flow is ∼69 s⁻¹, close to the maximum rate measured in the presence of DCMU. In Fig. 1, the photochemical rate R_ph ∼117 s⁻¹ has been measured in conditions that the Benson–Calvin cycle and the linear flow are largely inactivated (see Fig. 7), which implies that an efficient cyclic flow is also operating in noninfiltrated leaf. The PSI centers (∼50%) that participate to the linear flow are involved in the fast transfer of electrons from PSII to the pool of soluble PSI acceptors (Fig. 7). The reduction of Q_A observed beyond 1-s illumination implies that all of the carriers involved in the linear chain, including the cyt f of the appressed region, are fully reduced. We thus conclude that the fraction of cyt f oxidized after 1.7-s illumination (∼37%) exclusively belongs to the cyclic chain localized in the nonappressed region and is not in equilibrium with the granal cyt f. This finding implies that the carriers included in the supercomplex are not in equilibrium with the freely diffusing PC pool (Scheme S1).

Effect of Antimycin A.

Contrary to the literature (ref. 36 and for a review, ref. 6), we do not observe any inhibitory effect of antimycin A on the cyclic flow. On the other hand, we do observe an inhibitory effect of antimycin A on the linear electron flow, because of the inhibition of the Benson–Calvin cycle (Fig. 6). As myxothiazol acts as antimycin A, we suggest that this inhibition is associated with that of the respiratory electron transfer chain. We propose that ATP and ADP equilibrate between mitochondria and chloroplasts, as already reported for Chlamydomonas (37). In higher plants, Gardeström and Lernmark (38) have observed that the addition of oligomycin, which inhibits the mitochondrial ATPase, induces a pronounced delay in the photosynthetic induction. The inhibition of the respiratory chain would induce a decrease of the ATP concentration in the chloroplast compartment that affects the steps of the Benson–Calvin cycle, in which ATP acts as a substrate. Antimycin A would decrease the concentration of 1,3-diphosphoglycerate involved in the oxidation of NADP. In agreement with this hypothesis, we have observed that the addition of uncouplers (nigericin and nonactin), which induce ATP hydrolysis, also induces the inhibition of the Benson–Calvin cycle.

Under conditions where the Benson–Calvin cycle is inhibited, the pathway involved in the reoxidation of PSI acceptors is blocked (R_out ≅ 0). If the freely diffusing PC were able to transfer electrons to the supercomplex, the reductive power induced by PSII turnover would induce a rapid reduction of all photosynthetic carriers (including PSI acceptors) and therefore the inhibition of both the cyclic and the linear pathways. The high efficiency of the cyclic pathway we observe implies that the electrons accumulated in the granal PQ pool and in the PC pool have no access to the cyclic chain, as proposed in the preceding paragraph. As depicted in Scheme S1, the positive charges formed on the donor side of the PSI included in the supercomplex were transferred to the luminal side of cyt bf complex by way of a trapped PC molecule. We observed that the carriers involved in the cyclic pathway are in a more reduced state in the presence of antimycin A than in the control, which suggests that a slow electron leak (R_in) occurs between the soluble PC pool and the supercomplexes. Increasing R_in would lead to a further reduction of the cyclic electron carriers, thus inducing the reduction of the PSI acceptors and the inhibition of the cyclic pathway. Some physiological variability in R_in and R_out values could explain the contradictions between our results and those reported in the literature on the effect of antimycin A.

Conclusion

The large efficiency of the cyclic electron flow observed in aerobic conditions requires a structural separation of the cyclic and linear electron transfer chains. PQ-mediated electron exchange between PSII and the cyt bf complex present in the nonappressed region is prevented first by the segregation of PSII and PSI centers in the appressed and nonappressed regions, respectively, and second by the restricted diffusion of PQ. The trapping of a PC molecule in a supercomplex prevents a PC-mediated electron transfer between linear and cyclic chains whereas the trapping of an Fd molecule prevents electron exchange between Fd and the pool of soluble PSI acceptors. In the case of C4 plants, separation between cyclic and linear pathways have been pushed to an extreme, as the two processes occur in different types of cells, bundle sheath, and mesophyll, respectively (39).

In our view, the main function of the cyclic flow is to increase the concentration of ATP, which limits the rate of the Benson–Calvin cycle after a period of dark adaptation. It is likely that for increasing time of illumination, the fraction of PSI participating to the cyclic flow decreases whereas that involved in the linear flow increases. This regulation can be achieved by varying the proportion of PSI included in the supercomplexes. We tentatively propose that the formation of supercomplexes be controlled by the ATP concentration. At low ATP concentration, all of the cyt bf complexes present in the nonappressed region are included in supercomplexes. The increase in the ATP concentration induced by the cyclic electron flow leads to a dissociation of the supercomplexes, thus increasing the fraction of PSI available for the linear electron flow and decreasing that involved in the cyclic flow.

Recent structural data showed that the electrical rotor of the ATPase includes 14 polypeptides (40). Thus, a complete rotation of the rotor is associated with the transfer of 14 protons (one per polypeptide) and with the synthesis of 3 ATP, which leads to an H⁺/ATP ratio of 14/3 = ∼4.7. As the transfer of 1 electron by means of the linear chain induces the transfer of a maximum of 3 protons through the membrane, the ATP/e⁻ ratio is 3/∼4.7 = ∼0.64 or ∼2.55 ATP per CO₂. This ratio is overestimated, as we have not taken into account the proton leak through the membrane. Thus, the amount of ATP synthesized by the photosynthetic electron transfer chain does not fulfil the ATP requirement of the Benson–Calvin cycle (3 ATP/CO₂) and of other ATP-consuming processes occurring in the stroma. We expect that, even in a light-adapted leaf, a noticeable fraction of PSI centers remains involved in the cyclic process that will decrease the quantum yield for oxygen formation. Actually the measured quantum requirement is of 10–11 quanta per O₂ molecule (41) to be compared with a theoretical value of 8 quanta required for a linear chain involving two photoreactions.

Abbreviations

cyt bf

cytochrome b₆/f

DCMU

3-(3,4-dichloro-phenyl)-1,1-dimethylurea

Fd

ferredoxin

FNR

Fd-NADP reductase

NDH

NADP dehydrogenase

PC

plastocyanin

PS

photosystem

PQ

plastoquinone