Abstract
Levofloxacin was administered orally to steady state to volunteers randomly in doses of 500 and 750 mg. Plasma and epithelial lining fluid (ELF) samples were obtained at 4, 12, and 24 h after the final dose. All data were comodeled in a population pharmacokinetic analysis employing BigNPEM. Penetration was evaluated from the population mean parameter vector values and from the results of a 1,000-subject Monte Carlo simulation. Evaluation from the population mean values demonstrated a penetration ratio (ELF/plasma) of 1.16. The Monte Carlo simulation provided a measure of dispersion, demonstrating a mean ratio of 3.18, with a median of 1.43 and a 95% confidence interval of 0.14 to 19.1. Population analysis with Monte Carlo simulation provides the best and least-biased estimate of penetration. It also demonstrates clearly that we can expect differences in penetration between patients. This analysis did not deal with inflammation, as it was performed in volunteers. The influence of lung pathology on penetration needs to be examined.
Treatment of lower respiratory tract infections depends, explicitly, upon delivering drug to the site of infection. For extracellular pathogens, determination of drug concentration in the epithelial lining fluid (ELF) is currently the best estimate for ascertaining the degree of drug exposure for these organisms. Because of the nature of the sampling process, it is difficult to obtain multiple estimates of ELF drug concentration from an individual patient. Consequently, to ascertain ELF drug penetration, clinical trial designs randomize patients to different drug doses and sampling times.
Analysis of these data is often limited to obtaining ratios of drug concentrations in the ELF to those determined simultaneously in plasma. For drugs with multicompartmental behavior, these ratios will change as a function of the sampling time. Such time dependency makes this measure a poor one for understanding the penetration behavior of a drug.
Gotfried and colleagues (3) had previously published a study on the simultaneous determination of steady-state concentrations in plasma and ELF of either ciprofloxacin or levofloxacin, with the latter drug being administered in doses of either 500 or 750 mg.
Previously, we had population modeled the penetration of levofloxacin into the prostate (2). To improve the understanding of drug penetration in a population sense, we employed Monte Carlo simulation to evaluate the full range of variability seen with penetration into the prostate. Given the importance of having adequate drug concentrations at the site of infection, we wished to population model the data from the Gotfried study (3) and to perform a Monte Carlo simulation for the penetration of a 750-mg dose of levofloxacin, as this dose is currently being studied for the therapy of nosocomial infection.
Healthy volunteers, 18 years of age or older, were studied. Patients were randomized to receive either ciprofloxacin or levofloxacin and, within the levofloxacin group, to receive either 500 or 750 mg once daily, by mouth, for 5 days. Only the data from the levofloxacin group were analyzed in this work.
Plasma and ELF specimens were collected at 4, 12, and 24 h postdose at day 5. Methods for the ELF sampling were provided previously (3). Likewise, the assay for levofloxacin and urea in plasma and ELF and their performance was set forth in this previous publication.
All data from all subjects (n = 24) were simultaneously comodeled using BigNPEM as implemented at the UCSD Supercomputer Center (5). A three-compartment, open model with first-order input and first-order elimination was employed. A specific volume term was employed for estimation of ELF volume. MAP-Bayesian estimates were obtained using the population-of-one utility within NPEM.
A 1,000-subject Monte Carlo simulation was performed. The mean parameter vector and covariance matrix from the NPEM analysis were embedded in subroutine PRIOR of the ADAPT II package of programs of D'Argenio and Schumitzky (University of Southern California). Both normal and log-normal distributions were evaluated. The choice between distributions was made on the ability to recreate the original mean parameter vector and the standard deviations (SDs) of the parameters.
The levofloxacin concentrations in plasma at 4, 12, and 24 h (mean ± SD) were 5.29 ± 1.23, 3.06 ± 0.93, and 0.60 ± 0.10 mg/liter, and those in ELF were 9.94 ± 2.74, 6.46 ± 2.48, and 0.70 ± 0.41 mg/liter for the 500-mg dose. For the 750-mg dose, these values in plasma were, respectively, 11.98 ± 2.99, 4.06 ± 0.51, and 1.69 ± 1.14 mg/liter, and those in ELF were 22.13 ± 14.92, 9.17 ± 5.34, and 1.45 ± 0.76 mg/liter.
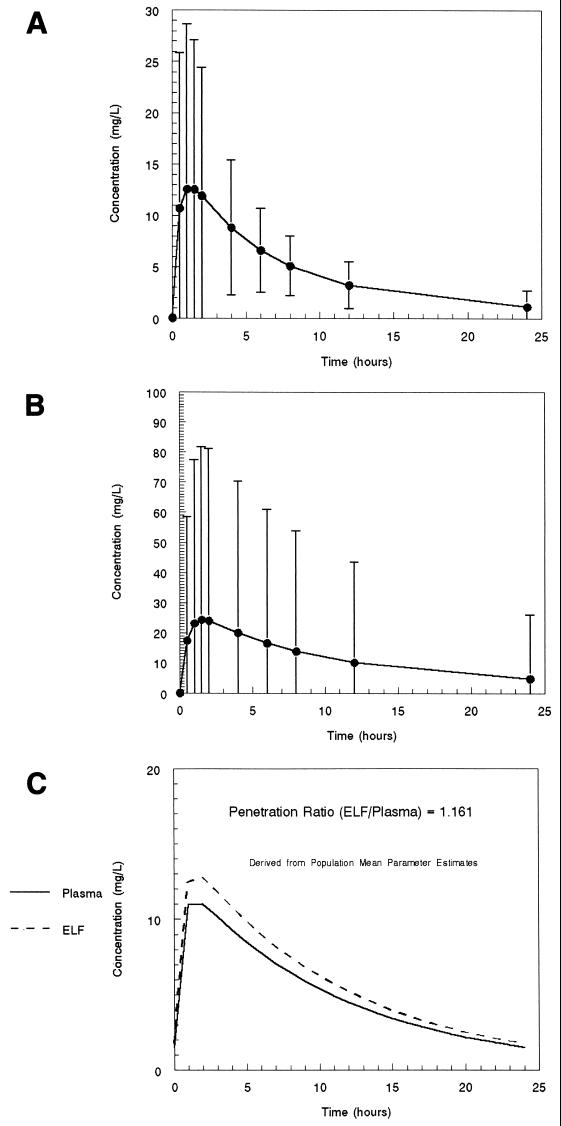
The values for the mean parameter values and the covariance matrix from the NPEM analysis are presented in Tables 1 and 2. The mean plasma concentration-time profile for levofloxacin in plasma and ELF and their 95% confidence intervals, as derived from the Monte Carlo simulation for the 750-mg dose, are presented in Fig. 1A and B.The concentration-time profiles for plasma and ELF as derived from the mean parameter vector are displayed in Fig. 1C. The area under the concentration-time curve (AUC) in ELF/AUC in plasma ratio determined from this calculation is 1.16.
TABLE 1.
Mean parameter vector for levofloxacin penetration into ELFa
| Parameter | Mean | SD |
|---|---|---|
| Vc/F (liters) | 22.54 | 16.15 |
| SCL/F (liters/h) | 5.97 | 1.02 |
| K12 (h−1) | 6.88 | 5.35 |
| K21 (h−1) | 10.89 | 5.91 |
| K13 (h−1) | 14.21 | 4.55 |
| K31 (h−1) | 11.26 | 6.33 |
| VELF/F (liters) | 24.50 | 26.66 |
| Ka (h−1) | 2.11 | 0.72 |
Vc/F and VELF/F are apparent volumes of distribution for the central and ELF compartments, respectively; SCL/F is the apparent serum clearance (these terms are divided by the bioavailability [F], as this is an unknown in this analysis); K12, K21, K13, and K31 are first-order intercompartmental transfer rate constants; Ka is the first order rate constant of drug absorption.
TABLE 2.
Covariance matrix for levofloxacin penetration into ELFa
| Parameter | Covariance with:
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Vc/F | SCL/F | K12 | K21 | K13 | K31 | VELF/F | Ka | |
| Vc/F | 260.75 | |||||||
| SCL/F | 6.85 | 1.03 | ||||||
| K12 | −10.86 | −0.67 | 28.60 | |||||
| K21 | 38.90 | −0.35 | 3.79 | 34.94 | ||||
| K13 | −7.06 | −2.07 | −1.46 | 11.62 | 20.73 | |||
| K31 | 31.82 | −0.90 | −19.49 | −4.50 | 2.99 | 40.05 | ||
| VELF/F | 41.44 | −3.31 | −1.15 | 34.64 | 19.00 | −77.70 | 711.05 | |
| Ka | −4.15 | 0.17 | 0.47 | −3.00 | −1.29 | −0.57 | −6.10 | 0.51 |
See footnote a to Table 1 for further details.
FIG. 1.
(A) Population mean concentration-time profile in plasma and 95% confidence interval for a 750-mg dose of levofloxacin administered orally, as derived from a 1,000-subject Monte Carlo simulation. (B) Population mean concentration-time profile in ELF and 95% confidence interval for a 750-mg dose of levofloxacin administered orally, as derived from a 1,000-subject Monte Carlo simulation. (C) Steady-state population mean concentration-time profiles in plasma and ELF for a 750-mg dose of levofloxacin administered orally, as derived from a simulation employing the mean parameter vector.
When the penetration ratio is developed from a Monte Carlo simulation, we find the mean penetration ratio is 3.18, with a median of 1.43. The SD is 5.71, with a 95% confidence interval from 0.143 to 19.12. Overall, 61% of simulations had a penetration ratio that exceeded 1.0.
Determination of drug penetration into sites such as ELF, cerebrospinal fluid, prostate, eye, and bone (among others) is problematic because of the difficulty of obtaining multiple samples within a patient because of the invasive or destructive nature of the sampling process. Study designs have concentrated on obtaining paired penetration site and plasma samples. Often, only a single time point has been empirically chosen. Further, analysis has most frequently been limited to taking the ratio of the concentration in the penetration site to that in plasma at the same sampling time. The difficulty with such an analysis is that, unless all the points are in pseudo-distribution equilibrium (absorption and distribution are completely over) the ratio of penetration must change with time in a manner that has nothing to do with random error. An index of penetration that changes with time is, on the face of it, a poor index of the ability of the drug to penetrate to that site.
While a study design and analysis plan based on paired samples was acceptable when more robust methods of analysis were unavailable, this is clearly no longer the case. Population analysis has been employed in an animal study of ciprofloxacin penetration into rabbit eye (1). More recently, our group has published a population pharmacokinetic analysis of levofloxacin penetration into the prostate (2). This analysis was linked to Monte Carlo simulation to provide a measure of dispersion for drug penetration. Other groups have used similar approaches (but without the Monte Carlo simulation) to examine penetration of a protease inhibitor into cerebrospinal fluid (4). This type of analysis should become the standard for penetration studies.
Levofloxacin penetrates well into ELF, with a mean penetration ratio of 1.16 to 3.18, depending on whether simulation from the mean parameter vector or the average penetration from the Monte Carlo simulation is employed. The average value for the Monte Carlo simulation is skewed because of outliers, as is evident when one examines the median value of the penetration ratio of 1.43, quite consistent with the simulation from the mean parameter values. It is important to recognize that levofloxacin is quite reliable in its penetration, with >61% of subjects in the Monte Carlo simulation having a penetration ratio exceeding 1.0. Many more subjects are near a penetration ratio of 1.0 (circa 0.8 to 1.0). This indicates that sampling the plasma and determining an AUC will provide a reasonable (and in the majority of instances, conservative) estimate of how much drug the pathogens in the ELF are being exposed to.
Levofloxacin is being examined for use in nosocomial pneumonia as a single agent. Given that the average AUC expected in the plasma for a 750-mg dose from the data in this study is approximately 125, it is clear that levofloxacin will provide robust coverage for the most common causes of nosocomial pneumonia. Exceptions may be Pseudomonas aeruginosa isolates, for which the MICs are greater than 1 mg/liter, and methicillin-resistant Staphylococcus aureus (MRSA). Additionally, treatment with a second agent for serious Pseudomonas infection may be appropriate in any case. For methicillin-resistant S. aureus, another drug such as vancomycin or linezolid would be appropriate.
We have examined the penetration of levofloxacin into ELF in this study. However, in order to provide the greatest insight into the utility of this agent for different pathogens causing pneumonia, it is important to examine the penetration in the presence of the pathological process for which the agent is being employed. The presence of pneumonia will have significant inflammation attendant to it. It is likely that this inflammation will alter penetration in a time-dependent way. The inflammation will likely peak early in the process, with a maximal effect on tight junctions and penetration occurring in the first few days after introduction of the drug. As the agent starts the resolution process, it is further likely that penetration will decrease. These issues need to be adequately studied if we are to gain the fullest understanding of drug penetration and its effect on the pathological process of pneumonia.
REFERENCES
- 1.Drusano, G. L., W. Liu, R. Perkins, A. Madu, C. Madu, M. Mayers, and M. H. Miller. 1995. The determination of robust ocular pharmacokinetic parameters from the serum and vitreous humor of albino rabbits following the systemic administration of ciprofloxacin from sparse data sets, using IT2S, a population pharmacokinetic modeling program. Antimicrob. Agents Chemother. 39:1683-1687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Drusano, G. L., S. L. Preston, M. Van Guilder, D. North, M. Gombert, M. Oefelein, L. Boccumini, B. Weisinger, M. Corrado, and J. Kahn. 2000. A population pharmacokinetic analysis of the penetration of the prostate by levofloxacin. Antimicrob. Agents Chemother. 44:2046-2051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gotfried, M. H., L. H. Danziger, and K. A. Rodvold. 2001. Steady state plasma and intrapulmonary concentrations of levofloxacin and ciprofloxacin in healthy adult subjects. Chest 119:1114-1122. [DOI] [PubMed] [Google Scholar]
- 4.Letendre, S. L., E. V. Capparelli, R. J. Ellis, and J. A. McCutchan. 2000. Indinavir population pharmacokinetics in plasma and cerebrospinal fluid. Antimicrob. Agents Chemother. 44:173-175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schumitzky, A., R. Jelliffe, and M. van Guilder. 1994. NPEM. A program for pharmacokinetic population analysis. Clin. Pharmacol. Ther. 55:163. [Google Scholar]