Abstract
The therapeutic and toxic effects of amikacin are known to depend on its concentration in plasma, but the pharmacokinetics of this drug in neonates, infants, and children and the influences of clinical and biological variables have been only partially assessed. Therapeutic drug monitoring data collected from 155 patients (49 neonates, 77 infants, and 29 children) receiving amikacin were analyzed by a nonparametric population-based approach, the nonparametric maximum-likelihood method. We assessed the effects of gestational and postnatal age, weight, Apgar score, and plasma creatinine and urea concentrations on pharmacokinetic parameters. There is no specific formulation of amikacin for neonates and infants. We therefore used an error model to account for errors due to dilution during preparation of the infusion. The covariates that reduced the variance of clearance from plasma and the volume of distribution by more than 10% were postnatal age (43 and 28%, respectively) and body weight (30.4 and 17.4%, respectively). The expected reduction of clearance was about 10% for the plasma creatinine concentration. The other covariates studied (Apgar scores, plasma urea concentration, gestational age, sex) were found to have little effect. Simulations showed that a smaller percentage of patients had a maximum concentration in plasma/MIC ratio greater than 8 with a regimen of 7.5 mg/kg of body weight twice daily than with a regimen of 15 mg/kg once a day for MICs of 1 to 8 mg/liter.
Amikacin is widely used in neonates and infants, as well as in adults, for the treatment of severe infections caused by gram-negative bacteria. Previous studies have shown that both the therapeutic response and toxic effects depend on plasma amikacin concentrations. Achieving a therapeutic maximum concentration of amikacin in plasma is associated with a significant decrease in the rate of mortality due to infection in critically ill patients (2, 36, 37), and a relationship has also been found between the minimum plasma amikacin concentration and renal toxicity (20, 49). Interindividual variability in the pharmacokinetics of amikacin may therefore make it difficult to achieve safe and effective treatment. The pharmacokinetics of aminoglycosides have been shown to be highly variable in neonates and children. Several factors account for the pharmacokinetic variabilities of other aminoglycosides in this population (50). The pharmacokinetics of netilmicin and gentamicin depend on gestational age, postnatal age, weight, renal clearance, and Apgar score (6, 9, 11, 12, 14, 18, 21, 43, 46, 47, 51-53). Very few data are available concerning the effects of clinical and biological covariates on the pharmacokinetics of amikacin in neonates and the changes in the pharmacokinetic profile of amikacin that occur from birth into infancy. The lack of data on the pharmacokinetics of many drugs in neonates and children is related to blood sampling limitations for this population. One way around this problem is to collect a few samples from many individuals and analyze the data by means of a population-based approach (7, 10, 13, 14, 29, 34, 51, 54). The administration of aminoglycosides once daily has been shown to be as well tolerated as or better tolerated than the conventional schedules (twice daily or thrice daily) in adults and children. Once-daily administration also has potential pharmacodynamic and nursing advantages (15, 16, 38, 44). No data have been published concerning the plasma amikacin concentrations in neonates treated with a regimen of once per day.
The aims of the study were (i) to describe amikacin pharmacokinetics in populations of neonates, infants, and children by the nonparametric maximum-likelihood (NPML) method (30) applied to drug monitoring data routinely collected from 155 patients; (ii) to determine the extent to which various covariates (gestational and postnatal age, weight, Apgar score, serum urea and creatinine concentrations) accounted for interindividual variability (30, 31, 44); and (iii) to compare the performances of a once-daily regimen and a twice-daily regimen in our population by simulating concentrations in plasma at various times from Bayesian individual parameter estimates.
MATERIALS AND METHODS
Patients and treatments.
Therapeutic drug monitoring data were retrospectively collected from 155 patients: 49 neonates (23 girls, 26 boys), 77 infants (28 girls, 49 boys), and 29 children (14 girls, 15 boys). These individuals were hospitalized in the Pediatrics Department of Saint-Vincent de Paul Hospital, Paris, France, and received amikacin for a suspected infection. Descriptive statistics for the biological and clinical data collected from these patients are given in Table 1. The drug was administered by infusion for a short period of time. The median dose administered was 7.44 mg/kg of body weight for all patients (dose range, 2.47 to 14.9 mg/kg). The duration of the infusion was not recorded for about 40% of drug administrations but was recorded for all administrations immediately preceding the measurement of plasma amikacin concentrations. If the duration of the infusion was unknown, we assumed that its value was the median value for both groups (i.e., 0.5 h). For each patient, we assessed the dose received, the infusion and sampling times, and plasma amikacin concentrations. We measured plasma amikacin concentrations by a fluorescence polarization immunoassay (TDx; Abbott). The lower limit of detection was 0.8 mg/liter. The coefficient of variation was less than 3.5% for all concentrations. Data were available for a total of 470 time points for the 155 patients, for a mean of 3.03 samples per patient, a median of 3 samples per patient, and a range of 1 to 8 samples per patient. For about 25% of the patients, the plasma amikacin concentration was determined only once after drug administration. A blood sample was systematically taken just before the start of the first infusion to determine the plasma amikacin concentration and to check whether the subject had previously received amikacin so that this information could be taken into account, if necessary, to calculate an appropriate drug regimen. This pretreatment sample was not taken into account in the analysis of the plasma amikacin concentration but was considered in the modeling study. Most of the other blood samples were drawn immediately after the first administration. The following information was recorded: gestational and postnatal ages; body weights; Apgar scores at 1, 5, and 10 min; and plasma creatinine and urea concentrations.
TABLE 1.
Descriptive statistics for biological and clinical data collected from patientsa
| Characteristic | Mean | CVb (%) | Median | Range |
|---|---|---|---|---|
| Gestational age (wk) | 38 | 6 | 39 | 30-41 |
| Postnatal age (days) | 450 | 185 | 69 | 1-3,650 |
| Body wt (kg) | 7.38 | 84 | 4.83 | 1.35-33 |
| Apgar score at: | ||||
| 1 min | 8.93 | 24 | 10 | 1-10 |
| 5 min | 9.94 | 2 | 10 | 9-10 |
| 10 min | 9.83 | 7 | 10 | 5-10 |
| Plasma creatinine concn (mmol/liter) | 54 | 40 | 49 | 24-114 |
| Plasma urea concn (mmol/liter) | 4.3 | 48 | 3.9 | 0.9-15.2 |
n = 155.
CV, coefficient of variation.
Pharmacokinetic model.
The pharmacokinetics of amikacin in pediatric populations are generally described by a two-compartment model (1, 19, 22, 45), and one three-compartment model has even been developed (1). However, in this study most of the kinetic data were collected between 5 min and 3 h after the end of infusion; thereafter, only one further measurement was made, at most, just before the next drug administration. As a result, the preliminary nonlinear regressions for each patient, carried out whenever possible with a two-compartment model, produced inaccurate second elimination constants. We therefore used a one-compartment model to describe our kinetic data, as already proposed by Botha et al. (4) and Padovani et al. (39) for a previously studied pediatric population. The two parameters were clearance (CL) and the volume of distribution (V), from which the elimination half-life (t1/2) was derived.
Statistical model.
An additive zero-mean normal-error model was assumed for all measurements. Its variance was modeled as being proportional to the square of the measurements, and its coefficient of variation was set at 5%. As dilution is required when preparing infusions for neonates, infants, and children, the errors in the amount of drug actually administered are in some cases large (42). Therefore, analytical errors are probably not the largest source of deviation between predicted and observed values. The coefficient of variation of this dose error can be estimated by measuring the concentration of the drug in the syringe after various dilution procedures for several target dose levels. Based on the results of previous studies on aminoglycoside dose errors due to dilution (42, 51), the coefficient of variation for dose error was assumed to be 20% for the neonates. As infants, and children in particular, are much heavier than neonates, dilution rates are generally lower when preparing the drug for such patients, and related procedures are simpler. Therefore, dose errors due to dilution are probably lower for infants and children than for neonates, and the coefficient of variation of the errors was assumed to be 5%. In any case, errors in the doses administered were assumed to be uncorrelated, and for a given concentration measurement, only the dose error for the infusion immediately preceding the measurement was considered.
Population analysis.
Our group of 155 pediatric patients was randomly divided into a learning sample containing two-thirds of the subjects and a validation sample made up of the remaining one-third. Kinetic data for the learning subgroup, eight continuous covariates (gestational age; postnatal age at the start of treatment; body weight; 1-, 5-, and 10-min Apgar scores; plasma urea and creatinine concentrations), and one categorical covariate (sex, coded 0 or 1) were analyzed by the NPML method (31, 42, 51). This method was used to estimate the joint distribution of the kinetic parameters and covariates in the population of patients. No assumptions about the shape of this distribution are required. Moreover, no mathematical relationship between kinetic parameters and covariates needs to be specified. From this distribution estimated by the NPML method, we obtained descriptive statistics for each kinetic parameter and covariate. We investigated the extent to which each covariate accounted for the variability of each parameter by calculating the relative expected reduction of variance of the parameter distribution associated with each covariate. These values were then compared, and the relationships between each of the parameter-covariate pairs were ranked. The relationships (if any) between parameters and covariates were explored by plotting the conditional mean of each parameter distribution for several percentiles of each covariate. The shape of the curve representing the relationship between parameter and covariate were investigated in more detail by using a Gaussian kernel smoother (40) to smooth the plots and examining the results by eye (32). Given the large number of possible combinations of parameters and covariates in this study, only parameter-covariate pairs with a relative expected reduction of variance greater than 10% were explored by this graphical method.
Validation.
The goodness of fit of the model was assessed for the learning group by plotting the predicted concentrations against the observed concentrations and by plotting the weighted residuals against the predicted concentrations. For each patient, we calculated the predicted concentration from estimated individual pharmacokinetic parameters obtained from the parameter distribution provided by the NPML method and from either the patient covariates only (i.e., population predictions) or both individual concentrations in plasma and covariates (i.e., Bayesian predictions). The mean and variance of the weighted residuals, the mean square error, and the root mean square error (RMSE) were also calculated. The ability to predict the concentration in new patients was tested with the data from the validation group. Standardized prediction errors, which for the validation group were equivalent to the weighted residuals, were also calculated (14). We also plotted predicted concentrations versus observed concentrations and standardized prediction errors against predicted concentrations for both population and Bayesian predictions. The mean and variance of the standardized prediction errors, the mean square error, and the RMSE were also calculated in each case. We used a nonparametric validation approach, proposed by Mesnil et al. (33) and based on a Kolmogorov-Smirnov test.
Assessment of dosing schedules.
Various dosing schedules for amikacin have been proposed for neonates, infants, and children, but no real consensus exists. For infants and children, the manufacturer recommends a dose of 15 mg/kg/day administered intravenously or intramuscularly and divided into two or three doses. For neonates, a loading dose of 10 mg/kg followed by a maintenance dose of 7.5 mg/kg every 12 h administered intravenously over 1 to 2 h has been recommended by the manufacturer, as V of amikacin is higher in neonates than in infants and children (26, 45). However, many other regimens have been proposed (23, 41, 45). Once-daily regimens have been suggested for children (20 mg/kg [25] or 15 mg/kg [5]) and neonates (24, 27, 28). We did not aim to assess every dose schedule mentioned in this nonexhaustive list. Two commonly encountered drug dosing regimens were considered for the simulation of the plasma amikacin concentration. In the first drug dosing regimen, neonates received a loading dose of 10 mg/kg followed by a maintenance dose of 7.5 mg/kg every 12 h administered intravenously over 1 h. For infants and children, a dose of 7.5 mg/kg every 12 h (no loading dose) given as a 1-h infusion was considered. In the second drug dosing regimen, we considered an infusion of 15 mg/kg every 24 h given over 1 h for all patients (i.e., neonates, infants, and children). We planned to measure the minimum concentrations in plasma at three time points: 24, 48, and 72 h after the beginning of the treatment. Maximum concentrations in plasma were assumed to occur half an hour after the end of a given infusion. Two determinations of maximum concentrations in plasma were made: at 1.5 and 25.5 h after the beginning of the treatment (48). These dosing schedules were applied to our group of 155 patients, and the concentrations in plasma at the five sampling times (two maximum concentrations in plasma and three minimum concentrations in plasma) were simulated from the one-compartment pharmacokinetic model and from Bayesian individual kinetic parameter estimates. Bayesian kinetic parameters were estimated for each patient from the parameter distribution estimated by the NPML method and individual kinetic data and covariates. At each sampling time, descriptive statistics were obtained from these predicted concentrations. The percentages of Bayesian predicted concentrations within the therapeutic range (i.e., maximum concentration in plasma/MIC of greater than 8 [8] and minimum concentration in plasma below 10 mg/liter [48]) were calculated for each regimen and for six MICs (1, 2, 3, 4, 6, and 8 mg/liter). The ratio of the peak concentration to the MIC is a good indicator of aminoglycoside activity (8).
RESULTS
Population characteristics.
Descriptive statistics for the population kinetic parameters and covariates estimated by the NPML method for the learning subgroup are presented in Table 2. In this sample, 49 of the 155 patients were neonates and 17 of the 49 neonates were 7 days old or younger. The interindividual variability of CL was very high, as shown by the coefficient of variation (about 52%) and by the ratio of the estimated maximum value to the estimated minimum value, which was about 25. The interindividual variability of V was lower than that of CL, but it was still high (about 38%). There was considerable interindividual variability of t1/2, from about 0.5 to 22 h, with the values differing by a factor of more than 40.
TABLE 2.
Population kinetic parameters, t1/2s, and covariates estimated by the NPML method with data from the learning populationa
| Parameter or characteristic | Mean | CVb (%) | Median | Range |
|---|---|---|---|---|
| CL (liter h−1 kg−1) | 1.23 × 10−1 | 52 | 1.16 × 10−1 | 9.95 × 10−3-2.50 × 10−1 |
| V (liter kg−1) | 3.37 × 10−1 | 39 | 3.12 × 10−1 | 1.38 × 10−1-8.46 × 10−1 |
| t1/2 (h) | 2.77 | 98 | 2.04 | 0.52-21.76 |
| Gestational age (wk) | 38 | 5 | 38 | 34-41 |
| Postnatal age (days) | 431 | 183 | 75 | 1-3,283 |
| Body wt (kg) | 7.41 | 80 | 4.77 | 1.99-32.94 |
| Apgar score at: | ||||
| 1 min | 8.69 | 10 | 9 | 7-10 |
| 5 min | 9.53 | 3 | 10 | 9-10 |
| 10 min | 9.54 | 3 | 10 | 9-10 |
| Plasma creatinine concn (mmol/l) | 56 | 36 | 48 | 10-100 |
| Plasma urea concn (mmol/liter) | 4.6 | 32 | 4.5 | 1.9-7.2 |
n = 104.
CV, coefficient of variation.
Covariate analysis.
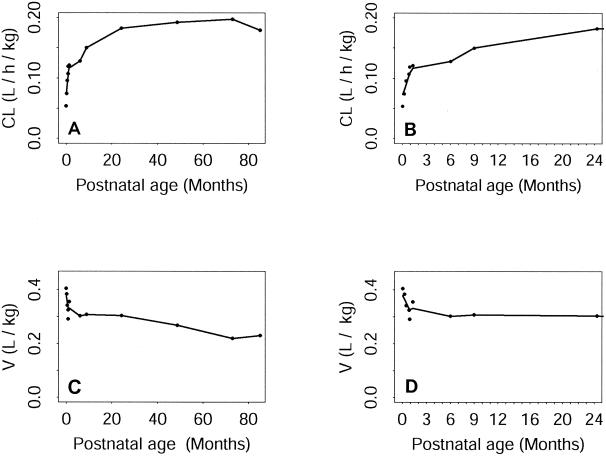
When calculating the relative expected reductions of variance of the two kinetic parameter distributions due to the introduction of each covariate into the analysis, two variables were found to account for a large proportion of the interindividual variability of both CL and V: postnatal age and body weight. Postnatal age gave an expected variance reduction of 43% for CL and 28% for V. For body weight the equivalent reductions were 30.4% for CL and 17.4% for V, and body weight had an effect even if the model parameters were standardized with respect to this factor. The plasma creatinine concentration also accounts for a large proportion of interindividual variability in CL, but the effect of this factor is less pronounced than that of body weight or postnatal age, with an expected reduction of about 10%. Apgar scores, the plasma urea concentration, gestational age, and sex were found to have little effect, inducing reductions of less than 5%. The pattern of change in mean clearance normalized to body weight as a function of postnatal age is shown for the whole population (i.e., neonates, infants and children) in Fig. 1A. It can be seen that mean CL increases considerably with postnatal age. This increase is extremely pronounced during the first few weeks of life and then becomes more moderate until about the age of 2 years. During childhood, CL continues to increase with age, but this trend is not pronounced and CL seems to reach a plateau at about 7 years of age. The scale of the postnatal age axis in Fig. 1A makes it difficult to determine accurately what happens during the very first months of life. Therefore, in Fig. 1B we restricted our attention specifically to neonates and infants, which made it possible to plot the data with a more appropriate x-axis scale. The mean CL increased very rapidly during the first month of life and continued to increase, but much less rapidly, thereafter (i.e., when neonates became infants). Figure 1C shows the pattern of change in mean V, normalized with respect to body weight, as a function of postnatal age for the whole population (i.e., neonates, infants, and children). Unlike CL, V decreased rapidly during the very first weeks of life and continued to decrease thereafter, although it decreased more slowly. However, there is no marked break in this trend at about 100 weeks (i.e., when infants became children), in contrast to what was observed for CL. If we focused only on neonates and infants, the mean V was found to decrease rapidly during the first 4 weeks of life (Fig. 1D). At the end of this period (when neonates became infants), the trend changed, and mean V then decreased very moderately until the age of 6 months, when V reached a plateau. CL, even if it was standardized with respect to body weight, increased with body weight. V decreased unevenly as body weight increased. CL seemed to decrease linearly as the plasma creatinine concentration increased.
FIG. 1.
(A and B) Variation of mean CL with respect to postnatal age for neonates, infants, and children (A) and for neonates and infants only (B). (C and D) Variation of V with respect to postnatal age for neonates, infants, and children (C) and for neonates and infants only (D). In every plot, each dot represents a point estimate of the mean CL or V for a given value of postnatal age. Solid lines correspond to the smoothed data.
Model evaluation.
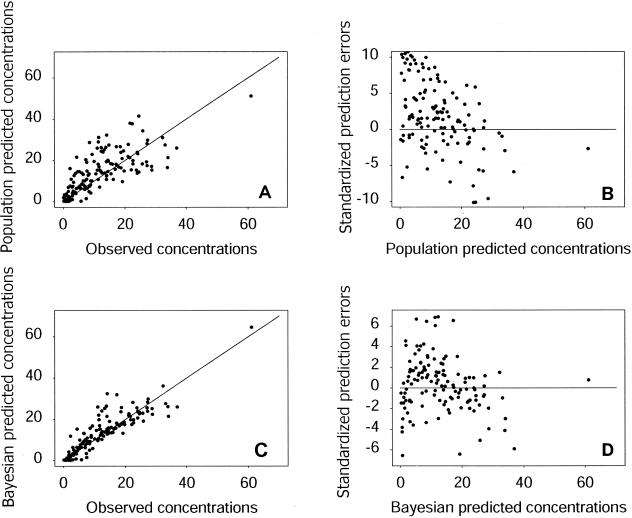
The Bayesian individual predicted and observed concentrations were similar for the learning group: the 325 datum points in the plot of predicted concentrations against observed concentrations were close to the line of unit slope. No trend was observed in the plot of weighted residuals versus predicted concentrations. The mean of the weighted residuals was 0.004, which is very close to 0, and its variance was 2.29, which is not significantly different from 1. The RMSE was 2.34. Figure 2 summarizes the assessment of the population model for the validation sample. The datum points for population predicted concentrations plotted against observed concentrations were, with few exceptions, not far from the unit slope (Fig. 2A). However, the model slightly overestimated concentration, as confirmed by the plot of standardized prediction errors versus predicted concentrations (Fig. 2B). The mean of the standardized prediction error was 0.85, its variance was 4.1, and the RMSE was 3.71. The Kolmogorov-Smirnov test statistic was found to be 0.1123, which is just below the threshold (0.1129) for rejection of the null hypothesis for a sample of 145 observations and a risk of 5%. Figure 2C shows a plot of the Bayesian predicted concentrations versus the observed concentrations for the validation sample, and Fig. 2D shows the corresponding standardized prediction errors with respect to the Bayesian predicted concentrations. The points are less scattered than those for the population predictions, and the slope of the regression line was not significantly different from 1 (P = 0.76). The mean standardized prediction error (0.11) and its variance (3.23) were both lower. The same held true for RMSE, for which a value of 2.70 was obtained. The Kolmogorov-Smirnov test statistic was 0.097, below the threshold of 0.1129 for rejection of the null hypothesis, for 145 observations and a risk of 5%.
FIG. 2.
Validation sample. (A) Population predicted concentrations versus observed concentrations. (B) Standardized prediction errors versus population predicted concentrations. (C) Bayesian predicted versus observed concentrations. (D) Standardized prediction errors versus Bayesian predicted concentrations. Concentrations are expressed in milligrams per liter.
Assessment of dosing schedules.
The results for the first dosing schedule evaluated (i.e., for neonates, a dose of 10 mg/kg followed by a maintenance dose of 7.5 mg/kg every 12 h administered intravenously over 1 h; for infants and children, a dose of 7.5 mg/kg every 12 h [no loading dose] given as a 1-h infusion) are given in Table 3. The mean and median predicted minimum concentrations were much lower than 10 mg/liter at 24, 48, and 72 h. Moreover, the percentage of subjects with concentrations below this limit was close to 100% at the three time points considered. The mean and median predicted maximum concentrations were about 17 mg/liter. The interindividual variability of the predicted minimum concentration in plasma was high, whereas that for the maximum concentration in plasma was moderate.
TABLE 3.
Descriptive statistics for Bayesian predicted amikacin concentrations for the sample of 155 patients at five sampling times from a standard dosing schedulea
| Sample designation | Sampling time (h)b | Statistics for predicted concn
|
|||
|---|---|---|---|---|---|
| Mean (mg/liter) | Median (mg/liter) | CVc (%) | Range (mg/liter) | ||
| First peak (0.5 h after end of first infusion) | 1.5 | 17.9 | 16.5 | 34 | 6.6-35.3 |
| First trough level (just before third infusion) | 24 | 1.4 | <0.8 | 180 | <0.8-14.7 |
| Second peak (0.5 h after end of third infusion) | 25.5 | 17.3 | 16.4 | 32 | 6.8-35.7 |
| Second trough level (just before fifth infusion) | 48 | 1.5 | <0.8 | 191 | <0.8-17.6 |
| Third trough level (just before seventh infusion) | 72 | 1.6 | <0.8 | 193 | <0.8-18.1 |
The standard dosing schedules were as follows: for neonates, a dose of 10 mg/kg followed by a maintenance dose of 7.5 mg/kg every 12 h administered intravenously over 1 h; for infants and children, 7.5 mg/kg every 12 h (no loading dose) given as a 1-h infusion.
Time zero was the beginning of treatment.
CV, coefficient of variation.
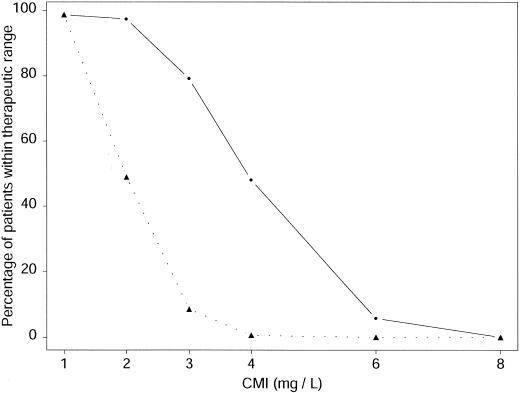
The results for the second dosing schedule evaluated (i.e., 15 mg/kg every 24 h administered intravenously over 1 h for every subject) are given in Table 4. Mean and median predicted minimum concentrations in plasma were below the limit of quantification at times of 24, 48, and 72 h; and the plasma of all patients had concentrations of less than 10 mg/liter at these time points. The mean and median maximum predicted concentrations were about 33 mg/liter, about twice those obtained with the other therapeutic schedule. The interindividual variability of the predicted maximum concentration in plasma was lower than that for the predicted minimum concentration in plasma, as was the case for the first regimen. Figure 3 presents the percentage of patients whose plasma had concentrations within the therapeutic range for the two regimens studied and six MICs. For each MIC, the percentage of patients with concentrations within the therapeutic range was higher for the once-daily regimen than for the twice-daily regimen.
TABLE 4.
Descriptive statistics for Bayesian predicted amikacin concentrations for sample of 155 patients at five sampling times from a standard dosing schedulea
| Sample designation | Sampling time (h)b | Statistics for predicted concn
|
|||
|---|---|---|---|---|---|
| Mean (mg/liter) | Median (mg/liter) | CVc (%) | Range (mg/liter) | ||
| First peak (0.5 h after end of first infusion) | 1.5 | 32.3 | 31.6 | 28 | 13.2-62.1 |
| First trough level (just before second infusion) | 24 | <0.8 | <0.8 | 289 | <0.8-9 |
| Second peak (0.5 h after end of second infusion) | 25.5 | 32.7 | 32.4 | 28 | 13.2-62.3 |
| Second trough level (just before third infusion) | 48 | <0.8 | <0.8 | 305 | <0.8-10.7 |
| Third trough level (just before fourth infusion) | 72 | <0.8 | <0.8 | 308 | <0.8-11.1 |
The standard dosing schedule was a dose of 15 mg/kg every 24 h administered intravenously over 1 hr.
Time zero was the beginning of treatment.
CV, coefficient of variation.
FIG. 3.
Percentages of patients with concentrations within the therapeutic range for the two regimens studied and six MICs. The triangles correspond to the first schedule (i.e., for neonates, a dose of 10 mg/kg followed by a maintenance dose of 7.5 mg/kg every 12 h administered intravenously over 1 h; for infants and children, 7.5 mg/kg every 12 h [no loading dose] given as a 1-h infusion), whereas the dots correspond to the second schedule (i.e., 15 mg/kg every 24 h administered intravenously over 1 h for every subject).
DISCUSSION
Our results reveal the existence of considerable interindividual variability in pharmacokinetic parameters within the population studied, as shown by the large coefficient of variation. Postnatal age reduced the expected relative variance of the CL distribution by more than 10% in the population studied. Gestational age gave no major reduction of variance of the amikacin CL. This may be because the age range of the population was not sufficiently large due to a lack of very premature neonates. These results are consistent with the results of previous studies on the pharmacokinetics of netilmicin (51), gentamicin (17), and amikacin (1, 39, 45) in neonates but not with the results of others suggesting that gestational age affects the clearance of gentamicin (43) and amikacin (45). The available data suggest that gestational age may have an effect only during the very first days of life (17, 43, 45). Some investigators have focused on the relationship between amikacin CL and postconceptional age. However, this covariate, which is the sum of gestational age and postnatal age, is probably not as relevant as gestational age and postnatal age considered separately, as the profile of renal function maturation differs during the gestational and postnatal periods (6). Few data on amikacin CL are available for infants and children (22). The design of our study made it possible to detect age-dependent changes in amikacin CL after the neonatal period. We found that the rate of increase in CL varies during the first 7 years of life, with a sharp increase during the first few weeks of life, followed by a slow increase until the age of 7 years. Amikacin CL, expressed in milliliters per minute per kilogram, was also affected by body weight. This is consistent with the results obtained in a previous study on the pharmacokinetics of netilmicin in neonates (51). This result is of physiological relevance, as it has been shown that changes in renal clearance, expressed in milliliters per minute, are not linearly related to body weight (6). Body weight is strongly correlated with postnatal age, a more direct measure of maturity.
Apgar score was found to have no effect in our population. However, most of our neonates were recruited in a neonatal ward rather than an intensive care unit and therefore had not experienced a severe perinatal challenge. These data are consistent with those previously obtained with netilmicin for a population recruited in the same setting (51).
The value of V dramatically decreased during the very first weeks of life. These pharmacological data are consistent with physiological observations, such as the fact that amikacin is hydrophilic and the fact that total body and extracellular water contents decrease with age during this period of life (3). The V of amikacin, expressed in milliliters per kilogram, was also affected by postnatal age.
To ensure the efficacy of amikacin treatment, we aimed to achieve a peak concentration/MIC ratio of at least 8 for MICs of 1 to 8 mg/liter, with minimum concentrations of less than 10 mg/liter, as recommended for adults and children (8, 23, 37, 48). With a dose of 7.5 mg/kg given every 12 h in neonates and children and with a loading dose of 10 mg/kg in neonates, only 50% of patients had adequate plasma amikacin concentrations for MICs of 2 mg/liter. This regimen therefore seems to be inappropriate for this population. The use of once-daily dose administration has been suggested as a means of obtaining high maximum concentrations. In neonates this regimen has been shown to be as safe as a thrice-daily or a twice-daily regimen (24, 27). Indeed, the predicted minimum concentrations obtained with this regimen were below 10 mg/liter for all patients, and the percentage of patients with a maximum concentration/MIC ratio greater than 8 with this regimen was much lower than the percentage of patients with a maximum concentration/MIC ratio greater than 8 with a regimen of 15 mg/kg once daily for MICs of 1 to 8 mg/liter. For example, for an MIC of 2 mg/liter, predicted maximum concentrations were outside the target concentration range for less than 5% of the patients with a once-daily regimen, whereas they were outside the target concentration range for 50% of the patients with a twice-daily regimen (Fig. 3). These results are consistent with those obtained by evaluation of a once-daily dosing regimen for gentamicin in neonates (52). They have important clinical implications, as the outcome depends on the maximum concentration in plasma in patients treated with aminoglycosides (2, 35-37). The higher the maximum concentration, the better the outcome. In conclusion, we recommend that neonates, infants, and children receive the same once-daily dosing regimen with a daily dose of 15 mg/kg, as this regimen gives higher maximum concentrations than the concentrations obtained with a twice-daily regimen.
REFERENCES
- 1.Assael, B. M., R. Parini, F. Rusconi, and G. Cavanna. 1982. Influence of intrauterine maturation on the pharmacokinetics of amikacin in the neonatal period. Pediatr. Res. 16:810-815. [DOI] [PubMed] [Google Scholar]
- 2.Beaucaire, G., O. Leroy, C. Beuscart, P. Karp, C. Chidiac, and M. Caillaux. 1991. Clinical and bacteriological efficacy, and practical aspects of amikacin given once daily for severe infections. J. Antimicrob. Chemother. 27(Suppl. C):91-103. [DOI] [PubMed] [Google Scholar]
- 3.Blackfan, K. 1961. Body water compartments in children: changes during growth and related changes in body composition. Pediatrics 28:169-181. [PubMed] [Google Scholar]
- 4.Botha, J. H., M. J. du Preez, R. Miller, and M. Adhikari. 1998. Determination of population pharmacokinetic parameters for amikacin in neonates using mixed-effect models. Eur. J. Clin. Pharmacol. 53:337-341. [DOI] [PubMed] [Google Scholar]
- 5.Bouffet, E., C. Fuhrmann, D. Frappaz, D. Couillioud, V. Artiges, C. Charra, D. Bouhour, and M. Brunat Mentigny. 1994. Once daily antibiotic regimen in paediatric oncology. Arch. Dis. Child. 70:484-487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bueva, A., and J. P. Guignard. 1994. Renal function in preterm neonates. Pediatr. Res. 36:572-577. [DOI] [PubMed] [Google Scholar]
- 7.Burtin, P., E. Jacqz-Aigrain, P. Girard, R. Lenclen, J. Magny, P. Betremieux, C. Tahiry, L. Desplanques, and P. Mussat. 1994. Population pharmacokinetics of midazolam in neonates. Clin. Pharmacol. Ther. 56:615-625. [DOI] [PubMed] [Google Scholar]
- 8.Craig, W. A. 2001. Does the dose matter? Clin. Infect. Dis. 33(Suppl. 3):S233-S237. [DOI] [PubMed] [Google Scholar]
- 9.Davies, M. W., and D. W. Cartwright. 1998. Gentamicin dosage intervals in neonates: longer dosage interval--less toxicity. J. Paediatr. Child. Health 34:577-580. [DOI] [PubMed] [Google Scholar]
- 10.Dehoog, M., R. C. Schoemaker, J. W. Mouton, and J. N. Vandenanker. 1997. Tobramycin population pharmacokinetics in neonates. Clin. Pharmacol. Ther. 62:392-399. [DOI] [PubMed] [Google Scholar]
- 11.Dodge, W. F., R. W. Jelliffe, C. J. Richardson, R. A. McCleery, J. A. Hokanson, and W. R. Snodgrass. 1991. Gentamicin population pharmacokinetic models for low birth weight infants using a new nonparametric method. Clin. Pharmacol. Ther. 50:25-31. [DOI] [PubMed] [Google Scholar]
- 12.Ettlinger, J. J., K. A. Bedford, A. M. Lovering, D. S. Reeves, B. D. Speidel, and A. P. MacGowan. 1996. Pharmacokinetics of once-a-day netilmicin (6 mg/kg) in neonates. J. Antimicrob. Chemother. 38:499-505. [DOI] [PubMed] [Google Scholar]
- 13.Falcao, A. C., M. M. Fernandez de Gatta, M. F. Delgado Iribarnegaray, D. Santos Buelga, M. J. Garcia, A. Dominguez-Gil, and J. M. Lanao. 1997. Population pharmacokinetics of caffeine in premature neonates. Eur. J. Clin. Pharmacol. 52:211-217. [DOI] [PubMed] [Google Scholar]
- 14.Fattinger, K., S. Vozeh, A. Olafsson, J. Vlcek, M. Wenk, and F. Follath. 1991. Netilmicin in the neonate: population pharmacokinetic analysis and dosing recommendations. Clin. Pharmacol. Ther. 50:55-65. [DOI] [PubMed] [Google Scholar]
- 15.Ferriols-Lisart, R., and M. Alos-Alminana. 1996. Effectiveness and safety of once-daily aminoglycosides: a meta-analysis. Am. J. Health Syst. Pharm. 53:1141-1150. [DOI] [PubMed] [Google Scholar]
- 16.Freeman, C. D., D. P. Nicolau, P. P. Belliveau, and C. H. Nightingale. 1997. Once-daily dosing of aminoglycosides: review and recommendations for clinical practice. J. Antimicrob. Chemother. 39:677-686. [DOI] [PubMed] [Google Scholar]
- 17.Hayani, K. C., F. K. Hatzopoulos, A. L. Frank, M. R. Thummala, M. J. Hantsch, B. M. Schatz, E. G. John, and D. Vidyasagar. 1997. Pharmacokinetics of once-daily dosing of gentamicin in neonates. J. Pediatr. 131:76-80. [DOI] [PubMed] [Google Scholar]
- 18.Isemann, B. T., U. R. Kotagal, S. M. Mashni, E. J. Luckhaupt, and C. J. Johnson. 1996. Optimal gentamicin therapy in preterm neonates includes loading doses and early monitoring. Ther. Drug Monit. 18:549-555. [DOI] [PubMed] [Google Scholar]
- 19.Iwai, N., A. Sasaki, Y. Taneda, F. Mizoguchi, H. Nakamura, M. Kawamura, N. Tauchi, T. Ozaki, T. Ichikawa, and S. Matsui. 1987. Pharmacokinetics in neonates and infants following administration of amikacin. Jpn. J. Antibiot. 40:1157-1175. (In Japanese.) [PubMed] [Google Scholar]
- 20.Jaresko, G. S., B. A. Boucher, E. J. Dole, E. A. Tolley, and T. C. Fabian. 1989. Risk of renal dysfunction in critically ill trauma patients receiving aminoglycosides. Clin. Pharmacol. 8:43-48. [PubMed] [Google Scholar]
- 21.Jensen, P. D., B. E. Edgren, and R. C. Brundage. 1992. Population pharmacokinetics of gentamicin in neonates using a nonlinear, mixed-effects model. Pharmacotherapy 12:178-182. [PubMed] [Google Scholar]
- 22.Kafetzis, D. A., C. A. Sinaniotis, C. J. Papadatos, and J. Kosmidis. 1979. Pharmacokinetics of amikacin in infants and pre-school children. Acta Paediatr. Scand. 68:419-422. [DOI] [PubMed] [Google Scholar]
- 23.Kenyon, C. F., D. C. Knoppert, S. K. Lee, H. M. Vandenberghe, and G. W. Chance. 1990. Amikacin pharmacokinetics and suggested dosage modifications for the preterm infant. Antimicrob. Agents Chemother. 34:265-268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kotze, A., P. R. Bartel, and D. K. Sommers. 1999. Once versus twice daily amikacin in neonates: prospective study on toxicity. J. Paediatr. Child. Health 35:283-286. [DOI] [PubMed] [Google Scholar]
- 25.Krivoy, N., S. Postovsky, R. Elhasid, and M. W. Ben Arush. 1998. Pharmacokinetic analysis of amikacin twice and single daily dosage in immunocompromised pediatric patients. Infection 26:396-398. [DOI] [PubMed] [Google Scholar]
- 26.Lanao, J. M., A. Dominguez-Gil, A. A. Dominguez-Gil, S. Malaga, M. Crespo, and F. Nuno. 1982. Modification in the pharmacokinetics of amikacin during development. Eur. J. Clin. Pharmacol. 23:155-160. [DOI] [PubMed] [Google Scholar]
- 27.Langhendries, J. P., O. Battisti, J. M. Bertrand, A. Francois, J. Darimont, S. Ibrahim, P. M. Tulkens, A. Bernard, J. P. Buchet, and E. Scalais. 1993. Once-a-day administration of amikacin in neonates: assessment of nephrotoxicity and ototoxicity. Dev. Pharmacol. Ther. 20:220-230. [DOI] [PubMed] [Google Scholar]
- 28.Langhendries, J. P., O. Battisti, J. M. Bertrand, A. Francois, M. Kalenga, J. Darimont, E. Scalais, and P. Wallemacq. 1998. Adaptation in neonatology of the once-daily concept of aminoglycoside administration: evaluation of a dosing chart for amikacin in an intensive care unit. Biol. Neonate 74:351-362. [DOI] [PubMed] [Google Scholar]
- 29.Lee, T. C., B. G. Charles, G. J. Harte, P. H. Gray, P. A. Steer, and V. J. Flenady. 1999. Population pharmacokinetic modeling in very premature infants receiving midazolam during mechanical ventilation--midazolam neonatal pharmacokinetics. Anesthesiology 90:451-457. [DOI] [PubMed] [Google Scholar]
- 30.Mallet, A. 1986. Maximum likelihood estimation method for random coefficient regression models. Biometrika 73:645-656. [Google Scholar]
- 31.Mallet, A., F. Mentre, J. L. Steimer, and F. Lokiec. 1988. Nonparametric maximum likelihood estimation for population pharmacokinetics, with application to cyclosporin. J. Pharmacokinet. Biopharm. 16:311-327. [DOI] [PubMed] [Google Scholar]
- 32.Mentre, F., F. Pousset, E. Comets, B. Plaud, B. Diquet, G. Montalescot, A. Ankri, A. Mallet, and P. Lechat. 1998. Population pharmacokinetic-pharmacodynamic analysis of fluindione in patients. Clin. Pharmacol. Ther. 63:64-78. [DOI] [PubMed] [Google Scholar]
- 33.Mesnil, F., C. Dubruc, F. Mentre, S. Huet, A. Mallet, and J. P. Thenot. 1997. Pharmacokinetic analysis of mizolastine in healthy young volunteers after single oral and intravenous doses: noncompartmental approach and compartmental modeling. J. Pharmacokinet. Biopharm. 25:125-147. [DOI] [PubMed] [Google Scholar]
- 34.Mirochnick, M., E. Capparelli, W. Dankner, R. S. Sperling, R. van Dyke, and S. A. Spector. 1998. Zidovudine pharmacokinetics in premature infants exposed to human immunodeficiency virus. Antimicrob. Agents Chemother. 42:808-812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Moore, R. D., P. S. Lietman, and C. R. Smith. 1987. Clinical response to aminoglycoside therapy: importance of the ratio of peak concentration to minimal inhibitory concentration. J. Infect. Dis. 155:93-99. [DOI] [PubMed] [Google Scholar]
- 36.Moore, R. D., C. R. Smith, and P. S. Lietman. 1984. The association of aminoglycoside plasma levels with mortality in patients with gram-negative bacteremia. J. Infect. Dis. 149:443-448. [DOI] [PubMed] [Google Scholar]
- 37.Moore, R. D., C. R. Smith, and P. S. Lietman. 1984. Association of aminoglycoside plasma levels with therapeutic outcome in gram-negative pneumonia. Am. J. Med. 77:657-662. [DOI] [PubMed] [Google Scholar]
- 38.Munckhof, W. J., M. L. Grayson, and J. D. Turnidge. 1996. A meta-analysis of studies on the safety and efficacy of aminoglycosides given either once daily or as divided doses. J. Antimicrob. Chemother. 37:645-663. [DOI] [PubMed] [Google Scholar]
- 39.Padovani, E. M., C. Pistolesi, V. Fanos, A. Messori, and N. Martini. 1993. Pharmacokinetics of amikacin in neonates. Dev. Pharmacol. Ther. 20:167-173. [DOI] [PubMed] [Google Scholar]
- 40.Parzen, E. O. 1962. On estimation of probability density function and model. Ann. Math. Stat. 33:1065-1076. [Google Scholar]
- 41.Petersen, P. O., T. G. Wells, and G. L. Kearns. 1991. Amikacin dosing in neonates: evaluation of a dosing chart based on population pharmacokinetic data. Dev. Pharmacol. Ther. 16:203-211. [PubMed] [Google Scholar]
- 42.Philips, J. B. D., M. Geerts, A. Dew, and G. Cassady. 1983. The accuracy of amikacin administration in neonates. Pediatr. Pharmacol. (New York) 3:127-130. [PubMed] [Google Scholar]
- 43.Pons, G., P. d'Athis, E. Rey, D. de Lauture, M. O. Richard, J. Badoual, and G. Olive. 1988. Gentamicin monitoring in neonates. Ther. Drug Monit. 10:421-427. [DOI] [PubMed] [Google Scholar]
- 44.Rybak, M. J., B. J. Abate, S. L. Kang, M. J. Ruffing, S. A. Lerner, and G. L. Drusano. 1999. Prospective evaluation of the effect of an aminoglycoside dosing regimen on rates of observed nephrotoxicity and ototoxicity. Antimicrob. Agents Chemother. 43:1549-1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sardemann, H., H. Colding, J. Hendel, J. P. Kampmann, E. F. Hvidberg, and R. Vejlsgaard. 1976. Kinetics and dose calculations of amikacin in the newborn. Clin. Pharmacol. Ther. 20:59-66. [DOI] [PubMed] [Google Scholar]
- 46.Semchuk, W., J. Borgmann, and L. Bowman. 1993. Determination of a gentamicin loading dose in neonates and infants. Ther. Drug Monit. 15:47-51. [DOI] [PubMed] [Google Scholar]
- 47.Skopnik, H., R. Wallraf, B. Nies, K. Troster, and G. Heimann. 1992. Pharmacokinetics and antibacterial activity of daily gentamicin. Arch. Dis. Child. 67:57-61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Taddio, A. 1998. Is there evidence for routine therapeutic drug monitoring in paediatric patients?, p. 353-376. In G. Koren and O. Diav-Citrin (ed.), Paediatric pharmacology: toward evidence-based drug therapy, vol. 6. Baillere Tindall, London, United Kingdom. [Google Scholar]
- 49.Townsend, P. L., M. P. Fink, K. L. Stein, and S. G. Murphy. 1989. Aminoglycoside pharmacokinetics: dosage requirements and nephrotoxicity in trauma patients. Crit. Care Med. 17:154-157. [PubMed] [Google Scholar]
- 50.Treluyer, J., E. Rey, and G. Pons. 1998. Pharmacokinetic principles in paediatric pharmacology: proof of differences beyond the neonatal period, p. 399-418. In G. Koren and O. Diav-Citrin (ed.), Paediatric pharmacology: toward evidence-based drug therapy, vol. 6. Baillere Tindall, London, United Kingdom. [Google Scholar]
- 51.Treluyer, J. M., Y. Merle, A. Semlali, and G. Pons. 2000. Population pharmacokinetic analysis of netilmicin in neonates and infants with use of a nonparametric method. Clin. Pharmacol. Ther. 67:600-609. [DOI] [PubMed] [Google Scholar]
- 52.Vervelde, M. L., C. M. Rademaker, T. G. Krediet, A. Fleer, P. van Asten, and A. van Dijk. 1999. Population pharmacokinetics of gentamicin in preterm neonates: evaluation of a once-daily dosage regimen. Ther. Drug Monit. 21:514-519. [DOI] [PubMed] [Google Scholar]
- 53.Weber, W., G. Kewitz, K. L. Rost, M. Looby, M. Nitz, and L. Harnisch. 1993. Population kinetics of gentamicin in neonates. Eur. J. Clin. Pharmacol. 44(Suppl. 1):S23-S25. [DOI] [PubMed] [Google Scholar]
- 54.Wiest, D. B., J. B. Pinson, P. S. Gal, R. C. Brundage, S. Schall, J. L. Ransom, R. L. Weaver, D. Purohit, and Y. Brown. 1991. Population pharmacokinetics of intravenous indomethacin in neonates with symptomatic patent ductus arteriosus. Clin. Pharmacol. Ther. 49:550-557. [DOI] [PubMed] [Google Scholar]