Phylogenetic and Familial Estimates of Mitochondrial Substitution Rates: Study of Control Region Mutations in Deep-Rooting Pedigrees

Abstract

We studied mutations in the mtDNA control region (CR) using deep-rooting French-Canadian pedigrees. In 508 maternal transmissions, we observed four substitutions (0.0079 per generation per 673 bp, 95% CI 0.0023–0.186). Combined with other familial studies, our results add up to 18 substitutions in 1,729 transmissions (0.0104), confirming earlier findings of much greater mutation rates in families than those based on phylogenetic comparisons. Only 12 of these mutations occurred at independent sites, whereas three positions mutated twice each, suggesting that pedigree studies preferentially reveal a fraction of highly mutable sites. Fitting the data through use of a nonuniform rate model predicts the presence of 40 (95% CI 27–54) such fast sites in the whole CR, characterized by the mutation rate of 274 per site per million generations (95% CI 138–410). The corresponding values for hypervariable regions I (HVI; 1,729 transmissions) and II (HVII; 1,956 transmissions), are 19 and 22 fast sites, with rates of 224 and 274, respectively. Because of the high probability of recurrent mutations, such sites are expected to be of no or little informativity for the evaluation of mutational distances at the phylogenetic time scale. The analysis of substitution density in the alignment of 973 HVI and 650 HVII unrelated European sequences reveals that the bulk of the sites mutate at relatively moderate and slow rates. Assuming a star-like phylogeny and an average time depth of 250 generations, we estimate the rates for HVI and HVII at 23 and 24 for the moderate sites and 1.3 and 1.0 for the slow sites. The fast, moderate, and slow sites, at the ratio of 1:2:13, respectively, describe the mutation-rate heterogeneity in the CR. Our results reconcile the controversial rate estimates in the phylogenetic and familial studies; the fast sites prevail in the latter, whereas the slow and moderate sites dominate the phylogenetic-rate estimations.

Introduction

The mitochondrial genome, and its control region (CR) in particular, is the most analyzed DNA sequence in human evolutionary studies. This popularity is due to the nucleotide diversity of mtDNA, which surpasses that of the nuclear genome, and to its small size, which renders this genetic system easy to analyze. Furthermore, the maternal-only inheritance of the mitochondrial genome and the lack of recombination allow easy reconstruction of the phylogenetic and genealogical connections between individual mitochondrial sequences. The resulting information adds to our understanding of human mtDNA evolution. However, answering questions about the history of human populations also requires accurate timing of genetic and demographic events from the evolutionary past. This timing can be evaluated from the observed mtDNA-sequence variability, given proper calibration of the “mitochondrial clock.” However, striking discrepancies in the CR mutation rates estimated in different studies have indicated problems with this calibration.

The molecular clock calibration typically relies on phylogenetic comparisons. On the basis of the comparisons of human and primate sequences, Ward et al. (1991) estimated the overall rate for hypervariable region I (HVI) at 4.95 per site per million generations (these units, unless otherwise stated, will be used throughout this article). Tamura and Nei (1993) considered the whole CR and determined a lower rate, 1.5. Their estimate was similar to those obtained by Horai et al. (1995): 2.08 and 1.48 for HVI and hypervariable region II (HVII), respectively. Mutation-rate estimates based on interspecific sequence comparison (e.g., between humans and chimpanzees or other extant species) may be skewed by the presence of recurrent mutations due to the too-long phylogenetic branches. To circumvent this problem, Torroni et al. (1994) calibrated the clock on the basis of intraspecific sequence differences. They measured the mtDNA divergence between human populations with documented archeological records, whereby the time of their fission could be inferred with good confidence. The original analysis of the mtDNA sequence screened by restriction enzyme digestion was subsequently extended to the CR sequences and led to a rate estimate, in this segment, of 5.4 (Forster et al. 1996). The pedigree studies reported values ranging from 0 (Soodyall et al. 1997) to 50 (Howell et al. 1996; Parsons et al. 1997), which exceeded by an order of magnitude those estimated by means of phylogenetic comparisons.

It is important to note that different authors have been expressing the mutation rate in a variety of ways, so that it is often difficult to directly compare the reported values. When expressed as number of mutations per segment, the rate estimates for the HVI region (for example) were based on the analysis of fragments of different lengths (<300–360 nucleotides). When the conversion to the per-site–per-year units was applied, the time used as the length of a generation varied: 20, 26, or 30 years. For this reason, we normalized all the rates we referred to by recalculating them into the units used above (per site per million generations). This calculation assumed an average generation time of 20 years for the estimates involving comparisons of human and chimp sequences, and of 30 years for intraspecies comparisons of different human populations. A generation time of 30 years in human populations was suggested by the recent studies by Tremblay and Vezina (2000) and Sigurdardottir et al. (2000) and will be retained throughout this paper for all estimations involving Homo sapiens populations.

The variance in the reported mitochondrial mutation-rate estimates can be due to (i) differences in size and origin of the data sets, (ii) different mutation models, (iii) different assumptions of the divergence time between compared lineages and/or the generation time, (iv) recurrent mutations, especially when the phylogenetic branches are too long, and (v) rate heterogeneity among the sites in segments analyzed (Hasegawa et al. 1993; Wakeley 1993; Excoffier and Yang 1999; Meyer et al. 1999). In this context, perhaps, the difference between the mutation rates estimated from the human pedigree studies and from the earlier phylogenetic studies should not seem surprising (Macaulay et al. 1997; Jazin et al. 1998; Stoneking 2000). As discussed by Sigurdardottir et al. (2000), it is, rather, a phylogenetic rate estimate that may be biased. The familial data, although not plagued by these ambiguities, are by their nature scarce and fragmentary and are subject to a great stochastic variance. In this context, using genealogically related samples is very interesting, because it increases the power of familial studies (Soodyall et al. 1997; Sigurdardottir et al. 2000). For this reason, in the present study, we estimated the mutation rate in the mitochondrial CR using deep-rooting pedigrees in the Quebec population. By combining our results with other data from pedigree studies, we found that mutations, which were preferentially detected in these studies, affected a small fraction of sites characterized by very high substitution rates. We proposed a simple model to take this rate heterogeneity into account and analyzed these results further in the context of the substitution density distribution in an alignment of a large set of nonrelated European mtDNA sequences. Our model, extended to such a data set, confirmed the mutation-rate heterogeneity in the CR region. We conclude that the apparent discordance between the mutation-rate estimates based on the familial and phylogenetic studies simply reflects the “observation window bias” that is introduced by the two approaches if the mutation-rate heterogeneity is not considered; we propose a simple model for taking it into account.

Material and Methods

Pedigrees

Among a large pool of DNA samples from Saguenay region (northeastern Quebec) studied by sequencing of the HVI and HVII regions, we identified 61 maternally related individuals. They belonged to 16 pedigrees in the genealogical database already described (Heyer et al. 1997). The number of generations (corresponding to maternal transmissions) was calculated from the reconstructed genealogies shown in figure 1.

Figure 1.

Maternal pedigrees relating 61 analyzed individuals shown at the tips of the genealogical trees. The individuals in whom substitutions were found are indicated by a number reflecting the position of the mutated site.

Molecular Analysis

DNA from the peripheral blood leukocytes were obtained by standard methods. The genomic samples were used to amplify the mitochondrial CR between positions 15926 and 00580, using primers MTL 15926 (5′-TCA AAG CTT ACA CCA GTC TTG TAA ACC) and MTH 00580 (5′-TTG AGG AGG TAA GTC ACA TA). Reactions were performed in 20-μl aliquots, using 15 ng DNA in 20 mM Tris-HC1 (pH 8.4), 50 mM KCl, 1 μM each primer, 2.5 mM of MgCl₂, 0.2 mM each dNTP, and 1.5 U of Taq DNA Polymerase (Gibco BRL). The amplification was performed in an automatic cycler for 37 cycles of denaturation at 94°C for 45 s, annealing at 50°C for 1 min, and elongation at 72°C for 2 min.

The sequence of HVI was determined between positions 15998 and 16400 by use of primers MTL15997 (5′-CAC CAT TAG CAC CCA AAG CT) and MTH 16401 (5′-TGA TTT CAC GGA GGA TGG TG), and the sequence of HVII was determined between positions 00021 and 000428 by use of primers MTL00020 (5′-GAT CAC AGG TCT ATC ACC CT) and MTH00429 (5′-CTG TTA AAA GTG CAT ACC GCC). However, following Sigurdardottir et al. (2000), only 360 nucleotides between positions 16024 and 16383 of HVI and 313 nucleotides between positions 58 and 370 of HVII were considered in the analysis.

Sequencing was carried out using the Thermo Sequenase kit from Amersham, following manufacturer’s recommendations. Reaction products were revealed by electrophoresis in a 6%-acrylamide denaturing gel, followed by autoradiography (exposure for 12 h at room temperature to a BIOMAX X-ray Kodak film). Since our objective was to reveal the differences rather than to determine the already known sequence, the reaction products ending with a particular base were loaded side-by-side, facilitating the “differential” reading.

European CR sequences

The European sequences were obtained directly from HVRbase (Handt et al. 1998), and only those which represented the “full length” HVI (360 nt) and HVII (313 nt) sequences were retained for the analysis. For HVI, 973 sequences comprised samples from Austria (n=101 [Parson et al. 1998]), Germany (n=321 [Richards et al. 1996; Baasner et al. 1998; Lutz et al. 1998]), Norway (n=216 [Opdal et al. 1998]), Switzerland (n=76 [Pult et al. 1994]), Italy (n=57 [Di Rienzo and Wilson 1991; Francalacci et al. 1996; Brown et al. 1998]), Great Britain (n=100 [Anderson et al. 1981; Piercy et al. 1993]), Finland (n=23 [Pult et al. 1994]), France (n=50 [Rousselet and Mangin 1998]), Bulgaria (n=30 [Calafell et al. 1996]), and mixed Europeans (n=11 [Vigilant et al. 1991; Brown et al. 1998]). For HVII, 650 sequences were from Great Britain (n=96 [Anderson et al. 1981; Piercy et al. 1993]), Austria (n=101 [Parson et al. 1998]), Bulgaria (n=30 [Calafell et al. 1996]), Italy (n=5 [Brown et al. 1998]), France (n=50 [Rousselet and Mangin 1998]), Germany (n=317 [Hofmann et al. 1997; Baasner et al. 1998; Lutz et al. 1998]), mixed Europeans (n=22 [Vigilant et al. 1991; Brown et al. 1998]), and Hispanics from the United States (n=29 [Reynolds et al. 2000]).

Statistical Analyses

Both (1) the analysis of the data by nonlinear regression curve fitting, according to equations defined in the text, and (2) the simulation of the theoretical curves were done using the GraphPad Prism v.3.02 program package. The fits were robust, converging to the same values for a variety of initial parameters. The goodness of fit was judged by the sum of squares and r², as well as by visual inspection of the resulting plots. The maximum-likelihood approach yielded the same results. The counting of the number of substitutions per position (site occupancies) in the alignment of sequences was computer assisted, using a program written by M. O’Gleman.

Results

Pedigree Analysis

The mitochondrial CR sequences were analyzed in 61 individuals traceable to 16 “founding mothers” from the Charlevoix/Saguenay region. The 16 corresponding pedigrees included a total of 508 independent maternal transmissions, 4–89 per genealogy (fig. 1). The sequences were obtained for both HVI and HVII regions of the CR sequence. To be consistent with other studies (see Sigurdardottir et al. [2000] and references therein), we considered HVI as being delimited by positions 16024–16383 and HVII by positions 58–370 (numbering according to Anderson et al. [1981]), for a total of 360 and 313 base pairs, respectively. Two substitutions were detected in HVI, at positions 16298 and 16311; each was found in a different pedigree and within a different haplotype. Two substitutions were also observed in HVII, at positions 146 and 195; here, however, both were in the same haplotype and the same pedigree. All substitutions represented transitions involving pyrimidines: 16311T→C on the background of haplogroup H sequence (according to Macaulay et al. 1999), 16298C→T on the background of haplogroup V, and 146T→C and 195T→C on the background of haplogroup K. The proposed direction of mutations is from the major to minor allele in the pedigree. For each mutation detected, the CR was amplified and sequenced again and, when available, a closely related individual was also sequenced (3 of 4 cases). We assumed that each confirmed change within a pedigree reflected a mutation and not a case of illegitimacy. The rate of illegitimacy in the Quebec population is very low. On the basis of the molecular analysis of the Y chromosomes in the paternal pedigree, it was estimated at 1/83 for a male transmission (Heyer et al. 1997); therefore, it can be expected that this rate is much lower for the female transmission.

Given four substitutions in 508 meioses, the overall CR mutation rate can be estimated at 0.0079 per 673-bp segment per generation—that is, 11.7 per site per million generations, with 95% confidence interval [CI] 3.4–27.5. The per-site mutation-rate estimates calculated separately for HVI and HVII segments have the same value, 11.7, with 95% CI 2.1–31.6. In addition, we found five instances of length changes within the oligo-C tract, starting at position 308 in HVII: three were length reductions by one C, one was a C addition, and one was also a change of one C, but, in this instance, we could not determine the direction of change. The rate of indels at this oligo-C tract, which is effectively a single multiallelic site, was thus 5 per 508 generations or ∼9,840 per million generations (95% CI of 3,500–21,000)—almost the same as the rate of 9,900 estimated elsewhere (Sigurdardottir et al. 2000). Because of its known high mutation rate (Hauswirth and Clayton 1985), the (C₃₀₈)_n site was considered separately and was not included in the following analysis.

Mutation-Rate Heterogeneity

The compilation of the data from different familial studies (table 1) shows that sites 16093, 195, and 207 each mutated twice. Is this to be expected under a uniform-rate model (see references in table 1)? If rare events, such as substitutions, occur randomly—that is, if they affect all sites of the analyzed sequence with similar probabilities—their distribution is expected to be Poisson: P(X)=e^-λλ^X/X!, where X=0, 1, 2,…, etc. and is the number of substitutions per site (site occupancy), and P(X) is the probability of sequence sites having exactly X substitutions. The site occupancy denotes the number of substitutions per site, and the sites that share the same number of substitutions fall within the same occupancy class (X=0, 1, 2, etc.). In an alignment of sequences (see below) the site occupancy refers to the count of a minor allele at a given sequence position. The Poisson parameter λ corresponds to the observed density of mutations (i.e., 18/673 in the collective data on CR from table 1) and relates the mutation rate μ with the length of the tree T, such that λ=μT. For the pedigree data from table 1, we can directly count the number of transmissions, which corresponds to the size of the tree and equals 1,729 generations.

Table 1.

Mutations Observed in the Familial Studies

Region, Reference(No. of Transmissions),and Position	Mutation	Ref.Allelea	EuropeanFrequency(%)
HVIb:
Parsons et al. 1997 (327):
16092	C→T	T	99.1
16093	T→C	T	94.4
16256	T→C	T	94.4
Sigurdardottir et al. 2000 (705):
16093	T→C	T	94.4
16111	G→A	C	99.5
Present study (508):
16298	C→T	T	96.5
16311	T→C	T	87.0
Soodyall et al. 1997 (108)	None	…	…
Howell et al. 1996 (81)	None	…	…
HVIIc:
Parsons et al. 1997 (327):
94	G→A	G	99.8
185	G→A	G	94.6
189	A→G	A	97.7
207	G→A	G	97.3
207	A→G	G	97.3
234	A→G	A	99.8
Present study (508):
146	T→C	T	93.1
195	T→C	T	82.3
Howell et al. 1996 (81):
152	T→C	T	83.8
195	T→C	T	82.3
Sigurdardottir et al. 2000 (705):
153	A→G	A	95.4
Soodyall et al. 1997 (108)	None	…	…
Jazin et al. 1998 (229)	None	…	…

^aAllele as in the reference sequence (Anderson et al. 1981).

^b1,729 total transmissions; 7 total substitutions.

^c1,956 total transmissions; 11 total substitutions.

To estimate the expected count of sequence positions LP(X) within each site-occupancy class X (X=0, 1, 2,…, etc.), given the random distribution λ and the length L of the sequence, we have to multiply the Poisson probability P(X) by the number of sequence sites L, such that

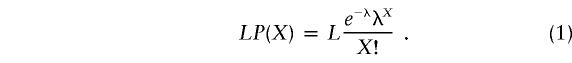Using λ=18/673 (or 0.0267) and L=673 for the CR, we obtain LP(0)=655.3, LP(1)=17.5, and LP(2)=0.2, which do not match the observed values (table 1) of 658, 12, and 3, respectively. This provides a formal demonstration of the inconsistency of the homogenous mutation-rate model for the CR sequence. To account for the heterogeneity in the mutation rate we considered the existence of at least two classes of sites, one characterized by fast and the other by slow substitution rate (f and l, respectively, where f=μ_f and l=μ_l). We assumed that these two classes of sites represent fractions a_f and 1-a_f, respectively, of the total analyzed sequence L. The expected number of sites having accumulated X=0, 1, 2,…, etc. substitutions may be thus described by the two-rate Poisson distribution:

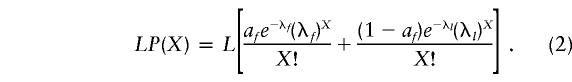Fitting this model’s parameters, we obtain LP(0)=658.0, LP(1)=12.0, and LP(2)=2.9, which represent the data much better (F test ratio 355 for P<.0001, favoring eq. [2] over eq. [1]). Given the limited number of mutations observed, it was reasonable to assume that the fast sites dominated the data and that practically no information about the remaining sites existed. The estimate of the rate f in the range of 200–300 per site per million generations (table 2) was obtained by fixing the slow mutation rate l at 0; the fit progressively deteriorated for l>0. The f estimates were very similar for the whole CR and for the HVI and HVII considered separately. The proportion a_f of the fast sites (0.06) also agreed almost perfectly between the whole CR and both HV segments (table 2).

Table 2.

Parameters of the Fast Sites from the Pedigree Data

Parameter	CR	HVI	HVII
L	673	360	313
g	1,729	1,729	1,956
Fitted parameter:
f (95% CI)a	274 ± 32 (138–412)	224 ± 21 (134–314)	274 ± 36 (121–315)
af (95% CI)	.060 ± .004 (.041–.079)	.053 ± .003 (.039–.067)	.071 ± .006 (.047–.096)
Lf=afL (95% CI)	40 ± 3 (28–53)	19 ± 1 (14–24)	22 ± 2 (15–30)

^aPer site per million generations.

In conclusion, the familial data from table 1 are better represented by assuming a double-rate model (eq. 2) than a single-rate one (eq. 1). This, in fact, is not a novel observation; the mutation-rate heterogeneity in the mitochondrial CR has already been recognized in earlier studies (Di Rienzo and Wilson 1991; Hasegawa and Horai 1991; Hasegawa et al. 1993; Wakeley 1993; Macaulay et al. 1997; Jazin et al. 1998; Excoffier and Yang 1999; Meyer et al. 1999; Stoneking 2000; and many others). The double-rate model, in spite of its simplicity, provides a straightforward explanation of the discrepancy between the familial and phylogenetic estimates of the mitochondrial mutation rate. The high rate of substitution appears to characterize only a small fraction of sites. When fitted to a gamma distribution, this heterogeneity in mutation rate leads to a shape parameter α of 0.0487. The very large confidence interval (0.0149–0.298) around this value indicates that, in our case, such an approach seems less powerful than a two-rate Poisson model. Interestingly, the (C₃₀₈)_n microsatellite mutation rate (of 9,840) is 30–40 times faster than the substitution rates (of 224–274) for the fast sites within the CR sequence (table 2), suggesting that its variability is due to a different mutation mechanism.

Substitution-Density Distribution in the Alignment of Nonrelated Sequences

To investigate how the pedigree-based mutation-rate estimates compare to the phylogenetic estimates from the alignments of population samples, we analyzed European CR sequences from the HVRbase (Handt et al. 1998). In a “starlike” phylogeny that is characteristic of mtDNA evolution (Rogers and Harpending 1992; Sherry et al. 1994; Watson et al. 1997; Richards et al. 1998; Torroni et al. 1998), one expects random distribution of the number of mutations among individual sequence positions representing distinct lineages, as in the sequences from deep-rooting pedigrees. In a simple model of a stationary population followed by demographic expansion, most of the mutations will occur during the expansion phase (see Appendix). Since relatively fewer data were available for the whole CR, we analyzed separately the HVI and HVII segments. The alignments of 973 HVI sequences (360 bp long) and of 650 HVII sequences (313 bp long) were obtained from the HVRbase (March 2001). The distribution of the substitution density in the analyzed HVI and HVII alignments is shown in figures 2 and 3, respectively. Here, the count of sites within the same occupancy class is shown on the Y-axis, thus grouping sequence positions in the alignment sharing the same number of substitutions (i.e., the same site occupancy X=0, 1, 2,…, etc.) as indicated on the X-axis.

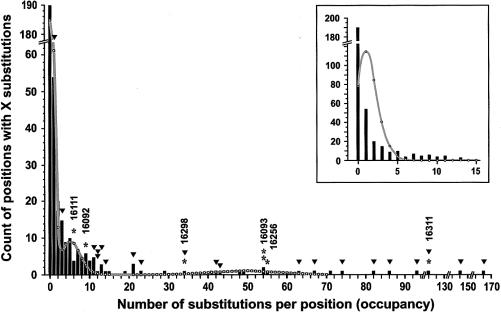
Figure 2.

Substitution-density distribution among the sites in the alignment of 973 HVI sequences from Europe (HVI being delimited by positions 16024–1683). Bars represent the counts of the positions characterized by a given site occupancy (i.e., X=0, 1, 2, 3,…; for each position, the occupancy describes the number of sequences in the alignment that carry the less frequent allele). Note that, to accommodate all data, the scales on both axes are not kept uniform. The continuous line is the theoretical curve based on the fitted parameters describing “slow” and “moderate” sites (table 3). Asterisks (*) indicate the sites that were mutated in the familial studies from table 1; the corresponding sequence positions are shown above. The mean mutation density of 48, used to draw the theoretical curve for the “fast” sites, represented the average substitution density among these “familial” sites; we assumed 19 such sites in the whole sequence (table 2). Inverted triangles indicate the sites found to be correlated with the haplogroups; if not rapidly mutating, these sites should be IBD. Inset shows the low-occupancy sites (bars) and a theoretical curve generated according to a single-rate model (eq. [3]) using a cumulative substitution density of the sites up to X=12.

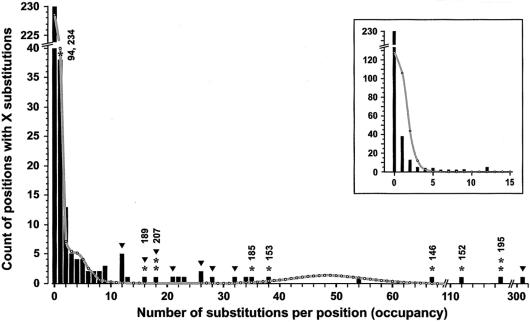
Figure 3.

Substitution-density distribution among the sites in 650 European HVII sequences (HVII being delimited by positions 58–370). The mean mutation density used to draw the theoretical curve for the fast sites was 48.9, and their number was assumed to be 22 (according to table 2). The meaning of the bars, asterisks, numbers, and triangles is the same as in figure 2. Inset shows the low-occupancy sites (bars) and a theoretical curve generated according to a single-rate model (eq. [3]) using a cumulative substitution density of the sites up to X=12.

Inspection of the histograms (in figs. 2 and 3) reveals a heterogeneous group of sites with occupancy of up to a few hundred (the right side of the distribution). This group comprises most of the fast sites that were seen mutated in the familial studies (reported in table 2 and indicated in figs. 2 and 3 by asterisks and the corresponding sequence position above). Intermingled with these sites are those that are likely to be identical by descent (IBD; indicated by inverted triangles); they have been identified elsewhere (Richards et al. 1996; Torroni et al. 1996; Macaulay et al. 1999) and found to correlate with (or to be “diagnostic” for) the European mitochondrial lineages or haplogroups (see also the Discussion section). The low-occupancy sites are on the left side of the distribution. Note that the shape of this part of the distribution is related to the number of sequences compared; when more sequences are analyzed (as in HVI), the sites with no substitutions (X=0) are relatively less numerous. Nevertheless, in both hypervariable regions (figs. 2 and 3) the low-occupancy sites distribution appears biphasic, suggesting the presence of two separate groups, of “slow” and “moderate” sites. To find the parameters that would best describe the substitution density among these sites, we again compared the data with the theoretical expectation according to a single-rate mutation model,

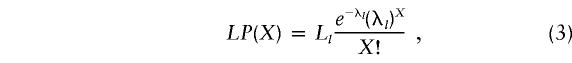and a double-rate mutation model,

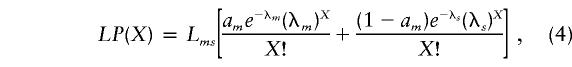where L_l=L_ms denotes the number of sequence positions involved (i.e., the length of the sequence minus the rapidly mutating f sites), a_m is the fraction of moderate sites within L_ms, and λ=μT, as in the previous section. In this case, T=gn, where n corresponds to the number of sequences in the alignment and g to the average time depth, in generations, of a starlike phylogeny (or to the average time since expansion; see Appendix). Here, we have λ_l=lgn, λ_m=mgn, and λ_s=sgn, where l, m, and s denote mutation rates (μ_l, μ_m, and μ_s, respectively), either a single one for all low occupancy sites, or separate for moderate sites and slow sites, respectively.

Equation (3), with the substitution-density characteristics of the low-occupancy sites (here, the sites with X=12), fails to adequately represent the data (see insets in figs. 2 and 3). Comparison of the fits of the two models represented by equations (3) and (4) indicates again that the double-rate Poisson distribution better describes the low-occupancy sites (see the corresponding theoretical curve). The fitted parameters of the double-rate model are given in table 3. They did not significantly differ from those obtained when the high-occupancy sites in figures 2 and 3 were disregarded during the fitting (not shown), indicating that the high-occupancy sites weighted little in the fit according to double-rate Poisson distribution. The absolute estimates of s and m mutation rates presented in table 3 were calculated with the time since expansion in Europe assumed to be 250, 500, or 1,000 generations, to cover the time range of 7,500, 15,000, or 30,000 years, respectively, with time per generation assumed to be 30 years (Sigurdardottir et al. 2000; Tremblay and Vezina 2000).

Table 3.

Parameters of the Moderate and Slow Sites Based on the Alignment of European Sequences

Fitted Parameter	HVIa			HVIIb
Lms (95% CI)	310 (263–358)			297 (256–337)
am (95% CI)	.173 (.111–.235)			.088 (.04–.13)
Lm=Lam (95% CI)	54 (34–73)			6 (13–40)
	g=250	g=500	g=1,000	g=250	g=500	g=1,000
mc (95% CI)	23.0 (17.4–28.8)	11.5 (8.7–14.4)	5.8 (4.3–7.2)	24.4 (15.2–33.6)	12.2 (7.6–16.8)	6.1 (3.8–8.4)
sc (95% CI)	1.35 (.88–1.52)	.67 (.44–.91)	.34 (.22–.45)	1.05 (.62–1.47)	.52 (.31–.74)	.26 (.16–.37)

^aL=360; n=973.

^bL=313; n=650.

^cPer site per million generations.

Phylogenetic Perspective and the “Fast” Sites

For the majority of the “familial” sites observed to be mutated in the pedigree studies (table 1), their placement within the mutation-density distribution (indicated by asterisks in figs. 2 and 3) clearly shows that they represent a distinct class of “fast” sites occurring outside the biphasic m and s distribution. The average mutation density λ_f for these particular sites was calculated as a sum of their observed site occupancy, divided by the number of sequence positions involved (table 1). The resulting values were 48 for the HVI segment and 49 for the HVII segment. Using these λ_f values as the Poisson parameter describing fast sites in the alignments (this parameter being a product of the mutation rate, the average number of generations since expansion, and the number of sequences in the analyzed alignment—i.e., λ_f=fgn) and taking 19 and 22 as the corresponding number of fast sites (L_f) in HVI and HVII, respectively, as well as the corresponding estimates of f (see table 2), we generated the rightmost segments of the theoretical curves in figures 2 and 3. However, the observed fast sites exhibit great variance and overlap poorly with the expected theoretical distribution. Nevertheless, assuming that this distribution represents an idealized average, one can use the average substitution densities λ_f to evaluate the historical depth of the starlike phylogeny. For the HVI sequences, we obtained 220 generations or 6,600 years, and for the HVII sequences 275 generations or 8,250 years. Although each of these values is associated with a large variance, they both point to ∼7,000–8,000 years and, therefore, to the early Neolithic as the time of expansion. However, we have to consider that the sequences contributing to the alignment are mostly of northern European origin (see Material and Methods section) and that perhaps, given the great variance, the estimate of 250 generations is not significantly different from 500 generations. The estimated time since expansion is close to the real one when the effective population size before expansion is small (see Appendix). Furthermore, this is an overall estimate, and ages of the contributing lineages may differ substantially (Torroni et al. 1998; Richards et al. 2000). On the other hand, note that each substitution at the “familial” sites was conservatively assumed to represent an independent mutation event; assuming the substitutions at these sites to be IBD, rather than independent, would further reduce the time depth estimated in this way. In this context, among the absolute rate estimates s and m for slow and moderate sites in table 3, those calculated assuming a matching historical depth of 250 generations may be considered as the most likely.

In conclusion, significant substitution rate heterogeneity observed in HVI and HVII can be explained in terms of three classes of sequence sites. These classes, characterized by the high, moderate, and small occupancy, are characterized by the substitution rates in the order of 250, 24, and 1.2 substitutions per site per million generations (or ∼8, 0.8, and 0.04 per site per million years), respectively, and, in the whole CR (673 positions), they occur at the proportions of 1:2:13 (tables 2 and 3).

However, not all the sites can be accounted for by these three categories. Some of the sites in the heterogeneous high-occupancy class, indicated by inverted triangles in figures 2 and 3, have no “familial” mutations reported but have been shown elsewhere to correlate with the European haplogroups (Torroni et al. 1996; Macaulay et al. 1999). This suggests that, rather than representing mutational hot spots, these sites reflect the identity by descent due to the early partitioning of the mitochondrial lineages. In other words, these sites can be considered as “diagnostic” positions discriminating between distinct branches of the European mitochondrial tree. On the other hand, some of these IBD sites appear to represent mutational hot spots as well (Excoffier and Yang 1999), suggesting that the correlation of the diagnostic substitutions with the phylogenetic branching of the European haplogroups might not be absolute at the CR level, as pointed out elsewhere (Torroni et al. 1994; Macaulay et al. 1999). In the Appendix we show, in a plausible model of mtDNA evolution, that the sites with higher mutation rate have a higher probability of being IBD. All this, taken together, may increase even further the distribution variance of the familial sites observed in figures 2 and 3, thus undermining our conservative assumption that substitutions at these sites appeared independently.

Discussion

Our overall CR mutation-rate estimate of 11.6 per site per million generations (or 0.0078 per segment per generation) was based on 508 transmissions in deep-rooting pedigrees. This is higher, but not significantly different, than the value of 6.3 reported in the recent pedigree study of a comparable sample size (three mutations in 705 transmissions [Sigurdardottir et al. 2000]). In another study (Soodyall et al. 1997), no mutations were detected in 108 transmissions. On the other hand, two substitutions were observed in 81 transmissions by Howell et al. (1996), and nine substitutions were observed in 327 transmissions by Parsons et al. (1997). Combining all these data (1,729 transmissions) results in the mutation rate of 15.5 (CI 10.3–22.1). Taking into account only those from deep-rooting pedigrees (1,321 transmissions) (Soodyall et al. 1997; Sigurdardottir et al. 2000; the present study) leads to the value of 7.9. The latter, by avoiding experimental problems with heteroplasmy, may provide a more realistic approximation of the overall mutation rate.

On the other hand, we realize that—in spite of its usefulness in evolutionary and population genetic studies—the notion of the overall mutation rate has no real physical meaning in a sequence with rate heterogeneity. The overall rate per site is a virtual quantity that is of use in comparative debates if the compared systems are investigated under ideal conditions, using a sufficient sample size that covers a sufficient time window and using comparable methods of mutation detection. In familial studies, each transmission is monitored (or almost every one, when deep-rooting pedigrees are used), and, in principle, every mutation can be detected, whether it occurs in a hot spot or at a slow site (see discussion by Sigurdadottir et al. [2000]). However, because of the limited number of maternal transmissions studied, the time window is short, favoring observation of fast sites over those where substitutions occur rarely. In other words, the familial studies, which up to now collectively represent <2,000 transmissions (table 1), tended to miss slowly mutating sites. In contrast, the effective time window in an analysis of 1,000 sequences, representing a population whose historical depth exceeds 250 generations, covers >250,000 transmissions. In such an analysis, even sites where substitutions occur once per million generations will be well represented in a sequence of >500 nucleotides. However, the substitution rate at a small fraction of mutational hot spots in this sequence will be difficult to assess, because of recurrent events that cannot be directly observed, unlike those in the familial studies. The problem of recurrent mutations is even less tractable in the “true” phylogenetic analyses involving interspecies sequence comparisons, where two compared sequences are separated by half a million generations (e.g., chimpanzee and human) or more (see discussion by Sigurdardottir et al. [2000]). Since the advent of mtDNA studies in human population genetics, the problem of recurrent mutations has been recognized with the observation of a multiplicity of the most-parsimonious trees representing the phylogeny of the sampled human sequences (Vigilant et al. 1991; Templeton 1992). To circumvent this problem, maximum-parsimony analysis was used by different authors to identify sites with recurrent mutations (Wakeley 1993; Excoffier and Yang 1999; Meyer et al. 1999), and new approaches were developed by creating median networks of mitochondrial sequences, taking into account reticulations due to recurrent mutations (Bandelt et al. 1995). The phenomenon of rate heterogeneity in the mitochondrial sequence has been recognized in early papers on mitochondrial phylogeny (Di Rienzo and Wilson 1991; Vigilant et al. 1991; Hasegawa et al. 1993; Tamura and Nei 1993; Wakeley 1993; Horai et al. 1995; Excoffier and Yang 1999; Meyer et al. 1999) and has been indicated as a major problem in the proper calibration of the mitochondrial clock in dating human evolutionary events. Several authors used gamma distribution as a realistic approximation of the rate heterogeneity (Tamura and Nei 1993; Wakeley 1993; Horai et al. 1995; Excoffier and Yang 1999; Meyer et al. 1999). The advantage of this approach is that, with a limited number of parameters, one can accommodate a large spectrum of sites mutating at very different rates. Use of adjustable parameters may facilitate fitting of the data; however, these parameters may substantially differ among different studies (varying from 0.11 to 0.47). In practice, the authors preferred to work with the discrete classes that can be assigned to describe particular sequence sites (see Richards et al. 1998). Our study shows significant substitution-rate heterogeneity in HVI and HVII that can be described in terms of three classes of sequence sites. These classes are characterized by fast, moderate, and slow mutation rates, on the order of 250, 24, and 1.2 substitutions per site per million generations, respectively, (or ∼8, 0.8, and 0.04 per site per million years, respectively), and in the CR they occur at the proportions of 1:2:13 (tables 2 and 3). We realize that these values may need substantial correction because of the uncertainties associated with their determinations.

The analysis presented in the present article was inspired by that of the repetitive Alu elements that are ubiquitous in the human genome (Labuda and Striker 1989). These elements spread in waves of amplifications throughout the history of the primate lineage (Deininger and Batzer 1993; Jurka 1995; Zietkiewicz et al. 1998). Different Alu subfamilies representing these waves could be recognized by their distinct diagnostic positions and by the fact that they spread in different evolutionary periods. The time of their dispersal could be dated (i) by counting separately fast-mutating positions, within CpG dinucleotides and non-CpG positions, that obey a much slower non-CpG evolutionary clock and (ii) by removing the diagnostic IBD positions from the calculations. The substitutions in slowly mutating non-CpG positions were shown to be Poisson distributed, whereas those at fast CpG positions, mutating according to the CpG clock, followed a binomial distribution. The same applies to the phylogenies of other retroposons, such as B1 elements that proliferated within the rodent genomes or the S1 elements from the plant genomes (Labuda and Striker 1989; Labuda et al. 1991; Deragon et al. 1994). Both calibrations provided congruent estimates of the time of dispersal of different Alu subfamilies in the primate lineage (Batzer and Deininger 1991; Zietkiewicz et al. 1994; Jurka 1995). The fast CpG clock tends to provide more information in a shorter time window and is useful in the analysis of young Alu subfamilies, whereas random mutations at slowly mutating non-CpG positions are more practical in the case of old Alu subfamilies. A similar “Alu paradigm”—that is, separating classes of sites that obey different mutation rates and subtracting positions that are IBD or “diagnostic”—can be used to time the age (since expansion) of different lineages of the mtDNA, whose evolution can be approximated by a starlike phylogeny (Sherry et al. 1994; Watson et al. 1997; Richards et al. 1998; Torroni et al. 1998; Richards et al. 2000). The task here is more difficult and less straightforward than simply separating methylable-CpG and non-CpG position in nuclear DNA sequences or separating synonymous and nonsynonymous sites in protein-coding segments (Horai et al. 1995). However, rapidly accumulating mitochondrial data make the approach feasible. In the HVRbase, we have found 597 European sequences representing “full-length” 673-bp CR (including both HV segments). After subdividing these sequences into haplogroups according to Macaulay et al. (1999), we compared the mutation densities λ_m and λ_s for the global sample of sequences (n=597) and for their subset (n=240) representing the haplogroup H (this is a tentative haplogroup assignment, since a rigorous analysis would require the knowledge of RFLP sites in the coding region that are not included in HVRbase). The densities, obtained by fitting the equation (4) parameters to the substitution distribution data, were: λ_m=3.41 and λ_s=0.17 for the global sample and λ_m=2.6 and λ_s=0.11 for the H sequences. To compare mutation rates based on the values of λ estimated from the alignments, we have to take into account different n values, since λ/n=μg. Then, assuming that the rates μ (either m or s) were the same in the global sample and in the subset of H sequences, we estimated the relative time since expansion of the H haplogroup. Assuming, for the global sample, an average depth of 250 generations since expansion, we obtain an estimate of 474 generations (or ∼14,200 years), based on the m sites, and one of 402 generations (or ∼12,000 years), based on the s sites. These estimates for the H haplogroup sequences agree very well with the corresponding values reported earlier, of 12,600–14,100 years (see table 6 of Torroni et al. [1998]) and ∼15,000 years (see fig. 1 of Richards et al. [2000]). This result additionally validates our estimate of ∼250 generations as an average time depth since expansion in our sample of the European HVI and HVII sequences analyzed separately above (see table 3). Our approach therefore appears to be valuable in dating past human expansions. Nevertheless, additional data from familial studies, and especially those from deep-rooting pedigrees, will be needed to assist the appropriate assignment of sites within different classes and thus the dissection of the multirate mitochondrial clock. Only this will allow us to use the mitochondrial clock (or clocks) adequately, according to the time resolution needed given the depth of the population history we are looking at.

Appendix A

Rogers and Harpending (1992) analyzed nucleotide mismatch distribution in mtDNA data, using a demographic model of a bottleneck followed by a sudden population expansion that occurred in the past. In their analysis, even if the coalescence of the lineages that survived through the bottleneck can go far back in time, it is the population age since expansion that is estimated from the data. Studies by Torroni et al. (1996, 1998), Richards et al. (1996, 1998, 2000), Macaulay et al. (1999), and others have shown that the European mitochondrial pool does not result from a single founder effect but is composed of different lineages (haplogroups) that have expanded at different time periods. Put simply, the Rogers and Harpending (1992) scenario repeated itself locally several times (Takahata 1994). Thus, rather than seeing the European mitochondrial pool as a result of a unique founder effect followed by expansion, a network of starlike phylogenies of different lineages is presented (Richards et al. 1996; Torroni et al. 1996; Richards et al. 1998; Torroni et al. 1998; Macaulay et al. 1999; Richards et al. 2000). The age of each of the lineages corresponds to the time of the underlying founder effect.

In a simple model of population history, a founder effect can be presented as an expansion preceded by a stationary phase. Let g_s generations be the time depth of the stationary phase (height of the tree) and g_e the duration of the expansion (thus g_t=g_s+g_e is the time to the most recent common ancestor). Let N_s be the effective population size during the stationary phase of population history, T the total length of the tree (in generations), T_e the length of the tree during population expansion, and T_s the length during the stationary phase (thus, T=T_e+T_s).

For the expansion, assuming a perfect starlike tree, we have T_e=ng_e, with n representing the sample size. For the stationary phase, the expectation of

where k corresponds to the number of sequences that passed from the stationary phase and were sampled at the end of the expansion. In the case of a perfect starlike expansion, k=n.

Since the expected height of the tree for the stationary phase is g_s=2N_s(1-1/n), and, thus, 2N_s=g_sn/(n-1), the expected total length of the tree is

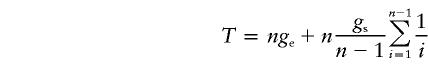and

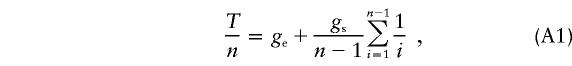while the mutation density λ=Tμ, where μ is the mutation rate. Knowing λ and T, we may calculate the mutation rate as μ=λ/T, as in our cumulative pedigree data, where μ= 18/673/1,729. In an alignment of sequences, assuming starlike phylogeny, we use λ=μgn, where g=T/n is equated with g_e, thus neglecting the second term in equation (A1).

In other words, assumption of a starlike phylogeny in computation of μ, when g>g_e, would underestimate the mutation rate. Using the same model, estimatation of g from λ while knowing μ would overestimate the time since expansion. How important are these effects? From equation (A1), we obtain that g exceeds g_e by

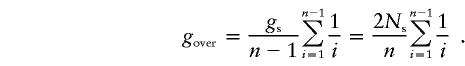For N_s=100 and n=100, g_over=10.46; for N_s=100 and n=500, g_over=2.72. For N_s=1,000, we obtain 104.6 and 27.2, respectively, whereas, for N_s=5,000, we obtain 522 and 136.

In general, therefore, g is very close to g_e, if N_s is not too large and the effect of the latter is substantially reduced by increasing the sample size n. In practice, we have to consider separately the case of simple lineages (haplogroups) and that of the alignment of a collective sample of European sequences. For distinct European haplogroups, it seems likely that N_s was very small (Richards and Macaulay 2001). Therefore, even if their cumulative tree coalesces in the Near East and eventually in Africa (Richards et al. 2000), the previous history of the founding sequences should not weigh much in the estimation of the age of expansion in Europe. Interestingly, on the basis of the above analysis, this conclusion can be tested by estimating the age of the expansion of the lineages at different values of n. If constant as a function of n, it would indicate a severe population bottleneck; if the estimate significantly decreased with n, this would indicate an important contribution of the preceding stationary phase. When considering a mixed sample of European sequences, we cannot neglect their previous common history, preceding the outbursts of individual founding sequences that led to the distinct haplogroups. This preceding history can be modeled within the stationary phase. The mutations occurring at this stage are likely to appear as IBD in different lineages. The probability of a given mutation occurring at this time period rather than during the expansion and thus being IBD is proportional to

with g_over as defined above. For n=500 and g_e=500, the proportion of IBD mutations is expected to be 0.4%, 5%, and 20%, assuming N_s=100, N_s=1,000, and N_s=5,000, respectively. Note that if N_s is small, T_s is small as well. The probability of a given site mutating during the stationary phase is 1-e^-μT_s. Hence, it is more likely that these mutations will occur at fast-mutating sites. This is interesting by itself, since it appears to be the case with many sites that are diagnostic for distinct haplogroups (Macaulay et al. 1999). Importantly, the majority of the IBD sites, like those characterized by a fast mutation rate, appear within the high-occupancy classes (on the right in the distribution in figs. 2 and 3). They are therefore excluded from (or weigh very little in) the fit of the slow and moderate sites, thus reducing the effect of stationary phase mutations on the estimate of mutation density accumulated throughout the expansion phase. This further supports the robustness of the proposed approach to estimation of either the overall age of expansion or that of individual lineages in a population characterized by a starlike phylogeny. The procedure effectively eliminates the IBD sites and the mutation hot spots, thus limiting the analyzed information to the expansion period. By the same token, however, it extracts the sites that are likely to have mutated during the stationary phase and that hence could be informative in a phylogenetic analysis.