Linkage Disequilibrium Mapping of Quantitative-Trait Loci by Selective Genotyping

Abstract

The principles of linkage disequilibrium mapping of dichotomous diseases can be well applied to the mapping of quantitative-trait loci through the method of selective genotyping. In 1999, M. Slatkin considered a truncation selection (TS) approach. We propose in this report an extended TS approach and an extreme-rank-selection (ERS) approach. The properties of these selection approaches are studied analytically. By using a simulation study, we demonstrate that both the extended TS approach and the ERS approach provide remarkable improvements over Slatkin’s original TS approach.

Linkage disequilibrium (LD) mapping has attracted considerable attention from geneticists in recent years. Thompson and Neel (1997) established that LD between closely linked genes is a common phenomenon in human populations. They argued that, for a rare disease, because it is likely the result of a gene variant of relatively recent origin, significant LD between markers separated by a distance ⩽0.5 cM is the usual expectation. In isolated, rapidly expanding populations, the LD is even more striking. In studies of the Finnish disease heritage, LD between markers separated by a distance of 3–13 cM has been observed (Peltonen et al. 1995). With the existence of LD, markers in the vicinity of a disease locus can be used as surrogates in the detection of the disease locus. LD mapping has been successfully applied to dichotomous diseases (MacDonald et al. 1992; Hästbacka et al. 1994; Xiong and Guo 1997; Rannala and Slatkin 1998).

LD mapping has also been applied to QTLs. An appealing method among the existing approaches to LD mapping of QTLs is to dichotomize the quantitative trait so that the same logic as that for dichotomous diseases applies. Laitinen et al. (1997) used an approach to classify individuals into a high group and a low group without the use of selection. Slatkin (1999) used a truncation selection (TS) approach. The TS approach has been considered by Xiong et al. (2002) for LD mapping involving multiple QTLs. Their theoretical results showed how the change in haplotype frequencies caused by TS depends on the effects of gene substitution at an individual trait locus and the epistatic effects between trait loci. The TS approach has been used in other contexts as well (Risch and Zhang 1995; Szatkiewicz and Feingold 2004).

In this report, we make an extension of Slatkin’s TS approach. By taking into account the feasibility of the screening procedure, we also propose an alternative approach—extreme rank selection (ERS)—for selective genotyping. The properties of these selection approaches are analytically studied. A simulation study was conducted to compare these selection approaches in terms of their power in LD mapping.

Let X be the quantitative trait of concern and Q be the QTL. Denote the genotypes of Q by QQ, Qq, and qq. Assume that the Q allele is associated with larger trait values. Let p_Q be the frequency of the Q allele. It is assumed that p_Q is very small. The frequency of the genotype with l Q alleles is denoted by p_l, and the density function of the quantitative trait, given this genotype, is denoted by f_l(x), where l=0,1,2. Let M be a marker in the vicinity of the QTL. Denote the genotypes of M by MM, Mm, and mm. Suppose that the marker is in LD with the QTL. Then the genotypes of M will show an association with the trait. Suppose that the allele M is linked with the Q allele—that is, M is associated with larger trait values.

Let β be a specified upper quantile of the trait distribution. By Slatkin’s TS approach, an upper sample is obtained by screening individuals chosen randomly and then selecting those with trait values exceeding β. In addition to the upper sample, a simple random sample is taken as well. These two samples are then used to test whether there is association between the quantitative trait and the marker under investigation. Slatkin established that the expected frequency of the Q allele in the upper sample is given by

where the second term on the right-hand side of the equation is positive. The genotype QQ is ignored here because of its negligible frequency, p²_Q. Slatkin (1999) also derived that the expected frequency of the M allele in the upper sample is given by

where D is the disequilibrium measure.

We extend Slatkin’s TS approach as follows. Instead of a simple random sample, we draw another selected sample—a lower sample. Besides the upper quantile β, let α be a specified lower quantile. By the extended TS approach, randomly chosen individuals are screened, and those with trait values exceeding β are put into the upper sample and those with trait values less than α are put into the lower sample. The two selected samples are then used for the test. As in the case of the upper sample, it can be established that the expected frequency of the Q allele in the lower sample is given by

where, however, the second term on the right-hand side of the equation is negative. Similarly, the expected frequency of the M allele in the lower sample is given by

It is clear that the difference in the expected Q-allele (or M-allele) frequencies between an upper sample and a lower sample is larger than that between an upper sample and a simple random sample. The increment in the difference between the Q-allele (or M-allele) frequencies accounts for an increment in power for the extended TS approach.

The ERS approach is as follows. Let k be a specified integer. For each selection, k individuals are chosen at random from the population. The trait values of these k individuals are measured and ordered from smallest to largest. Then, the individual with rank 1 is selected as a member of the lower sample and the individual with rank k is selected as a member of the upper sample.

Let p^U_QERS, p^L_QERS, p^U_MERS, and p^L_MERS denote the expected frequencies of the Q allele and M allele in the upper and lower samples obtained by the ERS approach. Our results, which are derived in appendix A, are as follows:

and

where F is the cumulative distribution function of the trait X and where the integrals in equation (1) are all positive and those in (2) are all negative. The equalities (1) and (2) imply that the ERS approach increases the frequency of the Q allele in the upper sample and reduces the frequency of the Q allele in the lower sample. The equalities (3) and (4) imply that the same is true for the M allele if the marker is in LD with the QTL.

Slatkin considered three tests for the original TS approach. These tests can also be applied in the extended TS approach and the ERS approach. In what follows, we describe the tests, with slight modifications.

The first test checks for a significant difference in allele frequencies between the upper sample and the lower sample (or a simple random sample) by using a classical χ² statistic. Let n_L and n_U be the sample sizes of the lower and upper samples, respectively. Let N_L and N_U be the numbers of Q alleles (or M alleles) in the lower and upper samples, respectively. Let

The test statistic is of the form

Under the null hypothesis that there is no QTL (or that the marker is not in LD with the QTL), T₁ has an asymptotic χ² distribution with 1 df.

The second test checks for a significant difference between the mean trait values for different genotypes of the locus under investigation, by use of a t statistic. Only the upper sample is used in this test. Let denote the average trait value and n_l denote the number of zygotes in the upper sample that have l Q alleles (or M alleles), where l=0,1. The zygotes with genotype QQ are ignored because of their negligible number. The second test is based on the t statistic

where

Under the null hypothesis, T₂ has an asymptotic standard normal distribution. A one-sided test using T₂ is adopted for testing the null hypothesis. Slatkin originally used T²₂ as the test statistic, which is equivalent to a two-sided test using T₂.

The third test is derived from the fact that the first and second tests are asymptotically independent, as argued by Slatkin. Let P₁ and P₂ be the P values of the first and second tests, respectively. The third test is based on the statistic

Under the null hypothesis, T₃ has an asymptotic χ² distribution with 4 df.

We compare the three selection approaches by using a simulation study. Hereafter, the original and extended TS approaches will be referred to as the “TS-I” and “TS-II” approaches, respectively. To make a fair comparison, the total sample size n (=n_L+n_U) must be the same for all the approaches, and the screening size must also be approximately the same. In the TS-II approach, let the specified lower and upper quantiles be the τth and (1-τ)th quantiles, respectively. For the ERS and TS approaches to have approximately the same screening size, we take k in ERS to be k=(1/τ). Thus, with the total sample size n, the screening size for the ERS procedure is the fixed number kn/2, and the screening size for the TS procedures is a random variable with mean kn/2.

It is assumed, in the simulation study, that the effects of the QTL alleles are additive—that is, the distribution of trait X has mean 0, ε, and 2ε when the genotype of the QTL is qq, Qq, and QQ, respectively. The frequency of the Q allele (p_Q) is taken to be 0.01 throughout the simulation study. To compare the power among the different approaches, we considered the simulation parameter values as follows. In the case in which the tested locus is a marker locus, we take p_M=0.01 and 0.03; D^′=0.95, 0.85, and 0.50; ε=1.03 and 1.65; and n=400, where D^′=D/[p_Q(1-p_M)]. The two values of ε are chosen such that the heritability is ∼0.02 and 0.05, respectively. In the case in which the tested locus is a putative QTL, we considered eight values of ε in a range from 0.1 to 1.5, with an equal distance of 0.2 between them. The batch size in ERS, k, is taken to be 10 and 20, and the corresponding τ in TS is taken to be 0.1 and 0.05. The power comparison among the different approaches is meaningful only if the type I errors are controlled at approximately the same level. Although the type I errors are controlled at the nominal level asymptotically, we needed to investigate the type I errors for finite sample sizes. To assess the type I errors, we simulated data with ε=0 and p_M=0.01 and 0.03.

For each set of simulation parameter values, 1,000 replicates of ERS samples and TS samples are generated. To mimic the implementation in practice, each replicate of samples is generated as follows. (1) First, nk/2 copies of (X,Q,M) are independently generated, where X is the trait value and Q and M are the genotypes at the QTL and the marker, respectively. (2) To obtain the ERS samples, these nk/2 copies are divided into n/2 sets in sequel, each of size k, and the units in each set are ranked with respect to X, after which the unit with the smallest rank is put into the lower sample and the unit with the largest rank is put into the upper sample. (3) To obtain the upper and lower samples for the TS-II approach, the first half of the nk/2 copies are used to estimate the lower and upper quantiles. The estimated quantiles are then used to screen the whole nk/2 copies, to select the upper and lower samples. If <n units are selected when all the nk/2 copies have been screened, additional copies of (X,Q,M) are generated until the total sample size reaches n. (4) For the TS-I approach, the upper sample is obtained in the same way as in step (3), but the procedure continues until the upper sample size reaches n/2. A simple random sample of size n/2 is then generated separately.

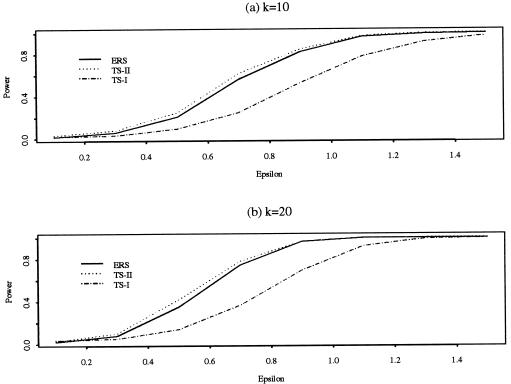
The three tests are performed on the basis of each sample. The nominal size of the tests is set at α=0.01. The proportion of rejections of each test with the same approach among the 1,000 replicates is counted. In the case ε=0, this proportion provides an approximation of the probability of type I error. In the case ε≠0, this proportion provides an approximation of the power of the test. The simulated results for a tested marker locus are reported in table 1. The entries corresponding to h=0 in table 1 are simulated levels (i.e., probabilities of type I error) and those corresponding to h≠0 are simulated powers. The simulated powers for tested putative QTLs are depicted in figure 1 (see also the Statistical Source Web site).

Table 1.

Power Comparison of the Tests at Nominal Level α=0.01 with the TS-I, TS-II, and ERS Approaches

				Simulated Level (Type I Error Probability) or Power of
Parameter Values(pQ=.01)				Test 1			Test 2			Test 3
k	h	pM	D′	ERS	TS-II	TS-I	ERS	TS-II	TS-I	ERS	TS-II	TS-I
10	.00	.01	−	.005	.003	.005	.008	.015	.015	.022	.023	.028
10	.00	.03	−	.007	.008	.007	.014	.012	.015	.010	.012	.010
10	.02	.01	.95	.863	.941	.507	.413	.336	.336	.896	.928	.636
10	.02	.01	.85	.736	.861	.418	.351	.280	.277	.808	.828	.553
10	.02	.01	.50	.250	.362	.134	.164	.148	.147	.366	.385	.250
10	.02	.03	.95	.373	.477	.232	.233	.188	.207	.500	.557	.366
10	.02	.03	.85	.306	.417	.174	.204	.173	.165	.441	.471	.304
10	.02	.03	.50	.094	.113	.061	.079	.082	.084	.144	.169	.107
10	.05	.01	.95	.999	.999	.935	.955	.906	.905	1.00	1.00	.990
10	.05	.01	.85	.985	.997	.885	.927	.876	.856	.999	1.00	.985
10	.05	.01	.50	.599	.745	.435	.655	.604	.582	.861	.878	.782
10	.05	.03	.95	.820	.905	.683	.872	.828	.850	.976	.978	.954
10	.05	.03	.85	.712	.819	.605	.790	.738	.756	.944	.954	.922
10	.05	.03	.50	.255	.346	.191	.438	.403	.417	.562	.589	.525
20	.00	.01	−	.005	.004	.007	.014	.014	.014	.023	.027	.029
20	.00	.03	−	.009	.009	.007	.012	.011	.013	.011	.012	.014
20	.02	.01	.95	.988	.997	.818	.437	.340	.305	.982	.988	.857
20	.02	.01	.85	.945	.982	.706	.359	.303	.293	.941	.959	.750
20	.02	.01	.50	.461	.585	.297	.184	.164	.167	.543	.584	.365
20	.02	.03	.95	.658	.778	.479	.296	.219	.202	.748	.793	.562
20	.02	.03	.85	.539	.655	.403	.241	.194	.205	.636	.694	.497
20	.02	.03	.50	.156	.211	.121	.124	.109	.098	.239	.269	.177
20	.05	.01	.95	1.00	1.00	1.00	.987	.947	.942	1.00	1.00	1.00
20	.05	.01	.85	1.00	1.00	.999	.971	.904	.901	1.00	1.00	1.00
20	.05	.01	.50	.910	.972	.853	.779	.644	.644	.982	.991	.936
20	.05	.03	.95	.988	.999	.973	.955	.887	.880	1.00	1.00	.996
20	.05	.03	.85	.962	.994	.936	.924	.830	.804	.997	.999	.989
20	.05	.03	.50	.545	.663	.516	.548	.473	.477	.803	.828	.756

Figure 1.

Power curves of test 3 with the three selection approaches, ERS, TS-II, and TS-I. a, k=10. b, k=20.

The simulated levels when p_M=0.3 are very close to the nominal level, 0.01. Although there is some discrepancy between the simulated levels and the nominal level when p_M=0.1, the simulated levels among all three approaches are comparable, which implies that the type I errors for all three approaches are controlled at about the same level. Since the critical values in all three approaches are determined by asymptotic theory, we expect that, when the sample size gets larger, the discrepancy between the simulated levels and the nominal level would disappear. To investigate this effect, we also simulated the levels with n=800. It turned out that the discrepancy disappeared, as expected. We do not present these results here, for the sake of brevity. Some features of the power comparison can be summarized as follows. First, both the TS-II approach and the ERS approach are remarkably more powerful than the TS-I approach in all cases. Second, when the additional information contained in the trait observations of the upper sample is incorporated into the detection of QTLs through test 3, by combining tests 1 and 2, a significant gain in power can be achieved, especially if the power of test 1 is relatively low and if the ERS approach is used. Third, the TS-II approach has the largest power, compared with the other approaches, in all cases. However, the power of the ERS approach is only slightly smaller than and thus is quite comparable to the power of the TS-II approach. Finally, the screening size has a considerable effect on the powers of the tests. When k is changed from 10 to 20 (i.e., the screening size is doubled), the powers are greatly increased.

We conclude this report with some further discussion. Although the TS-II approach is slightly more powerful than the ERS approach, it is more difficult to implement in certain situations than is the ERS. With the TS approach, a prescreening process is necessary for the estimation of the cutoff quantiles if they are not known a priori, which is usually the case in practice. The selection procedure can be performed only after the estimated cutoff quantiles are obtained. For example, in their study that involved the use of sib pair models for the mapping of genes that regulate blood pressure, Xu et al. (1999) prescreened 40,000 individuals to estimate the cutoff quantiles of blood pressure, whereas >160,000 individuals were eventually screened to select extremely discordant sib pairs. In situations like this, to keep the records of the individuals involved in the prescreening process and to recall them for genotyping, usually after quite a long period, is not a simple matter. A sizable extra cost may be incurred, unnecessary errors may be caused, some individuals may be lost to follow-up, and so forth. In contrast, however, the ERS approach does not require a prescreening process. The selection is done in batches of k individuals. The number k is usually small and well within the manageable range. Therefore, if a large-scale prescreening is needed to estimate the cutoff quantiles and the process would incur a nonnegligible cost and other troubles, the ERS provides a reasonable alternative to the TS-II approach because of its comparable power and convenience of implementation.

There are situations in which only a finite population is of concern in the study and the trait values of the individuals are completely known. For example, in the study of serum immunoglobulin E concentration in patients with asthma conducted by Laitinen et al. (1997), the study population was a group of 487 asthmatic patients, and the serum immunoglobulin E concentrations in all these patients were known. In such situations, the TS-II approach can be applied without any screening. What needs to be done is to order the trait values of all the individuals and then to take the upper τ fraction as the upper sample and the lower τ fraction as the lower sample.

Another issue is how to determine τ (or k) in the selective-genotyping approaches. From a purely theoretical point of view, the smaller the τ (or the larger the k), the more powerful the tests. In practice, however, τ cannot be chosen to be too small. Lander and Botstein (1989) warned that very extreme trait values might have causes other than genetic effects. They suggested that the selected upper or lower percentage should not be <5%. Subject to this restriction, the determination of τ could be made by a cost consideration. In selective genotyping, there are two kinds of cost involved: the cost of screening the trait values and the cost of genotyping the selected individuals. The power of the tests is determined by both the sample size n and the selection fraction τ (or k), whereas other factors are fixed. We may assume that the effects of n and τ on the power of tests are independent from other factors. In the cost consideration, it is more convenient to consider k than τ. Let the power of a test be denoted by p(k,n). Let the cost for screening one individual be denoted by C_s and the cost for genotyping one individual be denoted by C_g. The total cost of the selective genotyping is roughly C=n(kC_s/2+C_g). With fixed cost C, p(k,n) can be maximized with respect to k and n, subject to C=n(kC_s/2+C_g). For a given pair (k,n), the power p(k,n) can be simulated for the particular situation. This procedure can simultaneously determine the desired sample size n and the selection fraction τ. We do not elaborate on this procedure here, but it is worthy of further research.

Appendix A: Derivation of Results Related to the ERS Approach

Let

Let (X,δ₀,δ₁,δ₂) be the observation for a randomly chosen individual from the population. Denote by H the cumulative distribution function of the nongenetic component of X. Assume that the genotypic values are -a, d, and a when the genotypes of the QTL are qq, Qq, and QQ, respectively. Let F₀(x)=H(x+a), F₁(x)=H(x-d), and F₂(x)=H(x-a). Denote by f₀, f₁, and f₂ their corresponding probability density functions (PDFs). Then the joint PDF of (X,δ₀,δ₁,δ₂) is given by

The marginal PDF of X is given by

Let F denote the cumulative distribution function corresponding to f. Then . The conditional distribution of δ_l, given X, is

For the QTL, we use the notations p_l and p_l(r), where l=0,1,2 and r=1,k. For the marker, we use the notations q_l and q_l(r), where l=0,1,2 and r=1,k. In these notations, l refers to the number of Q or M alleles and r refers to the samples: 1 for the lower sample and k for the upper sample. For example, p_1(k) is the expected frequency of genotype Qq in the upper sample. Let X_(r) denote the rth order statistic of a simple random sample of size k from the distribution of X. Let δ_l(r) denote the induced order statistic of δ_l.

We have

Similarly, we have

Thus, we have

Replacing X_(k) and F(x) by X₍₁₎ and 1-F(x), respectively, we obtain

Since F₀(x)>F₁(x)>F₂(x), F^k-1(x) is increasing, and [1-F(x)]^k-1 is decreasing, the integrals in equation (A1) are all positive and the integrals in equation (A2) are all negative. In fact, we have, for example,

The positiveness and negativeness of the other integrals follow similarly.

Let p_M denote the frequency of the M allele and p_m=1-p_M. The haplotypes at the QTL and the marker locus together with their frequencies are given below. Note that D is the measure of LD.

Haplotype	Frequency
QM	τ1=pQpM+D
Qm	τ2=pQpm-D
qM	τ3=pqpM-D
qm	τ4=pqpM+D

Let α₁=τ₁/p_Q and α₃=τ₃/p_q. The conditional marker genotype frequencies, given the QTL genotypes, are as follows.

	MM	Mm	mm
QQ	α21	2α1(1-α1)	(1-α1)2
Qq	α1α3	α1(1-α3)+α3(1-α1)	(1-α1)(1-α3)
qq	α23	2α3(1-α3)	(1-α3)2

Note that, if D=0, then α₁=α₃=p_M.

For the frequencies with the marker, we obtain from the table above that

and

Then, some straightforward algebra yields

and