Assessment of Parent-of-Origin Effects in Linkage Analysis of Quantitative Traits

Abstract

Methods are presented for incorporation of parent-of-origin effects into linkage analysis of quantitative traits. The estimated proportion of marker alleles shared identical by descent is first partitioned into a component derived from the mother and a component derived from the father. These parent-specific estimates of allele sharing are used in variance-components or Haseman-Elston methods of linkage analysis so that the effect of the quantitative-trait locus carried on the maternally derived chromosome is potentially different from the effect of the locus on the paternally derived chromosome. Statistics for linkage between trait and marker loci derived from either or both parents are then calculated, as are statistics for testing whether the effect of the maternally derived locus is equal to that of the paternally derived locus. Analyses of data simulated for 956 siblings from 263 nuclear families who had participated in a linkage study revealed that type I error rates for these statistics were generally similar to nominal values. Power to detect an imprinted locus was substantially increased when analyzed with a model allowing for parent-of-origin effects, compared with analyses that assumed equal effects; for example, for an imprinted locus accounting for 30% of the phenotypic variance, the expected LOD score was 4.5 when parent-of-origin effects were incorporated into the analysis, compared with 3.1 when these effects were ignored. The ability to include parent-of-origin effects within linkage analysis of quantitative traits will facilitate genetic dissection of complex traits.

Introduction

For some chromosomal regions, the genomic segment inherited from one parent is inactivated, so that expression of an allele in one of these regions is dependent on the sex of the parent from whom it was inherited. This phenomenon, known as “genomic imprinting,” plays an important role in several genetic diseases in humans, notably Prader-Willi syndrome, most cases of which are caused by a chromosome 15q deletion carried on the paternally derived chromosome (MIM 176270). Similarly, Angelman syndrome is caused by a chromosome 15q deletion carried on the maternally derived chromosome (MIM 105830). Imprinting may play a role in the inheritance of complex diseases, and a potential role for imprinting has been suggested for diseases such as bipolar affective disorder (Grigoroiu-Serbanescu et al. ¹⁹⁹⁵), atopy (Ruiz et al. 1992; Sandford et al. ¹⁹⁹³), and both type 1 and type 2 diabetes mellitus (Margaritte-Jeannin et al. ¹⁹⁹⁵; Huxtable et al. ²⁰⁰⁰; Lindsay et al. ^2000a). To facilitate detection of imprinted loci influencing susceptibility to disease, a number of methods have been developed to incorporate parent-of-origin effects into linkage analysis. These methods have generally employed parametric models (Heutink et al. 1992; Stine et al. ¹⁹⁹⁵; Strauch et al. ²⁰⁰⁰) or have assessed allele sharing between pairs of affected siblings (Gershon et al. 1996; Paterson et al. ¹⁹⁹⁹). Methods for incorporation of parent-of-origin effects into the linkage analysis of quantitative traits have received little attention. In the present article, allele-sharing methods for linkage analysis of quantitative traits are extended to incorporate parent-of-origin effects, and the statistical properties of the resulting methods are assessed via simulation.

Methods

Parent-Specific Allele Sharing in Siblings

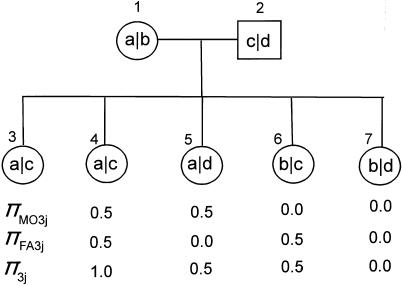
The most widely used nonparametric methods for linkage analysis of quantitative traits are the variance-components method (Amos 1994) and the regression method of Haseman and Elston (1972). Both methods are based on the principle that, if a marker is closely linked to a locus influencing a trait, pairs of relatives who share a larger proportion of marker alleles identical by descent (IBD) will tend to have more-similar trait values than are seen in pairs of relatives who share fewer alleles IBD. Consequently, a critical part of these methods is estimation of the proportion of marker alleles shared IBD between pairs of relatives (denoted as “π_ij,” where i and j denote the two individuals constituting the pair). A pair of siblings, for example, may share 0, 1, or 2 alleles IBD, corresponding to π_ij=.0, .5, and 1.0, respectively, and, on average, π_ij=.5 for sibling pairs. To assess parent-of-origin effects, it is necessary to partition π_ij into a component representing the proportion of alleles shared IBD derived from the mother (a component denoted as “π_MOij”) and a component derived from the father (a component denoted as “π_FAij”; see fig. 1). For sibling pairs, both π_MOij and π_FAij can be either .0 or .5 and will average .25. Note that, as presently defined, π_MOij+π_FAij=π_ij.

Figure 1.

Calculation of parent-specific IBD for a hypothetical family containing five siblings. Individual identification numbers are shown above the symbols, and alleles (designated “a,” “b,” “ c,” or “d”) at a hypothetical marker locus are shown within the symbols. For each of the siblings numbered “4”–“7,” calculation of allele sharing with individual 3 is shown for maternally derived alleles (π_MO3j), paternally derived alleles (π_FA3j), and all alleles (π_3j).

If markers are not perfectly informative, π_ij must be estimated. A number of algorithms have been developed to accomplish this; in the present analyses, a modification of the method described by Curtis and Sham (1994) was employed. This method makes use of the risk-calculation facility of the LINKAGE program (Lathrop and Lalouel 1984; Lathrop et al. ¹⁹⁸⁴). One member of a pair of relatives is considered affected by a hypothetical rare recessive disease, and risk calculation is performed for the other member of the pair, under the assumptions that there is no recombination between the marker and disease loci and that the affection status of all other members of the family is unknown. In these conditions, π_ij can be derived from the probability that the individual is a homozygous carrier (P_HOM) and the probability that the individual is a heterozygous carrier (P_HET), according to the equation π_ij=P_HOM+(P_HET/2). For siblings (and half-siblings), it is straightforward to extend this method to estimate parent-specific IBD, by employing separate recombination fractions for females (θ_MO) and males (θ_FA). To estimate the maternal contribution to allele sharing, the calculation is performed under the assumption that θ_MO=.0 and θ_FA=.5. Since, with θ_FA=.5, transmission of the hypothetical disease allele from the father is independent of the marker, the paternal contribution to the resulting estimate of π_ij will equal the expected value of π_FAij: E(π_FAij)=.25 for siblings. Thus, the maternal contribution to allele sharing can be calculated from the extent to which total allele sharing deviates from this expectation: π_MOij=P_HOM+(P_HET/2)-E(π_FAij). Similarly, π_FAij can be derived by setting θ_MO=.5 and θ_FA=.0 and subtracting E(π_MOij) from the estimated allele sharing.

Variance-Components Linkage Analysis

The variance-components method is a widely used and powerful tool for linkage analysis of quantitative traits. It involves fitting a linear “mixed” model, which estimates the trait mean (μ) and partitions the variance into a number of components (Amos 1994). Three components of variance are generally included: σ²_Q, a monogenic component that reflects the influence of a quantitative-trait locus linked to the region of interest; σ²_G, a “polygenic” component that reflects the effects of unlinked genes or other familial influences, including environmental factors shared by families; and σ²_E, an “environmental” component that reflects effects unique to the individual. Under the assumptions of no recombination between trait and marker loci and multivariate normality, the phenotypic variance-covariance matrix (Ω) between individuals in a pedigree is

where Π is a matrix of the proportion of marker alleles shared IBD (i.e., the elements are the individual estimates of π_ij), Φ is a matrix of the expected proportion of alleles shared IBD (.5 for sibling pairs), and I is an identity matrix.

The logarithm of the likelihood (lnL) for a pedigree with n individuals is

where (x_i-μ) represents a vector of the differences between the individual trait values x_i and the mean and where C is a constant whose value depends on n (Lange et al. 1976). The parameters of these models are estimated by maximizing the sum of lnL over all pedigrees. Evidence for linkage is typically assessed by the likelihood-ratio test comparing the value of twice the negative of lnL from a model in which σ²_Q is estimated versus that from a model in which σ²_Q is constrained to equal 0. Conventionally, variance components are constrained to be ⩾0, in order to preserve a biologically meaningful interpretation. With this constraint, the distribution of the likelihood-ratio test under the null hypothesis (σ²_Q=0) is not the usual χ² with 1 df but, instead, is a mixture of distributions that is one-half-part χ² with 1 df and one-half-part point mass at 0 (Hopper and Mathews 1982; Self and Liang ¹⁹⁸⁷). To account for the one-sided nature of the test, the P value for the likelihood-ratio test is typically calculated by dividing the corresponding P value for a 1 df χ² by 2. Such P values are asymptotically valid, provided that the assumption of multivariate normality is not violated (Allison et al. 1999). The likelihood-ratio test can also be converted to a LOD score, by division by 2×log_e(10).

To accommodate parent-of-origin effects, the monogenic component of variance can be partitioned into (a) a component that reflects the influence of the quantitative-trait locus carried on the maternally derived chromosome (σ²_QMO) and (b) a component that reflects the influence of the locus carried on the paternally derived chromosome (σ²_QFA). The phenotypic variance-covariance matrix then becomes

where Π_MO is a matrix of the proportion of marker alleles shared IBD that are derived from the mother, Π_FA is a matrix of the proportion of alleles shared IBD that are derived from the father, and Φ and I are defined as above.

A number of statistical tests for linkage are possible under this model. In a fashion analogous to that described for the model without parent-of-origin effects, the likelihood-ratio test can be used to test for a trait-influencing locus on either the maternally derived chromosome (LOD_MO) or the paternally derived chromosome (LOD_FA). If both tests are conducted and the maximum of either LOD_MO or LOD_FA (MAXLOD_MO,FA) is taken as the evidence for linkage, then one would expect inflation of the type I error rate unless a correction for the fact that two statistical tests have been conducted is applied. This can be accomplished with a Bonferroni correction, by which the corrected P value is calculated as 1-(1-P_max)² , where P_max is the nominal P value associated with the maximum of either LOD_MO or LOD_FA (Ott 1991). Alternatively, a global test for linkage with alleles derived from either or both parents can be conducted by comparing the model allowing for imprinting (eq. [2]) versus a model in which both monogenic components are constrained to equal 0 (LOD_IMP). In this case, the distribution of the likelihood-ratio test under the null hypothesis will be a mixture of distributions that is one-fourth-part χ² with 2 df, one-half-part χ² with 1 df and one-fourth-part point mass at 0 (Hopper and Mathews 1982; Self and Liang ¹⁹⁸⁷). To account for the constraints on the variance components, the P value associated with LOD_IMP can be calculated by dividing the P value associated with the 2 df χ² distribution by 2, in a fashion analogous to the approach used for one component of variance. Since Π_MO+Π_FA=Π, the model in equation (1) is a special case of that in equation (2)—a special case in which σ²_QMO and σ²_QFA are constrained to be equal. Therefore, the usual test for linkage, assessed in the absence of parent-of-origin effects (eq. [1]), can also be seen as a test of the null hypothesis that both monogenic variance components are 0 versus the alternative that both are >0 and equal to one another (H_A: σ²_QMO=σ²_QFA>0). For the purposes of the present article, this conventional linkage test will therefore be termed “LOD_EQ.” Finally, statistical significance of parent-of-origin effects can be assessed by comparison of the full model allowing for such effects (eq. [2]) versus the model in which the monogenic components are constrained to be equal (eq. [1]). The P value for this test of whether the monogenic components are different (P_diff) can be calculated from a χ² distribution with 1 df.

Haseman-Elston Regression

The Haseman-Elston regression method is another technique that is widely used for linkage analysis of quantitative traits, especially for sibling pairs (Haseman and Elston 1972). In this method, the squared difference between the trait values for a pair of relatives, (x_i-x_j)², is regressed against the proportion of marker alleles shared IBD, π_ij):

A negative value of β reflects a tendency for siblings to be more similar with respect to the trait as they share a greater proportion of marker alleles IBD and, thus, implies linkage between the trait and marker loci. Therefore, a test of the null hypothesis, that β=0, against the alternative, that β<0, provides statistical assessment of the evidence for linkage—analogous to that provided by LOD_EQ in the variance-components method. The model parameters can be estimated by ordinary least-squares regression, but the P value is calculated from a t-statistic with a reduced number of degrees of freedom, to account for any nonindependence introduced by analysis of multiple pairs within sibships (Wilson and Elston 1993).

The Haseman-Elston method can be readily extended to accommodate parent-of-origin effects, by estimation of separate β coefficients, according to the source of allele sharing:

Linkage with the maternally or paternally derived chromosome can be assessed by testing whether β_MO<0 (i.e., LOD_MO) or β_FA<0 (i.e., LOD_FA), and the statistic with the strongest evidence for linkage (MAXLOD_MO,FA) can be taken, by employing a Bonferroni correction, as for the variance-components analysis. The global test for linkage (i.e., LOD_IMP) can be conducted with an F-test (with 2 df in the numerator) to test the null hypothesis that β_MO and β_FA are both 0. Since the linear-regression method does not constrain β_MO and β_FA to be <0, adjustment of the P value to produce an equivalent to a one-sided test is appropriate only if both β_MO and β_FA are <0; if this is not the case, then linkage should be declared only if strong evidence for linkage is seen with at least one of the parental chromosomes. Determining the significance of the parent-of-origin effect requires an assessment of whether β_MO=β_FA, and this can be accomplished by dividing the difference between β_MO and β_FA by its standard error, determined from the variances of β_MO and β_FA and from the covariance between the β coefficients (Kleinbaum et al. 1982):

The two-tailed P value for the resulting statistic (P_diff) can be calculated from a t-distribution, with calculation, as described above, of the number of degrees of freedom. Null and alternate hypotheses associated with the various statistics are shown in table 1, for both variance-components and Haseman-Elston methods.

Table 1.

Null and Alternate Hypotheses for Statistics Used in Variance-Components and Haseman-Elston Analyses Allowing for Parent-of-Origin Effects^[Note]

	Variance-Components Analyses		Haseman-Elston Analyses
Statistic	Null Hypothesis	Alternate Hypothesis	Null Hypothesis	Alternate Hypothesis
LODMO	σ2QMO=0	σ2QMO>0	βMO=0	βMO<0
LODFA	σ2QFA=0	σ2QFA>0	βFA=0	βFA<0
MAXLODMO,FA	σ2QMO=σ2QFA=0	σ2QMO>0 or σ2QFA> 0	βMO=βFA=0	βMO<0 or βFA< 0
LODIMP	σ2QMO=σ2QFA=0	σ2QMO>0 or σ2QFA> 0	βMO=βFA=0	βMO<0 or βFA< 0
LODEQ	σ2QMO=σ2QFA=0 (σ2Q=0)	σ2QMO=σ2QFA>0 (σ2Q>0)	βMO=βFA=0 (β=0)	βMO=βFA<0 (β<0)
Pdiff	σ2QMO=σ2QFA	σ2QMO≠σ2QFA	βMO=βFA	βMO≠βFA

Note.— Hypotheses are defined in terms of equation (2), for the variance-components method, and in terms of equation (4), for the Haseman-Elston method; in parentheses are LOD_EQ hypotheses, which are defined in terms of equation (1), for the variance-components method, and in terms of equation (3), for the Haseman-Elston method.

Simulations

A simulation study was conducted to assess the performance of these methods. Genotypic and phenotypic data were simulated under a number of genetic models for a set of nuclear families that had participated in a genomewide linkage study of loci influencing susceptibility to type 2 diabetes mellitus and related traits (Hanson et al. 1998). The ability to partition, into maternal and paternal components, alleles shared IBD requires genotypic data on at least one parent (either measured directly or inferred through extended relationships), and the present sample was selected to approximate the subset of families, from the linkage study, for which this information was available and to which we first applied this method (Lindsay et al. ^2000b). The data set consisted of 263 nuclear families containing 956 siblings; the median sibship size was 3, with a range of 2–11. Genotypic data were considered to be available from both parents in 32% of the families, from the mother only in 48%, and from the father only in 20%, as was the case in the families with at least one parent genotyped that had been reported in our previous study (Hanson et al. 1998).

Data were simulated by SLINK (Ott 1989; Weeks et al. ¹⁹⁹⁰) and by programs written by the authors of the present article. Two unlinked biallelic loci with equally frequent alleles were initially generated, and a marker locus with four equally frequent alleles that was tightly linked (θ=0) to one of the biallelic loci was also simulated. A total of 500 replicates of genotypic data were thus created. Quantitative-trait data were generated by allowing the two biallelic loci to influence the trait, with sampling of values from a mixture of normal distributions. To assess type I error, the trait locus linked to the marker was assumed to have no influence on the trait, whereas the unlinked trait locus was assumed to have an effect that resulted in a heritability (h²) of .5. To assess type I error under a variety of conditions, data were generated for a model in which only the maternally derived allele at the unlinked trait locus was expressed and for a model with no imprinting; in addition, data were generated for a model in which the trait was influenced by a factor shared among all siblings, as might occur, for example, in mitochondrial inheritance or with an environmental factor affecting an entire sibship. To assess power, data were generated for models in which the biallelic locus linked to the marker influenced the quantitative trait, with varying locus-specific heritability. To determine power for assessment of parent-of-origin effects, data were simulated such that only the maternally derived allele at the biallelic locus linked to the marker influenced the trait. The biallelic locus not linked to the marker also influenced the trait, but without an imprinting effect, such that the total heritability was .5; this allows power to be examined for cases in which there is oligogenic inheritance. To determine type I error in detection of parent-of-origin effects (P_diff) and to compare power to detect imprinted loci versus that to detect nonimprinted loci, data were also generated under models in which the trait locus linked to the marker was not imprinted. In these simulations, the maternally derived allele at the unlinked trait locus was also assumed to influence the trait, such that the total heritability was .5; this allows type I error for P_diff to be determined for the case in which a locus linked to the marker is not imprinted but in which an imprinted locus occurs elsewhere in the genome. Models employed in the simulations are summarized in table 2.

Table 2.

Summary of Models Used in Simulation Studies

	Trait Locus Linked to Marker		Trait Locus Unlinked to Marker
	Mechanism of Action	h2	Mechanism of Action	h2	Total h2
	Models Used to Assess Type I Error of Linkage Statistics
Maternal expression	…	.00	Maternally expressed	.50	.50
Nonimprinted	…	.00	Nonimprinted	.50	.50
Common sibling	…	.00	…	.00	.50a
	Models Used to Assess Power to Detect Nonimprinted Loci
Locus-specific h2:
.10	Nonimprinted	.10	Maternally expressed	.40	.50
.20	Nonimprinted	.20	Maternally expressed	.30	.50
.30	Nonimprinted	.30	Maternally expressed	.20	.50
.40	Nonimprinted	.40	Maternally expressed	.10	.50
.50	Nonimprinted	.50	…	.00	.50
	Models Used to Assess Power to Detect Imprinted Loci
.10	Maternally expressed	.10	Nonimprinted	.40	.50
.20	Maternally expressed	.20	Nonimprinted	.30	.50
.30	Maternally expressed	.30	Nonimprinted	.20	.50
.40	Maternally expressed	.40	Nonimprinted	.10	.50
.50	Maternally expressed	.50	…	.00	.50

^aNeither genetic locus influenced the trait, but a familial factor influenced the trait to give a total h² of .50.

Analyses of linkage between the simulated markers and quantitative traits were conducted by use of the procedures outlined above. The FASTLINK (Cottingham et al. 1993; Schäffer et al. ¹⁹⁹⁴) modification of the LINKAGE program (Lathrop and Lalouel 1984; Lathrop et al. ¹⁹⁸⁴) was used to estimate parent-specific IBD for pairs of siblings, at each simulated marker. Variance components were estimated by the scoring algorithm (Lange et al. 1976), implemented in PROC IML of SAS. Haseman-Elston analyses were conducted in SAS, by use of standard regression methods.

Results

Type I error rates for the various linkage statistics, determined by analysis of replicates generated under models in which there was no linkage between the trait and marker loci, are shown in table 3. For both variance-components and Haseman-Elston methods, type I error rates were similar to the nominal values, for all statistics. When the evidence for linkage was maximized over both maternal and paternal chromosomes (MAXLOD_MO,FA), correction for multiple testing was necessary; in the absence of the Bonferroni correction, type I error rates for MAXLOD_MO,FA were approximately double the values reported in table 3.

Table 3.

Type I Error Rates (with 95% Confidence Intervals) for Linkage Statistics from Models Incorporating Parent-of-Origin Effects

	Type I Error Rate (95% Confidence Interval)
	Variance-Components Analysis		Haseman-Elston Analysisa
Generating Model and Statistic	P<.05	P<.01	P<.05	P<.01
Maternal expression:b
LODEQ	.070 (.050–.097)	.010 (.004–.025)	.050 (.033–.074)	.010 (.004–.025)
LODMO	.062 (.043–.088)	.008 (.003–.022)	.050 (.033–.074)	.012 (.005–.027)
LODFA	.038 (.024–.060)	.004 (.001–.016)	.046 (.030–.069)	.008 (.003–.022)
MAXLODMO,FAc	.046 (.030–.069)	.008 (.003–.022)	.046 (.030–.069)	.012 (.005–.027)
LODIMP	.040 (.025–.062)	.006 (.002–.019)	.044 (.028–.067)	.012 (.005–.027)
Nonimprinted:b
LODEQ	.038 (.024–.060)	.006 (.002–.019)	.034 (.021–.055)	.008 (.003–.022)
LODMO	.054 (.037–.079)	.010 (.004–.025)	.044 (.028–.067)	.010 (.004–.025)
LODFA	.042 (.027–.065)	.008 (.003–.022)	.054 (.037–.079)	.010 (.004–.025)
MAXLODMO,FAc	.044 (.028–.067)	.004 (.001–.016)	.054 (.037–.079)	.012 (.005–.027)
LODIMP	.042 (.027–.065)	.002 (.0001–.013)	.046 (.030–.069)	.010 (.004–.025)
Common sibling:b
LODEQ	.038 (.024–.060)	.010 (.004–.025)	.046 (.030–.069)	.010 (.004–.025)
LODMO	.040 (.025–.062)	.002 (.0001–.013)	.048 (.032–.072)	.004 (.001–.016)
LODFA	.032 (.019–.053)	.010 (.004–.025)	.034 (.021–.055)	.012 (.005–.027)
MAXLODMO,FAc	.032 (.019–.053)	.006 (.002–.019)	.042 (.027–.065)	.006 (.002–.019)
LODIMPc	.022 (.012–.040)	.006 (.002–.019)	.036 (.022–.057)	.008 (.003–.022)
Combined:b
LODEQ	.049 (.039–.061)	.009 (.005–.015)	.043 (.034–.055)	.009 (.005–.016)
LODMO	.052 (.042–.065)	.007 (.003–.013)	.047 (.037–.060)	.009 (.005–.015)
LODFA	.037 (.029–.049)	.007 (.004–.014)	.045 (.035–.057)	.010 (.006–.017)
MAXLODMO,FAc	.041 (.031–.052)	.006 (.003–.012)	.047 (.037–.060)	.010 (.006–.017)
LODIMP	.035 (.026–.046)	.005 (.002–.010)	.042 (.033–.054)	.010 (.006–.017)

^aFor Haseman-Elston analyses, results are considered positive only if both β_MO and β_FA are <0 or if linkage, at the relevant P value, is seen with at least one of the parental chromosomes.

^bResults are based on analysis of 500 replicates for each model; thus, “Combined” represents 1,500 replicates. Confidence intervals were calculated as described by Fleiss (1981).

^cA Bonferroni correction is applied to the nominal P value from the maximum of LOD_MO and LOD_FA.

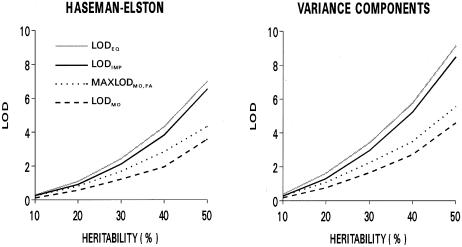
Median LOD scores for replicates generated under models in which a nonimprinted trait locus was linked to the marker are shown in figure 2. The analysis model that did not incorporate parent-of-origin effects (LOD_EQ) was the most powerful, as expected, since its alternative hypothesis corresponds most closely to the generating model. The general test allowing for parent-of-origin effects (i.e., LOD_IMP) was modestly less powerful, a consequence of the additional degree of freedom required for estimation of the additional parameter. Tests of linkage that were specific to alleles shared from a single parent (i.e., LOD_MO and LOD_FA) were substantially less powerful, and this loss of power was only modestly overcome by use of the maximum LOD score for either parent. Variance-components analyses were somewhat more powerful than Haseman-Elston analyses, for all statistics. Table 4 shows type I error rates for tests of parent-of-origin effects derived from analyses of these replicates. Type I error rates for the variance-components analyses were close to the nominal values, but those for the Haseman-Elston methods were slightly higher than the nominal values. To examine the possibility that the inflated type I error rates reflect the failure of the Haseman-Elston method to adequately account for nonindependence of pairs in sibships with more than two siblings, data were analyzed for one sibling pair selected at random from each family. In this situation, the type I error rates for the Haseman-Elston method were close to the nominal values (although the expected LOD scores were much lower).

Figure 2.

Median LOD scores, in analysis of 500 replicates generated for a nonimprinted quantitative-trait locus, for each of the tests of linkage, by the proportion of phenotypic variance attributed to the locus (heritability). Values for LOD_FA were virtually identical to those for LOD_MO and, thus, are not shown. For comparability, P values for LOD_IMP and MAXLOD_MO,FA have been converted to equivalent LOD scores.

Table 4.

Type I Error Rates (with 95% Confidence Intervals) at P_diff<.05, for Tests of Parent-of-Origin Effects, by h²

	Type I Error Rate (95% Confidence Interval)a
		Haseman-Elston Analysis
h2	Variance-Components Analysis	All Pairs	One Pair per Sibship
.10	.034 (.021–.055)	.072 (.052–.099)	.034 (.021–.055)
.20	.032 (.019–.053)	.086 (.064–.115)	.056 (.038–.081)
.30	.054 (.037–.079)	.102 (.078–.133)	.048 (.032–.072)
.40	.040 (.025–.062)	.130 (.102–.163)	.032 (.019–.053)
.50	.050 (.033–.074)	.116 (.090–.148)	.048 (.032–.072)
Overall	.042 (.035–.051)	.101 (.090–.114)	.044 (.036–.053)

^aBased on analysis of 500 replicates for each value of h²; confidence intervals were calculated as described by Fleiss (1981).

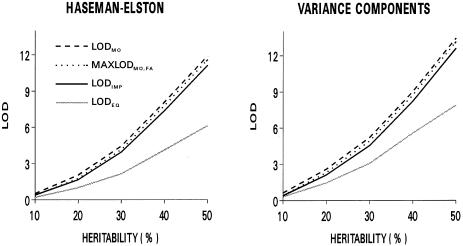
Median LOD scores for replicates generated under a model with an imprinted maternally expressed quantitative-trait locus linked to the marker are shown in figure 3. In this case, the statistic assessing linkage to the maternal chromosome (i.e., LOD_MO) was the most powerful, which is not surprising, since this statistic provides the most direct test of the generating model; however, taking the maximum of LOD_MO and LOD_FA was only slightly less powerful (the power loss being a consequence of the correction for multiple testing), and the general test allowing for parent-of-origin effects (i.e., LOD_IMP) was only modestly less powerful, than LOD_MO. Although linkage analysis that did not allow for imprinting (i.e., LOD_EQ) provided some power for detection of an imprinted locus, it was substantially less powerful than the tests that explicitly allowed for parent-of-origin effects. Again, the variance-components method was more powerful than the Haseman-Elston method. To further examine the potential increase in power for analyses that account for imprinting, the distribution of LOD_EQ was examined for replicates in which analyses accounting for imprinting gave some evidence for linkage (LOD_IMP>1.18; P<.01). The results show that, in a significant number of situations for which linkage can be detected by LOD_IMP, the analysis ignoring imprinting gives little to no evidence for linkage, particularly for loci with more-moderate effects (table 5); for example, for an imprinted locus accounting for 10% of the phenotypic variance, only 60% of replicates with LOD_IMP>1.18 also had LOD_EQ>1.18, and 11% had LOD_EQ⩽0.59 (P⩾.05).

Figure 3.

Median LOD scores, in analysis of 500 replicates generated for a maternally expressed quantitative-trait locus, for each of the tests of linkage, by the proportion of phenotypic variance attributed to the locus (heritability). Values for LOD_FA were 0 for all values of heritability and, thus, are not shown. For comparability, P values for LOD_IMP and MAXLOD_MO,FA have been converted to equivalent LOD scores.

Table 5.

Distribution of LOD_EQ Scores for Replicates Generated under an Imprinted Model for Which an Analysis Accounting for Imprinting Gave Evidence for Linkage (LOD_IMP>1.18), by h^2[Note]

	Variance-Components Analysis				Haseman-Elston Analysis
		Proportion of N				Proportion of N
h2	Na	LODEQ⩽0.59	0.59<LODEQ⩽1.18	LODEQ>1.18	Na	LODEQ⩽0.59	0.59<LODEQ⩽1.18	LODEQ>1.18
.1	93	.108	.290	.602	85	.306	.200	.494
.2	382	.055	.194	.754	331	.160	.245	.595
.3	485	.016	.072	.911	462	.052	.113	.835
.4	499	.002	.004	.994	495	.014	.020	.966
.5	500	.000	.002	.998	499	.004	.010	.986

Note.— P values corresponding to LOD scores of 1.18 and .59 are .01 and .05, respectively.

^aN = number of replicates (of a total of 500) for which LOD_IMP>1.18.

The power of the tests for assessment of parent-of-origin effects in analyses of data generated under a model with an imprinted maternally expressed locus is shown in table 6. For models with a locus-specific heritability of 10%, the power to detect these effects was low, but it increased rapidly for loci with larger effects. Restriction of the Haseman-Elston analysis to a single sibling pair for each sibship resulted in a substantial loss of power, versus analysis of all pairs.

Table 6.

Proportion (with 95% Confidence Intervals) of Replicates Demonstrating Statistically Significant Parent-of-Origin Effects at P_diff<.05, for Data Generated under Imprinted Models, by h²

	Proportion (95% Confidence Interval) of Replicates with Significant Parent-of-Origin Effects at Pdiff<.05a
		Haseman-Elston Analysis
h2	Variance-Components Analysis	All Pairs	One Pair per Sibship
.10	.196 (.163–.234)	.212 (.178–.251)	.042 (.027–.065)
.20	.622 (.578–.664)	.592 (.547–.635)	.076 (.055–.104)
.30	.904 (.874–.928)	.858 (.824–.887)	.232 (.196–.272)
.40	.994 (.981–.998)	.978 (.960–.988)	.340 (.299–.384)
.50	.998 (.987–.9999)	.994 (.981–.998)	.520 (.475–.564)

^aBased on analysis of 500 replicates for each value of h²; 95% confidence intervals were calculated as described by Fleiss (1981).

Discussion

The knowledge that genomic imprinting plays an important role in some human diseases—and the possibility that it might be involved in others—has led several investigators to incorporate parent-of-origin effects into linkage analyses. These efforts have been largely conducted by use of likelihood-based parametric-linkage methods. Parent-of-origin effects can be incorporated into such analyses by classification of families according to the sex of the transmitting parent (Stine et al. 1995; Nöthen et al. ¹⁹⁹⁹); by the use of different penetrances, depending on whether an individual has an affected father or mother (Heutink et al. 1992; Meijers-Heijboer et al. ¹⁹⁹²); or by allowance for different penetrances, depending on the parental origin of the disease allele (Strauch et al. 2000). In addition, family-based tests of allelic association can be extended to allow for differential effects, according to the sex of the transmitting parent, by use of either the transmission/disequilibrium test or log-linear models (Rice et al. 1995; Weinberg ¹⁹⁹⁹). Affected-sib-pair methods of linkage analysis can also be stratified by the sex of the transmitting parent (Gershon et al. 1996) and can be modified to assess allele sharing according to parent of origin, in a fashion similar to that employed in the present analyses (Paterson et al. 1999); however, methods for incorporation of parent-of-origin effects into linkage analysis of quantitative traits have received little attention. The present work shows that standard allele-sharing methods for linkage analysis of quantitative traits, such as the variance-components and Haseman-Elston methods, can be extended to incorporate parent-of-origin effects and that this approach can result in substantially increased power to detect imprinted loci, versus analyses that ignore parent-of-origin effects. Statistical tests can also be conducted to determine whether the effects of a locus differ according to parent of origin, thus allowing one to directly assess the hypothesis of imprinting.

Analyses of simulated data showed that type I error rates were close to the nominal values for statistics assessing linkage between the trait and marker loci (statistics such as LOD_EQ, LOD_MO, LOD_FA, MAXLOD_MO,FA, and LOD_IMP). The extent to which results of analyses of simulated data can be generalized beyond the family structures and genetic models for which the data were simulated is uncertain, but the present analyses were conducted for families that had participated in a linkage study, and they incorporated a number of features likely to be encountered in practice; these features include variable sibship size, less than perfectly informative markers, and missing genotypic data on some parents. Thus, the present analyses suggest that these factors do not produce substantial inflation of type I error rates. Similar results have been found, in a variety of situations, for both variance-components and Haseman-Elston analyses that do not include parent-of-origin effects (Amos et al. 1996; Pratt et al. ²⁰⁰⁰). The present simulations were not designed to produce the severe departures from multivariate normality (e.g., kurtosis) that, at least for variance-components analyses, can produce inflation of type I error rates (Allison et al. 1999). Application of the present methods to linkage analysis of traits with severely kurtotic distributions may require either the use of a normalizing transformation or the calculation of empirical P values by simulation. Tests of statistical significance of parent-of-origin effects (P_diff) had type I error rates for the variance-components method that were near the nominal values but had type I error rates for the Haseman-Elston method that were somewhat inflated. The inflation of type I error rates for the Haseman-Elston method appears to reflect the failure of this method to account adequately for the nonindependence of sibling pairs derived from sibships with more than two siblings. Although restriction of the Haseman-Elston analysis to a single pair from each sibship results in appropriate type I error rates, this strategy can result in a substantial loss of power to detect parent-of-origin effects.

The power of linkage analysis depends on the quantity and structure of the available family material, as well as on the effect of the locus in question. Simulations for nonimprinted loci have suggested that, for sample sizes typical of linkage studies, quantitative-trait loci need to have at least moderate effects (accounting for 20%–30% of the phenotypic variance) in order to have reasonable power to detect strong (LOD >3) linkage (Amos et al. 1996; Almasy and Blangero ¹⁹⁹⁸). The present analyses are consistent with this and show that power to detect imprinted loci is comparable to that for nonimprinted loci. Obviously, power is greatest for those analyses that best capture the underlying genetic architecture—for example, LOD_MO for maternally expressed loci and LOD_EQ for nonimprinted loci. If linkage is assessed for both parental chromosomes separately, the LOD scores need to be adjusted accordingly, in the form of either a Bonferroni correction for MAXLOD_{MO, FA} or an extra degree of freedom for LOD_IMP, in order to reduce type I error. This will result in some loss of power. The variance-components method was more powerful than the Haseman-Elston method, for detection of both linkage and parent-of-origin effects. This finding has also been seen in other analyses of simulated data on nonimprinted loci (Pugh et al. 1997; Pratt et al. ²⁰⁰⁰); it is probably due to additional information derived from the covariance between siblings, information that is not contained in the squared trait difference (Drigalenko 1998).

The present analyses were restricted to sibships, and additional work is needed to devise analytic strategies for detection of imprinted quantitative-trait loci in extended pedigrees. For many collections of family data, however, it is likely that sibships provide most of the information for assessment of parent-of-origin effects. The variance-components method can readily accommodate more-distant relatives (Almasy and Blangero 1998), but, to account for additional sources of familial resemblance, analyses of such data may require models more complex than those employed here. In analyses including both siblings and half-siblings, for example, it is probably necessary to partition the polygenic variance (i.e., σ²_G) into components representing maternal and paternal contributions; these separate polygenic components are not identifiable in analyses of sibships.

Recombination rates are sex specific; for most chromosomal regions, θ_MO>θ_FA, and, on average, the genetic distance between markers is 1.6 times greater for females than for males (Broman et al. 1998). Significant parent-of-origin effects detected with the present methods may thus reflect greater recombination between trait and marker loci in females versus that in males, or vice versa, rather than genomic imprinting. To examine the sensitivity of the present analyses to sex-specific differences in recombination, additional data were simulated under a model that included a nonimprinted quantitative-trait locus (h²=.5) linked to a marker with different θ_FA and θ_MO values. Results of analyses of these data (table 7) suggest that, even with a fairly strong effect of the locus, the method is not very sensitive to modest sex differences in recombination (i.e., a ratio of sex-specific genetic distances <10). It is difficult to distinguish, statistically, between imprinting and a sex difference in recombination, since imprinting will result in recombination rates that are apparently different between sexes (Smalley 1993). However, it may be possible to determine the plausibility of each mechanism by examination of both the female:male ratio of genetic distance and the pattern of parent-specific linkage results in the region of interest.

Table 7.

Proportion (with 95% Confidence Intervals) of Replicates with P_diff<.05 in Simulations of a Nonimprinted Locus Influencing the Quantitative Trait (h²=.5) with Variable Differences between θ_FA and θ_MO ^[Note]

		Proportion (95% Confidence Interval) of Replicates with Pdiff<.05
θFA	θMO	Variance-Components Analysis	Haseman-Elston Analysis
.01	.02	.04 (.01–.11)	.08 (.04–.16)
.01	.05	.09 (.04–.17)	.14 (.08–.23)
.01	.10	.08 (.04–.16)	.14 (.08–.23)
.01	.15	.15 (.09–.24)	.21 (.14–.31)
.01	.20	.34 (.25–.44)	.31 (.22–.41)

Note— Results are based on analysis of 100 replicates for each combination of θ_FA and θ_MO. Confidence intervals were calculated as described by Fleiss (1981).

These methods recently have been applied to data from a genomic scan to detect loci influencing obesity and type 2 diabetes in Pima Indians (Hanson et al. 1998; Lindsay et al. ^2000b). Analyses that allowed for imprinting detected tentative evidence for linkage in additional regions that were not detected in the initial analyses, which did not take into account the parent of origin. For body-mass index, for example, evidence was obtained for a maternally expressed locus on chromosome 5p (LOD_MO=1.7; LOD_FA=0; LOD_IMP=1.2; LOD_EQ=0.1; P_diff=.01) and for a paternally expressed locus on chromosome 10p (LOD_MO=0; LOD_FA=1.7; LOD_IMP=1.1; LOD_EQ=0.7; P_diff=.04). The strongest evidence for linkage with body-mass index was seen in a chromosome 11 region that was detected in the initial analyses; this locus did not appear to be imprinted (LOD_IMP=2.1; LOD_EQ=2.7; P_diff=.60). Assessment of parent-of-origin effects requires that genotypic data be available from at least one parent, and this resulted in exclusion of some families that could be used in the analyses that did not take into account the parent of origin. The results of the initial analyses of a larger sample, therefore, gave stronger evidence for linkage on chromosome 11 (LOD_EQ=3.6) than was seen in analyses of families informative for parent-of-origin effects (LOD_EQ=2.7).

The optimal strategy for conducting linkage analyses with parent-of-origin effects depends on the nature of the available families and on the characteristics of the trait being analyzed. To maximize power to detect nonimprinted loci and to minimize false-positive signals, it may be reasonable to conduct initial analyses that do not allow for imprinting (i.e., LOD_EQ) and to test for parent-of-origin effects in regions that show suggestive linkage. This approach, however, may result in failure to detect imprinted loci that could be detected if a genomewide linkage analysis accounting for imprinting was conducted. It therefore may be useful to assess a priori whether imprinted loci are likely—by use of epidemiologic data, for example. Of course, if imprinting is strongly suspected, then the optimal approach would be to assess linkage to the chromosome of the parent whose alleles are putatively expressed. The extent to which the human genome is imprinted is currently unknown. It is likely, on the basis of homology with the mouse genome, that several large blocks of imprinted genes exist but that most of the genome is probably not imprinted (Shire 1989; Bartolomei and Tilghman ¹⁹⁹⁷). Many of the known imprinted genes influence fetal development (Bartolomei and Tilghman 1997), and, therefore, incorporation of parent-of-origin effects into linkage analyses may be particularly useful for study of development-related traits, such as birth weight. Regardless of the strategy by which linkage is detected initially, knowledge regarding parent-of-origin effects may be useful for positional cloning efforts. The ability to conduct quantitative-trait linkage analyses incorporating parent-of-origin effects thus provides a useful tool for genetic dissection of complex traits.