A New Statistical Method for Haplotype Reconstruction from Population Data

Abstract

Current routine genotyping methods typically do not provide haplotype information, which is essential for many analyses of fine-scale molecular-genetics data. Haplotypes can be obtained, at considerable cost, experimentally or (partially) through genotyping of additional family members. Alternatively, a statistical method can be used to infer phase and to reconstruct haplotypes. We present a new statistical method, applicable to genotype data at linked loci from a population sample, that improves substantially on current algorithms; often, error rates are reduced by >50%, relative to its nearest competitor. Furthermore, our algorithm performs well in absolute terms, suggesting that reconstructing haplotypes experimentally or by genotyping additional family members may be an inefficient use of resources.

Introduction

Haplotype information is an essential ingredient in many analyses of fine-scale molecular-genetics data—for example, in disease mapping (e.g., Risch and Merikangas ¹⁹⁹⁶; Hodge et al. ¹⁹⁹⁹; Rieder et al. ¹⁹⁹⁹), or inferring population histories (e.g., Harding et al. ¹⁹⁹⁷). Our focus here is population data, for which routine genotyping methods typically do not provide phase information. This can be obtained, at considerable cost, experimentally, or (partially) through genotyping of additional family members (e.g., Sobel and Lange ¹⁹⁹⁶). Alternatively, a statistical method can be used to infer phase at linked loci from genotypes and thus reconstruct haplotypes. The two most popular existing methods are maximum likelihood, implemented via the expectation-maximization (EM) algorithm (Excoffier and Slatkin 1995; Hawley and Kidd ¹⁹⁹⁵; Long et al. ¹⁹⁹⁵), and a parsimony method created by Clark (1990). We present a new statistical method that improves on these by exploiting ideas from population genetics and coalescent theory that make predictions about the patterns of haplotypes to be expected in natural populations. Our method is Bayesian, allowing us to use these a priori expectations to inform haplotype reconstruction. Our method outperforms and is more widely applicable than existing algorithms; often, it reduces error rates by >50% relative to its nearest competitor. A novel feature is that it also estimates the uncertainty associated with each phase call. This avoids inappropriate overconfidence in statistically reconstructed haplotypes, and—crucially—it allows subsequent experimental phase confirmation to be targeted effectively. Our results suggest that, in many cases, our statistical method is sufficiently accurate that reconstructing haplotypes experimentally, or by genotyping additional family members, may be an inefficient use of resources.

Statistical Methods of Haplotype Reconstruction

Suppose we have a sample of n diploid individuals from a population. Let G=(G₁,…,G_n) denote the (known) genotypes for the individuals, let H=(H₁,…,H_n) denote the (unknown) corresponding haplotype pairs, let F=(F₁,…,F_M) denote the set of (unknown) population haplotype frequencies, and let f=(f₁,…,f_M) denote the set of (unknown) sample haplotype frequencies (the M possible haplotypes are arbitrarily labeled 1,…,M).

EM Algorithm

The EM algorithm (see, e.g., Excoffier and Slatkin ¹⁹⁹⁵; Hawley and Kidd ¹⁹⁹⁵; Long et al. ¹⁹⁹⁵) is a way of attempting to find the F that maximizes the likelihood

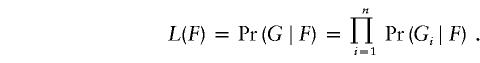Here,

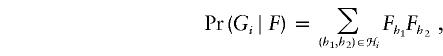where ℋ_i is the set of all (ordered) haplotype pairs consistent with the multilocus genotype G_i. Note that this likelihood is just the probability of observing the sample genotypes, as a function of the population haplotype frequencies, under the assumption of Hardy–Weinberg equilibrium (HWE).

We implemented the EM algorithm to obtain an estimate 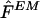for the population haplotype frequencies F, as described by Excoffier and Slatkin (1995). We used this as an estimate 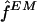for the sample haplotype frequencies f (that is, we used 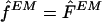). Since the estimate found by the EM algorithm typically depends on the starting point, for each data set we applied the algorithm using 100 different starting points and took the estimate of F that gave the highest likelihood. Following Excoffier and Slatkin (1995), the first starting point was computed by finding all haplotypes that could occur in the sample, given the genotypes, and setting each of these haplotypes to have equal frequency. (We found it helpful to add a small random perturbation to each frequency, to avoid the algorithm's converging to a saddle point in the likelihood.) Each of the 99 other starting points was obtained by randomly sampling the frequencies of all possible haplotypes from a (multivariate) uniform distribution.

Although, in theory, the EM algorithm can be applied to any number of loci with any number of alleles, in practice, implementations are limited by the need to store estimated haplotype frequencies for every possible haplotype in the sample. These storage requirements increase exponentially with the number of loci; for example, if any of the individuals is heterozygous at ⩾k loci, then the number of possible haplotypes in the sample is ⩾2^k-1. In our implementation, we imposed an arbitrary limit of 10⁵ on the number of possible haplotypes and did not apply the algorithm to data sets that exceeded this limit.

Within the maximum-likelihood framework, it is not clear how best to reconstruct the haplotypes themselves. We take perhaps the most natural and common approach, reconstructing haplotypes by choosing 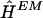to maximize 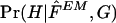—that is, by choosing the most probable haplotype assignment, given the genotype data and the estimated population haplotype frequencies .

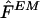Clark’s Algorithm

Clark’s algorithm (1990) can be viewed as an attempt to minimize the total number of haplotypes observed in the sample and, hence, as a sort of parsimony approach. The algorithm begins by listing all haplotypes that must be present unambiguously in the sample. This list comes from those individuals whose haplotypes are unambiguous from their genotypes—that is, those individuals who are homozygous at every locus or are heterozygous at only one locus. If no such individuals exist, then the algorithm cannot start (at least, not without extra information or manual intervention). Once this list of “known” haplotypes has been constructed, the haplotypes on this list are considered one at a time, to see whether any of the unresolved genotypes can be resolved into a “known” haplotype plus a complementary haplotype. Such a genotype is considered resolved, and the complementary haplotype is added to the list of “known” haplotypes. The algorithm continues cycling through the list until all genotypes are resolved or no further genotypes can be resolved in this way. The solution obtained can (and often does) depend on the order in which the genotypes are entered. In our comparisons, we entered the genotypes once, in a random order, and ignored cases in which the algorithm could not start or completely resolve all genotypes. A program, HAPINFERX, implementing the algorithm was kindly provided by A. G. Clark. When it successfully resolves all genotypes, Clark’s algorithm results in an estimate, 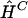, of H. We estimated sample haplotype frequencies f by the frequencies of the haplotypes reconstructed by the algorithm.

Our Phase Reconstruction Method

Our phase reconstruction method regards the unknown haplotypes as unobserved random quantities and aims to evaluate their conditional distribution in light of the genotype data. To do this, we use Gibbs sampling, a type of Markov chain–Monte Carlo (MCMC) algorithm (see Gilks et al. [1996] for background), to obtain an approximate sample from the posterior distribution of H given G, Pr(H∣G). Informally, the algorithm starts with an initial guess H⁽⁰⁾ for H, repeatedly chooses an individual at random, and estimates that individual's haplotypes under the assumption that all the other haplotypes are correctly reconstructed. Repeating this process enough times results in an approximate sample from Pr(H∣G). Formally, our method involves constructing a Markov chain H⁽⁰⁾,H⁽¹⁾,H⁽²⁾,…, with stationary distribution Pr(H∣G), on the space of possible haplotype reconstructions, using an algorithm of the following form.

Algorithm 1. Start with some initial haplotype reconstruction H⁽⁰⁾. For t=0,1,2,…, obtain H^(t+1) from H^(t) using the following three steps:

• 1. Choose an individual, i, uniformly and at random from all ambiguous individuals (i.e., individuals with more than one possible haplotype reconstruction).
• 2. Sample H^(t+1)_i from Pr(H_i∣G,H^(t)_-i), where H_-i is the set of haplotypes excluding individual i.
• 3. Set H^(t+1)_j=H^(t)_j for j=1,…,n, j≠i.

That this produces a Markov chain with the required stationary distribution follows from the proof for a general Gibbs sampler (see, e.g., Gilks et al. [1996]).

The difficulty in implementing the above algorithm lies in step 2. Not only does the conditional distribution Pr(H_i∣G,H_-i), which we are required to sample from, depend on assumptions about the genetic and demographic models (or, equivalently, on a “prior” for the population haplotype frequencies F), but this distribution is not even known for most models (or priors) of interest. Nonetheless, it turns out to be helpful to rewrite the conditional distribution as follows.

For any haplotype pair H_i=(h_i1,h_i2) consistent with genotypes G_i, we have

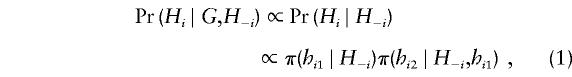where π(·∣H) is the conditional distribution of a future-sampled haplotype, given a set H of previously sampled haplotypes. This conditional distribution is also not known in general. However, it is known in the particular case of parent-independent mutation, in which the type of a mutant offspring is independent of the type of the parent. Although this model is unrealistic for the kinds of systems in which we are interested (e.g., DNA sequence, multilocus microsatellite, and single-nucleotide polymorphism [SNP] data), it leads to a simple algorithm (see Appendix A) whose performance is roughly comparable to the EM algorithm (data not shown) and has at least two advantages over EM: it can be applied to very large numbers of loci, and it naturally captures the uncertainty associated with haplotype reconstructions. This simple algorithm also provides a convenient way of determining a good starting point for the improved algorithm that we now describe.

Our improved algorithm arises from making more realistic assumptions about the form of the conditional distribution π(·∣H). Although, for most mutation or demographic models, the conditional distribution π(·∣H) is unknown, Stephens and Donnelly (2000) suggest an approximation (their definition 1). Formally, for a general mutation model with types in the countable set E, and (reversible) mutation matrix P, the approximation is

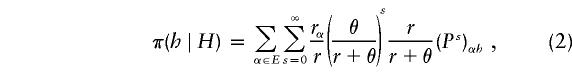where r_α is the number of haplotypes of type α in the set H, r is the total number of haplotypes in H, and θ is a scaled mutation rate. Informally, this corresponds to the next sampled haplotype, h, being obtained by applying a random number of mutations, s, to a randomly chosen existing haplotype, α, whereas s is sampled from a geometric distribution. The approximation (2) arose from consideration of the distribution of the genealogy relating randomly sampled individuals, as described by the coalescent (see Hudson [1991] for a review), and of what that distribution predicts about how similar a future-sampled chromosome and a previously sampled chromosome are likely to be. In particular, future-sampled chromosomes will tend to be more similar to previously sampled chromosomes as the sample size r increases and as the mutation rate θ decreases. See Stephens and Donnelly [2000] for further theoretical and empirical evidence that the approximation is sensible.

The key to the increased accuracy of our algorithm is that the approximation (2) captures the idea that the next haplotype is likely to look either exactly the same as or similar to a haplotype that has already been observed; see Figure 1 for illustration. Our new statistical method for haplotype reconstruction is based on substituting (2) into (1) to implement Step 2 of the Gibbs sampler. There are several other minor issues, both technical and practical (including, for example, how to estimate θ); details of these are given in Appendix B.

Figure 1.

Illustration of how our method uses the fact that unresolved haplotypes tend to be similar to known haplotypes. Suppose that we have a list of haplotypes, as shown on the left side of the figure, that are known without error (e.g., from family data or because some individuals are homozygous). Then, intuitively, the most likely pair of haplotypes for ambiguous individual 1 consists of two haplotypes that have high population frequency, as shown. All methods considered here will correctly identify this as the most likely reconstruction. However, ambiguous individual 2 cannot possess any of the haplotypes in the known list, and the most plausible reconstruction for this individual consists of two haplotypes that are similar, but not identical, to two haplotypes that have high population frequency, as shown. Of the methods considered here, only our method uses this kind of information, leading to the improved performance we observed.

For each run of our algorithm, we applied R successive update steps to obtain haplotype reconstructions H⁽¹⁾,…,H^(R), discarded the first b values of H as burn-in, and thinned the remainder by storing the result every k iterations. For the simulation studies, where we applied the method to many data sets, we used relatively small values of R and b to keep the computational burden manageable: R=200,000, b=100,000, k=100. For the examples we looked at, much shorter runs produced similar average performance (data not shown), but for more complex problems larger values may be necessary to obtain reliable results. We estimate f by the mean of the empirical haplotype frequencies in the thinned sample and use methods outlined in Appendix B to obtain a single point estimate, 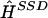, of H, together with estimates of Q=(q_ij), where q_ij denotes the probability that the phase call for individual i at locus j is correct. Software implementing our method will be made available at the Oxford Mathematical Genetics Group Web site.

Results

To compare the performance of the statistical methods of haplotype reconstruction, we simulated various types of DNA sequence and tightly linked multilocus microsatellite data with known phase. (The details of how these data were simulated are given in the relevant figure captions.) We randomly paired simulated haplotypes and compared the methods on their ability to reconstruct these haplotypes from the resulting genotype data, in which phase information is ignored. There are many possible aims for statistical methods of haplotype reconstruction. We concentrate on two particular tasks:

• I. Reconstruction of the haplotypes of sampled individuals, which is the main focus of Clark (1990).
• II. Estimation of sample haplotype frequencies, which is the main focus of Excoffier and Slatkin (1995).

For (I), we measure performance by the error rate, being the proportion of individuals with ambiguous phase whose haplotypes are incorrectly inferred. For (II), we use the discrepancy between the estimated and true sample haplotype frequencies:

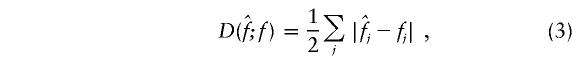with summation over all possible haplotypes, where 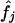and f_j denote, respectively, the estimated and true sample frequency of the jth haplotype. The discrepancy is equivalent to the I_f score used by Excoffier and Slatkin (1995): D=1-I_f.

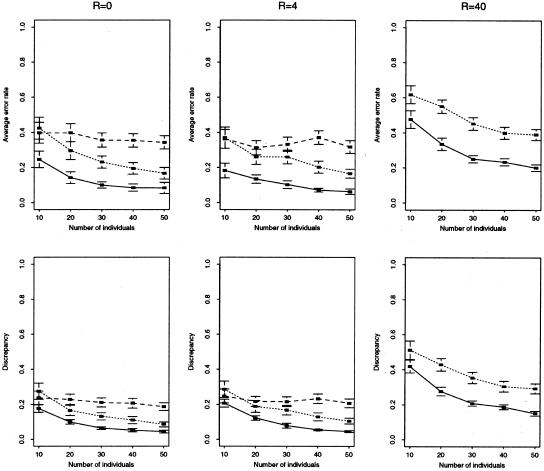
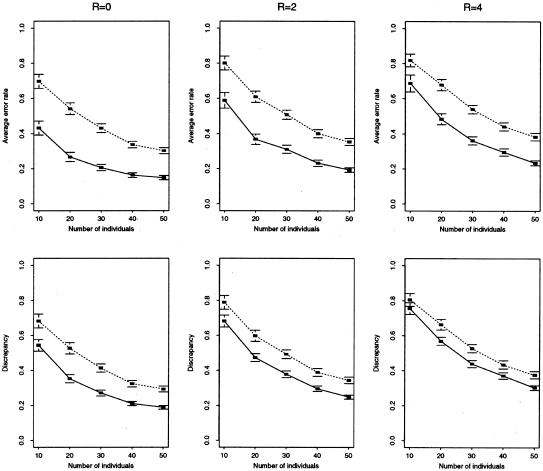
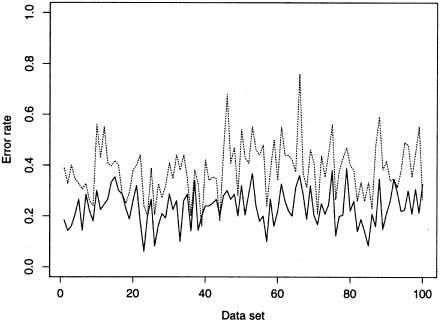
The results of our comparisons, shown in table 1 and figures 2 and 3, demonstrate that the accuracy of our new method substantially improves on both the EM algorithm and Clark’s method, with mean error rates often reduced by >50%. Not only is our average performance improved, but this improvement is achieved by a consistent improvement across many data sets, rather than an extreme improvement in a minority of cases. For example, figure 4 shows that, for the simulated microsatellite data sets with n=50 and R=4, the EM algorithm gave a smaller error rate than our method for only 3 data sets out of 100.

Table 1.

Comparison of Accuracy of Our Method and Clark’s Method for Long-Sequence Data (∼60–100 Segregating Sites)^[Note]

Method	Mean Error Rate	Standard Error
Clark’s	.42	.03
Ours	.20	.02

Note.— Error rate is defined in the text. Results are averages over 15 simulated data sets, each of n=50 individuals, simulated with θ=4N_eμ=16 and R=4N_er=16, where N_e is the effective population size, μ is the total per-generation mutation rate across the region sequenced, and r is the length, in Morgans, of the region sequenced. We simulated 20 independent data sets for a constant-sized panmictic population under the infinite-sites model, with recombination, using a coalescent-based program kindly provided by R. R. Hudson. Each simulated data set consisted of 100 haplotypes randomly paired to form 50 genotypes. Clark’s algorithm produced a unique haplotype reconstruction for 15 of these, and we discarded the other 5. The simulated data sets contained ∼60–100 segregating sites; for comparison, recent studies report 78 segregating sites in a 9.7-kb region (Nickerson et al. 1998) and 88 segregating sites in a 24-kb region (Rieder et al. 1999). Implementations of the EM algorithm typically cannot cope with these kinds of data, as the number of possible haplotypes is too large.

Figure 2.

Comparison of accuracy of our method (solid line) versus EM (dotted line) and Clark’s method (dashed line) for short sequence data (∼5–30 segregating sites). Top row, mean error rate (defined in text) for haplotype reconstruction. Bottom row, mean discrepancy (defined in text) for estimation of haplotype frequencies. We simulated data sets of 2n haplotypes, randomly paired to form n genotypes, under an infinite-sites model, with θ=4 and different assumptions about the local recombination rate R (R and θ are defined in the note to table 1), using a coalescent-based program kindly provided by R. R. Hudson. For each combination of parameters considered, we generated 100 independent data sets and discarded those data sets for which the total number of possible haplotypes was >10⁵ (the limit of our implementation of the EM algorithm), which typically left >90 data sets on which to compare the methods. Each point thus represents an average over 90–100 simulated data sets. Horizontal lines above and below each point show approximate 95% confidence intervals for this average (±2 standard errors). The results for Clark’s algorithm for R=40 are omitted, as we had difficulty getting the algorithm to consistently provide a unique haplotype reconstruction for these data.

Figure 3.

Comparison of accuracy of our method (solid line) versus EM (dotted line) for microsatellite data. Top row, mean error rate (defined in text) for haplotype reconstruction. Bottom row, mean discrepancy (defined in text) for estimation of haplotype frequencies. We simulated data sets of 2n haplotypes, randomly paired to form n genotypes, for 10 equally spaced linked microsatellite loci, from a constant-sized population, under a symmetric stepwise mutation model, using a coalescent-based program kindly provided by P. N. Fearnhead. We assumed θ=4N_eμ=8 (where μ is the per-generation mutation rate per locus, assumed to be constant across loci) and various values for the scaled recombination rate between neighboring loci, R=4N_er, where N_e is the effective population size and r is the genetic distance, in Morgans, between loci. For example, for humans, assuming N_e=10⁴, and the genomewide average recombination rate, 1 cM = 1 Mb, the right-hand column would correspond to 10 kb between loci. For each combination of parameters considered, we generated 100 independent data sets. Each point thus represents an average over 100 simulated data sets. Horizontal lines above and below each point show approximate 95% confidence intervals for this average (±2 standard errors). We had difficulty getting Clark’s algorithm to consistently provide a unique haplotype reconstruction for these data.

Figure 4.

Graph of error rates using our method (solid line) and the EM algorithm (dotted line) for each of the 100 simulated microsatellite data sets with n=50 and R=4. The EM algorithm gives a smaller error rate than our method for only 3 of the 100 data sets.

An important and novel feature of our method is that it quantifies the uncertainty in its phase calls by outputting an estimate of the probability that each call is correct. Table 2 shows the method to be well calibrated, in that, on average, phases called with x% certainty are correct ∼x% of the time. This is another substantial advantage of our method, and, in this sense, the performance improvements illustrated in figures 2 and 3 and table 1 underrepresent the gains achieved.

Table 2.

Results of Calibration Tests^[Note]

	Estimated Probability of Correct Call
Data Type	.5–.6	.6–.7	.7 –.8	.8 –.9	.9–1.0
Long sequence	.59	.82	.82	.82	.99
Short sequence:
R = 0	.58	.82	.87	.89	.95
R = 4	.60	.86	.88	.90	.98
R = 40	.62	.72	.77	.84	.96
Microsatellite:
R = 0	.60	.73	.81	.87	.99
R = 2	.60	.69	.78	.86	.98
R = 4	.60	.70	.76	.83	.97

Note.— Table entries show, for the simulated data sets used for table 1 and figures 2 and 3, proportion of all phase calls at ambiguous loci or sites, made with a given degree of confidence, that were actually correct. We regard the phase call in individual i at locus j as incorrect if the alternative call would give strictly fewer differences between the true and estimated haplotypes; otherwise, we regard the call as correct. Formally, the entries in each row of the table show #{(i,j):x%<q_ij⩽(x+10)%∩ Phase call for individual i at locus j is correct} /#{(i,j):x%<q_ij⩽(x+10)%}, for x=50,60,70,80,90, where #A denotes the number of members of the set A. The results suggest that our method tends, on average, to be slightly conservative in its estimate of the probability of having made a correct call.

We assessed the effect on our method of departures from HWE in data. Published haplotype data from a world sample (Harding et al. 1997) were randomly combined in pairs, first under HWE and then in a way that respected geographical structure. Table 3 shows that these departures from HWE have little effect. The type of geographical structure we modeled will tend to increase the amount of homozygosity in the sample, which, as pointed out by Fallin and Schork (2000), tends to reduce the number of ambiguous individuals. Deviations from HWE in the other direction (an increased proportion of heterozygotes) will tend to make things more difficult for all haplotype-reconstruction methods.

Table 3.

Illustration of Effect on Our Method of Deviations from HWE in Data^[Note]

Data Set	Mean Error Rate	Mean Discrepancy
HW	.21 (.006)	.16 (.002)
NHW	.21 (.008)	.16 (.004)

Note.— Results are averages over 20 simulated data sets, with standard errors for this average in parentheses. Data set HW was formed under HWE, and NHW was formed under an assumption of geographical structure (see below). The results suggest that deviations from HWE have little effect on our method’s average performance (though the performance is slightly more variable). To create the data sets HW and NHW, we used published, experimentally determined haplotype data from a 3-kb region of the beta-globin gene, sequenced in 253 chromosomes (appendix A of Harding et al. ¹⁹⁹⁷), kindly provided electronically by R. M. Harding. Six subpopulations were represented in the sample: Vanuatu, Papua New Guinea, Sumatra, the Gambia, the United Kingdom, and the Nuu-Chah-Nulth. We used these data to create HW and NHW by repeating the following procedure 20 times: (a) remove one chromosome at random from each subpopulation with an odd number of chromosomes in the sample, leaving 250 haplotypes, and (b) form 125 genotypes, by (i) (for HW) randomly pairing all haplotypes or (ii) (for NHW) randomly pairing haplotypes within each subpopulation.

Discussion

Haplotypes are the raw material of many genetic analyses, but the rapid growth of high-throughput genotyping techniques has not been matched by similar advances in cheap experimental haplotype determination. We have introduced a new statistical method for haplotype reconstruction that has three major advantages over existing statistical methods: increased accuracy, wider applicability, and the facility to assess accurately the uncertainty associated with each phase call.

The key to our increased accuracy is the use, in addition to the likelihood, of the fact that, a priori, unresolved haplotypes tend to be similar to known haplotypes (see fig. 1). The particular quantitative way in which we capture this prior expectation is motivated by coalescent theory. It amounts to specifying a statistical model (or, depending on your philosophy, a “prior”) for the population-genetics aspect of the problem—namely, the results of the evolutionary process that generated the haplotypes in the first place. Of course, we would expect the method to perform well if this is exactly the model that is generating the data, but, for real data, this will never be the case. Thus, what matters, in practice, is whether the model used and the implicit prior it induces on haplotype structure do a reasonable job of capturing important features of the haplotype structure in real data. If so, then we would expect the method to perform well and to outperform methods (including those to which it is compared here) that do not model the haplotype structure in the population.

Unfortunately, there simply do not exist enough real data sets, with known haplotypes for sequence or closely linked markers, to allow sensible statistical comparisons of different methods. However, coalescent methods have proved useful for a wide range of molecular-genetics data, and so it seems reasonable, a priori, to expect their use here to helpfully capture some of the key population genetics aspects of real data. Further, our simulation results provide evidence that the performance of our method is relatively robust to deviations in data from our underlying modeling assumptions. We note in particular that (1) the data underlying table 1 and figure 1 were simulated under a mutation model different from that used to derive the prior in our method; (2) the majority of data sets were simulated with recombination, which is not included in our model; and (3) in none of the tests of our method did we use the actual parameter values under which data were generated (as described in Appendix B, these were estimated within the method via simple summary statistics). Despite these deviations from our model, our method performed well. Thus, although our method makes more-explicit assumptions than the other methods we consider, it would be a mistake to conclude that it requires all these assumptions to hold to provide a useful improvement in performance. (It is, however, true that, in analysis of some real microsatellite data, it may be prudent to drop the assumption of a strict stepwise mutation mechanism; this option will be implemented in our software.)

In addition to the modeling assumptions that underlie our method, the likelihood used here and by the EM algorithm assumes HWE. Fallin and Schork (2000) provide a good discussion of the general consequences of departures from HWE in data and show that the EM algorithm can still give good results when HWE is not strictly satisfied. Our own results, shown in table 2, suggest that geographical structure of the sort plausible for human populations does not affect the average accuracy of our method. In light of this, it would be a misunderstanding to assume that either method “relies” on HWE for its validity; both methods are better thought of as “black box” estimation methods, and it is appropriate to assess their performance for data generated under a range of scenarios, as we have here.

Our method is also directly applicable to SNP data. In fact, the final column of figure 2 corresponds to SNP data (10–30 SNPs over 100 kb, under the assumption that 1 cM = 1 Mb) in which ascertainment of SNPs is independent of their sample frequencies. Performance is encouraging. This ascertainment assumption will not be valid for many real data sets. Although different studies use different ascertainment strategies, most of these strategies tend to preferentially select SNPs with higher frequencies. Higher-frequency variants produce, on average, a larger total number of ambiguous phases (through greater heterozygosity), but these phases are typically easier to estimate statistically than are those of lower-frequency variants (e.g., there is no information about phase for variants that appear only once in the sample). For these reasons, we would expect that—although our method, when applied to real SNP data, would typically give more incorrect phase calls (in absolute terms) than it would when applied to the corresponding SNP data that we simulated without taking ascertainment into account—a higher proportion of ambiguous phases would be called correctly with the real data.

Our method does not use information about genetic distances between loci or sites and is best suited to cases where the loci are tightly linked. Nonetheless, our simulation results show that it continues to perform well in the presence of moderate amounts of recombination (loci or segregating sites spread over ∼100 kb in humans, provided there are no recombination hotspots in the region). Our method could be extended to deal with loci or sites spread over larger genetic distances by replacement of the approximation (2) with an approximation that takes genetic distance between loci into account (e.g., the approximation used by Fearnhead and Donnelly [available online]).

As well as being more accurate, our method is also more widely applicable than other available methods. Existing implementations of the EM algorithm are limited in the size of problem they can tackle. For example, they are typically impracticable for sequence data containing individuals whose phase is ambiguous at more than ∼30 sites. Similarly, they cannot cope with large numbers of linked SNPs. Clark’s algorithm can deal with very long sequences (or large numbers of SNPs) but may fail either to start or to resolve all genotypes completely. These problems with Clark’s algorithm arose in many of the settings we examined. In contrast, our method suffers from neither limitation, although the running time required will increase with the size and complexity of the problem. For the simulated data sets we considered, the running time for our method ranged from a few minutes to a few hours (on a PC with a 500-MHz processor), whereas the EM algorithm and Clark’s method typically took only seconds for those problems to which they could be applied successfully. However, since the cost of a few hours of calculation on a computer is small, relative to the costs of data collection and experimental haplotype reconstruction, we argue that this kind of difference in speed is not a particularly important consideration in this context. It is difficult to make general statements about the maximum size of problem that our method might reasonably be expected to tackle, but we believe that, given reasonably modern computing resources, our method should be practicable for hundreds of individuals typed at ⩾100 sites.

An important and novel feature of our method is that it provides estimates of the uncertainty associated with each phase call. Quantification of uncertainty is, of course, good practice in any statistical estimation procedure. Formally, our method provides a sample from a distribution over possible haplotype reconstructions. Although it might be tempting to hope that one could summarize the posterior distribution by a few most-common configurations, in the cases we have looked at, the support is typically spread rather thinly over an enormous number of possible haplotype configurations. We therefore chose to summarize the posterior distribution by a single “best” phase call at each position and an estimate of the marginal probability that each phase call is correct. In practice, this risks discarding some of the information in the posterior distribution, particularly complex dependencies between the phase calls at different positions both within and between individuals. Nonetheless, we believe our summary to be a helpful way of visualizing the full joint distribution over possible haplotype reconstructions. Development of more-sophisticated ways to summarize complex high-dimensional posterior distributions provides a challenging problem for the future, both here and in other contexts.

Unless haplotype reconstruction is an end in itself, it is natural to make use of a sample from the posterior distribution of haplotype reconstructions in subsequent analyses. Any statistical procedure that uses haplotype data can easily be applied independently to several sampled haplotype reconstructions. For certain inference problems—particularly those using Bayesian methods, which provide posterior distributions over parameters of interest—uncertainty in the haplotype reconstruction can then be taken into account by averaging results of the independent analyses. However, in many inference problems (e.g., estimation of recombination rates), it would be preferable to develop a method of jointly inferring haplotypes and parameters of interest, and, in other settings, (e.g., significance testing) the best way to combine the results of independent analyses is far from clear (see the literature on multiple imputation—e.g., the work of Little and Rubin [1987]). As a practical general solution, we suggest performance of independent analyses using 10 sampled haplotype reconstructions to investigate the robustness of conclusions to inferred haplotypes. If conclusions differ among the 10 analyses, then experimental methods for haplotype reconstruction may be required to confirm findings.

Statistical methods can be used in conjunction with experimental methods to provide more-accurate estimates of individual haplotypes. Although we have treated Clark’s algorithm as an automatic method for haplotype reconstruction (as did Clark [1990]), in published applications (e.g., Nickerson et al. ¹⁹⁹⁸; Rieder et al. ¹⁹⁹⁹), it has often been used as an exploratory tool to suggest putative haplotype reconstructions, which could then be confirmed by allele-specific PCR. This seems a powerful approach, and our method can also be used in this way. The ability of our method to accurately assess the uncertainty associated with the phase call at each individual site (or locus) gives it the substantial practical advantage of allowing experimental effort to be directed at sites or loci whose phases are most difficult to reconstruct statistically. Our software can use experimentally verified phase information (either for complete individuals or for specific sites or loci) in estimation of the unknown haplotypes, and this will usually produce a substantial further reduction in error rate.

The availability of family data can also improve statistical estimation of haplotypes. In the case where triples of mother, father, and child have been collected, the child’s genotype information can be used to infer the parental haplotypes at many loci or sites (e.g., Excoffier and Slatkin ¹⁹⁹⁸, Hodge et al. ¹⁹⁹⁹), and (provided that the genetic distance across the region is not too large) our method can then use this known phase information in estimation of the remaining ambiguous phases. The accuracy of our method in simulation studies suggests that the pessimistic conclusions of Hodge et al. (1999) for markers in linkage equilibrium will not apply to markers in disequilibrium. For data from extended pedigrees, the situation is often more complex. Current methods of haplotype reconstruction in pedigrees (e.g., Sobel and Lange ¹⁹⁹⁶) ignore population-genetics considerations and rely on information in transmission events to infer haplotypic phase. These transmission events carry information on haplotypes over much larger genetic distances than we consider here, and pedigree methods can thus be effective even for widely spaced markers. However, the use of ideas from population genetics to model founder haplotypes in such pedigrees could lead to worthwhile performance improvements, particularly as denser maps of markers become available.

Fallin and Schork (2000) have recently published a simulation study to assess the performance of the EM algorithm for reconstructing phase from genotype data at linked biallelic loci. Their general conclusion is that the performance of the EM algorithm is good. The most substantial difference between our simulation study and theirs is that we have considered rather “larger” problems. Fallin and Schork (2000) considered five linked biallelic loci. We have considered long sequence data (60–100 segregating sites; table 1), short-sequence data (5–30 segregating sites; fig. 2), and 10 linked microsatellite loci (fig. 3). Haplotype reconstruction is much harder for these larger (but realistic) problems, and we believe that the improvement made by our method over EM is practically important.

A more technical, less substantial methodological difference between the approaches is that we assessed accuracy of haplotype sample frequency estimates using the discrepancy (effectively following Excoffier and Slatkin [1995]), whereas Fallin and Schork (2000) use the mean squared error (MSE). Use of MSE to measure accuracy of haplotype sample frequency estimates gives results that seem to favor our method more strongly than use of the discrepancy (data not shown).

A common and important problem with MCMC algorithms is knowing how long one needs to run the algorithm to obtain reliable results. (Often, this problem is referred to in terms of diagnosing “convergence” of the Markov chain.) Checking (and, indeed, attaining) convergence is, in general, notoriously difficult, so it is important to note that our algorithm does not necessarily need to “converge” in order to improve on the accuracy of other methods. In particular, the results of our simulation experiments did not rely on checking convergence of the algorithm and so provide direct evidence that, for the size of problem we considered, the runs were sufficiently long to give a substantial average gain in accuracy over other methods, regardless of whether the Markov chain had actually “converged” in each instance. Nonetheless, it is helpful to be aware of potential problems caused by lack of convergence. The main danger is that the algorithm could get “stuck” in a local mode of the posterior distribution of haplotype reconstructions and fail to find other, perhaps more strongly supported, modes. Depending on the severity of the problem, this kind of behavior can be difficult to identify on the basis of a single run of the algorithm, since this run could remain stuck in a single local mode for a very long time and give no clue that other modes exist. We therefore prefer to investigate convergence using multiple runs of the algorithm, with different initial values for the seed of the random-number generator (an approach suggested by Gelman and Rubin [1992]). If the algorithm tends to get stuck in local modes, then these different runs may give qualitatively quite different results, effectively diagnosing the problem. (Although more-formal approaches are possible, most are based on diagnosing convergence for a small set of continuous parameters, which is not the situation here.) Where possible, the length of the runs should be increased until they all give qualitatively similar results. If this proves impractical, then further experimental investigation may be necessary to decide between competing haplotype reconstructions.

Our method could usefully be extended to allow it to deal with missing genotype data in some individuals at some loci. This is straightforward in principle, by the usual trick of augmenting the space that the MCMC scheme explores to include the missing data. Similarly, the method could be extended to allow for the possibility of genotyping error. For realistic amounts of missing data and realistic probabilities of genotyping error, these extensions seem unlikely to greatly increase the computational time our method requires. (Indeed, incorporation of the possibility of genotyping error may even provide a way to improve the mixing of the MCMC scheme, as it will tend to flatten out modes in the posterior distribution.)

An alternative approach to the whole problem would be to assume more-explicit models for mutation, recombination, and population demography and to jointly estimate haplotypes with the parameters of these models. Kuhner and Felsenstein (2000) describe an MCMC scheme that could be used to do this, although their primary focus is estimation of parameters, rather than reconstruction of haplotypes. Their MCMC scheme makes explicit use of the genetic distance between markers and is a modified version of the scheme for known haplotypes described by Kuhner et al. (2000). However, because of its computational complexity, this scheme is currently practical only for very small genetic distances (see Kuhner and Felsenstein ^2000; Kuhner et al. ²⁰⁰⁰; Fearnhead and Donnelly [available online]) and so (we believe) could not usefully be applied to most of the data sets we consider here.

In conclusion, we note that, for many of the data sets we considered, our new statistical method succeeded in correctly reconstructing the haplotypes of ⩾80% of the sample. Although explicit conclusions will depend on power calculations for specific analyses, the accuracy of our method suggests that, in many settings, the optimal use of experimental resources will be to maximize the number of unrelated individuals genotyped. In others, it will be most efficient to target experimental effort on those phase calls that are identified as having a moderate probability of being wrong or that are critical to the conclusions of the study.

Appendix A

We consider here the “naive” version of the Gibbs sampler that arises from algorithm 1 if we assume that the type of a mutant offspring is h with probability ν_h, independent of the type of the parent. In this case (for a constant-sized panmictic population), the conditional distribution π(h∣H) is known to be

where r_h is the number of haplotypes of type h in H, r is the total number of haplotypes in H, and θ is a scaled mutation rate (see Donnelly ¹⁹⁸⁶).

In principle, we can substitute (A1) into (1) to calculate (up to a normalizing constant) Pr(H_i∣G,H_-i) for all possible values of H_i, and thus we can implement step 2 of algorithm 1. However, this is impractical if the number of possible values of H_i is too large; if k denotes the number of loci at which individual i is heterozygous, then there are 2^k-1 different possible values for H_i, and if k is large, this causes problems. However, if we take ν_h=1/M for all h, where M is the total number of different possible haplotypes that could be observed in the population, then we can solve these problems by exploiting the fact that, for those haplotype reconstructions H_i that do not contain any of the haplotypes in H_-i, the probabilities Pr(H_i∣G,H_-i) are all equal. This leads to algorithm 2, below, which is practical for large samples and large numbers of loci.

Algorithm 2. Starting with an initial guess H for the haplotype reconstructions of all individuals, make a list consisting of the haplotypes h=(h₁,…,h_m) present in H, together with counts r=(r₁,…,r_m) of how many times each haplotype appears.

• 1. Pick an individual i uniformly at random, and remove his or her two current haplotypes from the list (h,r) (so the list now contains the haplotypes in H_-i). Let k be the number of loci at which i is heterozygous.
• 2. Calculate a vector p=(p₁,…,p_m) as follows. For j=1,…,m, check whether the genotype G_i could be made up of the haplotype h_j plus a complementary haplotype, h^′. If not, set p_j=0; if so, search for h^′ in the list (h₁,…,h_m). If h^′ is in the list, h^′=h_k, then set p_j=(r_j+θ/M)(r_k+θ/M)-(θ/M)²; otherwise, set p_j=r_j(θ/M).
• 3. With probability 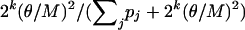, reconstruct the haplotype for individual i completely at random (i.e., by randomly choosing the phase at each heterozygous locus). Otherwise, reconstruct the haplotype for individual i as h_j plus the corresponding complementary haplotype, with probability .
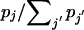• 4. Add the reconstructed haplotype for individual i to the list (h,r).

The accuracy of this algorithm is similar to that of the EM algorithm (data not shown). Note that the case θν_h=1 (for all h) corresponds to a uniform prior on the population allele frequencies F,, and that, under this uniform prior, the mode of the posterior distribution for F will be the same as the maximum-likelihood estimate sought by the EM algorithm. This approach thus could be used to perform maximum-likelihood estimation in problems that are too large for the EM algorithm.

Appendix B

We consider here the more sophisticated Gibbs sampler that arises from using (2) and (1) to perform step 2 of algorithm 1. (In fact, the algorithm we present is actually a “pseudo-Gibbs sampler,” in the sense of Heckerman et al. ²⁰⁰⁰, because the conditional distributions from which we sample are approximations that do not correspond to an explicit prior and likelihood.)

There are two main problems to be overcome here. First, for multilocus data, the expression (2) is not easy to compute, because the matrix P has the same dimension as the number of possible haplotypes and, therefore, is potentially huge. Stephens and Donnelly (2000) describe (in their appendix 1) how to approximate (2) using Gaussian quadrature, and we make use of this approximation here. The approximation requires the specification of a mutation mechanism and a scaled mutation rate, θ_j, at each locus or site. Note the contrast with the definition of θ in (2), which is the overall scaled mutation rate across sites or loci.

For the sequence data, we treated the polymorphic sites as linked biallelic loci, where a mutation at a locus causes the allele at that locus to change, and where recurrent mutations are permitted. We ignored nonpolymorphic sites, since these sites add no ambiguity to the haplotypes (and, in any case, the program we used to simulate the sequence data outputs only the polymorphic sites). For our method, this is formally equivalent to setting θ_j=0 at nonpolymorphic sites. We set θ_j=1/log(2n) for each polymorphic site in the sample, where n is the number of diploid individuals in the sample. This choice of θ_j gives, a priori, an expectation of approximately one mutation at each polymorphic site during the ancestry of the sample subsequent to its most recent common ancestor. It also corresponds to an estimate, θ=S/log(2n), for the total scaled mutation rate across the region, where S is the number of polymorphic sites observed. This is, for moderate values of n, approximately Watterson’s estimate for θ (Watterson 1977). To assess sensitivity of our results to choice of θ, we looked at other choices for θ_j at the polymorphic sites, in the range θ_j=0.1-1.0, for a few of the data sets with n=50. From our limited investigations, these values seemed to perform slightly less well, though the results were still a substantial improvement over the other methods considered.

For the microsatellite data, we used a symmetric stepwise mutation model, with 50 alleles and reflecting boundaries, and set

where H_j is the observed heterozygosity at locus j (see, e.g., Kimmel et al. ¹⁹⁹⁸).

The second problem is that, as in Appendix A above, although, in principle, we can use (2) and (1) to calculate (up to a normalizing constant) Pr(H_i∣G,H_-i) for all possible values of H_i and thus implement step 2 of algorithm 1, this approach is impractical if the number of possible values of H_i is too large. The trick we used in Appendix A to solve this problem will not work here. Instead, we adjust the Gibbs sampler (algorithm 1) so that, at each iteration, we update only a subset of the loci of a randomly chosen individual, as follows.

Algorithm 3. Start with some initial haplotype reconstruction, H⁽⁰⁾. For t=0,1,2,…, obtain H^(t+1) from H^(t), using the following three steps:

• 1. Choose an individual i uniformly at random from all ambiguous individuals.
• 2. Select a subset S of ambiguous loci (or sites) in individual i to update. (In the absence of family, or other experimental data, the ambiguous loci are those for which individual i is heterozygous.) Let H(S) denote the haplotype information for individual i at the loci in S, and let H(-S) denote the complement of H(S), including haplotype information on all other individuals (so H(S)∪H(-S)=H). Sample H^(t+1)(S) from Pr[H(S)∣G,H^(t)(-S)].
• 3. Set H^(t+1)(-S)=H^(t)(-S).

This modification of the algorithm does not affect its stationary distribution, regardless of how the subset S is chosen. We formed S by choosing five loci uniformly at random from the ambiguous loci in individual i (or all ambiguous loci if there were fewer than five ambiguous loci in individual i). At each iteration, it is then necessary to compute Pr[H(S)∣G,H^(t)(-S)] for, at most, 2⁵=32 values of H(S). Note that, for H(S) consistent with G,

and so the necessary probabilities can still be computed, up to a normalizing constant, using (2). From experience, we have found that updating up to five loci at a time in this way produces reasonable mixing in small problems. However, the algorithm can have trouble mixing effectively for larger data sets, and choice of starting point can then be important. For our simulations, we used a short preliminary run of algorithm 2 (which updates all loci simultaneously in the chosen individual), from a random starting point, to provide a “good” starting point for algorithm 3.

Finally, we summarize the information in the posterior distribution for H by a point estimate for H, and a matrix Q representing an estimate of the probability that each phase call is incorrect. We do this by specifying a loss function 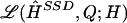, which gives the loss for reporting the estimates 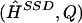when the true haplotypes are H, and attempting to minimize the posterior expected loss by means of methods analogous to those in Stephens (2000). The particular loss function we used was

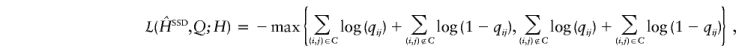where (i,j)∈C if the phase call in 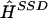for individual i at locus j is correct. There are other good summaries, corresponding to other sensible loss functions, for which the results in this study are similar.