Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 1994 May;66(5):1573–1579. doi: 10.1016/S0006-3495(94)80949-X

Hydrodynamic properties of a double-helical model for DNA.

J Garcia de la Torre 1, S Navarro 1, M C Lopez Martinez 1
PMCID: PMC1275877  PMID: 8061206

Abstract

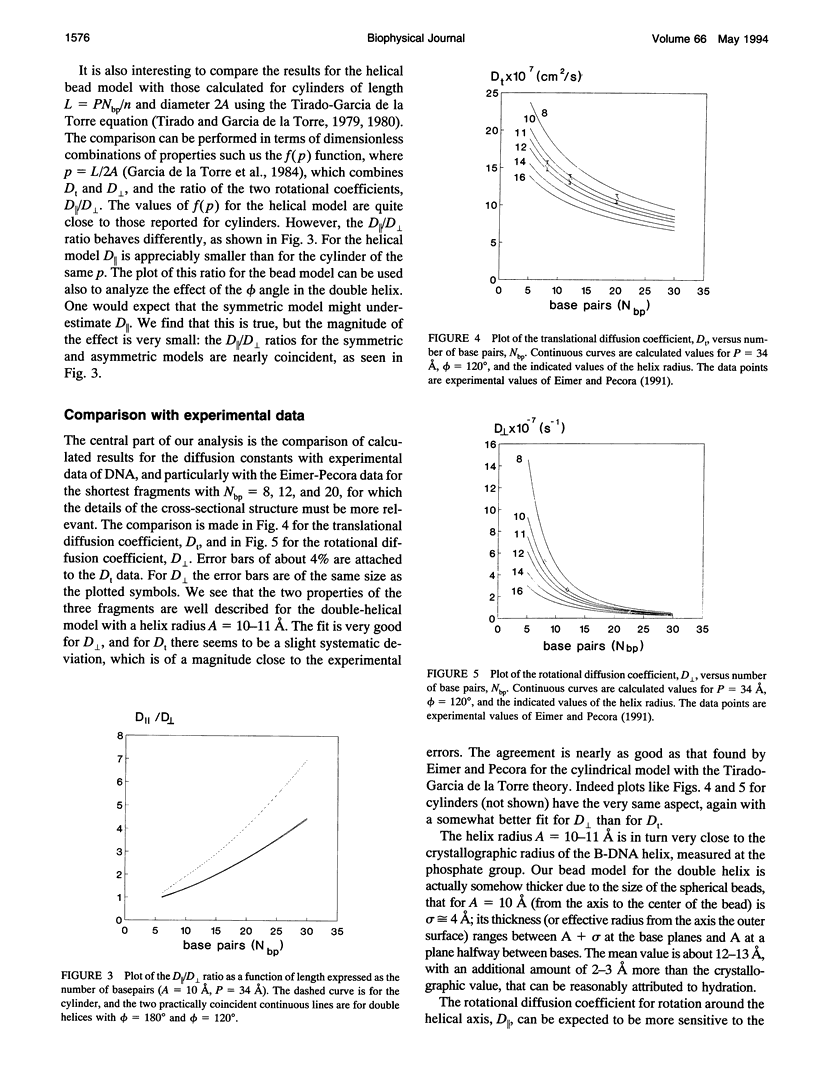
The translational and rotational diffusion coefficients of very short DNA fragments have been calculated using a double-helical bead model in which each nucleotide is represented by one bead. The radius of the helix is regarded as an adjustable parameter. The translational coefficient and the perpendicular rotation coefficient agree very well with experimental values for oligonuclotides with 8, 12, and 20 base pairs, for a single value of the helical radius of about 10 A. We have also calculated a nuclear magnetic resonance relaxation time in which the coefficient for rotation about the main axis is involved. As found previously with cylindrical models, the results deviate from experimental values, indicating that the internal motion of the bases has a remarkable amplitude. An attempt to quantify the extent of internal motions is presented.

Full text

PDF
1573

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Birchall A. J., Lane A. N. Anisotropic rotation in nucleic acid fragments: significance for determination of structures from NMR data. Eur Biophys J. 1990;19(2):73–78. doi: 10.1007/BF00185089. [DOI] [PubMed] [Google Scholar]
  2. Bloomfield V., Dalton W. O., Van Holde K. E. Frictional coefficients of multisubunit structures. I. Theory. Biopolymers. 1967 Feb;5(2):135–148. doi: 10.1002/bip.1967.360050202. [DOI] [PubMed] [Google Scholar]
  3. Boutonnet N., Hui X., Zakrzewska K. Looking into the grooves of DNA. Biopolymers. 1993 Mar;33(3):479–490. doi: 10.1002/bip.360330314. [DOI] [PubMed] [Google Scholar]
  4. Diekmann S., Hillen W., Morgeneyer B., Wells R. D., Pörschke D. Orientation relaxation of DNA restriction fragments and the internal mobility of the double helix. Biophys Chem. 1982 Jul;15(4):263–270. doi: 10.1016/0301-4622(82)80009-4. [DOI] [PubMed] [Google Scholar]
  5. Eimer W., Williamson J. R., Boxer S. G., Pecora R. Characterization of the overall and internal dynamics of short oligonucleotides by depolarized dynamic light scattering and NMR relaxation measurements. Biochemistry. 1990 Jan 23;29(3):799–811. doi: 10.1021/bi00455a030. [DOI] [PubMed] [Google Scholar]
  6. Garcia de la Torre J. G., Bloomfield V. A. Hydrodynamic properties of complex, rigid, biological macromolecules: theory and applications. Q Rev Biophys. 1981 Feb;14(1):81–139. doi: 10.1017/s0033583500002080. [DOI] [PubMed] [Google Scholar]
  7. García M. M., Jiménez Rios M. A., García Bernal J. M. Translational diffusion and intrinsic viscosity of globular proteins. Theoretical predictions using hydrated hydrodynamic models. Application to BPTI. Int J Biol Macromol. 1990 Feb;12(1):19–24. doi: 10.1016/0141-8130(90)90077-n. [DOI] [PubMed] [Google Scholar]
  8. Kovacic R. T., van Holde K. E. Sedimentation of homogeneous double-strand DNA molecules. Biochemistry. 1977 Apr 5;16(7):1490–1498. doi: 10.1021/bi00626a038. [DOI] [PubMed] [Google Scholar]
  9. Porschke D., Antosiewicz J. Permanent dipole moment of tRNA's and variation of their structure in solution. Biophys J. 1990 Aug;58(2):403–411. doi: 10.1016/S0006-3495(90)82386-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Schurr J. M., Fujimoto B. S. The amplitude of local angular motions of intercalated dyes and bases in DNA. Biopolymers. 1988 Oct;27(10):1543–1569. doi: 10.1002/bip.360271003. [DOI] [PubMed] [Google Scholar]
  11. Venable R. M., Pastor R. W. Frictional models for stochastic simulations of proteins. Biopolymers. 1988 Jun;27(6):1001–1014. doi: 10.1002/bip.360270609. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES