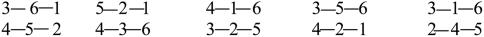A geometric construction determines all permissible strand arrangements of sandwich proteins

Abstract

For a large class of proteins called sandwich-like proteins (SPs), the secondary structures consist of two β-sheets packed face-to-face, with each β-sheet consisting typically of three to five β-strands. An important step in the prediction of the three-dimensional structure of a SP is the prediction of its supersecondary structure, namely the prediction of the arrangement of the β-strands in the two β-sheets. Recently, significant progress in this direction was made, where it was shown that 91% of observed SPs form what we here call “canonical motifs.” Here, we show that all canonical motifs can be constructed in a simple manner that is based on thermodynamic considerations and uses certain geometric structures. The number of these structures is much smaller than the number of possible strand arrangements. For instance, whereas for SPs consisting of six strands there exist a priori 900 possible strand arrangements, there exist only five geometric structures. Furthermore, the few motifs that are noncanonial can be constructed from canonical motifs by a simple procedure.

Predicting the secondary structures (α-helices and β-strands) from a given amino acid sequence has now become a routine procedure, although its accuracy is only ≈80% (1–4). For β-proteins, i.e., for proteins whose secondary structure consists of only β-sheets, predicting the arrangement of the strands in space (supersecondary structure) remains an important open problem. To address this problem, structural biologists have used the fact that β-protein structures exhibit a number of regularities (5–12), for example the ubiquitous occurrence of Richardson's Greek key. Furthermore, they have used several different algorithms, some of which are based on neural networks and on hidden Markov models (13–19).

For sandwich-like proteins (SPs), we suggest that the above problem can be solved in two steps: (i) Given a number of strands n, where n is typically between 6 and 11, construct all canonical motifs. (ii) Given the amino acid sequence of n strands, identify a single motif among the motifs constructed in step i. In what follows, we present the solution of step i. Step ii has yet to be performed.

Canonical motifs are defined as strand arrangements that satisfy the structural rules of ref. 20 (see also definitions below). Although this definition can be used in principle for the construction of all canonical motifs with a given number of strands, the implementation of this construction is complicated. Here, we will introduce an alternative characterization of canonical motifs that allows one to construct all canonical motifs with a given number of strands in a simple manner. Furthermore, our analysis reveals the existence of certain invariant topological objects, which are more fundamental than canonical motifs. Indeed, all canonical motifs are generated from these topological objects that we call “geometric structures.”

An important feature of the above geometric construction is that it can be explained from biological considerations. Indeed, the formation of the geometric structures is a consequence of simple thermodynamic principles.

Materials and Methods

Material Considered. Proteins of 69 superfamilies in 38 protein folds have been described as SPs [see folds 1.2.1–1.2.38 in Structure Classification of Proteins Release 1.59 (21, 22)]. Some SPs, in addition to the “main” sandwich sheets, contain “auxiliary” β-sheets. Here, we have analyzed only SPs consisting of two main sheets. By analyzing the H bonds between main-chain atoms, we have determined the strands (secondary structure) and the arrangements of the strands in space (supersecondary structure). We have analyzed the arrangement of strands of 177 protein domains. Each domain consists of a total of 6–11 strands. Our analysis has revealed that there are 58 supersecondary motifs that describe all these domains, see table 1 of ref. 20. Observed motifs with an even number of strands (i.e., motifs consisting of 6, 8, or 10 strands), as well as 11 of 13 motifs with 7 strands, 15 of 17 motifs with 9 strands, and 2 of 3 motifs with 11 strands, are canonical. Overall, 53 of the 58 observed motifs are canonical (91.4%).

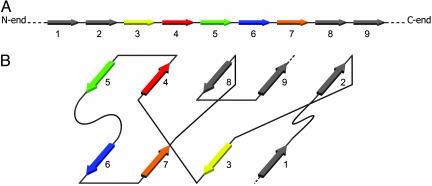
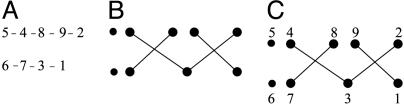
Determination of the Supersecondary Structure. The protein of Fig. 1 is a typical SP; it consists of nine strands arranged in two β-sheets. The supersecondary structure of Fig. 1B can be represented in the simplified form of Fig. 2A, where each line denotes a H bond. This canonical motif is actually the most commonly observed motif of SPs consisting of nine strands (20).

Fig. 1.

The schematic representation of the strands and the arrangement of the strands in the two β-sheets. (A) The strands are consequently numbered starting from the N-terminal of the chain. (B) Arrangements of the strands in two main β-sheets.

Fig. 2.

Different schematic representations of strand arrangements. (A)A canonical motif. (B) The geometric structure generating the canonical motif of A. (C) The canonical motif of A is generated from the geometrical structure of B by placing strands 1 and 2 at the lower and upper right positions, respectively.

Definitions. We first recall some definitions of ref. 20. Neighboring strands (NSs) are strands found in the same β-sheet and connected by H bonds between the main-chain atoms. Each strand has two NSs unless it occurs at the edge of the sheet (for example, in Fig. 2 A, strands 7 and 1 are the left and right NSs, respectively, of strand 3). Two consecutive strands i and i + 1 are called a jumping pair (JP) if they are in different sheets. If both i and i + 1 are at the edges of the same side of the two sheets, then the JP is called an edge JP (EJP); otherwise it is called an internal JP (IJP) (for example, in Fig. 2 A, strands 2/3, 3/4, 7/8, and 9/1 are IJPs, whereas strands 1/2 and 5/6 are EJPs). Throughout this article we assume cyclic ordering, i.e., the first strand of the domain follows the last strand (for example, in Fig. 2 A, strands 9 and 1 are considered consecutive strands; thus 9/1 form an IJP). Two IJPs, i/i + 1 and k/k + 1, form an interlock (23) if i/k are NSs, if i + 1/k + 1 are also NSs, and if i is to the left (right) of k and i + 1 is to the right (left) of k + 1 (Fig. 3). For example, in Fig. 2 A, the pairs of strands 2/3 and 9/1 and the pairs 3/4 and 7/8 form interlocks.

Fig. 3.

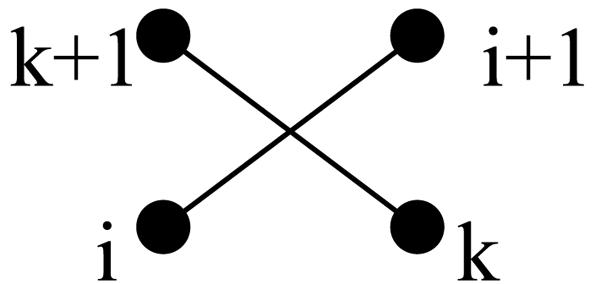
The schematic representation of an interlock.

We note that there exist EJPs at both ends of Fig. 2 A; furthermore, all IJPs appear in the form of interlocks. These are the manifestations of rules III and I, respectively, of ref. 20. Rule II of ref. 20 describes the possible arrangements of four consecutive strands. We define a canonical motif as any strand arrangement that obeys Rules I, II, and III.

Observed canonical motifs with six strands involve one interlock, those with seven and eight strands involve one or two interlocks, those with nine strands involve one, two, or three interlocks, and those with 10 and 11 strands involve two or three interlocks.

The evolutionary preservation of residues in the strands forming interlocks has been recently experimentally established in ref. 22 through the use of protein engineering.

We will denote each strand with a dot and each interlock by a pair of intersecting line segments connecting the strands of each JP, as in Fig. 3.

Geometric Structures. All canonical motifs can be obtained by using what we call geometric structures, which can be constructed as follows. Let n be the number of strands. A geometric structure is a collection of interlocks placed in sequence and of strands so that the total number of strands is n. Let m be the number of interlocks. We assume that there is at least one interlock (i.e., m ≥ 1). The number of interlocks cannot exceed (n - 2)/2 if n is even or (n - 3)/2 if n is odd. For example, if n = 9, then m may be equal to 1, 2, or 3. A possible geometric structure is depicted in Fig. 2B for m = 2.

For a given n, it is straightforward to construct all possible geometric structures. It turns out that it is sufficient to consider only structures within an equivalence class, where two structures are equivalent if one can be obtained from the other by interchanging either the two sheets or the left with the right sides or both. For example, if n = 6, m may be equal to 1 or 2 and we find five distinct geometric structures, those shown in Fig. 4.

Fig. 4.

The five canonical geometric structures for six strands.

Construction of Canonical Motifs from Geometric Structures. Each geometric structure gives rise to a multitude of canonical motifs as follows: Place strand number 1 at one of the positions and then place the remaining strands cyclically observing the definition of an interlock. After placing strand 1, there exist two choices for placing strand 2, and each of these choices yields a unique motif. For example, placing strand 1 at the lower right position of the structure of Fig. 2B and strand 2 in the upper right position, we find Fig. 2C, i.e., the canonical motif of Fig. 2 A (the other choice, as dictated by the interlock, would be to place strand 2 to the left of the upper right position).

Example: Construction of All Possible Canonical Motifs with Six Strands. We must use all possible geometric structures for six strands, i.e., those of Fig. 4. Let us for example show how to construct the five observed canonical motifs analyzed in ref. 20 and presented in Fig. 5. By placing strand 1 at the upper right position of Fig. 4A, it follows that one choice is to place strand 2 at the lower right position, and the other choice is to place strand 2 to the left of strand 1. These two choices yield the first two canonical motifs of Fig. 5. Similarly, placing strand 1 at the upper center position of Fig. 4A and placing 2 at the lower center position (following the IJP), we find the third canonical motif of Fig. 5. The fourth and the fifth canonical motifs of Fig. 5 are produced from the geometric structure of Fig. 4B, by placing strand 1 at the lower right position (respectively at the lower center position) and strand 2 at the lower center strand (respectively at the lower left). In the same way, one can construct all possible canonical motifs with six strands.

Fig. 5.

Observed SPs with six strands.

The geometric structure shown in Fig. 4E does not generate observed canonical motifs. This structure can be excluded by requiring the additional restriction that there exist at least two consecutive strands in at least one sheet. Actually, this restriction can be adopted in general because it is valid for all observed canonical motifs of six to 11 strands.

Thermodynamically Motivated Structural Principles and Geometric Structures. The formation of geometric structures is a consequence of simple thermodynamic considerations. Indeed, if one postulates that (i) two strands adjacent in the same sheet are antiparallel (with the possible exception of the case involving the first and the last strands) and that (ii) loops neither cross nor overlap, then it can be shown that one essentially arrives at the above geometric structures. These two structural principles, which have been observed by several authors, have a simple thermodynamic explanation (24). For principle i, loops connecting parallel and antiparallel strands bend by 2π and π, respectively, and, because the energy of bending is approximately proportional to the square of the angle of bent, antiparallel strands are preferred. For principle ii, if loops were to cross or overlap, then one loop would be forced into the hydrophobic core of the protein, and, because loops have many potential groups for forming hydrogen bonds, this would lead to instability. The reason for allowing strands that occur at the edges of SP to be parallel is that such strands can be connected by loops that do not create overlaps, which, together with cyclic ordering, implies that there exist two types of interlocks: One type consists of JPs with only antiparallel strands (like strands 3/4 and 7/8 in Fig. 1B), and the other type consists of JPs, some of which involve parallel strands (like strands 9/1 in Fig. 1B).

We now present a brief outline of the (extensive) analysis that demonstrates that the geometric structures arise from the preceding principles i and ii. Consider the possible connections between two consecutive strands in the schematic representation of a canonical motif, as in the typical case of Fig. 1B. The two consecutive strands may lie in the same sheet or in different sheets. First note that principles i and ii imply that there do not exist connections between the back and front of the two sheets, except possibly in the case of two strands at the same edge whose connection, being on the side of the motif, does not cause a loop crossing or overlap. (Thus, in Fig. 1B, the connections from strands 3 to 4, from 6 to 7, and from 8 to 9 lie entirely in the front, and those from 2 to 3, 4 to 5, and 7 to 8 lie entirely in the back; the two edge connections, i.e., from 1 to 2 and from 5 to 6, extend from back to front and from front to back, respectively.) Next, note that two consecutive strands in the same sheet are necessarily NSs, otherwise the existence of a strand between them would cause a loop overlap and a violation of principle ii. Then, a careful examination of all potential strand arrangements (and the exclusion of certain cases that do not occur in observed motifs) lead to the following conclusions. (i) The two strands at each edge are consecutive (including the case of the last and first strand); thus, they form an EJP. (ii) The only possible IJPs occur in pairs and form interlocks (one IJP may involve the last and first strands). Thus, a canonical motif consists of consecutive strands in the same sheet, the two EJPs and one or more interlocks.

Noncanonical Motifs. These motifs can be constructed from canonical motifs simply by changing the order of consecutive strands in the same sheet. For example, the geometric structure of Fig. 4D yields canonical motifs with strands 3, 1, 6, and 5 in one sheet and strands 2 and 4 in the other. By changing the order of consecutive strands 6 and 5, we find a noncanonical motif with strands 3, 1, 5, and 6 in one sheet. Proteins with this motif exist, but they were not analyzed in ref. 20 because they involve auxiliary sheets (see Note Added in Proof).

Discussion

Geometric structures provide a straightforward and systematic way of generating all canonical motifs. In addition, their number and the number of the corresponding canonical motifs is dramatically smaller than the number of all possible a priori motifs. Moreover, this number can be further restricted because some of the canonical motifs can be eliminated on the basis that they violate the requirement of the right-handedness (24) and of antiparallelism. Also, structural rearrangements needed for a protein to progress from a collapsed chain to the native fold, may eliminate some additional protein topologies, i.e., some motifs may be eliminated not from thermodynamic but from kinetic requirements (25).

Noncanonical motifs can be constructed through a simple modification of canonical motifs.

Current ab initio prediction algorithms are mainly based on thermodynamic considerations and search for the configuration with the lowest free energy. Imposing severe topological constraints of the type presented here, should have a major impact on the design of more efficient search algorithms.

The problem of protein engineering (26) can be considered as the inverse of the problem of protein prediction. Hence, the solution of the protein prediction problem of SPs should have important implications for the rational design of protein engineering.

Note Added in Proof. Recently, proteins involving auxiliary sheets have been analyzed by appropriately embedding them in a two-sheets structure (Y. S. Chiang and A.E.K., personal communication). The motifs of these proteins are consistent with our analysis. For example, some of the proteins with six strands have the motif with strands 1 and 4 in one sheet and strands 6, 5, 2, and 3 in the other. These proteins can be constructed from the geometric structure of Fig. 4C and, therefore, were predicted to exist by our construction.