GIS-Based Estimation of Exposure to Particulate Matter and NO₂ in an Urban Area: Stochastic versus Dispersion Modeling

Abstract

Stochastic modeling was used to predict nitrogen dioxide and fine particles [particles collected with an upper 50% cut point of 2.5 μm aerodynamic diameter (PM_2.5)] levels at 1,669 addresses of the participants of two ongoing birth cohort studies conducted in Munich, Germany. Alternatively, the Gaussian multisource dispersion model IMMIS^net/em was used to estimate the annual mean values for NO₂ and total suspended particles (TSP) for the 40 measurement sites and for all study subjects. The aim of this study was to compare the measured NO₂ and PM_2.5 levels with the levels predicted by the two modeling approaches (for the 40 measurement sites) and to compare the results of the stochastic and dispersion modeling for all study infants (1,669 sites). NO₂ and PM_2.5 concentrations obtained by the stochastic models were in the same range as the measured concentrations, whereas the NO₂ and TSP levels estimated by dispersion modeling were higher than the measured values. However, the correlation between stochastic- and dispersion-modeled concentrations was strong for both pollutants: At the 40 measurement sites, for NO₂, r = 0.83, and for PM, r = 0.79; at the 1,669 cohort sites, for NO₂, r = 0.83 and for PM, r = 0.79. Both models yield similar results regarding exposure estimate of the study cohort to traffic-related air pollution, when classified into tertiles; that is, 70% of the study subjects were classified into the same category. In conclusion, despite different assumptions and procedures used for the stochastic and dispersion modeling, both models yield similar results regarding exposure estimation of the study cohort to traffic-related air pollutants.

Recent interest has focused on traffic-related air pollution and the potential health effects associated with exposure (Kunzli et al. 2000). The acute health effects of short-term exposures to traffic-related pollution have been widely demonstrated, but much less is known about the chronic effects of exposure. Several studies have found associations between chronic morbidity or mortality and traffic-related pollution (e.g., Brunekreef et al. 1997; Heinrich and Wichmann 2004; Hoek et al. 2002a; Weiland et al. 1994; Wjst et al. 1993). On the other hand, a number of studies have found no detectable effects (Magnus et al. 1998; Wilkinson et al. 1999). Thus, the extent to which the long-term exposure to air pollution contributes to chronic health effects remains unknown. Much of the uncertainty relates to the problems of potential confounding variables and of reliable estimates of exposure to traffic-related pollution at the individual or small-area level, across large populations and cities. To date, most assessments of the health impacts of long-term exposure have involved between-city comparisons using a limited number of monitors within each city. Such between-city comparisons are subject to exposure misclassification because they rely on a small number of monitors. A recently conducted study in four European countries [SAVIAH (Small-Area Variation in Air Pollution and Health)] found important variations in the concentrations of nitrogen dioxide and sulfur dioxide on a small scale within cities (Lebret et al. 2000). Several other studies have documented important within-city variation of concentration, especially related to nearness to motorized traffic and location within the city—for example, center versus suburb (Bernard et al. 1997; Cyrys et al. 1998; Raaschou-Nielsen et al. 2000).

To overcome these problems, some studies used surrogate variables, such as distance to major road or traffic intensity (objectively determined or self-reported) (Brunekreef et al. 1997; van Vliet et al. 1997; Weiland et al. 1994; Wjst et al. 1993) to account for within-city variability in exposure. A disadvantage of these exposure indicators is that they are frequently not validated, and it may therefore be unclear what the actual exposure contrast is.

A potential solution to these problems is the use of geographic information systems (GIS) in which geographic data can be either used for the development of dispersion models (Bellander et al. 2001; Pershagen et al. 1995) or combined with concentration measurements to estimate exposures for individual members of large study populations by regression (stochastic) models (Brauer et al. 2003; Briggs et al. 1997; Gehring et al. 2002).

So far, epidemiologic studies used either stochastic or dispersion modeling, but not both in parallel. Only in the international collaborative study on the risks of development of childhood asthma and other allergic diseases [TRAPCA (Traffic-Related Air Pollution on Childhood Asthma) study (Brauer et al. 2002; Gehring et al. 2002)] were both approaches (stochastic and dispersion modeling) used in parallel to predict the out-door exposure to NO₂ and particulate matter (PM) for 1,669 study participants. For the stochastic modeling, NO₂ and particles collected with an upper 50% cut point of 2.5 μm aerodynamic diameter (PM_2.5) were measured at 40 sites spread over the city area to estimate the annual average concentrations of these pollutants. This data set offers the unique opportunity to evaluate the result of the dispersion and stochastic modeling. The aim of the study is to compare the measured levels of the two pollutants with the levels predicted by the two modeling approaches (for the 40 measurement sites) and to compare the results of the stochastic and dispersion modeling for all 1,669 study participants.

Materials and Methods

Study area and study cohort.

The study was conducted in the city of Munich, the capital of Bavaria, situated in the south of Germany. In 1999 Munich had a population of approximately 1.32 millions inhabitants in an area of 310.4 km², and approximately 700,000 cars were registered (Statistic Agency of the Provincial Capital Munich 2005).

Exposure to traffic-related air pollutants (NO₂ and PM) was modeled for two ongoing birth cohort studies [GINI (German Infant Nutrition Intervention Programme) and LISA (Influence of Lifestyle Factors on the Development of the Immune System and Allergies in East and West Germany)] conducted in Munich. A total of 1,757 infants—1,084 from the GINI cohort and 673 from the LISA cohort—were selected for this purpose. These infants were born in Munich (excluding surrounding communities, postal codes 80000–81999) and remained in Munich at least for the first year of life. For 1,756 study subjects, birth addresses could be converted into geographic coordinates. However, because some children shared the same home address, the final data set for the present analysis consists of 1,669 different cohort addresses.

Exposure modeling.

Because it was not feasible to measure outdoor exposure for all 1,669 cohort addresses, we used GIS-based stochastic and dispersion exposure modeling to predict annual average concentrations for each cohort address.

Stochastic (regression) modeling.

For the stochastic modeling, we conducted a 1-year measurement program for NO₂ and PM_2.5 at 40 measurement sites. To capture all of the variation in air pollution concentrations that might be experienced by the study subjects, we selected 17 street sites that were located both at main roads and at side roads, and 23 background sites. A detailed description of the site selection criteria is provided elsewhere (Cyrys et al. 2003; Hoek et al. 2002b).

The measurement program was performed from 16 March 1999 to 21 July 2000. At each site, four 14-day measurements were conducted such that each site was measured in each season once. PM_2.5 samples were collected with Harvard impactors (Marple et al. 1987), and NO₂ concentrations were measured by Palmes tubes (Palmes et al. 1976). All measurements were conducted according to a standard operating procedure (SOP) TRAPCA 2.0 (Hoek et al. 2001). A detailed description of the measurement program is provided elsewhere (Cyrys et al. 2003; Hoek et al. 2002b; Lewne et al. 2004).

For all pollutants, we calculated annual averages as described by Hoek et al. (2002b). In brief, measurements at the 40 sites were not performed simultaneously. Therefore, differences among the sites may have occurred because of temporal variation; because we intended these measurements to incorporate spatial variability only, the annual averages were adjusted for the impact of temporal variability using data from one site where continuous measurements were made over the entire study period.

In addition, we collected traffic-related variables (e.g., traffic intensity and population density) for the 40 measurement sites and for all cohort addresses using GIS. The annual average concentrations were then related to a set of predictor variables obtained from a GIS, using stochastic modeling. The following GIS variables were collected using GIS ARCVIEW (version 3.2; ESRI, Redlands, CA, USA): traffic density and heavy vehicles intensity in three different circular buffers around the measurement sites (50, 250, and 1,000 m radius), and household density and population density (300, 1,000, and 5,000 m radius). The relation between the geographic variables (independent variables) and the annual average air pollution concentrations (dependent variables) for the 40 sites was analyzed by multiple linear regression. The selection of the most relevant spatial scale for the geographic variables (with the highest adjusted R²) is described in detail by Brauer et al. (2003).

The final linear regression models used for the calculation of cohort exposures are presented in Table 1. These two models include only variables that were also available for the cohort addresses and therefore could be used for the calculation of cohort exposures. Using these developed models, we obtained quantitative estimates of exposure to outdoor NO₂ and PM_2.5 for all study subjects.

Table 1.

Results of regression models for PM_2.5 (μg/m3) and NO₂ (μg/m3; intercept = 11.92 for PM_2.5, and 18.91 for NO₂).

	NO2			PM2.5
Variable	Slope	SE	R2 full modela	Slope	SE	R2 full modela
			0.62			0.56
Traffic intensity (50–250 m)b (per 1,000 vehicles/day)	6.22 × 10−5	4.30 × 10−5	0.36	1.35 × 10−5	3.28 × 10−6	0.29
Traffic intensity (50 m)b (per 1,000 vehicles/day)	1.12 × 10−4	4.30 × 10−5	0.15	3.32 × 10−5	1.02 × 10−5	0.19
Address density (300 m)b (per 1,000 addresses)	1.93 × 10−3	6.16 × 10−4	0.09	3.26 × 10−4	1.27 × 10−4	0.08
Address density (300–5,000 m)b (per 1,000 addresses)	1.24 × 10−5	1.03 × 10−5	0.02	—	—	—

^aIndividual variables added to previously entered variables already in the model.

^bDistances refer to the radius of the buffer zone (in meters) around the sampling site.

We evaluated the validity of the regression models by a cross-validation procedure. This involved fitting the regression model for 39 of the measurement sites to predict the concentration at the remaining site. This procedure was conducted for each of the 40 sites, and these results were compared with the measured annual average concentrations determined for each of the sites. The root mean squared error (RMSE) was calculated as the square root of the sum of the squared differences of the observed concentration at site i and the predicted concentration at site i from a model developed without site i (Hoek et al. 2001). The RMSE was 1.35 μg/m³ for PM_2.5 and 6.12 μg/m³ for NO₂; that is, it was small compared with the range in concentration across sites (11.18–19.69 μg/m³ for PM_2.5 and 15.86–50.64 μg/m³ for NO₂).

Dispersion modeling.

We used a Gaussian multisource dispersion model IMMIS^net (IVU Umwelt GmbH, Sexau, Germany) for the calculation of annual mean values for NO₂ and total suspended particles (TSP; defined as airborne particles with a diameter < 30 μm) concentrations. The dispersion models were developed on the basis of GIS data for the addresses of the 40 measurement sites and for the 1,669 cohort addresses.

IMMIS^net is a model for calculating the spatial extent of concentration levels of air pollution. The model describes the dilution and transport of pollutants from point, line, and area sources as a stationary process, using a Gaussian normal distribution. Gaussian dispersion models are instruments that have been tried and tested for many years within the framework of plans for maintaining air quality, or planning permit procedures, in line with the German Technical Directive on Air Pollution Control TA-Luft 1986 (TA Luft 1986).

Based on the Gaussian smoke plume equation, the model calculates concentration contributions from the emissions of the area, line, or point sources considered. Statistical parameters, such as the mean value or percentiles of the cumulative frequency, are calculated for each of the defined receptors from the individual concentrations determined for all the hours of the year. In addition, IMMIS^net can prepare all the background input data for microscale street canyon models.

The input values in IMMIS^net consist of the emission data for the sources under consideration, broken down into a number of polluter groups, and a climatologic frequency distribution or a time series of meteorologic parameters. The model operates chronologically; that is, the concentration contributions of all the data sources considered are calculated for every hour of the year. The representative meteorologic conditions for any particular hour are selected randomly from the climatologic distribution of meteorologic cases in a meteorologic frequency distribution. The model determines hourly emissions from the annual emissions, using polluter-group–specific monthly, weekly, and daily cycles.

The specific emissions data of the different categories of sources (traffic, industry, domestic fuel) were not available for the measurement period from March 1999 to July 2000. Thus, the data for the emissions of the traffic were determined based on the road network of the city of Munich from 1997 (by the use of the program IMMIS^em). Large single emitters such as industrial plants or power stations were taken out of the emission inventory for Munich from 1986. Because the emission inventory contains only emissions data for TSP and not for PM_2.5, the dispersion model estimated TSP levels. The spatial distribution of domestic heating emissions was obtained from the data for energy consumption in Munich in 1997 and the data of the building structure. Therefore, the estimated NO₂ and TSP levels are more valid for 1997 than for the study period (March 1999 through July 2000).

The annual concentrations are calculated for defined coordinates including a 1.5-m height above ground level. The regional background level was determined as the difference between the modeled and the measured NO_x and TSP concentrations (as measured at the network station in Munich Johanneskirchen). The background concentration was 21.5 μg/m³ for NO_x and 33.2 μg/m3 for TSP. The NO₂ values were calculated from the estimated NO_x values using the following formula (Romberg et al. 1996):

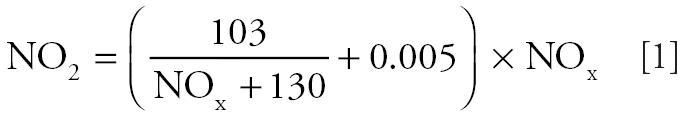To validate the IMMIS^net/em model, we compared the annual means of NO₂ and TSP measured in 1997 at the network stations in Munich (n = 7 for NO₂ and n = 6 for TSP) with the estimated NO₂ and TSP values. The comparison showed that the mean difference between the measured and modeled NO₂ concentrations is 3.8 ± 4.8 μg/m³ (7.6 ± 10.2%). The mean difference between the measured and modeled TSP levels is –1.6 ± 9.7 μg/m³ (–3.6 ± 18.4%). The coefficient of variation is 8.1% for NO₂ and 12.9% for TSP.

Quality assurance.

During each of the approximately 16 measurement periods, a PM_2.5 field blank and field duplicate were collected. The detection limit was 3.4 μg/m³, and all samples were above the detection limit. The coefficient of variance was low (3.3%); that is, the precision of PM_2.5 was good.

To answer the question whether the Palmes tube measurements were not underestimating the true NO₂, we compared the Palmes tube measurements during every 2-week sampling period with a chemiluminescence monitor (Ecophysics CLD 700 AL; Ecophysics GmbH, Munich, Germany) at three sites. The Palmes tubes were located in direct vicinity to the inlet of the chemiluminescence equipment. There was a high correlation between 2-week average NO₂ concentrations from Palmes tubes and parallel continuous monitoring measurements (r = 0.94). The overall ratio of the Palmes tube reading and the corresponding chemiluminescence value was 1.01. For more details, see Hoek et al. (2002b) and Lewne et al. (2004).

Statistical methods.

The Pearson correlation coefficients were calculated to describe the associations between air pollutants concentration derived from the two different sets of models.

To compare the stochastic and dispersion model, the modeled concentrations were classified into 3 categories: high, middle, and low concentrations for the two models separately. Tertiles were used as cutoff values to ensure equal distribution of the values between the three categories. Finally, the concordance of the cohort address classification by the two models was considered.

Generalized additive models were used to investigate the functional relationship between NO₂ and PM concentrations estimated by stochastic and dispersion modeling, respectively. We computed LOESS smoothers with pointwise ± 2 SE bands and a span of 0.4 for the smooth curves with S-Plus (version 6.0; Insightful Corporation, Seattle, WA, USA).

Results

Comparison of measured air pollution, stochastic-modeled air pollution, and dispersion-modeled air pollution (for 40 measurements sites).

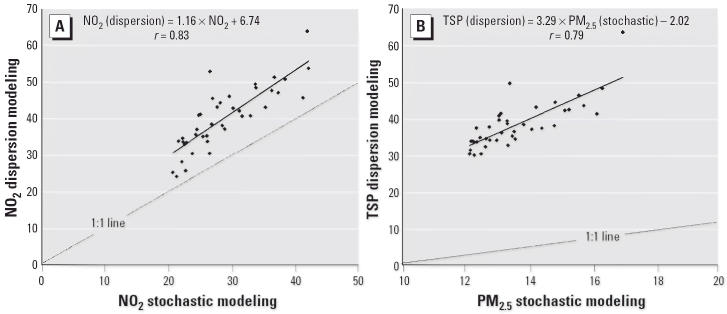
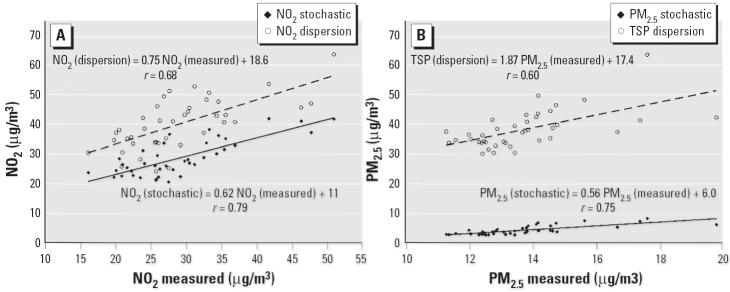
The annual average air pollution concentrations measured and estimated for the 40 measurement sites are shown in Table 2. There is a substantial range in annual average concentrations for NO₂ and for PM. The ratio of the measured NO₂ concentrations to the NO₂ levels estimated by the dispersion model is 0.71. The ratio of the measured PM_2.5 concentrations to the TSP values estimated by the dispersion model is 0.31.

Table 2.

Description of the measured and modeled NO₂ and PM_2.5 (TSP) annual average concentration across the 40 measurements site.

Variable	Type	Mean	Minimum	Maximum	SD
NO2	Measured	28.8	15.9	50.6	7.8
NO2	Stochastic	28.8	20.6	42.1	6.1
NO2	Dispersion	40.2	24.3	63.8	8.6
PM2.5	Measured	13.6	11.2	19.7	1.8
PM2.5	Stochastic	13.6	12.2	17.0	1.3
TSP	Dispersion	42.8	35.8	64.5	5.5

The relationship between the stochastic and dispersion NO₂ values is shown in Figure 2A. Figure 2B shows the relationship between the stochastic PM_2.5 and dispersion TSP levels. The regression equation for NO₂ differs significantly from the one for PM_2.5:TSP. The intercept of the regression equation for NO₂ is clearly higher than the intercept of the regression equation for PM_2.5:TSP (6.8 vs. –2.0). The slope of the stochastic versus dispersion NO₂ regression equation is only slightly > 1, whereas the slope of the PM_2.5 versus TSP regression equation is > 3.

Figure 2.

(A) Relationship between stochastic- and dispersion-modeled NO₂ concentration (40 measurement sites). (B) Relationship between stochastic-modeled PM_2.5 and dispersion-modeled TSP concentration (40 measurement sites).

Note that, although the correlation between measured NO₂ and PM_2.5 concentrations was 0.84, the correlation between modeled NO₂ and PM concentrations was almost 1 for both models (data not shown).

Comparison of stochastic-modeled air pollution and dispersion-modeled air pollution (for 1,669 cohort addresses).

We applied the regression models described in Table 1 to the 1,669 home addresses of the cohort, and we applied the dispersion model to the home addresses of the cohort. A description of the estimated exposure for the study cohort is presented in Table 3. The mean values estimated for the cohort are very similar to those for the 40 measurement sites, whereas the range of the estimated pollutant levels increased for the study cohort. Apparently, the selection of 40 sampling sites did not include some of the more extreme traffic conditions encountered in the cohort. Exactly 18 cohort addresses were estimated to have higher NO₂ or PM values than the highest measured values in the 40 measurement sites. All 18 addresses are located in the vicinity of the Munich city circular highway (Mittlerer Ring), with an extremely high traffic density, so the estimate for these addresses requires extrapolation.

Table 3.

Description of the measured and modeled NO₂ and PM_2.5 (TSP) annual concentration for the study cohort (n = 1,669).

Variable	Type	Mean	Minimum	Maximum	SD
NO2	Stochastic	27.7	19.5	66.9	6.2
NO2	Dispersion (IMMIS)	38.8	20.6	73.8	7.7
PM2.5	Stochastic	13.4	11.9	21.9	1.3
TSP	Dispersion (IMMIS)	41.8	34.5	83.9	4.5

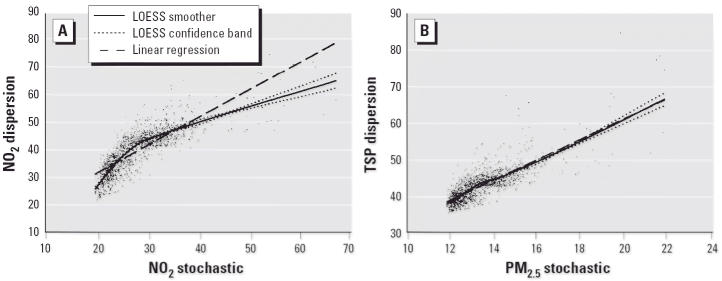
The relationship between the stochastic and dispersion NO₂ values for the whole study cohort is shown in Figure 3A. The estimated LOESS smooth curve differs substantially from the linear regression curve. The relation between the NO₂ levels estimated by means of the two models is nonlinear. However, the correlation between the stochastic and dispersion NO₂ levels is strong. The Spearman rank-order correlation coefficient (instead of Pearson correlation coefficient) is 0.86.

Figure 3.

(A) Relationship between stochastic- and dispersion-modeled NO₂ concentration for all study subjects (n = 1,669); r (Spearman) = 0.86. (B) Relationship between stochastic-modeled PM_2.5 and dispersion-modeled TSP concentration for all study subjects (n = 1,669); r (Spearman) and r (Pearson) = 0.79.

Figure 3B shows the relationship between the stochastic PM_2.5 and dispersion TSP levels for all study subjects. For PM the estimated LOESS smooth curve does not differ substantially from the linear regression curve. The linear regression equation for all study subjects [TSP (dispersion) = 2.78 × PM_2.5 (stochastic) + 4.57] is similar to the regression equation found for the 40 measurement sites. The Pearson correlation coefficient (r = 0.79) has the same value as that for the 40 measurement sites.

As previously shown for the 40 measurements, we also found for the study cohort very strong correlations between the stochastic estimated levels of NO₂ and PM_2.5 (r = 0.98) as well as between NO₂ and TSP levels estimated by dispersion modeling (r = 0.99) (data not shown).

Numerous epidemiologic studies do not use individual exposure estimates for NO₂ for study subjects; rather, the estimates are categorized in several groups, with each group including a comparable number of subjects. For this reason, we compare the categorization of the subjects made by means of the results of both models. Table 4 shows the classification of the study addresses into three categories (described in “Materials and Methods”). For 70% of the cohort addresses, the exposure estimates for NO₂ remain in the same category; a change between the highest and the lowest category is very rare (< 1%). The changes between the highest and the middle or between the middle and the lowest category were < 10% for the specific relationship, but approximately 30% in total. A similar pattern was observed for PM_2.5:TSP (64% agreement). The highest degree of disagreement is found for the middle–middle category (45% for NO₂ and 53% for PM), whereas the disagreement in the low–low or high–high category is substantially lower (between 20 and 30%).

Table 4.

Comparison of the categorization of the study subjects made by means of the stochastic and dispersion modeling [n (%)].

Category	High(dispersion)	Middle(dispersion)	Low(dispersion)	Total(dispersion)
NO2
High(stochastic)	412 (24.7)	143 (8.6)	1 (0.1)	556
Middle(stochastic)	142 (8.5)	307 (18.4)	108 (6.5)	557
Low(stochastic)	2 (0.1)	107 (6.4)	447 (26.8)	556
Total(stochastic)	556	557	556	1,669
PM
High(stochastic)	400 (24.0)	152 (9.1)	4 (0.2)	556
Middle(stochastic)	142 (8.5)	264 (15.8)	151 (9.1)	557
Low(stochastic)	14 (0.8)	141 (8.5)	401 (24.0)	556
Total(stochastic)	556	557	556	1,669

Discussion

Comparison of measured air pollution, stochastic-modeled air pollution, and dispersion-modeled air pollution (for 40 measurements sites).

The NO₂ levels estimated by the dispersion model are clearly higher than the concentrations of NO₂ at the 40 measurement sites. For the comparison of the measured PM_2.5 with the modeled TSP levels, the typical PM_2.5:TSP ratio for Munich should be considered. To our knowledge, there are no simultaneous measurements of PM_2.5 and TSP in Munich available at the present. However, one of our 40 measurement sites (background station where PM_2.5 was measured) was located approximately 2 km from the network background station in Munich Johanniskirchen (where TSP was measured). The calculated average PM_2.5:TSP ratio for those two stations is 0.40. The PM_{2.5(measured)}:TSP_(modeled) ratio estimated in our study is lower (0.31), which suggests an overestimation of the TSP levels by the dispersion model.

This assumption is supported by the consideration of the PM_2.5:TSP ratios observed for other European cities. Gomiśćek et al. (2004) estimated the PM_2.5:TSP ratios over a 1-year period for three urban sites in Austria. The ratios are 0.45 for Linz, 0.52 for Vienna, and 0.54 for Graz, with negligible differences between the winter and the summer seasons. Similar PM_2.5:TSP ratios (0.46 ± 0.09 for the summer and 0.59 ± 0.07 for the winter season) were estimated for Erfurt, Germany, over a 5-year period from 1996 through 2000 (Heinrich J, personal communication). Lall et al. (2004) estimated the mean PM_2.5:TSP ratios for the United States based on PM data collected over the last three decades (mean ratio = 0.30). The PM_2.5:TSP ratios show a strong spatial trend across the United States, with the northeastern and eastern parts of the country having among the highest fine mass fractions (PM_2.5:TSP between 0.45 and 0.55). The higher PM_2.5:TSP ratios in the eastern United States are consistent with the presence of stronger sources of fine particulate emissions in the U.S. east coast, with its high degree of urbanization. In the light of the findings here, one can assume that the typical PM_2.5:TSP ratios expected for the Central European ambient air quality situation as well as climatic conditions should be between 0.40 and 0.60.

The overestimation of the NO₂ and TSP levels calculated by the dispersion model could be caused by the use of older emission data (emission inventory for industrial plants or power stations from 1986, traffic and house fire emissions from 1997). It can be assumed that especially the emissions from large single emitters and domestic heating decreased significantly during the nineties. However, even if the estimated levels of NO₂ and TSP could be overestimated, the within-city variability in concentrations across the study participants does not change.

It seems that the difference between the stochastic- and dispersion-modeled NO₂ concentrations is rather constant for all measurement sites (slope of the regression equation ~1), whereas the difference between the stochastic-modeled PM_2.5 levels and dispersion- modeled TSP values is more site specific and increases for higher PM concentrations (slope of the regression equation > 3).

The correlations between the values obtained by the measurements and the stochastic model were somewhat higher than the correlations between the measured values and the dispersion values. This is not unexpected, because the stochastic modeling includes the multiple linear regression analysis based on the 40 measured values. Notable is the very strong correlation between the exposure estimates for NO₂ and PM_2.5 within the two models. This could be explained by the similarity of the predictors used for the two pollutants both in the regression and in the dispersion modeling.

Comparison of stochastic-modeled air pollution and dispersion-modeled air pollution (for 1,669 cohort addresses).

The regression equation for PM_2.5 (stochastic) versus TSP (dispersion) at the 1,669 cohort addresses is very similar to that observed for the 40 measurement sites. Because the two models contain different PM characteristics (PM_2.5 or TSP), the direct comparison of the two models is allowed only if the spatial variation of TSP is to a large extent driven by the PM_2.5 spatial variation. It means that PM_2.5 and TSP should be strongly correlated over the whole study area. Unfortunately, we do not have any information about the correlation between PM_2.5 and TSP in Munich. However, as shown by Cyrys et al. (2003), the Pearson correlation coefficient estimated on 36 sites across the whole TRAPCA study area (Munich, Stockholm, and the Netherlands) between PM_2.5 and PM₁₀ is 0.78. The correlation between PM_2.5 and PM₁₀ restricted only to Munich (12 measurement sites) is stronger (r = 0.95). This strong correlation between annual averages of PM_2.5 and PM₁₀ documents that a large portion of the spatial variation of PM₁₀ was caused by PM_2.5. Although PM₁₀ is not TSP, we might assume that TSP is also strongly correlated to PM_2.5 in the urban area of Munich and that the comparison of both variables (PM_2.5 and TSP) as shown in Figures 2A and 3B has some meaning.

Because of the similar classification of the study subject generated by the two models, one would expect that the choice of one model (regression or dispersion) should not affect the results of the epidemiologic studies. In both cases, similar results regarding the estimated association between health effects and traffic-related pollutants are expected. This assumption is valid only if simple categorization in tertiles is used for epidemiologic studies. However, epidemiologic studies are also using more than three exposure categories or even continuous air pollution data that need to be considered.

In choosing between the two models, other aspects should also be considered. The dispersion models require input data, specifically for emissions and background pollution, which may not be readily available. For this reason, we were able to estimate only the TSP and not the PM_2.5 concentrations by dispersion modeling. On the other hand, the regression modeling requires a monitoring program, which may be much more expensive because of the high equipment and personnel costs.

Conclusions

Despite different assumptions and approaches made by the two models, the NO₂ and PM_2.5 values predicted by stochastic model were strongly correlated with the corresponding NO₂ and TSP concentrations predicted by the dispersion model. Both models led to similar classifications of the cohort addresses regarding the exposure to traffic-related air pollution. Thus, we assume that similar results regarding the estimated association between health effects and traffic-related pollutants are expected by use of the two modeling approaches. However, this assumption is valid only if similar categorization in tertiles is used for epidemiologic analysis. Further verification of this conclusion is needed—for example, an epidemiologic analysis with continuous exposure data and comparison of the findings coming from the two different approaches (stochastic and dispersion).

Other model aspects should be considered in choosing one specific model. The regression modeling requires a monitoring program, which may be very expensive because of high equipment and personnel costs. On the other hand, the dispersion models require input data, specifically for emissions and background pollution, which may not be readily available. For this reason, we were not able to estimate the PM_2.5 concentrations by dispersion modeling, but only the TSP levels.

Both models have common shortcomings: Because traffic intensity and household density were the most important predictors for both pollutants, the correlations between modeled NO₂ and PM_2.5 (stochastic model) or between modeled NO₂ and TSP concentrations (dispersion model) were almost 1 for both modeling methods. This does not allow a sufficient discrimination of the two pollutants regarding their associations with the health of the study cohort members.

Figure 1.

(A) Relationship between modeled and measured NO₂ concentration (40 measurement sites). (B) Relationship between modeled and measured PM_2.5 concentration (40 measurement sites).