Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1989 Aug;56(2):273–280. doi: 10.1016/S0006-3495(89)82673-6

Evidence for chaotic behavior in driven ventricles.

G V Savino 1, L Romanelli 1, D L González 1, O Piro 1, M E Valentinuzzi 1
PMCID: PMC1280476  PMID: 2505870

Abstract

Toad ventricles were externally driven by periodic pulses while monophasic action potential (MAP) signals were recorded in seven excised and seven in situ ventricles. As the frequency was slowly increased in steps, the stimulated tissue displayed several dynamic characteristics. Hierarchies of periodic behavior, like phase-locking and period-doubling sequences leading to chaos, were observed. Results showed that subharmonic bifurcations (order one and two) and chaotic-like behavior may systematically occur in the MAP signal within a definite frequency interval in the 1:1 phase locking regime. The chaotic, or more cautiously expressed, chaotic-like behavior is characterized by the power spectrum, the autocorrelation function, the Poincaré map, and the reconstructed 2-D phase portrait. It is concluded that (a) bifurcations of order one and two and the characteristic irregular behavior are evidences of local universal chaotic dynamics in cardiac tissue; (b) there are no qualitative differences in the dynamics of the in situ and excised ventricles; and (c) fibrillation seems to be related to chaotic behavior, but whether they are similar or equivalent phenomena still remains to be seen.

Full text

PDF

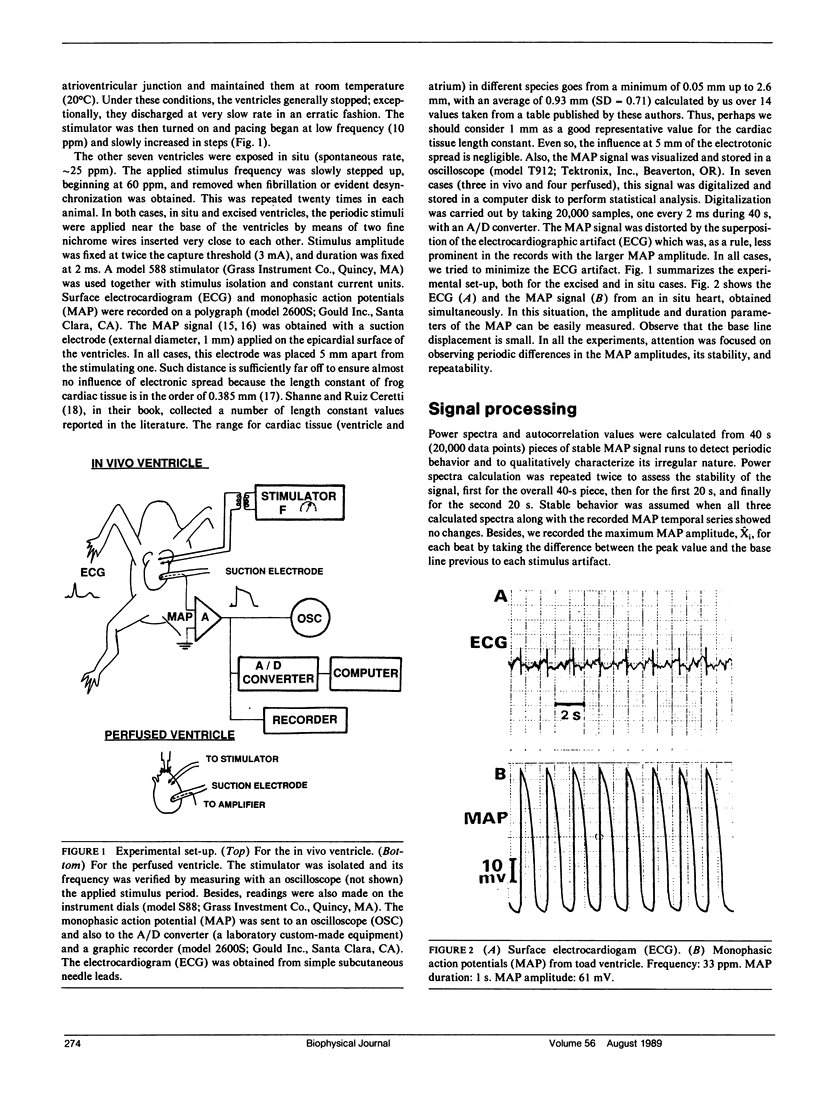
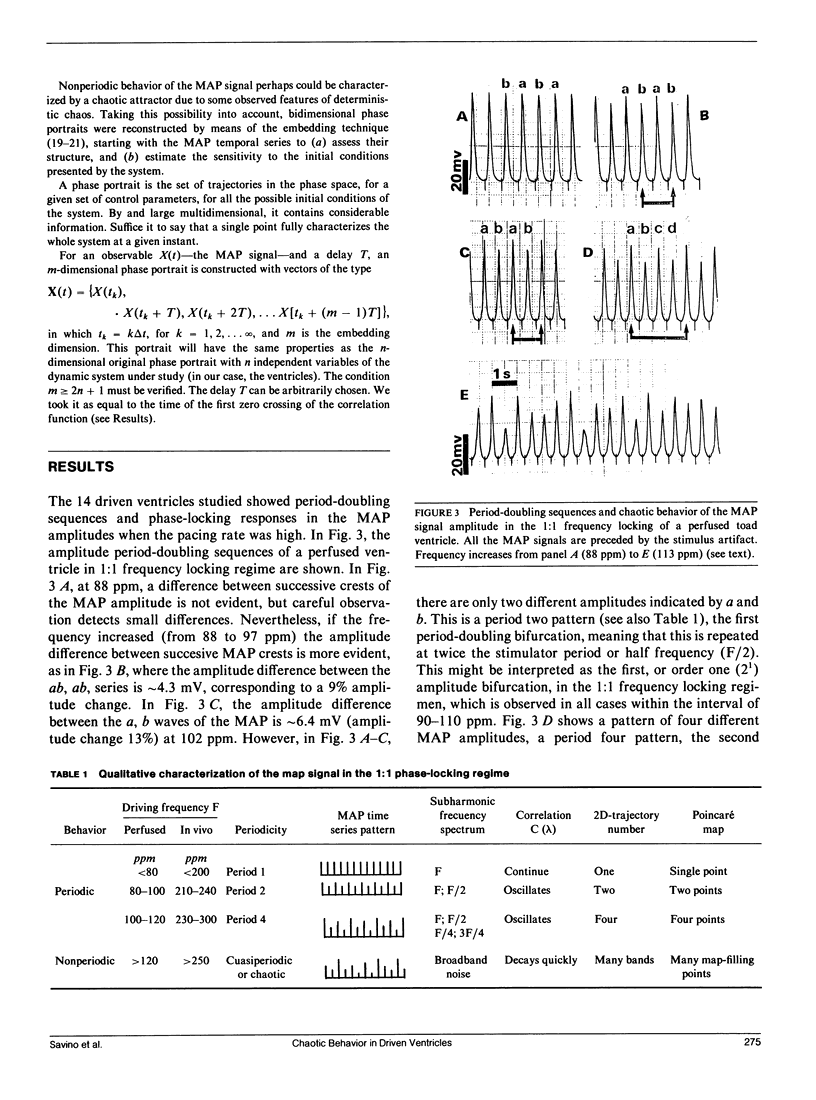
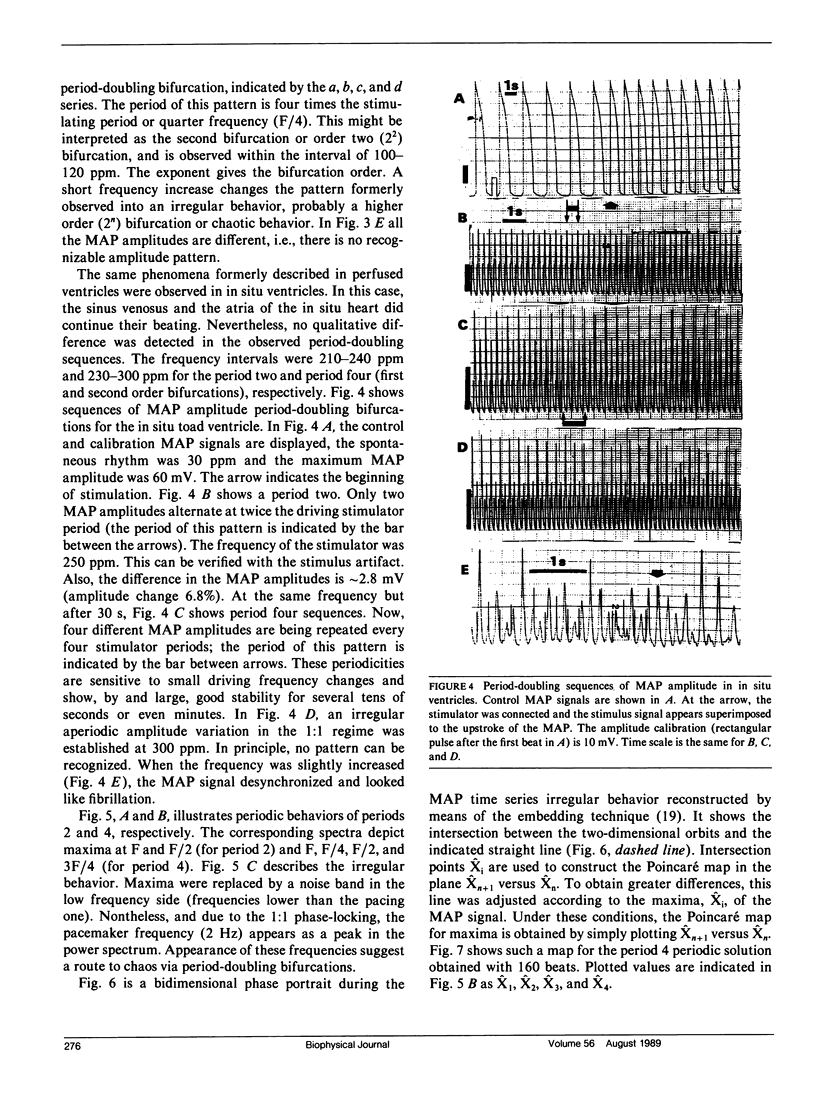
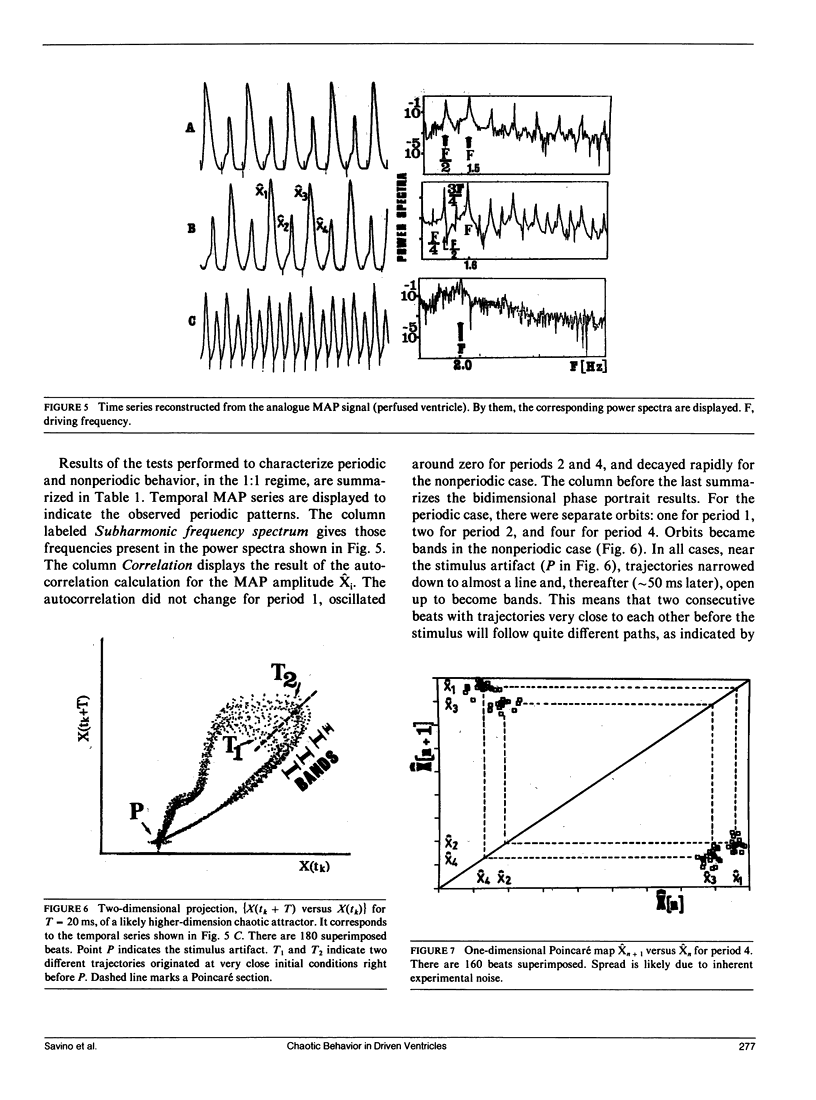
Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Beeler G. W., Reuter H. Reconstruction of the action potential of ventricular myocardial fibres. J Physiol. 1977 Jun;268(1):177–210. doi: 10.1113/jphysiol.1977.sp011853. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Best E. N. Null space in the Hodgkin-Huxley Equations. A critical test. Biophys J. 1979 Jul;27(1):87–104. doi: 10.1016/S0006-3495(79)85204-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. CRANEFIELD P. F., EYSTER J. A. E., GILSON W. E. Electrical characteristics of injury potentials. Am J Physiol. 1951 Nov;167(2):450–456. doi: 10.1152/ajplegacy.1951.167.2.450. [DOI] [PubMed] [Google Scholar]
  4. Chay T. R., Lee Y. S. Phase resetting and bifurcation in the ventricular myocardium. Biophys J. 1985 May;47(5):641–651. doi: 10.1016/S0006-3495(85)83960-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chialvo D. R., Jalife J. Non-linear dynamics of cardiac excitation and impulse propagation. Nature. 1987 Dec 24;330(6150):749–752. doi: 10.1038/330749a0. [DOI] [PubMed] [Google Scholar]
  6. González DL, Piro O. Symmetric kicked self-oscillators: Iterated maps, strange attractors, and symmetry of the phase-locking Farey hierarchy. Phys Rev Lett. 1985 Jul 1;55(1):17–20. doi: 10.1103/PhysRevLett.55.17. [DOI] [PubMed] [Google Scholar]
  7. Grebogi C., Ott E., Yorke J. A. Chaos, strange attractors, and fractal basin boundaries in nonlinear dynamics. Science. 1987 Oct 30;238(4827):632–638. doi: 10.1126/science.238.4827.632. [DOI] [PubMed] [Google Scholar]
  8. Guevara M. R., Glass L. Phase locking, period doubling bifurcations and chaos in a mathematical model of a periodically driven oscillator: a theory for the entrainment of biological oscillators and the generation of cardiac dysrhythmias. J Math Biol. 1982;14(1):1–23. doi: 10.1007/BF02154750. [DOI] [PubMed] [Google Scholar]
  9. Guevara M. R., Glass L., Shrier A. Phase locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cardiac cells. Science. 1981 Dec 18;214(4527):1350–1353. doi: 10.1126/science.7313693. [DOI] [PubMed] [Google Scholar]
  10. HOFFMAN B. F., CRANEFIELD P. F., LEPESCHKIN E., SURAWICZ B., HERRLICH H. C. Comparison of cardiac monophasic action potentials recorded by intracellular and suction electrodes. Am J Physiol. 1959 Jun;196(6):1297–1301. doi: 10.1152/ajplegacy.1959.196.6.1297. [DOI] [PubMed] [Google Scholar]
  11. Jalife J., Antzelevitch C. Phase resetting and annihilation of pacemaker activity in cardiac tissue. Science. 1979 Nov 9;206(4419):695–697. doi: 10.1126/science.493975. [DOI] [PubMed] [Google Scholar]
  12. Kremers M. S., Miller J. M., Josephson M. E. Electrical alternans in wide complex tachycardias. Am J Cardiol. 1985 Aug 1;56(4):305–308. doi: 10.1016/0002-9149(85)90854-9. [DOI] [PubMed] [Google Scholar]
  13. Mines G. R. On dynamic equilibrium in the heart. J Physiol. 1913 Jul 18;46(4-5):349–383. doi: 10.1113/jphysiol.1913.sp001596. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ritzenberg A. L., Adam D. R., Cohen R. J. Period multupling-evidence for nonlinear behaviour of the canine heart. Nature. 1984 Jan 12;307(5947):159–161. doi: 10.1038/307159a0. [DOI] [PubMed] [Google Scholar]
  15. Savino G. V., Valentinuzzi M. E. Ventricular fibrillation-defibrillation in the toad Bufo paracnemis. Int J Cardiol. 1988 Apr;19(1):19–25. doi: 10.1016/0167-5273(88)90186-6. [DOI] [PubMed] [Google Scholar]
  16. Surawicz B. Ventricular fibrillation. J Am Coll Cardiol. 1985 Jun;5(6 Suppl):43B–54B. doi: 10.1016/s0735-1097(85)80526-x. [DOI] [PubMed] [Google Scholar]
  17. TARR M., SPERELAKIS N. WEAK ELECTROTONIC INTERACTION BETWEEN CONTIGUOUS CARDIAC CELLS. Am J Physiol. 1964 Sep;207:691–700. doi: 10.1152/ajplegacy.1964.207.3.691. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES