Modeling lateral geniculate nucleus cell response spectra and Munsell reflectance spectra with cone sensitivity curves

Abstract

We find that the cell response spectra of lateral geniculate nucleus cells, as well as the reflectance spectra of Munsell color chips, may be modeled by using the cone sensitivity functions of the long and medium cones. We propose a simple model for how the neural signals from the photoreceptors might be combined in the retina to closely approximate the reflectance spectra of Munsell color chips without input from the short cone.

Recent research reveals that lateral geniculate nucleus (LGN) cell response spectra are fairly smoothly distributed in Munsell perceptual color space in a manner similar to the reflectance spectra of Munsell color chips (1). The findings were based on data reported by De Valois et al. (2), who measured spectral response data on 147 LGN cells. Neural signals reach the LGN through the optic nerve, which consists of the axons of ganglion cells in the retina. Each axon carries signals aggregated from a number of photoreceptors. The aim of this paper is to examine the LGN response spectra for clues as to how the responses of the long (L), medium (M), and short (S) cones (photoreceptors) are aggregated through the various layers of the retina to produce the LGN response spectra. From these clues, we construct a simple model of how the reflectance spectra of the Munsell chips might be represented by these aggregation processes.

We assume that the color appearance of objects originates in their reflectance spectra that, together with the illumination source, determine the light stimuli reaching the photoreceptors or cones in the retina. We seek understanding of how photoreceptors are combined in the retina to produce a distribution of the LGN response spectra that is similar in distribution to the reflectance spectra of objects (1). First, we explore the contribution of the cones to the basis functions of the LGN spectral response curves. We recognize that these representations are statistical constructions and do not necessarily represent how the neural system actually functions. However, we can obtain some insight into the way the system might function from such an examination. We then propose a model of how the cone sensitivity curves might be combined to produce response spectra that closely approximate reflectance spectra of ordinary objects such as flowers, fruits, and Munsell color chips.

Cone Contributions to the Basis Functions of the LGN Neurons

In a reanalysis of the De Valois et al. data, Young (3) reported the first three loadings (designated by Young as E1, E2, and E3) of the LGN cells obtained from a principal components analysis (PCA). He further demonstrated that the LGN response spectra were well represented in the normalized cone sensitivity space of Derrington et al. (4). In this section, we reanalyze the De Valois et al. data with the aim of understanding the quantitative relationship between cone sensitivity curves and the LGN response spectra. All the data analyzed in this section of the paper are published in ref. 1.

We denote the data consisting of the response spectra of the 147 LGN cells as R_N×M, where N = 147 cells and M = 12 sampled wavelength locations with responses measured in spikes per second (each cell was measured at three light intensities, and the 147 values are means of the three measures). We used the raw recorded data uncorrected for base firing rates. In general, PCA or singular value decomposition analyzes a matrix such as R in the following way (5)

[1]

where both UU^T and VV^T are identity matrices, and Δ_K×K = (√λ_k) is a diagonal matrix. Values of λ_k(>0) and v_jk are obtained, respectively, as eigenvalues and eigenvectors of X^TX and U = XVΔ^-1. In our case, we find that K = 3 provides an adequate agreement between the two sides of Eq. 1. We can write

[2]

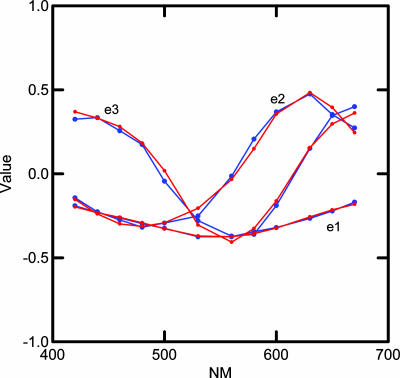
The adequacy of the approximation may be seen by comparing the sum of squares of the original data with that of the reconstructed data based on the first three basis functions. The sum of the squares of the full rank = 12 matrix R, taken element-wise, is 526,991, whereas the sum of squares of R̂, also taken element-wise, is 510,618 (smaller because it is reconstructed with 3 instead of 12 dimensions), which means that 96.9% of the sum of squares is accounted for in the three-dimensional approximation. We call E_12×3 = (e_jk) basis functions and refer to them as e₁, e₂, and e₃. With a Stewart-Love (6) redundancy index = 0.998, these basis functions are almost identical to the principal component loadings, E1, E2, and E3, found by Young (3) without taking means. We have carried out the calculations in this section with Young's loadings as well as with our basis functions and the substantive conclusions are similar, therefore, we only report details for the basis functions. To a close approximation, all the LGN cell response spectra may be reconstructed by combining the basis functions in the appropriate proportions. The blue lines in Fig. 1 show a plot of the observed basis functions.

Fig. 1.

Curves showing the three LGN cell basis functions in blue and estimated basis functions, based on best fitting combination of L and M cones, in red.

Our first task is to investigate ways of combining cone sensitivity curves that model each of these basis functions. The red lines in Fig. 1 show the results of a regression analysis that estimates the basis functions from L and M cone sensitivity curves as described below. For the regression analysis, we first computed four multiple regression analyses for each basis function. In each analysis, the basis functions were the dependent variables. The cone sensitivity curves of Stockman and Sharpe (7) constituted the basis for constructing the four sets of independent variables for computing the predictions as follows: {L, M, S} {L, M} {L^⅓, M^⅓, S^⅓} {L^⅓, M^⅓}. A constant (indicated by K in Table 1) was used in each case. The cube root cone response transformation was included because it had been shown in the previous analysis by Young (3) to produce a good approximation to the LGN spectral response curves. Table 1 shows the adjusted (for differing degrees of freedom) multiple R² values obtained from these calculations.

Table 1. Value of adjusted R² (with associated F ratios) for each of the three basis functions of the LGN spectra for each of four different models, with the preferred model in bold.

Model	e1	F ratio	e2	F ratio	e3	F ratio
K + L + M + S	0.879	27.64	0.914	40.16	0.982	196.04
K + L + M	0.880	41.32	0.724	15.46	0.981	297.15
K + L⅓ + M⅓ + S⅓	0.987	290.10	0.988	302.22	0.932	51.56
K + L⅓ + M⅓	0.988	456.91	0.989	486.88	0.937	83.28

The results tabulated in Table 1 seem to indicate that fits may be obtained without input from the S cone that are as adequate as can be obtained using the S cone. Given the small sample of spectral locations (n = 12), tests of the significance of the differences in correlations are all nonsignificant. Because we need all the evidence we can get, we have included the associated F ratios. We have highlighted in boldface the model for each basis function that seems best, based on both the magnitude of the correlation and the F ratio. Our tentative conclusion that e₁ and e₂ are best fit with the cube root of the cone sensitivity curves, whereas e₃ is best fit with unpowered cone sensitivity curves, is unproven. It is an open question as to whether our conclusion will be verified by further research. The apparent lack of input from the S cone is so contrary to our expectations that we have carefully checked for possible artifacts or errors in our statistical procedures. Because the cone sensitivity curves are so highly correlated with each other, the results could be due to collinearity effects. Another possibility is that the use of a constant in the equation could somehow confound the results and mask the effects of the S cone. Therefore, we performed tests of the contribution of each term in the preferred equations using all three cone types. In these calculations, the null hypothesis H₀ that we are testing with the P value is that the regression coefficient of the predicting variable is zero. The results are shown in Table 2.

Table 2. Results from testing for the effects of three cone sensitivity curves in accounting for the basis functions.

Effect	Coefficient	SE	Lower 95%	Upper 95%	t value	Two-tail P value
Basis function e1
Constant	−0.108	0.015	−0.141	−0.074	−7.338	0.000
L⅓	−0.137	0.037	−0.222	−0.051	−3.697	0.006
M⅓	−0.134	0.027	−0.197	−0.072	−4.946	0.001
S⅓	−0.011	0.014	−0.043	0.022	−0.752	0.473
Basis function e2
Constant	−0.171	0.062	−0.315	−0.27	−2.742	0.025
L⅓	1.886	0.157	1.523	2.248	11.989	0.000
M⅓	−1.806	0.115	−2.072	−1.540	15.641	0.000
S⅓	0.037	0.060	−0.101	0.175	0.614	0.557
Basis function e3
Constant	0.403	0.026	0.343	0.462	15.642	0.000
L	−0.631	0.065	−0.781	−0.482	−9.740	0.000
M	−0.217	0.61	−0.358	−0.075	−3.525	0.007
S	−0.041	0.043	−0.141	0.059	−0.945	0.372

If we use a cutoff probability value of 0.05 and recompute the remaining terms, we get the following prediction equations for the basis functions

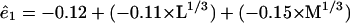[3]

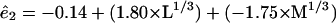[4]

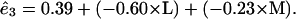[5]

The red curves in Fig. 1 show a plot of values obtained from these equations without any S cone input. It can be seen that the basis functions can be well approximated by combinations of the L and M cones.

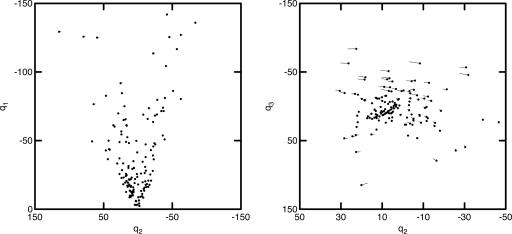
Using Q, we can plot the LGN cells as a configuration of points {Q_ik} in a K-dimensional space spanned by orthogonal coordinate axes q, plots of which are shown in Fig. 2. From Eq. 2 we see that Q_147×3 = R_147×12E_12×3, which allows us to calculate estimates of Q based on estimates of E obtained with Eqs. 3-5. These estimated values are plotted in Fig. 2 as the end of the vectors radiating from the points {Q_ik} represented as filled circles. The fit is so close that many vectors do not extend beyond the filled circle. We conclude that the location of the cells in this representation may be adequately estimated with no input from S cones. The fact that the S cones do not contribute significantly to the response spectra of cells in the parvocellular layers of LGN is the critical clue needed for the construction of the model developed below.

Fig. 2.

Euclidean representation of the 147 cells of the LGN based on the basis functions (filled circles) compared to estimates (ends of vectors) based only on the L and M cones.

A Model of How Cone Sensitivity Curves Are Aggregated in the Retina to Match Munsell Reflectance Spectra

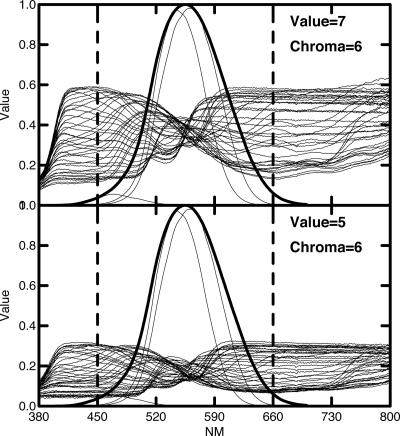
We now use the findings of the last section to construct a model of how cones might be aggregated in the retina to emulate the reflectance spectra of Munsell color chips. To understand our task better, we need to review some of the characteristics of the reflectance spectra and how they relate to color appearance. Fig. 3 shows two sets of reflectance spectra of Munsell color chips representing all 40 possible hues. Fig. 3 Upper shows all Munsell hues of chroma level 6 (fairly saturated colors) and value level 7 (fairly light). Fig. 3 Lower shows spectra from chips similar in all respects except they are at value level 5 (much less light). In both cases, the superimposed thick line curve is the luminous efficiency function of Judd's 1951 modification of CIE 1924 standard observer V(λ) for photopic vision (8) and is a linear combination of the L and M cone sensitivity curves of Stockman and Sharpe (7) with a peak at 555 nm. The three thin line curves show the L, M, and S cone sensitivity curves multiplied by V(λ), which is an estimate of the relative sensitivity of the three cones in the photopic range. The small contribution of the S cone is consistent with Wald's finding that “when the total foveal sensitivity is given a maximal height of 1.0, the heights of the B, G, and R curves are as 0.053:0.575:0.542 at the corneal level” (p. 1011 of ref. 9).

Fig. 3.

Two plots of the reflectance spectra of Munsell color chips of all 40 hues at Munsell chroma value of 6. (Upper) Munsell value 7. (Lower) Munsell value 5. The fine lines are plots of the three cone sensitivity curves times v(λ), and the thick line shows v(λ).

Note that the various physical spectra shown in Fig. 3 cross at ≈555 nm, which produces a butterfly effect centering on that point. The vast majority of the meaningful variation in the shape of the spectra, as well as the vast majority of the human visual sensitivity in the photopic or high luminosity range, lies between the vertical dotted lines. Therefore, we will restrict our model to apply to the effective photopic range from 450 nm to 660 nm [which includes 98.7% of the area of V(λ)]. We assume that this is the range of vision for full daylight conditions in which color vision seems to function at its best. The photopic luminosity efficiency function has been carefully measured with various independent measuring methods, including heterochromatic flicker photometry and judging minimally distinct borders, and these “is no measurable contribution from the S cones to the photopic luminous efficiency function that can be distinguished from experimental error” (p. 459 of ref. 10).

Romney and Indow (11) examined the Euclidean structure of the Munsell reflectance spectra. In general, there is a rather remarkable correspondence between the structure of the physical spectra and the perceptual color system. The reflectance spectra of ordinary objects (we exclude things such as fluorescence, incandescence, etc.) in the photopic range are closely approximated by three basis functions. They reported the basis functions for both the Munsell color samples and the 708 natural objects reported by Vrhel et al. (12) as being virtually identical.

If we represent the Munsell reflectance spectra as a matrix, S_1269×211, measured on 1,269 chips at 1-nm steps from 450 to 660 nm, we can perform an analysis parallel to that on the LGN cells as summarized in Eq. 2 by writing

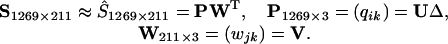[6]

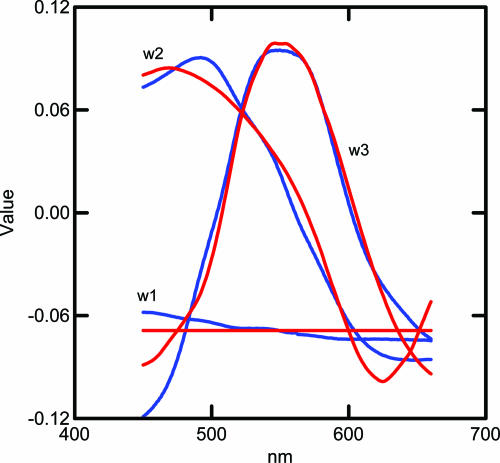
The adequacy of the approximation may be seen by comparing the sum of squares of the original data with that of the reconstructed data based on the first three basis functions. The sum of the squares of S, taken element-wise, is 44,169.3, while the sum of squares of Ŝ, is 43,955.9 which means that 99.5% of the sum of squares is accounted for in the three-dimensional approximation. Fig. 4 shows the first three basis functions of the Munsell sample computed on 1,269 chips plotted with blue lines. The data are a subset of that used in ref. 4. Note that the first basis function is close to flat (achromatic), whereas the second and third basis functions are associated with chromaticity and the color circle of hues. We assume that the universe of possible reflectance spectra consists of all combinations of these basis functions in the 450-660 nm range with reflectance values between 0 and 1. All reflectance spectra of both natural and artificial objects, obtained from personal measurements as well as from the literature, can be closely approximated with these three basis functions.

Fig. 4.

Plots of the first three basis functions of the Munsell reflectance spectra (blue curves) compared to a model based on L and M cones (red curves). See text for formula.

If each spectral curve is scaled to a value of zero at its observed reflectance value at 555 nm, then the area bounded by the minimum and maximum reflectance values, when bisected into a lower and upper half at 550 nm, results in two approximately equal areas of opposite sign. The implication of this is that the value of any spectra at 555 nm is approximately the mean of the spectra and corresponds to the first basis function, which is highly proportional to the mean value of the spectra. This characteristic of the spectra helps account for the butterfly effect and is related to the fact that the majority of the information about color is clustered around 555 nm. From an engineering perspective, photoreceptors located 10-15 nm on each side of 555 nm and with a combined peak sensitivity at 555 nm are close to ideal. Munsell value is defined as a function of V(λ) (8), a linear combination of L and M cones with a peak at 555 nm. We have found that Munsell chroma may be approximated as a function of the standard deviation of the cube rooted spectra (from 450 to 660 nm).

We now use the clues from the LGN basis functions to provide a solution to the question of how cone sensitivity curves might be combined to produce an approximation to the basis functions of physically measured spectra. We first note that the second and third basis functions of the LGN cells and the second and third basis functions of the color samples are fairly similar in shape. Because the second loading was best represented as the difference between the cube roots of the L and M cones, whereas the third was best represented as a simple weighted average of the L and M cones, we tried the same thing for the Munsell basis functions. The estimated basis functions are arrived at by regression analysis as for ê₂ and ê₃ in Eqs. 4 and 5. The formulas used are as follows

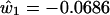[7]

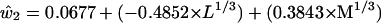[8]

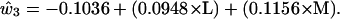[9]

These values are plotted in red in Fig. 4. It would make very little difference to the outcome if the coefficients in parentheses in Eq. 8 and 9 were made equal to each other within each equation. The first basis function is simply a flat function consisting of the mean of the empirical basis function. The fit between the blue lines obtained from 1,269 physically measured spectra through complicated matrix calculations and the red lines obtained solely from simple differences and sums of the L and M cone sensitivity curves appears to offer a simple and economical solution to the puzzle of how LGN cell response data can emulate reflectance spectra without input from the S cone.

The empirical and estimated curves are qualitatively similar. The curves are within the bounds of individual variation among individuals in expressed opsins (13). A final test of how well the reflectance spectra can be approximated by just the L and M cones may be made by comparing the location of the sample spectra derived from the empirical basis functions with the location of the sample spectra derived from estimated basis functions based on the L and M cone sensitivity curves. Romney and Indow (5, 11) demonstrated that the dot product of the reflectance spectra and basis functions results in coordinates that locate the spectra in a three-dimensional Euclidean space (see, for example, figure 4 in ref. 11, similar except for illumination by D65).

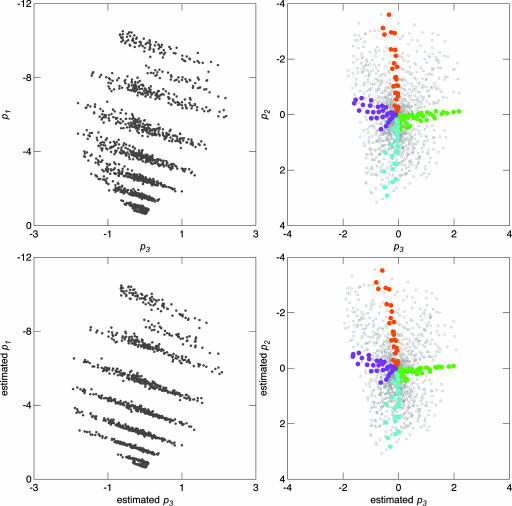
In Fig. 5 we compare results of locating the chips on the basis of the actual basis functions with the estimated basis functions obtained with P̂_1269×3 = S_1269×211 Ŵ_211×3, where Ŵ_211×3 is calculated with Eqs. 7-9. We have plotted the actual results in Fig. 5 Upper and the estimated results in Fig. 5 Lower. To show the orientation of the figure, we have highlighted the location of the polar extremes of the two basis functions. The exact chips highlighted in terms of Munsell area and hue are as follows: top, 2.5 YR; right, 5 GY; bottom, 2.5 B; and left, 7.5 P. The similarity of the two sets of figures demonstrates that Munsell reflectance spectra can be closely fit with just the L and M cone spectral sensitivity curves.

Fig. 5.

Plots showing the location of the 1,269 Munsell samples. (Upper) Scaling of actual spectra. (Lower) Scaling based on estimated basis functions using L and M cones. The color highlights Munsell area, and hue is as follows: orange, 2.5 YR; green, 5 GY; blue, 2.5 B; and purple, 7.5 P.

A possible model might consist of three components. The first would require the existence of a rapidly responding component to adjust the visual system to the existing illumination level. This component would operate in the retina prior to the chromaticity component that we associate with the parvocellular level LGN signals analyzed in this paper. A process that does exactly this is described by Rinner and Gegenfurtner (14). They demonstrated “that perceptual colour constancy measured by achromatic adjustments is in large part complete after 25 ms” (p. 733 of ref. 14). In our model, this sets the first basis function of the visual field to a flat function at a mean value from which calculations as to perceived lightness (or Munsell value) can be made.

The second component models the second and third basis functions as two subunits, the outputs of which are merged by some neural interconnecting mechanism in the retina (or, much less likely, the LGN). The first subunit would correspond to the second basis function and consist of De Valois et al.'s (2) spectrally opponent cells or to type I cells (with the exception of the blue, on-center cells) as defined by Wiesel and Hubel (15), whereas the second subunit would correspond to De Valois et al.'s (2) spectrally nonopponent cells and type III cells (except without input from the S cone) as defined by Wiesel and Hubel (15). Basically, the second component utilizes signals from two well established LGN cell types and posits that they are somehow interconnected to produce the response spectra observed in the LGN. Processes in the second component are simple additive and subtractive functions, the on center and off surround (and vice versa) of the opponent cell provide obvious mechanisms for such functions.

The third component we posit is necessary for processing lightness (Munsell value) and may be associated with the magnocellular layer of the LGN and is probably more or less identical to V(λ). Because V(λ) is similar in shape to the second subunit above, the two processes would be very difficult to distinguish. Another possibility for the computation of lightness or value is to extract it with some neural function that performs the calculation of regression with a constant. We have correlated the second and third basis functions estimated from using just the L and M cones. Computing a regression equation including a constant for each of the 1,269 Munsell chip spectra results in three variables: the constant term is correlated perfectly with the mean of the spectra and the two coefficients correlated virtually perfectly with the eigenvectors in the matrix P in Eq. 6 that correspond to the second and third basis functions.

Discussion

We can speculate about the many unsolved problems raised by the model. First, the reason the cube root applies to one subunit and not the other is not clear. The fact that the red/green opponent process equilibria is linear (16), whereas the yellow/blue opponent process equilibria involves nonlinearity in the long-wavelength cone response (17), is suggestive in this regard. Second, the model posits some mechanism for combining the effects of two subunits that is unspecified. Third, the model provides no answer to the question of how the physical representation is transformed into a perceptual representation. The answer provided by D'Andrade and Romney (18) now appears to need revision because it required significant input from the S cone.

Just because the reflectance spectra may be recovered without any input from the S cone does not imply that the S cone is simply an appendix-like evolutionary fossil. It does suggest that we take a second look at some contemporary views of the opponent process theory as consisting of categorically different type signals reaching the LGN and later integrated by using higher-order processes in the cortex, as implied by Conway and Livingstone (19). Because there is clearly subsequent processing for color perceptions at higher cortical levels, the fact that the space of Munsell reflectance spectra can be spanned by LGN cell response spectral functions need not imply that these signals are turned directly into color sensations at the subcortical level. However, this study indicates that an adequate neural representation of Munsell reflectance spectra is already present at the level of LGN.

We speculate that, when the Old World primate visual system evolved, separate L and M cone opsin genes in place of a single L/M arrangement, as is still found in most New World primates, the S cone became more or less redundant and has declined since that time in its contribution to color vision. This is clearly reflected in a number of obvious ways: the paucity of type I blue on-center cells in Wiesel and Hubel's study (15), the relatively low occurrence of S cones in the retina (20), the almost total absence of S cones in the fovea (20), and the low level of the sensitivity of the S cone in the photopic range compared to the L and M cones as illustrated in Fig. 3. D'Zmura and Lennie (21) summarize the situation as follows: “Although some chromatically opponent ganglion cells and neurons in the LGN receive inputs from all three classes of cone, when adapted to white light most show no discernible input from blue cones” (p. 1671). Clearly, some activity of the S cone can be demonstrated in various experiments with light stimuli (e.g., bleaching with intense lights in the yellow region of the spectra to cancel out the L and M cones, and observing that the world appears blue). However, it remains a fact the yellow/blue opponent process has always been somewhat less well defined than the red/green opponent process.

We can speculate further as to the functions the S cone might serve to drive the evolutionary selective pressure to maintain the frequency of occurrence that we observe in the retina. First, the L and M cones reside on the X chromosome, which accounts for the higher rate of vision deficits among males than females. It is possible that, when either the L or M cone opsins are deficient, the S cone comes into play as a backup and the visual system reverts to resemble the New World primate system. Second, the system we posit is for normal daylight environments. When there is a sudden change to darkness, it takes some minutes for the scoptic rod vision to fully adapt and reach reasonable sensitivity. It is possible that the S cone, which would be much quicker reacting, might play an important role in mesopic light conditions.