Cooperative cargo transport by several molecular motors

Abstract

The transport of cargo particles that are pulled by several molecular motors in a cooperative manner is studied theoretically in this article. The transport properties depend primarily on the maximal number N of motor molecules that may pull simultaneously on the cargo particle. Because each motor must unbind from the filament after a finite number of steps but can also rebind to it again, the actual number of pulling motors is not constant but varies with time between zero and N. An increase in the maximal number N leads to a strong increase of the average walking distance (or run length) of the cargo particle. If the cargo is pulled by up to N kinesin motors, for example, the walking distance is estimated to be 5^N–1/N micrometers, which implies that seven or eight kinesin molecules are sufficient to attain an average walking distance in the centimeter range. If the cargo particle is pulled against an external load force, this force is shared between the motors, which provides a nontrivial motor–motor coupling and a generic mechanism for nonlinear force–velocity relationships. With increasing load force, the probability distribution of the instantaneous velocity is shifted toward smaller values, becomes broader, and develops several peaks. Our theory is consistent with available experimental data and makes quantitative predictions that are accessible to systematic in vitro experiments.

Cytoskeletal motors that perform active movements along cytoskeletal filaments drive the long-range transport of vesicles, organelles, and other types of cargo in biological cells. In this article, we will consider processive motors, which can complete many chemo-mechanical cycles while remaining bound to the filaments. During the last decade, the properties of single processive motors, such as kinesin on microtubules and myosin V on actin filaments, have been characterized in some detail by using in vitro motility assays and novel experimental techniques for the visualization and manipulation of single molecules (1, 2). However, in vivo, force generation and transport is typically performed by several motor molecules in a cooperative fashion as revealed by electron microscopy (3, 4) and by tracking of the cargo particles with optical methods (5–7). It also has been found that some cargo particles bind different types of motors simultaneously so that these particles can reverse their direction of motion along microtubules (5, 7) or switch from microtubules to actin filaments (8).

The force generated by a single cytoskeletal motor is rather small and of the order of a few piconewtons. Larger forces can be generated if several motors pull on the same cargo. This larger force is necessary, e.g., for the fast transport of large organelles through the cytoplasm, which is a highly viscous medium (9). Likewise, large forces arising from many motors also are required for specific motor functions such as the extraction of membrane tubes from vesicles (10, 11).

Another important consequence of the cooperative action of several motors is that it increases the walking distance (or run length) of the cargo particles. Because the binding energy of such a cargo particle is necessarily finite, it can be overcome by thermal fluctuations, which are ubiquitous in cells. If the cargo particle is pulled by a single processive motor, its walking distance is typically of the order of one micrometer (12). If the cargo particle is pulled by several motors, the walking distance is strongly increased because the cargo continues to move along the filament unless all motors unbind simultaneously. In addition, as long as the cargo particle is still connected to the filament by at least one motor, all unbound motors can rebind rather fast, because they are prevented from diffusing away from the filament. It also has been shown by using in vitro motility assays that cargo particles pulled by many motors can switch tracks and move along several filaments at the same time, so that huge walking distances can be achieved that exceed the length of a single filament (13).

In this article, we study these cooperative transport phenomena from the theoretical point of view. First, we introduce a generic transition rate model for the transport of cargo particles, which are pulled by up to N motors, and obtain general expressions for the average number of pulling motors, for the average velocity of the bound cargo particle, for its effective unbinding rate, and for the distribution of its walking distances. Next, we focus on the case of cargo particles with a dilute motor coverage, which should be directly applicable to typical bead assays. In the absence of an external load force, we obtain an explicit expression for the average walking distance of the cargo particles. Using this expression for particles that are pulled by up to N kinesin motors, we estimate the walking distance to grow as 5^N–1/N. We also calculate the distribution of the walking distances, which is found to exhibit a tail with an extended plateau region for N ≥ 3.

An external load force leads to a nontrivial coupling between the different motors because the unbinding rates of the motors increase with increasing force. As a consequence, the average number of bound motors decreases as the load force is increased, which provides a generic mechanism for nonlinear force–velocity relationships. We argue that the motor transport becomes ineffective at a critical force for which the average walking distance becomes comparable with the step size of a single motor. For N ≥ 2, this critical force is found to be small compared to the maximal stall force that can be sustained by N motors. Finally, we calculate the probability distribution of the instantaneous velocity of the bound cargo particle. As the load force is increased, this velocity distribution is shifted toward smaller values, becomes broader, and develops several peaks.

We will focus on the transport by kinesin motors, which pull cargo particles along microtubules, because, in this case, all input parameters for our theory have been determined experimentally, but our analysis is rather general and can be applied to other types of cytoskeletal motors as well. All experimental data that are available for cargo transport by several kinesin motors are consistent with our theoretical results.

Model and General Solution

Transition Rate Model. We consider cargo particles that are transported by N motors, see Fig. 1. These motors are irreversibly attached to the cargo particle but can bind to and unbind from the filament along which they move. Thus, the number n of motor molecules that are bound to the filament can vary between n = 0 and n = N. We will distinguish N + 1 different states of the cargo particle corresponding to the unbound state with n = 0 and to N bound states with n = 1,2,... N. Each of these bound states contains N!/(N – n)!n! substates corresponding to the different combinations of connecting n motor molecules to the filament. If the cargo particle is linked to the filament through n motors, it moves with velocity v_n. Unbinding of a motor from the filament and binding of an additional motor to the filament occur with rates ε_n and π_n, respectively.

Fig. 1.

A cargo particle is transported cooperatively by N molecular motors along a filament. The motors are firmly attached to the cargo but unbind from and rebind to the filament. Each state of the system, denoted by |n 〉, is characterized by the number n of bound motors that pull on the cargo particle. The latter number can vary between n = N (on the left) and n = 0 (on the right). In state |n 〉, the cargo particle has velocity v_n, a motor unbinds from the filament with rate ε_n, and an additional motor binds to the filament with rate π_n.

We first derive general expressions for the transport properties of cargo particles pulled by up to N motors without specifying how the rates ε_n and π_n and the velocities v_n depend on the number n of bound motors. We derive the distributions of the number of bound motors, of the binding times, and of the walking distances from which we then obtain the effective unbinding rate, the average walking distance, and the average velocity. All these quantities can be directly measured by particle tracking both in vivo and in vitro.

Distribution of the Number of Bound Motors. We first calculate the distribution of the number of bound motors. We denote by P_n the probability that the cargo particle is in state |n 〉, i.e., bound to the filament by n motors. These probabilities satisfy the master equation

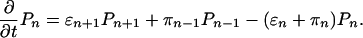[1]

We are interested in the transport properties of bound cargo particles. Because all movements of bound cargo particles begin and end with n = 0, every step from state |n 〉 to |n + 1 〉 implies a backward step at some later time. To determine the transport properties of the bound cargo particles, we can therefore focus on the stationary solution of the master equation, which is characterized by

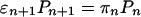[2]

for 0 ≤ n ≤ N – 1.

Subsequently expressing all P_n in terms of P₀ and using the normalization 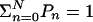, we obtain

[3]

To determine the transport properties of cargo particles bound to the filament, we normalize these probabilities with respect to the bound states, i.e., we consider the probabilities P_n/(1 – P₀) that a bound cargo particle is bound to the filament by n motors. For example, the average number of bound motors is given by

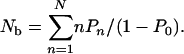[4]

Average Velocity. The distribution of the number of bound motors as given by Eq. 3 implies the distribution of velocities

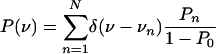[5]

of the cargo particle moving along the filament. The latter quantity can be determined experimentally as the histogram of velocities averaged over short time intervals. The average velocity of the cargo particle moving along the filament is then given by

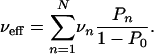[6]

If the velocity of the cargo particle is independent of the number of bound motors, v_n = v, the effective velocity is equal to the single-motor velocity v.

Effective Unbinding Rate. Finally, the distribution of the number of bound motors also implies an explicit expression for the effective detachment or unbinding rate. In the stationary state, the effective binding and unbinding rates, π_eff and ε_eff, fulfill the simple relation

[7]

where (1 – P₀) is again the probability that the cargo particle is bound to the filament through at least one motor. The effective binding rate is given by π_eff = π₀ because the cargo–filament link is established as soon as one motor binds to the filament, so that ε_eff = π₀P₀/(1 – P₀).†

With the distribution of the number of bound motors as given by Eq. 3, we obtain

[8]

where the summation now starts with n = 1. For N = 2 motors, this result reduces to ε_eff = ε₁/(1 + π₁/ε₂). An alternative derivation of Eq. 8 based on first passage times is presented in A.1. Mean First Passage Times in Supporting Text, which is published as supporting information on the PNAS web site.

Distributions of Binding Times and Walking Distances. The effective unbinding rate as given by Eq. 8 determines only the average time that the cargo particle is bound to the filament. The actual binding time Δt_b of the cargo particles is, however, a stochastic quantity that is governed by a certain probability distribution .

This probability distribution governs the passage from the state with one motor connecting the cargo to the filament at time t (immediately after binding) to the unbound state at time t + Δt_b. This distribution can be obtained by solving a recursion relation as shown in A.2. Distribution of Unbinding Times in Supporting Text. The general solution is a sum of exponentials,

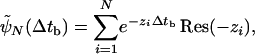[9]

where the scales –z_i of the exponentials and the prefactors Res(–z_i) are the poles and the corresponding residues, respectively, of a continued fraction that is given in the supporting information. The time scales and prefactors are functions of the binding and unbinding rates and should not be considered as independent fit parameters when analyzing experimental data.

The distribution of the walking distances, ψ_N(Δx_b), is obtained from the distribution of binding times by substituting Δt_b by Δx_b, ε_n by ε_n/v_n, and π_n by π_n/v_n, i.e., by expressing the rates in units of inverse distance traveled rather than in units of inverse time. The distribution ψ_N(Δx_b) is therefore also given by a sum of N exponentials as in Eq. 9 and has the general form

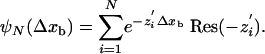[10]

The same substitution leads to an explicit expression for the average walking distance 〈Δx_b 〉 as given by

[11]

which again applies to a cargo particle pulled by N motors.

Results

Cargo Particles with Dilute Motor Coverage. Let us now consider specific examples and specify the dependence of the rates π_n and ε_n and of the velocity v_n on the number n of bound motors. First, we consider the case where the cargo particle is transported by N motor molecules, which have well separated anchor points on the particle surface and, thus, do not experience mutual interactions. In the absence of an external load force, the parameters ε_n, π_n, and v_n are then given by

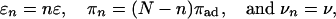[12]

where ε, π_ad, and v are the unbinding rate, the binding rate, and the velocity of a single motor, respectively.‡

In the following, we use parameter values for kinesin motors as summarized in Table 1 to determine numerical results, but the general expressions also can be applied to other types of motors. Our model with rates as specified by Eq. 12 has three parameters that can be determined from the studies of single motor molecules: the velocity v, the unbinding rate ε, and the binding rate π_ad. The first two quantities have been measured for many types of motors. For kinesin, the velocity is ≈1μm/s, and the unbinding rate is ≈1/s (14, 15). The binding rate is more difficult to measure. If π_ad is regarded as an unknown quantity, our results for the effective unbinding rate or the distribution of walking distances can be used to determine π_ad experimentally. Here, we use π_ad ≃ 5/s as measured for kinesins linking a membrane tube (which acts as the cargo particle) to a microtubule (11).

Table 1. Model parameters for single motors and values for conventional kinesin.

Parameter	Symbol	Value for kinesin	Ref(s).
Velocity	v	1 μm/s	14, 15
Unbinding rate	ε	1/s	14, 15
Binding rate	πad	5/s	11
Stall force	Fs	6 pN	22, 24
Detachment force	Fd	3 pN	24

For the parameters as specified by Eq. 12, the general expression Eq. 4 for the average number of bound motors implies the explicit relation

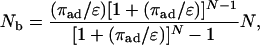[13]

which implies the simple asymptotic behavior

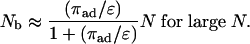Likewise, the general expression Eq. 11 for the average walking distance 〈Δx_b 〉 can be evaluated analytically, which leads to

[14]

For strongly binding motors with π_ad/ε » 1, the walking distance behaves as 〈Δx_b 〉 ≈ (v/Nε)(π_ad/ε)^N–1 and essentially increases exponentially with increasing number of motors. For weakly binding motors with π_ad/ε « 1, one has

where the leading term v/ε corresponds to the walking distance of a single motor.

Kinesin binds rather strongly with π_ad/ε ≃ 5, so that the average walking distance, which is 1 μm for a single motor, increases quickly with N and is 3.5 μm, 14 μm, 65 μm, and 311 μm for cargoes pulled by 2, 3, 4, or 5 motors, respectively. These large walking distances exceed the length of a single microtubule but can still be realized if several microtubules are aligned in a parallel and isopolar fashion so that, via unbinding and rebinding, the motors can step from one microtubule to another. Such an organization of microtubules is typical for axons (16) and has also been engineered in vitro (13).

Our results for the walking distance distributions of kinesin-pulled cargoes are shown in Fig. 2. With increasing motor number N, the slope of the distribution becomes increasingly steep for small walking distances, but the distribution becomes flatter and flatter for large walking distances. For more than three kinesins, the distribution is nearly constant for walking distances between 5 and 20 μm, see Fig. 2.

Fig. 2.

Probability distribution ψ_N of walking distance Δx_b for cargo particles pulled by N = 1, 2, 3, 4, and 5 kinesin motors with parameters as given in Table 1. The same distributions are plotted on a linear scale (a) and on a semilogarithmic scale (b).

If the motors are densely packed onto the cargo particle, exclusion effects (12, 17) modify the rates (Eq. 12) as shown in B. Mutual Exclusion of Motors in Supporting Text and Fig. 6, which is published as supporting information on the PNAS web site. For typical motor numbers N ≲ 10, the effect of exclusion on the velocity and the average walking distance is rather small. For very dense packing, however, a reduction of the velocity to ≃35% of the value without exclusion is obtained, in agreement with experimental results (18).

Movement Against External Load Force. Let us now consider cargo transport against a constant external force that could be applied, e.g., by optical tweezers or other single-molecule manipulation techniques. This force is shared equally between the n bound motors and induces an effective interaction of the motors, because, via the force-dependence, the transport parameters of the motors now depend on the presence of the other motors.

The velocity of a single motor decreases essentially linearly with the force imposed against the motor movement (19–22). We therefore use the linear force–velocity relation

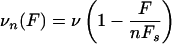[15]

for 0 ≤ F ≤ nF_s and take the velocity to be constant with v_n(F) = v for F < 0 and v_n(F) = 0 for F > F_s (compare ref. 23). The force scale F_s is given by the stall force at which a single motor stalls and stops moving. For kinesin, stall forces of F_s ≃ 5–7 pN have been reported (19–22). In the following, we use the typical value F_s ≃ 6 pN.

The force dependence of the unbinding rates ε_n is given by

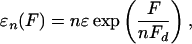[16]

as obtained from the measurements of the walking distance of a single motor as a function of load (24) in agreement with Kramers' rate theory (25). The detachment force F_d, which sets the force scale here, is, in general, not equal to the stall force, although both can be expected to have the same order of magnitude. The force scale F_d may be expressed as F_d ≡ k_BT/d, which depends on the thermal energy k_BT and on the extension d of the potential barrier between the bound and unbound state. For kinesins, the length scale d has been reported to be d ≃ 1.3 nm, so that the detachment force is F_d ≃ 3 pN (24).

It is more difficult to estimate the force dependence of the binding rates π_n because there are no experimental data about this dependence. An external load force should lead to a decrease of the binding rate π₀ from the unbound state, but this binding rate does not affect the properties of the bound motor. The binding rates π_n with n ≥ 1, on the other hand, are expected to depend only weakly on F because a pulling motor that is subject to a certain strain arising from F will relax this strain as soon as it becomes unbound and will then rebind from such a relaxed state. In other words, unbinding and rebinding occur along different reaction coordinates, i.e., along different paths in configuration space. Therefore, we take the binding rates π_n with n ≥ 1 to be force-independent, so that π_n = (N – n)π_ad for n ≥ 1 as before. In Eqs. 15 and 16, v and ε are the velocity and unbinding rate of a single motor in the absence of load, in agreement with Eq. 12. A similar type of binding/unbinding dynamics but without the active movement in the bound state arises for the forced rupture of adhesion molecule clusters (26–28).§

The force–velocity relationships for cargo particles pulled by N motors are shown in Fig. 3a. Even though the force–velocity curve is linear for a single motor, it is nonlinear for N > 1, an effect that arises from the force-dependence of the unbinding rate, which implies that the average number of bound motors decreases with increasing force, see Fig. 3b. At high forces, a cargo particle is most likely bound to the filament by a single motor, and this single motor then has a high unbinding rate, because it is pulled off from the filament by the total force.¶ For N > 2, the velocity decreases quickly for small and intermediate forces but approaches zero rather slowly for forces close to the stall force. Indeed, the actual stall force for a cargo particle pulled by N motors is equal to N times the stall force F_s of a single motor, but the cargo movement will become undetectable already at much smaller forces.

Fig. 3.

Transport properties of cargo particles pulled by up to N motors against a constant external load force F. (a) Average velocity v_eff. (b) Average number N_b of bound motors. (c) Average walking distance 〈Δx_b 〉. The chosen parameter values are for kinesin as in Table 1. The horizontal line in c indicates the step size of 8 nm. For forces for which 〈Δx_b 〉 becomes comparable to or smaller than the step size, the motors become unprocessive.

The force-dependent increase of the unbinding rate also is reflected in the corresponding decrease of the average walking distance, which is approximately exponential with increasing force F for N ≥ 2 as shown in Fig. 3c.∥ For very strong forces that exceed a critical force F_c, the average walking distance becomes comparable to the motor step size 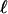, and the motors become unprocessive. This critical force can be estimated from the implicit equation 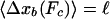. For kinesin, which has a step size 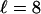nm, we obtain F_c = 5.7, 8.8, 10.6, and 13.8 pN for particles pulled by n = 1, 2, 3, and 5 motors, respectively. For N ≥ 2, these values are considerably smaller than the corresponding stall forces. Force-dependent distributions of the walking distances are shown in Fig. 4.

Fig. 4.

Probability distribution ψ_N of walking distance Δx_b for cargo particles pulled by up to N = 1 (solid lines), 2 (dashed lines), 3 (dotted lines), and 5 (dashed-dotted lines) motors against an external load force F. For F = 10 pN, cargoes pulled by a single motor do not move, and the distribution ψ_N contains a delta function at Δx_b = 0. The distributions are plotted on a semilogarithmic scale as in Fig. 2b.

In the presence of an external load force, the velocity depends on the number of motors that pull the cargo, which implies that the velocity of such a cargo particle is switched stochastically when a motor binds to or unbinds from the filament. The trajectory of such a cargo therefore consists of segments with constant velocity as has been observed recently for vesicles dragged through the cytoplasm (6, 7). The distribution of these velocities is shown in Fig. 5. With increasing load force, the observed velocities decrease, but in addition, the velocity distribution P(v) becomes broader and develops several peaks. The latter feature is again consistent with the in vivo experiments in refs. 6 and 7.

Fig. 5.

Probability distribution P of the instantaneous velocity v for cargo particles that are pulled by N = 5 motors in the presence of an external load force F. The chosen parameter values are given in Table 1 and apply to kinesin. The white bar in the graph for F = 1 pN indicates the distribution for vanishing external force. For F = 10 pN and F = 12 pN, the particles are stalled with a nonzero probability P(v = 0), because no movement occurs if the cargo particle is pulled by a single motor for F = 10 pN or by one or two motors for F = 12 pN.

Discussion and Applications

We have presented a theoretical study of the transport properties of cargo particles that are pulled by several molecular motors in a cooperative fashion. Let us now discuss some applications of our results to cellular systems.

The most prominent example for long-range transport over distances that by far exceed the walking distances of single motors is the transport in axons (16). The cargo particles that belong to the slow transport component, such as neurofilaments, exhibit alternating periods of directed movement with velocities of the order of 1 μm/s and pausing periods where essentially no movement can be detected, so that their effective velocity is of the order of 10^–3–10^–2 μm/s or 0.1–1 mm per day. The walking distances of the active movements are typically a few microns (see refs. 29 and 30). These observations are consistent with the assumption that these slow cargoes are transported by one or two motors. On the other hand, cargo particles of fast axonal transport, such as vesicles, move with velocities of ≈1 μm/s over distances of at least centimeters. Using Eq. 14, we can estimate that the cooperation of seven to eight kinesin motors is sufficient for a walking distance in the centimeter range. A walking distance of approximately 1 m, as necessary in the longest axons, is obtained if 10 motors drive the movement.

Our theory also gives a quantitative explanation for the effect of microtubule-associated proteins (MAPs) such as the tau protein on the processivity of cargo particles. On the one hand, the presence of tau reduces the binding rate of kinesin to microtubules in single-molecule experiments but has no effect on the velocity and walking distance of the bound kinesins (31). On the other hand, the movements of vesicles in cells transfected with tau exhibit reduced walking distances (32). It has been proposed (31) that these apparently contradictory experimental findings can be reconciled if the vesicles with reduced walking distance were transported by several motors. Our theory supports this idea, because Eq. 11 implies that the walking distance of a cargo particle pulled by more than one motor is affected by changes in the binding rate. At a ratio of two tau molecules per tubulin dimer, the binding rate of a single kinesin molecule is reduced to approximately 50% of its value in the absence of tau (31). For cargoes pulled by two, three, and four kinesin motors, this reduction of the binding rate implies a reduction of the walking distance to 64%, 40%, and 16% of the corresponding value in the absence of tau, respectively.

Finally, we have calculated the transport properties of cargo particles pulled by several motors against an external load force. This situation is accessible to in vitro experiments, using, for example, bead assays and optical traps that exert constant forces. For such experiments, our theory makes quantitative predictions about the force–velocity relationships, the walking distances, and the distribution of the instantaneous cargo velocities.

In addition, our theory can be applied to the movement of large organelles in cells that experience viscous forces of a few piconewtons comparable to the stall force of a single motor (9). If the cargo particle moves with velocity v_n, it experiences the Stokes force F_n = γv_n, where γ is the corresponding friction coefficient. In the presence of such a force, our relation (Eq. 15) leads to

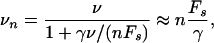[17]

where the asymptotic equality applies to large friction coefficients γ. For such a situation, two groups (6, 7) recently have measured the distribution of the instantaneous velocities as given by Eq. 5. They found that the vesicles switch between different values of the velocity that are peaked at integer multiples of the smallest observed velocity. If the friction coefficient is large compared to nF_s/v, such a linear behavior is indeed predicted by Eq. 17.

In summary, we have presented a theoretical study of the cooperative transport of cargo particles that are pulled by up to N molecular motors. We have determined the transport properties of these cargo particles such as their effective velocity and average walking distance (or run length). The latter quantity is strongly affected by the maximal number N of pulling motors, and the cooperation of several motors enables efficient transport over large distances. Our approach provides a quantitative theoretical basis for the interpretation of a number of recent experiments and makes quantitative predictions that can be tested experimentally. The theoretical framework introduced here can be extended to more complex situations such as the transport of cargo particles that are attached to several species of motors. These different species may have different velocities or may even move in opposite directions. Likewise, our theory can be extended to load forces that depend on the displacement of the cargo particle or change with time. A relatively simple example for such a variable load force is provided by laser traps, which are used in motility assays to exert harmonic force potentials for small particle displacements. More complex examples are found for the cytoskeletal transport in biological cells, where the cargo particle is pulled through a meshwork of membranes and filaments that can act as steric barriers or adhesive surfaces and, thus, can exert various types of position-dependent forces on this particle.