Abstract
One of the longest running debates in ecology is whether chance or determinism structures biotic communities, and this question is often studied by looking for the presence or absence of community inertia (lack of change) over time or space. Results have been equivocal. We adopted three tactics for a fresh approach: (i) allowing the answer to vary with the geographic, temporal, and taxonomic scale of study, (ii) using appropriate reference points for the amount of inertia in random biological systems, and (iii) using a robust approach for measurement of inertia. We examined fossil assemblages of mammalian communities across almost 1,000,000 years and at sites spanning ≈3,500 km. We showed that in general there is good evidence for inertia but that the results change in a quantifiable fashion with taxonomic, spatial, and temporal scales. By using neutral theory we place a reference point on the degree of inertia and demonstrate that empirical mammalian communities show greater inertia than neutral communities over time scales >3,000 year. Although our results do not specifically reveal mechanism, they emphasize that deterministic forces are at work in structuring communities over millennia.
Keywords: neutral theory, paleoecology
One of the oldest debates in ecology (1) is between the view that there are deterministic processes that lead to predictable patterns in the structure of communities and the idea that random or at least unpredictable factors dominate that structure. A specific debate within this broad question is whether or not communities retain a coherent structure as abiotic forcing conditions change across space and time. We will call this putative coherency “community inertia.” Although this is an important and old question (2, 3), it is still largely unresolved and hotly debated today. Traditionally, community inertia has been quantified by studying whether relative abundances of taxa change across time or space. Neoecologists have made claims of inertia (4–6) and lack of inertia (7) in space as well as inertia (4) and lack thereof (8) in time. Paleoecologists have primarily focused on time and have also produced claims of inertia (9–16) and lack of inertia (17–21). Much of the debate has been of the unproductive form of “there's inertia in my system” vs. “there's not inertia in my system” (but see refs. 11, 14, and 15). Perhaps Simberloff (22) is correct in suggesting that communities are too contingent and context-dependent for general rules to be found. However, we suggest that improved methods for analyzing community dynamics may yet yield general rules. Full and careful consideration of three challenges can begin to provide a resolution to this debate. We elaborate these three factors in the next three paragraphs.
One obvious challenge is that the patterns obtained depend on (and may well change with) temporal, spatial, and taxonomic scale (23, 24). Yet rarely have there been attempts to make statements specific to scale (but see ref. 14). To fully address the question in the context of scale is a four-dimensional problem (inertia is a function of spatial, temporal, and taxonomic scale), which may further change for different groups of organisms. Such concerns are not realistically addressable by one data set, researcher, or manuscript. But it is crucial to begin to include these dimensions in studies of community inertia. In this article, we choose to explore the effects of scale along the time dimension with a strong secondary emphasis on taxonomic scale and a minor emphasis on space. We also focus on a single taxonomic group (small mammals), but our approach can be adopted for other taxonomic groups.
The second challenge is that it is impossible to give a simple yes/no answer to the question of whether there is community inertia or not. The correct answer is “both;” there is always some inertia and some change. There are no purely deterministic, noise-free systems and no truly random (white noise) systems. Suppose we measure community inertia on a scale of 0 (complete randomness) to 1 (full inertia). We call this a community inertia index (CII). Measurements of CII are invariably intermediate (between 0 and 1). Whether to call this result a sign of inertia has been largely determined by subjective assessments of what qualifies as a little or a lot of inertia (but see ref. 19). In practice, it would be useful if we could place reference points on this scale of 0–1 that would allow us to say that a system has more or less inertia than a meaningful reference point. But it has been very difficult to select an appropriate model of stochasticity in community ecology (25). There is now an obvious reference point to help calibrate the scale (15), the neutral theory of biogeography (26, 27), which explicitly incorporates a random dynamic process based on ecologically identical species. This stochastic process results in a drift of abundance within communities that can act as a reference point for the measurement of community inertia. The neutral model also includes the idea of ongoing immigration and reassembly from a regional pool (metacommunity), which has been considered an appropriate null model by paleontologists for analyzing community inertia (19).
The third challenge is the method of quantification of similarity of communities (i.e., the CII). Dozens of measures have been proposed (28). At one extreme are measures that ignore abundance and only use presence/absence, such as the Jaccard index. At the other extreme are measures that place heavy emphasis on small differences in rare species, such as the squared chord distance (SCD), because a change in abundance from one individual to two represents a 100% increase (29). It has been argued, for example, that the identification of nonanalog (noninertial) communities relies on these properties of the SCD (29). Our approach to this problem is based on the idea of robustness. We focus on results that hold true across a variety of CIIs.
Methods
Because we want to emphasize the time dimension, we necessarily chose a paleontological system. Neoecological time series rarely span >30 years and almost never go beyond ≈200 years. The choice of a paleontological system affects our ability to examine the taxonomic and spatial dimensions. The effect on the taxonomic dimension is small; there is a diminished ability to resolve at the species level but higher taxonomic levels are largely maintained. However, for our system the resolution of the spatial dimension is diminished because there are only a few sites that provide data that span the time frames needed and meet our requirements (come from a single biome type, identify to species where possible, measure abundances rather than just presence/absence, and contain large faunal lists indicating good sampling of the communities).
We examined fossil assemblages of communities of small mammals, taking published data from four sites across North America: Kennewick Roadcut, WA (30); Baker's Bluff, TN (31); Porcupine Cave, CO (32); and Lamar Cave, WY (33, 34). All of these sites were in mixed grassland–coniferous forests at the time of deposition. A complete description of the sites and the taxa are in Supporting Text, which is published as supporting information on the PNAS web site. The last three sites are all woodrat (Neotoma spp.) middens. Kennewick has a different and somewhat unclear taphonomy. There is good evidence that woodrat middens provide an excellent sample of the local community at the time of deposition (34, 35), and any inertia we find between sites with different taphonomic origins further confirms that the inertia found is not a taphonomic artifact. Each site had multiple stratigraphic layers, with successively lower layers being older in deposition time. All sites with appropriately aged strata were dated by 14C methods (Lamar Cave and Baker's Bluff); other strata were dated by paleomagnetics, ash chronology, and biostratigraphy. Lamar Cave spans 0–3000 years before present (ybp), Baker's Bluff spans 270–19,100 ybp, Kennewick spans ≈7,000–200,000 ybp, and Porcupine Cave spans 840,000-950,000 ybp. Thus we achieved a time span of 0 ybp to almost 1 million ybp. Clearly this time span includes a great deal of climatic change with as many as 10 glacial/interglacial cycles.
We limited the fossils to small mammals (Rodentia, Lagomorpha, Insectivora, and small Carnivora), because this group was most heavily sampled (because of smaller bones and greater abundance in the original communities) and members were similar enough in habitat use to constitute an interacting community. We used the number of bones identified to species or genus as a proxy for individual abundance.
Bones were identified to the lowest taxonomic level possible, producing 72 taxa. Many of these taxa were at the species level, some at the genus, and for one the lowest taxon was at the family level (Leporidae). Full details are in Table 2, which is published as supporting information on the PNAS web site. Thus analysis at the family and order level are 100% accurate, and analysis at the genus level is highly accurate (the one group Leporidae actually contains several genera). Analysis at the species level is more problematic because in the older caves (Kennewick and Porcupine) some bones were identified only to the genus level. We report species-level analyses, eliminating bones identified only to genus.
To derive our CII, we transformed abundances at a given site and/or level by adding one and taking the log, thereby roughly normalizing the data and avoiding the log of 0. If a taxon was absent from two sites, we eliminated its comparison (no 0 vs. 0 comparisons) because the taxon might be absent from the two sites for very different reasons (e.g., outside of species range at one site and competitively excluded at the other) (28). We then calculated the CII on a scale of –1 through 0 (total randomness) to +1 by taking the Pearson correlation coefficient, r, of the transformed data. Engen et al. (36) show that Pearson's r on log-transformed data is a natural measure of community similarity under a bivariate lognormal distribution that can be derived from stochastic models. A variety of other options exist, but we focus on this simple Pearson r on log-transformed data because it is well known and easily supports tests of significance. The point 0 represents complete randomness and is the null hypothesis for significance tests. We demonstrate robustness of our results in Supporting Text by presenting parallel results with a variety of markedly different indices of CII, showing qualitatively similar results.
We calculated the CII for all possible pairs of communities under three sets of conditions. First, we chose only layers that met three a priori criteria: (i) the layer was assigned an age (ybp); (ii) the layer had a number of identified specimens >50; and (iii) the layer was in the top 60% of abundance for layers at that site, which gave a total of 15 “good” layers (six, four, two, and three layers, respectively for the Lamar, Baker, Kennewick, and Porcupine sites). We then performed three types of comparisons. The first type (“between site”) was between any one of the 15 layers with any other of the 15 layers (excluding same-layer comparisons but including within-site comparisons), giving 105 total comparisons. These comparisons use time and space simultaneously. Thus, there is confoundment between time and space in these data to the degree that time and space are correlated in our sample sites. The second type (“within site, between time”) compared layers only with other layers found in the same site, giving 25 comparisons. This process gave the highest-quality measure of the effect of time alone. The third type (“whole-site”) compared one site with another site by pooling all layers of a site, producing a time-averaged sample. This process gave six comparisons.
We used standard linear model statistical techniques to analyze the data from these comparisons, including regression and analysis of covariance. To look at the confoundment between space and time in the between-site comparisons, we used a Mantel test to examine the correlation of the 4 × 4 matrix of distance between sites with the 4 × 4 matrix of times between the midpoints of the span of the fossil records at each site.
To calibrate our CII we calculated neutral model predictions of CII as follows. We implemented a spatially explicit version of the neutral model (i.e., the metacommunity consists of many local communities added together) (26, 27) derived from previously published computer code (37). The model was parameterized and sensitivity analyses were performed (Supporting Text). We chose a local community size, J, of 10,000, a conservatively large estimate of the effective population size of small rodent communities (although not reported, runs for J = 100,000 showed similar results for our analysis with only a longer transient time). Because good empirical estimates of migration rate, m, are rare, we report sensitivity analysis with m ranging from 0 (no migration) to 1 (total migration). Most results in this article are presented for M = m × J (the number of individuals migrating rather than the percentage), because the role of migration in a stochastic drift process depends only on M = m × J (38). According to this body of theory (38), significant between-site drift occurs only if M « 4 (or «2 in some spatial models). Most simulations were run with C = 20 local communities. In the case of full migration (m = 1), the effective population size for the rate of drift would be J × C. We converted model time steps to years to allow comparison with paleontological data (see Supporting Text for details). Neutral CIIs were calculated as the average across 20 simulations.
Analyzing data at higher taxonomic levels required careful treatment. In particular, any time a set of data are lumped into groups of any sort and then summed or averaged by group and then used in correlations, the strength of correlation increases. To control for this effect we performed “empirical aggregations” from the lowest taxonomic level to higher levels such as genus, family, or order based on actual taxonomic affiliations. We contrasted this with “random aggregations” where the same number of lower-level and higher-level taxa were used but the lower taxa were randomly reassigned to the higher taxa (reshuffled) while keeping the distributions of counts of species among genera, etc. For example, there is one genus, Sorex, containing eight species and an “unidentified Sorex” category, so in the reshuffling one genus received nine random species. This reshuffling destroyed any taxonomic associations and provides a null for the effect of aggregation when analyzing higher taxonomic levels.
One issue that must be addressed is the question of time averaging. Paleontological data are assigned to a layer or stratigraphic unit, which represents a span of time (typically tens to thousands of years for our data), and it is known that averaging abundances over time can change the apparent structure of a community (39). This averaging could potentially be a problem in comparing empirical data with different degrees of time averaging or comparing empirical data with data from neutral model simulations that have no time averaging. In particular, our third type of comparison (whole-site) does have an unusually high degree of time averaging relative to the first two types of comparisons and might suffer from these problems to a greater degree, but we include this analysis because of its conceptual simplicity and confirm any results obtained in this analysis with the other types of comparisons. For the first two types of analyses, we believe that time averaging did not affect our results because (i) time-averaged woodrat data such as we mostly used have been shown to be a good predictor of modern day (i.e., not time-averaged) communities (34, 40); (ii) time averaging introduces distortions to the abundances of rare species that varies significantly with the amount of time averaging (such as between our layers of greatly different duration) (39) and is therefore primarily a source of increased noise in the empirical data and thereby conservatively should create lower CII and favor neutral (unaveraged) data; and (iii) the degree of difference found between neutral and empirical data was large enough so it seems unlikely that a factor such as time averaging could affect this result, especially over just a few hundreds or thousands of years.
Results
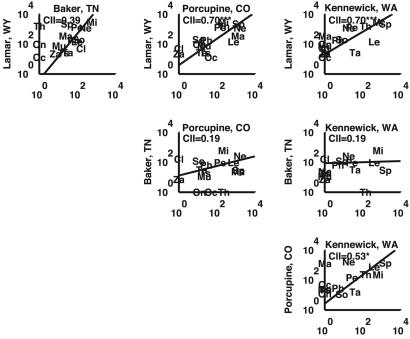
Whole-site comparisons indicated that abundances of taxa among sites were positively correlated among all pairs of sites (Fig. 1 and Table 3, which is published as supporting information on the PNAS web site). Three of the comparisons were statistically significant. The odds of achieving three significant tests of six by chance (for α = 0.05) are minimal (P < 0.0001 binomial test). This finding provides evidence for community inertia, but the role of historical contingency (41) was also clear in the empirical data. The three least similar comparisons all involve Baker's Bluff. On these comparisons, Ochotona (pikas), Thomomys (pocket gophers), and Clethrionomys (red-backed voles) were outliers, being reasonably common at one site and not present at the other. Ochotona and Thomomys are taxa only found in the western United States and thus have no possibility of being present in Baker's Bluff. A post hoc removal of these two species causes the Lamar/Baker's Bluff correlation to rise to r = 0.52 with P < 0.05. Likewise, Clethrionomys arrived from Eurasia after the deposition in Porcupine Cave so additionally removing this genus from the analysis causes the Porcupine/Baker's Bluff comparison to become significant (r = 0.51, P < 0.05). Hence, the cause of the three nonsignificant but positive correlations between communities involved historical/biogeographic contingency involving these three species.
Fig. 1.
Inertia in community structure. The similarity of community structure is plotted for all six pairwise combinations of the four sites. The axes are log10-scale in units of number of identified bones. Each taxon is represented by its first two letters, except Tamiascurius, represented by Ts. The Pearson r is reported in the upper left corner, with * denoting P < 0.05 and *** denoting P < 0.001. The line is a ranged major axis regression (28). The abundance for a given site was summed across all levels. The distance in km and average separation in years between sites are summarized in Table 3.
A more sophisticated comparison takes into account the fact that community inertia may behave differently at different spatial, temporal, and taxonomic scales and avoids the large degree of time averaging in the previous analysis. We repeated this analysis by using the between-sites and within-sites and between-time comparisons, and the results are summarized in Fig. 2 and in Table 4, which is published as supporting information on the PNAS web site. Again, some comparisons (Table 4) showed significant (α = 0.05) differences from a null model of CII = 0 and some did not, but a binomial test suggested that the probability of the observed number of significant results by chance is vanishingly small (P « 0.001) for both types of comparison.
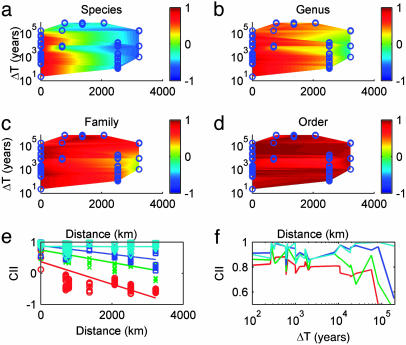
Fig. 2.
How temporal and spatial scales affect community inertia. (a–d) Plots of the CII as a function of the time between communities (log scale) and the spatial distance between communities for four taxonomic scales. The CII ranges from –1 (complete reversal) through 0 (random reshuffling) to +1 (identical abundance proportions). The CII at any point is indicated by the color of the surface at that point as indicated by the color bars to the right; cool colors correspond to negative CII (blue = –1) to green = 0 to warm color indicating positive CII or inertia (dark red =+1). The blue circles represent the comparisons actually performed. The surface is a simple linear extrapolation between these points. (e) The between-sites comparison is used to look at how CII varies with distance. The four lines show different taxonomic levels (red = species, green = genus, blue = family, and cyan = order). (f) The within-sites, between-times comparison is used to look at how CII varies with time (lines represent different taxonomic levels as in e).
CII decreased with both temporal and spatial distance between communities. A Mantel test on matrices of distance and time between sites suggests that time and space are independent in the between-site comparisons (r = –0.44, P = 0.79, but the power is low). A visual examination of the locations of points in Fig. 2 a–d suggests that time and space are not strongly correlated with each other, but nor are they fully independent. An inspection of Fig. 2 shows that distance effects strongly dominated time effects. Therefore, to analyze the effect of time, within-site comparisons are much more accurate. Thus time and space both had statistically significant effects for species, genus, and family and are nonsignifcant for order (although clearly trending significant for time) (Table 4).
An examination of Fig. 2 e and f suggests the possibility of some intriguing nonlinearities as well. For example, it appears (especially for species) that most of the decrease in CII happens exponentially in the first 700 km and slows to almost no decrease over the next 2,500+ km, but we did not have data points between 0 and 700 km to quantify this idea further. Similarly, the decrease with time appears largely linear, except that there is a rapid, steep drop-off in CII after 200,000 years. But this difference is caused by one data point, comparing the top and bottom layers at Kennewick, and may be an artifact; more data are needed in these time ranges.
CII also decays more slowly with increasing taxonomic level. An analysis of covariance showed that the slopes vary significantly by taxon (i.e., the interaction term for taxon level vs. the slope for CII over distance or time is significant, P < 0.001 for both comparison types). The graphs in Fig. 2 suggest that community similarity increases with taxonomic level, although using analysis of covariance with its assumption of independence to calculate the magnitude and significance of the effects is inappropriate because of the issues related to aggregation of data mentioned in Methods.
We used random reshuffles of taxonomic associations as a null model to evaluate the effects of analysis at different taxonomic levels vs. a null model of aggregation in a randomized fashion (Table 1). These results suggest that at least for small mammals of the Quaternary the taxonomic level of analysis has no effect on analysis of community inertia within sites (time dimension only), but has a significant effect on analysis of community inertia between sites. Between sites, analyzing at higher levels (genus-order) increases estimates of community inertia by ≈0.25–0.30, which is highly significant statistically. Some caution is needed in the analysis of species-level data because the older sites contain fewer bones identified to the species level. Thus the significant effect of taxonomic level on rate of decrease of inertia with space and time (Fig. 2 and analysis of covariance presented earlier) is entirely caused by the nonbiological effect of aggregating data for comparisons across time within a site, but between sites it appears to be largely caused by some biological effect of taxonomic aggregation.
Table 1. Effect of empirical aggregation vs. randomized aggregation.
| Between sites/times (n = 105)
|
Within sites (n = 25)
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Data set | Species | Genus | Family | Order | Species | Genus | Family | Order |
| MeanAct | -0.120 | 0.474 | 0.697 | 0.856 | 0.766 | 0.836 | 0.918 | 0.936 |
| MeanRnd | -0.114 | 0.231 | 0.444 | 0.549 | 0.722 | 0.828 | 0.878 | 0.930 |
| MeanDelt | -0.006 | 0.243 | 0.254 | 0.308 | 0.044 | 0.008 | 0.040 | 0.007 |
| SD | 0.103 | 0.301 | 0.385 | 0.484 | 0.112 | 0.097 | 0.110 | 0.115 |
| SE | 0.020 | 0.058 | 0.074 | 0.093 | 0.044 | 0.038 | 0.043 | 0.045 |
| P | 0.5838 | <0.0001 | <0.0001 | <0.0001 | 0.0619 | 0.6855 | 0.0855 | 0.7737 |
The effects of taxonomic aggregation are summarized. The data are for the between-sites comparison and the within-sites comparison. MeanAct gives the average CII for the comparison at the taxonomic level indicated. MeanRnd gives the average CII if the same taxonomic level is used but the 72 detailed taxa are randomly reshuffled with respect to which higher taxa they are part of. MeanDelt gives the “effect size” or true increase in CCI caused by studying at a higher level after removing the increase caused purely by using aggregated data (i.e. MeanDelt = MeanAct - MeanRnd). SD and SE give the standard deviation and standard error at each level, respectively and P gives the P value for MeanDelt being significantly different from zero (paired t test). Repeated randomizations with different starting values for the random seed suggest that these results are robust, and in particular show that the three levels for the between-site values are highly significant (and with approximately similar effect sizes), but the species and family within-site values do not trend near significance (usually have much higher P values than in the run reported).
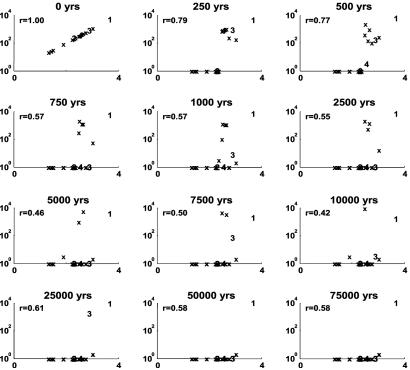
Having addressed the effects of temporal, spatial, and taxonomic scale on the question of inertia, we now turn to the use of neutral theory as a context for making comparative statements (there is/is not a lot of inertia relative to a drift model). A typical example of the simulated neutral community is shown in Fig. 3. Two facts about the drift of community structure in the neutral model are obvious. First, the neutral model loses rare species at a very high rate (see also Fig. 5, which is published as supporting information on the PNAS web site). Second, the relative abundances of species in a neutral community drift significantly, with moderately rare species becoming common and vice versa. For example after t = 7,500 years, the second and fourth most common species have gone extinct, whereas two moderately rare species are common (contrast Fig. 5 with Fig. 1).
Fig. 3.
Drift in community structure between a neutral community and itself over time. Shown is one Monte Carlo simulation comparing a community with itself for inertia or drift as the time between the points of comparison increases. Thus a single local community was selected at random and the community structure at various points in the future is compared with the initial community structure. Abundances in the initial community are plotted on the horizontal axis, and abundances at the specified amount of time later in the same community are plotted on the vertical axis. As a result, initially rare species appear on the left, and initially common species appear on the right. The four most common species in the metacommunity are numbered 1–4, and the rest are denoted by x. As a species becomes more common within the local community it moves up, and if it crosses the y = x line it is more common than it was initially in the community. Similarly, a species moves down as it becomes rarer, hitting the x axis when it becomes locally extinct. CII (Pearson r) values are reported as in Fig. 1. Species are randomly assigned to a genus and analyzed at the genus level to compare with Fig. 1. Notice how most taxa, including all but the most common, go extinct. Model values are: θ = 6, M = 1(m = 1/J), J = 1e4. See note in Supporting Text on artificially high r values for later years.
Results averaged across 20 local communities and also across 20 Monte Carlo replicates are summarized in Fig. 4 and confirm that the rapid loss of species and high degree of drift in community structure is a general result of the neutral model. Thus, even for the highest migration rates (m = 1.0), half the species are lost from the average local community in ≈300 years and two-thirds of all species are lost in 1,000 years (Fig. 5), leaving only three to five of the more common species in the community. Thus a major finding is that whereas extinctions can occur over the time scales explored, the neutral model causes both rare and moderately abundant species to go extinct at extremely high rates relative to the empirical data (42) (in our empirical data, none of the small mammal species experience extinction). This result is related to the unusually high rate of speciation necessary to make the neutral theory fit empirical data (42). Real communities apparently possess an additional mechanism not found in neutral communities that allows rare species to persist over time and space.
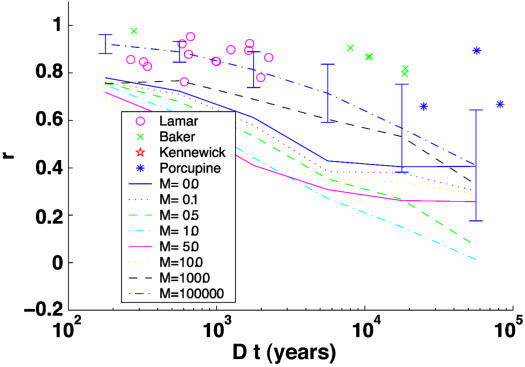
Fig. 4.
Comparison of empirical data with the neutral model. CII is plotted vs. time. For empirical and neutral data the CII for all possible comparisons was calculated and plotted along the ordinate as the difference in time between the pair of communities. Symbols represent the within-site, between-time empirical comparisons. For neutral data only the line through the means is plotted with a 95% confidence interval based on ±2 SE added to the m = 1.0 line (95% range of observed points gave very similar intervals). After ≈2,500 years, the empirical data are always above the neutral model even for the case of M = J or total panmixia. The Kennewick case for difference in time = 190,000 years, r = 0.46, is left off the plot although it is above the M = 1 line for five Monte Carlo replicates extended out to 200,000 years. Model parameters are θ = 6, M = various, J = 1e4, C = 20.
We were unable to calibrate migration rate with distance for the neutral model. To do this calibration would require a precise estimate of how M varies with distance in small mammal communities, which is difficult to obtain. Thus we can only compare our within-site, between-time analysis with the neutral model. In the neutral model, the local community structure is compared against the same local community at a different point in time. The results are shown in Fig. 4, where CII (Pearson's r) is plotted vs. time. The empirical data show a much greater degree of community inertia than does the neutral drift model over extended periods of time (with r ≈ 0.9 for time periods <10,000 years and r ≈ 0.7–0.9 out to 100,000 years). For time periods of <1,000 ybp (Lamar Cave only), there is considerable noise and the empirical data and neutral model overlap each other as the drift begins. For the time scale between 1,000 and 3,000 ybp, the empirical data fall in the same range as the neutral model for M » 4, but well above the range for M ≤ 4. M » 4 would have to be considered to be a much higher migration rate than the rate of M < 1 most small mammals experience (43, 44), especially when the biases of the FST estimation method (45) are taken into account. For time periods >3,000 years, the empirical data are all well above the neutral simulations, even for the highly unrealistic scenario of M = J (m = 1.0, complete replacement of the community by migrants each year or total panmixia). When the time span exceeds 3,000 years (allowing for initial transients in the neutral model), the empirical data always show more inertia than the neutral model (a binomial test gives P « 0.001; seven of eight empirical points are above the 95% confidence interval for the neutral M = J or m = 1.0 line). These results are conservative because the empirical data also contains measurement error, decreasing the CII (Pearson r), whereas the neutral does not. The neutral model further shows (Fig. 4 vs. Fig. 6, which is published as supporting information on the PNAS web site) that decay occurs faster across space than time (at least for the scales studied here), just as was found in the empirical data.
A good confirmation of the accuracy of our neutral-model simulations was given by the fact that, as expected from analytical results (38), the neutral model displays three distinct groups depending on M » 4, M ≈ 4, or M « 4 (data not shown but the three groups decay to CIIs of about r = 0.8, 0.6, and 0.4, respectively over the first 10,000 years, see also comparison between sites in Fig. 6).
Finally, we address our third challenge: that of choice of CII. We reanalyzed the within-site, between-time comparisons for both empirical and neutral data and the between sites for empirical data (Figs. 2 and 4 and Table 4 compared with Tables 5 and 6 and Fig. 7, which are published as supporting information on the PNAS web site) by using the Jaccard, Whittaker, squared chord distance, and our own percentage swap measures of similarity or distance as CII. Only minor changes were found (see details in Supporting Text). This finding demonstrates that our results are independent of the choice of CII. We suggest that this robustness to the exact measure of CII should be demonstrated before making claims for or against community inertia.
Discussion
All our results are concordant and support a nonrandom view of communities through space and time. It appears that between sites at the level of species change occurs that is so extensive that it is nonrandom (CII < 0), although some caution is needed for interpretation of our results at the species level. This one exception is probably caused by (i) the historical contingencies discussed earlier and (ii) the nonrandom, systematic replacement of species by congenerics between sites (and to a much lesser degree replacements of genera by confamilial genera). In all other instances (higher taxonomic levels between sites, all taxonomic levels within sites), there is strong evidence of community inertia (CII = 0.9 for time <10,000 years and CII = 0.7–0.9 for time <100,000 years). It is usually statistically significant against the null hypothesis of total randomness (CII = 0). Moreover, in the case where we were able to develop a calibrated comparison (within sites over time), the inertia is also greater than a neutral drift model for time spans larger than ≈3,000 years. Community inertia remains positive but decreases with increasing spatial and temporal scales in a quantifiable fashion (Table 4), e.g., CII decreases by 0.20/1,000 km and 0.21/100,000 years at the genus level). Despite calls for the inclusion of scale in ecological studies, this inclusion is still rarely done. The results herein suggest that not only is this possible, but it is interesting and important. All of these strong, precise statements are possible because of addressing the three methodological challenges that we outlined (scale, reference points, and robustness to CII definition). Obviously, the results are currently limited to small mammal communities in grassland/conifer zones, but we hope this methodology will prove useful in analyzing other locations and groups.
The use of two reference points lends credence that deterministic forces of some sort must be at work. In particular, the CII = 0 point corresponds to the common stochastic model of independent identically distributed or white noise with no autocorrelation, whereas the neutral model is a form of a random walk or brown noise with very high autocorrelation. In a formal sense, these two models represent the two endpoints of a continuum of stochastic models (fractal Brownian motion) and most empirical time series fall between these two extremes (including 1/frequency noise) (46, 47). The fact that observed community inertia falls outside the range of inertia produced by this continuum of models suggests that most stochastic models are unable to generate observed CII, and thus it is likely that deterministic forces are involved. Using fossil pollen data, Clark and McLachlan (48) made a similar point for variation in abundance of individual species rather than the community-level measure (CII) used herein.
The observed inertia is remarkable in the context of the amount of major environmental change against which it occurred (up to seven glacial/interglacial cycles). Such constancy in the face of massive external forcing begs the question of why? This study has been primarily observational (with appropriate null hypotheses). We have not suggested mechanisms. But given the high levels of inertia, some deterministic forces must be involved at these scales. The fact that a mammal species typically survives for ≈1,000,000 years and is thus adapted to change is clearly one factor. Another clear candidate mechanism would be classical niche-based ecology (7, 49, 50). Ecologists need to begin developing a more synthetic approach to community ecology that gives the deterministic forces their due importance while also including the stochastic forces that have been emphasized in recent decades. This approach is needed urgently as scientists attempt to understand the effects of global change and habitat destruction on biotic communities, some of which may be at least 1,000,000 years old.
Supplementary Material
Acknowledgments
We thank all of the workers who labored to collect the paleontological data, without which this study would not be possible; J. Roughgarden, A. Axel, J. Bruzgul, Y. Chan, G. Nesslage, K. O'Keefe, H. Peters, U. Ramakrishnan, J. Skillen, P. Spaeth, and M. van Tuinen for providing feedback on this work; and A. Barnosky for the Porcupine Cave data. This work was supported by a National Science Foundation Bioinformatics postdoctoral fellowship (to B.J.M.) and a Terman fellowship (to E.A.H.).
Author contributions: B.J.M., E.A.H., and B.A.M. designed research; B.J.M., E.A.H., and B.A.M. performed research; B.J.M., E.A.H., and B.A.M. analyzed data; and B.J.M. wrote the paper.
Conflict of interest statement: No conflicts declared.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: CII, community inertia index; ybp, years before present.
References
- 1.Maurer, B. A. (1999) Untangling Ecological Complexity (Univ. Chicago Press, Chicago).
- 2.Clements, F. E. (1936) J. Ecol. 24, 252–284. [Google Scholar]
- 3.Gleason, H. A. (1926) Torrey Botan. Club 53, 7–26. [Google Scholar]
- 4.McGowan, J. A. & Walker, P. W. (1985) Ecol. Monogr. 55, 103–118. [Google Scholar]
- 5.Terborgh, J., Foster, R. B. & Nunez, P. V. (1996) Ecology 77, 561–567. [Google Scholar]
- 6.Pitman, N. C. A., Terborgh, J. W., Silman, M. R., Nunez, P., Neill, D. A., Ceron, C. E., Palacios, W. A. & Aulestia, M. (2001) Ecology 82, 2101–2117. [Google Scholar]
- 7.Whittaker, R. H. (1975) Communities and Ecosystems (MacMillan, New York).
- 8.Brown, J. H., Whitam, T. G., Ernest, S. K. M. & Gehring, C. A. (2001) Science 293, 643–650. [DOI] [PubMed] [Google Scholar]
- 9.Boucot, A. J. (1996) Palaeogeogr. Palaeoclimatol. Palaeoecol. 127, 339–359. [Google Scholar]
- 10.Brett, C. E., Ivany, L. C. & Schopf, K. M. (1996) Palaeogeogr. Palaeoclimatol. Palaeoecol. 127, 1–20. [Google Scholar]
- 11.DiMichele, W. A. (1994) Paleobiology 20, 89–92. [Google Scholar]
- 12.DiMichele, W. A. & Philips, T. L. (1996) Paleogeogr. Palaeoclimatol. Palaeoecol. 127, 83–105. [Google Scholar]
- 13.Pandolfi, J. (1996) Paleobiology 22, 152–176. [Google Scholar]
- 14.Pandolfi, J. (2002) Coral Reefs 21, 13–23. [Google Scholar]
- 15.DiMichele, W. A., Behrensmeyer, A. K., Olszewski, T. D., Labandeira, C. C., Pandolfi, J. M., Wing, S. L. & Bobe, R. (2004) Annu. Rev. Ecol. Evol. System. 35, 285–322. [Google Scholar]
- 16.Prothero, D. R. & Heaton, T. H. (1996) Palaeogeogr. Palaeoclimatol. Palaeoecol. 127, 257–283. [Google Scholar]
- 17.Westrop, S. R. (1996) Palaeogeogr. Palaeoclimatol. Palaeoecol. 127, 33–46. [Google Scholar]
- 18.Alroy, J. (1996) Palaeogeogr. Palaeoclimatol. Palaeoecol. 127, 285–311. [Google Scholar]
- 19.Holterhoff, P. F. (1996) Palaeogeogr. Palaeoclimatol. Palaeoecol. 127, 47–81. [Google Scholar]
- 20.FAUNMAP Working Group, Graham, R. W., Lundelius, E. L., Jr., Graham, M. A., Schroeder, E. K., Toomey, R. S., III, Anderson, E., Barnosky, A. D., Burns, J. A., Churcher, C. S., et. al. (1996) Science 272, 1601–1606. [DOI] [PubMed] [Google Scholar]
- 21.Overpeck, J. T., Webb, R. S. & Webb, T. I. (1992) Geology 20, 1071–1074. [Google Scholar]
- 22.Simberloff, D. (2004) Am. Nat. 163, 787–799. [DOI] [PubMed] [Google Scholar]
- 23.Levin, S. A. (1992) Ecology 73, 1943–1967. [Google Scholar]
- 24.Rosenzweig, M. L. (1995) Species Diversity in Space and Time (Cambridge Univ. Press, Cambridge, U.K.).
- 25.Gotelli, N. J. & Graves, G. R. (1996) Null Models in Ecology (Smithsonian Institution, Washington, DC).
- 26.Hubbell, S. P. (2001) A Unified Theory of Biodiversity and Biogeography (Princeton Univ. Press, Princeton).
- 27.Bell, G. (2001) Science 293, 2413–2418. [DOI] [PubMed] [Google Scholar]
- 28.Legendre, P. & Legendre, L. (1998) Numerical Ecology (Elsevier, Amsterdam).
- 29.Bulman, D. & Kershaw, P. (1993) in INQUA Working Group on Data-Handling Methods, Newsletter 10, ed. Maher, L. J., Jr. Available at www.kv.geo.uu.se/inqua/news10/n10-db.htm.
- 30.Rensberger, J. M. & Barnosky, A. D. (1993) in Morphological Change in Quaternary Mammals of North America, eds. Martin, R. A. & Barnosky, A. D. (Cambridge Univ. Press, Cambridge, U.K.), pp. 299–342.
- 31.Guilday, J. E., Hamilton, H. W., Anderson, E. & Parmalee, P. W. (1978) The Baker Bluff Cave Bone Deposit, Tennessee, and the Late Pleistocene Faunal Gradient (Carnegie Museum of Natural History, Pittsburgh).
- 32.Barnosky, A. D. & Bell, C. J. (2004) Biodiversity Response to Climate Change in the Middle Pleistocene: The Porcupine Cave Fauna from Colorado (University of Calif. Press, Berkeley).
- 33.Hadly, E. A. (1996) Quaternary Res. 46, 298–310. [Google Scholar]
- 34.Hadly, E. A. (1999) Paleogeogr. Palaeoclimatol. Palaeoecol. 149, 389–409. [Google Scholar]
- 35.Hadly, E. A. (2003) Paleobiology 29, 197–204. [Google Scholar]
- 36.Engen, S., Lande, R., Walla, T. & DeVries, P. J. (2002) Am. Nat. 160, 60–73. [DOI] [PubMed] [Google Scholar]
- 37.McGill, B. J. (2003) Nature 422, 881–885. [DOI] [PubMed] [Google Scholar]
- 38.Slatkin, M. (1993) Evolution 47, 264–279. [DOI] [PubMed] [Google Scholar]
- 39.McGill, B. J. (2003) Ecol. Lett. 6, 766–773. [Google Scholar]
- 40.Hadly, E. A. & Maurer, B. A. (2001) Evol. Ecol. Res. 3, 477–486. [Google Scholar]
- 41.Ricklefs, R. E. & Schluter, D. (1993) in Species Diversity in Ecological Communities: Historical and Geographical Perspectives, eds. Ricklefs, R. E. & Schluter, D. (Univ. of Chicago Press, Chicago).
- 42.Ricklefs, R. E. (2003) Oikos 100, 185–192. [Google Scholar]
- 43.Martino, A. M. G., Capanna, E. & Filipucci, M. G. (2001) Genetics 110, 163–175. [DOI] [PubMed] [Google Scholar]
- 44.Mahida, H., Campbell, G. K. & Taylor, P. J. (1999) South African J. Zool. 34, 91–101. [Google Scholar]
- 45.Whitlock, M. C. & McCauley, D. E. (1999) Heredity 82, 117–125. [DOI] [PubMed] [Google Scholar]
- 46.Halley, J. M. (1996) Trends Ecol. Evol. 11, 33–37. [DOI] [PubMed] [Google Scholar]
- 47.Hastings, H. M. & Sugihara, G. (1993) Fractals: A User's Guide for the Natural Sciences (Oxford Univ. Press, Oxford).
- 48.Clark, J. S. & McLachlan, J. S. (2003) Nature 423, 635–638. [DOI] [PubMed] [Google Scholar]
- 49.Pianka, E. R. (1988) Evolutionary Ecology (Harper & Row, Cambridge, MA).
- 50.MacArthur, R. H. (1972) Geographical Ecology: Patterns in the Distribution of Species (Princeton Univ. Press, Princeton).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.